 整数の性質
整数の性質
 整数の性質
整数の性質
【正答率1%】3つの方法で桁数を求めます【一橋大学 入試問題 数学】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$(2\times3\times5\times7\times11\times13)^{10}$の桁数は?
一橋大過去問
この動画を見る
$(2\times3\times5\times7\times11\times13)^{10}$の桁数は?
一橋大過去問
範囲を考えろ!整数問題の入試問題【慶応義塾大学】【数学】

単元:
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$ x^2+y^2<9,x^2\leqq y^2$を満たす整数の組$(x,y)$は全部で$\Box$個ある。
慶應義塾大過去問
この動画を見る
$ x^2+y^2<9,x^2\leqq y^2$を満たす整数の組$(x,y)$は全部で$\Box$個ある。
慶應義塾大過去問
nを求めよ 整数問題 高校入試 佼成学園

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
自然数$n^3-n$が51の倍数となるような自然数nのうち最小のものを求めよ
佼成学園高等学校
この動画を見る
自然数$n^3-n$が51の倍数となるような自然数nのうち最小のものを求めよ
佼成学園高等学校
福田の数学〜九州大学2022年理系第3問〜約数と倍数と不定方程式の自然数解

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
福田次郎
問題文全文(内容文):
自然数m,nが
$n^4=1+210m^2 \ldots①$
を満たすとき、以下の問いに答えよ。
(1)$\frac{n^2+1}{2},\ \frac{n^2-1}{2}$は互いに素な整数であることを示せ。
(2)$n^2-1$は168の倍数であることを示せ。
(3)①を満たす自然数の組(m,n)を1つ求めよ。
2022九州大学理系過去問
この動画を見る
自然数m,nが
$n^4=1+210m^2 \ldots①$
を満たすとき、以下の問いに答えよ。
(1)$\frac{n^2+1}{2},\ \frac{n^2-1}{2}$は互いに素な整数であることを示せ。
(2)$n^2-1$は168の倍数であることを示せ。
(3)①を満たす自然数の組(m,n)を1つ求めよ。
2022九州大学理系過去問
福田の数学〜九州大学2022年理系第2問〜商と余りの関係と極限

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$n$を3以上の自然数、$\alpha,\beta$を相異なる実数とするとき、以下の問いに答えよ。
(1)次を満たす実数A,B,Cと整式Q(x)が存在することを示せ。
$x^n=(x-\alpha)(x-\beta)^2Q(x)+A(x-\alpha)(x-\beta)+B(x-\alpha)+C$
(2)(1)のA,B,Cを$n,\alpha,\beta$を用いて表せ。
(3)(2)のAについて、nと$\alpha$を固定して、$\beta$を$\alpha$に近づけたときの極限
$\lim_{\beta \to \alpha}A$を求めよ。
2022九州大学理系過去問
この動画を見る
$n$を3以上の自然数、$\alpha,\beta$を相異なる実数とするとき、以下の問いに答えよ。
(1)次を満たす実数A,B,Cと整式Q(x)が存在することを示せ。
$x^n=(x-\alpha)(x-\beta)^2Q(x)+A(x-\alpha)(x-\beta)+B(x-\alpha)+C$
(2)(1)のA,B,Cを$n,\alpha,\beta$を用いて表せ。
(3)(2)のAについて、nと$\alpha$を固定して、$\beta$を$\alpha$に近づけたときの極限
$\lim_{\beta \to \alpha}A$を求めよ。
2022九州大学理系過去問
愛媛大(医)合同式で楽々

単元:
#数A#大学入試過去問(数学)#約数・倍数・整数の割り算と余り・合同式#愛媛大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$33^{20}$を90で割った余りを求めよ.
愛媛大(医)過去問
この動画を見る
$33^{20}$を90で割った余りを求めよ.
愛媛大(医)過去問
福田の数学〜神戸大学2022年文系第3問〜指数方程式と整数解

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a,b$を実数とし、$1 \lt a \lt b$とする。以下の問いに答えよ。
(1)x,y,zを0でない実数とする。$a^x=b^y=(ab)^z$ならば$\frac{1}{x}+\frac{1}{y}=\frac{1}{z}$であることを示せ。
(2)$m,n$を$m \gt n$を満たす自然数とし、$\frac{1}{m}+\frac{1}{n}=\frac{1}{5}$とする。$m,n$の値を求めよ。
(3)$m,n$を自然数とし、$a^m=b^n=(ab)^5$とする。bの値をaを用いて表せ。
2022神戸大学文系過去問
この動画を見る
$a,b$を実数とし、$1 \lt a \lt b$とする。以下の問いに答えよ。
(1)x,y,zを0でない実数とする。$a^x=b^y=(ab)^z$ならば$\frac{1}{x}+\frac{1}{y}=\frac{1}{z}$であることを示せ。
(2)$m,n$を$m \gt n$を満たす自然数とし、$\frac{1}{m}+\frac{1}{n}=\frac{1}{5}$とする。$m,n$の値を求めよ。
(3)$m,n$を自然数とし、$a^m=b^n=(ab)^5$とする。bの値をaを用いて表せ。
2022神戸大学文系過去問
福田の数学〜神戸大学2022年理系第5問〜指数方程式と整数解

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
a,bを実数、$p$を素数とし、$1 \lt a \lt b$とする。以下の問いに答えよ。
(1)x,y,zを0でない実数とする。$a^x=b^y=(ab)^z$ならば$\frac{1}{x}+\frac{1}{y}=\frac{1}{z}$であることを示せ。
(2)m,nを$m \gt n$を満たす自然数とし、$\frac{1}{m}+\frac{1}{n}=\frac{1}{p}$とする。m,nの値をpを用いて表せ。
(3)m,nを自然数とし、$a^m=b^n=(ab)^p$とする。bの値をa,pを用いて表せ。
2022神戸大学理系過去問
この動画を見る
a,bを実数、$p$を素数とし、$1 \lt a \lt b$とする。以下の問いに答えよ。
(1)x,y,zを0でない実数とする。$a^x=b^y=(ab)^z$ならば$\frac{1}{x}+\frac{1}{y}=\frac{1}{z}$であることを示せ。
(2)m,nを$m \gt n$を満たす自然数とし、$\frac{1}{m}+\frac{1}{n}=\frac{1}{p}$とする。m,nの値をpを用いて表せ。
(3)m,nを自然数とし、$a^m=b^n=(ab)^p$とする。bの値をa,pを用いて表せ。
2022神戸大学理系過去問
【シンプルな問題の実態は…?】整数:大東文化大学第一高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$300$を$2$けたの自然数$N$で割ると,商があまりの$2$倍になった.
$N$を求めよ.
大東文化第一高校過去問
この動画を見る
$300$を$2$けたの自然数$N$で割ると,商があまりの$2$倍になった.
$N$を求めよ.
大東文化第一高校過去問
下4桁!でも簡単

合同式の基本

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
m,nを自然数とする.
$ n^2-m!=2001 $を満たす(m,n)をすべて求めよ.
この動画を見る
m,nを自然数とする.
$ n^2-m!=2001 $を満たす(m,n)をすべて求めよ.
整数問題【一橋大学】【数学 入試問題】

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$x$は0でない実数とする。$x-\dfrac{1}{x}$が0以外の整数ならば$x^2-\dfrac{1}{x^2}$は整数でないことを示せ。
一橋大過去問
この動画を見る
$x$は0でない実数とする。$x-\dfrac{1}{x}$が0以外の整数ならば$x^2-\dfrac{1}{x^2}$は整数でないことを示せ。
一橋大過去問
簡単な問題

単元:
#数A#数Ⅱ#複素数と方程式#整数の性質#約数・倍数・整数の割り算と余り・合同式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \omega=1(\omega \neq 1)$であり,
$x=a+b $
$y=a\omega+b\omega^2 $
$z=a\omega^2+b\omega $である.
$ x^3+y^3+z^3$の値をa,bで表せ.
この動画を見る
$ \omega=1(\omega \neq 1)$であり,
$x=a+b $
$y=a\omega+b\omega^2 $
$z=a\omega^2+b\omega $である.
$ x^3+y^3+z^3$の値をa,bで表せ.
【まず、2分でOK!一度は当たりたい!】整数:八代白百合学園高等学校~全国入試問題解法
単元:
#数学(中学生)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
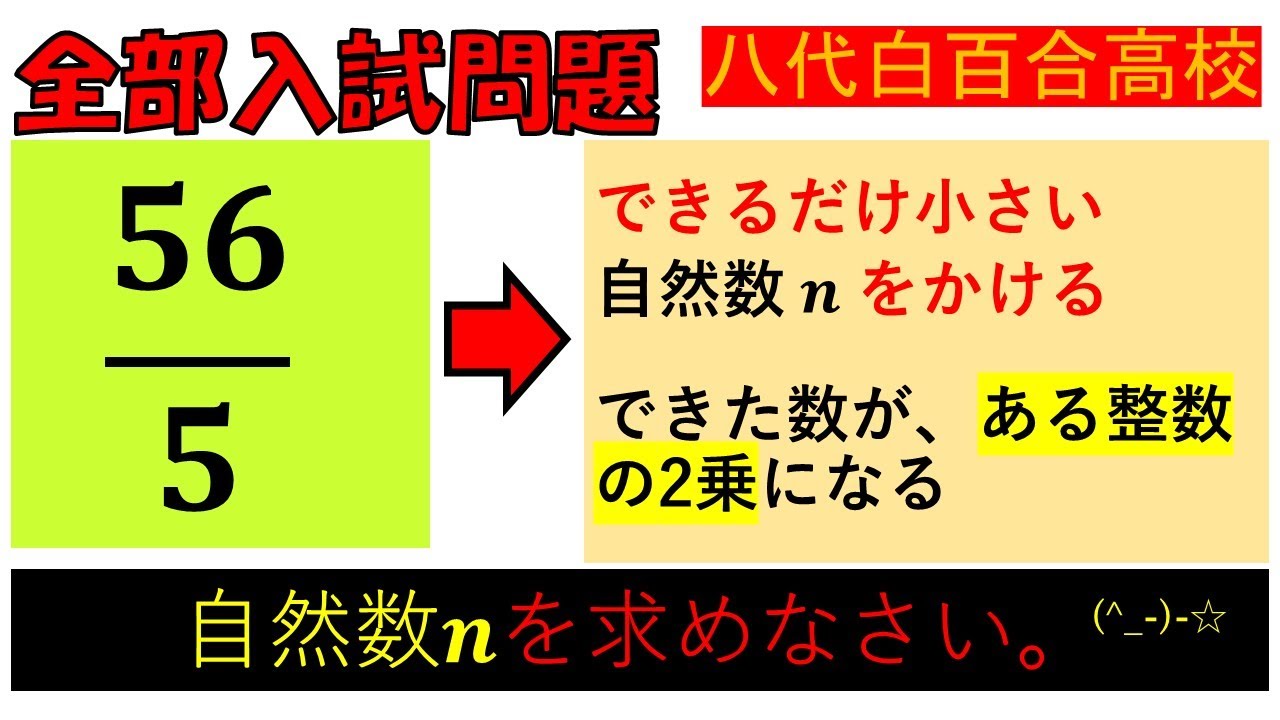
できるだけ小さい自然数$n$をかける.
できた数が,ある整数の2乗になる.
自然数$n$を求めなさい.
八代白百合学園高等学校過去問
この動画を見る
できるだけ小さい自然数$n$をかける.
できた数が,ある整数の2乗になる.
自然数$n$を求めなさい.
八代白百合学園高等学校過去問
福田の数学〜一橋大学2022年文系第1問〜2と3の累乗の積2個で2022を作る

単元:
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\ 2^a3^b+2^c3^d=2022$を満たす0以上の整数a,b,c,dの組を求めよ。
2022一橋大学文系過去問
この動画を見る
$\ 2^a3^b+2^c3^d=2022$を満たす0以上の整数a,b,c,dの組を求めよ。
2022一橋大学文系過去問
整数の良問だよ!やや難?
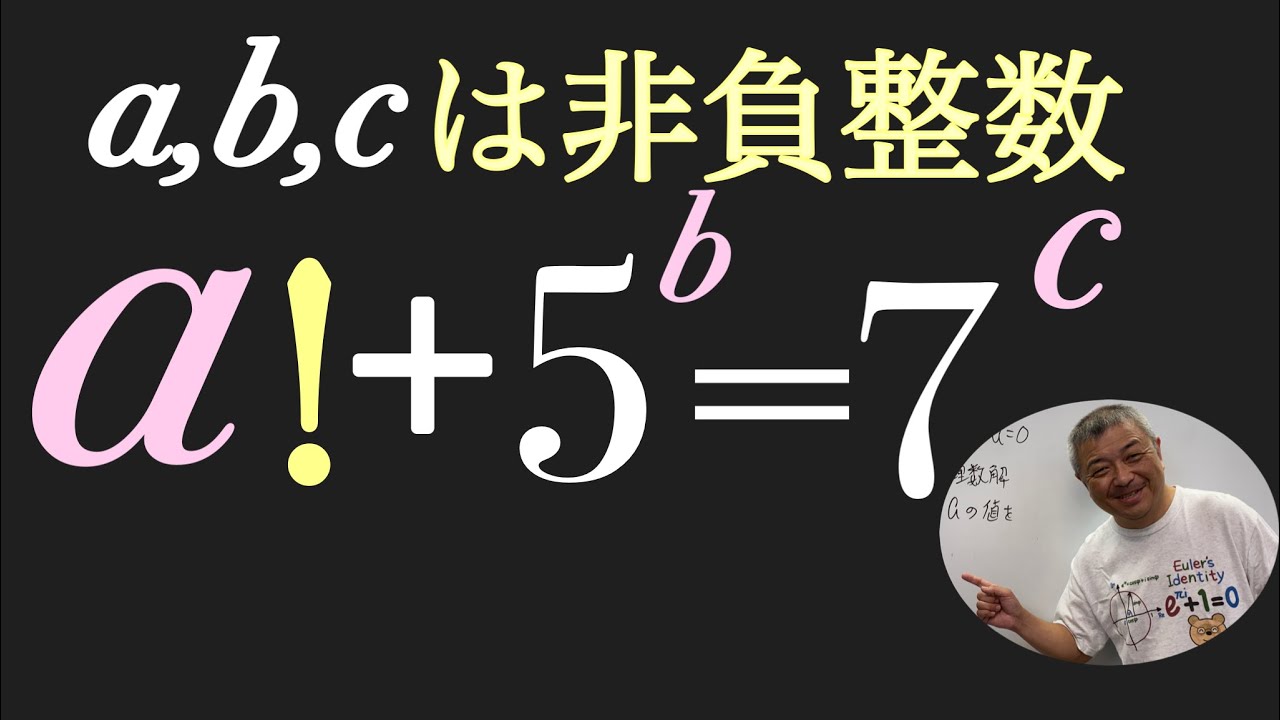
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b,c$は非負整数である.
$a!+5^b=7^c$を満たす$(a,b,c)$をすべて求めよ.
この動画を見る
$a,b,c$は非負整数である.
$a!+5^b=7^c$を満たす$(a,b,c)$をすべて求めよ.
整数の良問だよ!やや難?
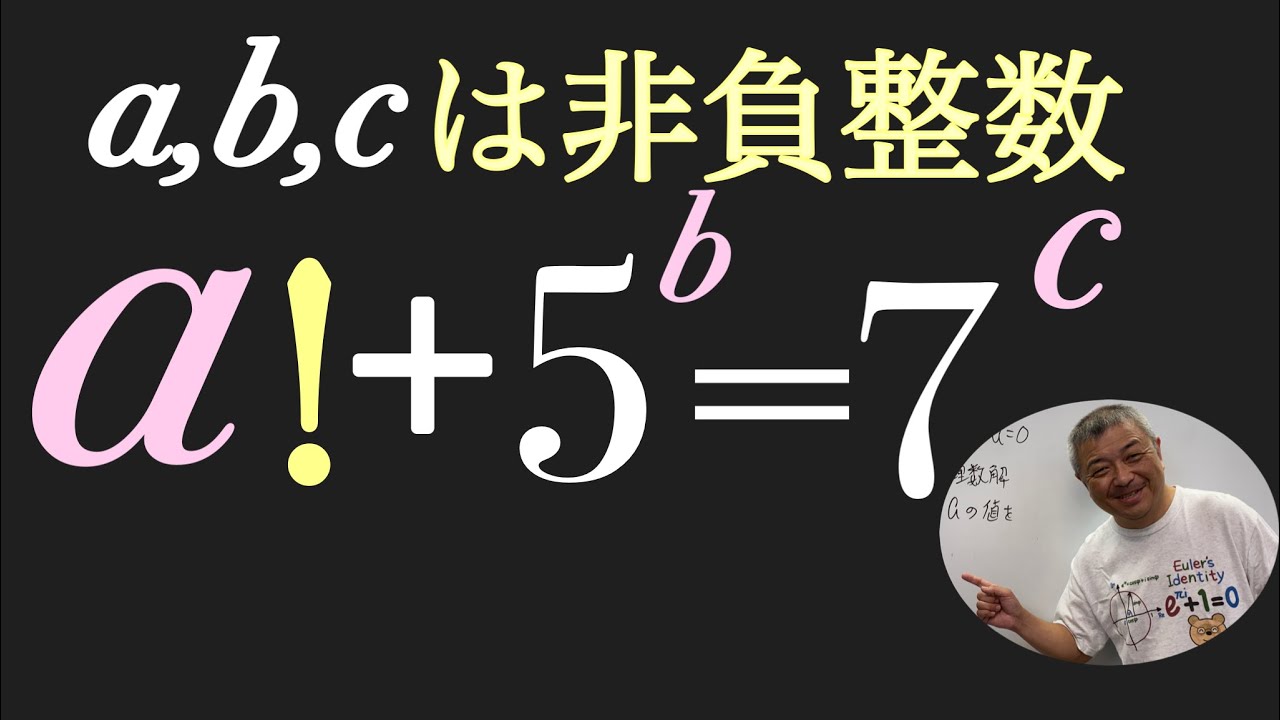
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
a,b,cは非負整数である.
$ a!+5^b=7^c $を満たす(a,b,c)をすべて求めよ.
この動画を見る
a,b,cは非負整数である.
$ a!+5^b=7^c $を満たす(a,b,c)をすべて求めよ.
【不定方程式の特解はこれで楽勝】合同式を使った不定方程式の解き方を解説!〔数学 高校数学〕

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
合同式を使った不定方程式の解き方について解説します。
この動画を見る
合同式を使った不定方程式の解き方について解説します。
素数に関する整数問題

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^3+5$が素数となる素数xは何コ?
京都教育大学附属高等学校
この動画を見る
$x^3+5$が素数となる素数xは何コ?
京都教育大学附属高等学校
福田の数学〜名古屋大学2022年理系第1問〜割り算の余りと異なる実数解の個数

単元:
#数A#数Ⅱ#大学入試過去問(数学)#複素数と方程式#整数の性質#約数・倍数・整数の割り算と余り・合同式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学
指導講師:
福田次郎
問題文全文(内容文):
a,bを実数とする。
(1)整式$x^3$を2次式$(x-a)^2$で割った時の余りを求めよ。
(2)実数を係数とする2次式$f(x)=x^2+\alpha x+\beta$で整式$x^3$を割った時の余りが
$3x+b$とする。bの値に応じて、このようなf(x)が何個あるかを求めよ。
2022名古屋大学理系過去問
この動画を見る
a,bを実数とする。
(1)整式$x^3$を2次式$(x-a)^2$で割った時の余りを求めよ。
(2)実数を係数とする2次式$f(x)=x^2+\alpha x+\beta$で整式$x^3$を割った時の余りが
$3x+b$とする。bの値に応じて、このようなf(x)が何個あるかを求めよ。
2022名古屋大学理系過去問
整数の基本問題

【足元をすくわれるな!】整数:八代白百合学園高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の問いに答えなさい.
$-2.7$より大きく$\dfrac{14}{3}$より小さい整数は全部で何個あるか.
八代白百合学園高等学校過去問
この動画を見る
次の問いに答えなさい.
$-2.7$より大きく$\dfrac{14}{3}$より小さい整数は全部で何個あるか.
八代白百合学園高等学校過去問
ハルハル様の作成問題 手筋連発

単元:
#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x$についての方程式
$x^3+x^2-x-5=0$の最小の実数解を$\alpha$とする。
$\alpha^5$の整数部分を求めよ。
この動画を見る
$x$についての方程式
$x^3+x^2-x-5=0$の最小の実数解を$\alpha$とする。
$\alpha^5$の整数部分を求めよ。
解けるように作られた問題 ガウス少年なら一瞬

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ f(x)=\dfrac{25^x}{25^x+5}$である.
$ f \left(\dfrac{1}{100}\right)+f \left(\dfrac{2}{100}\right)+
・・・・・・+f \left(\dfrac{98}{100}\right)+\left(\dfrac{99}{100}\right)$の値を求めよ.
この動画を見る
$ f(x)=\dfrac{25^x}{25^x+5}$である.
$ f \left(\dfrac{1}{100}\right)+f \left(\dfrac{2}{100}\right)+
・・・・・・+f \left(\dfrac{98}{100}\right)+\left(\dfrac{99}{100}\right)$の値を求めよ.
【考え方が理解で得意になる!!】合同式がこの一本でできるようになる!プチ演習付き〔数学、高校数学〕

基本問題

基本問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整数$m$をすべて求めよ.
$\dfrac{8^m-2^m}{6^m-3^m}=2$
この動画を見る
整数$m$をすべて求めよ.
$\dfrac{8^m-2^m}{6^m-3^m}=2$
福田の数学〜東京工業大学2022年理系第2問〜3つの数の最大公約数

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
3つの正の整数a,b,cの最大公約数が1であるとき、次の問いに答えよ。
(1)$a+b+c,ab+bc+ca,abc$の最大公約数は1であることを示せ。
(2)$a+b+c,a^2+b^2+c^2,a^3+b^3+c^3$の最大公約数となるような正の整数を
全て求めよ。
2022東京工業大学理系過去問
この動画を見る
3つの正の整数a,b,cの最大公約数が1であるとき、次の問いに答えよ。
(1)$a+b+c,ab+bc+ca,abc$の最大公約数は1であることを示せ。
(2)$a+b+c,a^2+b^2+c^2,a^3+b^3+c^3$の最大公約数となるような正の整数を
全て求めよ。
2022東京工業大学理系過去問
ちょっと難しいか...?

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
32,7,105,98,64,606,73
この中から2つの整数を選ぶとその差が必ず6で割り切れるものがあることを説明せよ
この動画を見る
32,7,105,98,64,606,73
この中から2つの整数を選ぶとその差が必ず6で割り切れるものがあることを説明せよ
ざ・見掛け倒し

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \displaystyle \sum_{n=1}^{2022} n^{2022}$
$ =1^{2022}+2^{2022}+3^{2022}+・・・・・・$
$+2021^{2022}+2022^{2022}$
を13で割った余りを求めよ.
この動画を見る
$ \displaystyle \sum_{n=1}^{2022} n^{2022}$
$ =1^{2022}+2^{2022}+3^{2022}+・・・・・・$
$+2021^{2022}+2022^{2022}$
を13で割った余りを求めよ.
