整数の性質
整数の性質
【理数個別の過去問解説】2007年度千葉大学 数学 第2問解説
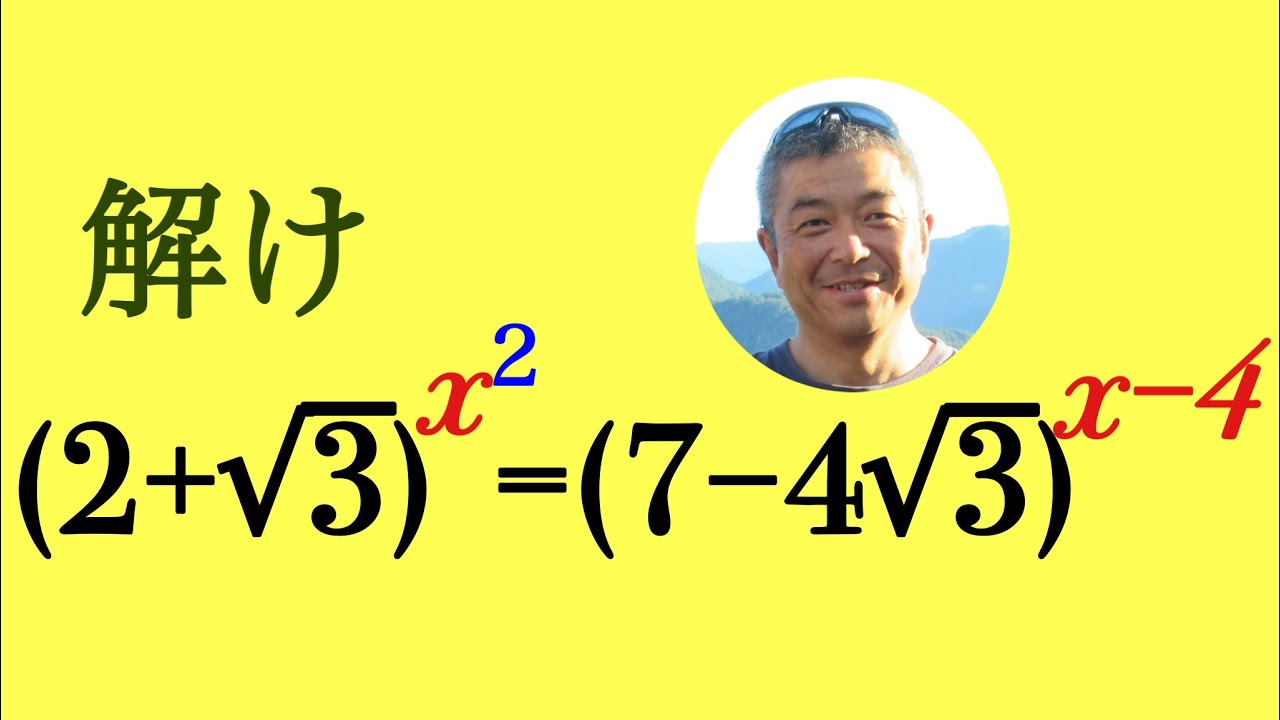
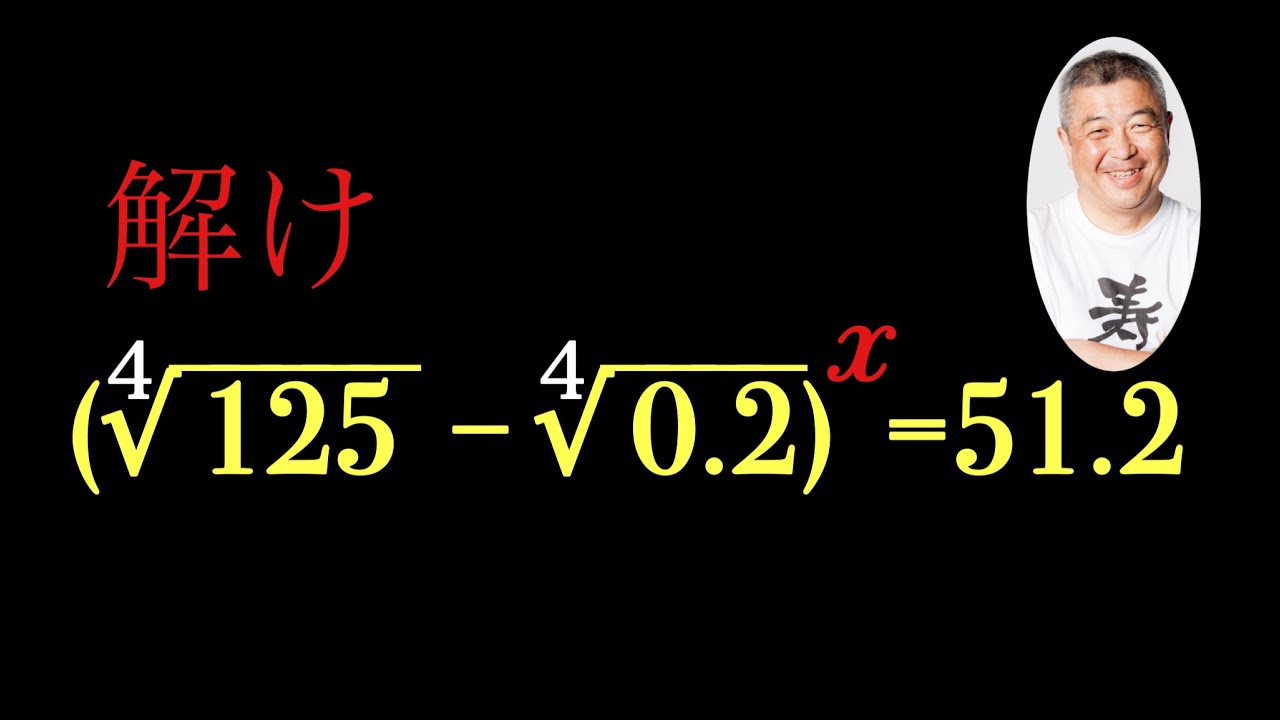
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
nは奇数とする。このとき、次のことを証明せよ。
(1)n²-1は8の倍数である。
(2)n⁵-nは3の倍数である。
(3)n⁵-nは120の倍数である。
千葉大学(文理共通)2007年第2問より
この動画を見る
nは奇数とする。このとき、次のことを証明せよ。
(1)n²-1は8の倍数である。
(2)n⁵-nは3の倍数である。
(3)n⁵-nは120の倍数である。
千葉大学(文理共通)2007年第2問より
16京都府教員採用試験（数学：5番 整数問題）
単元：
#数Ⅰ#数A#数と式#集合と命題（集合・命題と条件・背理法）#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
5⃣ $\frac{1}{2015} , \frac{2}{2015} , \cdots , \frac{2014}{2015},\frac{2015}{2015}$のうち既約分数の個数を求めよ。
この動画を見る
5⃣ $\frac{1}{2015} , \frac{2}{2015} , \cdots , \frac{2014}{2015},\frac{2015}{2015}$のうち既約分数の個数を求めよ。
自作 整数問題
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$10^{2020}-1$を$3^5$で割った余りを求めよ.
この動画を見る
$10^{2020}-1$を$3^5$で割った余りを求めよ.
整数問題
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\dfrac{3n^2-5n+218}{3n-2}$が整数となる自然数$n$を求めよ.
この動画を見る
$\dfrac{3n^2-5n+218}{3n-2}$が整数となる自然数$n$を求めよ.
13東京都教員採用試験（数学：1番 整数問題）
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
1⃣ 33x+55y+60z=935を満たす$x,y,z \in \mathbb{ N }$を求めよ。
この動画を見る
1⃣ 33x+55y+60z=935を満たす$x,y,z \in \mathbb{ N }$を求めよ。
京大院生 古賀真輝 フェルマーの小定理を証明する
自作 整数問題
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$n^{12}-15n^6+21$が素数となる自然数$n$を求めよ.
この動画を見る
$n^{12}-15n^6+21$が素数となる自然数$n$を求めよ.
14奈良県教員採用試験（数学：2-1番 整数問題）
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
2⃣-(1)
$\sqrt{n^2+211}$が整数となる$n \in \mathbb{ N }$を求めよ。
この動画を見る
2⃣-(1)
$\sqrt{n^2+211}$が整数となる$n \in \mathbb{ N }$を求めよ。
15東京都教員採用試験（数学：1-1 整数問題）
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
1⃣-(1)
$m^2-mn+3m-3n-7=0$
をみたす自然数の組(m,n)を求めよ。
この動画を見る
1⃣-(1)
$m^2-mn+3m-3n-7=0$
をみたす自然数の組(m,n)を求めよ。
自作 整数問題２
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$3^n=k^4+k^2+1$
整数$(k,n)$をすべて求めよ.
この動画を見る
$3^n=k^4+k^2+1$
整数$(k,n)$をすべて求めよ.
自作 整数問題
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$13^n=k^2+672$
自然数$(k,n)$をすべて求めよ.
この動画を見る
$13^n=k^2+672$
自然数$(k,n)$をすべて求めよ.
13奈良県教員採用試験（数学：1-1番 整数問題）
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
1⃣-(1)
$\frac{1}{x}+\frac{2}{y}=\frac{1}{4}$を満たす正の整数の組(x,y)を求めよ。
この動画を見る
1⃣-(1)
$\frac{1}{x}+\frac{2}{y}=\frac{1}{4}$を満たす正の整数の組(x,y)を求めよ。
15奈良県教員採用試験（数学：中-4番 整数問題）
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
中-4⃣
$x^2-2xy+2y^2-2x-3y+5=0$を満たす整数x,yの組を求めよ。
この動画を見る
中-4⃣
$x^2-2xy+2y^2-2x-3y+5=0$を満たす整数x,yの組を求めよ。
灘中 難関大学並の整数問題
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$A=123456789$
$A$の2つの数を入れかえてできる数を小さい順に$a_1,a_2･･････a_{36}$とする.
$a_1=123456798$
$a_{36}=923456781$
$b_k=a_k-A,1\leqq k\leqq 36$である.
(1)$1000$で割り切れる$b_k$の個数を求めよ.
(2)$37$で割り切れる$b_k$の個数を求めよ.
(3)$b_1 \times b_2 \times b_3 \times ･･･\times b_{36}$は3で何回割り切れるか
2016灘中過去問
この動画を見る
$A=123456789$
$A$の2つの数を入れかえてできる数を小さい順に$a_1,a_2･･････a_{36}$とする.
$a_1=123456798$
$a_{36}=923456781$
$b_k=a_k-A,1\leqq k\leqq 36$である.
(1)$1000$で割り切れる$b_k$の個数を求めよ.
(2)$37$で割り切れる$b_k$の個数を求めよ.
(3)$b_1 \times b_2 \times b_3 \times ･･･\times b_{36}$は3で何回割り切れるか
2016灘中過去問
小樽商科大 整数問題
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\dfrac{2n-2}{n^2+2n+2}$が整数となる整数$n$を求めよ.
2018小樽商科大過去問
この動画を見る
$\dfrac{2n-2}{n^2+2n+2}$が整数となる整数$n$を求めよ.
2018小樽商科大過去問
信州大2020 指数方程式の解の存在条件
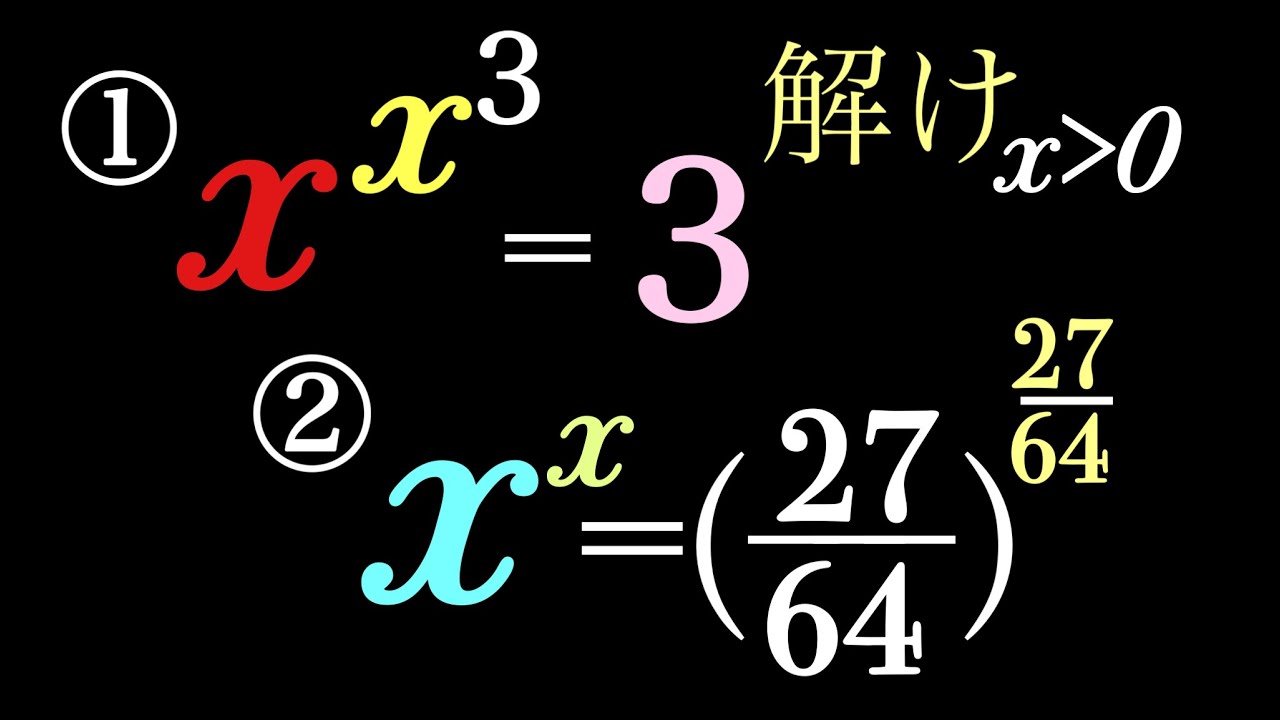
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$9^x-k(3^x+3^{-x})+9^{-x}+\dfrac{k^2}{4}+k-17=0$
が実数解をもつ$k$の範囲を求めよ.
2020信州大過去問
この動画を見る
$9^x-k(3^x+3^{-x})+9^{-x}+\dfrac{k^2}{4}+k-17=0$
が実数解をもつ$k$の範囲を求めよ.
2020信州大過去問
16神奈川県教員採用試験（数学：整数問題）
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
2⃣$n \leqq 300$,nの約数の個数が9個となる$n \in \mathbb{ N }$を求めよ。
この動画を見る
2⃣$n \leqq 300$,nの約数の個数が9個となる$n \in \mathbb{ N }$を求めよ。
パスラボ宇佐見さん登場 整数問題
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$7^n=k^2-99$
整数$k,n$を全て求めよ.
この動画を見る
$7^n=k^2-99$
整数$k,n$を全て求めよ.
整数問題
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$2^a+m^2=n^4$
$a,m,n$は自然数で,$m,n$は奇数であることを示せ.
この動画を見る
$2^a+m^2=n^4$
$a,m,n$は自然数で,$m,n$は奇数であることを示せ.
熊本大2020整数問題
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x^2+5y^2=2z^2$を満たす自然数$(x,y,z)$は存在しないことを示せ.
2020熊本大過去問
この動画を見る
$x^2+5y^2=2z^2$を満たす自然数$(x,y,z)$は存在しないことを示せ.
2020熊本大過去問
広島大 約数の総和
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$m,n$は0以上の整数である.
$3^{2m+1}・7^{2n+1}$の正の約数のうち,4で割って1余るものの総和を求めよ.
広島大過去問
この動画を見る
$m,n$は0以上の整数である.
$3^{2m+1}・7^{2n+1}$の正の約数のうち,4で割って1余るものの総和を求めよ.
広島大過去問
整数問題
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$n^2+2n-1$と$n^5-5$がともに7の倍数となる$n$のうち3桁で最小のものを求めよ.
この動画を見る
$n^2+2n-1$と$n^5-5$がともに7の倍数となる$n$のうち3桁で最小のものを求めよ.
14兵庫県教員採用試験（数学：1-1番 整数問題）
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
1⃣-(1)
$2^{2x}-3^{2y} =55$を満たす、$x,y \in \mathbb{ Z }$を求めよ。
この動画を見る
1⃣-(1)
$2^{2x}-3^{2y} =55$を満たす、$x,y \in \mathbb{ Z }$を求めよ。
東工大 ガウス記号
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$n$は$10000$以下の自然数である.
$[\sqrt{n}]$が$n$の約数となる.$n$は何個あるか.
2012東工大過去問
この動画を見る
$n$は$10000$以下の自然数である.
$[\sqrt{n}]$が$n$の約数となる.$n$は何個あるか.
2012東工大過去問
早稲田大 ガウス記号
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x$は実数であり,$n$は自然数である.
①$\left[\dfrac{1}{2}x\right]-\left[\dfrac{1}{2}[x]\right]=0$示せ.
②$\left[\dfrac{1}{n}x\right]-\left[\dfrac{1}{n}[x]\right]=0$を求めよ.
2009早稲田大過去問
この動画を見る
$x$は実数であり,$n$は自然数である.
①$\left[\dfrac{1}{2}x\right]-\left[\dfrac{1}{2}[x]\right]=0$示せ.
②$\left[\dfrac{1}{n}x\right]-\left[\dfrac{1}{n}[x]\right]=0$を求めよ.
2009早稲田大過去問
素数問題
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$5m^2+4mn-n^2$が素数となる自然数$(m,n)$は無限にあることを示せ.
この動画を見る
$5m^2+4mn-n^2$が素数となる自然数$(m,n)$は無限にあることを示せ.
大阪府立大 整数問題
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$m,n$は整数であり,$0\leqq n\leqq m$とする.
①$3m^2+mn-2n^2$が素数となる($m,n$)
②$m^4-3m^2n^2-4n^4-6m^2-16n^2-16$が素数となる$(m,n)$
2019大阪府立大過去問
この動画を見る
$m,n$は整数であり,$0\leqq n\leqq m$とする.
①$3m^2+mn-2n^2$が素数となる($m,n$)
②$m^4-3m^2n^2-4n^4-6m^2-16n^2-16$が素数となる$(m,n)$
2019大阪府立大過去問
高知大（医）整数問題
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
整数$(p,q)$の組は何個あるか.
①$p^2-q^2=250$
②$p^2-q^2=210000$
2020高知大(医)過去問
この動画を見る
整数$(p,q)$の組は何個あるか.
①$p^2-q^2=250$
②$p^2-q^2=210000$
2020高知大(医)過去問
お茶の水女子大 不定方程式
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$2x+25y=1993$を満たす整数$x,y$のうち,$x$と$y$の差の絶対値が最小となる$x,y$を求めよ.
お茶の水女子大過去問
この動画を見る
$2x+25y=1993$を満たす整数$x,y$のうち,$x$と$y$の差の絶対値が最小となる$x,y$を求めよ.
お茶の水女子大過去問
17東京都教員採用試験（数学1-1番 整数問題）
単元：
#数Ⅰ#数A#数Ⅱ#２次関数#式と証明#2次方程式と2次不等式#整数の性質#約数・倍数・整数の割り算と余り・合同式#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
1⃣$m^2-mn+2n^2=28$
$m,n \in \mathbb{ N } (m>n)$を求めよ。
この動画を見る
1⃣$m^2-mn+2n^2=28$
$m,n \in \mathbb{ N } (m>n)$を求めよ。