 整数の性質
整数の性質
 整数の性質
整数の性質
答え方が困る?? 整数問題 (高校数学です)

福田のおもしろ数学208〜必要条件で絞って十分で切り返す

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$f(x)=ax^3+bx^2+c$ がある。
すべての整数 $n$ に対して $f(n)$ が整数となるための $a,b,c$ の必要十分条件を求めよ。
この動画を見る
$f(x)=ax^3+bx^2+c$ がある。
すべての整数 $n$ に対して $f(n)$ が整数となるための $a,b,c$ の必要十分条件を求めよ。
大学入試問題#885「油断したら沼るかも」 #奈良県立医科大学(2014) 三角関数と整数問題
単元:
#数A#数Ⅱ#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#三角関数#学校別大学入試過去問解説(数学)#数学(高校生)#奈良県立医科大学
指導講師:
ますただ
問題文全文(内容文):
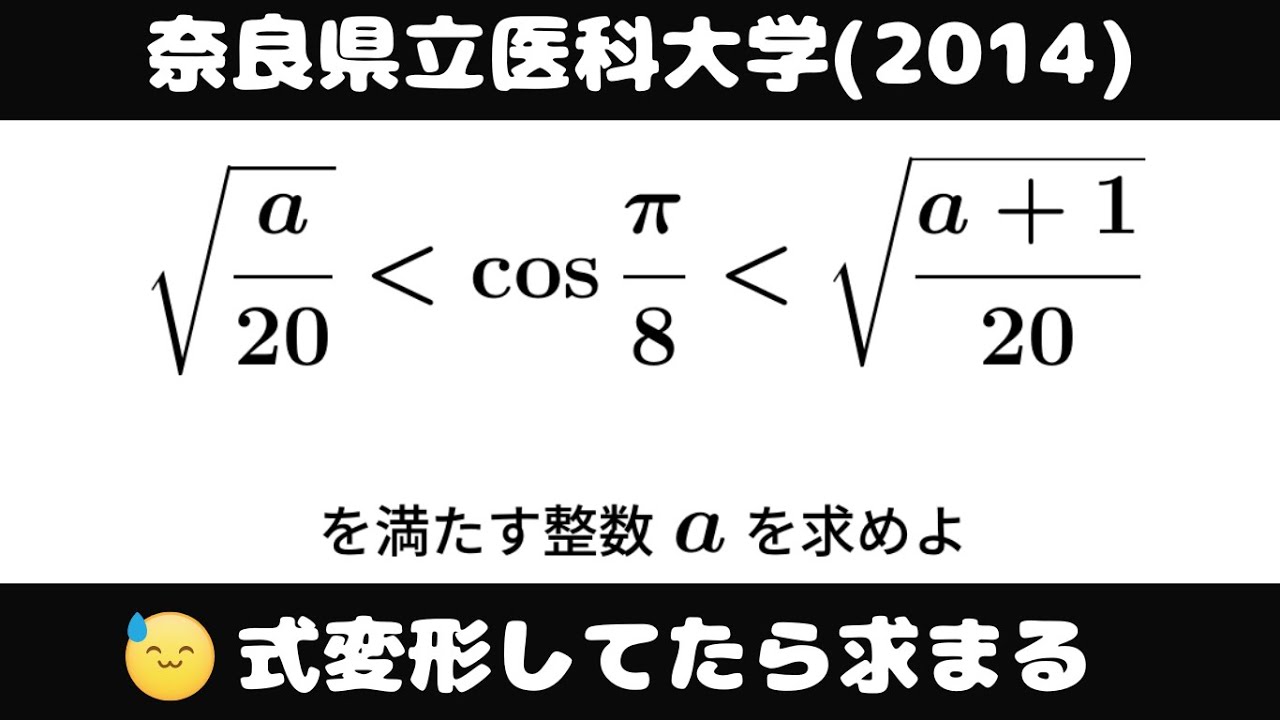
$\sqrt{ \displaystyle \frac{a}{20} } \lt \cos\displaystyle \frac{\pi}{8} \lt \sqrt{ \displaystyle \frac{a+1}{20} }$を満たす整数$a$を求めよ。
出典:2014年奈良県立医科大学
この動画を見る
$\sqrt{ \displaystyle \frac{a}{20} } \lt \cos\displaystyle \frac{\pi}{8} \lt \sqrt{ \displaystyle \frac{a+1}{20} }$を満たす整数$a$を求めよ。
出典:2014年奈良県立医科大学
福田のおもしろ数学203〜整数を取る4変数の最大値

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a,b,c,d$はすべて正の整数とする。
$a+b+c+d=63$のとき$ab+bc+cd$の最大値を求めよ。
この動画を見る
$a,b,c,d$はすべて正の整数とする。
$a+b+c+d=63$のとき$ab+bc+cd$の最大値を求めよ。
大学入試問題#880「基本の基本!」 #聖マリアンナ医科大学(2021) #整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#聖マリアンナ医科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$n,\sqrt{ n^2+2021 }$がともに自然数のとき、$n$の値をすべて求めよ。
$2021=43\times47$を利用してよい
出典:2021年聖マリアンナ医科大学
この動画を見る
$n,\sqrt{ n^2+2021 }$がともに自然数のとき、$n$の値をすべて求めよ。
$2021=43\times47$を利用してよい
出典:2021年聖マリアンナ医科大学
298 ユークリッドの互除法2:余りを計算して効率的に最大公約数を求めよう! #shorts
単元:
#数A#情報Ⅰ(高校生)#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)#プログラミング#プログラムによる動的シミュレーション
指導講師:
めいちゃんねる
問題文全文(内容文):
298 ユークリッドの互除法2:余りを計算して効率的に最大公約数を求めよう! #shorts
【問題文】
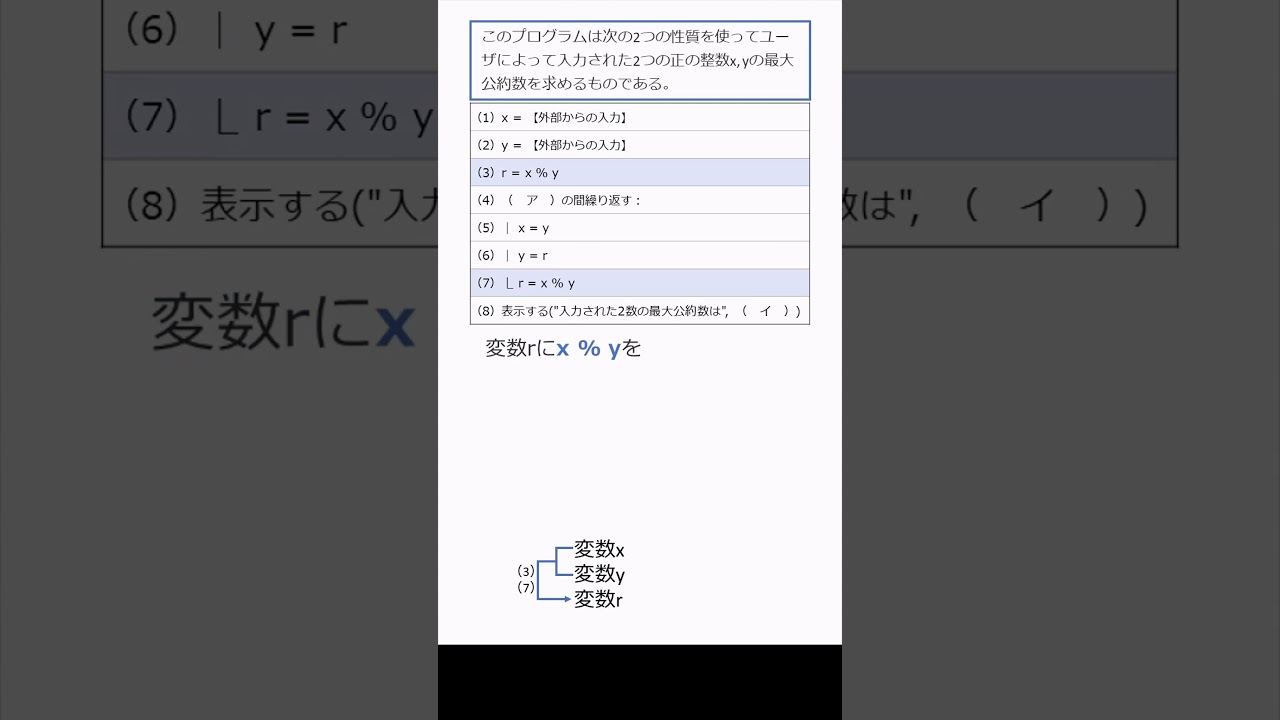
このプログラムは次の2つの性質を使って最大公約数を求めるものである。
性質1)xをyで割ったあまりが0のとき、xとyの最大公約数はyである。
性質2)xをyで割ったあまりが0と異なるとき、xとyの最大公約数はyとxをyでわったあまりの最大公約数に等しい。
空欄に入る最も適切なものを選べ。
※プログラムは動画内参照
この動画を見る
298 ユークリッドの互除法2:余りを計算して効率的に最大公約数を求めよう! #shorts
【問題文】
このプログラムは次の2つの性質を使って最大公約数を求めるものである。
性質1)xをyで割ったあまりが0のとき、xとyの最大公約数はyである。
性質2)xをyで割ったあまりが0と異なるとき、xとyの最大公約数はyとxをyでわったあまりの最大公約数に等しい。
空欄に入る最も適切なものを選べ。
※プログラムは動画内参照
298 ユークリッドの互除法2:余りを計算して効率的に最大公約数を求めよう! #shorts

単元:
#数A#情報Ⅰ(高校生)#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)#プログラミング#プログラムによる動的シミュレーション
指導講師:
めいちゃんねる
問題文全文(内容文):
298 ユークリッドの互除法2:余りを計算して効率的に最大公約数を求めよう! #shorts
【問題文】
このプログラムは次の2つの性質を使って最大公約数を求めるものである。
性質1)xをyで割ったあまりが0のとき、xとyの最大公約数はyである。
性質2)xをyで割ったあまりが0と異なるとき、xとyの最大公約数はyとxをyでわったあまりの最大公約数に等しい。
空欄に入る最も適切なものを選べ。
この動画を見る
298 ユークリッドの互除法2:余りを計算して効率的に最大公約数を求めよう! #shorts
【問題文】
このプログラムは次の2つの性質を使って最大公約数を求めるものである。
性質1)xをyで割ったあまりが0のとき、xとyの最大公約数はyである。
性質2)xをyで割ったあまりが0と異なるとき、xとyの最大公約数はyとxをyでわったあまりの最大公約数に等しい。
空欄に入る最も適切なものを選べ。
297 ユークリッドの互除法1:引き算だけを使って最大公約数を求めよう! #shorts
単元:
#数A#情報Ⅰ(高校生)#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)#プログラミング#プログラムによる動的シミュレーション
指導講師:
めいちゃんねる
問題文全文(内容文):
297 ユークリッドの互除法1:引き算だけを使って最大公約数を求めよう! #shorts
【問題文】
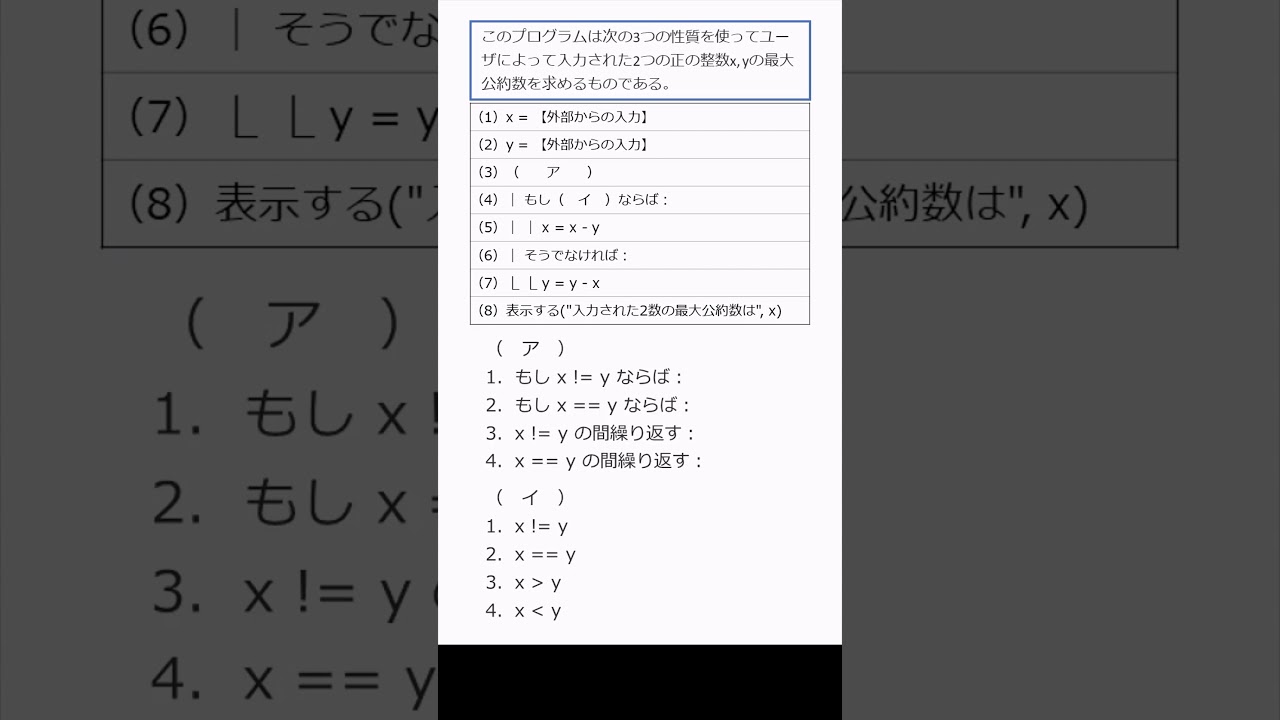
このプログラムは次の3つの性質を使って最大公約数を求めるものである。
性質1)xとyの値が等しいとき、xとyの最大公約数はxである。
性質2)xがyより大きいとき、xとyの最大公約数は(x - y)とyの最大公約数に等しい。
性質3)xがyより小さいとき、xとyの最大公約数はxと(y - x)の最大公約数に等しい。
空欄に入る最も適切なものを選べ。
※プログラムは動画内参照
この動画を見る
297 ユークリッドの互除法1:引き算だけを使って最大公約数を求めよう! #shorts
【問題文】
このプログラムは次の3つの性質を使って最大公約数を求めるものである。
性質1)xとyの値が等しいとき、xとyの最大公約数はxである。
性質2)xがyより大きいとき、xとyの最大公約数は(x - y)とyの最大公約数に等しい。
性質3)xがyより小さいとき、xとyの最大公約数はxと(y - x)の最大公約数に等しい。
空欄に入る最も適切なものを選べ。
※プログラムは動画内参照
297 ユークリッドの互除法1:引き算だけを使って最大公約数を求めよう! #shorts

単元:
#数A#情報Ⅰ(高校生)#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)#プログラミング#プログラムによる動的シミュレーション
指導講師:
めいちゃんねる
問題文全文(内容文):
297 ユークリッドの互除法1:引き算だけを使って最大公約数を求めよう! #shorts
【問題文】
このプログラムは次の3つの性質を使って最大公約数を求めるものである。
性質1)xとyの値が等しいとき、xとyの最大公約数はxである。
性質2)xがyより大きいとき、xとyの最大公約数は(x - y)とyの最大公約数に等しい。
性質3)xがyより小さいとき、xとyの最大公約数はxと(y - x)の最大公約数に等しい。
空欄に入る最も適切なものを選べ。
この動画を見る
297 ユークリッドの互除法1:引き算だけを使って最大公約数を求めよう! #shorts
【問題文】
このプログラムは次の3つの性質を使って最大公約数を求めるものである。
性質1)xとyの値が等しいとき、xとyの最大公約数はxである。
性質2)xがyより大きいとき、xとyの最大公約数は(x - y)とyの最大公約数に等しい。
性質3)xがyより小さいとき、xとyの最大公約数はxと(y - x)の最大公約数に等しい。
空欄に入る最も適切なものを選べ。
これなんで? フルは↑
単元:
#数Ⅰ#数A#数Ⅱ#数と式#複素数と方程式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#複素数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
これなんで? フルは↑
【問題文】20×20
この動画を見る
これなんで? フルは↑
【問題文】20×20
福田の数学〜立教大学2024年理学部第1問(2)〜17のn乗の1の位

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (2)$17^n$の1の位の数が1になる最小の自然数$n$は$\boxed{\ \ イ\ \ }$である。また、$17^{555}$の1の位の数を求めると、$\boxed{\ \ ウ\ \ }$である。
この動画を見る
$\Large{\boxed{1}}$ (2)$17^n$の1の位の数が1になる最小の自然数$n$は$\boxed{\ \ イ\ \ }$である。また、$17^{555}$の1の位の数を求めると、$\boxed{\ \ ウ\ \ }$である。
「20+20=200」になる理由を解説

単元:
#数Ⅰ#数A#数Ⅱ#数と式#複素数と方程式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#複素数#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
「20+20=200」になる理由を解説しています。
この動画を見る
「20+20=200」になる理由を解説しています。
福田の数学〜慶應義塾大学2024年経済学部第5問〜ある対数とそれを超えない最大の整数

単元:
#数A#数Ⅱ#大学入試過去問(数学)#整数の性質#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{5}}$ $x$を正の実数とする。$m$と$n$は、それぞれ$m$≦$\displaystyle\log_4\frac{x}{8}$, $n$≦$\displaystyle\log_2\frac{8}{x}$ を満たす最大の整数とし、さらに、$\alpha$=$\displaystyle\log_4\frac{x}{8}$-$m$, $\beta$=$\displaystyle\log_2\frac{8}{x}$-$n$ とおく。
(1)$\log_2x$を、$m$と$\alpha$を用いて表せ。
(2)$2\alpha$+$\beta$ の取りうる値を全て求めよ。
(3)$n$=$m$-1 のとき、$m$と$n$の値を求めよ。
(4)$n$=$m$-1 となるために$x$が満たすべき必要十分条件を求めよ。
この動画を見る
$\Large{\boxed{5}}$ $x$を正の実数とする。$m$と$n$は、それぞれ$m$≦$\displaystyle\log_4\frac{x}{8}$, $n$≦$\displaystyle\log_2\frac{8}{x}$ を満たす最大の整数とし、さらに、$\alpha$=$\displaystyle\log_4\frac{x}{8}$-$m$, $\beta$=$\displaystyle\log_2\frac{8}{x}$-$n$ とおく。
(1)$\log_2x$を、$m$と$\alpha$を用いて表せ。
(2)$2\alpha$+$\beta$ の取りうる値を全て求めよ。
(3)$n$=$m$-1 のとき、$m$と$n$の値を求めよ。
(4)$n$=$m$-1 となるために$x$が満たすべき必要十分条件を求めよ。
1➕1🟰10

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
以下を解いてください。
$\begin{array}{r}
11 \\[-3pt]
\underline{+\phantom{0}1}\\[-3pt]
\end{array}$
この動画を見る
以下を解いてください。
$\begin{array}{r}
11 \\[-3pt]
\underline{+\phantom{0}1}\\[-3pt]
\end{array}$
福田の数学〜慶應義塾大学2024年経済学部第1問(1)〜2次方程式が整数解をもつ条件

単元:
#数A#数Ⅱ#大学入試過去問(数学)#複素数と方程式#整数の性質#ユークリッド互除法と不定方程式・N進法#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)$p$を実数とする。$x$の2次方程式$x^2$-($p$-9)$x$-$p$+1=0 の解は整数$m$<0<$n$が成り立つとする。このとき$mn$+$m$+$n$=$\boxed{\ \ アイ\ \ }$なので、$m$=$\boxed{\ \ ウエ\ \ }$, $n$=$\boxed{\ \ オ\ \ }$, $p$=$\boxed{\ \ カキ\ \ }$ である。
この動画を見る
$\Large\boxed{1}$ (1)$p$を実数とする。$x$の2次方程式$x^2$-($p$-9)$x$-$p$+1=0 の解は整数$m$<0<$n$が成り立つとする。このとき$mn$+$m$+$n$=$\boxed{\ \ アイ\ \ }$なので、$m$=$\boxed{\ \ ウエ\ \ }$, $n$=$\boxed{\ \ オ\ \ }$, $p$=$\boxed{\ \ カキ\ \ }$ である。
文章題それとも整数問題!?

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
毎日開いている店に4日ごとにくる客と
6日ごとにくる客が、ある日曜日に会った。
次に日曜日に会うのは何日後?
この動画を見る
毎日開いている店に4日ごとにくる客と
6日ごとにくる客が、ある日曜日に会った。
次に日曜日に会うのは何日後?
福田のおもしろ数学163〜連続する奇数が互いに素である証明

福田の数学〜神戸大学2024年文系第2問〜さいころの目と約数に関する確率

単元:
#数A#場合の数と確率#整数の性質#確率#約数・倍数・整数の割り算と余り・合同式#神戸大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ $n$を自然数とする。以下の問いに答えよ。
(1)1個のサイコロを投げて出た目が必ず$n$の約数となるような$n$で最小のものを求めよ。
(2)1個のサイコロを投げて出た目が$n$の約数となる確率が$\displaystyle\frac{5}{6}$であるような$n$で最小のものを求めよ。
(3)1個のサイコロを3回投げて出た目の積が20の約数となる確率を求めよ。
この動画を見る
$\Large\boxed{2}$ $n$を自然数とする。以下の問いに答えよ。
(1)1個のサイコロを投げて出た目が必ず$n$の約数となるような$n$で最小のものを求めよ。
(2)1個のサイコロを投げて出た目が$n$の約数となる確率が$\displaystyle\frac{5}{6}$であるような$n$で最小のものを求めよ。
(3)1個のサイコロを3回投げて出た目の積が20の約数となる確率を求めよ。
福田の数学〜神戸大学2024年理系第3問〜さいころの目と約数に関する確率

単元:
#数A#場合の数と確率#整数の性質#確率#約数・倍数・整数の割り算と余り・合同式#神戸大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ $n$を自然数とする。以下の問いに答えよ。
(1)1個のサイコロを投げて出た目が必ず$n$の約数となるような$n$を小さい順に3つ求めよ。
(2)1個のサイコロを投げて出た目が$n$の約数となる確率が$\displaystyle\frac{5}{6}$であるような$n$を小さい順に3つ求めよ。
(3)1個のサイコロを3回投げて出た目の積が160の約数となる確率を求めよ。
この動画を見る
$\Large\boxed{3}$ $n$を自然数とする。以下の問いに答えよ。
(1)1個のサイコロを投げて出た目が必ず$n$の約数となるような$n$を小さい順に3つ求めよ。
(2)1個のサイコロを投げて出た目が$n$の約数となる確率が$\displaystyle\frac{5}{6}$であるような$n$を小さい順に3つ求めよ。
(3)1個のサイコロを3回投げて出た目の積が160の約数となる確率を求めよ。
福田の数学〜大阪大学2024年文系第3問〜素数を小さい順に並べた数列の特徴

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#大阪大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 素数を小さい順に並べて得られる数列を
$p_1$, $p_2$, ..., $p_n$, ...
とする。
(1)$p_{15}$の値を求めよ。
(2)$n$≧12のとき、不等式$p_n$>$3n$が成り立つことを示せ。
この動画を見る
$\Large\boxed{3}$ 素数を小さい順に並べて得られる数列を
$p_1$, $p_2$, ..., $p_n$, ...
とする。
(1)$p_{15}$の値を求めよ。
(2)$n$≧12のとき、不等式$p_n$>$3n$が成り立つことを示せ。
福田のおもしろ数学155〜6の倍数である証明

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
自然数$n$に対し、$n(n^2+5)$が6の倍数であることを示せ。
この動画を見る
自然数$n$に対し、$n(n^2+5)$が6の倍数であることを示せ。
福田の数学〜大阪大学2024年理系第5問〜互いに素な整数の個数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 自然数1, 2, 3, ..., $n$のうち、$n$と互いに素であるものの個数を$f(n)$とする。
(1)自然数$a$, $b$, $c$及び相異なる素数$p$, $q$, $r$に対して、等式
$f(p^ap^bp^c)$=$p^{a-1}p^{b-1}p^{c-1}(p-1)(q-1)(r-1)$
が成り立つことを示せ。
(2)$f(n)$が$n$の約数となる5以上100以下の自然数$n$をすべて求めよ。
この動画を見る
$\Large\boxed{5}$ 自然数1, 2, 3, ..., $n$のうち、$n$と互いに素であるものの個数を$f(n)$とする。
(1)自然数$a$, $b$, $c$及び相異なる素数$p$, $q$, $r$に対して、等式
$f(p^ap^bp^c)$=$p^{a-1}p^{b-1}p^{c-1}(p-1)(q-1)(r-1)$
が成り立つことを示せ。
(2)$f(n)$が$n$の約数となる5以上100以下の自然数$n$をすべて求めよ。
福田のおもしろ数学147〜3変数の不定方程式の一般解

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
35x+91y+65z=3 を満たす整数x, y, zを求めよ。
この動画を見る
35x+91y+65z=3 を満たす整数x, y, zを求めよ。
福田のおもしろ数学146〜3m+5nで作れない自然数を求める

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$X$=$3m$+$5n$ ($m$, $n$は0以上の整数)の形で表せない自然数$X$を全て求めよ。
この動画を見る
$X$=$3m$+$5n$ ($m$, $n$は0以上の整数)の形で表せない自然数$X$を全て求めよ。
福田のおもしろ数学144〜連続する6個の自然数を積の等しい2グループに分けられない証明

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
連続する6個の自然数を2つのグループに分けて、それぞれのグループに属する自然数の積を等しくすることはできない。
これを示せ。
この動画を見る
連続する6個の自然数を2つのグループに分けて、それぞれのグループに属する自然数の積を等しくすることはできない。
これを示せ。
福田の数学〜慶應義塾大学2024年商学部第2問(3)〜最小公倍数の変化と個数

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ (3)1から$n$までの$n$個の自然数の最小公倍数を$a_n$とする。
・$a_n$=$a_{n+1}$を満たす最小の自然数$n$は$\boxed{ケ}$である。
・$a_{n+1}$=$2a_n$を満たす10000以下の自然数$n$は$\boxed{コサ}$個ある。
この動画を見る
$\Large\boxed{2}$ (3)1から$n$までの$n$個の自然数の最小公倍数を$a_n$とする。
・$a_n$=$a_{n+1}$を満たす最小の自然数$n$は$\boxed{ケ}$である。
・$a_{n+1}$=$2a_n$を満たす10000以下の自然数$n$は$\boxed{コサ}$個ある。
方程式
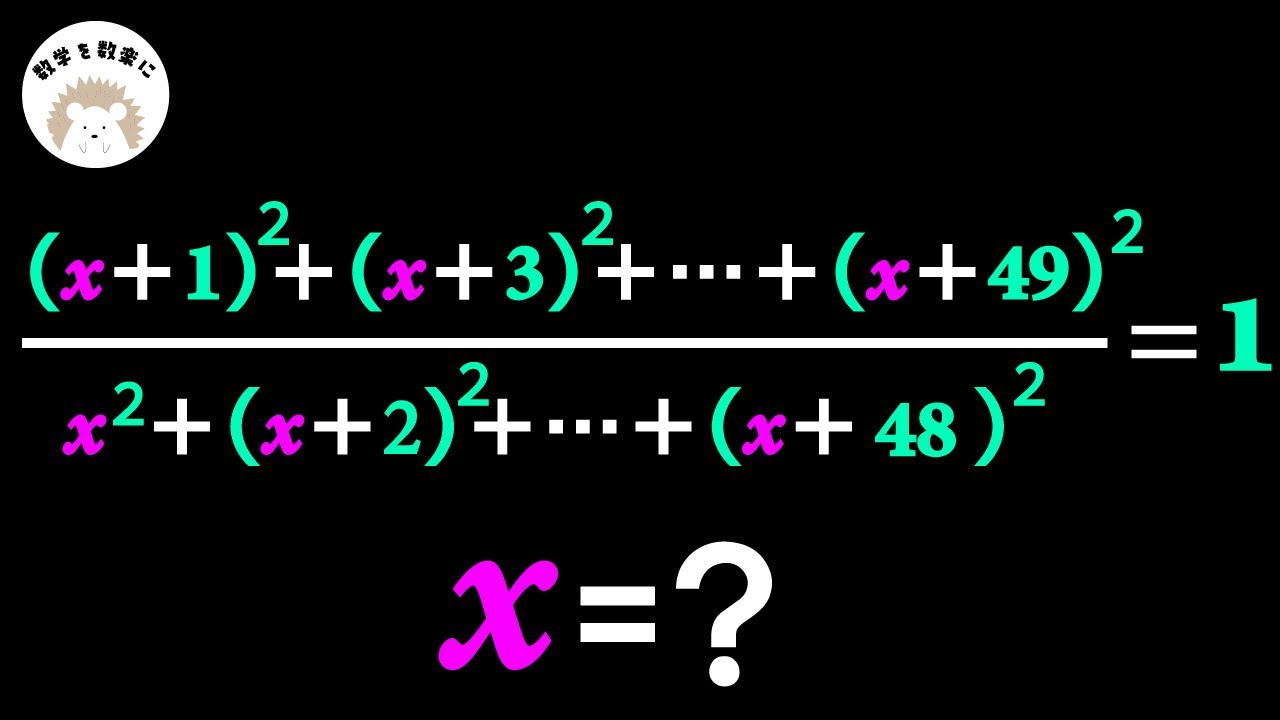
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{(x+1)^2+(x+3)^2+(x+5)^2+ \cdots +(x+49)^2}{x^2+(x+2)^2+(x+4)^2+ \cdots +(x+48)^2}=1$
この動画を見る
$\frac{(x+1)^2+(x+3)^2+(x+5)^2+ \cdots +(x+49)^2}{x^2+(x+2)^2+(x+4)^2+ \cdots +(x+48)^2}=1$
福田の数学〜慶應義塾大学2024年商学部第1問(3)〜不定方程式の自然数解

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$
(3)$a$<$b$<$c$かつ $\displaystyle\frac{1}{a}$+$\displaystyle\frac{2}{b}$+$\displaystyle\frac{3}{c}$=$2$ を満たす自然数の組($a$, $b$, $c$)をすべて求めよ。
この動画を見る
$\Large\boxed{1}$
(3)$a$<$b$<$c$かつ $\displaystyle\frac{1}{a}$+$\displaystyle\frac{2}{b}$+$\displaystyle\frac{3}{c}$=$2$ を満たす自然数の組($a$, $b$, $c$)をすべて求めよ。
大学入試問題#818「なんてことはない問題」 #京都大学(1979)

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \frac{2^n}{n} \gt n$を満たす自然数$n$の範囲を求めよ。
出典:1979年京都大学 入試問題
この動画を見る
$\displaystyle \frac{2^n}{n} \gt n$を満たす自然数$n$の範囲を求めよ。
出典:1979年京都大学 入試問題
いやらしい方程式を解け!!

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
方程式を解け
(1)$x=x$
(2)$x=x+1$
この動画を見る
方程式を解け
(1)$x=x$
(2)$x=x+1$
