 数A
数A
 数A
数A
333‥‥33が2021の倍数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$333・・・・・・33$のように,すべての位の数が3である数の中には必ず$2021$の倍数があることを示せ.
この動画を見る
$333・・・・・・33$のように,すべての位の数が3である数の中には必ず$2021$の倍数があることを示せ.
200! 12進法で表すと末尾に0何個?

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
十進法の$200!$を12進法で表すと末尾に$0$が何個並ぶか.
この動画を見る
十進法の$200!$を12進法で表すと末尾に$0$が何個並ぶか.
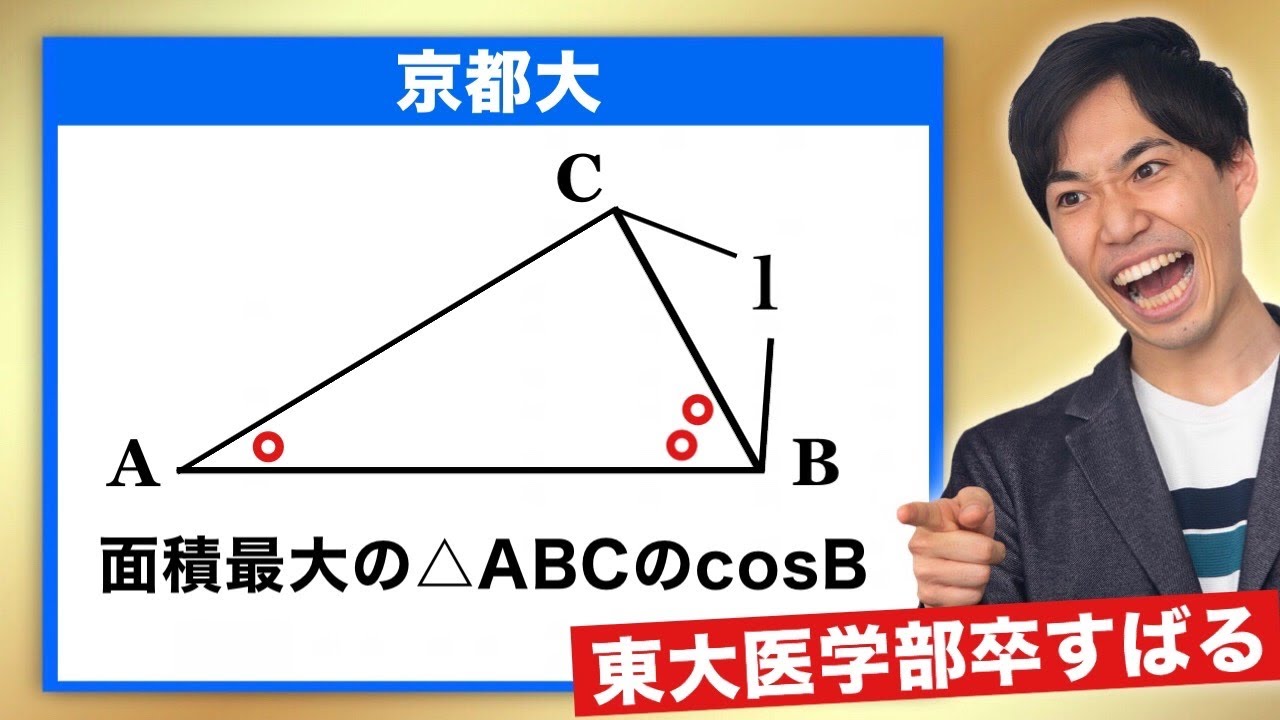
京都大 東大医学部卒パスラボ宇佐見さん3度目登場
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
三角形のうち面積が最大のとき,$\cos \angle B$を求めよ.
京大過去問
この動画を見る
三角形のうち面積が最大のとき,$\cos \angle B$を求めよ.
京大過去問
名古屋大 分野不明

単元:
#数Ⅰ#数A#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt{n}$は整数でなく,小数第一位が$0$で$2$倍は$0$でない.
$\sqrt{n}=\boxed{A}.0\boxed{b}・・・$
(1)最小の$n$を求めよ.
(2)小さい順で$10$番目の$n$を求めよ.
2019名古屋大過去問
この動画を見る
$\sqrt{n}$は整数でなく,小数第一位が$0$で$2$倍は$0$でない.
$\sqrt{n}=\boxed{A}.0\boxed{b}・・・$
(1)最小の$n$を求めよ.
(2)小さい順で$10$番目の$n$を求めよ.
2019名古屋大過去問
【数A】整数の性質:次の条件を全て満たす3つの自然数の組(a,b,c)をすべて求めよ。・a,b,cの最大公約数は6・b,cの最大公約数は24最小公倍数は144・a,bの最小公倍数は240(a<b<c)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の条件を全て満たす3つの自然数の組(a,b,c)をすべて求めよ。
・a,b,cの最大公約数は6
・b,cの最大公約数は24最小公倍数は144
・a,bの最小公倍数は240(a<b<c)
この動画を見る
次の条件を全て満たす3つの自然数の組(a,b,c)をすべて求めよ。
・a,b,cの最大公約数は6
・b,cの最大公約数は24最小公倍数は144
・a,bの最小公倍数は240(a<b<c)
【数A】整数の性質:√n²+40が自然数となるような自然数nをすべて求めよ。

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\sqrt{n^2+40}$が自然数となるような自然数nをすべて求めよ。
この動画を見る
$\sqrt{n^2+40}$が自然数となるような自然数nをすべて求めよ。
山口大 フェルマー素数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整数$n \geqq 0$,$F_n=2^{2^n}+1$とする.
(1)$F_{n+1}=F_0F_1F_2・・・・・・F_n+2$を示せ.
(2)$m\neq n$であり,$F_m$と$F_n$は互いに素を示せ.
2005山口大過去問
この動画を見る
整数$n \geqq 0$,$F_n=2^{2^n}+1$とする.
(1)$F_{n+1}=F_0F_1F_2・・・・・・F_n+2$を示せ.
(2)$m\neq n$であり,$F_m$と$F_n$は互いに素を示せ.
2005山口大過去問
同志社大 最大公約数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2^{32}+1$と$2^{16}+1$の最大公約数を求めよ.
2002同志社大過去問
この動画を見る
$2^{32}+1$と$2^{16}+1$の最大公約数を求めよ.
2002同志社大過去問
08大阪府教員採用試験(数学:1番 整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣ $n \in \mathbb {Z}$
$n^5-n$が30の倍数である
この動画を見る
1⃣ $n \in \mathbb {Z}$
$n^5-n$が30の倍数である
素数判定

単元:
#数A#数Ⅱ#整数の性質#約数・倍数・整数の割り算と余り・合同式#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$30^{17}+17^{30}$は素数か.
この動画を見る
$30^{17}+17^{30}$は素数か.
京都大 整数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b$は自然数であり,$d,p$は素数である.
$a^p-b^p=d$ならば$d$を$2p$で割った余りは1であることを示せ.
1995京都大過去問
この動画を見る
$a,b$は自然数であり,$d,p$は素数である.
$a^p-b^p=d$ならば$d$を$2p$で割った余りは1であることを示せ.
1995京都大過去問
数学オリンピック予選 合同式の「割り算‼️」

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学オリンピック#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
${}_{40}\mathrm{C}_{20}$を41で割った余りを求めよ.
数学オリンピック過去問
この動画を見る
${}_{40}\mathrm{C}_{20}$を41で割った余りを求めよ.
数学オリンピック過去問
【数A】整数の性質:合同式② a,bは3で割り切れない整数とする。このとき、a⁴+a²b²+b⁴は3で割り切れることを証明せよ。

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
a,bは3で割り切れない整数とする。このとき、$a^4+a^2b^2+b^4$は3で割り切れることを証明せよ。
この動画を見る
a,bは3で割り切れない整数とする。このとき、$a^4+a^2b^2+b^4$は3で割り切れることを証明せよ。
【数A】整数の性質:合同式① 整数a,b,cがa²+b²=c²を満たすとき、a,b,cのうち少なくとも1つは5の倍数である。このことを合同式を利用して証明せよ。

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)整数a,b,cが$a^2+b^2=c^5$を満たすとき、a,b,cのうち少なくとも1つは5の倍数である。このことを合同式を利用して証明せよ。
(2)nが自然数のとき、$n^3+1$が3で割り切れるものをすべて求めよ。
この動画を見る
(1)整数a,b,cが$a^2+b^2=c^5$を満たすとき、a,b,cのうち少なくとも1つは5の倍数である。このことを合同式を利用して証明せよ。
(2)nが自然数のとき、$n^3+1$が3で割り切れるものをすべて求めよ。
19愛知県教員採用試験(数学:4番 整数問題(数列系))

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
4⃣$N=\mathbb{ p }^n×5^n$
(1)正の約数の個数が8個
(2)正の約数の総和が90のとき、$\mathbb{ p }$とNを求めよ。
この動画を見る
4⃣$N=\mathbb{ p }^n×5^n$
(1)正の約数の個数が8個
(2)正の約数の総和が90のとき、$\mathbb{ p }$とNを求めよ。
千葉大 n次方程式の整数解

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$P$は素数であり,$n\geqq 2$は自然数とする.
$x^n-p^n x-p^{n+1}=0$は整数解をもたないことを示せ.
2009千葉大過去問
この動画を見る
$P$は素数であり,$n\geqq 2$は自然数とする.
$x^n-p^n x-p^{n+1}=0$は整数解をもたないことを示せ.
2009千葉大過去問
変な方程式
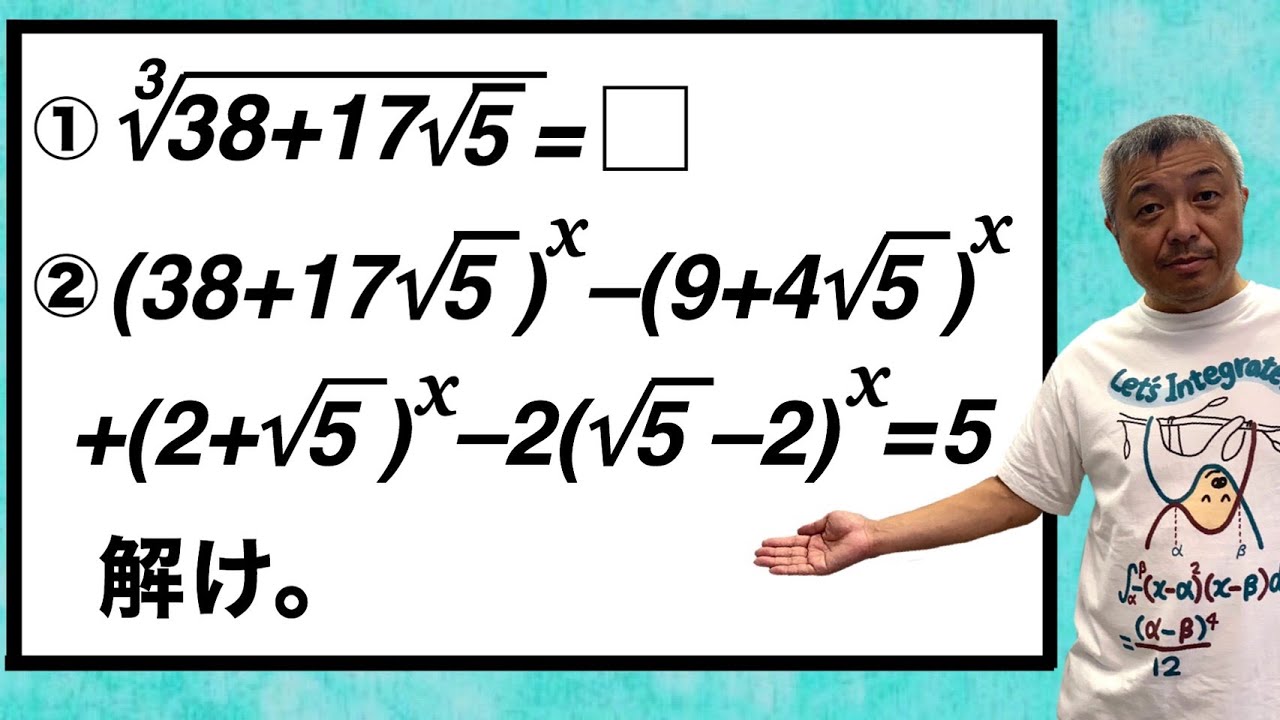
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
①$\sqrt[3]{38+17\sqrt5}=\Box$
②$(38+17\sqrt5)^x-(9+4\sqrt5)^x+(2+\sqrt5)^x$
$-2(\sqrt5-2)^x=5$を解け.
この動画を見る
これを解け.
①$\sqrt[3]{38+17\sqrt5}=\Box$
②$(38+17\sqrt5)^x-(9+4\sqrt5)^x+(2+\sqrt5)^x$
$-2(\sqrt5-2)^x=5$を解け.
漸化式と整数の融合問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=2$,$a_{n+1}=2^{n^2+2n-1}・a^2_n$
$a_n$の1の位が2になるのは$a_1$のみであることを示せ.
この動画を見る
$a_1=2$,$a_{n+1}=2^{n^2+2n-1}・a^2_n$
$a_n$の1の位が2になるのは$a_1$のみであることを示せ.
16愛知県教員採用試験(数学:2番 整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
2⃣自然数$N=2^a×3^b$の
(1)正の約数の個数が20コ
(2)正の約数の総和が1240をみたすa,bの値を求めよ。
この動画を見る
2⃣自然数$N=2^a×3^b$の
(1)正の約数の個数が20コ
(2)正の約数の総和が1240をみたすa,bの値を求めよ。
整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$7^{7^{7^{7^{7^{7}}}}}$を$13$で割った余りを求めよ.
この動画を見る
$7^{7^{7^{7^{7^{7}}}}}$を$13$で割った余りを求めよ.
漸化式と整数問題の融合

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は自然数である.
$a_1=10,a_{n+1}=2a_n+3^{n+1}$
$a_n$が7の倍数となるような$n$を求めよ.
この動画を見る
$n$は自然数である.
$a_1=10,a_{n+1}=2a_n+3^{n+1}$
$a_n$が7の倍数となるような$n$を求めよ.
東大 座標上の鋭角三角形

単元:
#数A#図形の性質#平面上の曲線#三角形の辺の比(内分・外分・二等分線)#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b$は実数であり,$b\neq 0$である.
$O(0,0).P(1,0),Q(a,b)$
(1)$\triangle OPQ$が鋭角三角形になる$a,b$の条件を不等式で表せ.
(2)$m,n$整数,$a,b$は(1)の条件を満たすとき,$(m+na)^2-(m+na)+n^2b^2 \geqq 0$を示せ.
1998東大過去問
この動画を見る
$a,b$は実数であり,$b\neq 0$である.
$O(0,0).P(1,0),Q(a,b)$
(1)$\triangle OPQ$が鋭角三角形になる$a,b$の条件を不等式で表せ.
(2)$m,n$整数,$a,b$は(1)の条件を満たすとき,$(m+na)^2-(m+na)+n^2b^2 \geqq 0$を示せ.
1998東大過去問
京都大 三角形の辺の長さ
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
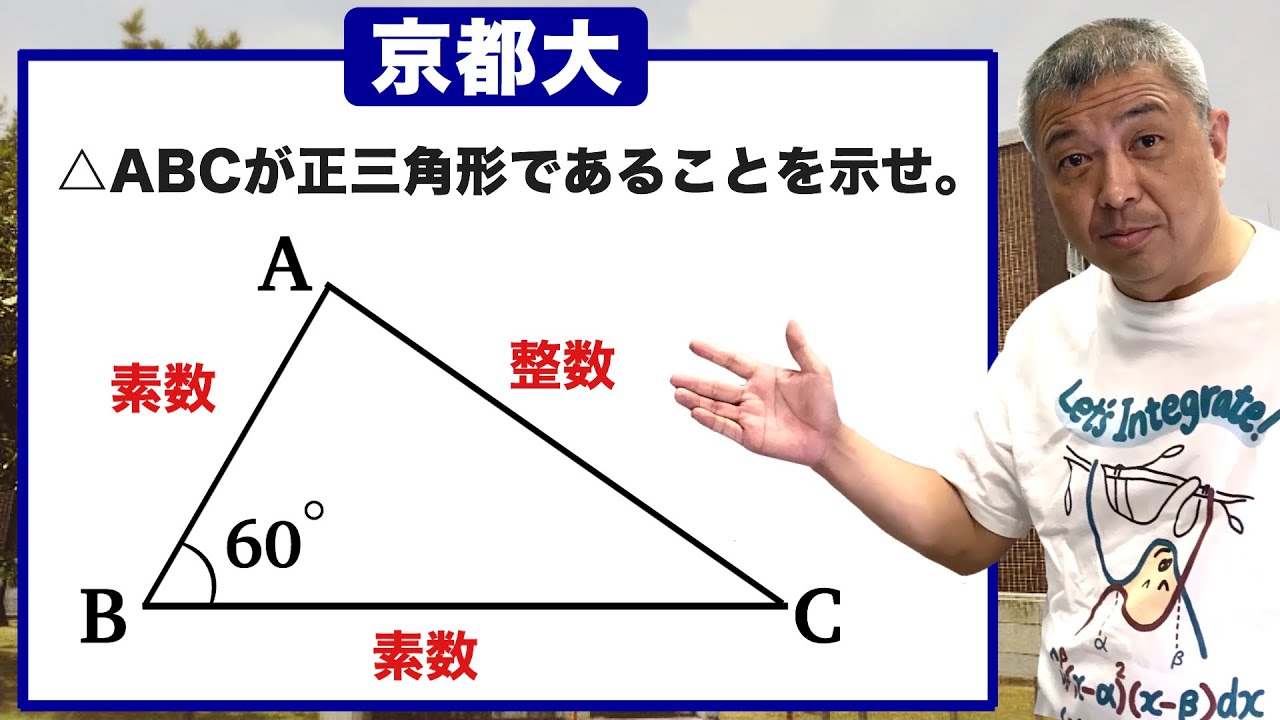
$a,c$は素数である.
$b$が整数のとき,$\triangle ABC$は正三角形であることを示せ
1990京都大過去問
この動画を見る
$a,c$は素数である.
$b$が整数のとき,$\triangle ABC$は正三角形であることを示せ
1990京都大過去問
図書館情報大 整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2^{(3^n)}+1$は$3$で何回割り切ることができるか.
1991図書館情報大過去問
この動画を見る
$2^{(3^n)}+1$は$3$で何回割り切ることができるか.
1991図書館情報大過去問
19愛知県教員採用試験(数学:1-1,2番 整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
1⃣2x+5y=43$\cdots$※
(1)※をみたす自然数の組(x,y)
(2)※をみたしx-2yがx+3yで割り切れる整数の組(x,y)の個数
この動画を見る
1⃣2x+5y=43$\cdots$※
(1)※をみたす自然数の組(x,y)
(2)※をみたしx-2yがx+3yで割り切れる整数の組(x,y)の個数
慶應義塾大 指数方程式の解の個数

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$8^x-3a4^x+4a=0$の実数解の個数を求めよ.$a$は実数である.
1997慶應(経)過去問
この動画を見る
$8^x-3a4^x+4a=0$の実数解の個数を求めよ.$a$は実数である.
1997慶應(経)過去問
数学オリンピック 整数問題

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学オリンピック#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$1111^{2018}$を$11111$で割った余りを求めよ.
この動画を見る
$1111^{2018}$を$11111$で割った余りを求めよ.
19大阪府教員採用試験(数学:2番 フェルマーの小定理)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
2⃣ ℙ:素数、(a,ℙ)=1
(1)$a,2a,3a, \cdots ,(ℙ-1)a$の余りは全て異なる
(2)$a^{ℙ-1}$はℙの倍数
(3)$2018^{1800}$を181で割った余り
この動画を見る
2⃣ ℙ:素数、(a,ℙ)=1
(1)$a,2a,3a, \cdots ,(ℙ-1)a$の余りは全て異なる
(2)$a^{ℙ-1}$はℙの倍数
(3)$2018^{1800}$を181で割った余り
サイコロ確率

【数A】確率:2019年第2回高2K塾記述模試の第4問を解説!「難しそうだから手を付けませんでした...」と言っていた生徒と状況整理をしながら解いていくと「簡単でしたね!」となりました。

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#全統模試(河合塾)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
Oを原点とする座標平面上に点Pがある。最初、Pは原点Oにあり、1個のサイコロを1回投げるごとに次の(規則)に従ってPを動かす。
(規則)
・1,2いずれかの目が出たときはx軸の正の方向に1だけ動かす。
・3の目が出たときはx軸の正の方向に2だけ動かす。
・4,5,6いずれかの目が出たときはy軸の正の方向に1だけ動かす。
例えば、さいころを2回投げて、1回目に2の目、2回目に5の目が出たとき、Pは O(0,0)→点(1,0)→点(1,1) と動く。
(1)サイコロを3回投げたとき、Pの座標が(3,0)である確率を求めよ。
(2)サイコロを3回投げたとき、Pのy座標が2である確率を求めよ。
(3)サイコロを6回投げたとき、Pの座標が(5,2)である確率を求めよ。
(4)サイコロを6回投げたとき、Pのx座標が5であったという条件のもとで、Pのy座標が2である条件付き確率を求めよ。
この動画を見る
Oを原点とする座標平面上に点Pがある。最初、Pは原点Oにあり、1個のサイコロを1回投げるごとに次の(規則)に従ってPを動かす。
(規則)
・1,2いずれかの目が出たときはx軸の正の方向に1だけ動かす。
・3の目が出たときはx軸の正の方向に2だけ動かす。
・4,5,6いずれかの目が出たときはy軸の正の方向に1だけ動かす。
例えば、さいころを2回投げて、1回目に2の目、2回目に5の目が出たとき、Pは O(0,0)→点(1,0)→点(1,1) と動く。
(1)サイコロを3回投げたとき、Pの座標が(3,0)である確率を求めよ。
(2)サイコロを3回投げたとき、Pのy座標が2である確率を求めよ。
(3)サイコロを6回投げたとき、Pの座標が(5,2)である確率を求めよ。
(4)サイコロを6回投げたとき、Pのx座標が5であったという条件のもとで、Pのy座標が2である条件付き確率を求めよ。
