複素数
複素数
愛が１番！
i=1⁉️からくりは通常動画で❗️ #short
神戸大 ３次方程式の基本問題
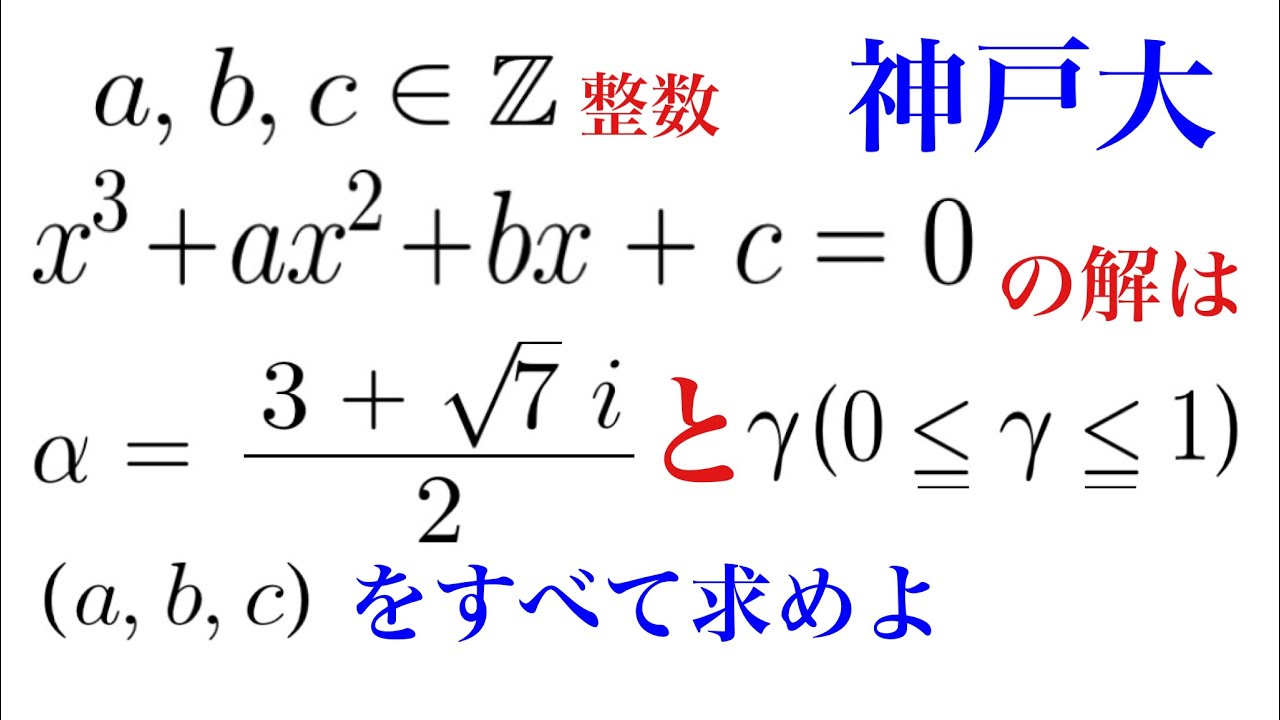
単元：
#数Ⅰ#数Ⅱ#数と式#複素数と方程式#複素数平面#一次不等式（不等式・絶対値のある方程式・不等式）#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#複素数平面#数学(高校生)#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a,b,c$は整数である。
$x^3+ax^2+bx+c=0$は$\alpha=\dfrac{3+\sqrt{7}i}{2}$と0以上1以下の解をもつ(a,b,c)をすべて求めよ.
神戸大過去問
この動画を見る
$a,b,c$は整数である。
$x^3+ax^2+bx+c=0$は$\alpha=\dfrac{3+\sqrt{7}i}{2}$と0以上1以下の解をもつ(a,b,c)をすべて求めよ.
神戸大過去問
久留米大（医）４次方程式
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#数学(高校生)#久留米大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x=1+\sqrt{3}c$が解である$x^4+ax^3+ax^2+(6-a)x+b=0$の
実数$a,b$を求めよ.
久留米大(医)過去問
この動画を見る
$x=1+\sqrt{3}c$が解である$x^4+ax^3+ax^2+(6-a)x+b=0$の
実数$a,b$を求めよ.
久留米大(医)過去問
大学入試問題#483「作成時間がありませんでした」 近畿大学医学部(2023) #解と係数の関係
単元：
#数Ⅱ#複素数と方程式#複素数#解と判別式・解と係数の関係#数列#漸化式#数B
指導講師：
ますただ
問題文全文(内容文)：
$x^2-x+1=0$の解を$\alpha,\beta$とする
$\alpha^9+\beta^9$の値を求めよ
出典：2023年近畿大学医学 入試問題
この動画を見る
$x^2-x+1=0$の解を$\alpha,\beta$とする
$\alpha^9+\beta^9$の値を求めよ
出典：2023年近畿大学医学 入試問題
昭和大（医学部）複素数の計算
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#数学(高校生)#昭和大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ Z=\cos\dfrac{2}{5}\pi+i\sin\dfrac{2}{5}\pi,w=Z+Z^3$とするとき,
①$w+\bar{w}$
②$w･\bar{w}$
の値を求めよ.
昭和大(医)過去問
この動画を見る
$ Z=\cos\dfrac{2}{5}\pi+i\sin\dfrac{2}{5}\pi,w=Z+Z^3$とするとき,
①$w+\bar{w}$
②$w･\bar{w}$
の値を求めよ.
昭和大(医)過去問
愛があれば解決する。愛はなくても問題ない
単元：
#数Ⅱ#式と証明#複素数と方程式#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#複素数
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x+2\sqrt{3}y=\dfrac{x}{x^2+y^2} \\
2\sqrt{3}x-2y=\dfrac{y}{x^2+y^2}
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け.
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x+2\sqrt{3}y=\dfrac{x}{x^2+y^2} \\
2\sqrt{3}x-2y=\dfrac{y}{x^2+y^2}
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け.
虚数係数の二次方程式
単元：
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$(1-i)x^2+(3k-6i)x+8-5ki+2i=0$が実数解をもつような整数ｋとそのときの解を求めよ.
愛知大過去問
この動画を見る
$(1-i)x^2+(3k-6i)x+8-5ki+2i=0$が実数解をもつような整数ｋとそのときの解を求めよ.
愛知大過去問
大学入試問題#422「基本性質を利用」 自治医科大学2016 #複素数
単元：
#数Ⅱ#複素数と方程式#複素数
指導講師：
ますただ
問題文全文(内容文)：
$z$：複素数
$\displaystyle \sum_{k=0}^9 z^k=0$のとき
$\displaystyle \frac{|z-2|^2+|z+2|^2}{5}$の値を求めよ
出典：2016年自治医科大学 入試問題
この動画を見る
$z$：複素数
$\displaystyle \sum_{k=0}^9 z^k=0$のとき
$\displaystyle \frac{|z-2|^2+|z+2|^2}{5}$の値を求めよ
出典：2016年自治医科大学 入試問題
福田の数学〜北里大学2020年医学部第１問(1)〜虚数係数の３次方程式の解
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large{\boxed{1}}$ (1)$p,q$を実数の定数、$i$を虚数単位とする。$x$の方程式
$x^3-(p-i)x^2+(q-pi)x-2p+\displaystyle\frac{3p}{2}i=0$
が$2+i$を解にもつとする。このとき、$p=\boxed{\ \ ア\ \ }$,$q=\boxed{\ \ イ\ \ }$である。また、この方程式の$2+i$以外の解を$\alpha$,$\beta$(ただし、|$\alpha$| $\lt$ |$\beta$|)とおくと$\left(\displaystyle\frac{\beta-i}{\alpha}\right)^7=\boxed{\ \ ウ \ \ }$である。
2020北里大学医学部過去問
この動画を見る
$\Large{\boxed{1}}$ (1)$p,q$を実数の定数、$i$を虚数単位とする。$x$の方程式
$x^3-(p-i)x^2+(q-pi)x-2p+\displaystyle\frac{3p}{2}i=0$
が$2+i$を解にもつとする。このとき、$p=\boxed{\ \ ア\ \ }$,$q=\boxed{\ \ イ\ \ }$である。また、この方程式の$2+i$以外の解を$\alpha$,$\beta$(ただし、|$\alpha$| $\lt$ |$\beta$|)とおくと$\left(\displaystyle\frac{\beta-i}{\alpha}\right)^7=\boxed{\ \ ウ \ \ }$である。
2020北里大学医学部過去問
ナイスな連立４元三次方程式
単元：
#数A#数Ⅱ#複素数と方程式#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#複素数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\begin{eqnarray}
\left\{
\begin{array}{l}
a+bcd=30 \\\
b+acd=30 \\
c+abd=30 \\
d+abc=30
\end{array}
\right.
\end{eqnarray}$
を解け.
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
a+bcd=30 \\\
b+acd=30 \\
c+abd=30 \\
d+abc=30
\end{array}
\right.
\end{eqnarray}$
を解け.
連立二元４次方程式
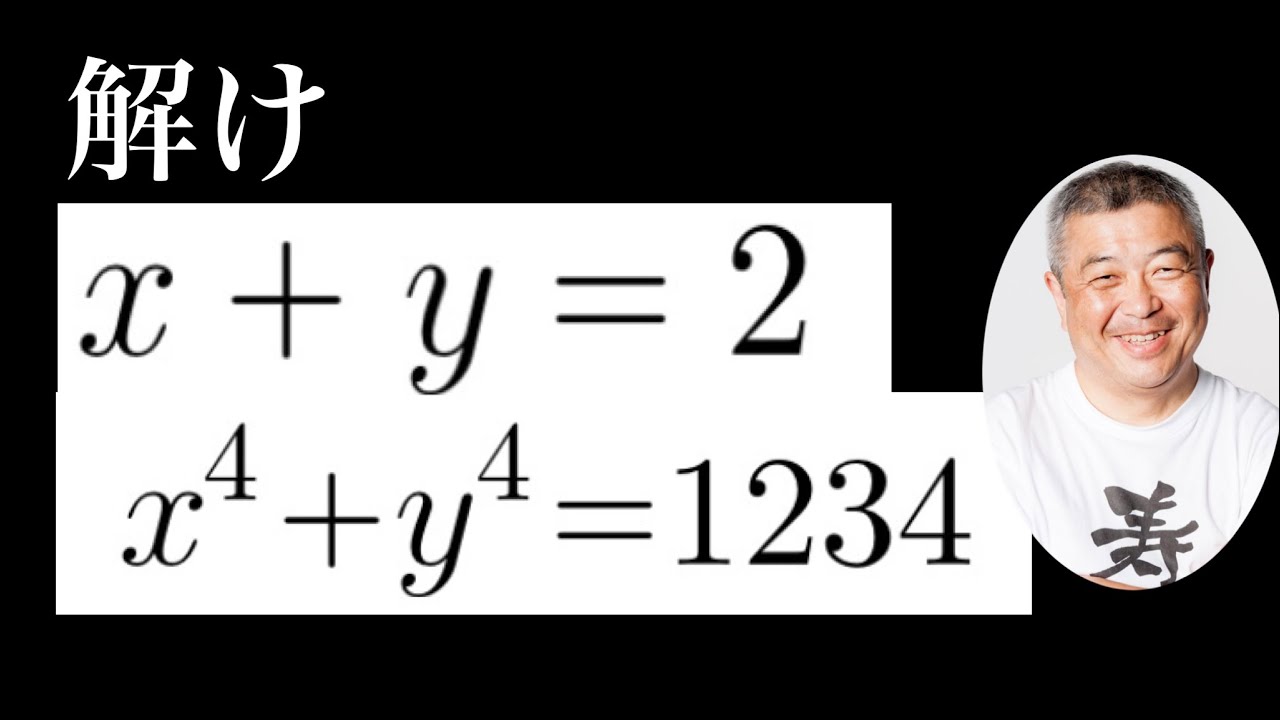
単元：
#数Ⅰ#数Ⅱ#数と式#２次関数#複素数と方程式#2次方程式と2次不等式#複素数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=2 \\
x^4+y^4=1234
\end{array}
\right.
\end{eqnarray}$
この動画を見る
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=2 \\
x^4+y^4=1234
\end{array}
\right.
\end{eqnarray}$
大学入試問題#396「基本問題」 慶應義塾大学(2009) #複素数
単元：
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$a,b$：実数
$(a+bi)^3=4+\mathit{i}$のとき、
$\displaystyle \frac{(a-b\mathit{i})^3}{2+3\mathit{i}}$の値を求めよ
出典：2009年慶應義塾大学 入試問題
この動画を見る
$a,b$：実数
$(a+bi)^3=4+\mathit{i}$のとき、
$\displaystyle \frac{(a-b\mathit{i})^3}{2+3\mathit{i}}$の値を求めよ
出典：2009年慶應義塾大学 入試問題
暗算？
単元：
#数Ⅱ#複素数と方程式#複素数平面#複素数#複素数平面#数学(高校生)#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ x^2-\sqrt3x+1=0$のとき,
$x^{30}+\dfrac{1}{x^{30}}$の値を求めよ.
この動画を見る
$ x^2-\sqrt3x+1=0$のとき,
$x^{30}+\dfrac{1}{x^{30}}$の値を求めよ.
俺のアイデアを聞いて
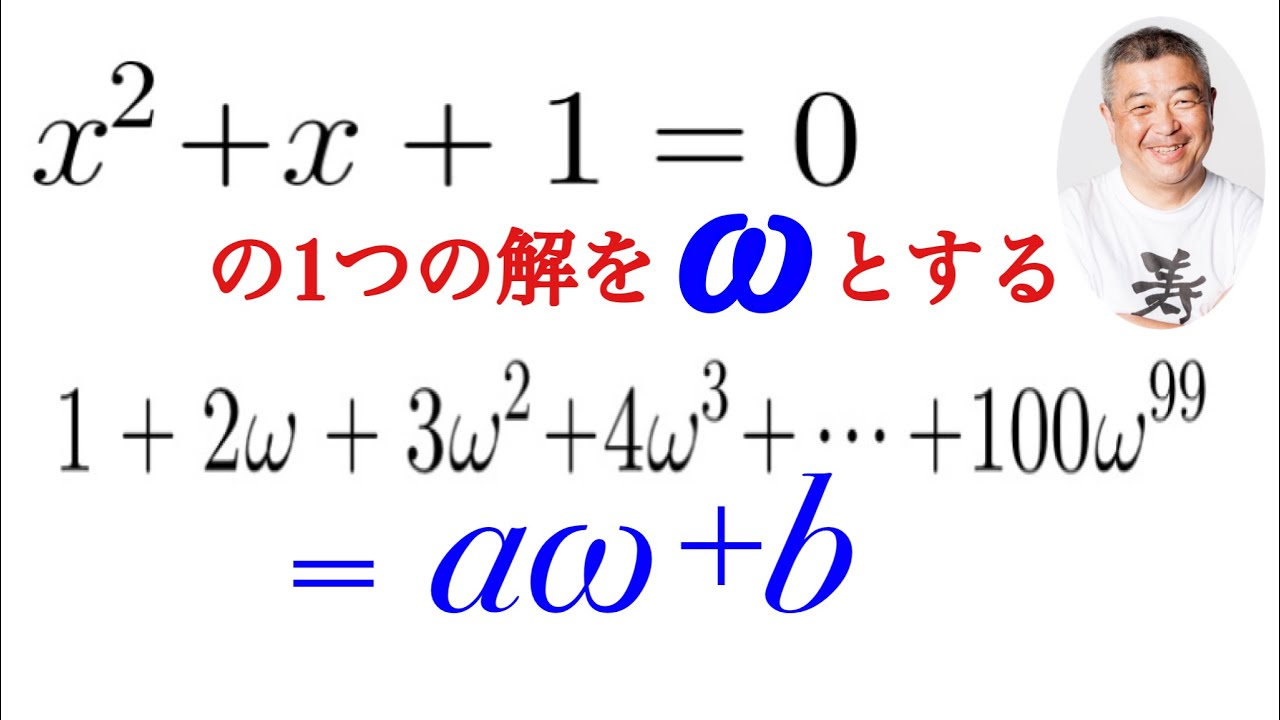
単元：
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ x^2+x+1=$の1つの解を$\omega$とする.
$1+2\omega+3\omega^2+4\omega^3+…+100\omega^{99}=a\omega+b$である.a.bの値を求めよ.
この動画を見る
$ x^2+x+1=$の1つの解を$\omega$とする.
$1+2\omega+3\omega^2+4\omega^3+…+100\omega^{99}=a\omega+b$である.a.bの値を求めよ.
分からないので教えてください！ふさわしくない解は？
単元：
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ x-\dfrac{4}{x}=\sqrt x+\dfrac{2}{\sqrt x}$
これを解け.
この動画を見る
$ x-\dfrac{4}{x}=\sqrt x+\dfrac{2}{\sqrt x}$
これを解け.
【高校数学あるある】二項定理と1の3乗根ωの融合問題 #Shorts
単元：
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$x^2+x+1=0$の解の一つを$\omega$とするとき
${}_9 \mathrm{ C }_0+{}_9 \mathrm{ C }_1\omega+{}_9 \mathrm{ C }_2\omega+……+{}_9 \mathrm{ C }_9\omega^9$の値を求めよ。
この動画を見る
$x^2+x+1=0$の解の一つを$\omega$とするとき
${}_9 \mathrm{ C }_0+{}_9 \mathrm{ C }_1\omega+{}_9 \mathrm{ C }_2\omega+……+{}_9 \mathrm{ C }_9\omega^9$の値を求めよ。
愛のある二次方程式
福田の数学〜早稲田大学2022年人間科学部第４問〜3変数の基本対称式と解と係数の関係
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#複素数#解と判別式・解と係数の関係#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\large\boxed{4}}$互いに異なる実数$a,b,c$について、
$a+b+c=0,\ bc+ca+ab=-3$であるとき、
$abc$のとりうる値の範囲は、$\boxed{\ \ ア\ \ } \lt abc \lt \boxed{\ \ イ\ \ }$である。
さらに$a \lt b \lt c$のとき、$a,b,c$のとりうる値の範囲は
$\boxed{\ \ ウ\ \ } \lt a \lt \boxed{\ \ エ\ \ } \lt b \lt \boxed{\ \ オ\ \ } \lt c \lt \boxed{\ \ カ\ \ }$である。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{4}}$互いに異なる実数$a,b,c$について、
$a+b+c=0,\ bc+ca+ab=-3$であるとき、
$abc$のとりうる値の範囲は、$\boxed{\ \ ア\ \ } \lt abc \lt \boxed{\ \ イ\ \ }$である。
さらに$a \lt b \lt c$のとき、$a,b,c$のとりうる値の範囲は
$\boxed{\ \ ウ\ \ } \lt a \lt \boxed{\ \ エ\ \ } \lt b \lt \boxed{\ \ オ\ \ } \lt c \lt \boxed{\ \ カ\ \ }$である。
2022早稲田大学人間科学部過去問
５次式の因数分解 R15中学生はご遠慮ください
単元：
#数Ⅰ#数と式#複素数と方程式#式の計算（整式・展開・因数分解）#複素数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ x^5+16x+32$
これを因数分解(整数係数)せよ.
この動画を見る
$ x^5+16x+32$
これを因数分解(整数係数)せよ.
ハルハル様の作成問題③ #複素数
単元：
#数Ⅱ#複素数と方程式#複素数平面#複素数#複素数平面#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$z$：複素数
$a$：実数
$2Z^2+3|Z|Z=a$を解け
この動画を見る
$z$：複素数
$a$：実数
$2Z^2+3|Z|Z=a$を解け
数学オリンピック予選
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数#解と判別式・解と係数の関係#数学オリンピック#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
有理数係数の2次方程式
$ x^{2n}+a_1x^{2n-1}+a_2x^{2n-2}+$
$･･････+a_{2n-1}x+a_{2n}=0$
の解はすべて$x^2+5x+7=0$の解にもなっている.
$a_1$の値を求めよ.
この動画を見る
有理数係数の2次方程式
$ x^{2n}+a_1x^{2n-1}+a_2x^{2n-2}+$
$･･････+a_{2n-1}x+a_{2n}=0$
の解はすべて$x^2+5x+7=0$の解にもなっている.
$a_1$の値を求めよ.
虚数解の６乗が実数
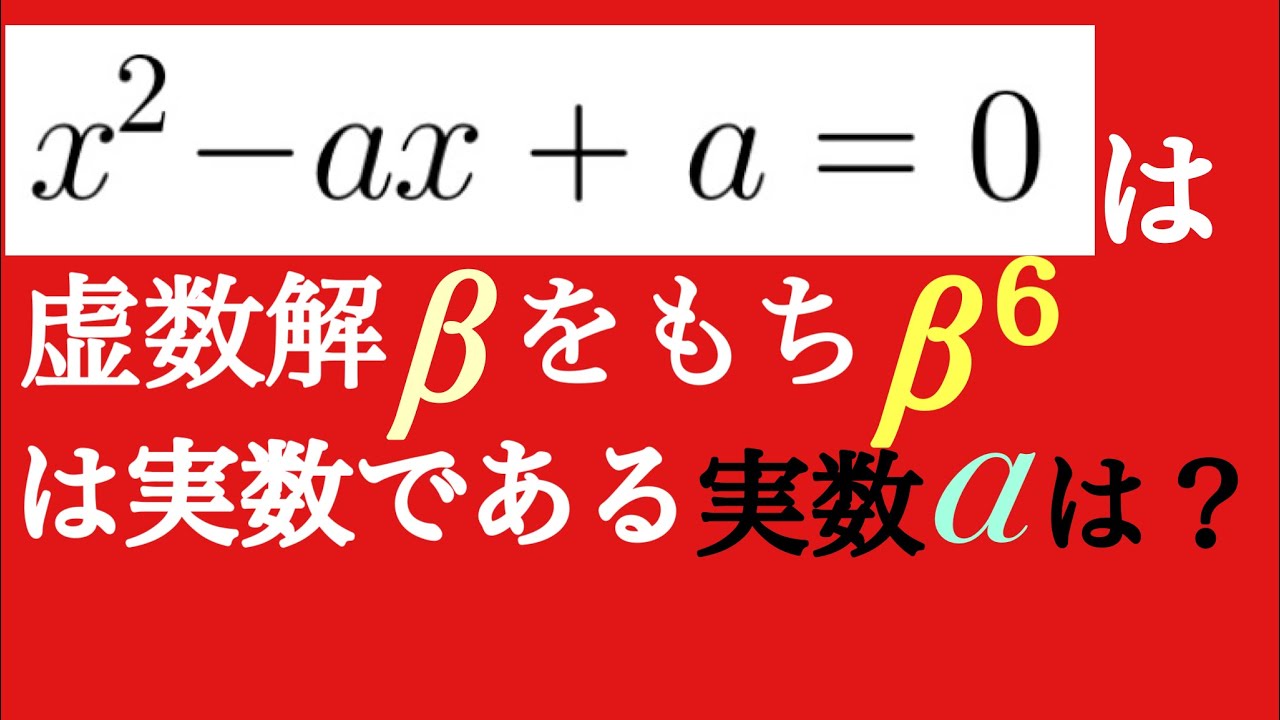
単元：
#数Ⅱ#複素数と方程式#複素数#解と判別式・解と係数の関係
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ x^2-ax+a=0$は虚数解$\beta$をもち$\beta^6$は実数である.
aの値を求めよ.
この動画を見る
$ x^2-ax+a=0$は虚数解$\beta$をもち$\beta^6$は実数である.
aの値を求めよ.
何乗しても実数にならない数
複素数の２次方程式・２通りの解法で
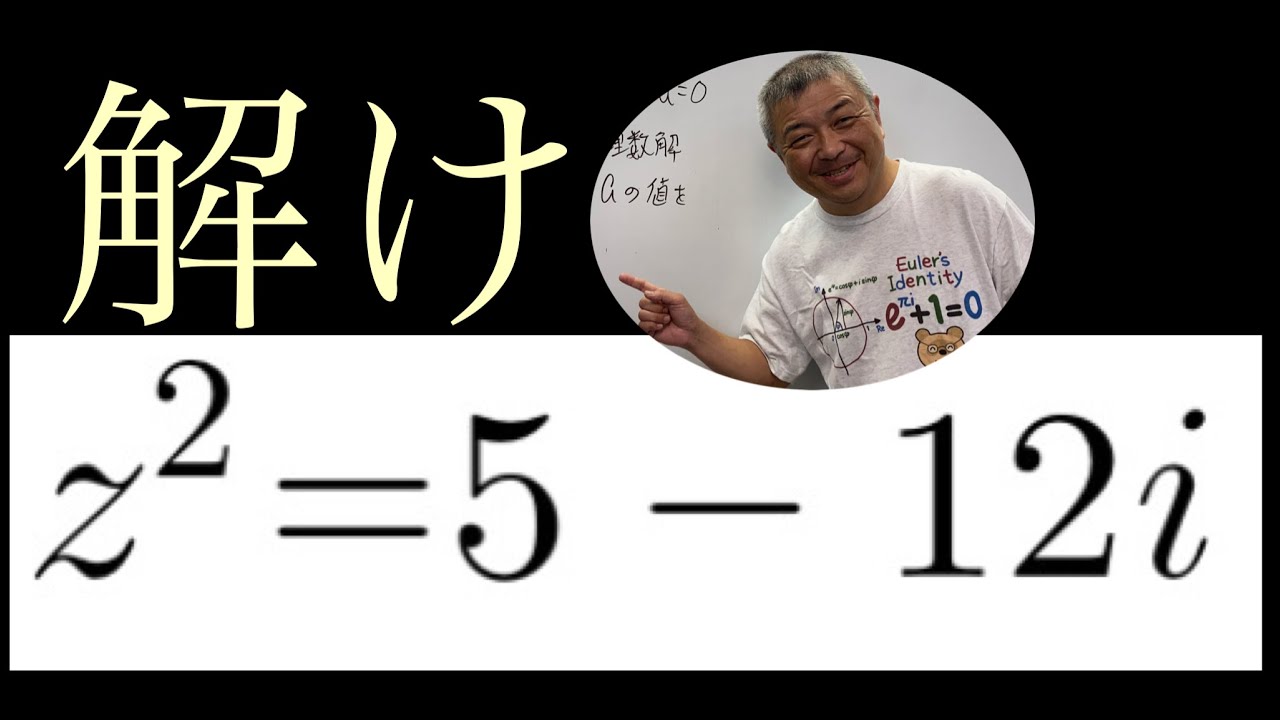
大学入試問題#228 愛知教育大学(2012) 3乗根の計算
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#数学(高校生)#愛知教育大学
指導講師：
ますただ
問題文全文(内容文)：
$\alpha=\sqrt[ 3 ]{ 5\sqrt{ 2 }+7 }-\sqrt[ 3 ]{ 5\sqrt{ 2 }-7 }$
（1）$\alpha^3$を$\alpha$で表せ
（2）$\alpha$は整数であることを示せ
出典：2012年愛知教育大学 入試問題
この動画を見る
$\alpha=\sqrt[ 3 ]{ 5\sqrt{ 2 }+7 }-\sqrt[ 3 ]{ 5\sqrt{ 2 }-7 }$
（1）$\alpha^3$を$\alpha$で表せ
（2）$\alpha$は整数であることを示せ
出典：2012年愛知教育大学 入試問題
４次方程式の解でできた式の値
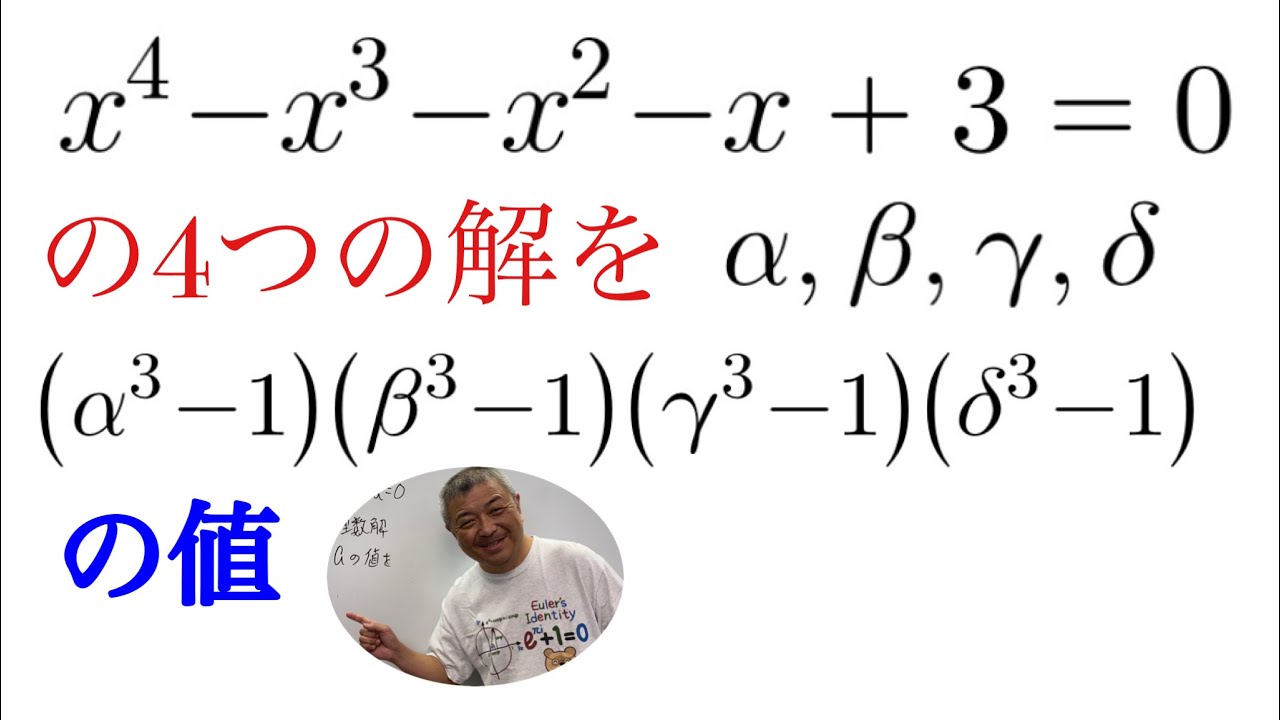
単元：
#数Ⅱ#複素数と方程式#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ x^4-x^3-x^2-x+3=0$の4つの解を$\alpha,\beta,\delta,\zeta$とする.
$(\alpha^3-1)(\beta^3-1)(\delta^3-1)(\zeta^3-1)$の値を求めよ.
この動画を見る
$ x^4-x^3-x^2-x+3=0$の4つの解を$\alpha,\beta,\delta,\zeta$とする.
$(\alpha^3-1)(\beta^3-1)(\delta^3-1)(\zeta^3-1)$の値を求めよ.
藤田医科大学 式の最小値
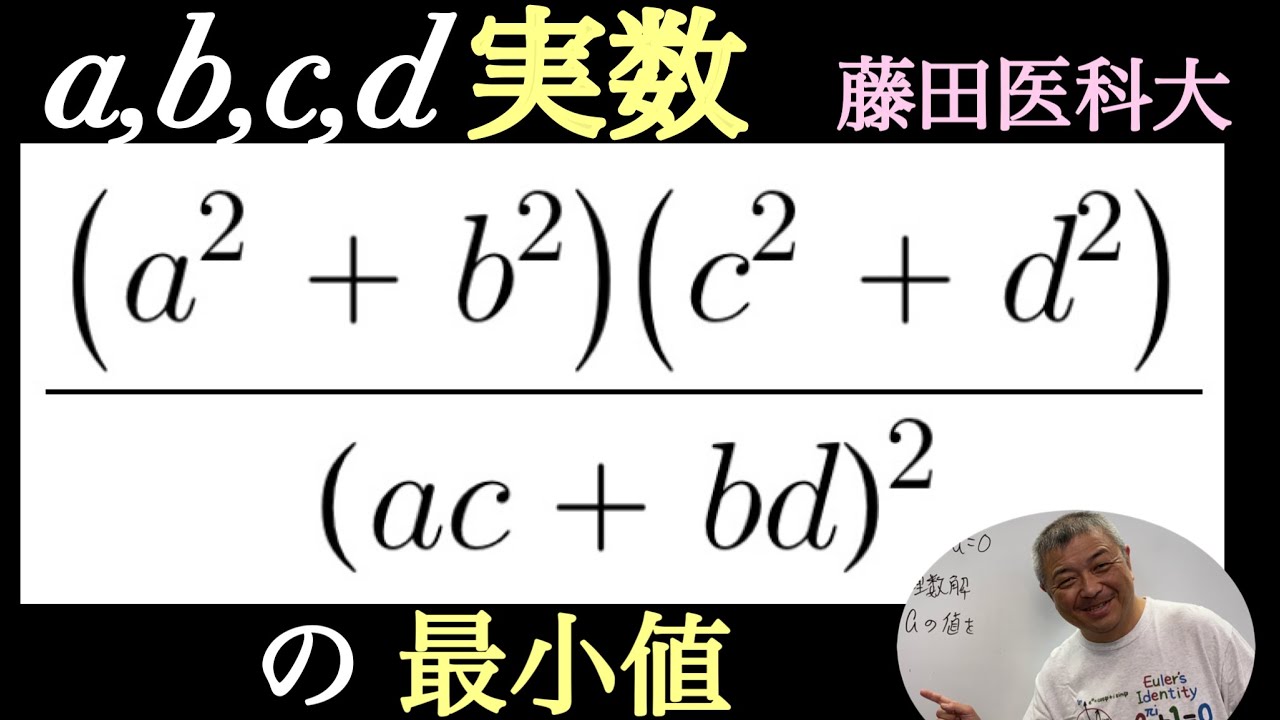
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#複素数#複素数平面#数学(高校生)#藤田医科大学#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ a,b,c,dは実数である.
$\dfrac{(a^2+b^2)(c^2+d^2)}{(ac+bd)^2}$の最小値を求めよ.
この動画を見る
$ a,b,c,dは実数である.
$\dfrac{(a^2+b^2)(c^2+d^2)}{(ac+bd)^2}$の最小値を求めよ.
立命館（文系）複素数の計算
単元：
#数Ⅱ#複素数と方程式#複素数#大学入試過去問(英語)#立命館大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x^6=1$の4つの虚数解のうちの1つを$\alpha$とする.
$(1-\alpha)(1-\alpha^3)(1-\alpha^5)$の値は$\Box$か$\Box$か.
立命館大(文系)過去問
この動画を見る
$x^6=1$の4つの虚数解のうちの1つを$\alpha$とする.
$(1-\alpha)(1-\alpha^3)(1-\alpha^5)$の値は$\Box$か$\Box$か.
立命館大(文系)過去問
早稲田（教育）見た目は数２か数３ 中身は中学入試
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#数列#早稲田大学#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ a_1=a_2=1,a_{n+2}=a_{n+1}+a_n,\displaystyle \sum_{n=1}^{2019} ia_n,$
$i$は虚数単位である.これを解け.
早稲田大(教育)過去問
この動画を見る
$ a_1=a_2=1,a_{n+2}=a_{n+1}+a_n,\displaystyle \sum_{n=1}^{2019} ia_n,$
$i$は虚数単位である.これを解け.
早稲田大(教育)過去問