剰余の定理・因数定理・組み立て除法と高次方程式
剰余の定理・因数定理・組み立て除法と高次方程式
3秒で答え出ます（剰余の定理）数II 割った余り
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$3x^2-2x+1$をx-1で割った余りは？
この動画を見る
$3x^2-2x+1$をx-1で割った余りは？
ざ・見掛け倒し 何次方程式？
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
実数解を求めよ.
$f(x)=x^2+6x+6$
$f(f(f(f(f(x)))))=0$
この動画を見る
実数解を求めよ.
$f(x)=x^2+6x+6$
$f(f(f(f(f(x)))))=0$
ちょっと工夫 連立三元方程式
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y+xy=26\\y+z+yz=41 \\
z+x+zx=125
\end{array}
\right.
\end{eqnarray}$
この動画を見る
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y+xy=26\\y+z+yz=41 \\
z+x+zx=125
\end{array}
\right.
\end{eqnarray}$
３次方程式の解の７乗の和
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x^3-x^2+1=0$の3つの解を$\alpha,\beta,\delta$とする.
$\alpha^7+\beta^7+\delta^7$の値を求めよ.
この動画を見る
$x^3-x^2+1=0$の3つの解を$\alpha,\beta,\delta$とする.
$\alpha^7+\beta^7+\delta^7$の値を求めよ.
高校入試だけど3次方程式 動画内に誘導あり！ 徳島文理（改）
単元：
#数学(中学生)#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$a^3+a^2-a-1$を因数分解
$(x+1)^3+(x+1)^2-x-2=0$を解け
徳島文理高等学校
この動画を見る
$a^3+a^2-a-1$を因数分解
$(x+1)^3+(x+1)^2-x-2=0$を解け
徳島文理高等学校
方程式を解け。
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$2^{x^{2}}=2x^2$を解け
（x:実数）
この動画を見る
$2^{x^{2}}=2x^2$を解け
（x:実数）
福田のわかった数学〜高校２年生012〜高次方程式の作成
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{II}$ 高次方程式
$\alpha=\sqrt{13}+\sqrt{9+2\sqrt{17}}+\sqrt{9-2\sqrt{17}}$
を解にもつ整数係数であり$x^4$の係数1の
4次方程式を作れ。また、残りの解を求めよ。
この動画を見る
数学$\textrm{II}$ 高次方程式
$\alpha=\sqrt{13}+\sqrt{9+2\sqrt{17}}+\sqrt{9-2\sqrt{17}}$
を解にもつ整数係数であり$x^4$の係数1の
4次方程式を作れ。また、残りの解を求めよ。
福田のわかった数学〜高校２年生第９回〜高次方程式の有理数解
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{II}$ 高次方程式
$a,b,c$を整数とするとき、3次方程式
$x^3+ax^2+bx+c=0$
が有理数解$s$をもつなら、$s$は整数である。
これを示せ。
この動画を見る
数学$\textrm{II}$ 高次方程式
$a,b,c$を整数とするとき、3次方程式
$x^3+ax^2+bx+c=0$
が有理数解$s$をもつなら、$s$は整数である。
これを示せ。
ただの４次方程式 その２
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを解け.
$x^4+2x^2-400x=9991$
この動画を見る
これを解け.
$x^4+2x^2-400x=9991$
ただの４次方程式
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
実数解を求めよ.
$(x-1)(x-3)(x-9)(x-27)=56x^2$
この動画を見る
実数解を求めよ.
$(x-1)(x-3)(x-9)(x-27)=56x^2$
慶應（経済）実数解を持たない４次方程式
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
次の$4$次方程式が実数解をもたない実数$a$の範囲を求めよ.
$x^4-ax^3+(-2a^2+a+4)x^2+(-2a^2+4a)x$
$+4a=0$
1999慶應(経)
この動画を見る
次の$4$次方程式が実数解をもたない実数$a$の範囲を求めよ.
$x^4-ax^3+(-2a^2+a+4)x^2+(-2a^2+4a)x$
$+4a=0$
1999慶應(経)
福田の１日１題わかった数学〜高校２年生第１回〜高次方程式
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{II}$ 高次方程式
3次方程式$x^3+ax+b=0$の
3つの解を$\alpha,\beta,\gamma$とし、
$t_n=\alpha^n+\beta^n+\gamma^n$
のとき、$at_5+bt_4$を$a,b$で表せ。
この動画を見る
数学$\textrm{II}$ 高次方程式
3次方程式$x^3+ax+b=0$の
3つの解を$\alpha,\beta,\gamma$とし、
$t_n=\alpha^n+\beta^n+\gamma^n$
のとき、$at_5+bt_4$を$a,b$で表せ。
ただの３次方程式 複数の解法で
数学「大学入試良問集」【2−4 剰余の定理•商と余り】を宇宙一わかりやすく
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#鹿児島大学
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
次の問いに答えよ。
（1）
$x$の整式$p(x)$を$x-3$で割った余りは$2,(x-2)^2$で割った余りは$x+1$である。
$p(x)$を$(x-2)^2$で割った商は$q(x)$とするとき、$q(x)$を$x-3$で割った余りを求めよ。
（2）
$p(x)$は（1）と同じ条件を満たすものとする。
このとき、$xp(x)$を$(x-3)(x-2)^2$で割った余りを求めよ。
この動画を見る
次の問いに答えよ。
（1）
$x$の整式$p(x)$を$x-3$で割った余りは$2,(x-2)^2$で割った余りは$x+1$である。
$p(x)$を$(x-2)^2$で割った商は$q(x)$とするとき、$q(x)$を$x-3$で割った余りを求めよ。
（2）
$p(x)$は（1）と同じ条件を満たすものとする。
このとき、$xp(x)$を$(x-3)(x-2)^2$で割った余りを求めよ。
数学「大学入試良問集」【2−2 高次方程式と解】を宇宙一わかりやすく
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
$\alpha=\displaystyle \frac{3+\sqrt{ 7 }\ i}{2}$とする。
ただし、$i$は虚数単位である。次の問いに答えよ。
（1）
$\alpha$を解にもつような2次方程式$x^2+px+q=0(p,q$は整数)を求めよ。
（2）
整数$a,b,c$を係数とする3次方程式$x^3+ax^2+bx+c=0$について、解の1つは$\alpha$であり、また$0 \leqq x \leqq 1$の範囲に実数解を1つもつとする。
このような整数の組$(a,b,c)$を全て求めよ。
この動画を見る
$\alpha=\displaystyle \frac{3+\sqrt{ 7 }\ i}{2}$とする。
ただし、$i$は虚数単位である。次の問いに答えよ。
（1）
$\alpha$を解にもつような2次方程式$x^2+px+q=0(p,q$は整数)を求めよ。
（2）
整数$a,b,c$を係数とする3次方程式$x^3+ax^2+bx+c=0$について、解の1つは$\alpha$であり、また$0 \leqq x \leqq 1$の範囲に実数解を1つもつとする。
このような整数の組$(a,b,c)$を全て求めよ。
方程式
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを解け.$x$を実数とする.
$\sqrt{x^2+3x+2}-\sqrt{x^2+2x+5}=3-x$
この動画を見る
これを解け.$x$を実数とする.
$\sqrt{x^2+3x+2}-\sqrt{x^2+2x+5}=3-x$
2021同志社大 ４次方程式４つの虚数解
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$c$は実数であり,定数である.
$x^4+cx^3+cx^2+cx+1=0$の$4$つの解がすべて虚数となる.$c$の必要十分条件である.
$4$つの虚数解が複素平面上で正方形になる$c$の値を求めよ.
2021同志社過去問
この動画を見る
$c$は実数であり,定数である.
$x^4+cx^3+cx^2+cx+1=0$の$4$つの解がすべて虚数となる.$c$の必要十分条件である.
$4$つの虚数解が複素平面上で正方形になる$c$の値を求めよ.
2021同志社過去問
2021早稲田 ４次方程式の解
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x^4+5x^3-3x^2+4x+2=0$は$\dfrac{1+\sqrt3 i}{2}$を解にもつ.
実数解を求めよ.
2021早稲田(教)
この動画を見る
$x^4+5x^3-3x^2+4x+2=0$は$\dfrac{1+\sqrt3 i}{2}$を解にもつ.
実数解を求めよ.
2021早稲田(教)
明治大 ３倍角の公式と３次方程式
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$3$倍角の公式を利用して$x^3-3x-1=0$の$3$つの解を$cos$を用いて答えよ.
2020明治大過去問
この動画を見る
$3$倍角の公式を利用して$x^3-3x-1=0$の$3$つの解を$cos$を用いて答えよ.
2020明治大過去問
2021東京医科大学 そんなやり方もあるか！４次方程式の解
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x^4+11x^3+31x^2+11x+1=0$の$4$つの解を$\alpha,\beta,\delta,\zeta$とする.
$x+\dfrac{1}{x}=y$として,$y$の方程式を求めよ.
①$\dfrac{1}{\alpha}+\dfrac{1}{\beta}+\dfrac{1}{\delta}+\dfrac{1}{\zeta}$
②$\alpha^2+\beta^2+\delta^2+\zeta^2$
③$\alpha^3+\beta^3+\delta^3+\zeta^3$
2021東京医科大過去問
この動画を見る
$x^4+11x^3+31x^2+11x+1=0$の$4$つの解を$\alpha,\beta,\delta,\zeta$とする.
$x+\dfrac{1}{x}=y$として,$y$の方程式を求めよ.
①$\dfrac{1}{\alpha}+\dfrac{1}{\beta}+\dfrac{1}{\delta}+\dfrac{1}{\zeta}$
②$\alpha^2+\beta^2+\delta^2+\zeta^2$
③$\alpha^3+\beta^3+\delta^3+\zeta^3$
2021東京医科大過去問
2021久留米大（医）三次方程式と複素平面
単元：
#数Ⅱ#複素数と方程式#複素数平面#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#複素数平面#数学(高校生)#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a\lt 0,a,b$は実数である.
$x^3-2(a+1)x^2+(5a^2+1)x+b-0$の3つの解は$2,z,\omega$である.
複素平面上で3点,$2,z,\omega$を結ぶと直角二等辺三角形になる.
$a,b,z,\omega$を求めよ.
2021久留米(医)
この動画を見る
$a\lt 0,a,b$は実数である.
$x^3-2(a+1)x^2+(5a^2+1)x+b-0$の3つの解は$2,z,\omega$である.
複素平面上で3点,$2,z,\omega$を結ぶと直角二等辺三角形になる.
$a,b,z,\omega$を求めよ.
2021久留米(医)
式の値
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x+\dfrac{1}{x}=\sqrt3$のとき,$x^{18}+x^{12}+x^6+1$の値を求めよ.
この動画を見る
$x+\dfrac{1}{x}=\sqrt3$のとき,$x^{18}+x^{12}+x^6+1$の値を求めよ.
３次方程式
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを解け.
$126x^3-3x^2+3x-1=0$
この動画を見る
これを解け.
$126x^3-3x^2+3x-1=0$
４次方程式
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$4$つの解を求めよ.
$(x-7.5)^4+(x-8.5)^4=1$
この動画を見る
$4$つの解を求めよ.
$(x-7.5)^4+(x-8.5)^4=1$
4次方程式
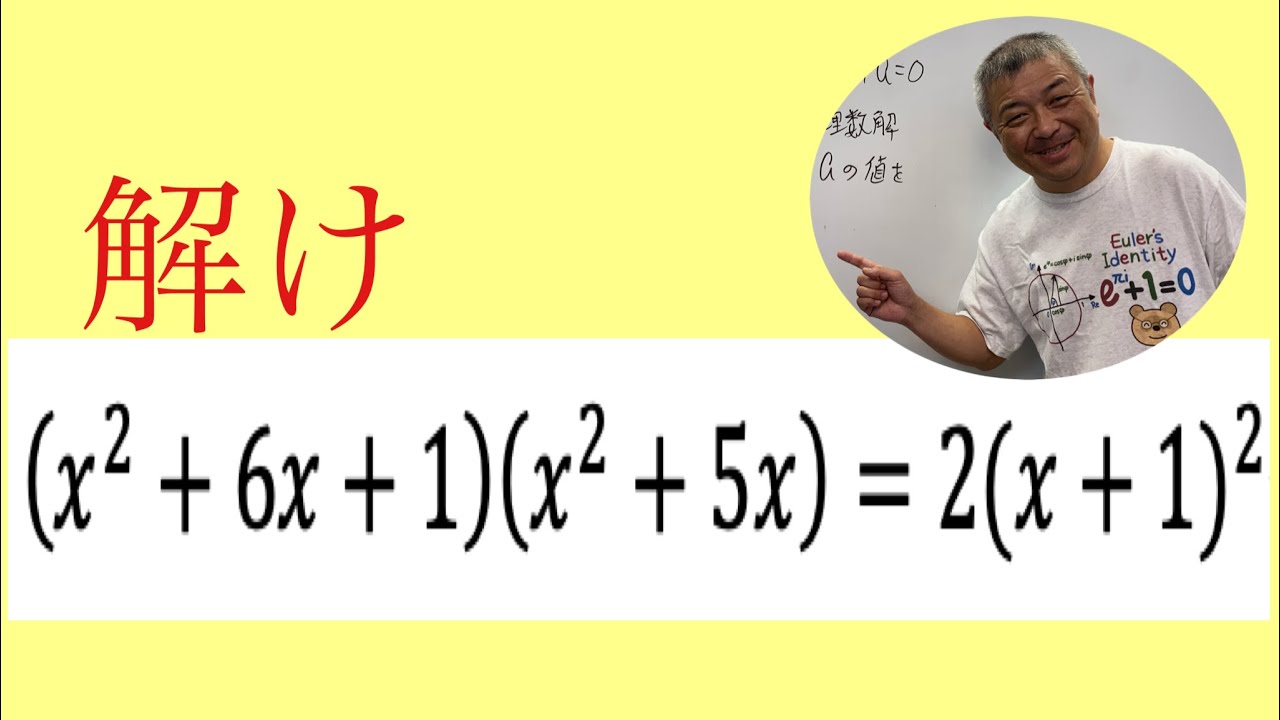
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを解け.
$(x^2+2x-6)^2+2(x^2+2x-6)-6=x$
この動画を見る
これを解け.
$(x^2+2x-6)^2+2(x^2+2x-6)-6=x$
剰余
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$111^{2021}$を$1111$で割った余りを求めよ.
この動画を見る
$111^{2021}$を$1111$で割った余りを求めよ.
武蔵工業大 ６次方程式の解
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$z^6+z^3+1=0$を満たす複素数$z$の偏角$\theta$をすべて求めよ.
2005武蔵工業大過去問
この動画を見る
$z^6+z^3+1=0$を満たす複素数$z$の偏角$\theta$をすべて求めよ.
2005武蔵工業大過去問
一橋大 整数解をもつ三次方程式
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$k$は整数である.
$x^3-13x+k=0$は$3$つの異なる整数解をもつ.$k$とこれらの整数解をすべて求めよ.
一橋大過去問
この動画を見る
$k$は整数である.
$x^3-13x+k=0$は$3$つの異なる整数解をもつ.$k$とこれらの整数解をすべて求めよ.
一橋大過去問
一橋大 三次方程式
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a,b,m$は整数である.$(b \neq 0)$
$f(x)=x^3+8x^2+mx+60$
$f(a+bi)=0$を満たすものが存在するような$m$を求めよ.そのときの解も求めよ.
2007一橋大過去問
この動画を見る
$a,b,m$は整数である.$(b \neq 0)$
$f(x)=x^3+8x^2+mx+60$
$f(a+bi)=0$を満たすものが存在するような$m$を求めよ.そのときの解も求めよ.
2007一橋大過去問
横浜市立大（医）３次方程式の虚数解の絶対値
単元：
#数Ⅰ#数Ⅱ#数と式#複素数と方程式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#一次不等式（不等式・絶対値のある方程式・不等式）#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x^3-x^2-x+k=0(k\gt 1)$である.
(1)実数解は1個であることを示せ.
(2)3つの解の絶対値はいずれも1より大きいことを示せ.
横浜市立(医)過去問
この動画を見る
$x^3-x^2-x+k=0(k\gt 1)$である.
(1)実数解は1個であることを示せ.
(2)3つの解の絶対値はいずれも1より大きいことを示せ.
横浜市立(医)過去問