 図形と方程式
図形と方程式
 図形と方程式
図形と方程式
福田の数学〜東京大学2025文系第2問〜三角形の3頂点を中心とする3つの円で3辺を含む条件と三角形を含む条件

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
平面上で$AB=AC=1$である
二等辺三角形$ABC$を考える。
正の実数$r$に対し、$A,B,C$それぞれを中心とする
半径$r$の円$3$つを合わせた領域を$D_r$とする。
ただし、この問いでは、
三角形と円は周とその内部からなるものとする。
辺$AB,AC,BC$がすべて$D_r$に
含まれるような最小の$r$を$s$、
三角形$ABC$が
$D_r$に含まれるような最小の$r$を$t$と表す。
(1)$\angle BAC=\dfrac{\pi}{3}$のとき、$s$と$t$を求めよ。
(2)$\angle BAC=\dfrac{2\pi}{3}$のとき、$s$と$t$を求めよ。
(3)$0\lt \theta \lt \pi$を満たす$\theta$に対して、
$\angle BAC=\theta$のとき、$s$と$t$を$\theta$を用いて表せ。
$2025$年東京大学文系過去問題
この動画を見る
$\boxed{2}$
平面上で$AB=AC=1$である
二等辺三角形$ABC$を考える。
正の実数$r$に対し、$A,B,C$それぞれを中心とする
半径$r$の円$3$つを合わせた領域を$D_r$とする。
ただし、この問いでは、
三角形と円は周とその内部からなるものとする。
辺$AB,AC,BC$がすべて$D_r$に
含まれるような最小の$r$を$s$、
三角形$ABC$が
$D_r$に含まれるような最小の$r$を$t$と表す。
(1)$\angle BAC=\dfrac{\pi}{3}$のとき、$s$と$t$を求めよ。
(2)$\angle BAC=\dfrac{2\pi}{3}$のとき、$s$と$t$を求めよ。
(3)$0\lt \theta \lt \pi$を満たす$\theta$に対して、
$\angle BAC=\theta$のとき、$s$と$t$を$\theta$を用いて表せ。
$2025$年東京大学文系過去問題
福田の数学〜東京大学2025理系第6問〜複素数平面上の点の軌跡と実部の最大最小

単元:
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#軌跡と領域#複素数平面#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{6}$
複素数平面上の点$\dfrac{1}{2}$を中心とする
半径$\dfrac{1}{2}$の円の周から原点を除いた曲線を
$C$とする。
(1)曲線$C$上の複素数$z$に対し、$\dfrac{1}{z}$の実部は
$1$であることを示せ。
(2)$\alpha,\beta$を曲線$C$上の相異なる複素数とするとき、
$\dfrac{1}{alpha^2}+\dfrac{1}{\beta^2}$がとりうる範囲を
複素数平面上に図示せよ。
(3)$\nu $を(2)で求めた範囲に属さない複素数とするとき、
$\dfrac{1}{\gamma}$の実部がとりうる値の
最大値と最小値を求めよ。
$2025$年東京大学理系過去問題
この動画を見る
$\boxed{6}$
複素数平面上の点$\dfrac{1}{2}$を中心とする
半径$\dfrac{1}{2}$の円の周から原点を除いた曲線を
$C$とする。
(1)曲線$C$上の複素数$z$に対し、$\dfrac{1}{z}$の実部は
$1$であることを示せ。
(2)$\alpha,\beta$を曲線$C$上の相異なる複素数とするとき、
$\dfrac{1}{alpha^2}+\dfrac{1}{\beta^2}$がとりうる範囲を
複素数平面上に図示せよ。
(3)$\nu $を(2)で求めた範囲に属さない複素数とするとき、
$\dfrac{1}{\gamma}$の実部がとりうる値の
最大値と最小値を求めよ。
$2025$年東京大学理系過去問題
福田の数学〜東京大学2025理系第3問〜平行四辺形を囲む長方形の面積の最大値

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed {3} $
平面四辺形$ABCD$において、
$\angle ABC = \dfrac {\pi} {6} , AB = a , BC = b , a \leqq b$とする。
次の条件を満たす長方形$EFGH$を考え、
その面積を$S$とする。
条件:点$A,B,C,D$はそれぞれ
$\quad$辺$EF,FG,GH,HE$上にある。
$\quad$ただし、辺はその両端の点も含むものとする。
(1)$\angle BCG=\theta$とするとき、
$S$を$a,b,\theta$を用いて表せ。
(2)$S$とりうる値の最大値を$a,b$を用いて表せ。
$2025$年東京大学理系過去問題
この動画を見る
$\boxed {3} $
平面四辺形$ABCD$において、
$\angle ABC = \dfrac {\pi} {6} , AB = a , BC = b , a \leqq b$とする。
次の条件を満たす長方形$EFGH$を考え、
その面積を$S$とする。
条件:点$A,B,C,D$はそれぞれ
$\quad$辺$EF,FG,GH,HE$上にある。
$\quad$ただし、辺はその両端の点も含むものとする。
(1)$\angle BCG=\theta$とするとき、
$S$を$a,b,\theta$を用いて表せ。
(2)$S$とりうる値の最大値を$a,b$を用いて表せ。
$2025$年東京大学理系過去問題
福田のおもしろ数学405〜√2+√3が円周率πよりも大きいことの証明

function : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study #test
単元:
#数Ⅱ#軌跡と領域#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2点$A(1,7),B(6,-2)$
$y=ax+2とABが共有する点を持つようaの値の範囲を求めよ$
この動画を見る
2点$A(1,7),B(6,-2)$
$y=ax+2とABが共有する点を持つようaの値の範囲を求めよ$
軌跡の難問!軌跡は苦手意識を持った人も多いので差がつきます【東京大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
長さlの線分が、その両端を放物線y=x^2にのせて動く。この線分の中点Mがx軸に最も近い場合のMの座標を求めよ。ただし、l≧1とする。
この動画を見る
長さlの線分が、その両端を放物線y=x^2にのせて動く。この線分の中点Mがx軸に最も近い場合のMの座標を求めよ。ただし、l≧1とする。
福田の数学〜早稲田大学2024社会科学部第1問〜領域における最大最小

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$$連立不等式
y≦-\frac{2}{3}x+4, y≧x-1,x≧0,y≧0
の表す領域をDとする。点(x,y)が領域Dを動くとき、次の問いに答えよ。
$$(1)領域Dを座標平面上に図示せよ。$$
$$(2)-2x+yの最大値と、そのときのx,yの値を求めよ。$$
$$(3)2x+yの最大値と、そのときのx,yの値を求めよ。$$
$$(4)aがすべての実数を動くとき、ax+yの最大値をaで分類せよ。$$
この動画を見る
$$連立不等式
y≦-\frac{2}{3}x+4, y≧x-1,x≧0,y≧0
の表す領域をDとする。点(x,y)が領域Dを動くとき、次の問いに答えよ。
$$(1)領域Dを座標平面上に図示せよ。$$
$$(2)-2x+yの最大値と、そのときのx,yの値を求めよ。$$
$$(3)2x+yの最大値と、そのときのx,yの値を求めよ。$$
$$(4)aがすべての実数を動くとき、ax+yの最大値をaで分類せよ。$$
福田の数学〜早稲田大学2024教育学部第1問(4)〜領域と奇跡

単元:
#数Ⅰ#数Ⅱ#2次関数#図形と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$
\begin{eqnarray}
\fcolorbox{#000}{ #fff }{$1$} \ (4) \\
\end{eqnarray}
$
$xy$平面上に3点$O(0,0),A(1,0),B(1,1)$をとる。点$(x,y)$が三角形$OAB$の周および内部を動くときに点$(x+y,xy)$が動く範囲の面積を求めよ。
この動画を見る
$
\begin{eqnarray}
\fcolorbox{#000}{ #fff }{$1$} \ (4) \\
\end{eqnarray}
$
$xy$平面上に3点$O(0,0),A(1,0),B(1,1)$をとる。点$(x,y)$が三角形$OAB$の周および内部を動くときに点$(x+y,xy)$が動く範囲の面積を求めよ。
福田の数学〜慶應義塾大学2024総合政策学部第5問〜線形計画法

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
領域 $D$ $ \begin{eqnarray}
\left\{
\begin{array}{l}
x^2 + y^2 \leq 4 \\
(\sqrt{2}x^2 - 2y) (x-2y+2) \leq 0
\end{array}
\right.
\end{eqnarray} $
を点 $(x,y)$ が動くとき $x-2y$ の最大値、最小値を求めよ。
$ax+y$ が $(\frac{6}{5}, \frac{8}{5})$ で最大となる $a$ の範囲は?
そのときの $ax+y$ のとりうる範囲は?
この動画を見る
領域 $D$ $ \begin{eqnarray}
\left\{
\begin{array}{l}
x^2 + y^2 \leq 4 \\
(\sqrt{2}x^2 - 2y) (x-2y+2) \leq 0
\end{array}
\right.
\end{eqnarray} $
を点 $(x,y)$ が動くとき $x-2y$ の最大値、最小値を求めよ。
$ax+y$ が $(\frac{6}{5}, \frac{8}{5})$ で最大となる $a$ の範囲は?
そのときの $ax+y$ のとりうる範囲は?
福田の数学〜上智大学2024TEAP利用型文系第3問(4)〜線分の通過範囲の面積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#軌跡と領域#学校別大学入試過去問解説(数学)#不定積分・定積分#面積、体積#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}(4)$座標平面上で放物線$y=x^2$上の点P$(t,t^2)(0 \leqq t \leqq 1)$における接線$y=-(x+1)^2$の二つの共有点の中点をQとする。ただし、共有点が1つの場合は、その共有点をQとする。Qの座標は$(\boxed{ユ}t+\boxed{ヨ}
,\boxed{ラ}t^2+\boxed{リ}t+\boxed{ル})$である。
tが$0 \leqq t \leqq1$の範囲を動くとき線分PQが動いてできる図形の面積は$\frac{\boxed{レ}}{\boxed{ロ}}$である
この動画を見る
$\boxed{2}(4)$座標平面上で放物線$y=x^2$上の点P$(t,t^2)(0 \leqq t \leqq 1)$における接線$y=-(x+1)^2$の二つの共有点の中点をQとする。ただし、共有点が1つの場合は、その共有点をQとする。Qの座標は$(\boxed{ユ}t+\boxed{ヨ}
,\boxed{ラ}t^2+\boxed{リ}t+\boxed{ル})$である。
tが$0 \leqq t \leqq1$の範囲を動くとき線分PQが動いてできる図形の面積は$\frac{\boxed{レ}}{\boxed{ロ}}$である
福田の数学〜上智大学2024TEAP利用型文系第3問(1)〜対数指数不等式と領域に含まれる格子点の個数

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}(1)$整数の組$(x,y)$で条件\begin{eqnarray}
\left\{
\begin{array}{l}
\log_{ \frac{π}{4} } y \lt log_{\frac{1}{2}}(x-1) \\
2^{y-1} \lt 8^x
\end{array}
\right.
\end{eqnarray}
を満たすものは全部で$\boxed{ヒ}$個ある。
この動画を見る
$\boxed{3}(1)$整数の組$(x,y)$で条件\begin{eqnarray}
\left\{
\begin{array}{l}
\log_{ \frac{π}{4} } y \lt log_{\frac{1}{2}}(x-1) \\
2^{y-1} \lt 8^x
\end{array}
\right.
\end{eqnarray}
を満たすものは全部で$\boxed{ヒ}$個ある。
福田の数学〜青山学院大学2024理工学部第3問〜2次方程式の解の条件と領域

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$p,qを実数の定数とし、xについての2次方程式$
$x^2+px+q=0 \cdots (\ast)$
を考える。2次方程式$(\ast)$が異なる2つの実数解$\alpha,\beta(\alpha\lt\beta)$をもち、かつ$\alpha,\beta$が
$\displaystyle \frac{\alpha}{2}\leqq\beta\leqq2\alpha$
を満たすとき、以下の問いに答えよ。
(1)点$(p,q)$のとりうる範囲を座標平面上に図示せよ。
(2)$\alpha,\beta$がさらに
$(\alpha+1)(\beta+1)\leqq 3$
を満たすとする。このとき、pの値が最小となるような$(p,q)$を求めよ。
(3)(2)で求めた$(p,q)$に対して、2次方程式$(\ast)$の解$\alpha,\beta$を求めよ。
この動画を見る
$p,qを実数の定数とし、xについての2次方程式$
$x^2+px+q=0 \cdots (\ast)$
を考える。2次方程式$(\ast)$が異なる2つの実数解$\alpha,\beta(\alpha\lt\beta)$をもち、かつ$\alpha,\beta$が
$\displaystyle \frac{\alpha}{2}\leqq\beta\leqq2\alpha$
を満たすとき、以下の問いに答えよ。
(1)点$(p,q)$のとりうる範囲を座標平面上に図示せよ。
(2)$\alpha,\beta$がさらに
$(\alpha+1)(\beta+1)\leqq 3$
を満たすとする。このとき、pの値が最小となるような$(p,q)$を求めよ。
(3)(2)で求めた$(p,q)$に対して、2次方程式$(\ast)$の解$\alpha,\beta$を求めよ。
福田の数学〜明治大学2024理工学部第3問〜放物線と折れ線の位置関係
単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#2次関数とグラフ#図形と方程式#点と直線#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
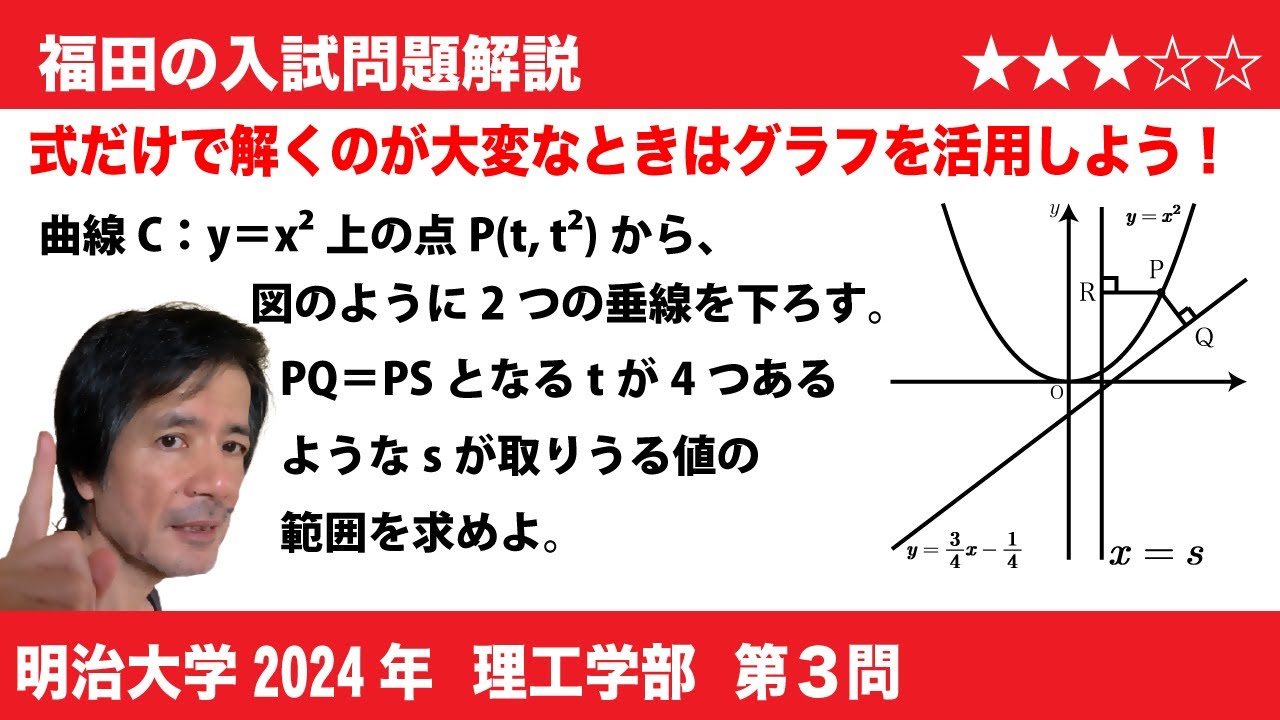
$\boxed{3}$座標平面上も曲線$y=x^2$を$C$、直線$y=\frac{3}{4}x-\frac{1}{4}$を$l$とする。$s$を実数とし、直線$x=s$を$m$とする。曲線$C$上の点$P(t,t^2)$に対し、$P$から直線$l$との交点$Q$とする。また、$P$から直線$m$に下ろした垂線と$m$との交点を$R$とする。
$(1)$点$P$と点$Q$の距離$PQ$を$l$の式で表すと、$PQ=\boxed{け}$である。
$(2)$点$P$と点$R$の距離$PR$を$s$と$l$の式で表すと、$PR=\boxed{こ}$である。
$(3)PQ$は$t=\boxed{さ}$のとき、最小値$\boxed{し}$をとる。
$(4)s=\frac{2}{5}$のとき、$PQ=PR$となる点$P$をすべて求め、その$x$座標を小さい順に並べると$\boxed{す}$となる。
$(5)$実数$s$を固定したとき、$PQ=PR$となるような点$P$の個数を$N_s$とする。$N_s=4$となる$s$の範囲は$\boxed{せ}$
この動画を見る
$\boxed{3}$座標平面上も曲線$y=x^2$を$C$、直線$y=\frac{3}{4}x-\frac{1}{4}$を$l$とする。$s$を実数とし、直線$x=s$を$m$とする。曲線$C$上の点$P(t,t^2)$に対し、$P$から直線$l$との交点$Q$とする。また、$P$から直線$m$に下ろした垂線と$m$との交点を$R$とする。
$(1)$点$P$と点$Q$の距離$PQ$を$l$の式で表すと、$PQ=\boxed{け}$である。
$(2)$点$P$と点$R$の距離$PR$を$s$と$l$の式で表すと、$PR=\boxed{こ}$である。
$(3)PQ$は$t=\boxed{さ}$のとき、最小値$\boxed{し}$をとる。
$(4)s=\frac{2}{5}$のとき、$PQ=PR$となる点$P$をすべて求め、その$x$座標を小さい順に並べると$\boxed{す}$となる。
$(5)$実数$s$を固定したとき、$PQ=PR$となるような点$P$の個数を$N_s$とする。$N_s=4$となる$s$の範囲は$\boxed{せ}$
定点の座標を求めよ 高校数学
定点の座標を求めよ 高校数学

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
定数kがどんな値を取っても
直線$kx-y+5k=0$が通る
定点の座標を求めよ
この動画を見る
定数kがどんな値を取っても
直線$kx-y+5k=0$が通る
定点の座標を求めよ
福田の数学〜浜松医科大学2024医学部第4問〜直線に関する対称点と絶対不等式

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#軌跡と領域#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
正方形の紙 $\alpha$ に下図のように座標軸をとり、 $2$ 点 $\mathrm{A}(0,1),$ $\mathrm{B}(-2,0)$ および、 $2$ 直線 $y=-1,$$x=2$ を定める(図は動画内参照)。以下この $2$ 直線をそれぞれ $l_1,l_2$ と表す。このとき、点 $\mathrm{A}$ を直線 $l_1$ 上の点 $\mathrm{A'}(a,-1)$ に重ねて $\alpha$ を折ったときにできる折り目の直線を $l_3(a)$ とする。ただし、 $\mathrm{A'}$ は $\alpha$ 上にとることとし、また、以下の操作はすべて $\alpha$ 上で行うこととする。以下の問いに答えよ。
$(1)$ 直線 $l_3(a)$ の方程式を、 $a$ を用いて表せ。
$(2)$ 点 $\mathrm{A}$ が直線 $l_1$ 上に位置するように $\alpha$ を折り、そのときできる折り目により、 $\alpha$ を $2$ つに分割する。このとき、点 $\mathrm{A}$ が直線 $l_1$ 上に位置するような、どのような折り方をしても、その折り目に対して常に点 $\mathrm{A}$ と同じ側にある点全体の集合の境界線の方程式を求めよ。
$(3)$ 点 $\mathrm{A}$ が直線 $l_1$ 上の点 $\mathrm{A'}$ に重なると同時に、点 $\mathrm{B}$ が直線 $l_2$ 上の点に重なるように $\alpha$ を折るとき、 $a$ の値を求めよ。
この動画を見る
正方形の紙 $\alpha$ に下図のように座標軸をとり、 $2$ 点 $\mathrm{A}(0,1),$ $\mathrm{B}(-2,0)$ および、 $2$ 直線 $y=-1,$$x=2$ を定める(図は動画内参照)。以下この $2$ 直線をそれぞれ $l_1,l_2$ と表す。このとき、点 $\mathrm{A}$ を直線 $l_1$ 上の点 $\mathrm{A'}(a,-1)$ に重ねて $\alpha$ を折ったときにできる折り目の直線を $l_3(a)$ とする。ただし、 $\mathrm{A'}$ は $\alpha$ 上にとることとし、また、以下の操作はすべて $\alpha$ 上で行うこととする。以下の問いに答えよ。
$(1)$ 直線 $l_3(a)$ の方程式を、 $a$ を用いて表せ。
$(2)$ 点 $\mathrm{A}$ が直線 $l_1$ 上に位置するように $\alpha$ を折り、そのときできる折り目により、 $\alpha$ を $2$ つに分割する。このとき、点 $\mathrm{A}$ が直線 $l_1$ 上に位置するような、どのような折り方をしても、その折り目に対して常に点 $\mathrm{A}$ と同じ側にある点全体の集合の境界線の方程式を求めよ。
$(3)$ 点 $\mathrm{A}$ が直線 $l_1$ 上の点 $\mathrm{A'}$ に重なると同時に、点 $\mathrm{B}$ が直線 $l_2$ 上の点に重なるように $\alpha$ を折るとき、 $a$ の値を求めよ。
福田の数学〜筑波大学2024理系第2問〜対数不等式が表す領域と面積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#指数関数と対数関数#微分法と積分法#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学
指導講師:
福田次郎
問題文全文(内容文):
(1)$x\gt 1, y\gt 1$のとき、$\log_{ x } y+\log_{ y } x\geqq 2$を示せ。
(2)座標平面において、連立不等式$x\gt 1, y\gt 1, \log_{ x } y+\log_{ y } x\lt \frac{5}{2}$の表す領域を図示せよ。
(3)(2)の領域の中で$x^2+y^2\lt 12$を満たす部分に境界線を含めた図形を$\mathit{D}$とする。$\mathit{D}$の面積を求めよ。
この動画を見る
(1)$x\gt 1, y\gt 1$のとき、$\log_{ x } y+\log_{ y } x\geqq 2$を示せ。
(2)座標平面において、連立不等式$x\gt 1, y\gt 1, \log_{ x } y+\log_{ y } x\lt \frac{5}{2}$の表す領域を図示せよ。
(3)(2)の領域の中で$x^2+y^2\lt 12$を満たす部分に境界線を含めた図形を$\mathit{D}$とする。$\mathit{D}$の面積を求めよ。
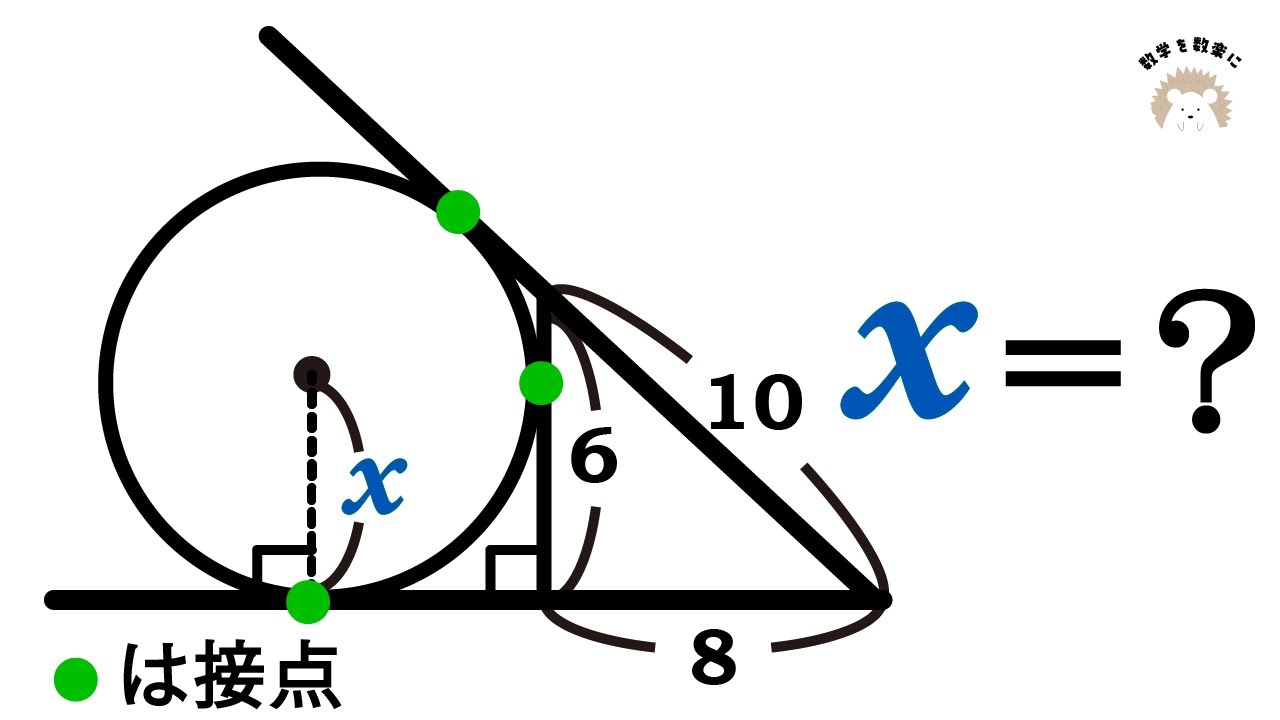
傍接円の半径を求める 解き方2通り
【高校数学】線形計画法(円と直線パターン)の考え方【数学のコツ】

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$x^2+y^2≦1, y≧0$のとき、$-2x+y$の最大値、最小値を求めよ。
この動画を見る
$x^2+y^2≦1, y≧0$のとき、$-2x+y$の最大値、最小値を求めよ。
【高校数学】円と直線が接するときの2パターンの考え方【数学のコツ】

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の円と直線が接するときのkの値と接点の座標を求めよ。
$x^2+y^2=4, y=x+k$
この動画を見る
次の円と直線が接するときのkの値と接点の座標を求めよ。
$x^2+y^2=4, y=x+k$
福田の数学〜神戸大学2024年理系第2問〜放物線と2接線た作る三角形の重心の軌跡

単元:
#数Ⅱ#図形と方程式#微分法と積分法#円と方程式#接線と増減表・最大値・最小値#面積、体積#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ $a$, $b$, $c$は実数で、$a$≠0とする。放物線$C$と直線$l_1$, $l_2$をそれぞれ
$C$:$y$=$ax^2$+$bx$+$c$
$l_1$:$y$=$-3x$+3
$l_2$:$y$=$x$+3
で定める。$l_1$, $l_2$がともに$C$と接するとき、以下の問いに答えよ。
(1)$b$を求めよ。$c$を$a$を用いて表せ。
(2)$C$が$x$軸と異なる2点で交わるとき、$\displaystyle\frac{1}{a}$のとりうる値の範囲を求めよ。
(3)$C$と$l_1$の接点をP、$C$と$l_2$の接点をQ、放物線$C$の頂点をRとする。$a$が(2)の条件を満たしながら動くとき、$\triangle PQR$の重心Gの軌跡を求めよ。
この動画を見る
$\Large\boxed{3}$ $a$, $b$, $c$は実数で、$a$≠0とする。放物線$C$と直線$l_1$, $l_2$をそれぞれ
$C$:$y$=$ax^2$+$bx$+$c$
$l_1$:$y$=$-3x$+3
$l_2$:$y$=$x$+3
で定める。$l_1$, $l_2$がともに$C$と接するとき、以下の問いに答えよ。
(1)$b$を求めよ。$c$を$a$を用いて表せ。
(2)$C$が$x$軸と異なる2点で交わるとき、$\displaystyle\frac{1}{a}$のとりうる値の範囲を求めよ。
(3)$C$と$l_1$の接点をP、$C$と$l_2$の接点をQ、放物線$C$の頂点をRとする。$a$が(2)の条件を満たしながら動くとき、$\triangle PQR$の重心Gの軌跡を求めよ。
福田のおもしろ数学154〜2変数関数の最大最小

単元:
#数Ⅱ#図形と方程式#円と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x$, $y$が実数で、$x^2$+$(y-1)^2$≦1 のとき、$z$=$\displaystyle\frac{x+y+1}{x-y+3}$ の最大値、最小値を求めよ。
この動画を見る
$x$, $y$が実数で、$x^2$+$(y-1)^2$≦1 のとき、$z$=$\displaystyle\frac{x+y+1}{x-y+3}$ の最大値、最小値を求めよ。
福田のおもしろ数学148〜円の面積
単元:
#数A#数Ⅱ#図形の性質#図形と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
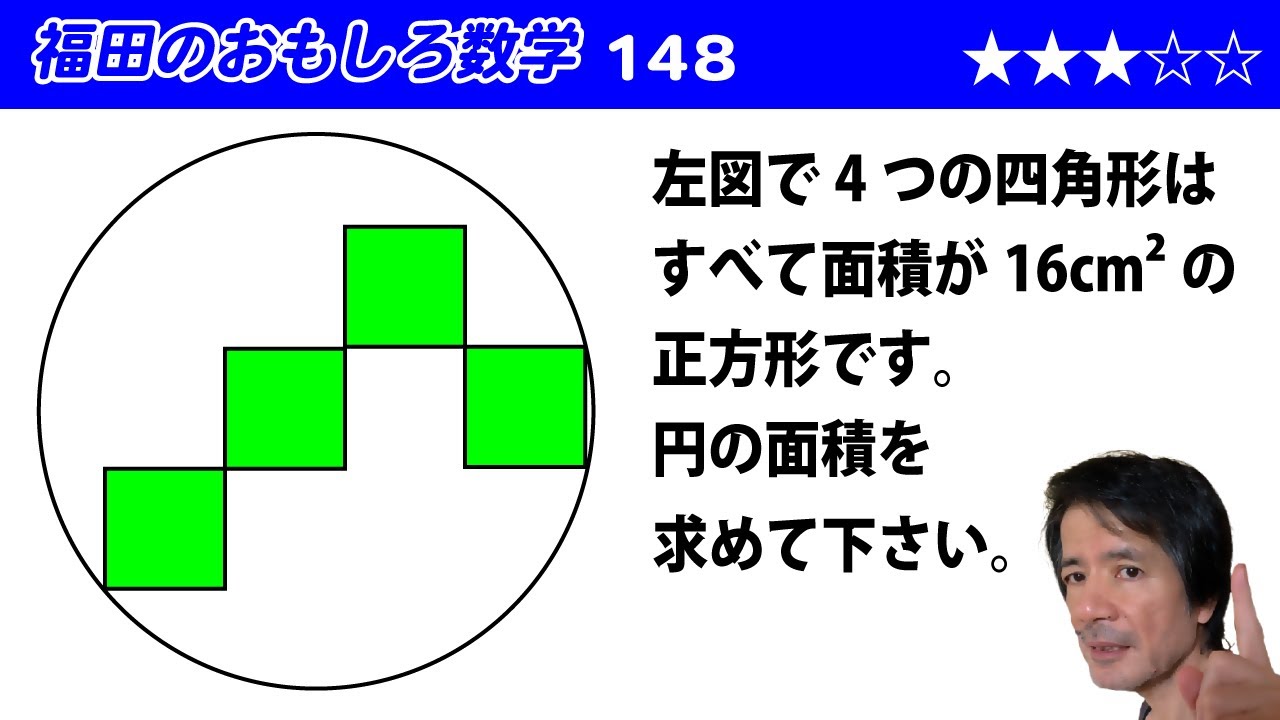
左図(※動画参照)で4つの四角形はすべて面積が$16 \textrm{cm}^2$の正方形です。
円の面積を求めて下さい。
この動画を見る
左図(※動画参照)で4つの四角形はすべて面積が$16 \textrm{cm}^2$の正方形です。
円の面積を求めて下さい。
福田の数学〜慶應義塾大学2024年商学部第2問(4)〜領域と集合の要素の個数

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ (4)$xy$平面上で、不等式$x$≦5 の表す領域を$A$, 不等式$x$+$y$≧10 の表す領域を$B$とする。また、$xy$平面上の点の集合$S$は以下の3つの条件をすべて満たす。
(条件1)$S$に含まれるどの点も、その$x$座標と$y$座標はともに1以上10以下の自然数である。
(条件2)$S$の要素で領域$A$に含まれるものは、領域$B$に含まれる。
(条件3)$S$の要素で領域$B$に含まれるものは、領域$A$に含まれる。
$S$を、条件1~3を満たす中で要素の個数が最大のものとするとき、その要素の個数は$\boxed{シス}$である。
この動画を見る
$\Large\boxed{2}$ (4)$xy$平面上で、不等式$x$≦5 の表す領域を$A$, 不等式$x$+$y$≧10 の表す領域を$B$とする。また、$xy$平面上の点の集合$S$は以下の3つの条件をすべて満たす。
(条件1)$S$に含まれるどの点も、その$x$座標と$y$座標はともに1以上10以下の自然数である。
(条件2)$S$の要素で領域$A$に含まれるものは、領域$B$に含まれる。
(条件3)$S$の要素で領域$B$に含まれるものは、領域$A$に含まれる。
$S$を、条件1~3を満たす中で要素の個数が最大のものとするとき、その要素の個数は$\boxed{シス}$である。
円を表す方程式
【高校数学】【図形と方程式】領域の超時短裏ワザ!後編

単元:
#数Ⅱ#図形と方程式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
定期考査直前、「この問題だけはできるようにしよう!」ってことで領域の問題を裏ワザで解説してみました。(割と有名なので知ってる人はゴメンナサイ)この動画は前編( • 【高校数学】【図形と方程式】領域の超時短裏ワザ!前編【後編は明日18時公開!】 )を見てからご覧ください!
この動画を見る
定期考査直前、「この問題だけはできるようにしよう!」ってことで領域の問題を裏ワザで解説してみました。(割と有名なので知ってる人はゴメンナサイ)この動画は前編( • 【高校数学】【図形と方程式】領域の超時短裏ワザ!前編【後編は明日18時公開!】 )を見てからご覧ください!
【高校数学】【図形と方程式】領域の超時短裏ワザ!前編【後編は明日18時公開!】

単元:
#数Ⅱ#図形と方程式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
定期考査直前、「この問題だけはできるようにしよう!」ってことで領域の問題を裏ワザで解説してみました。(割と有名なので知ってる人はゴメンナサイ)
この動画では「$x-2y-4\geqq 0$」を図示します!
この動画を見る
定期考査直前、「この問題だけはできるようにしよう!」ってことで領域の問題を裏ワザで解説してみました。(割と有名なので知ってる人はゴメンナサイ)
この動画では「$x-2y-4\geqq 0$」を図示します!
福田の数学〜早稲田大学2024年人間科学部第5問〜円の性質と切り取られる弦の長さ

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 2点A(-$\sqrt 2$-$\sqrt 6$, $\sqrt 2$-$\sqrt 6$), B($\sqrt 2$+$\sqrt 6$, $\sqrt 2$-$\sqrt 6$)と原点O(0, 0)について、$\theta$=$\angle\textrm{AOB}$ とするとき、$\theta$=$\displaystyle\frac{\boxed{ナ}}{\boxed{ニ}}\pi$ である。ただし、0≦$\theta$≦$\pi$ とする。さらに円$x^2$+$y^2$-$2x$-$10y$+22=0 を$C$とする。円$C$上の点P, Qは
$\angle\textrm{APB}$=$\angle\textrm{AQB}$=$\displaystyle\frac{5}{12}\pi$
を満たす点とする。このとき、PQ=$\displaystyle\boxed{ヌ}\sqrt{\frac{\boxed{\ \ ネ\ \ }}{\boxed{\ \ ノ\ \ }}}$ である。
この動画を見る
$\Large\boxed{5}$ 2点A(-$\sqrt 2$-$\sqrt 6$, $\sqrt 2$-$\sqrt 6$), B($\sqrt 2$+$\sqrt 6$, $\sqrt 2$-$\sqrt 6$)と原点O(0, 0)について、$\theta$=$\angle\textrm{AOB}$ とするとき、$\theta$=$\displaystyle\frac{\boxed{ナ}}{\boxed{ニ}}\pi$ である。ただし、0≦$\theta$≦$\pi$ とする。さらに円$x^2$+$y^2$-$2x$-$10y$+22=0 を$C$とする。円$C$上の点P, Qは
$\angle\textrm{APB}$=$\angle\textrm{AQB}$=$\displaystyle\frac{5}{12}\pi$
を満たす点とする。このとき、PQ=$\displaystyle\boxed{ヌ}\sqrt{\frac{\boxed{\ \ ネ\ \ }}{\boxed{\ \ ノ\ \ }}}$ である。
大学入試問題#802「ほんまに解いてほしい良問」 #岡山大学(2002) #通過領域

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#数学(高校生)#岡山大学
指導講師:
ますただ
問題文全文(内容文):
座標平面上に点$A(0,2)$と点$B(1,0)$があり線分$AB$上の点$P$から$x$軸、$y$軸におろした垂線の足をそれぞれ$Q,R$とする。
点$P$が$A$から$B$まで動くとき、線分$QR$の通過する部分の面積を求めよ。
出典:2002年岡山大学 入試問題
この動画を見る
座標平面上に点$A(0,2)$と点$B(1,0)$があり線分$AB$上の点$P$から$x$軸、$y$軸におろした垂線の足をそれぞれ$Q,R$とする。
点$P$が$A$から$B$まで動くとき、線分$QR$の通過する部分の面積を求めよ。
出典:2002年岡山大学 入試問題
福田のおもしろ数学116〜円の内部の点(a,b)に対してax+by=r^2はどんな直線を表しているか
単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
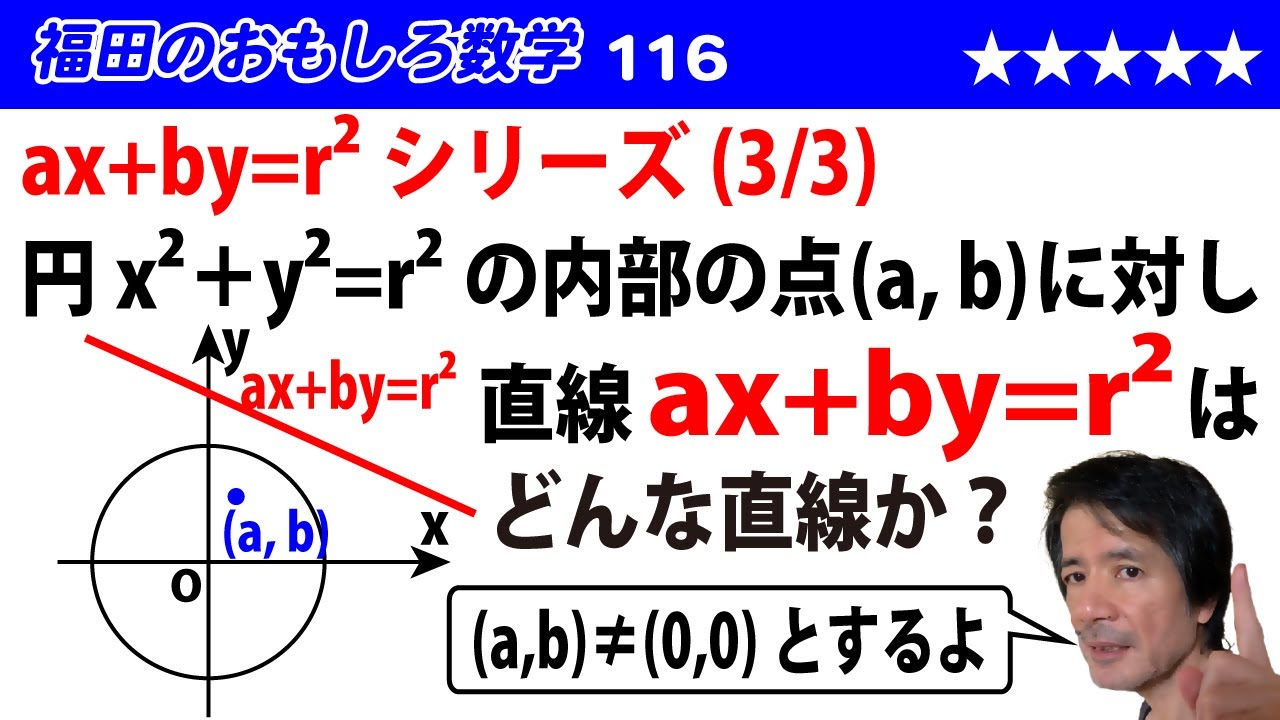
円$x^2$+$y^2$=$r^2$ の内部の点($a$,$b$)に対して直線$ax$+$by$=$r^2$ はどんな直線か。ただし、($a$,$b$)$\ne$(0,0)とする。
この動画を見る
円$x^2$+$y^2$=$r^2$ の内部の点($a$,$b$)に対して直線$ax$+$by$=$r^2$ はどんな直線か。ただし、($a$,$b$)$\ne$(0,0)とする。
