 指数関数
指数関数
 指数関数
指数関数
素数になる4次式

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
mは整数である.
$m^4+5m^3+6m^2+5m+1$が素数となるmをすべて求めよ.
この動画を見る
mは整数である.
$m^4+5m^3+6m^2+5m+1$が素数となるmをすべて求めよ.
福田の数学〜早稲田大学2022年教育学部第4問〜3次関数の増減と3次方程式の解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#指数関数と対数関数#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#指数関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{4}}$自然数$a,b$に対し、3次関数$f_{a,b}(x),g_{a,b}(x)$を
$f_{a,b}(x)=x^3+3ax^2+3bx+8$
$g_{a,b}(x)=8x^3+3bx^2+3ax+1$
で定める。次の問いに答えよ。
(1)次の条件$(\textrm{I})(\textrm{II})$の両方を満たす自然数の組(a,b)
で$a+b \leqq 9$となるものを全て求めよ。
$(\textrm{I})f_{a,b}(x)$が極値をもつ
$(\textrm{II})g_{a,b}(x)$が極値をもつ
(2)3次方程式$f_{a,b}(x)=0$の3つの解が$\alpha,\beta,\gamma$であるとき
3次方程式$g_{a,b}(x)=0$の解を$\alpha,\beta,\gamma$で表せ。
(3)次の条件$(\textrm{III})$を満たす自然数の組$(a,b)$で$a+b \leqq 9$となるものを全て求めよ。
$(\textrm{III})$3次方程式$f_{a,b}(x)=0$が相異なる3つの実数解をもつ。
2022早稲田大学教育学部過去問
この動画を見る
${\large\boxed{4}}$自然数$a,b$に対し、3次関数$f_{a,b}(x),g_{a,b}(x)$を
$f_{a,b}(x)=x^3+3ax^2+3bx+8$
$g_{a,b}(x)=8x^3+3bx^2+3ax+1$
で定める。次の問いに答えよ。
(1)次の条件$(\textrm{I})(\textrm{II})$の両方を満たす自然数の組(a,b)
で$a+b \leqq 9$となるものを全て求めよ。
$(\textrm{I})f_{a,b}(x)$が極値をもつ
$(\textrm{II})g_{a,b}(x)$が極値をもつ
(2)3次方程式$f_{a,b}(x)=0$の3つの解が$\alpha,\beta,\gamma$であるとき
3次方程式$g_{a,b}(x)=0$の解を$\alpha,\beta,\gamma$で表せ。
(3)次の条件$(\textrm{III})$を満たす自然数の組$(a,b)$で$a+b \leqq 9$となるものを全て求めよ。
$(\textrm{III})$3次方程式$f_{a,b}(x)=0$が相異なる3つの実数解をもつ。
2022早稲田大学教育学部過去問
解はあれだけですか?
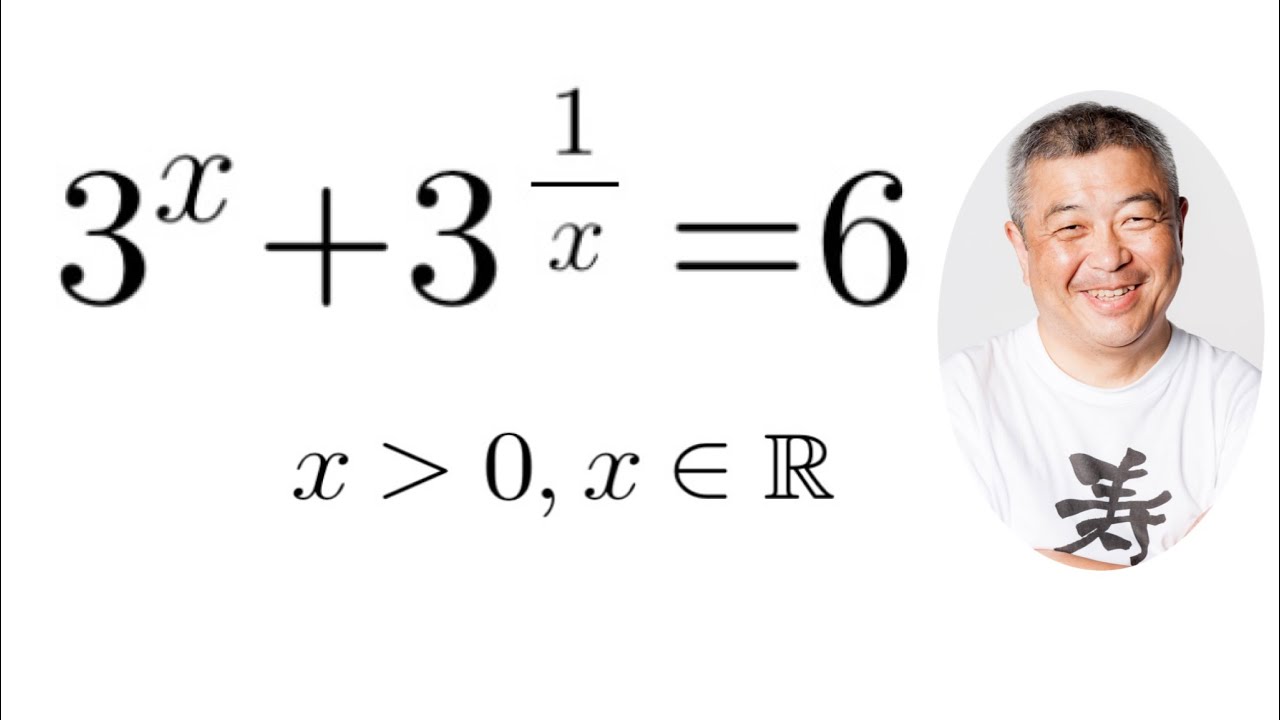
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
xは正の実数である.
$3^x+3^{\frac{1}{x}}=6$
これを解け.
この動画を見る
xは正の実数である.
$3^x+3^{\frac{1}{x}}=6$
これを解け.
わざとらしい連立方程式

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\dfrac{4x^2}{1+4x^2}=y$
$\dfrac{4y^2}{1+4y^2}=z$
$\dfrac{4z^2}{1+4z^2}=x$
これを解け.
この動画を見る
$\dfrac{4x^2}{1+4x^2}=y$
$\dfrac{4y^2}{1+4y^2}=z$
$\dfrac{4z^2}{1+4z^2}=x$
これを解け.
指数方程式
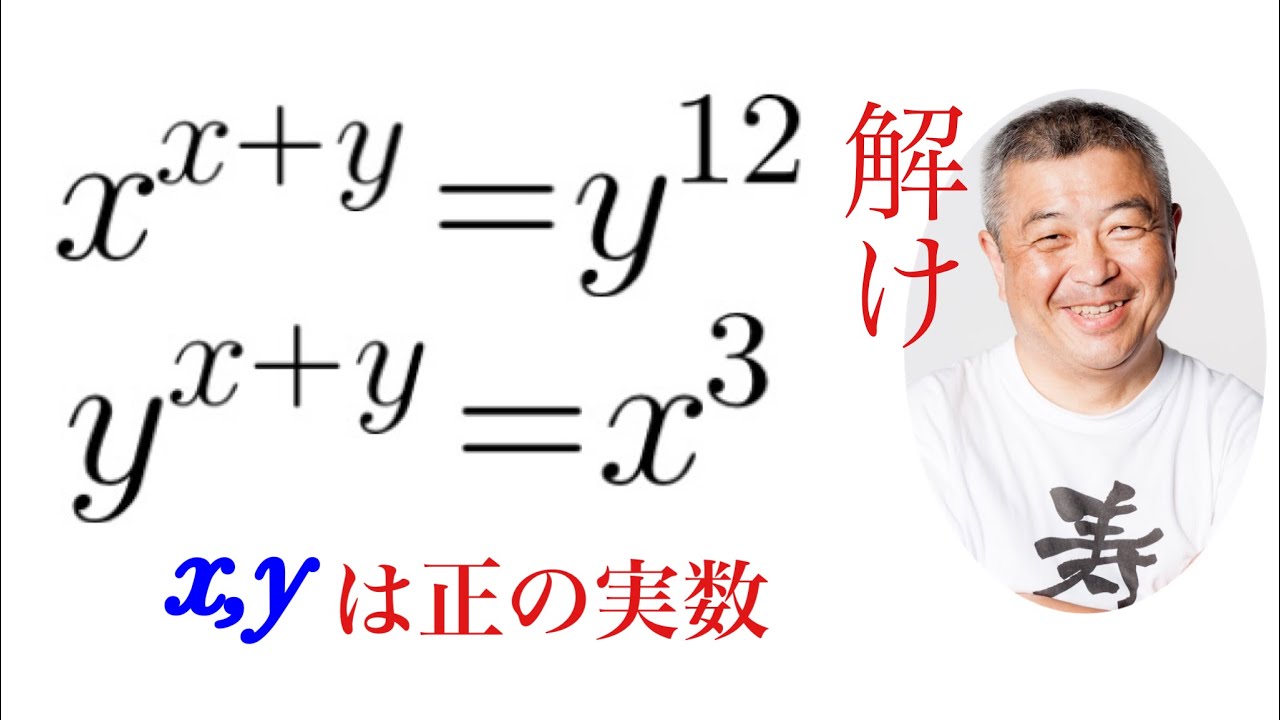
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
x,yは正の実数である.
$x^{x+y}=y^{12},y^{x+y}=x^3$
これを解け.
この動画を見る
x,yは正の実数である.
$x^{x+y}=y^{12},y^{x+y}=x^3$
これを解け.
指数の計算

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{2^{2022} + 2^{2020}}{10} = 2^▢$
▢=?
この動画を見る
$\frac{2^{2022} + 2^{2020}}{10} = 2^▢$
▢=?
ベトナム数学オリンピック
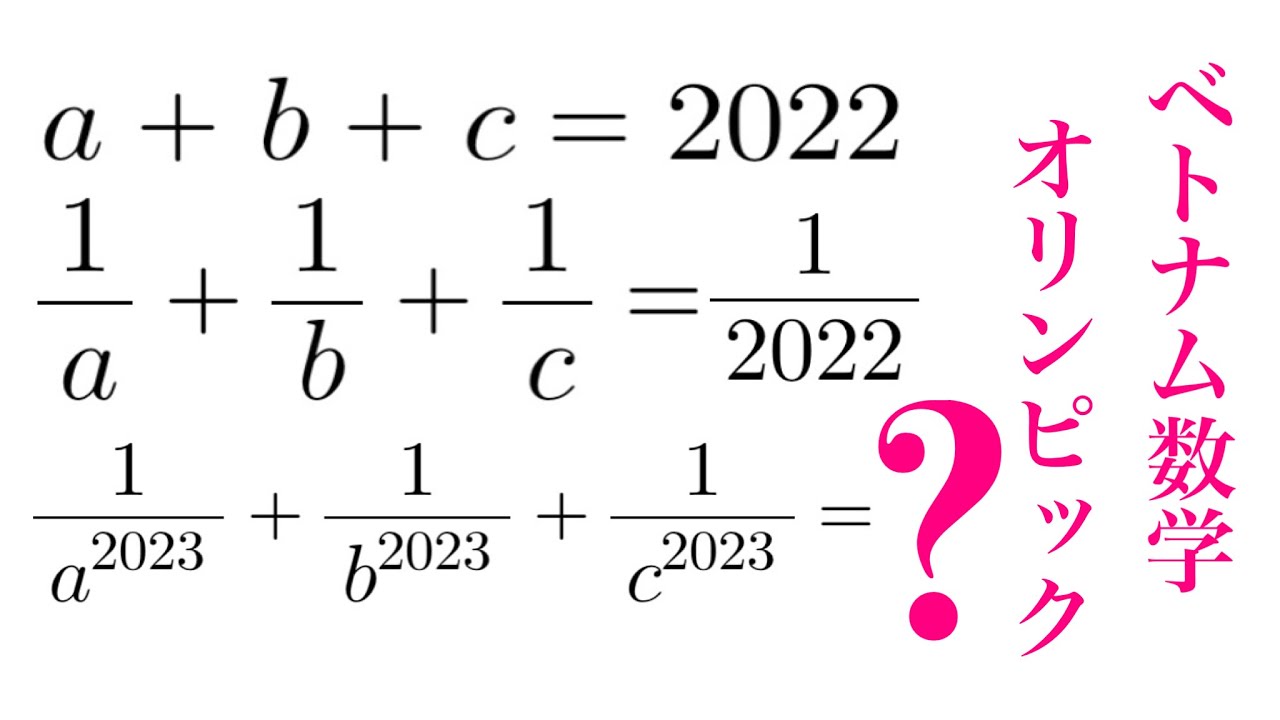
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a+b+c=2022$
$\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=\dfrac{1}{2022}$
$\dfrac{1}{a^{2023}}+\dfrac{1}{b^{2023}}+\dfrac{1}{c^{2023}}=?$
これを解け.
ベトナム数学オリンピック過去問
この動画を見る
$ a+b+c=2022$
$\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=\dfrac{1}{2022}$
$\dfrac{1}{a^{2023}}+\dfrac{1}{b^{2023}}+\dfrac{1}{c^{2023}}=?$
これを解け.
ベトナム数学オリンピック過去問
指数の基本問題
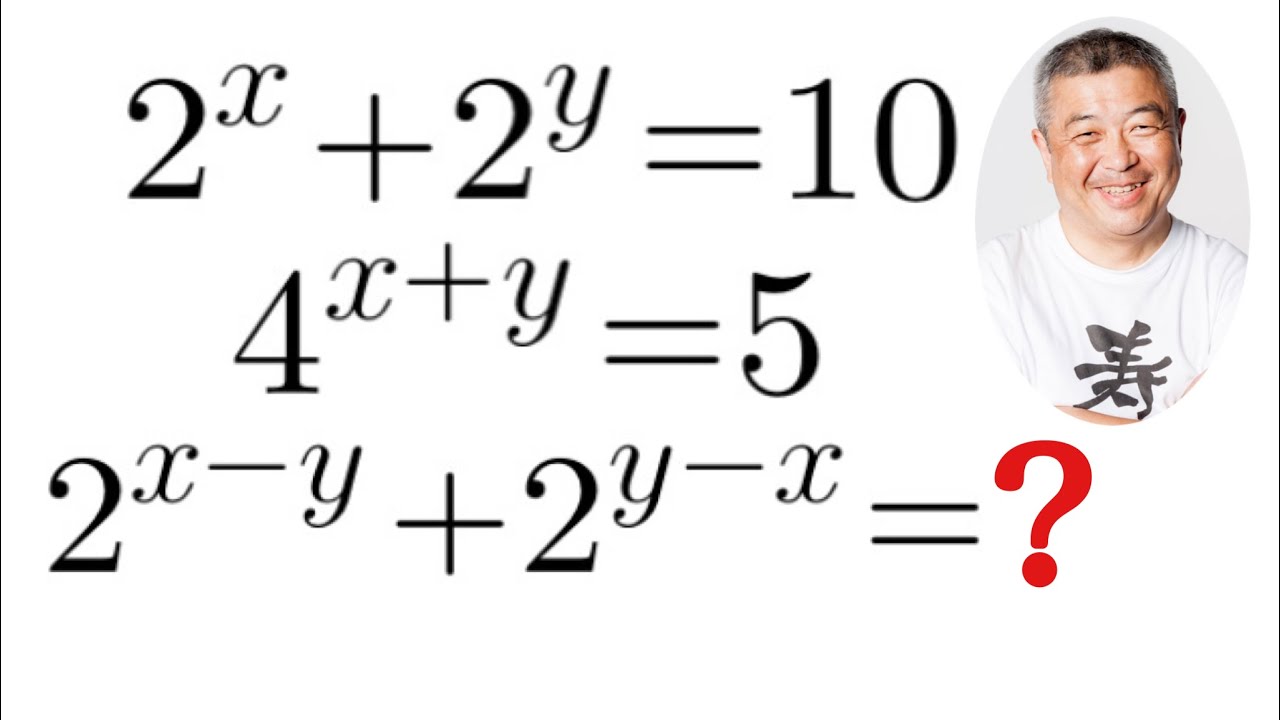
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
x,yは実数である.
$2^x+2^y=10,4^{x+y}=5,2^{x-y}+2^{y-x}=?$
これを解け.
この動画を見る
x,yは実数である.
$2^x+2^y=10,4^{x+y}=5,2^{x-y}+2^{y-x}=?$
これを解け.
指数の基本
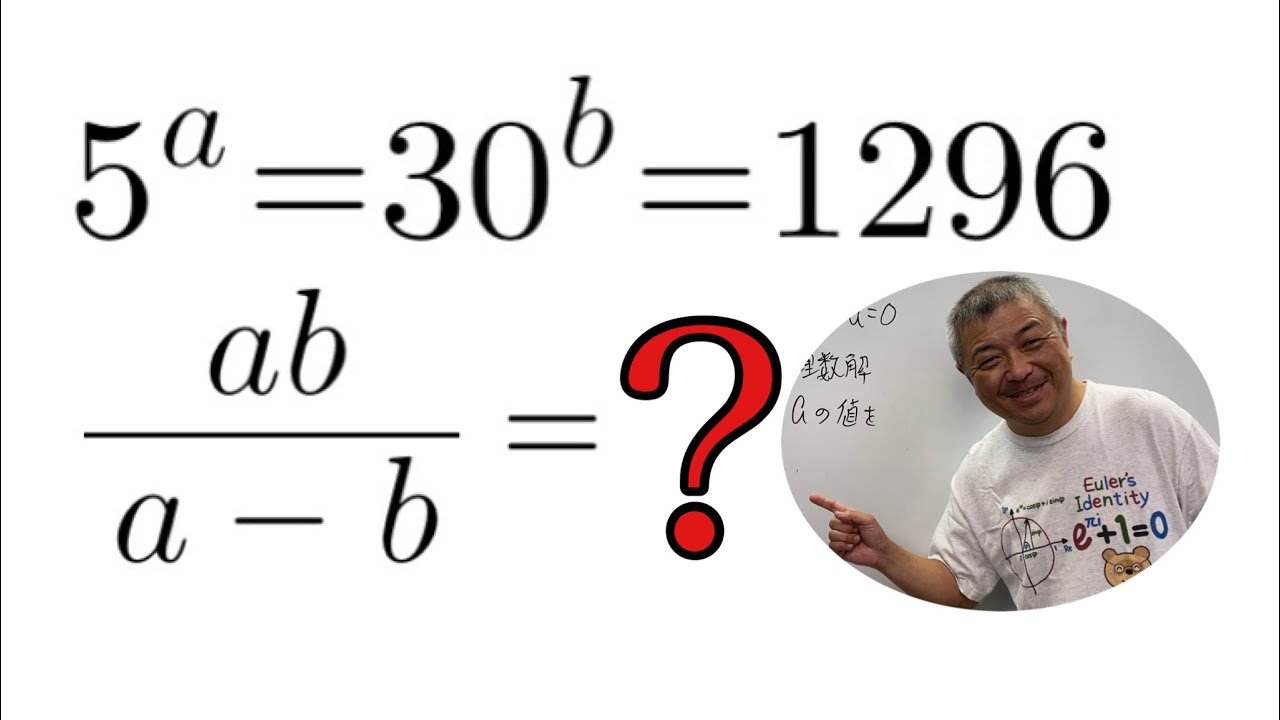
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 5^a=30^b=1296,\dfrac{ab}{a-b}$の値を求めよ.
この動画を見る
$ 5^a=30^b=1296,\dfrac{ab}{a-b}$の値を求めよ.
すっきりするただの計算問題

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x=\sqrt2+1$のとき,
$\dfrac{x^7-x}{x^8+1}$の値を求めよ.
この動画を見る
$ x=\sqrt2+1$のとき,
$\dfrac{x^7-x}{x^8+1}$の値を求めよ.
ただの約分

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \dfrac{1+2+3+4+8+・・・・・・+2^{2024}}{1+8+64+512+・・・・・・+2^{2022}}$
これを計算せよ.
この動画を見る
$ \dfrac{1+2+3+4+8+・・・・・・+2^{2024}}{1+8+64+512+・・・・・・+2^{2022}}$
これを計算せよ.
【数Ⅱ】指数関数のグラフと不等式【底が1より大きいか小さいかで全然違うグラフになる!】

【誘導あり:概要欄】大学入試問題#256 神戸大学2012 #極限 #はさみうちの定理

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#対数関数#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$2 \leqq n$自然数
$S_n=\displaystyle \sum_{k=1}^{n^3-1}\displaystyle \frac{1}{k\ log\ k}$
(1)
$2 \leqq k$:自然数
$\displaystyle \frac{1}{(k+1)log(k+1)} \lt \displaystyle \int_{k}^{k+1}\displaystyle \frac{dx}{x\ log\ x} \lt \displaystyle \frac{1}{k\ log\ k}$
(2)
$\displaystyle \lim_{ n \to \infty }S_n$を求めよ。
出典:2012年神戸大学 入試問題
この動画を見る
$2 \leqq n$自然数
$S_n=\displaystyle \sum_{k=1}^{n^3-1}\displaystyle \frac{1}{k\ log\ k}$
(1)
$2 \leqq k$:自然数
$\displaystyle \frac{1}{(k+1)log(k+1)} \lt \displaystyle \int_{k}^{k+1}\displaystyle \frac{dx}{x\ log\ x} \lt \displaystyle \frac{1}{k\ log\ k}$
(2)
$\displaystyle \lim_{ n \to \infty }S_n$を求めよ。
出典:2012年神戸大学 入試問題
福田の数学〜慶應義塾大学2022年看護医療学部第1問(2)〜指数計算

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
問題文全文(内容文):
${\large\boxed{1}}$(2)aを正の実数、pを実数とする。$a^{2p}=3$のとき、
$\frac{a^{2p}-a^{-2p}}{a^p-a^{-p}}$の値は$\boxed{\ \ ア\ \ }$である。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{1}}$(2)aを正の実数、pを実数とする。$a^{2p}=3$のとき、
$\frac{a^{2p}-a^{-2p}}{a^p-a^{-p}}$の値は$\boxed{\ \ ア\ \ }$である。
2022慶應義塾大学看護医療学科過去問
福田の数学〜慶應義塾大学2022年環境情報学部第3問〜4次関数のグラフの接線と囲まれた面積

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#微分法と積分法#指数関数#学校別大学入試過去問解説(数学)#不定積分・定積分#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{3}}$xy平面上の曲線Cを$y=x^2(x-1)(x+2)$とする。
(1)Cに2点で下から接する直線Lの方程式は
$y=\frac{\boxed{\ \ アイウ\ \ }}{\boxed{\ \ エオカ\ \ }}\ x+\frac{\boxed{\ \ キクケ\ \ }}{\boxed{\ \ コサシ\ \ }}$である。
(2)CとLが囲む図の斜線部分の面積(※動画参照)は
$\frac{\boxed{\ \ スセソ\ \ }\sqrt{\boxed{\ \ タチツ\ \ }}}{\boxed{\ \ テトナ\ \ }}$となる。
ただし、次の公式を使ってもかまわない(m,nは正の整数)
$\int_{\alpha}^{\beta}(x-\alpha)^m(x-\beta)^ndx=\frac{(-1)^nm!n!}{(m+n+1)!}(\beta-\alpha)^{m+n+1}$
2022慶應義塾大学環境情報学部過去問
この動画を見る
${\large\boxed{3}}$xy平面上の曲線Cを$y=x^2(x-1)(x+2)$とする。
(1)Cに2点で下から接する直線Lの方程式は
$y=\frac{\boxed{\ \ アイウ\ \ }}{\boxed{\ \ エオカ\ \ }}\ x+\frac{\boxed{\ \ キクケ\ \ }}{\boxed{\ \ コサシ\ \ }}$である。
(2)CとLが囲む図の斜線部分の面積(※動画参照)は
$\frac{\boxed{\ \ スセソ\ \ }\sqrt{\boxed{\ \ タチツ\ \ }}}{\boxed{\ \ テトナ\ \ }}$となる。
ただし、次の公式を使ってもかまわない(m,nは正の整数)
$\int_{\alpha}^{\beta}(x-\alpha)^m(x-\beta)^ndx=\frac{(-1)^nm!n!}{(m+n+1)!}(\beta-\alpha)^{m+n+1}$
2022慶應義塾大学環境情報学部過去問
大学入試問題#250 福井大学(2012) #定積分
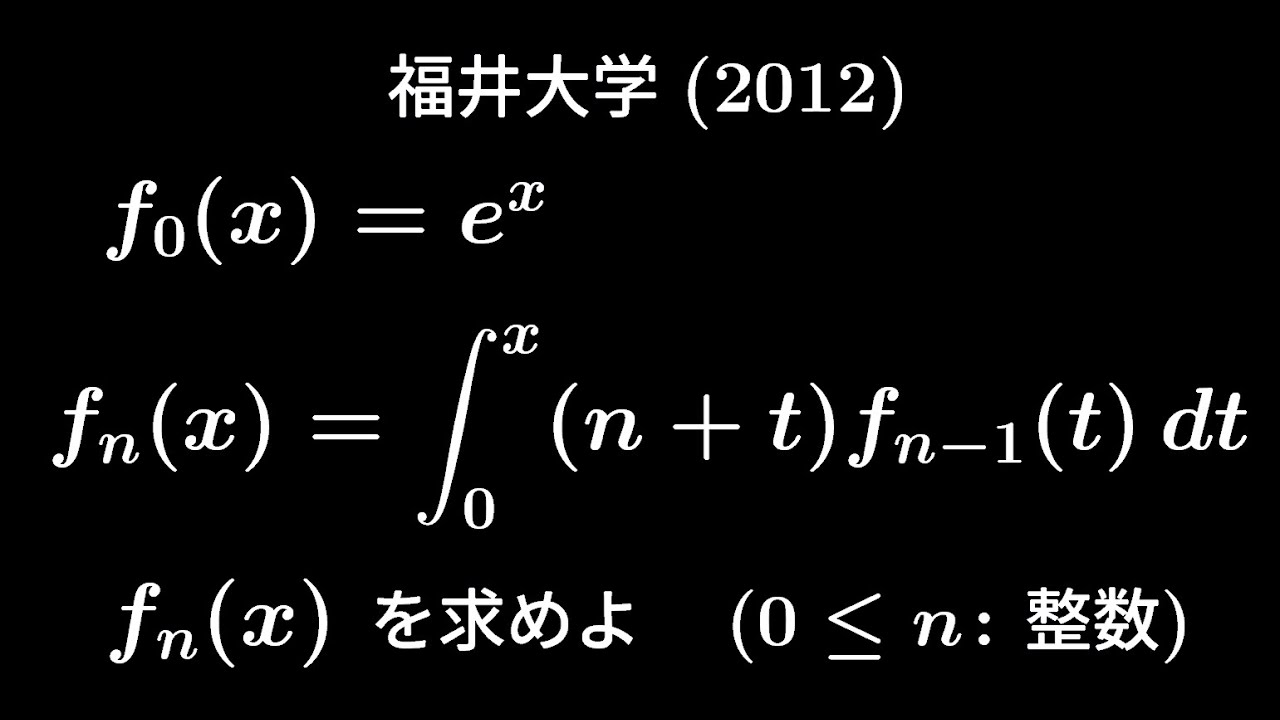
単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#数列#漸化式#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福井大学#数B#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$n$を0以上の整数とする。
次の2つの条件をみたす関数$f_n(x)$を求めよ。
(ⅰ)$f_0(x)=e^x$
(ⅱ)$f_n(x)=\displaystyle \int_{0}^{x}(n+t)f_{n-1}(t)dt$
出典:2012年福井大学 入試問題
この動画を見る
$n$を0以上の整数とする。
次の2つの条件をみたす関数$f_n(x)$を求めよ。
(ⅰ)$f_0(x)=e^x$
(ⅱ)$f_n(x)=\displaystyle \int_{0}^{x}(n+t)f_{n-1}(t)dt$
出典:2012年福井大学 入試問題
簡単な指数方程式

単元:
#数Ⅱ#複素数と方程式#指数関数と対数関数#剰余の定理・因数定理・組み立て除法と高次方程式#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 2^x-3^x=\sqrt{6^x-9^x}$
これの実数解を求めよ.
この動画を見る
$ 2^x-3^x=\sqrt{6^x-9^x}$
これの実数解を求めよ.
大学入試問題#241 早稲田大学(2014) #指数

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
関数$f(x)=(27^x+\displaystyle \frac{1}{27^x})-5(9^x+\displaystyle \frac{1}{9^x})$
$-5(3^x+\displaystyle \frac{1}{3^x})+1$の最小値と、そのときの$x$の値を求めよ。
出典:2014年早稲田大学 入試問題
この動画を見る
関数$f(x)=(27^x+\displaystyle \frac{1}{27^x})-5(9^x+\displaystyle \frac{1}{9^x})$
$-5(3^x+\displaystyle \frac{1}{3^x})+1$の最小値と、そのときの$x$の値を求めよ。
出典:2014年早稲田大学 入試問題
福田の数学〜慶應義塾大学2022年経済学部第5問〜指数対数の性質と格子点と2次関数の最大

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{5}}$aを2以上の整数、pを整数とし、$s=2^{2p+1}$とおく。実数$x,y$が等式
$2^{a+1}\log_23^x+2x\log_2(\frac{1}{3})^x=\log_s9^y$
を満たすとき、yをxの関数として表したものを$y=f(x)$とする。
(1)対数の記号を使わずに、$f(x)$を$a,p$およびxを用いて表せ。
(2)$a=2,\ p=0$とする。このとき、$n \leqq f(m)$を満たし、かつ、$m+n$が正となる
ような整数の組(m,n)の個数を求めよ。
(3)$y=f(x)(0 \leqq x \leqq 2^{a+1})$の最大値が$2^{3a}$以下となるような整数pの
最大値と最小値を、それぞれaを用いて表せ。
2022慶應義塾大学経済学部過去問
この動画を見る
${\Large\boxed{5}}$aを2以上の整数、pを整数とし、$s=2^{2p+1}$とおく。実数$x,y$が等式
$2^{a+1}\log_23^x+2x\log_2(\frac{1}{3})^x=\log_s9^y$
を満たすとき、yをxの関数として表したものを$y=f(x)$とする。
(1)対数の記号を使わずに、$f(x)$を$a,p$およびxを用いて表せ。
(2)$a=2,\ p=0$とする。このとき、$n \leqq f(m)$を満たし、かつ、$m+n$が正となる
ような整数の組(m,n)の個数を求めよ。
(3)$y=f(x)(0 \leqq x \leqq 2^{a+1})$の最大値が$2^{3a}$以下となるような整数pの
最大値と最小値を、それぞれaを用いて表せ。
2022慶應義塾大学経済学部過去問
2022乗

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(5+2 \sqrt 6)^{1011}(\sqrt 3 - \sqrt 2)^{2022}$
この動画を見る
$(5+2 \sqrt 6)^{1011}(\sqrt 3 - \sqrt 2)^{2022}$
福田の入試問題解説〜慶應義塾大学2022年医学部第4問〜4次関数の増減凹凸と曲線の長さ

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
座標平面上の点A(a,b)を1つ固定し、曲線$y=x^2$上の点P$(x,x^2)$と点A
との距離の2乗をg(x)とおく。関数$y=g(x)$のグラフが区間$(-\infty,\infty)$において下に凸
となるための条件は$b \leqq \boxed{\ \ ア\ \ }$となることである。$b \gt \boxed{\ \ ア\ \ }$のとき$y=g(x)$のグラフは
2つの変曲点をもち、そのx座標は$\boxed{\ \ イ\ \ }$及び$\boxed{\ \ ウ\ \ }$である。
ただし$\boxed{\ \ イ\ \ }\lt \boxed{\ \ ウ\ \ }$とする。また、関数$y=g(x)$が極小となるxがただ1つであるために
a,bが満たすべき条件を$b \leqq F(a)$と書くと、$F(a)=\boxed{\ \ エ\ \ }$ である。
$b= F(a)$のとき、関数$y=g(x)$は$x=\boxed{\ \ オ\ \ }$において最小値をとる。
さらに、連立不等式$x \geqq 0,\ y \geqq x^2$が表す領域をDとするとき、
曲線$y=F(x)$のDに含まれる部分の長さLを求めると、$L=\boxed{\ \ カ\ \ }$である。
2022慶應義塾大学医学部過去問
この動画を見る
座標平面上の点A(a,b)を1つ固定し、曲線$y=x^2$上の点P$(x,x^2)$と点A
との距離の2乗をg(x)とおく。関数$y=g(x)$のグラフが区間$(-\infty,\infty)$において下に凸
となるための条件は$b \leqq \boxed{\ \ ア\ \ }$となることである。$b \gt \boxed{\ \ ア\ \ }$のとき$y=g(x)$のグラフは
2つの変曲点をもち、そのx座標は$\boxed{\ \ イ\ \ }$及び$\boxed{\ \ ウ\ \ }$である。
ただし$\boxed{\ \ イ\ \ }\lt \boxed{\ \ ウ\ \ }$とする。また、関数$y=g(x)$が極小となるxがただ1つであるために
a,bが満たすべき条件を$b \leqq F(a)$と書くと、$F(a)=\boxed{\ \ エ\ \ }$ である。
$b= F(a)$のとき、関数$y=g(x)$は$x=\boxed{\ \ オ\ \ }$において最小値をとる。
さらに、連立不等式$x \geqq 0,\ y \geqq x^2$が表す領域をDとするとき、
曲線$y=F(x)$のDに含まれる部分の長さLを求めると、$L=\boxed{\ \ カ\ \ }$である。
2022慶應義塾大学医学部過去問
福田の入試問題解説〜慶應義塾大学2022年理工学部第4問〜指数関数と直線の位置関係と極限

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#関数と極限#微分とその応用#関数の極限#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
曲線$C:y=e^x$を考える。
(1)$a,b$を実数とし、$a \geqq 0$とする。曲線Cと直線$y=ax+b$が共有点をもつため
のaとbの条件を求めよ。
(2)正の実数tに対し、C上の点$A(t,e^t)$を中心とし、直線$y=x$に接する円Dを
考える。直線$y=x$と円Dの接点Bのx座標は$\boxed{\ \ タ\ \ }$であり、
円Dの半径は$\boxed{\ \ チ\ \ }$である。線分ABを3:2に内分する点をPとし、Pのx座標、y座標
をそれぞれX(t),Y(t)とする。このとき、等式
$\lim_{t \to \infty}\frac{Y(t)-kX(t)}{\sqrt{\left\{X(t)\right\}^2+\left\{Y(t)\right\}^2}}=0$
が成り立つような実数kを定めると$k=\boxed{\ \ ツ\ \ }$である。
ただし、$\lim_{t \to \infty}te^{-t}=0$である。
2022慶應義塾大学理工学部過去問
この動画を見る
曲線$C:y=e^x$を考える。
(1)$a,b$を実数とし、$a \geqq 0$とする。曲線Cと直線$y=ax+b$が共有点をもつため
のaとbの条件を求めよ。
(2)正の実数tに対し、C上の点$A(t,e^t)$を中心とし、直線$y=x$に接する円Dを
考える。直線$y=x$と円Dの接点Bのx座標は$\boxed{\ \ タ\ \ }$であり、
円Dの半径は$\boxed{\ \ チ\ \ }$である。線分ABを3:2に内分する点をPとし、Pのx座標、y座標
をそれぞれX(t),Y(t)とする。このとき、等式
$\lim_{t \to \infty}\frac{Y(t)-kX(t)}{\sqrt{\left\{X(t)\right\}^2+\left\{Y(t)\right\}^2}}=0$
が成り立つような実数kを定めると$k=\boxed{\ \ ツ\ \ }$である。
ただし、$\lim_{t \to \infty}te^{-t}=0$である。
2022慶應義塾大学理工学部過去問
福田の数学〜浜松医科大学2022年医学部第2問〜3次関数が区間で常に正である条件

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$s$を実数、tを0以上の実数とし、関数f(x)を
$f(x)=x^3-sx^2+(t-2s^2)\ x+st$
により定める。関数$f(x)$に対して次の条件pを考える。
$p:0 \leqq x \leqq 1$を満たすすべてのxに対して$f(x) \gt 0$である。
このとき、条件pを満たす点(s,t)の領域を図示せよ。
2022浜松医科大学医学部過去問
この動画を見る
$s$を実数、tを0以上の実数とし、関数f(x)を
$f(x)=x^3-sx^2+(t-2s^2)\ x+st$
により定める。関数$f(x)$に対して次の条件pを考える。
$p:0 \leqq x \leqq 1$を満たすすべてのxに対して$f(x) \gt 0$である。
このとき、条件pを満たす点(s,t)の領域を図示せよ。
2022浜松医科大学医学部過去問
自力で対数の範囲を求めて桁数を出す【数学 入試問題】【岐阜大学】

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#岐阜大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(1)不等式$\dfrac{3}{10}<log_{10} 2<\dfrac{4}{13}$を証明せよ。
(2)(1)を用いて、$2^{100}は何桁の数か答えよ。
岐阜大過去問
この動画を見る
(1)不等式$\dfrac{3}{10}<log_{10} 2<\dfrac{4}{13}$を証明せよ。
(2)(1)を用いて、$2^{100}は何桁の数か答えよ。
岐阜大過去問
解けるように作られた指数方程式

単元:
#数Ⅱ#複素数と方程式#指数関数と対数関数#剰余の定理・因数定理・組み立て除法と高次方程式#指数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x+y)^{x-y}=2 \\
2^{y-x},(x+y)=1
\end{array}
\right.
\end{eqnarray}$
これを解け.
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x+y)^{x-y}=2 \\
2^{y-x},(x+y)=1
\end{array}
\right.
\end{eqnarray}$
これを解け.
【超難問】4÷2できる?

ハルハル様の作成問題② 複雑な方程式の解

これ解けましたか?

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$5^x=7^y=1225$
$\displaystyle \frac{xy}{x+y}$の値を求めよ
この動画を見る
$5^x=7^y=1225$
$\displaystyle \frac{xy}{x+y}$の値を求めよ
これ解ける?

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$5^x=7^y=1225$
$\displaystyle \frac{xy}{x+y}$の値を求めよ
この動画を見る
$5^x=7^y=1225$
$\displaystyle \frac{xy}{x+y}$の値を求めよ
東京電機大 複素数のべき乗

単元:
#複素数と方程式#複素数#指数関数#数列
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(1+2i)^n=x_n+y_ni$
(1)$x^2_n+y^2_n$を求めよ.
(2)$x_{n+2}$を$x_{n+1}$と$x_n$で表せ.
(3)$x_n$と$y_n$の最大公約数を求めよ.
東京電機大過去問
この動画を見る
$(1+2i)^n=x_n+y_ni$
(1)$x^2_n+y^2_n$を求めよ.
(2)$x_{n+2}$を$x_{n+1}$と$x_n$で表せ.
(3)$x_n$と$y_n$の最大公約数を求めよ.
東京電機大過去問
