微分法と積分法
微分法と積分法
【数Ⅱ】【微分法と積分法】放物線と直線で囲まれた図形の面積 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#面積、体積#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の曲線と直線で囲まれた図形の面積Sを求めよ。
(1) $y=x^2-4x-2,x$軸
(2) $y=x^2+x,y=1-x$
(3) $y=|x^2-x-2|,y=x+1$
この動画を見る
次の曲線と直線で囲まれた図形の面積Sを求めよ。
(1) $y=x^2-4x-2,x$軸
(2) $y=x^2+x,y=1-x$
(3) $y=|x^2-x-2|,y=x+1$
【数Ⅱ】【微分法と積分法】1/6公式の利用 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$\int_{α}^β(x-α)(x-β)dx=-\dfrac{1}{6}(β-α)³$
を用いて、次の定積分を求めよ。
(1)$\int_{-1}^2(x²-x-2)dx$
(2)$\int_{1-\sqrt 2}^{1+\sqrt2}(x²-2x-1)dx$
(3)$\int_{3}^4(14x-24-2x²)dx $
この動画を見る
$\int_{α}^β(x-α)(x-β)dx=-\dfrac{1}{6}(β-α)³$
を用いて、次の定積分を求めよ。
(1)$\int_{-1}^2(x²-x-2)dx$
(2)$\int_{1-\sqrt 2}^{1+\sqrt2}(x²-2x-1)dx$
(3)$\int_{3}^4(14x-24-2x²)dx $
【数Ⅱ】【微分法と積分法】偶関数と奇関数の利用 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の定積分を求めよ。
(1)$\int_{-1}^1(4x³+3x²+3x+1)dx$
(2)$\int_{-2}^2(x³-x²-x+4)dx$
(3)$\int_{-2}^2(x⁴-5x³+x²+9x)dx $
この動画を見る
次の定積分を求めよ。
(1)$\int_{-1}^1(4x³+3x²+3x+1)dx$
(2)$\int_{-2}^2(x³-x²-x+4)dx$
(3)$\int_{-2}^2(x⁴-5x³+x²+9x)dx $
【数Ⅱ】【微分法と積分法】接線からの関数決定 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$f'(x)=x^2+2x+2$で、曲線$y=f(x)$は$y=-3x+1$に接している。この時、$f(x)$を求めよ。
この動画を見る
$f'(x)=x^2+2x+2$で、曲線$y=f(x)$は$y=-3x+1$に接している。この時、$f(x)$を求めよ。
【数Ⅱ】【微分法と積分法】係数比較から関数の決定 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
2次関数$f(x)$の1つの不定積分$F(x)$が$xf(x)-2x^3+3x^2$に等しく、$f(1)=0$であるとき、$f(x)$を求めよ。
この動画を見る
2次関数$f(x)$の1つの不定積分$F(x)$が$xf(x)-2x^3+3x^2$に等しく、$f(1)=0$であるとき、$f(x)$を求めよ。
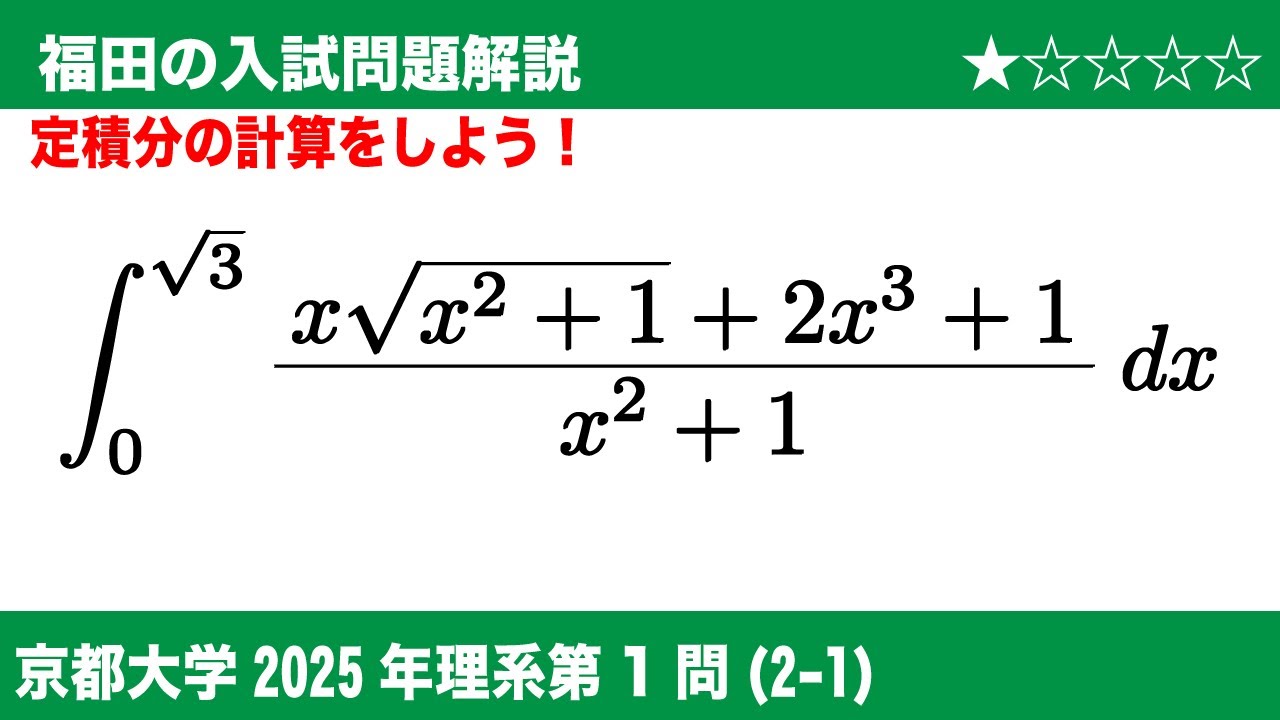
福田の数学〜京都大学2025理系第1問(2−1)〜定積分の計算
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(2-1)次の定積分の値を求めよ。
$\displaystyle \int_{0}^{\sqrt3} \dfrac{x\sqrt{x^2+1}+2x^3+1}{x^2+1}dx$
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{1}$
(2-1)次の定積分の値を求めよ。
$\displaystyle \int_{0}^{\sqrt3} \dfrac{x\sqrt{x^2+1}+2x^3+1}{x^2+1}dx$
$2025$年京都大学理系過去問題
福田の数学〜東京大学2025理系第2問〜はさみうちの原理を利用する極限
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
(1)$x\gt0$のとき、
不等式$\log x \leqq x - 1$を示せ。
(2)次の極限を求めよ。
$\displaystyle \lim_{n\to\infty} n \displaystyle \int_{1}^{2} \log \left(\dfrac{1+x^{\frac{1}{n}}}{2}\right)dx$
$2025$年東京大学理系過去問題
この動画を見る
$\boxed{2}$
(1)$x\gt0$のとき、
不等式$\log x \leqq x - 1$を示せ。
(2)次の極限を求めよ。
$\displaystyle \lim_{n\to\infty} n \displaystyle \int_{1}^{2} \log \left(\dfrac{1+x^{\frac{1}{n}}}{2}\right)dx$
$2025$年東京大学理系過去問題
【数Ⅱ】【微分法と積分法】方程式の解の個数5 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
方程式2x³-3x²-36x=aが1個の正の解と2個の負の解をもつように、定数aの値の範囲を定めよ。
この動画を見る
方程式2x³-3x²-36x=aが1個の正の解と2個の負の解をもつように、定数aの値の範囲を定めよ。
【数Ⅱ】【微分法と積分法】方程式の解の個数8 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
曲線C:y=x³+3x²について、次の問いに答えよ。
(1)C上の点P(t,t³+3t)におけるCの接線が点A(0,a)を通る時、等式2t³+3t²+a=0が成り立つことを示せ。
(2)Aを通るCの接線が3本存在するとき、aの値の範囲を求めよ。
この動画を見る
曲線C:y=x³+3x²について、次の問いに答えよ。
(1)C上の点P(t,t³+3t)におけるCの接線が点A(0,a)を通る時、等式2t³+3t²+a=0が成り立つことを示せ。
(2)Aを通るCの接線が3本存在するとき、aの値の範囲を求めよ。
【数Ⅱ】【微分法と積分法】方程式の解の個数7 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
方程式x³-3ax+a=0が異なる3個の実数解をもつとき、定数aの値の範囲を求めよ。
この動画を見る
方程式x³-3ax+a=0が異なる3個の実数解をもつとき、定数aの値の範囲を求めよ。
【数Ⅱ】【微分法と積分法】方程式の解の個数6 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
4次方程式x⁴-4x³-2x²+12x-a=0が異なる4個の実数解を持ち、そのうち2個は正、残りの2個は負であるとき、定数aの値の範囲を求めよ。
この動画を見る
4次方程式x⁴-4x³-2x²+12x-a=0が異なる4個の実数解を持ち、そのうち2個は正、残りの2個は負であるとき、定数aの値の範囲を求めよ。
【数Ⅱ】【微分法と積分法】極大極小の条件2 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
関数f(x)=x⁴+4x³+2ax²が極大値と極小値を持つように，定数aの値の範囲を定めよ。
この動画を見る
関数f(x)=x⁴+4x³+2ax²が極大値と極小値を持つように，定数aの値の範囲を定めよ。
【数Ⅱ】【微分法と積分法】極大極小の条件1 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
関数f(x)=x³+ax²+bx+cについて，次の問に答えよ。
（１）x=1で極大となるための条件を求めよ。
（２）x=-2で極小となるための条件を求めよ。
この動画を見る
関数f(x)=x³+ax²+bx+cについて，次の問に答えよ。
（１）x=1で極大となるための条件を求めよ。
（２）x=-2で極小となるための条件を求めよ。
【数Ⅱ】【微分法と積分法】極値の場合分け ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
aは定数とする。次の各場合に、関数y=x(x-a)²の極値を調べよ。
(1)a＜0
(2)a=0
(3)a＞0
この動画を見る
aは定数とする。次の各場合に、関数y=x(x-a)²の極値を調べよ。
(1)a＜0
(2)a=0
(3)a＞0
【数Ⅱ】【微分法と積分法】極値を持つ条件 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の条件に適するように、定数aの値の範囲を、それぞれ定めよ。
(1)関数$f(x)=\frac{1}{3}x^3+ax^2+(a+2)x+1$が極値をもつ。
(2)関数$g(x)=x^3+ax^2-3ax+2$が極値をもたない。
この動画を見る
次の条件に適するように、定数aの値の範囲を、それぞれ定めよ。
(1)関数$f(x)=\frac{1}{3}x^3+ax^2+(a+2)x+1$が極値をもつ。
(2)関数$g(x)=x^3+ax^2-3ax+2$が極値をもたない。
【数Ⅱ】【微分法と積分法】微分と接線7 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
2つの曲線y=x²，y=-(x-2)²の共通接線の方程式を求めよ。
この動画を見る
2つの曲線y=x²，y=-(x-2)²の共通接線の方程式を求めよ。
【数Ⅱ】【微分法と積分法】微分と接線6 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
2つの曲線y=x²+2，y=x²+ax+3の交点をPとする。Pにおけるそれぞれの曲線の接線が垂直であるとき，定数aの値を求めよ。
この動画を見る
2つの曲線y=x²+2，y=x²+ax+3の交点をPとする。Pにおけるそれぞれの曲線の接線が垂直であるとき，定数aの値を求めよ。
【数Ⅱ】【微分法と積分法】微分と接線5 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
(1)曲線y=x³+ax+1が直線y=2x-1に接するとき，定数aの値を求めよ。
(2)曲線y=x³+x²と放物線y=x²+ax+16は，ともにある点Pを通り，Pにおいて共通の接線を持つ。このとき、定数aの値と接線の方程式を求めよ。
この動画を見る
(1)曲線y=x³+ax+1が直線y=2x-1に接するとき，定数aの値を求めよ。
(2)曲線y=x³+x²と放物線y=x²+ax+16は，ともにある点Pを通り，Pにおいて共通の接線を持つ。このとき、定数aの値と接線の方程式を求めよ。
【数Ⅱ】【微分法と積分法】微分と接線4 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
曲線y=2x²-4x+3上の点A(0,3)を通り，点Aにおける曲線の接線に垂直な直線の方程式を求めよ。
この動画を見る
曲線y=2x²-4x+3上の点A(0,3)を通り，点Aにおける曲線の接線に垂直な直線の方程式を求めよ。
【数Ⅱ】【微分法と積分法】微分と接線3 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
曲線y=-x³+4x上の点(-2,0)における接線が，この曲線と交わるもう1つの点のx座標を求めよ。
この動画を見る
曲線y=-x³+4x上の点(-2,0)における接線が，この曲線と交わるもう1つの点のx座標を求めよ。
【数Ⅱ】【微分法と積分法】微分と接線2 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
曲線y=x³+3x²-6 について，傾きが9である接線の方程式を求めよ。
この動画を見る
曲線y=x³+3x²-6 について，傾きが9である接線の方程式を求めよ。
【数Ⅱ】【微分法と積分法】微分と接線1 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の曲線に，与えられた点から引いた接線の方程式と，接点の座標を求めよ。
(1) y=x²+3x+4 (0,0)
(2) y=x²-x+3 (1,-1)
(3) y=x³+2 (0,4)
この動画を見る
次の曲線に，与えられた点から引いた接線の方程式と，接点の座標を求めよ。
(1) y=x²+3x+4 (0,0)
(2) y=x²-x+3 (1,-1)
(3) y=x³+2 (0,4)
【数Ⅱ】【微分法と積分法】微分の基本6 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$k$は0ではない定数とする。次の等式を満たす2次関数$f(x)$を求めよ。
$f(x)-x^2f'(x)=k^2x^3-kx+5$
この動画を見る
$k$は0ではない定数とする。次の等式を満たす2次関数$f(x)$を求めよ。
$f(x)-x^2f'(x)=k^2x^3-kx+5$
【数Ⅱ】【微分法と積分法】微分の基本5 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の関数を求めよ。
(1) 等式 $f(x)+(x+2)f'(x)=9x^2+8x-3$ を満たす2次関数$f(x)$
(2) 等式 $g(x)+xg'(x)=4x^3+6x^2+4x+1$ を満たす3次関数$g(x)$
この動画を見る
次の関数を求めよ。
(1) 等式 $f(x)+(x+2)f'(x)=9x^2+8x-3$ を満たす2次関数$f(x)$
(2) 等式 $g(x)+xg'(x)=4x^3+6x^2+4x+1$ を満たす3次関数$g(x)$
【数Ⅱ】【微分法と積分法】微分の基本4 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
1辺の長さ$x$の正四面体がある。
(1)正四面体の表面積を$S$とするとき，$S$を$x$の関数で表せ。
(2)$x$が変化するとき，$S$の$x=5$における微分係数を求めよ。
この動画を見る
1辺の長さ$x$の正四面体がある。
(1)正四面体の表面積を$S$とするとき，$S$を$x$の関数で表せ。
(2)$x$が変化するとき，$S$の$x=5$における微分係数を求めよ。
【数Ⅱ】【微分法と積分法】微分の基本3 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$\{(ax+b)^n\}'=na(ax+b)^{n-1}$ ($n$ は正の整数) であることを用いて、次の関数を微分せよ。
$(1)\ y=(2x+1)^3$
$(2)\ y=(x-1)^4$
$(3)\ y=(-2x+1)^5$
この動画を見る
$\{(ax+b)^n\}'=na(ax+b)^{n-1}$ ($n$ は正の整数) であることを用いて、次の関数を微分せよ。
$(1)\ y=(2x+1)^3$
$(2)\ y=(x-1)^4$
$(3)\ y=(-2x+1)^5$
【数Ⅱ】【微分法と積分法】微分の基本2 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$f(x)=x^2-3x$ とする。
関数 $y=f(x)$ のグラフ上の2点 $(1,\,f(1)),\ (a,\,f(a))$ を結ぶ直線の傾きが、$x=b$ $(1< b < a)$ における微分係数 $f'(b)$ に等しい。
$b$ を $a$ で表せ。
この動画を見る
$f(x)=x^2-3x$ とする。
関数 $y=f(x)$ のグラフ上の2点 $(1,\,f(1)),\ (a,\,f(a))$ を結ぶ直線の傾きが、$x=b$ $(1< b < a)$ における微分係数 $f'(b)$ に等しい。
$b$ を $a$ で表せ。
【数Ⅱ】【微分法と積分法】微分の基本1 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の関数 $f(x)$ について、$x=a$ における微分係数 $f'(x)$ を求めよ。また、$f'(a)$ が、$x$ が $0$ から $2$ まで変化するときの平均変化率に一致するとき、$a$ の値を求めよ。
$(1)\ f(x)=x^2-x$
$(2)\ f(x)=x^3-x^2+1$
この動画を見る
次の関数 $f(x)$ について、$x=a$ における微分係数 $f'(x)$ を求めよ。また、$f'(a)$ が、$x$ が $0$ から $2$ まで変化するときの平均変化率に一致するとき、$a$ の値を求めよ。
$(1)\ f(x)=x^2-x$
$(2)\ f(x)=x^3-x^2+1$
【数Ⅱ】【微分法と積分法】極限の計算 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
(1)$\displaystyle \lim_{ x \to -2 } (x^2+1)(x-1)$
(2)$\displaystyle \lim_{ x \to 1 } (x^3-1)(x-1)$
(3)$\displaystyle \lim_{ x \to 2 } (x^2-x-2)(x^2+x-6)$
(4)$\displaystyle \lim_{ x \to -3 } \frac{1}{x+3}(\frac{12}{x-3}+2)$
この動画を見る
(1)$\displaystyle \lim_{ x \to -2 } (x^2+1)(x-1)$
(2)$\displaystyle \lim_{ x \to 1 } (x^3-1)(x-1)$
(3)$\displaystyle \lim_{ x \to 2 } (x^2-x-2)(x^2+x-6)$
(4)$\displaystyle \lim_{ x \to -3 } \frac{1}{x+3}(\frac{12}{x-3}+2)$
大学受験生が覚えてたら差がつく公式
