 数Ⅱ
数Ⅱ
 数Ⅱ
数Ⅱ
福田のおもしろ数学526〜数値評価
単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
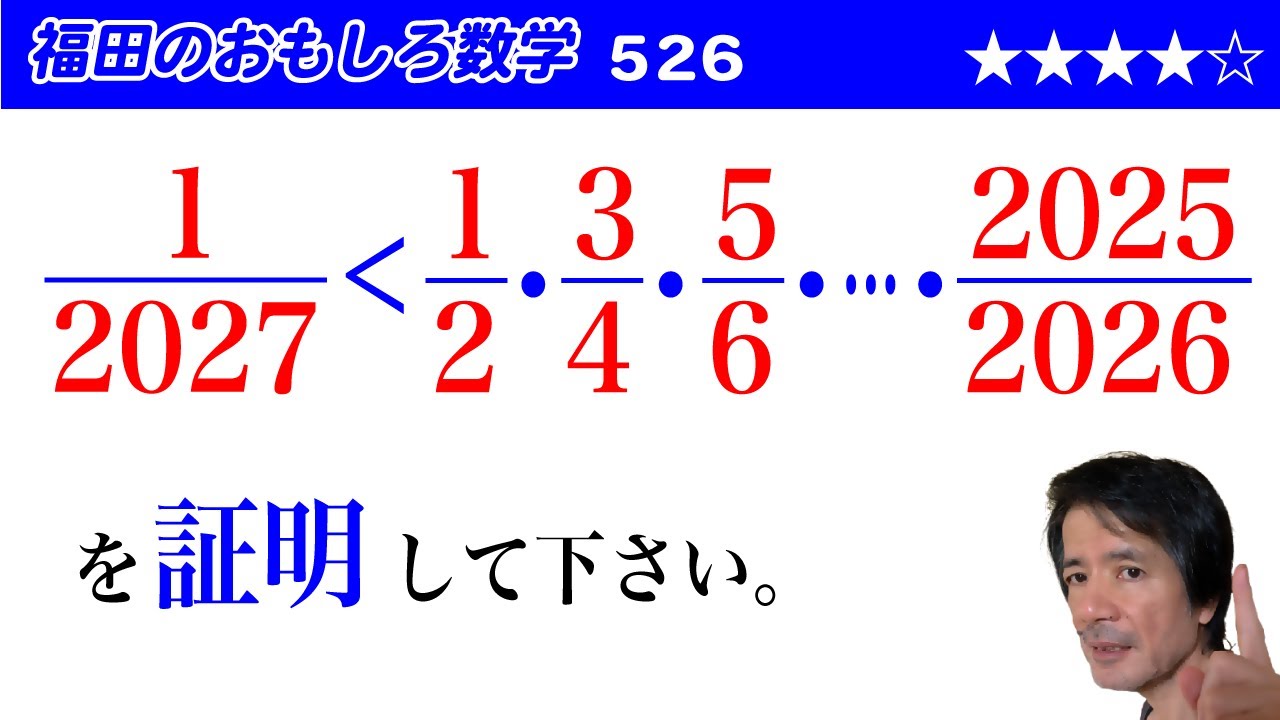
$\dfrac{1}{2027} \lt \dfrac{1}{2}・\dfrac{3}{4}・\dfrac{5}{6}・\cdots ・\dfrac{2025}{2026}$
を証明して下さい。
この動画を見る
$\dfrac{1}{2027} \lt \dfrac{1}{2}・\dfrac{3}{4}・\dfrac{5}{6}・\cdots ・\dfrac{2025}{2026}$
を証明して下さい。
福田のおもしろ数学525〜数値評価
単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
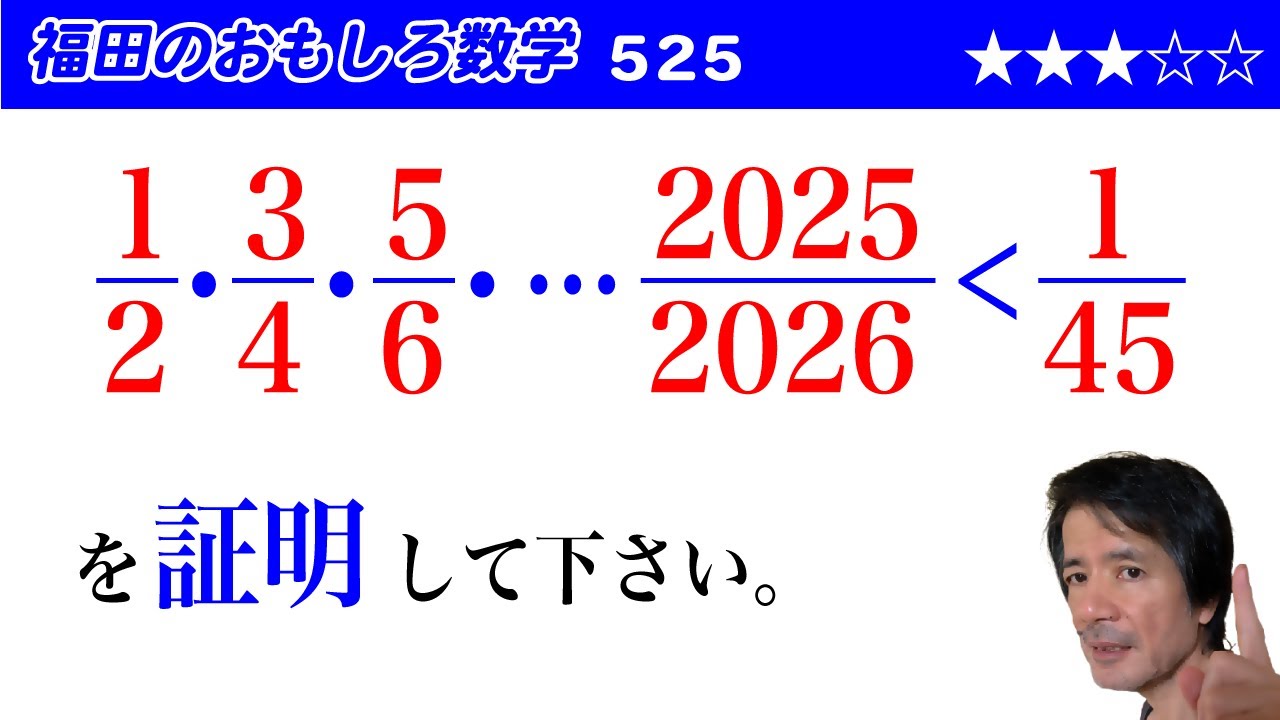
$\dfrac{1}{2}・\dfrac{3}{4}・\dfrac{5}{6}・\cdots \dfrac{2025}{2026}\lt \dfrac{1}{45}$
を証明して下さい。
この動画を見る
$\dfrac{1}{2}・\dfrac{3}{4}・\dfrac{5}{6}・\cdots \dfrac{2025}{2026}\lt \dfrac{1}{45}$
を証明して下さい。
equation : Shirotan's cute kawaii math show #数学 #小学生テスト #高校入試 #歌ってみた #高校受験 #占い

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
a¹⁰b⁸+a⁶b⁸-3a⁵b⁵=?
この動画を見る
a¹⁰b⁸+a⁶b⁸-3a⁵b⁵=?
福田のおもしろ数学524〜無限級数の和

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \sum_{k=1}^{\infty} \dfrac{k^2}{3^k}$を求めて下さい。
この動画を見る
$\displaystyle \sum_{k=1}^{\infty} \dfrac{k^2}{3^k}$を求めて下さい。
福田の数学〜立教大学2025理学部第2問〜三角関数の最大最小の定番

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
実数$x$に対し、関数$f(x)$を
$f(x)=\sin^3x+\cos^3x+4sin x \cos x$
により定める。
また、$t=\sin x+\cos x$とおく。次の問いに答えよ。
(1)$\sin x \cos x$を$t$を用いて表せ。
(2)$f(x)$を$t$を用いて表せ。
(3)$x$がすべてに実数を動くとき、
$t$のとりうる値の範囲を求めよ。
(4)$x$がすべてに実数を動くとき、
$f(x)$の最大値と最小値をそれぞれ求めよ。
$2025$年立教大学理学部過去問題
この動画を見る
$\boxed{2}$
実数$x$に対し、関数$f(x)$を
$f(x)=\sin^3x+\cos^3x+4sin x \cos x$
により定める。
また、$t=\sin x+\cos x$とおく。次の問いに答えよ。
(1)$\sin x \cos x$を$t$を用いて表せ。
(2)$f(x)$を$t$を用いて表せ。
(3)$x$がすべてに実数を動くとき、
$t$のとりうる値の範囲を求めよ。
(4)$x$がすべてに実数を動くとき、
$f(x)$の最大値と最小値をそれぞれ求めよ。
$2025$年立教大学理学部過去問題
福田のおもしろ数学520〜4次方程式が異なる3つの解をもつ条件

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
方程式
$(x^2-2mx-4(m^2+1))(x^2-4x-2m(m^2+1))=0$
が異なる$3$個の解をもつような
実数$m$をすべて求めよ。
この動画を見る
方程式
$(x^2-2mx-4(m^2+1))(x^2-4x-2m(m^2+1))=0$
が異なる$3$個の解をもつような
実数$m$をすべて求めよ。
福田のおもしろ数学518〜積分で表された関数の導関数

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#不定積分・定積分#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \int_{0}^{1} f(x-t)dt$
の導関数を求めよ。
この動画を見る
$\displaystyle \int_{0}^{1} f(x-t)dt$
の導関数を求めよ。
福田の数学〜立教大学2025理学部第1問(1)〜不等式と対数

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(1)自然数$n$に対して$a_n=2^n$とし、
積$a_1a_2\cdots a_n$を$A_n$とおく。
このとき、$A_n \geqq 10^{10}$を満たす最小の
$n$は$\boxed{ア}$である。
ただし、$\log_2 10=3.3219$とする。
$2025$年立教大学理学部過去問題
この動画を見る
$\boxed{1}$
(1)自然数$n$に対して$a_n=2^n$とし、
積$a_1a_2\cdots a_n$を$A_n$とおく。
このとき、$A_n \geqq 10^{10}$を満たす最小の
$n$は$\boxed{ア}$である。
ただし、$\log_2 10=3.3219$とする。
$2025$年立教大学理学部過去問題
福田のおもしろ数学517〜2つの楕円の共通部分の面積

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$2$つの楕円(内部を含む)
$\dfrac{x^2}{3}+y^2\leqq 1,x^2+\dfrac{y^2}{3} \leqq 1$
の共通部分の面積を求めよ。
この動画を見る
$2$つの楕円(内部を含む)
$\dfrac{x^2}{3}+y^2\leqq 1,x^2+\dfrac{y^2}{3} \leqq 1$
の共通部分の面積を求めよ。
福田の数学〜立教大学2025経済学部第3問〜3次関数のグラフと直線の共有点の個数

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
$k$を実数とする。
$3$次関数$f(x)=x^3-x^2+1$に対して、
座標平面上の曲線$C$を$C:y=f(x)$とする。
また、$C$上の点$P(1,1)$を通り、
傾きが$k$である直線を$\ell$とする。
このとき、次の問いに答えよ。
(1)$\ell$の方程式を$k$を用いて表せ。
(2)$f(x)$の導関数$f'(x)$を求めよ。
(3)$f(x)$の極値を求めよ。
また、そのときの$x$の値を求めよ。
(4)$\ell$と$C$がちょうど$2$個の共有点を
もつような$k$の値を求めよ。
(5)$\ell$と$C$が異なる$3$個の共有点をもつような
$k$の値の範囲を求めよ。
(6)(5)のとき、異なる$3$個の共有点の$y$座標を
小さい方から順に$y_1,y_2,y_3$とする。
このとき、
比の等式$(y_2-y_1):(y_3-y_2)=1:2$を
満たすような$k$の値を求めよ。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{3}$
$k$を実数とする。
$3$次関数$f(x)=x^3-x^2+1$に対して、
座標平面上の曲線$C$を$C:y=f(x)$とする。
また、$C$上の点$P(1,1)$を通り、
傾きが$k$である直線を$\ell$とする。
このとき、次の問いに答えよ。
(1)$\ell$の方程式を$k$を用いて表せ。
(2)$f(x)$の導関数$f'(x)$を求めよ。
(3)$f(x)$の極値を求めよ。
また、そのときの$x$の値を求めよ。
(4)$\ell$と$C$がちょうど$2$個の共有点を
もつような$k$の値を求めよ。
(5)$\ell$と$C$が異なる$3$個の共有点をもつような
$k$の値の範囲を求めよ。
(6)(5)のとき、異なる$3$個の共有点の$y$座標を
小さい方から順に$y_1,y_2,y_3$とする。
このとき、
比の等式$(y_2-y_1):(y_3-y_2)=1:2$を
満たすような$k$の値を求めよ。
$2025$年立教大学経済学部過去問題
福田の数学〜立教大学2025経済学部第2問〜2点の位置関係と三角関数

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
$p,q$を正の実数とする。
原点を$O$とする座標平面上に
点$A(1,0)$、点$P\left(p,\dfrac{1}{p}\right)$,点$Q\left(q,\dfrac{2}{q}\right)$がある。
$\angle AOP=\alpha,\angle AOQ=\beta$とおき、
$P,Q$は$\alpha \lt \beta$を満たしながら動くものとする。
三角形$OPQ$の面積を$S$とし、
また、$T=\tan(\beta-\alpha)$とおく。
(1)$\cos\alpha,\sin\alpha$をそれぞれ$p$を用いて表せ。
また、$\cos\beta,\sin\beta$をそれぞれ$q$を用いて表せ。
(2)$T$を$p,q$を用いて表せ。
(3)$S$を$p,q$を用いて表せ。
(4)$t=pq$とおく。$\dfrac{S}{T}$を$t$を用いて表せ。
(5)$\dfrac{S}{T}$の最小値を求めよ。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{2}$
$p,q$を正の実数とする。
原点を$O$とする座標平面上に
点$A(1,0)$、点$P\left(p,\dfrac{1}{p}\right)$,点$Q\left(q,\dfrac{2}{q}\right)$がある。
$\angle AOP=\alpha,\angle AOQ=\beta$とおき、
$P,Q$は$\alpha \lt \beta$を満たしながら動くものとする。
三角形$OPQ$の面積を$S$とし、
また、$T=\tan(\beta-\alpha)$とおく。
(1)$\cos\alpha,\sin\alpha$をそれぞれ$p$を用いて表せ。
また、$\cos\beta,\sin\beta$をそれぞれ$q$を用いて表せ。
(2)$T$を$p,q$を用いて表せ。
(3)$S$を$p,q$を用いて表せ。
(4)$t=pq$とおく。$\dfrac{S}{T}$を$t$を用いて表せ。
(5)$\dfrac{S}{T}$の最小値を求めよ。
$2025$年立教大学経済学部過去問題
福田のおもしろ数学514〜指数方程式の解

福田の数学〜立教大学2025経済学部第1問(5)〜絶対値の付いた関数の定積分の計算

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(5)定積分$\displaystyle \int_{0}^{2} (x+1)\vert x-1 \vert dx$
の値は$\boxed{キ}$である。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{1}$
(5)定積分$\displaystyle \int_{0}^{2} (x+1)\vert x-1 \vert dx$
の値は$\boxed{キ}$である。
$2025$年立教大学経済学部過去問題
福田のおもしろ数学513〜3つの数のうち少なくとも2つは等しいことの証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x,y,z$は正の実数であり、
任意の自然数$n$について$x^n,y^n,z^n$が
三角形の$3$辺をなすとき、
$x,y,z$の少なくとも$2$つは等しくことを
証明して下さい。
この動画を見る
$x,y,z$は正の実数であり、
任意の自然数$n$について$x^n,y^n,z^n$が
三角形の$3$辺をなすとき、
$x,y,z$の少なくとも$2$つは等しくことを
証明して下さい。
福田の数学〜立教大学2025経済学部第1問(4)〜2直線が1点で交わる条件

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(4)実数$a$は定数とする。
座標平面上の$2$つの直線$(a+1)x+ay=1$
$ax+(a+2)y=2$がただ$1$つの交点を持つための
$a$の条件は$\boxed{カ}$である。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{1}$
(4)実数$a$は定数とする。
座標平面上の$2$つの直線$(a+1)x+ay=1$
$ax+(a+2)y=2$がただ$1$つの交点を持つための
$a$の条件は$\boxed{カ}$である。
$2025$年立教大学経済学部過去問題
福田のおもしろ数学511〜50の50乗と49の51乗の大小比較

福田のおもしろ数学510〜(n+1/n)のn乗がeより小であることの証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$n$を正の整数とするとき
$\left(1+\dfrac{1}{n}\right)^n \lt e$
を証明して下さい。
$e$は自然対数の底とする。
この動画を見る
$n$を正の整数とするとき
$\left(1+\dfrac{1}{n}\right)^n \lt e$
を証明して下さい。
$e$は自然対数の底とする。
福田の数学〜立教大学2025経済学部第1問(1)〜指数不等式

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(1)$2^{1-3x} \geqq \left(\dfrac{1}{\sqrt2}\right)^x$を満たす
実数$x$の値の範囲は$\boxed{ア}$である。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{1}$
(1)$2^{1-3x} \geqq \left(\dfrac{1}{\sqrt2}\right)^x$を満たす
実数$x$の値の範囲は$\boxed{ア}$である。
$2025$年立教大学経済学部過去問題
福田の数学〜慶應義塾大学2025経済学部第6問〜放物線と直線で囲まれた図形の面積

単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{6}$
$C$を$y=3x^2$で定まる曲線とし、
$C$上に異なる$2$点$A(a,3a^2)$
$B(b,3b^2)$をとる。ただし、$a\lt b$とする。
(1)$C$と直線$AB$で囲まれた図形の面積$S$を、
$a$と$b$を用いて表せ。
ただし、積分を用いて計算し、
積分の計算過程も書くこと。
(2)$2$点$A,B$間の距離が$3$のとき、
(1)で求めた面積$S$の取りうる値の最大値$T$を
求めよ。
(3)$2$点$A,B$間の距離が$3$のとき、
直線$AB$は点$(0,7)$を通らないことを示せ。
$2025$年慶應義塾大学経済学部過去問題
この動画を見る
$\boxed{6}$
$C$を$y=3x^2$で定まる曲線とし、
$C$上に異なる$2$点$A(a,3a^2)$
$B(b,3b^2)$をとる。ただし、$a\lt b$とする。
(1)$C$と直線$AB$で囲まれた図形の面積$S$を、
$a$と$b$を用いて表せ。
ただし、積分を用いて計算し、
積分の計算過程も書くこと。
(2)$2$点$A,B$間の距離が$3$のとき、
(1)で求めた面積$S$の取りうる値の最大値$T$を
求めよ。
(3)$2$点$A,B$間の距離が$3$のとき、
直線$AB$は点$(0,7)$を通らないことを示せ。
$2025$年慶應義塾大学経済学部過去問題
福田の数学〜慶應義塾大学2025経済学部第4問〜指数不等式と対数

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#微分法と積分法#指数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
$p$を正の実数、$m$を自然数とし、
曲線$y=-x^2$上の点$(-p,-p^2)$における
接線と直線$y=2m$の交点を$P_m$とする。
$P_m$の$x$座標が$1$以下となる$m$の最大値を
$N$とする。
(1)$P_m$の$x$座標を、$p$と$m$を用いて表せ。
(2)$N=40$が成り立つ$p$の範囲を求めよ。
以下、$n$を自然数とし、
$a=3n\log_3 6-\log_2+n$とする。
(3)$3^a$は$2$以上の自然数である。
$3^a$の素因数分解を、$n$を用いて書け。
(4)$p=3^a$のとき、$N\lt 2^{1000}$となる
自然数$n$の最大値を求めよ。
なお、必要があれば$1.58 \lt \log_2 3 \lt 1.50$を用いよ。
$2025$年慶應義塾大学経済学部過去問題
この動画を見る
$\boxed{4}$
$p$を正の実数、$m$を自然数とし、
曲線$y=-x^2$上の点$(-p,-p^2)$における
接線と直線$y=2m$の交点を$P_m$とする。
$P_m$の$x$座標が$1$以下となる$m$の最大値を
$N$とする。
(1)$P_m$の$x$座標を、$p$と$m$を用いて表せ。
(2)$N=40$が成り立つ$p$の範囲を求めよ。
以下、$n$を自然数とし、
$a=3n\log_3 6-\log_2+n$とする。
(3)$3^a$は$2$以上の自然数である。
$3^a$の素因数分解を、$n$を用いて書け。
(4)$p=3^a$のとき、$N\lt 2^{1000}$となる
自然数$n$の最大値を求めよ。
なお、必要があれば$1.58 \lt \log_2 3 \lt 1.50$を用いよ。
$2025$年慶應義塾大学経済学部過去問題
福田のおもしろ数学506〜相加平均と相乗平均の商の極限

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
自然数$n+1,n+2,\cdots,n+n$の
相加平均を$A_n$、相乗平均を$B_n$とするとき
$\displaystyle \lim_{n\to\infty}\dfrac{A_n}{B_n}$
を求めて下さい。
この動画を見る
自然数$n+1,n+2,\cdots,n+n$の
相加平均を$A_n$、相乗平均を$B_n$とするとき
$\displaystyle \lim_{n\to\infty}\dfrac{A_n}{B_n}$
を求めて下さい。
福田のおもしろ数学504〜三角関数の最大値

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x$がすべての実数を動くとき
$\sin(\cos x)+\cos(\sin x)$の最大値を求めよ。
この動画を見る
$x$がすべての実数を動くとき
$\sin(\cos x)+\cos(\sin x)$の最大値を求めよ。
福田の数学〜慶應義塾大学2025経済学部第1問(2)〜2変数の不等式と領域

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(2)不等式
$\vert m+n-6 \vert + \vert m-n-2 \vert \leqq 6 \cdots ①$
を満たす整数$m,n$を考える。
$(m+n-6)(m-n-2)\geqq 0$のとき、$m$と$n$が
不等式①を満たすための必要十分条件は
$\boxed{セ} \leqq m \leqq \boxed{ソ}$
である。
同様に、$(m+n-6)(m-n-2)\leqq 0$のとき、
$m$と$n$が①を満たすための必要十分条件は
$\boxed{タチ}\leqq n \leqq \boxed{ツ}$
である。よって、$m$と$n$が①を満たすとき、
$(m-n)(m+n-6)$の最大値は、
$(m-n)(m+n-6)=(m-\boxed{テ})^2-(n-\boxed{ト})^2$
より$\boxed{ナニ}$である。
$2025$年慶應義塾大学経済学部過去問題
この動画を見る
$\boxed{1}$
(2)不等式
$\vert m+n-6 \vert + \vert m-n-2 \vert \leqq 6 \cdots ①$
を満たす整数$m,n$を考える。
$(m+n-6)(m-n-2)\geqq 0$のとき、$m$と$n$が
不等式①を満たすための必要十分条件は
$\boxed{セ} \leqq m \leqq \boxed{ソ}$
である。
同様に、$(m+n-6)(m-n-2)\leqq 0$のとき、
$m$と$n$が①を満たすための必要十分条件は
$\boxed{タチ}\leqq n \leqq \boxed{ツ}$
である。よって、$m$と$n$が①を満たすとき、
$(m-n)(m+n-6)$の最大値は、
$(m-n)(m+n-6)=(m-\boxed{テ})^2-(n-\boxed{ト})^2$
より$\boxed{ナニ}$である。
$2025$年慶應義塾大学経済学部過去問題
福田のおもしろ数学503〜複雑な三角方程式が実数解をもつ条件

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\cos^2\pi(a-x)-2\cos \pi(a-x)$
$+\cos\dfrac{3\pi x}{2a}\cos \left(\dfrac{\pi x}{2a}+\dfrac{\pi}{3}\right)+2=0$
が実数解をもつような
自然数$a$の最小値を求めよ。
この動画を見る
$\cos^2\pi(a-x)-2\cos \pi(a-x)$
$+\cos\dfrac{3\pi x}{2a}\cos \left(\dfrac{\pi x}{2a}+\dfrac{\pi}{3}\right)+2=0$
が実数解をもつような
自然数$a$の最小値を求めよ。
福田のおもしろ数学502〜(n/10)^(n/10)の最小となるnを求める

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\left(\dfrac{n}{10}\right)^{\frac{n}{10}}$を最小にする
自然数$n$を求めて下さい。
この動画を見る
$\left(\dfrac{n}{10}\right)^{\frac{n}{10}}$を最小にする
自然数$n$を求めて下さい。
福田の数学〜名古屋大学2025文系第1問〜放物線が囲む部分の面積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
実数$b,c$に対し、
放物線$y=f(x)=x^2+bx+c$が
$2$点$(p,0),(q,0)$を通ると仮定する(ただし$p\gt q$)。
また、条件$0\lt t \leqq 1$を満たす実数$t$に対し
実数$r,s$を次のように定める。
$r=\dfrac{1+t}{2}p+\dfrac{1-t}{2}q,s=\dfrac{1-t}{2}p+\dfrac{1+t}{2}q$
以下の問いに答えよ。
(1)$q-s,r-p,s+r,s-r$のそれぞれを
$b,c,t$で用いて表せ。
(2)$sr$および$s^2+r^2$を$b,c,t$を用いて表せ。
(3)放物線$y=f(x)$、直線$x=r,x=s$および
$x$軸が囲む領域の面積を$b,c,t$を用いて表せ。
$2025$年名古屋大学文系過去問題
この動画を見る
$\boxed{1}$
実数$b,c$に対し、
放物線$y=f(x)=x^2+bx+c$が
$2$点$(p,0),(q,0)$を通ると仮定する(ただし$p\gt q$)。
また、条件$0\lt t \leqq 1$を満たす実数$t$に対し
実数$r,s$を次のように定める。
$r=\dfrac{1+t}{2}p+\dfrac{1-t}{2}q,s=\dfrac{1-t}{2}p+\dfrac{1+t}{2}q$
以下の問いに答えよ。
(1)$q-s,r-p,s+r,s-r$のそれぞれを
$b,c,t$で用いて表せ。
(2)$sr$および$s^2+r^2$を$b,c,t$を用いて表せ。
(3)放物線$y=f(x)$、直線$x=r,x=s$および
$x$軸が囲む領域の面積を$b,c,t$を用いて表せ。
$2025$年名古屋大学文系過去問題
福田の数学〜名古屋大学2025理系第3問〜球の通過範囲の体積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
以下の問いに答えよ。
(1)実数$r,\alpha$は$0\lt r \leqq 1,0\leqq \alpha \lt \pi$をみたすとする。
$xy$平面内で、点$(1,0)$を中心にもつ半径$r$の
円周およびその内部を$C$とする。
$C$を原点$(0,0)$を中心に反時計回りに角度$\alpha$だけ
回転させるとき、$C$が通過する領域の面積を求めよ。
(2)実数$R,\alpha$は$0\lt R \leqq 1,0\leqq \alpha \lt \pi$をみたすとする。
$xyz$空間内で、点$(1,0,0)$を中心にもつ半径$R$の
球面およびその内部を$B$とする。
$B$を$z$軸のまわりに角度$\alpha$だけ回転させるとき、
$B$が通過する領域の体積を求めよ。
ただし、回転の向きは回転後の$B$の中心が
$(\cos \alpha,\sin \alpha,0)$になるように選ぶものとする。
$2025$年名古屋大学理系過去問題
この動画を見る
$\boxed{3}$
以下の問いに答えよ。
(1)実数$r,\alpha$は$0\lt r \leqq 1,0\leqq \alpha \lt \pi$をみたすとする。
$xy$平面内で、点$(1,0)$を中心にもつ半径$r$の
円周およびその内部を$C$とする。
$C$を原点$(0,0)$を中心に反時計回りに角度$\alpha$だけ
回転させるとき、$C$が通過する領域の面積を求めよ。
(2)実数$R,\alpha$は$0\lt R \leqq 1,0\leqq \alpha \lt \pi$をみたすとする。
$xyz$空間内で、点$(1,0,0)$を中心にもつ半径$R$の
球面およびその内部を$B$とする。
$B$を$z$軸のまわりに角度$\alpha$だけ回転させるとき、
$B$が通過する領域の体積を求めよ。
ただし、回転の向きは回転後の$B$の中心が
$(\cos \alpha,\sin \alpha,0)$になるように選ぶものとする。
$2025$年名古屋大学理系過去問題
mathematical formula : Shirotan's cute kawaii math show #数学 #小学生テスト #高校入試 #勉強 #高校受験

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
x²-5x+3=0の解a,b
1/a+1/b=?
この動画を見る
x²-5x+3=0の解a,b
1/a+1/b=?
福田のおもしろ数学496〜少なくとも1つは−1より大きくないことの証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
実数$a,b,c,d$が次の式を満たしている。
$a+b+c+d=-2$
$ab+ac+ad+bc+bd+cd=0$
このとき、$a,b,c,d$の少なくとも$1$つは
$-1$より大きくないことを証明して下さい。
この動画を見る
実数$a,b,c,d$が次の式を満たしている。
$a+b+c+d=-2$
$ab+ac+ad+bc+bd+cd=0$
このとき、$a,b,c,d$の少なくとも$1$つは
$-1$より大きくないことを証明して下さい。
福田のおもしろ数学495〜次数の高い連立方程式

単元:
#連立方程式#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^3+3ab^2+3ac^2-6abc=1 \\
b^3+3ba^2+3bc^2-6abc=1 \\\
c^2+3ca^2+3cb^2-6abc=1
\end{array}
\right.
\end{eqnarray}$
を満たす実数$a,b,c$を求めよ。
この動画を見る
連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^3+3ab^2+3ac^2-6abc=1 \\
b^3+3ba^2+3bc^2-6abc=1 \\\
c^2+3ca^2+3cb^2-6abc=1
\end{array}
\right.
\end{eqnarray}$
を満たす実数$a,b,c$を求めよ。
