 数列とその和(等差・等比・階差・Σ)
数列とその和(等差・等比・階差・Σ)
 数列とその和(等差・等比・階差・Σ)
数列とその和(等差・等比・階差・Σ)
計算しないで答えを出せ!奈良教育大

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#奈良教育大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$m, n$は自然数、$m$は定数
$S(n)=1+2+3+...+mn$
$T(n)=S(n)-(1~mn間のmの倍数の和)$
$\displaystyle \lim_{ n \to \infty } \frac {T(n)}{S(n)}$
この動画を見る
$m, n$は自然数、$m$は定数
$S(n)=1+2+3+...+mn$
$T(n)=S(n)-(1~mn間のmの倍数の和)$
$\displaystyle \lim_{ n \to \infty } \frac {T(n)}{S(n)}$
【数B】【数列】nは自然数とする。連立不等式0≦x≦n, y≧0, y≦n²-x²の表す領域に含まれる格子点の個数を求めよ。

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
nは自然数とする。連立不等式0≦x≦n, y≧0, y≦n²-x²の表す領域に含まれる格子点の個数を求めよ。
この動画を見る
nは自然数とする。連立不等式0≦x≦n, y≧0, y≦n²-x²の表す領域に含まれる格子点の個数を求めよ。
【数B】【数列】nは自然数とする。座標平面上の3点(0,0),(3n,0)(0,n)を頂点とする三角形の周および内部にある格子点の個数を求めよ。

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
nは自然数とする。座標平面上の3点(0,0),(3n,0)(0,n)を頂点とする三角形の周および内部にある格子点の個数を求めよ。
この動画を見る
nは自然数とする。座標平面上の3点(0,0),(3n,0)(0,n)を頂点とする三角形の周および内部にある格子点の個数を求めよ。
【数B】【数列】(x+1)(x+2)(x+3)……(x+n)の展開式において、次の係数を求めよ。(1)xのn-1乗の係数(2)xのn-2乗の係数(n≧2)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
(x+1)(x+2)(x+3)……(x+n)の展開式において、次の係数を求めよ。
(1)xのn-1乗の係数
(2)xのn-2乗の係数(n≧2)
この動画を見る
(x+1)(x+2)(x+3)……(x+n)の展開式において、次の係数を求めよ。
(1)xのn-1乗の係数
(2)xのn-2乗の係数(n≧2)
【高校数学】階差数列の漸化式~分かりやすく~ 3-17【数学B】

【数B】【数列】西暦2022年1月1日に100万円を年利率7で借りた人がいる。2022年12月31日を1回とし毎年年末に等額ずつ支払い、2024年年末に完済することにする。毎年年末に支払う金額を求めよ

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
西暦2022年1月1日に100万円を年利率7で借りた人がいる。この返済は、2022年12月31日を第1回とし、その後、毎年年末に等額ずつ支払い、2024年年末に完済することにする。毎年年末に支払う金額を求めよ。ただし、1.07³=1.255として計算し、1円未満は切り上げよ。
この動画を見る
西暦2022年1月1日に100万円を年利率7で借りた人がいる。この返済は、2022年12月31日を第1回とし、その後、毎年年末に等額ずつ支払い、2024年年末に完済することにする。毎年年末に支払う金額を求めよ。ただし、1.07³=1.255として計算し、1円未満は切り上げよ。
【数B】【数列】0<a<bとする。数列a,u,v,w,bが等差であり、数列a,x,y,z,bが等比(公比は実数)である。(1) uwとxzの大小を比較せよ。(2) u+wと、x+zの大小を比較せよ。

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
0<a<bとする。数列a,u,v,w,bが等差数列であり、数列a,x,y,z,bが等比数列(公比は実数)である。
(1) uwとxzの大小を比較せよ。
(2) u+wと、x+zの大小を比較せよ。
この動画を見る
0<a<bとする。数列a,u,v,w,bが等差数列であり、数列a,x,y,z,bが等比数列(公比は実数)である。
(1) uwとxzの大小を比較せよ。
(2) u+wと、x+zの大小を比較せよ。
福田のおもしろ数学579〜自然対数の底が階乗の逆数の和で表せる証明

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$a_n=\displaystyle \int_{0}^{1} \dfrac{(1-x)^{n-1}}{(n-1)!}e^x dx$を利用して
$e=1+\dfrac{1}{1!}+\dfrac{1}{2!}+\dfrac{1}{3!}+\cdots$
を証明して下さい。
この動画を見る
$a_n=\displaystyle \int_{0}^{1} \dfrac{(1-x)^{n-1}}{(n-1)!}e^x dx$を利用して
$e=1+\dfrac{1}{1!}+\dfrac{1}{2!}+\dfrac{1}{3!}+\cdots$
を証明して下さい。
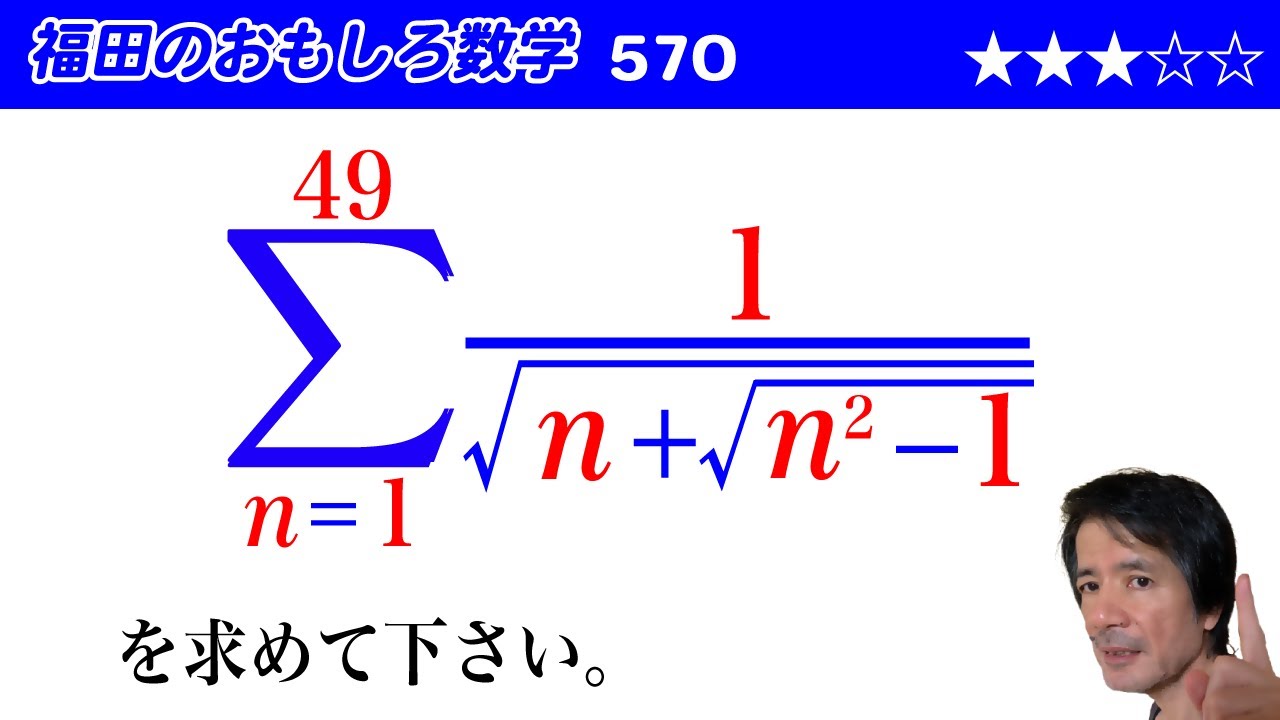
福田のおもしろ数学570〜無理式のシグマ計算
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \sum_{n=1}^{49} \dfrac{1}{\sqrt{n+\sqrt{n^2-1}}}$を求めて下さい。
この動画を見る
$\displaystyle \sum_{n=1}^{49} \dfrac{1}{\sqrt{n+\sqrt{n^2-1}}}$を求めて下さい。
福田のおもしろ数学562〜連立漸化式で定まる数列に関する証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
数列$\{a_k\},\{b_k\}$が$a_0=b_0=0$,
$a_{k+1}=b_k,b_{k+1}=\dfrac{a_k b_k+a_k+1}{b_k+1}$
で定義されている。
$a_{2024}+b_{2024}\geqq 88$
であることを証明して下さい。
この動画を見る
数列$\{a_k\},\{b_k\}$が$a_0=b_0=0$,
$a_{k+1}=b_k,b_{k+1}=\dfrac{a_k b_k+a_k+1}{b_k+1}$
で定義されている。
$a_{2024}+b_{2024}\geqq 88$
であることを証明して下さい。
福田の数学〜早稲田大学2025教育学部第1問(1)〜シグマ計算

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(1)$k$を自然数とする。次の数
$-1^2+2^2-3^2+4^2-5^2+6^2- \cdots -(2k-1)^2+(2k)^2$
を$k$を用いて表せ。
$2025$年早稲田大学教育学部過去問題
この動画を見る
$\boxed{1}$
(1)$k$を自然数とする。次の数
$-1^2+2^2-3^2+4^2-5^2+6^2- \cdots -(2k-1)^2+(2k)^2$
を$k$を用いて表せ。
$2025$年早稲田大学教育学部過去問題
福田の数学〜早稲田大学2025社会科学部第2問〜階差数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
数列$\{a_n\}$の階差数列を$\{b_n\}$、すなわち
$b_n=a_{n+1}-a_n \quad (n=1,2,3,\cdots)$
とする。次の問いに答えよ。
(1)$a_n=-\dfrac{1}{n}$のとき、
$b_n$を$n$の式で表す。
(2)$b_n=\dfrac{1}{n(n+1)}$のとき、
$a_n$を$n$の式で表せ。ただし、$a_1=1$とする。
(3)数列$\{b_n\}$が以下を満たすとき、
$a_n$を$n$の式で表せ。ただし、$a_1=1$とする。
$\begin{eqnarray}
\left\{
\begin{array}{l}
b_1=1 \\
b_n=n(n+1) \quad (n\geqq 2)
\end{array}
\right.
\end{eqnarray}$
$2025$念早稲田大学社会科学部過去問題
この動画を見る
$\boxed{2}$
数列$\{a_n\}$の階差数列を$\{b_n\}$、すなわち
$b_n=a_{n+1}-a_n \quad (n=1,2,3,\cdots)$
とする。次の問いに答えよ。
(1)$a_n=-\dfrac{1}{n}$のとき、
$b_n$を$n$の式で表す。
(2)$b_n=\dfrac{1}{n(n+1)}$のとき、
$a_n$を$n$の式で表せ。ただし、$a_1=1$とする。
(3)数列$\{b_n\}$が以下を満たすとき、
$a_n$を$n$の式で表せ。ただし、$a_1=1$とする。
$\begin{eqnarray}
\left\{
\begin{array}{l}
b_1=1 \\
b_n=n(n+1) \quad (n\geqq 2)
\end{array}
\right.
\end{eqnarray}$
$2025$念早稲田大学社会科学部過去問題
福田のおもしろ数学554〜nのn乗根の最大と最小

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$a_1=1,a_n=\sqrt[n]{n} \quad (n\geqq 2)$
で定める数列$\{a_n\}$について
(1)$n\geqq 3$のとき$\dfrac{a_{n+1}}{a_n} \lt 1$を示せ。
(2)この数列の最大の項と
最小の項を求めよ。
この動画を見る
$a_1=1,a_n=\sqrt[n]{n} \quad (n\geqq 2)$
で定める数列$\{a_n\}$について
(1)$n\geqq 3$のとき$\dfrac{a_{n+1}}{a_n} \lt 1$を示せ。
(2)この数列の最大の項と
最小の項を求めよ。
福田のおもしろ数学545〜最大公約数と最小公倍数の商で定まる数列

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
自然数の列$\{a_n\}$が次の性質を満たしている。
$a_n=\dfrac{Icm(a_{n-1},a_{n-2})}{gcd(a_{n-1},a_{n-2})} \quad (n\geqq 2)$
$a_{560}=560,a_{1600}=1600$のとき
$a_{2025}$を求めて下さい。
この動画を見る
自然数の列$\{a_n\}$が次の性質を満たしている。
$a_n=\dfrac{Icm(a_{n-1},a_{n-2})}{gcd(a_{n-1},a_{n-2})} \quad (n\geqq 2)$
$a_{560}=560,a_{1600}=1600$のとき
$a_{2025}$を求めて下さい。
福田のおもしろ数学539〜部分和がすべて正になるような数列を作れるか

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
総和が$1$である$2025$個の整数が円形に
並んでいる。
ある整数から出発して反時計回りでこれらの
整数を一列に並べ$a_1,a_2,a_3,\cdots, a_{2025}$とする。
これらの部分和$S_n=\displaystyle \sum_{k=1}^{n} a_k \quad (n=1,2,\cdots ,2025)$
がすべて正となるようにできるか?
この動画を見る
総和が$1$である$2025$個の整数が円形に
並んでいる。
ある整数から出発して反時計回りでこれらの
整数を一列に並べ$a_1,a_2,a_3,\cdots, a_{2025}$とする。
これらの部分和$S_n=\displaystyle \sum_{k=1}^{n} a_k \quad (n=1,2,\cdots ,2025)$
がすべて正となるようにできるか?
福田のおもしろ数学538〜数列の一般項を1つの式で表す

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
数列
$1,1,2,2,3,3,4,4,\cdots $
の一般項を$1$つの式で表せ。
この動画を見る
数列
$1,1,2,2,3,3,4,4,\cdots $
の一般項を$1$つの式で表せ。
【数B】【数列】初項4、公差5の等差数列{a_n}と、初項8,公差7の等差数列{b_n}について、これら2つの数列に共通に含まれている項を、順に並べてできる数列{c_n}の一般項を求めよ。

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
初項4、公差5の等差数列${a_n}$と、初項8,公差7の等差数列${b_n}$について、これら2つの数列に共通に含まれている項を、順に並べてできる数列${c_n}$の一般項を求めよ。
この動画を見る
初項4、公差5の等差数列${a_n}$と、初項8,公差7の等差数列${b_n}$について、これら2つの数列に共通に含まれている項を、順に並べてできる数列${c_n}$の一般項を求めよ。
【数B】【数列】初項a、公差dである等差数列の初項から第n項までの和をSnとする。m≠nであって、Sm=Snならば、Sn+m=0であることを証明せよ。

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
初項a、公差dである等差数列の初項から第n項までの和をSnとする。m≠nであって、$S_m=S_n$ならば、$S_{n+m}$=0であることを証明せよ。
この動画を見る
初項a、公差dである等差数列の初項から第n項までの和をSnとする。m≠nであって、$S_m=S_n$ならば、$S_{n+m}$=0であることを証明せよ。
【数B】【数列】a、bは、正の整数でa<bとする。aとbの間にあって、5を分母とするすべての分数(整数を除く)の和を求めよ。

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
a、bは、正の整数でa<bとする。aとbの間にあって、5を分母とするすべての分数(整数を除く)の和を求めよ。
この動画を見る
a、bは、正の整数でa<bとする。aとbの間にあって、5を分母とするすべての分数(整数を除く)の和を求めよ。
福田の数学〜大阪大学2025文系第2問〜漸化式と数列の和

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
次の条件によって定められる数列$\{ a_n\}$がある。
$a_1=1,a_{n+1}=\dfrac{2n-1}{2n}a_n \quad (n=1,2,3,\cdots)$
(1)正の整数$k,\ell$に対して
$\dfrac{k}{k+\ell-1}a_{k+1}a_{\ell}+\dfrac{\ell}{k+\ell-1}a_ka_{\ell+1}=a_ka_{\ell}$
が成り立つことを示せ。
(2)正の整数$m$に対して
$\displaystyle \sum_{k=1}^{m} a_ka_{m-K+1}=1$
が成り立つことを示せ。
$2025$年大阪大学文系過去問題
この動画を見る
$\boxed{2}$
次の条件によって定められる数列$\{ a_n\}$がある。
$a_1=1,a_{n+1}=\dfrac{2n-1}{2n}a_n \quad (n=1,2,3,\cdots)$
(1)正の整数$k,\ell$に対して
$\dfrac{k}{k+\ell-1}a_{k+1}a_{\ell}+\dfrac{\ell}{k+\ell-1}a_ka_{\ell+1}=a_ka_{\ell}$
が成り立つことを示せ。
(2)正の整数$m$に対して
$\displaystyle \sum_{k=1}^{m} a_ka_{m-K+1}=1$
が成り立つことを示せ。
$2025$年大阪大学文系過去問題
福田の数学〜大阪大学2025理系第5問〜確率漸化式

単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{5}$
投げたときに表と裏の出る確率が
それぞれ$\dfrac{1}{2}$のコインがある。
$A,B,C$の$3$文字を$BAC$のように$1$個ずつ
すべて並べて得られる文字列に対して、
コインを投げて次の操作を行う。
・表がで出たら文字列の左から$1$文字目と
$2$文字目を入れかえる。
・裏がで出たら文字列の左から$2$文字目と
$3$文字目を入れかえる。
例えば、文字列が$BAC$であるときに、
$2$回続けてコインを投げて表、裏の順に出た
とすると、文字列は$BAC$から$ABC$を経て
$ACB$となる。
最初の文字列は$ABC$であるとする。
コインを$n$回続けて投げたあとの文字列が
$ABC$である確率を$p_n$とし、
$BCA$である確率を$q_n$とする。
(1)$k$を正の整数とするとき、
$p_{2k}-q_{2k}$を求めよ。
(2)$n$を正の整数とするとき、
$p_n$を求めよ。
$2025$年大阪大学理系過去問題
この動画を見る
$\boxed{5}$
投げたときに表と裏の出る確率が
それぞれ$\dfrac{1}{2}$のコインがある。
$A,B,C$の$3$文字を$BAC$のように$1$個ずつ
すべて並べて得られる文字列に対して、
コインを投げて次の操作を行う。
・表がで出たら文字列の左から$1$文字目と
$2$文字目を入れかえる。
・裏がで出たら文字列の左から$2$文字目と
$3$文字目を入れかえる。
例えば、文字列が$BAC$であるときに、
$2$回続けてコインを投げて表、裏の順に出た
とすると、文字列は$BAC$から$ABC$を経て
$ACB$となる。
最初の文字列は$ABC$であるとする。
コインを$n$回続けて投げたあとの文字列が
$ABC$である確率を$p_n$とし、
$BCA$である確率を$q_n$とする。
(1)$k$を正の整数とするとき、
$p_{2k}-q_{2k}$を求めよ。
(2)$n$を正の整数とするとき、
$p_n$を求めよ。
$2025$年大阪大学理系過去問題
福田の数学〜立教大学2025経済学部第1問(3)〜等差中項と等比中項

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(3)$x,y,z$は実数であり、$x\lt y$を満たすとする。
$3$つの数$3,x,y$がこの順に等差数列となり、
さらに$4$つの数$4,x,y,z$がこの順に
等差数列となるとき、
$x=\boxed{ウ}、\boxed{エ}、\boxed{オ}$である。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{1}$
(3)$x,y,z$は実数であり、$x\lt y$を満たすとする。
$3$つの数$3,x,y$がこの順に等差数列となり、
さらに$4$つの数$4,x,y,z$がこの順に
等差数列となるとき、
$x=\boxed{ウ}、\boxed{エ}、\boxed{オ}$である。
$2025$年立教大学経済学部過去問題
福田のおもしろ数学505〜フィボナッチ数列の性質

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
フィボナッチ数列$\{f_n\}$
$f_1=f_2=1,f_{n+2}=f_{n+1}+f_n$
に対し、
$f_m・f_n=mn$
を満たす自然数の組$(m,n)$をすべて求めて下さい。
この動画を見る
フィボナッチ数列$\{f_n\}$
$f_1=f_2=1,f_{n+2}=f_{n+1}+f_n$
に対し、
$f_m・f_n=mn$
を満たす自然数の組$(m,n)$をすべて求めて下さい。
福田の数学〜慶應義塾大学2025経済学部第2問〜数列の和から一般項を求める

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
数列$\{a_n\}$に対して
$T_n=\displaystyle \sum_{k=1}^n \dfrac{(k+2)!}{(k-1)!}a_k (n=1,2,3,\cdots)$
とおくとき、
$T_n=\left(n-\dfrac{1}{2}\right)^2 (n=1,2,3,\cdots)$
が成り立つとする。ただし、$0!=1$である。
(1)$a_1=\dfrac{\boxed{ア}}{\boxed{イウ}},a_2=\dfrac{\boxed{エ}}{\boxed{オ}}$である。
(2)$n\geqq 2$に対して$T_n-T_{n-1}=\boxed{カ}n-\boxed{キ}$が
成り立つから、
$a_n=r^n\dfrac{n-\boxed{ク}}{(n+s)(n+t)(n+u)} (n=2,3,4,\cdots)$
である。ただし、ここに$r=\boxed{ケ}$であり、
$s\lt t \lt u$として$s=\boxed{コ},t=\boxed{サ},u=\boxed{シ}$である。
$2025$年慶應義塾大学経済学部過去問題
この動画を見る
$\boxed{2}$
数列$\{a_n\}$に対して
$T_n=\displaystyle \sum_{k=1}^n \dfrac{(k+2)!}{(k-1)!}a_k (n=1,2,3,\cdots)$
とおくとき、
$T_n=\left(n-\dfrac{1}{2}\right)^2 (n=1,2,3,\cdots)$
が成り立つとする。ただし、$0!=1$である。
(1)$a_1=\dfrac{\boxed{ア}}{\boxed{イウ}},a_2=\dfrac{\boxed{エ}}{\boxed{オ}}$である。
(2)$n\geqq 2$に対して$T_n-T_{n-1}=\boxed{カ}n-\boxed{キ}$が
成り立つから、
$a_n=r^n\dfrac{n-\boxed{ク}}{(n+s)(n+t)(n+u)} (n=2,3,4,\cdots)$
である。ただし、ここに$r=\boxed{ケ}$であり、
$s\lt t \lt u$として$s=\boxed{コ},t=\boxed{サ},u=\boxed{シ}$である。
$2025$年慶應義塾大学経済学部過去問題
福田のおもしろ数学499〜1分チャレンジ!数値計算

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\dfrac{(4\times 7+2)(6\times 9+2)(8\times 11+2)\cdots}{(5\times 8 +2)(7\times 10 +2)(9\times 12 +2)\cdots }$
$\dfrac{\cdots (100\times 103+2)}{\cdots (99\times 102+2)}$
を計算して下さい。
この動画を見る
$\dfrac{(4\times 7+2)(6\times 9+2)(8\times 11+2)\cdots}{(5\times 8 +2)(7\times 10 +2)(9\times 12 +2)\cdots }$
$\dfrac{\cdots (100\times 103+2)}{\cdots (99\times 102+2)}$
を計算して下さい。
福田の数学〜東京科学大学(旧・東京工業大学)2025理系第4問〜フィボナッチ数列と無限級数の和

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
数列$\{a_n\}$を
$a_1=a_2=1,a_{n+2}=a_{n+1}+a_n (n=1,2,3,\cdots)$
により定め、数列$\{b_n\}$を
$\tan b_n=\dfrac{1}{a_n}$
により定める。
ただし、$0\lt b_n \lt \dfrac{\pi}{2}$であるものとする。
(1)$n\geqq 2$に対して、$a_{n+1}a_{n-1}-{a_n}^2$を求めよ。
(2)$m\geqq 1$($m$は整数)に対して、
$a_{2m}・\tan(b_{2m+1}+b_{2m+2})$を求めよ。
(3)無限級数$\displaystyle \sum_{m=0}^{\infty} b_{2m+1}$を求めよ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
この動画を見る
$\boxed{4}$
数列$\{a_n\}$を
$a_1=a_2=1,a_{n+2}=a_{n+1}+a_n (n=1,2,3,\cdots)$
により定め、数列$\{b_n\}$を
$\tan b_n=\dfrac{1}{a_n}$
により定める。
ただし、$0\lt b_n \lt \dfrac{\pi}{2}$であるものとする。
(1)$n\geqq 2$に対して、$a_{n+1}a_{n-1}-{a_n}^2$を求めよ。
(2)$m\geqq 1$($m$は整数)に対して、
$a_{2m}・\tan(b_{2m+1}+b_{2m+2})$を求めよ。
(3)無限級数$\displaystyle \sum_{m=0}^{\infty} b_{2m+1}$を求めよ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
【暗記じゃない…!】数列:興南高等学校~全国入試問題解法
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
1/1,1/2,2/2,1/3,2/3,3/3,1/4,2/4,3/4,4/4,・・・
の時、左から85番目の分数?
この動画を見る
1/1,1/2,2/2,1/3,2/3,3/3,1/4,2/4,3/4,4/4,・・・
の時、左から85番目の分数?
【数B】【数列】自然数の式の証明3 ※問題文は概要欄

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
$n$は自然数とする。
$6^n+4= (5+1)^n+4$と変形することで、$6^n+4$が$5$の倍数であることを、二項定理を利用して証明せよ。
この動画を見る
$n$は自然数とする。
$6^n+4= (5+1)^n+4$と変形することで、$6^n+4$が$5$の倍数であることを、二項定理を利用して証明せよ。
【数B】【数列】自然数の式の証明2 ※問題文は概要欄

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
$n$は整数とする。
(1)連続する2個の整数には、必ず$2$の倍数が含まれることを利用して、 $n^2+3n$が$2$の倍数であることを証明せよ。
(2)連続する3個の整数には、必ず$3$の倍数が含まれることを利用して、 $4n^3+3n^2+2n$が$3$の倍数であることを証明せよ。
この動画を見る
$n$は整数とする。
(1)連続する2個の整数には、必ず$2$の倍数が含まれることを利用して、 $n^2+3n$が$2$の倍数であることを証明せよ。
(2)連続する3個の整数には、必ず$3$の倍数が含まれることを利用して、 $4n^3+3n^2+2n$が$3$の倍数であることを証明せよ。
【数B】【数列】自然数の式の証明1 ※問題文は概要欄

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1) 整数$n$を$2$で割った余りで分類することで、$3n^2-n$が$2$の倍数であることを証明せよ。
(2) 整数$n$を$3$で割った余りで分類することで、 $n^3-n+9$が$3$の倍数であることを証明せよ。
この動画を見る
(1) 整数$n$を$2$で割った余りで分類することで、$3n^2-n$が$2$の倍数であることを証明せよ。
(2) 整数$n$を$3$で割った余りで分類することで、 $n^3-n+9$が$3$の倍数であることを証明せよ。
