数列の極限
数列の極限
 数列の極限
数列の極限
信州大 三次方程式の解の極限値

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#数列の極限#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#信州大学#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2x^3+3nx^2-3(n+1)=0(n$自然数$)$
(1)
$n$の値に関わらず正の解をただ一つだけもつことを示せ
(2)
正の解を$\alpha_n$とする。
$\displaystyle \lim_{ n \to \infty }\alpha_n$を求めよ
出典:1998年信州大学 過去問
この動画を見る
$2x^3+3nx^2-3(n+1)=0(n$自然数$)$
(1)
$n$の値に関わらず正の解をただ一つだけもつことを示せ
(2)
正の解を$\alpha_n$とする。
$\displaystyle \lim_{ n \to \infty }\alpha_n$を求めよ
出典:1998年信州大学 過去問
素数の逆数の和は収束か発散か?杉山&ヨビノリたくみ

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \frac{1}{2}+\displaystyle \frac{1}{3}+\displaystyle \frac{1}{5}+…+\displaystyle \frac{1}{p}+…=?$
この動画を見る
$\displaystyle \frac{1}{2}+\displaystyle \frac{1}{3}+\displaystyle \frac{1}{5}+…+\displaystyle \frac{1}{p}+…=?$
もっちゃんと真面目に数学 素数、完全数、約数の個数、総和、メルセンヌ素数、調和級数発散のお話

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
素数、完全数、約数の個数、総和、メルセンヌ素数、調和級数発散 解説動画です
この動画を見る
素数、完全数、約数の個数、総和、メルセンヌ素数、調和級数発散 解説動画です
東工大 極限 東大大学院 数学科卒 杉山さん

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$自然数
半径$\displaystyle \frac{1}{n}$の円を重ならないように、半径1の円に外接させる。
外接する円の最大個数を$a_{n}$とする。
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{a_{n}}{n}$を求めよ
出典:1992年東京工業大学 過去問
この動画を見る
$n$自然数
半径$\displaystyle \frac{1}{n}$の円を重ならないように、半径1の円に外接させる。
外接する円の最大個数を$a_{n}$とする。
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{a_{n}}{n}$を求めよ
出典:1992年東京工業大学 過去問
What is e?? The essence of e. Why (e^x)’=e^x
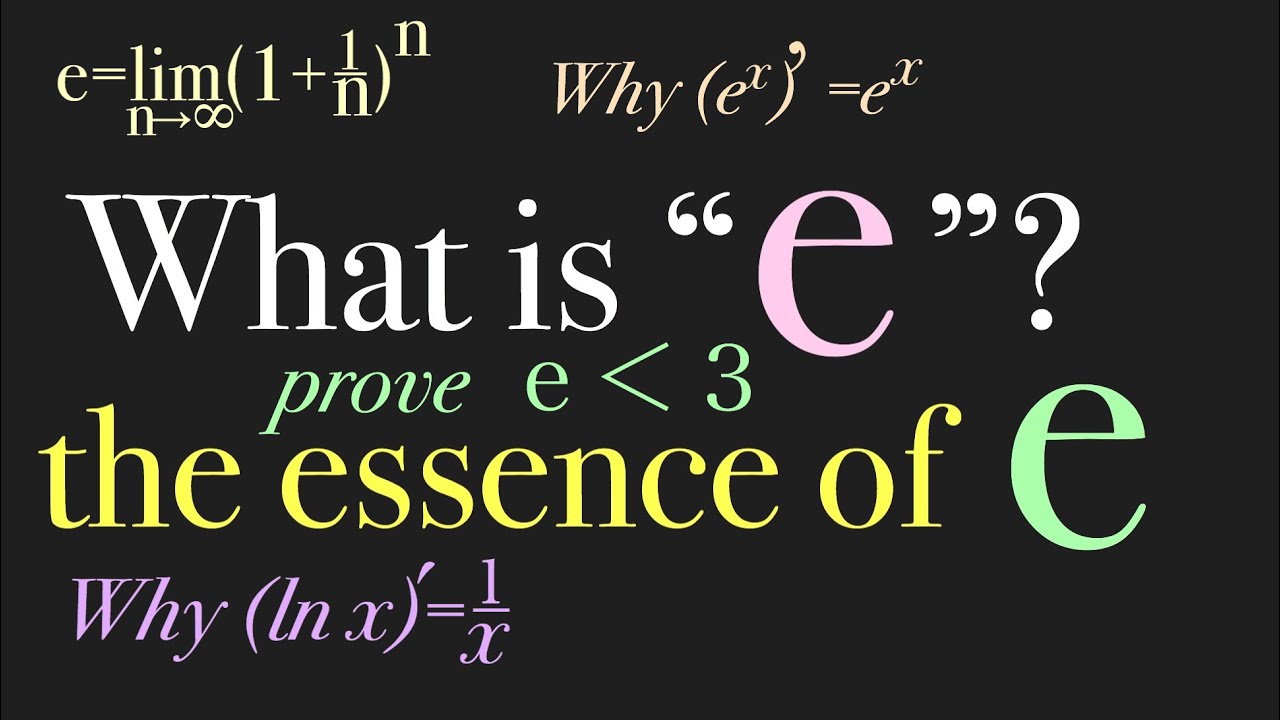
単元:
#関数と極限#微分とその応用#数列の極限#微分法#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)
$\displaystyle \lim_{ n \to \infty }(1+\displaystyle \frac{1}{n})^n$
$\displaystyle \lim_{ h \to \infty }(1+h)^{\displaystyle \frac{1}{h}}$
(2)
$y=e^x$
(3)
動画内の図を見て求めよ
(4)
$y=log_{e}x$
$y^1=\displaystyle \frac{1}{x}$
この動画を見る
(1)
$\displaystyle \lim_{ n \to \infty }(1+\displaystyle \frac{1}{n})^n$
$\displaystyle \lim_{ h \to \infty }(1+h)^{\displaystyle \frac{1}{h}}$
(2)
$y=e^x$
(3)
動画内の図を見て求めよ
(4)
$y=log_{e}x$
$y^1=\displaystyle \frac{1}{x}$
名古屋市立(医)積分 初のVチューバー解説 アイシアちゃん/仮の姿は東大数学科院卒杉山聡

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#積分とその応用#数列の極限#微分法#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#名古屋市立大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n:$自然数
$S_{n}:y=e^{-x}\sin x$と$y$軸の囲む面積$((n-1)\pi \leqq x \leqq n\pi)$
(1)
$S_{n}$は?
(2)
$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=1}^n S_{k}$は?
この動画を見る
$n:$自然数
$S_{n}:y=e^{-x}\sin x$と$y$軸の囲む面積$((n-1)\pi \leqq x \leqq n\pi)$
(1)
$S_{n}$は?
(2)
$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=1}^n S_{k}$は?
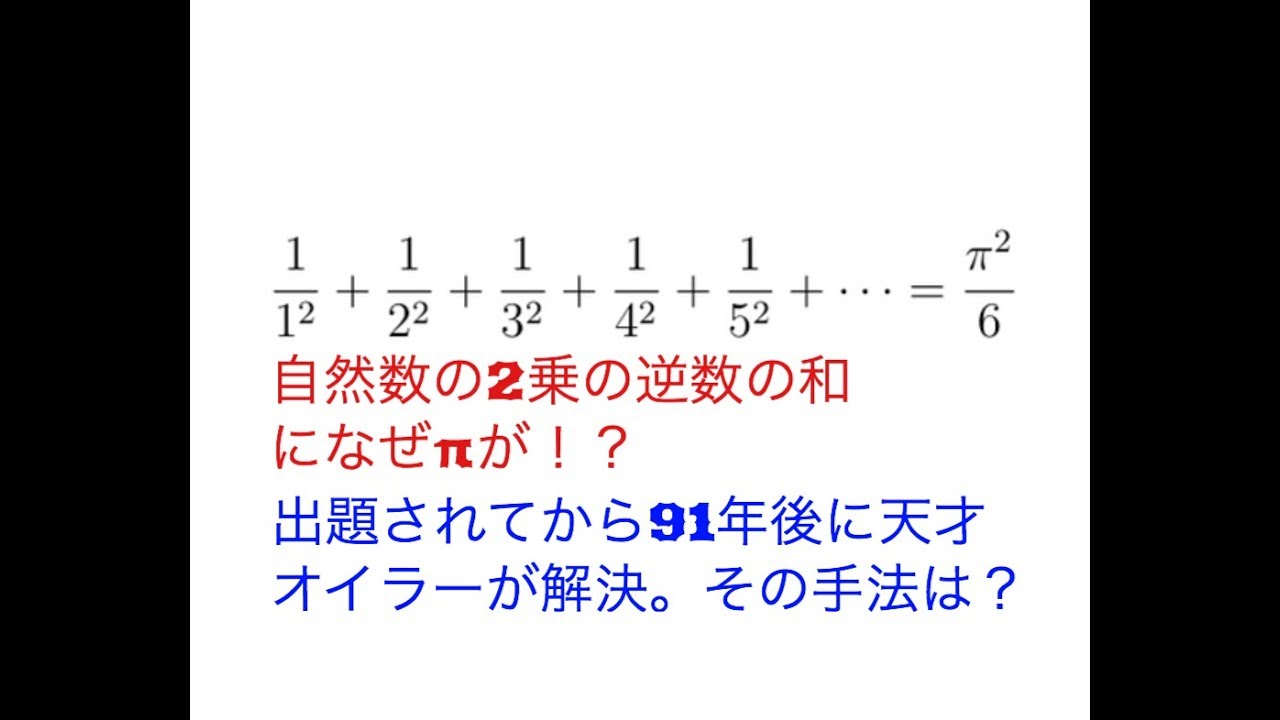
でんがんとヨビノリを脇に添えてもっちゃんとバーゼル問題を解く!

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\frac{1}{1^2}+$$\frac{1}{2^2}+$$\frac{1}{3^2}・・・+$$\frac{1}{n^2}=$$\frac{\pi^2}{6}$
この動画を見る
$\frac{1}{1^2}+$$\frac{1}{2^2}+$$\frac{1}{3^2}・・・+$$\frac{1}{n^2}=$$\frac{\pi^2}{6}$
慶應(医)3次方程式 ほぼ文系知識で解けます Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
慶応義塾大学過去問題
$8x^3-6x+1=0$の3つの解をα,β,γ
(1)0<x<1の範囲にある実数解の個数
(2)$\displaystyle\sum_{n=0}^{\infty}(α^n+β^n+γ^n)$
この動画を見る
慶応義塾大学過去問題
$8x^3-6x+1=0$の3つの解をα,β,γ
(1)0<x<1の範囲にある実数解の個数
(2)$\displaystyle\sum_{n=0}^{\infty}(α^n+β^n+γ^n)$
浜松医大 確率 サイコロ4個・n個 高校数学 Mathematics Japanese university entrance exam

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
浜松医科大学過去問題
(1)4個のサイコロを投げて1,1,2,2のように同じ目がちょうど2個ずつでる確率
(2)n=4,5,6・・・としてn個のサイコロを投げて、少なくとも(n-2)個のサイコロに同じ目がそろって出る確率$P_n$
また$\displaystyle\lim_{n \to \infty}\frac{P_n+1}{P_n}$
この動画を見る
浜松医科大学過去問題
(1)4個のサイコロを投げて1,1,2,2のように同じ目がちょうど2個ずつでる確率
(2)n=4,5,6・・・としてn個のサイコロを投げて、少なくとも(n-2)個のサイコロに同じ目がそろって出る確率$P_n$
また$\displaystyle\lim_{n \to \infty}\frac{P_n+1}{P_n}$
東大 入試問題 天才ヨビノリのたくみさんが解説 Mathematics Japanese university entrance exam

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
東京大学1990
$a_n=\displaystyle\sum_{k=1}^n\frac{1}{\sqrt k}$,$b_n=\displaystyle\sum_{k=1}^n\frac{1}{\sqrt {2k+1}}$
とするとき、$\displaystyle\lim_{n \to \infty}a_n,\displaystyle\lim_{n \to \infty}\frac{b_n}{a_n}$を求めよ。
この動画を見る
東京大学1990
$a_n=\displaystyle\sum_{k=1}^n\frac{1}{\sqrt k}$,$b_n=\displaystyle\sum_{k=1}^n\frac{1}{\sqrt {2k+1}}$
とするとき、$\displaystyle\lim_{n \to \infty}a_n,\displaystyle\lim_{n \to \infty}\frac{b_n}{a_n}$を求めよ。
東北大 確率漸化式 高校数学 Japanese university entrance exam questions

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
東北大学過去問題
立方体の上面に印をつける。床に接する面の4辺のうちから1辺を等確率で選び、その1辺を軸に立方体を倒す。
n回倒したとき、印の面が側面にくる確率を$a_n$,底面にくる確率を$b_n$
(1)$a_n$をnで表せ
(2)$b_n$をnで表し、$\displaystyle\lim_{n \to \infty}b_n$を求めよ
この動画を見る
東北大学過去問題
立方体の上面に印をつける。床に接する面の4辺のうちから1辺を等確率で選び、その1辺を軸に立方体を倒す。
n回倒したとき、印の面が側面にくる確率を$a_n$,底面にくる確率を$b_n$
(1)$a_n$をnで表せ
(2)$b_n$をnで表し、$\displaystyle\lim_{n \to \infty}b_n$を求めよ
日本医科大学 バーゼル問題 高校数学 Japanese university entrance exam questions

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
日本医科大学過去問題
$abc=1$ $a>0,b>0,c>0$
$\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \geqq \sqrt{a} + \sqrt{b} +\sqrt{c}$を示せ
$\frac{1}{a}+\frac{1}{b}+\frac{1}{c} - \sqrt{a} - \sqrt{b} -\sqrt{c}$
$n \to \infty \frac{3}{2} \leqq 1 + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots + \frac{1}{n^2} \leqq 2$
この動画を見る
日本医科大学過去問題
$abc=1$ $a>0,b>0,c>0$
$\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \geqq \sqrt{a} + \sqrt{b} +\sqrt{c}$を示せ
$\frac{1}{a}+\frac{1}{b}+\frac{1}{c} - \sqrt{a} - \sqrt{b} -\sqrt{c}$
$n \to \infty \frac{3}{2} \leqq 1 + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots + \frac{1}{n^2} \leqq 2$
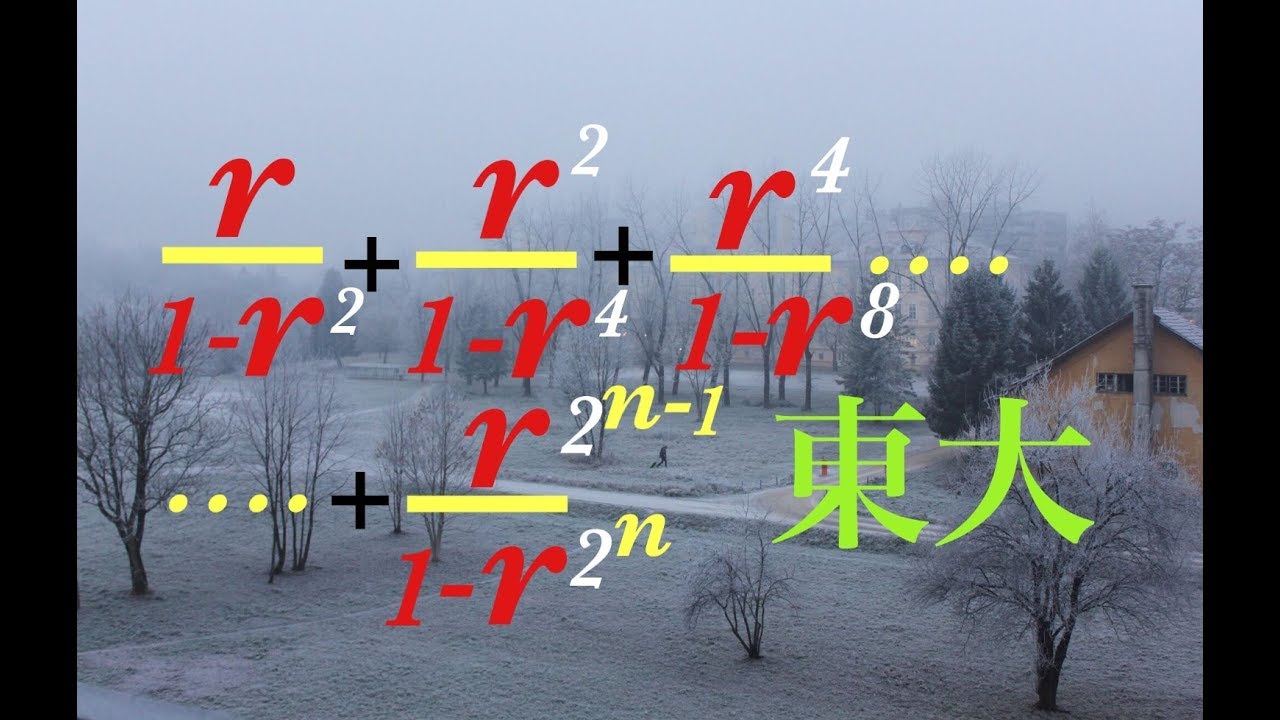
東大入試問題 無限級数 数列の和 Japanese university entrance exam questions Tokyo University
単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
東京大学過去問題
無限級数
$\frac{r}{1-r^2}$+$\frac{r^2}{1-r^4}$+$\frac{r^4}{1-r^8}$+$\cdots$+$\frac{r^{2^{n-1}}}{1-r^{2^{n}}}$
この動画を見る
東京大学過去問題
無限級数
$\frac{r}{1-r^2}$+$\frac{r^2}{1-r^4}$+$\frac{r^4}{1-r^8}$+$\cdots$+$\frac{r^{2^{n-1}}}{1-r^{2^{n}}}$
奇数の4乗の逆数の和 オイラー級数 πが登場

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\frac{1}{1^4}+\frac{1}{3^4}+\frac{1}{5^4}+\frac{1}{7^4}+\cdots=\dfrac{\pi^4}{96}$
この動画を見る
$\frac{1}{1^4}+\frac{1}{3^4}+\frac{1}{5^4}+\frac{1}{7^4}+\cdots=\dfrac{\pi^4}{96}$
分母が奇数の分数を無限に足したい引いたり、何故か答えにπが登場

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\frac{1}{1}-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}+\cdots=\dfrac{\pi}{4}$
この動画を見る
$\frac{1}{1}-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}+\cdots=\dfrac{\pi}{4}$
自然数の4乗の逆数の和 オイラー級数(Euler) やっぱりπが登場

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\frac{1}{1^4}$+$\frac{1}{2^4}$+$\frac{1}{3^4}$+$\frac{1}{4^4}$+$\cdots$$\frac{1}{n^4}$=$\frac{\pi^4}{90}$
この動画を見る
$\frac{1}{1^4}$+$\frac{1}{2^4}$+$\frac{1}{3^4}$+$\frac{1}{4^4}$+$\cdots$$\frac{1}{n^4}$=$\frac{\pi^4}{90}$
【高校数学】数Ⅲ-74 数列の極限⑩(無限等比級数)

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の無限級数が収束するような実数$x$の値の範囲と、
収束するときの和を求めよ。
①$1+\dfrac{x}{3}+\dfrac{x^2}{9}+\dfrac{x^3}{27}+・・・$
②$(x-4)+\dfrac{x(x-4)}{2x-4}+\dfrac{x^2(x-4)}{(2x-4)^2}+・・・ \quad (x \neq 2)$
この動画を見る
次の無限級数が収束するような実数$x$の値の範囲と、
収束するときの和を求めよ。
①$1+\dfrac{x}{3}+\dfrac{x^2}{9}+\dfrac{x^3}{27}+・・・$
②$(x-4)+\dfrac{x(x-4)}{2x-4}+\dfrac{x^2(x-4)}{(2x-4)^2}+・・・ \quad (x \neq 2)$
【高校数学】数Ⅲ-73 数列の極限⑨(無限等比級数)

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の無限級数の収束、発散を調べ、収束するときにはその和を求めよ。
①$4+2+1+\dfrac{1}{2}+・・・$
②$1-2+4-8+・・・$
③$3-3+3-3+・・・$
④$\displaystyle \sum_{n=1}^{\infty}2\left(-\dfrac{1}{3}\right)^{n-1}$
この動画を見る
次の無限級数の収束、発散を調べ、収束するときにはその和を求めよ。
①$4+2+1+\dfrac{1}{2}+・・・$
②$1-2+4-8+・・・$
③$3-3+3-3+・・・$
④$\displaystyle \sum_{n=1}^{\infty}2\left(-\dfrac{1}{3}\right)^{n-1}$
【高校数学】数Ⅲ-72 数列の極限⑧(無限級数)

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の無限級数の収束、発散を調べ、収束するときにはその和を求めよ。
①$\dfrac{1}{1・3}+\dfrac{1}{3・5}+・・・+\dfrac{1}{(2n-1)(2n+1)}+・・・$
②$\displaystyle \sum_{n=1}^{\infty}\dfrac{1}{\sqrt n+\sqrt{n+1}}$
この動画を見る
次の無限級数の収束、発散を調べ、収束するときにはその和を求めよ。
①$\dfrac{1}{1・3}+\dfrac{1}{3・5}+・・・+\dfrac{1}{(2n-1)(2n+1)}+・・・$
②$\displaystyle \sum_{n=1}^{\infty}\dfrac{1}{\sqrt n+\sqrt{n+1}}$
天才オイラーが解決した問題。奇数の平方の逆数の和にπが登場

【高校数学】数Ⅲ-70 数列の極限⑥(無限等比数列)

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の極限を求めよ。
①$\displaystyle \lim_{n\to\infty}\dfrac{1-r^n}{1+r^n}(r \neq -1)$
②$\displaystyle \lim_{n\to\infty}\dfrac{r^{2n+1}}{1+r^{2n}}$
この動画を見る
次の極限を求めよ。
①$\displaystyle \lim_{n\to\infty}\dfrac{1-r^n}{1+r^n}(r \neq -1)$
②$\displaystyle \lim_{n\to\infty}\dfrac{r^{2n+1}}{1+r^{2n}}$
【高校数学】数Ⅲ-69 数列の極限⑤(無限等比数列)

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の極限を求めよ。
①$\displaystyle \lim_{n\to\infty}3^n$
②$\displaystyle \lim_{n\to\infty}1^n$
③$\displaystyle \lim_{n\to\infty}\left(-\dfrac{1}{3}\right)^n$
④$\displaystyle \lim_{n\to\infty}(-3)^n$
⑤$\displaystyle \lim_{n\to\infty}\dfrac{3^n+4^n}{5^n}$
⑥$\displaystyle \lim_{n\to\infty}\dfrac{2^n}{1+2^n}$
⑦$\displaystyle \lim_{n\to\infty}\dfrac{5^n+3^n}{2^n-3^n}$
⑧$\displaystyle \lim_{n\to\infty}\dfrac{2^{n+1}-4^{n+1}}{3^n-4^n}$
この動画を見る
次の極限を求めよ。
①$\displaystyle \lim_{n\to\infty}3^n$
②$\displaystyle \lim_{n\to\infty}1^n$
③$\displaystyle \lim_{n\to\infty}\left(-\dfrac{1}{3}\right)^n$
④$\displaystyle \lim_{n\to\infty}(-3)^n$
⑤$\displaystyle \lim_{n\to\infty}\dfrac{3^n+4^n}{5^n}$
⑥$\displaystyle \lim_{n\to\infty}\dfrac{2^n}{1+2^n}$
⑦$\displaystyle \lim_{n\to\infty}\dfrac{5^n+3^n}{2^n-3^n}$
⑧$\displaystyle \lim_{n\to\infty}\dfrac{2^{n+1}-4^{n+1}}{3^n-4^n}$
【高校数学】数Ⅲ-68 数列の極限④ はさみうちの原理

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の数列の極限を求めよ。
①$\displaystyle \lim_{n\to\infty}\dfrac{(-1)^n}{n+3}$
②$\displaystyle \lim_{n\to\infty}\dfrac{1}{n}\sin^2 n\theta \quad $($\theta$は定数)
この動画を見る
次の数列の極限を求めよ。
①$\displaystyle \lim_{n\to\infty}\dfrac{(-1)^n}{n+3}$
②$\displaystyle \lim_{n\to\infty}\dfrac{1}{n}\sin^2 n\theta \quad $($\theta$は定数)
【高校数学】数Ⅲ-67 数列の極限③

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の極限を求めよ。
①$\displaystyle \lim_{n\to\infty}\dfrac{n^2-n+2}{3n^2-5}$
②$\displaystyle \lim_{n\to\infty}\dfrac{5n^2-1}{4+n}$
③$\displaystyle \lim_{n\to\infty}(\sqrt{n+1}-\sqrt n)$
④$\displaystyle \lim_{n\to\infty}(\sqrt{n^2-2n}-n)$
⑤$\displaystyle \lim_{n\to\infty}\dfrac{4n}{\sqrt{n^2+n}+3n}$
⑥$\displaystyle \lim_{n\to\infty}\dfrac{5}{\sqrt{n^2+2n}-n}$
この動画を見る
次の極限を求めよ。
①$\displaystyle \lim_{n\to\infty}\dfrac{n^2-n+2}{3n^2-5}$
②$\displaystyle \lim_{n\to\infty}\dfrac{5n^2-1}{4+n}$
③$\displaystyle \lim_{n\to\infty}(\sqrt{n+1}-\sqrt n)$
④$\displaystyle \lim_{n\to\infty}(\sqrt{n^2-2n}-n)$
⑤$\displaystyle \lim_{n\to\infty}\dfrac{4n}{\sqrt{n^2+n}+3n}$
⑥$\displaystyle \lim_{n\to\infty}\dfrac{5}{\sqrt{n^2+2n}-n}$
【高校数学】数Ⅲ-66 数列の極限②

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の極限を求めよ。
①$\displaystyle \lim_{n\to\infty}(-3n+8)$
②$\displaystyle \lim_{n\to\infty}(n-1)$
③$\displaystyle \lim_{n\to\infty}\left(5+\dfrac{2}{n}\right)$
④$\displaystyle \lim_{n\to\infty}(-3)^n$
⑤$\displaystyle \lim_{n\to\infty}\dfrac{n-3}{2n+1}$
⑥$\displaystyle \lim_{n\to\infty}(4n-3n^2)$
この動画を見る
次の極限を求めよ。
①$\displaystyle \lim_{n\to\infty}(-3n+8)$
②$\displaystyle \lim_{n\to\infty}(n-1)$
③$\displaystyle \lim_{n\to\infty}\left(5+\dfrac{2}{n}\right)$
④$\displaystyle \lim_{n\to\infty}(-3)^n$
⑤$\displaystyle \lim_{n\to\infty}\dfrac{n-3}{2n+1}$
⑥$\displaystyle \lim_{n\to\infty}(4n-3n^2)$
【高校数学】数Ⅲ-65 数列の極限①

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の数列の収束、発散を調べよ。
①$-3,-1,1,・・・2n-5,・・・$
②$1,\dfrac{3}{2},\dfrac{5}{3},・・・,2-\dfrac{1}{n},・・・$
③$-1,-4,-9,・・・,-n^2,・・・$
④$-4,16,-64,・・・,(-4)^n,・・・$
この動画を見る
次の数列の収束、発散を調べよ。
①$-3,-1,1,・・・2n-5,・・・$
②$1,\dfrac{3}{2},\dfrac{5}{3},・・・,2-\dfrac{1}{n},・・・$
③$-1,-4,-9,・・・,-n^2,・・・$
④$-4,16,-64,・・・,(-4)^n,・・・$
オイラー(Euler)が解決した「自然数の平方の逆数の和」。円とは無関係なのに結論にπが登場