関数の変化（グラフ・最大最小・方程式・不等式）
関数の変化（グラフ・最大最小・方程式・不等式）
福田の数学〜上智大学2021年理工学部第１問〜双曲線の方程式と回転体の体積
単元：
#大学入試過去問(数学)#平面上の曲線#微分とその応用#2次曲線#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#上智大学#数学(高校生)#数C#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
{\Large\boxed{1}} 媒介変数表示\\
x=\frac{2}{\cos\theta}, y=3\tan\theta+1\\
で表される図形Cを考える。\\
\\
(1)Cは頂点(±\boxed{\ \ ア\ \ },\ \boxed{\ \ イ\ \ })、焦点(±\sqrt{\boxed{\ \ ウ\ \ }},\ \boxed{\ \ エ\ \ })、\\
漸近線y=±\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}x+\boxed{\ \ キ\ \ }をもつ双曲線である。\\
(2)双曲線Cと直線x=4は、2点(4,\ \boxed{\ \ ク\ \ }±\boxed{\ \ ケ\ \ }\sqrt{\boxed{\ \ コ\ \ }})\\
で交わる。\\
(3)双曲線Cと直線x=4で囲まれる部分をy軸の周りに1回転\\
させてできる立体の体積は\ \boxed{\ \ サ\ \ }\sqrt{\boxed{\ \ シ\ \ }}\ \pi である。
\end{eqnarray}
2021上智大学理工学部過去問
この動画を見る
\begin{eqnarray}
{\Large\boxed{1}} 媒介変数表示\\
x=\frac{2}{\cos\theta}, y=3\tan\theta+1\\
で表される図形Cを考える。\\
\\
(1)Cは頂点(±\boxed{\ \ ア\ \ },\ \boxed{\ \ イ\ \ })、焦点(±\sqrt{\boxed{\ \ ウ\ \ }},\ \boxed{\ \ エ\ \ })、\\
漸近線y=±\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}x+\boxed{\ \ キ\ \ }をもつ双曲線である。\\
(2)双曲線Cと直線x=4は、2点(4,\ \boxed{\ \ ク\ \ }±\boxed{\ \ ケ\ \ }\sqrt{\boxed{\ \ コ\ \ }})\\
で交わる。\\
(3)双曲線Cと直線x=4で囲まれる部分をy軸の周りに1回転\\
させてできる立体の体積は\ \boxed{\ \ サ\ \ }\sqrt{\boxed{\ \ シ\ \ }}\ \pi である。
\end{eqnarray}
2021上智大学理工学部過去問
【数Ⅲ】微分法：対数微分、この計算式をどうしますか？
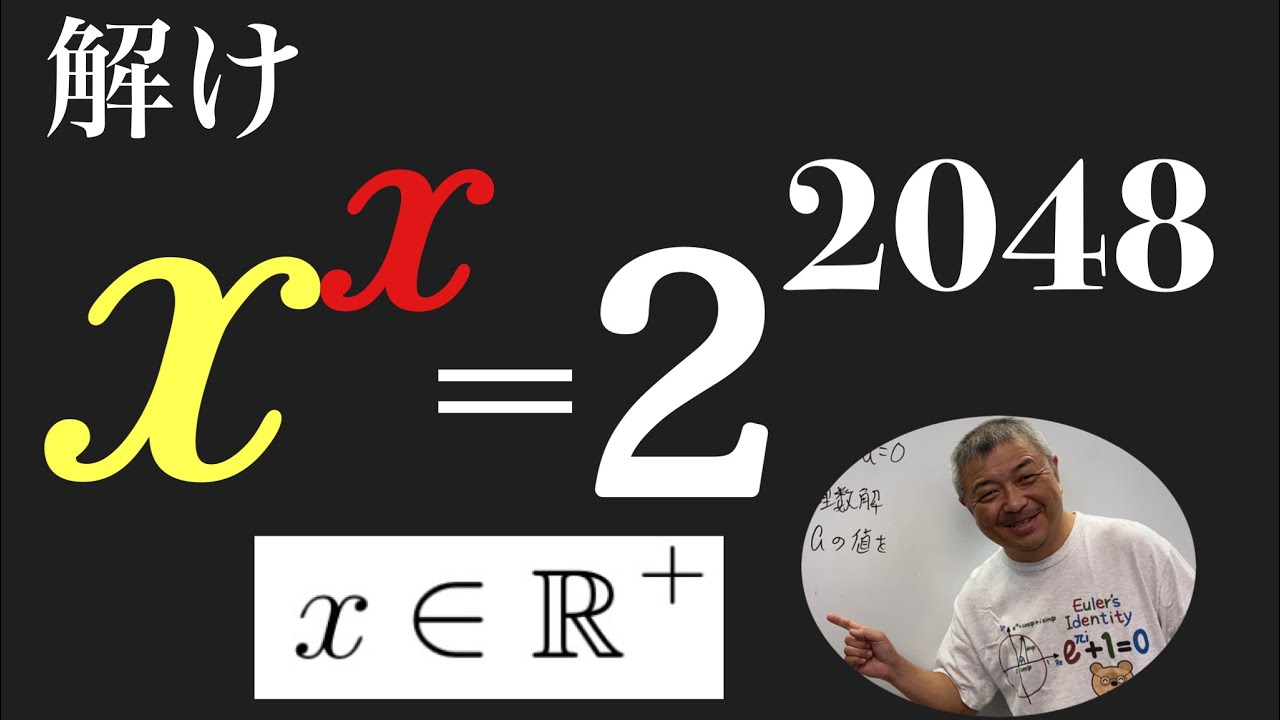
単元：
#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#数学(高校生)#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$f(x)=(1+a^x)^{\frac{1}{x}}$は,$0＜a＜1$の時単調である
[上級問題精講数学Ⅲ、416(1)]
この動画を見る
$f(x)=(1+a^x)^{\frac{1}{x}}$は,$0＜a＜1$の時単調である
[上級問題精講数学Ⅲ、416(1)]
福田の数学〜中央大学2021年理工学部第４問〜定積分と不等式、極限
単元：
#大学入試過去問(数学)#関数と極限#微分とその応用#積分とその応用#関数の極限#関数の変化（グラフ・最大最小・方程式・不等式）#定積分#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$自然数$n$に対し,$f_n(x)=x^{-1+\frac{1}{n}}(x\gt 0)$とおく.
また,正の実数$a_n$は$\displaystyle \int_{1}^{a_n}f_n(x)dx=1$満たすものとする.次の問い
答えよ.
(1)関数$f_n(x)$の不定積分を求めよ.
(2)$a_n$の値と極限$\displaystyle \lim_{n\to\infty}a_n$を求めよ.また,正の実数$b_n$が$\displaystyle \int_{1}^{b_n}f_{n+1}(x)dx=-1$を満たすとき,$b_n$の値と極限$\displaystyle \lim_{n\to\infty}b_n$を求めよ.
(3)2以上の自然数$k$に対して$\displaystyle \int_{k-1}^{k}f_n(x)dx \gt \dfrac{1}{k}$を示し,これを利用して$a_n\lt 4$を証明せよ.
(4)$\displaystyle \int_{1}^{a_n}f_{n+1}(x)dx\lt 1$を示し,これを利用して$a_n\lt a_{n+1}＄を証明せよ.
2021中央大理工学部過去問
この動画を見る
$\boxed{4}$自然数$n$に対し,$f_n(x)=x^{-1+\frac{1}{n}}(x\gt 0)$とおく.
また,正の実数$a_n$は$\displaystyle \int_{1}^{a_n}f_n(x)dx=1$満たすものとする.次の問い
答えよ.
(1)関数$f_n(x)$の不定積分を求めよ.
(2)$a_n$の値と極限$\displaystyle \lim_{n\to\infty}a_n$を求めよ.また,正の実数$b_n$が$\displaystyle \int_{1}^{b_n}f_{n+1}(x)dx=-1$を満たすとき,$b_n$の値と極限$\displaystyle \lim_{n\to\infty}b_n$を求めよ.
(3)2以上の自然数$k$に対して$\displaystyle \int_{k-1}^{k}f_n(x)dx \gt \dfrac{1}{k}$を示し,これを利用して$a_n\lt 4$を証明せよ.
(4)$\displaystyle \int_{1}^{a_n}f_{n+1}(x)dx\lt 1$を示し,これを利用して$a_n\lt a_{n+1}＄を証明せよ.
2021中央大理工学部過去問
福田のわかった数学〜高校３年生理系045〜極限(45)関数の連続性(2)
単元：
#関数と極限#微分とその応用#関数の極限#関数の変化（グラフ・最大最小・方程式・不等式）#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
数学\textrm{III} 関数の連続性(2)\\
f(x)=[x^2](x+1)\\
はx=0で連続かまた、x=1で連続か、調べよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{III} 関数の連続性(2)\\
f(x)=[x^2](x+1)\\
はx=0で連続かまた、x=1で連続か、調べよ。
\end{eqnarray}
数学「大学入試良問集」【18−7 球に外接する直円錐の最小体積】を宇宙一わかりやすく
単元：
#大学入試過去問(数学)#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京学芸大学
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
半径$a$の球に外接する直円錐について、次の各問いに答えよ。
（1）直円錐の底面の半径を$x$とするとき、その高さを$x$を用いて表せ。
（2）このような直円錐の体積の最小値を求めよ。
この動画を見る
半径$a$の球に外接する直円錐について、次の各問いに答えよ。
（1）直円錐の底面の半径を$x$とするとき、その高さを$x$を用いて表せ。
（2）このような直円錐の体積の最小値を求めよ。
数学「大学入試良問集」【18−4 微分と不等式の証明】を宇宙一わかりやすく
単元：
#大学入試過去問(数学)#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数Ⅲ
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
$0 \lt \theta \lt \displaystyle \frac{\pi}{2}$のとき、次の不等式が成り立つことを証明せよ。
$\displaystyle \frac{1}{\theta}(\sin\theta+\tan\theta) \gt 2$
この動画を見る
$0 \lt \theta \lt \displaystyle \frac{\pi}{2}$のとき、次の不等式が成り立つことを証明せよ。
$\displaystyle \frac{1}{\theta}(\sin\theta+\tan\theta) \gt 2$
数学「大学入試良問集」【18−1三角関数の微分】を宇宙一わかりやすく
単元：
#大学入試過去問(数学)#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#日本女子大学
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
関数$f(x)=\displaystyle \frac{\sin\ x}{3+\cos\ x}$の最大値を最小値を求めよ。
この動画を見る
関数$f(x)=\displaystyle \frac{\sin\ x}{3+\cos\ x}$の最大値を最小値を求めよ。
福田の数学〜慶應義塾大学2021年医学部第４問〜カテナリーと円の相接
単元：
#大学入試過去問(数学)#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
{\Large\boxed{4}} 曲線y=\frac{e^x+e^{-x}}{2} (x \gt 0)をCで表す。Q(X,Y)を中心とする半径rの円が曲線C\\
と、点P(t,\frac{e^t+e^{-t}}{2})\ (ただしt \gt 0)において共通の接線をもち、さらにX \lt tであるとする。\\
このときXおよびYをtの式で表すと\\
X=\boxed{\ \ (あ)\ \ }, Y=\boxed{\ \ (い)\ \ }\\
となる。tの関数X(t),Y(t)をX(t)=\boxed{\ \ (あ)\ \ },Y(t)=\boxed{\ \ (い)\ \ }により定義する。全て\\
のt \gt 0に対してX(t) \gt 0となるための条件は、rが不等式\boxed{\ \ (う)\ \ }を満たすことで\\
ある。\boxed{\ \ (う)\ \ }が成り立たないとき、関数Y(t)はt=\boxed{\ \ (え)\ \ }において最小値\boxed{\ \ (お)\ \ }\\
をとる。また\boxed{\ \ (う)\ \ }が成り立つとき、YをXの関数と考えて、(\frac{dY}{dX})^2+1をYの式で\\
表すと(\frac{dY}{dX})^2+1=\boxed{\ \ (か)\ \ } となる。\\
\end{eqnarray}
2021慶應義塾大学医学部過去問
この動画を見る
\begin{eqnarray}
{\Large\boxed{4}} 曲線y=\frac{e^x+e^{-x}}{2} (x \gt 0)をCで表す。Q(X,Y)を中心とする半径rの円が曲線C\\
と、点P(t,\frac{e^t+e^{-t}}{2})\ (ただしt \gt 0)において共通の接線をもち、さらにX \lt tであるとする。\\
このときXおよびYをtの式で表すと\\
X=\boxed{\ \ (あ)\ \ }, Y=\boxed{\ \ (い)\ \ }\\
となる。tの関数X(t),Y(t)をX(t)=\boxed{\ \ (あ)\ \ },Y(t)=\boxed{\ \ (い)\ \ }により定義する。全て\\
のt \gt 0に対してX(t) \gt 0となるための条件は、rが不等式\boxed{\ \ (う)\ \ }を満たすことで\\
ある。\boxed{\ \ (う)\ \ }が成り立たないとき、関数Y(t)はt=\boxed{\ \ (え)\ \ }において最小値\boxed{\ \ (お)\ \ }\\
をとる。また\boxed{\ \ (う)\ \ }が成り立つとき、YをXの関数と考えて、(\frac{dY}{dX})^2+1をYの式で\\
表すと(\frac{dY}{dX})^2+1=\boxed{\ \ (か)\ \ } となる。\\
\end{eqnarray}
2021慶應義塾大学医学部過去問
福田の数学〜早稲田大学2021年商学部第１問(2)〜整式と不等式
単元：
#大学入試過去問(数学)#微分とその応用#微分法#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
{\Large\boxed{1}} (2)nを正の整数とする。f(x)はxのn+1次式で表される関数で、xが0以上\\
n以下の整数のときf(x)=0であり、f(n+1)=n+1である。このとき、\\
\\
\sum_{k=0}^n\frac{(1-\sqrt2)^k}{f'(k)} \gt 2^{2021}\\
\\
を満たす最小のnは\boxed{\ \ イ\ \ }である。
\end{eqnarray}
2021早稲田大学商学部過去問
この動画を見る
\begin{eqnarray}
{\Large\boxed{1}} (2)nを正の整数とする。f(x)はxのn+1次式で表される関数で、xが0以上\\
n以下の整数のときf(x)=0であり、f(n+1)=n+1である。このとき、\\
\\
\sum_{k=0}^n\frac{(1-\sqrt2)^k}{f'(k)} \gt 2^{2021}\\
\\
を満たす最小のnは\boxed{\ \ イ\ \ }である。
\end{eqnarray}
2021早稲田大学商学部過去問
指数不等式
単元：
#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを解け.
$\left(\dfrac{5}{3}\right)^{\frac{x^2+x-3}{x+1}}\leqq \dfrac{2}{3}・\left(\dfrac{5}{2}\right)^{x-\left(\frac{3}{x+1}\right)}$
この動画を見る
これを解け.
$\left(\dfrac{5}{3}\right)^{\frac{x^2+x-3}{x+1}}\leqq \dfrac{2}{3}・\left(\dfrac{5}{2}\right)^{x-\left(\frac{3}{x+1}\right)}$
ただの不等式
単元：
#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを解け.
$30x^2-2・3^{x+1}+19x・3^x \gt 5x^2・3^{x+1}$
$+38x-12$
この動画を見る
これを解け.
$30x^2-2・3^{x+1}+19x・3^x \gt 5x^2・3^{x+1}$
$+38x-12$
立教大 関数の最小値
単元：
#微分とその応用#色々な関数の導関数#関数の変化（グラフ・最大最小・方程式・不等式）#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x\gt 0$とする.
$\left(x+\dfrac{1}{x}\right)\left(x+\dfrac{2}{x}\right)$の最小値を求めよ.
2021立教大過去問
この動画を見る
$x\gt 0$とする.
$\left(x+\dfrac{1}{x}\right)\left(x+\dfrac{2}{x}\right)$の最小値を求めよ.
2021立教大過去問
徳島大（医）放物線の法線
単元：
#大学入試過去問(数学)#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#数学(高校生)#徳島大学#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$C:y=x^2$上の$P(t,t^2)(t\gt 0)$における法線と$C$との交点を$Q(\neq P)$とする.
$PQ$の最小値を求めよ.
2020徳島大(医)過去問
この動画を見る
$C:y=x^2$上の$P(t,t^2)(t\gt 0)$における法線と$C$との交点を$Q(\neq P)$とする.
$PQ$の最小値を求めよ.
2020徳島大(医)過去問
岐阜薬科大 対数の不等式 良問
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\log_x y-\log_y x^{\frac{1}{2}}\lt -\dfrac{1}{2}$を満たす点$(x,y)$の領域を図示せよ.
岐阜薬科大過去問
この動画を見る
$\log_x y-\log_y x^{\frac{1}{2}}\lt -\dfrac{1}{2}$を満たす点$(x,y)$の領域を図示せよ.
岐阜薬科大過去問
【数Ⅲ-160】定積分で表された関数③(極値編)
単元：
#微分とその応用#積分とその応用#微分法#関数の変化（グラフ・最大最小・方程式・不等式）#定積分#数学(高校生)#数Ⅲ
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
数Ⅲ(定積分で表された関数③・極値編)
Q.次の関数の極値を求めよ。
①$f(x)=\int_0^xt\cos t \ dt(0 \lt x \lt \pi)$
➁$f(x)=\int_0^x (1-t^2)e^tdt$
この動画を見る
数Ⅲ(定積分で表された関数③・極値編)
Q.次の関数の極値を求めよ。
①$f(x)=\int_0^xt\cos t \ dt(0 \lt x \lt \pi)$
➁$f(x)=\int_0^x (1-t^2)e^tdt$
上智大 関数の最大最小
単元：
#大学入試過去問(数学)#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師：
問題文全文(内容文)：
$f(x)=\displaystyle \frac{x^2+ax+b}{x^2-x+1}$の最大値が$3$、最小値が$\displaystyle \frac{1}{3}$
$(a,b)$の値を求めよ
出典：2005年上智大学 過去問
この動画を見る
$f(x)=\displaystyle \frac{x^2+ax+b}{x^2-x+1}$の最大値が$3$、最小値が$\displaystyle \frac{1}{3}$
$(a,b)$の値を求めよ
出典：2005年上智大学 過去問
佐賀大 三次関数
単元：
#大学入試過去問(数学)#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$y=x^3-x$上を点$P$が原点から点$A(a,a^3-a)$まで動く
$(a \gt 0)\triangle OAP$の最大値を求めよ
出典：2005年佐賀大学 過去問
この動画を見る
$y=x^3-x$上を点$P$が原点から点$A(a,a^3-a)$まで動く
$(a \gt 0)\triangle OAP$の最大値を求めよ
出典：2005年佐賀大学 過去問
東北大 積分
単元：
#数Ⅱ#微分法と積分法#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$f(x)=x^3-6ax^2+bx+1$
$x=a(a \gt 0)$で極大値
$f(x)$と直線$y=f(a)$で囲まれた面積が$a^2$
$a$の値を求めよ
出典：1996年東北大学 過去問
この動画を見る
$f(x)=x^3-6ax^2+bx+1$
$x=a(a \gt 0)$で極大値
$f(x)$と直線$y=f(a)$で囲まれた面積が$a^2$
$a$の値を求めよ
出典：1996年東北大学 過去問
慶応義塾大 4次方程式
単元：
#関数と極限#微分とその応用#関数（分数関数・無理関数・逆関数と合成関数）#関数の極限#色々な関数の導関数#関数の変化（グラフ・最大最小・方程式・不等式）#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$3x^4-4x^3-12x^2-k=0$が相異なる4つの実数解をもつ$k$の範囲
そのときの4つの解のうち最大のものを$\alpha$とする。
$\alpha$の範囲を求めよ
出典：1989年慶應義塾大学 過去問
この動画を見る
$3x^4-4x^3-12x^2-k=0$が相異なる4つの実数解をもつ$k$の範囲
そのときの4つの解のうち最大のものを$\alpha$とする。
$\alpha$の範囲を求めよ
出典：1989年慶應義塾大学 過去問
甲南大 関数の最小値
単元：
#大学入試過去問(数学)#微分とその応用#色々な関数の導関数#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#甲南大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$f(x)=(x^2-x+a)^2-x^2+x$の最小値を求めよ
出典：甲南大学 過去問
この動画を見る
$f(x)=(x^2-x+a)^2-x^2+x$の最小値を求めよ
出典：甲南大学 過去問
熊本大 関数の領域
単元：
#大学入試過去問(数学)#微分とその応用#色々な関数の導関数#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#熊本大学#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\begin{eqnarray}
\left\{
\begin{array}{l}
y \geqq x^2-1 \\
y \leqq x+1
\end{array}
\right.
\end{eqnarray}$
$(x,y)$がこの領域を動く
$x^2+y^2-4y$の最大値・最小値を求めよ。
出典：2001年熊本大学 過去問
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
y \geqq x^2-1 \\
y \leqq x+1
\end{array}
\right.
\end{eqnarray}$
$(x,y)$がこの領域を動く
$x^2+y^2-4y$の最大値・最小値を求めよ。
出典：2001年熊本大学 過去問
信州大 三次方程式の解の極限値
単元：
#大学入試過去問(数学)#関数と極限#微分とその応用#数列の極限#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#信州大学#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$2x^3+3nx^2-3(n+1)=0(n$自然数$)$
（1）
$n$の値に関わらず正の解をただ一つだけもつことを示せ
（2）
正の解を$\alpha_n$とする。
$\displaystyle \lim_{ n \to \infty }\alpha_n$を求めよ
出典：1998年信州大学 過去問
この動画を見る
$2x^3+3nx^2-3(n+1)=0(n$自然数$)$
（1）
$n$の値に関わらず正の解をただ一つだけもつことを示せ
（2）
正の解を$\alpha_n$とする。
$\displaystyle \lim_{ n \to \infty }\alpha_n$を求めよ
出典：1998年信州大学 過去問
埼玉大 微分積分 三次関数極値の差 ヨビノリ技
単元：
#大学入試過去問(数学)#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$f(x)=x^3+ax^2+bx$は原点で$y=-x$に接し、
$($極大値$)-($極小値$)=4,$
$($極大値$)+($極小値$) \gt 0$である。
$a,b$の値を求めよ
出典：2018年埼玉大学 過去問
この動画を見る
$f(x)=x^3+ax^2+bx$は原点で$y=-x$に接し、
$($極大値$)-($極小値$)=4,$
$($極大値$)+($極小値$) \gt 0$である。
$a,b$の値を求めよ
出典：2018年埼玉大学 過去問
京都大 ３次関数 整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$f(x)=x^3+2x^2+2$
$|f(n)$と$|f(n+1)|$がともに素数となるような整数$n$を求めよ
出典：2019年京都大学 過去問
この動画を見る
$f(x)=x^3+2x^2+2$
$|f(n)$と$|f(n+1)|$がともに素数となるような整数$n$を求めよ
出典：2019年京都大学 過去問
東京海洋大 ３次関数
単元：
#大学入試過去問(数学)#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#東京海洋大学#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$f(x)=2x^3-15ax^2+24a^2x+a^2$
$y=f(x)$のグラフと$x$軸とが$0 \lt x \lt 1$の範囲でただ一つの共有点をもつための$a$の条件を求めよ
出典：2005年東京海洋大学 過去問
この動画を見る
$f(x)=2x^3-15ax^2+24a^2x+a^2$
$y=f(x)$のグラフと$x$軸とが$0 \lt x \lt 1$の範囲でただ一つの共有点をもつための$a$の条件を求めよ
出典：2005年東京海洋大学 過去問
京都大 関数
単元：
#大学入試過去問(数学)#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a,b$実数
$f(x)=\displaystyle \frac{ax+b}{x^2+x+1}$
すべての実数$x$にたいして不等式
$f(x) \leqq f(x)^3-2f(x)^2+2$が成り立つ$(a,b)$を図示せよ
出典：2014年京都大学 過去問
この動画を見る
$a,b$実数
$f(x)=\displaystyle \frac{ax+b}{x^2+x+1}$
すべての実数$x$にたいして不等式
$f(x) \leqq f(x)^3-2f(x)^2+2$が成り立つ$(a,b)$を図示せよ
出典：2014年京都大学 過去問
早稲田大（国際教養）微分
単元：
#大学入試過去問(数学)#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x^3-3mx+m-3=0$が3個の異なる実数解$\alpha ,\beta,\gamma$をもつ$(\alpha \lt \beta \lt \gamma)m,\alpha,\beta,\gamma$の範囲を求めよ
出典：2018年早稲田大学 過去問
この動画を見る
$x^3-3mx+m-3=0$が3個の異なる実数解$\alpha ,\beta,\gamma$をもつ$(\alpha \lt \beta \lt \gamma)m,\alpha,\beta,\gamma$の範囲を求めよ
出典：2018年早稲田大学 過去問
大阪大 ３次関数
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$f(x)=x^3-3ax+a$
$0 \leqq x \leqq 1$において$f(x) \geqq 0$となるような$a$の範囲
出典：2006年大阪大学 過去問
この動画を見る
$f(x)=x^3-3ax+a$
$0 \leqq x \leqq 1$において$f(x) \geqq 0$となるような$a$の範囲
出典：2006年大阪大学 過去問
二階微分＞０ なぜ下に凸・指数関数の微分 名古屋大の問題の補足
単元：
#大学入試過去問(数学)#微分とその応用#微分法#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
指数関数の微分の補足 解説動画です
この動画を見る
指数関数の微分の補足 解説動画です
名古屋大 微分/大小比較 東大大学院数学科卒の杉山さん代講
単元：
#大学入試過去問(数学)#微分とその応用#微分法#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a,b$実数
$0 \lt a \lt b \lt 1$
$\displaystyle \frac{2^a-2a}{a-1},\displaystyle \frac{2^b-2b}{b-1}$
大小比較せよ
出典：2004年名古屋大学 過去問
この動画を見る
$a,b$実数
$0 \lt a \lt b \lt 1$
$\displaystyle \frac{2^a-2a}{a-1},\displaystyle \frac{2^b-2b}{b-1}$
大小比較せよ
出典：2004年名古屋大学 過去問