積分とその応用
積分とその応用
【数Ⅲ】【積分とその応用】区間a≦x≦bでf(x)≧0曲線y=f(x)とx軸および2直線x=a,x=bで囲まれy軸の周りに1回転させてできる体積は2π∫[a→b]xf(x)dxで与えられることを示せ。
単元：
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材：
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師：
理数個別チャンネル
問題文全文(内容文)：
(1) 0≦a＜bとする。関数f(x)を区間a≦x≦bで単調に増加する関数とし、
区間a≦x≦bでf(x)≧0とする。曲線y=f(x)とx軸および2直線x=a,x=bで囲まれた部分を、
y軸の周りに1回転させてできる立体の体積Vは
$V=2\pi\int_a^bxf(x)dx$……①で与えられることを示せ。
(2) (1)の①は、一般の関数f(x) (ただし、a≦x≦bでf(x)≧0)についても成り立つ。
これを利用して、曲線y=-x²+2xとx軸で囲まれた部分を、
y軸の周りに1回転させてできる立体の体積を求めよ。
この動画を見る
(1) 0≦a＜bとする。関数f(x)を区間a≦x≦bで単調に増加する関数とし、
区間a≦x≦bでf(x)≧0とする。曲線y=f(x)とx軸および2直線x=a,x=bで囲まれた部分を、
y軸の周りに1回転させてできる立体の体積Vは
$V=2\pi\int_a^bxf(x)dx$……①で与えられることを示せ。
(2) (1)の①は、一般の関数f(x) (ただし、a≦x≦bでf(x)≧0)についても成り立つ。
これを利用して、曲線y=-x²+2xとx軸で囲まれた部分を、
y軸の周りに1回転させてできる立体の体積を求めよ。
【数Ⅲ】【積分とその応用】曲線y=e^{-x}上でx座標がnの点をP_nとし、線分P_{n-1}P_nと曲線y=e^{-x}で囲まれた部分の面積をS_nとするとき、次の無限級数の和を求めよ。
単元：
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材：
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師：
理数個別チャンネル
問題文全文(内容文)：
曲線$y=e^{-x}$上で$x$座標が$n$の点を$P_n$とし、
線分$P_{n-1}P_n$と曲線$y=e^{-x}$で囲まれた部分の面積を$S_n$とするとき、
次の無限級数の和を求めよ。
$S=S_1+S_2+S_3+\cdots\cdots+S_n+\cdots\cdots$
この動画を見る
曲線$y=e^{-x}$上で$x$座標が$n$の点を$P_n$とし、
線分$P_{n-1}P_n$と曲線$y=e^{-x}$で囲まれた部分の面積を$S_n$とするとき、
次の無限級数の和を求めよ。
$S=S_1+S_2+S_3+\cdots\cdots+S_n+\cdots\cdots$
数学IIIのこの問題、解けるかな？
単元：
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文)：
以下を満たすf(x)は？
f(x)=8x+2∫f(t)dt
この動画を見る
以下を満たすf(x)は？
f(x)=8x+2∫f(t)dt
定積分を含む関数f(x)を求める問題、解けてくれーー
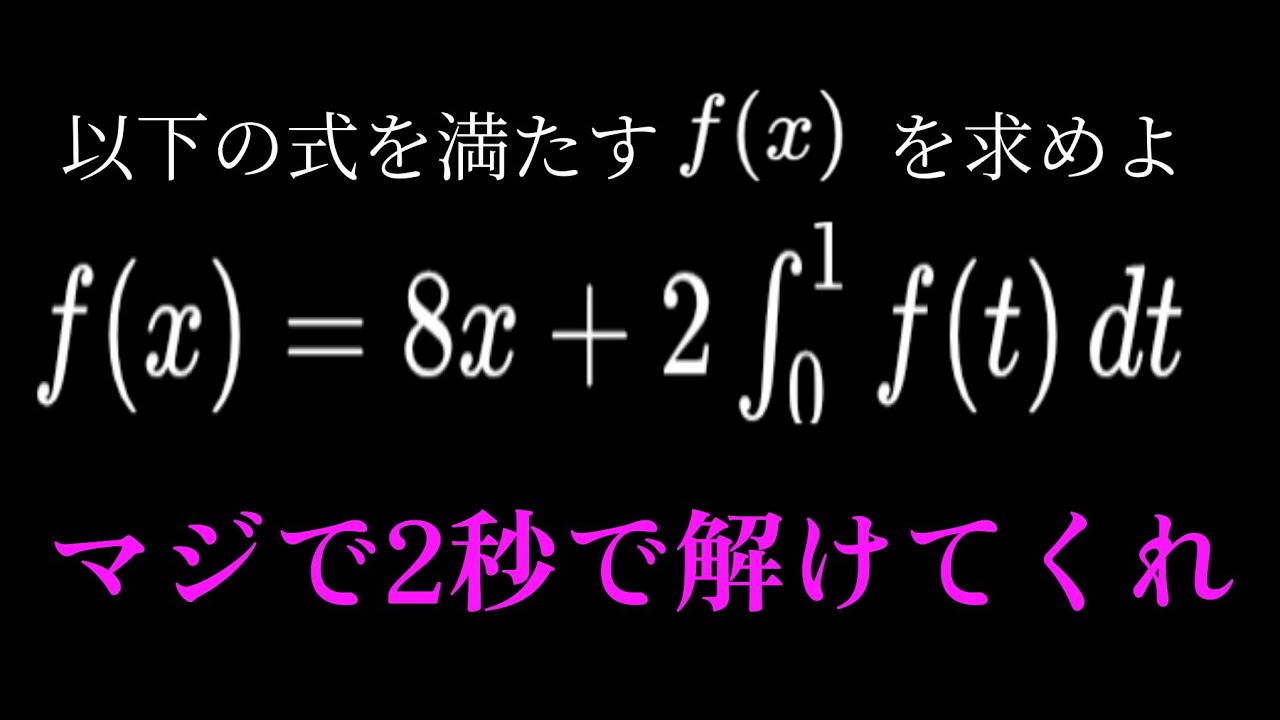
単元：
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文)：
以下を満たすf(x)は？
f(x)=8x+2∫f(t)dt
この動画を見る
以下を満たすf(x)は？
f(x)=8x+2∫f(t)dt
【数Ⅲ】【積分とその応用】シュワルツの不等式{∫[a→b]f(x)g(x)dx}²≦(∫[a→b]{f(x)}²dx)(∫[a→b]{g(x)}²dx) を利用して、次の不等式が成り立つことを証明せよ
単元：
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材：
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師：
理数個別チャンネル
問題文全文(内容文)：
シュワルツの不等式
\[
\left\{ \int_a^b f(x)g(x) \, dx \right\}^2 \leq
\left( \int_a^b \{ f(x) \}^2 dx \right)
\left( \int_a^b \{ g(x) \}^2 dx \right) \quad (a < b)
\]
を利用して、\( 0 < a < b, \, h(x) > 0 \) のとき、次の不等式が成り立つことを証明せよ。
(1)
\[
(b - a)^2 < \int_a^b x^2 \, dx \int_a^b \frac{dx}{x^2}
\]
(2)
\[
(b - a)^2 \leq \int_a^b h(x) \, dx \int_a^b \frac{dx}{h(x)}
\]
この動画を見る
シュワルツの不等式
\[
\left\{ \int_a^b f(x)g(x) \, dx \right\}^2 \leq
\left( \int_a^b \{ f(x) \}^2 dx \right)
\left( \int_a^b \{ g(x) \}^2 dx \right) \quad (a < b)
\]
を利用して、\( 0 < a < b, \, h(x) > 0 \) のとき、次の不等式が成り立つことを証明せよ。
(1)
\[
(b - a)^2 < \int_a^b x^2 \, dx \int_a^b \frac{dx}{x^2}
\]
(2)
\[
(b - a)^2 \leq \int_a^b h(x) \, dx \int_a^b \frac{dx}{h(x)}
\]
【数Ⅲ】【積分とその応用】次の極限値を求めよ。(1)lim[n→∞]{√(n+1)+√(n+2)+……+√(2n)}/{1+√2+√3+……+√n}他1問
単元：
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材：
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の極限値を求めよ。
(1) $\displaystyle \lim_{ n \to 0 }\dfrac{\sqrt{n+1}+\sqrt{n+2}+\sqrt{n+3}+…+\sqrt{2n}}{1+\sqrt{2}+\sqrt{3}+\sqrt{4}+…+\sqrt{n}}$
(2) $\displaystyle \lim_{ n \to 0 }\log{\sqrt[ n ]{ n+1 }}+\log{\sqrt[ n ]{ n+2 }}+\log{\sqrt[ n ]{ n+3 }}+…+\log{\sqrt[ n ]{ 2n }}-\log n$
この動画を見る
次の極限値を求めよ。
(1) $\displaystyle \lim_{ n \to 0 }\dfrac{\sqrt{n+1}+\sqrt{n+2}+\sqrt{n+3}+…+\sqrt{2n}}{1+\sqrt{2}+\sqrt{3}+\sqrt{4}+…+\sqrt{n}}$
(2) $\displaystyle \lim_{ n \to 0 }\log{\sqrt[ n ]{ n+1 }}+\log{\sqrt[ n ]{ n+2 }}+\log{\sqrt[ n ]{ n+3 }}+…+\log{\sqrt[ n ]{ 2n }}-\log n$
【数Ⅲ】【積分とその応用】次の極限値を求めよ。(1) lim[x→0]1/x∫[0→x]1/(1+cost)dt(2) lim[x→0]∫[0→x](1+sint)²/xdt他1問
単元：
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材：
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師：
理数個別チャンネル
問題文全文(内容文)：
導関数、定積分の定義を利用して、次の極限値を求めよ。
(1) $\displaystyle \lim_{ x \to 0 }\dfrac{1}{x}\int_0^x \dfrac{1}{1+cost}dt$
(2) $\displaystyle \lim_{ x \to 0 }\int_0^x \dfrac{(1+sint)^2}{x}dt$
(3) $\displaystyle \lim_{ x \to 0 }\int_0^{x^2} \dfrac{cos⁵t}{x}dt$
この動画を見る
導関数、定積分の定義を利用して、次の極限値を求めよ。
(1) $\displaystyle \lim_{ x \to 0 }\dfrac{1}{x}\int_0^x \dfrac{1}{1+cost}dt$
(2) $\displaystyle \lim_{ x \to 0 }\int_0^x \dfrac{(1+sint)^2}{x}dt$
(3) $\displaystyle \lim_{ x \to 0 }\int_0^{x^2} \dfrac{cos⁵t}{x}dt$
福田のおもしろ数学549〜無理関数の不定積分その2
単元：
#関数と極限#積分とその応用#関数（分数関数・無理関数・逆関数と合成関数）#不定積分#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
不定積分
$I=\displaystyle \int \sqrt{x^2-1}dx \ (x\gt 1)$を
$x=\sqrt{x^2-1}=t$
と置き換えて求めて下さい。
この動画を見る
不定積分
$I=\displaystyle \int \sqrt{x^2-1}dx \ (x\gt 1)$を
$x=\sqrt{x^2-1}=t$
と置き換えて求めて下さい。
福田のおもしろ数学548〜無理関数の不定積分
単元：
#関数と極限#積分とその応用#関数（分数関数・無理関数・逆関数と合成関数）#不定積分#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
不定積分$I=\displaystyle \int \sqrt{x^2-1}dx \ (x\gt 1)$を
$x=\dfrac{1}{\cos\theta}$と
置き換えて求めて下さい。
この動画を見る
不定積分$I=\displaystyle \int \sqrt{x^2-1}dx \ (x\gt 1)$を
$x=\dfrac{1}{\cos\theta}$と
置き換えて求めて下さい。
【数Ⅲ】【積分とその応用】点Pの座標(x,y)が 3x=t³+6t², 3y=2t³-3t²(1)点Pが座標(27,9)を通るときの速度を求めよ(2)点Pが時刻0からaまでに通過する道のりLを求めよ。
単元：
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材：
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師：
理数個別チャンネル
問題文全文(内容文)：
点Pの座標(x,y)が、時刻の関数として次のように表されている。
3x=t³+6t², 3y=2t³-3t²
(1)点Pが座標(27,9)を通るときの速度を求めよ。
(2)点Pが時刻0からa(a＞0)までに通過する道のりLを求めよ。
この動画を見る
点Pの座標(x,y)が、時刻の関数として次のように表されている。
3x=t³+6t², 3y=2t³-3t²
(1)点Pが座標(27,9)を通るときの速度を求めよ。
(2)点Pが時刻0からa(a＞0)までに通過する道のりLを求めよ。
【数Ⅲ】【積分とその応用】t秒後の速度が v=30-10t(m/s)となるように地上から真上に投げ上げられた物体は、何秒後に何mの高さまで上がって落ち始めるか。
単元：
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材：
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師：
理数個別チャンネル
問題文全文(内容文)：
t秒後の速度が v=30-10t(m/s)となるように地上から真上に投げ上げられた物体は、何秒後に何mの高さまで上がって落ち始めるか。
この動画を見る
t秒後の速度が v=30-10t(m/s)となるように地上から真上に投げ上げられた物体は、何秒後に何mの高さまで上がって落ち始めるか。
【数Ⅲ】【積分とその応用】曲線x=θcosθ、y=θsinθ(0≦θ≦2π)の長さは、曲線y=x²/2(0≦θ≦2π)の長さに等しいことを示せ。
単元：
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材：
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師：
理数個別チャンネル
問題文全文(内容文)：
曲線x=θcosθ、y=θsinθ(0≦θ≦2π)の長さは、曲線y=x²/2(0≦θ≦2π)の長さに等しいことを示せ。
この動画を見る
曲線x=θcosθ、y=θsinθ(0≦θ≦2π)の長さは、曲線y=x²/2(0≦θ≦2π)の長さに等しいことを示せ。
【数Ⅲ】【積分とその応用】次の曲線の長さLを求めよ。ただし、θは媒介変数a,p,qは定数であり、a＞0,0＜q＜π/2 を満たす。
単元：
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材：
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の曲線の長さLを求めよ。ただし、θは媒介変数a,p,qは定数であり、a＞0,0＜q＜π/2 を満たす。
(1) x=a(cosθ+θsinθ)、y=a(sinθ-θcosθ) (0≦θ≦p)
(2) y=log(cosx) (0≦θ≦p)
この動画を見る
次の曲線の長さLを求めよ。ただし、θは媒介変数a,p,qは定数であり、a＞0,0＜q＜π/2 を満たす。
(1) x=a(cosθ+θsinθ)、y=a(sinθ-θcosθ) (0≦θ≦p)
(2) y=log(cosx) (0≦θ≦p)
【数Ⅲ】【積分とその応用】半径がaである円Oの直径ABの両端AおよびBから出発して円Oの周上を同じ向きに動く2点P,QがPの速さはQの速さの2倍でAからBまで動くとき、△APQの面積の最大値を求めよ｡
単元：
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材：
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師：
理数個別チャンネル
問題文全文(内容文)：
半径がaである円Oの直径ABの両端AおよびBから出発して円Oの周上を同じ向きにそれぞれ一定の速さで動く2点P,Qがある｡Pの速さはQの速さの2倍で､PがAからBまで動くとき、△APQの面積の最大値を求めよ｡また,その時の∠BOQの大きさを求めよ｡
この動画を見る
半径がaである円Oの直径ABの両端AおよびBから出発して円Oの周上を同じ向きにそれぞれ一定の速さで動く2点P,Qがある｡Pの速さはQの速さの2倍で､PがAからBまで動くとき、△APQの面積の最大値を求めよ｡また,その時の∠BOQの大きさを求めよ｡
【数Ⅲ】【積分とその応用】点Ｐが原点Ｏを中心とする半径rの円の周上を等速円運動ＯＰが毎秒π/6ラジアンだけ回転するとき，点Ｐの速さと加速度の大きさを求めよ。
単元：
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材：
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師：
理数個別チャンネル
問題文全文(内容文)：
点Ｐが，原点Ｏを中心とする半径rの円の周上を，等速円運動。ＯＰが毎秒π/6ラジアンだけ回転するとき，点Ｐの速さと加速度の大きさを求めよ。ただし，Ｐは円周上の点（ｒ，０）から出発するものとする。
この動画を見る
点Ｐが，原点Ｏを中心とする半径rの円の周上を，等速円運動。ＯＰが毎秒π/6ラジアンだけ回転するとき，点Ｐの速さと加速度の大きさを求めよ。ただし，Ｐは円周上の点（ｒ，０）から出発するものとする。
【数Ⅲ】【積分とその応用】半径が10cm深さが20cmの直円錐形容器に毎秒3cm³の割合で静かに水を注ぐとき水の深さが6cmになった瞬間の水面の上昇する速さと水面の面積の増加する速さを求めよ。
単元：
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材：
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師：
理数個別チャンネル
問題文全文(内容文)：
上面の半径が10cm,深さが20cmの直円錐形の容器が，その軸を鉛直にして固定されている。この容器に毎秒3cm³の割合で静かに水を注ぐとき，水の深さが6cmになった瞬間の，水面の上昇する速さと，水面の面積の増加する速さを求めよ。
この動画を見る
上面の半径が10cm,深さが20cmの直円錐形の容器が，その軸を鉛直にして固定されている。この容器に毎秒3cm³の割合で静かに水を注ぐとき，水の深さが6cmになった瞬間の，水面の上昇する速さと，水面の面積の増加する速さを求めよ。
福田の数学〜立教大学2025理学部第1問(3)〜定積分の計算
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(3)定積分$\displaystyle \int_{0}^{\frac{7}{6}\pi}\sin x \sin 2x \ dx$の値は
$\boxed{エ}$である。
$2025$年立教大学理学部過去問題
この動画を見る
$\boxed{1}$
(3)定積分$\displaystyle \int_{0}^{\frac{7}{6}\pi}\sin x \sin 2x \ dx$の値は
$\boxed{エ}$である。
$2025$年立教大学理学部過去問題
【数Ⅲ】【積分とその応用】定積分の種々の問題6 ※問題文は概要欄
単元：
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材：
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の等式を満たす関数$f(x)$を求めよ。
(1) $\displaystyle f(x)=x+\int_0^2f(t)e^t~dt$
(2) $\displaystyle f(x)=\sin x-\int_0^\frac\pi3\{f(t)-\frac\pi3\}\sin t~dt$
この動画を見る
次の等式を満たす関数$f(x)$を求めよ。
(1) $\displaystyle f(x)=x+\int_0^2f(t)e^t~dt$
(2) $\displaystyle f(x)=\sin x-\int_0^\frac\pi3\{f(t)-\frac\pi3\}\sin t~dt$
【数Ⅲ】【積分とその応用】定積分の種々の問題5 ※問題文は概要欄
単元：
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材：
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の関数$f(x)$の最大値、最小値を求めよ。
(1) $\displaystyle f(x)=\int_0^x(1+2\cos t)\sin t~dt~~(0\leqq x\leqq2\pi)$
(2) $\displaystyle f(x)=\int_1^x(2-t)\log t~dt~~(1\leqq x\leqq e)$
この動画を見る
次の関数$f(x)$の最大値、最小値を求めよ。
(1) $\displaystyle f(x)=\int_0^x(1+2\cos t)\sin t~dt~~(0\leqq x\leqq2\pi)$
(2) $\displaystyle f(x)=\int_1^x(2-t)\log t~dt~~(1\leqq x\leqq e)$
【数Ⅲ】【積分とその応用】定積分の種々の問題4 ※問題文は概要欄
単元：
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材：
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師：
理数個別チャンネル
問題文全文(内容文)：
関数$\displaystyle f(x)=\int_0^{x}\sin 2t~dt~~(0\leqq x\leqq 2\pi)$
の極値を求めよ。
この動画を見る
関数$\displaystyle f(x)=\int_0^{x}\sin 2t~dt~~(0\leqq x\leqq 2\pi)$
の極値を求めよ。
【数Ⅲ】【積分とその応用】定積分の種々の問題3 ※問題文は概要欄
単元：
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材：
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師：
理数個別チャンネル
問題文全文(内容文)：
関数$\displaystyle F(x)=\int_x^{2x^2}(x+t)\sin t~dt$
を$x$について微分せよ。
この動画を見る
関数$\displaystyle F(x)=\int_x^{2x^2}(x+t)\sin t~dt$
を$x$について微分せよ。
【数Ⅲ】【積分とその応用】定積分の種々の問題2 ※問題文は概要欄
単元：
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材：
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の関数を$x$について微分せよ。
(1) $\displaystyle y=\int_x^{2x}\cos^2t~dt$
(2) $\displaystyle y=\int_x^{x^2}e^t\sin t~dt$
この動画を見る
次の関数を$x$について微分せよ。
(1) $\displaystyle y=\int_x^{2x}\cos^2t~dt$
(2) $\displaystyle y=\int_x^{x^2}e^t\sin t~dt$
【数Ⅲ】【積分とその応用】定積分の種々の問題1 ※問題文は概要欄
単元：
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の関数を$x$について微分せよ。
(1) $\displaystyle F(x)=\int_0^x(x+t)e^t~dt$
(2) $\displaystyle F(x)=\int_1^x(t-x)\log t~dt$
この動画を見る
次の関数を$x$について微分せよ。
(1) $\displaystyle F(x)=\int_0^x(x+t)e^t~dt$
(2) $\displaystyle F(x)=\int_1^x(t-x)\log t~dt$
福田のおもしろ数学498〜定積分で定義された関数の極限
単元：
#関数と極限#積分とその応用#関数の極限#定積分#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$0\lt t \leqq 1$に対し、
$f(t)=\dfrac{1}{t} \displaystyle \int_{0}^{\frac{\pi}{2}t} \vert \cos 2x \vert dx$とする。
$\displaystyle \lim_{t\to 0} f(t)$を求めよ。
この動画を見る
$0\lt t \leqq 1$に対し、
$f(t)=\dfrac{1}{t} \displaystyle \int_{0}^{\frac{\pi}{2}t} \vert \cos 2x \vert dx$とする。
$\displaystyle \lim_{t\to 0} f(t)$を求めよ。
福田の数学〜慶應義塾大学薬学部2025第3問〜逆関数と定積分
単元：
#大学入試過去問(数学)#関数と極限#積分とその応用#関数（分数関数・無理関数・逆関数と合成関数）#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
実数$x$に対して、関数
$f(x)=\dfrac{1}{3}x+\sqrt{\dfrac{1}{9}x^2+8}$
がある。ただし、定義域は$x\geqq 0$である。
$y=f(x)$の逆関数を$y=g(x)$とする。
(1)$g(x)$を求めると、$g(x)=\boxed{ナ}$であり、
$g(x)$定義域は$\boxed{ニ}$である。
(2)$\displaystyle \int_{2\sqrt2}^{4}g(x)dx$を求めると$\boxed{ヌ}$である。
(3)$\displaystyle \int_{0}^{3} f(x) dx$を求めると$\boxed{ネ}$である。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{3}$
実数$x$に対して、関数
$f(x)=\dfrac{1}{3}x+\sqrt{\dfrac{1}{9}x^2+8}$
がある。ただし、定義域は$x\geqq 0$である。
$y=f(x)$の逆関数を$y=g(x)$とする。
(1)$g(x)$を求めると、$g(x)=\boxed{ナ}$であり、
$g(x)$定義域は$\boxed{ニ}$である。
(2)$\displaystyle \int_{2\sqrt2}^{4}g(x)dx$を求めると$\boxed{ヌ}$である。
(3)$\displaystyle \int_{0}^{3} f(x) dx$を求めると$\boxed{ネ}$である。
$2025$年慶應義塾大学薬学部過去問題
福田の数学〜慶應義塾大学薬学部2025第1問(4)〜円柱を切ってできる立体の体積と側面積
単元：
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#立体図形#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(4)$xyz$空間において、
$xy$平面上に$(0,0,0)$を中心とする半径$2$の円がある。
この円と、$(0,0,2\sqrt3)$を中心とする半径$2$の円を
底面とする円柱を、
原点を通り$xz$平面と$30$度の角をなす平面によって
切断し、$2$つの立体に分ける。
いま$2$つの立体のうち、
体積の小さい方の立体について考える。
その立体の体積を$V$、切り口の面積を$S_1$、
円柱の側面であった部分の面積を$S_2$とする。
(i)$V=\boxed{ケ}$
(ii)$S_1=\boxed{コ},S_2=\boxed{サ}$である。
この動画を見る
$\boxed{1}$
(4)$xyz$空間において、
$xy$平面上に$(0,0,0)$を中心とする半径$2$の円がある。
この円と、$(0,0,2\sqrt3)$を中心とする半径$2$の円を
底面とする円柱を、
原点を通り$xz$平面と$30$度の角をなす平面によって
切断し、$2$つの立体に分ける。
いま$2$つの立体のうち、
体積の小さい方の立体について考える。
その立体の体積を$V$、切り口の面積を$S_1$、
円柱の側面であった部分の面積を$S_2$とする。
(i)$V=\boxed{ケ}$
(ii)$S_1=\boxed{コ},S_2=\boxed{サ}$である。
福田のおもしろ数学454〜積分に関するシュワルツの不等式の証明と等号成立条件
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#積分とその応用#不定積分#定積分#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$p\leqq x \leqq q$で定義された連続関数$f(x),ｇ(x)$に対して
$\left(\displaystyle \int_{p}^{q} f(x)^2 dx\right)\left(\displaystyle \int_{p}^{q}g(x)^2 dx \right) \geqq \left(\displaystyle \int_{p}^{q} f(x)g(x)dx\right)^2$
を証明して下さい。
また等号成立条件も調べて下さい。
この動画を見る
$p\leqq x \leqq q$で定義された連続関数$f(x),ｇ(x)$に対して
$\left(\displaystyle \int_{p}^{q} f(x)^2 dx\right)\left(\displaystyle \int_{p}^{q}g(x)^2 dx \right) \geqq \left(\displaystyle \int_{p}^{q} f(x)g(x)dx\right)^2$
を証明して下さい。
また等号成立条件も調べて下さい。
【数Ⅲ】【積分とその応用】面積13 ※問題文は概要欄
単元：
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$k > 0$とする。曲線$y=\sin2x~~(0\leqq x\leqq \dfrac\pi2)$と$x$軸で囲まれた部分の面積を$y=k\sin x$が2等分するように定数$k$の値を定めよ。
この動画を見る
$k > 0$とする。曲線$y=\sin2x~~(0\leqq x\leqq \dfrac\pi2)$と$x$軸で囲まれた部分の面積を$y=k\sin x$が2等分するように定数$k$の値を定めよ。
【数Ⅲ】【積分とその応用】面積15 ※問題文は概要欄
単元：
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$x$軸に平行な直線と曲線$y=\sin x~~(0\leqq x \leqq 3\pi)$が4点で交わるとき、この直線と曲線で囲まれた3つの部分の面積の和が最小となるような直線の方程式を求めよ。
この動画を見る
$x$軸に平行な直線と曲線$y=\sin x~~(0\leqq x \leqq 3\pi)$が4点で交わるとき、この直線と曲線で囲まれた3つの部分の面積の和が最小となるような直線の方程式を求めよ。
【数Ⅲ】【積分とその応用】面積14 ※問題文は概要欄
単元：
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$1\leqq a\leqq e$とする。曲線$y=e^x-a$と$x$軸、$y$軸および直線$x=1$で囲まれた部分の面積を$S(a)$とする。
(1) $S(a)$を求めよ。
(2) $S(a)$の最小値とそのときの$a$の値を求めよ。
この動画を見る
$1\leqq a\leqq e$とする。曲線$y=e^x-a$と$x$軸、$y$軸および直線$x=1$で囲まれた部分の面積を$S(a)$とする。
(1) $S(a)$を求めよ。
(2) $S(a)$の最小値とそのときの$a$の値を求めよ。