 図形への応用
図形への応用
 図形への応用
図形への応用
福田のおもしろ数学528〜平面幾何の証明
単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
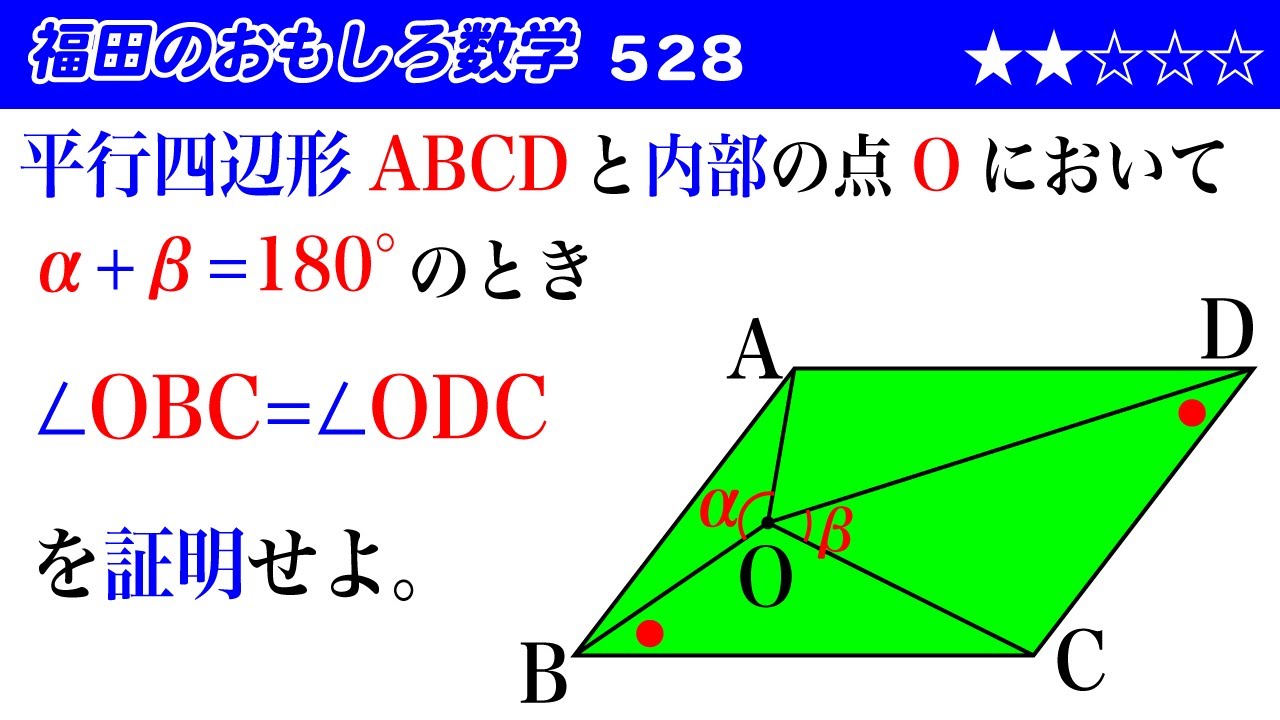
平行四辺形$ABCD$と内部の点$O$において
$\alpha+\beta=180°$のとき
$\angle OBC=\angle ODC$
を証明せよ。
図は動画内参照
この動画を見る
平行四辺形$ABCD$と内部の点$O$において
$\alpha+\beta=180°$のとき
$\angle OBC=\angle ODC$
を証明せよ。
図は動画内参照
【数C】【複素数平面】複素数と図形12 ※問題文は概要欄
単元:
#複素数平面#図形への応用#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#複素数平面
指導講師:
理数個別チャンネル
問題文全文(内容文):
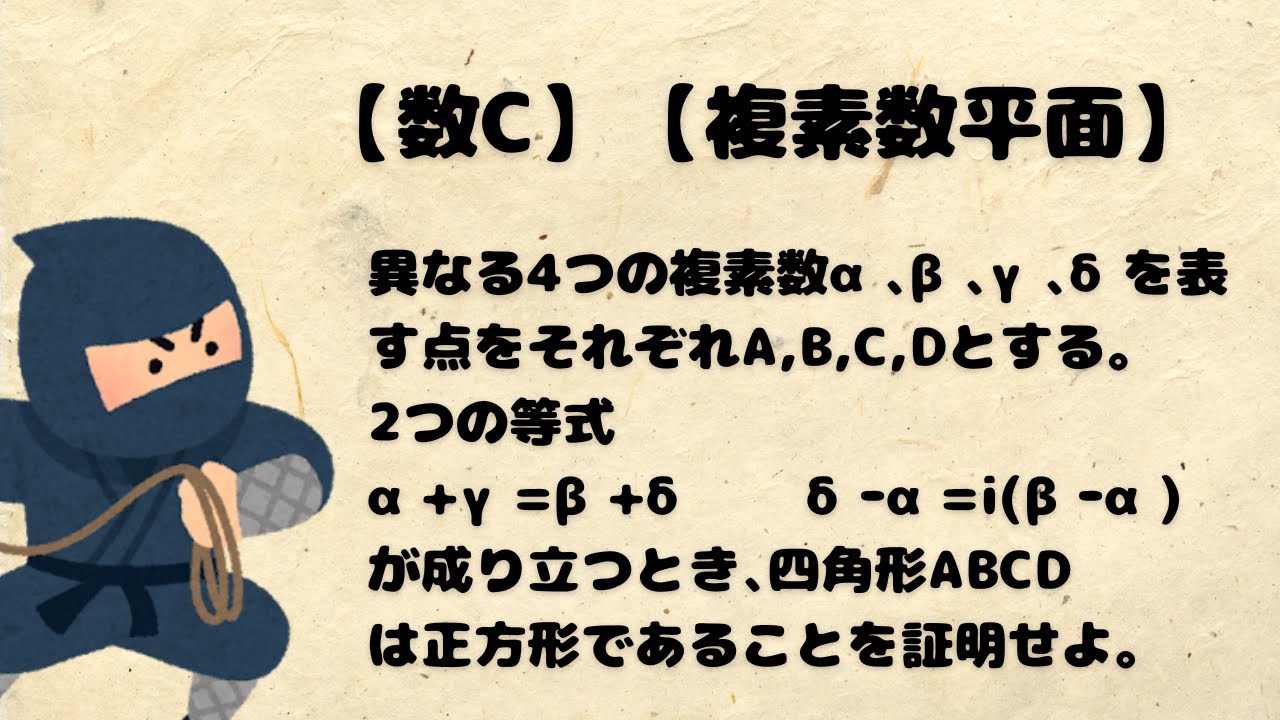
異なる4つの複素数α、β、γ、δを表す点を
それぞれA,B,C,Dとする。2つの等式
α+γ=β+δ δーα=i(βーα)
が成り立つとき、四角形ABCD
は正方形であることを証明せよ。
この動画を見る
異なる4つの複素数α、β、γ、δを表す点を
それぞれA,B,C,Dとする。2つの等式
α+γ=β+δ δーα=i(βーα)
が成り立つとき、四角形ABCD
は正方形であることを証明せよ。
【数C】【複素数平面】複素数と図形11 ※問題文は概要欄
単元:
#複素数平面#図形への応用#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#複素数平面
指導講師:
理数個別チャンネル
問題文全文(内容文):
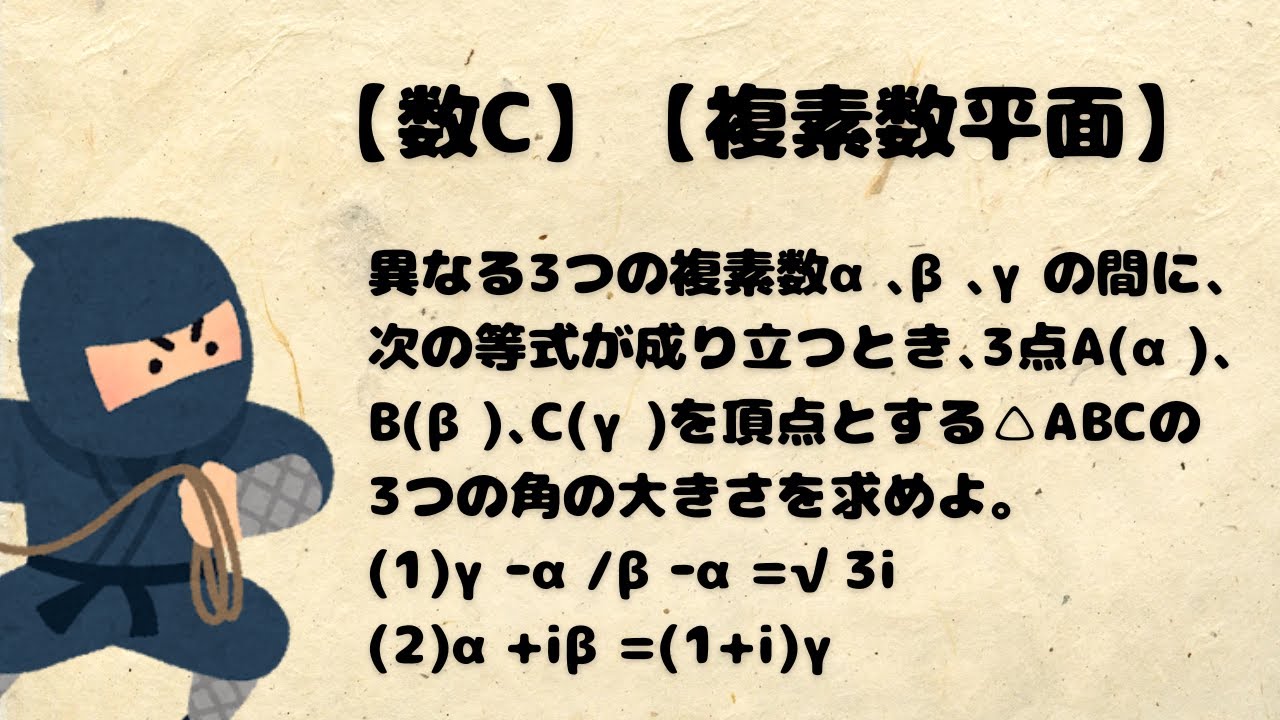
異なる3つの複素数α、β、γの間に、次の等式が成り立つとき、3点A(α)、B(β)、C(γ)を頂点とする△ABCの3つの角の大きさを求めよ。
(1)$\displaystyle \frac{γーα}{βーα}=\sqrt{3}i $
(2)$α+iβ=(1+i)γ$
この動画を見る
異なる3つの複素数α、β、γの間に、次の等式が成り立つとき、3点A(α)、B(β)、C(γ)を頂点とする△ABCの3つの角の大きさを求めよ。
(1)$\displaystyle \frac{γーα}{βーα}=\sqrt{3}i $
(2)$α+iβ=(1+i)γ$
【数C】【複素数平面】複素数と図形10 ※問題文は概要欄
単元:
#複素数平面#図形への応用#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#複素数平面
指導講師:
理数個別チャンネル
問題文全文(内容文):
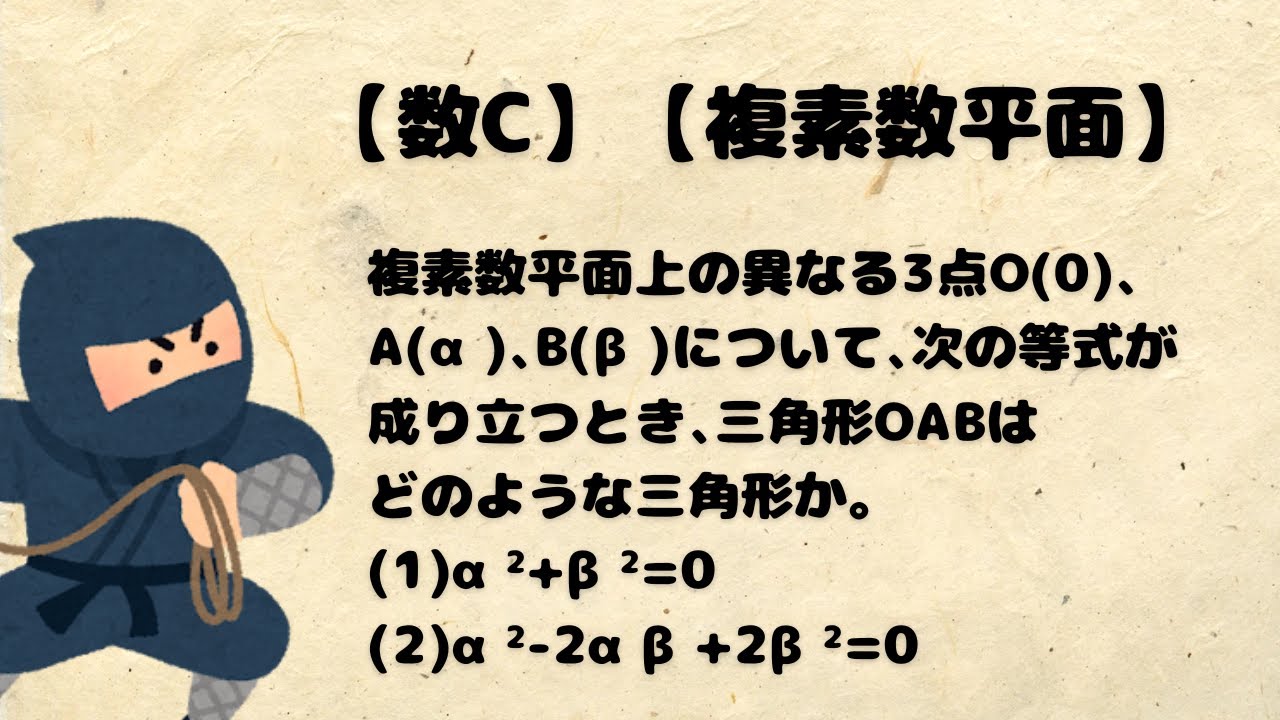
複素数平面上の異なる3点O(0)、A(α)、B(β)について、次の等式が成り立つとき、三角形OABはどのような三角形か。
(1)α²+β²=0
(2)α²-2αβ+2β²=0
この動画を見る
複素数平面上の異なる3点O(0)、A(α)、B(β)について、次の等式が成り立つとき、三角形OABはどのような三角形か。
(1)α²+β²=0
(2)α²-2αβ+2β²=0
【数C】【複素数平面】複素数と図形9 ※問題文は概要欄

単元:
#複素数平面#図形への応用#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#複素数平面
指導講師:
理数個別チャンネル
問題文全文(内容文):
複素数平面上の異なる2点A,Bを表す複素数をそれぞれ
1+i、4+3iとする。線分ABを1辺とする正方形の
他の2つの頂点を表す複素数をそれぞれ求めよ。
この動画を見る
複素数平面上の異なる2点A,Bを表す複素数をそれぞれ
1+i、4+3iとする。線分ABを1辺とする正方形の
他の2つの頂点を表す複素数をそれぞれ求めよ。
【数C】【複素数平面】複素数と図形8 ※問題文は概要欄

単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
複素数平面上の2点$\rm A,B$を表す複素数をそれぞれ$\alpha=1-2i,\beta=3+2i$とするとき
線分$\rm AB$を1辺とする正三角形の他の頂点$\rm C$を表す複素数$\gamma$を求めよ。
この動画を見る
複素数平面上の2点$\rm A,B$を表す複素数をそれぞれ$\alpha=1-2i,\beta=3+2i$とするとき
線分$\rm AB$を1辺とする正三角形の他の頂点$\rm C$を表す複素数$\gamma$を求めよ。
【数C】【複素数平面】複素数と図形7 ※問題文は概要欄

単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
原点を${\rm {O}}, \alpha=2-i,\beta=3+(2a-1)i$を表す点をそれぞれ$\rm A,B$とするとき、$\rm \angle AOB=\dfrac\pi4$を満たす実数$a$の値を求めよ。
この動画を見る
原点を${\rm {O}}, \alpha=2-i,\beta=3+(2a-1)i$を表す点をそれぞれ$\rm A,B$とするとき、$\rm \angle AOB=\dfrac\pi4$を満たす実数$a$の値を求めよ。
【数C】【複素数平面】複素数と図形6 ※問題文は概要欄

単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
複素数平面上の異なる4点$\rm A(\alpha),B(\beta),C(\gamma),D(\delta)$
について次のことが成り立つことを証明せよ。
2直線$\rm AB,CD$が垂直に交わる ⇔ $\dfrac{(\delta-\gamma)}{(\beta-\alpha)}$が純虚数
この動画を見る
複素数平面上の異なる4点$\rm A(\alpha),B(\beta),C(\gamma),D(\delta)$
について次のことが成り立つことを証明せよ。
2直線$\rm AB,CD$が垂直に交わる ⇔ $\dfrac{(\delta-\gamma)}{(\beta-\alpha)}$が純虚数
【数C】【複素数平面】複素数と図形5 ※問題文は概要欄

単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
点$z$が、点$-1$を通り実軸に垂直な直線上を動くとき、
点$w=\dfrac1z$ はどのような図形を描くか。
この動画を見る
点$z$が、点$-1$を通り実軸に垂直な直線上を動くとき、
点$w=\dfrac1z$ はどのような図形を描くか。
【数C】【複素数平面】複素数と図形3 ※問題文は概要欄

単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
点$z$が、原点$\rm O$を中心とする半径1の円上を動くとき、次の点$w$はどのような図形を描くか。
(1) $w=\dfrac{1+i}{z}$ (2) $w=\dfrac{6z-1}{2z-1}$
この動画を見る
点$z$が、原点$\rm O$を中心とする半径1の円上を動くとき、次の点$w$はどのような図形を描くか。
(1) $w=\dfrac{1+i}{z}$ (2) $w=\dfrac{6z-1}{2z-1}$
【数C】【複素数平面】複素数と図形2 ※問題文は概要欄

単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の方程式を満たす点$z$全体の集合はどのような図形か。
(1) $z+\bar{z}=2$ (2) $z-\bar{z}=2i$
この動画を見る
次の方程式を満たす点$z$全体の集合はどのような図形か。
(1) $z+\bar{z}=2$ (2) $z-\bar{z}=2i$
【数C】【複素数平面】複素数と図形1 ※問題文は概要欄

単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形の各辺の中点が$\alpha=-1+i,\beta=1+2i,\gamma=2$であるとき、この三角形の3つの頂点を表す複素数を求めよ。
この動画を見る
三角形の各辺の中点が$\alpha=-1+i,\beta=1+2i,\gamma=2$であるとき、この三角形の3つの頂点を表す複素数を求めよ。
福田の数学〜東京理科大学2024創域理工学部第1問(1)〜複素数と三角形の外接円

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}(1)a$を正の実数とする。$x$についての方程式
$(x^2+ax+2)(x^2-ax-1)=0・・・①$
が異なる2つの実数解と異なる2つの虚数解をもつのは
$\boxed{ア} \lt a \lt \boxed{イ}\sqrt{\boxed{ウ}}・・・②$
のときである。
以下では、$a$は不等式$②$を満たす最大の整数とし、$i$は虚数単位とする。このとき、複素数平面上において、方程式$①$の異なる2つの虚数解と$3+i$を頂点とする三角形の面積は$\boxed{エ}$であり、この三角形の外接円を複素数zの方程式で表すと
$|x-\boxed{オ}|=\sqrt{\boxed{カ}}$
である。
この動画を見る
$\boxed{1}(1)a$を正の実数とする。$x$についての方程式
$(x^2+ax+2)(x^2-ax-1)=0・・・①$
が異なる2つの実数解と異なる2つの虚数解をもつのは
$\boxed{ア} \lt a \lt \boxed{イ}\sqrt{\boxed{ウ}}・・・②$
のときである。
以下では、$a$は不等式$②$を満たす最大の整数とし、$i$は虚数単位とする。このとき、複素数平面上において、方程式$①$の異なる2つの虚数解と$3+i$を頂点とする三角形の面積は$\boxed{エ}$であり、この三角形の外接円を複素数zの方程式で表すと
$|x-\boxed{オ}|=\sqrt{\boxed{カ}}$
である。
福田のおもしろ数学214〜与えられた方程式の表すグラフが放物線であることの証明

単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\sqrt{x}+\sqrt{y}=1$のグラフは放物線の一部であることを示してください。
この動画を見る
$\sqrt{x}+\sqrt{y}=1$のグラフは放物線の一部であることを示してください。
福田の数学〜千葉大学2024年理系第4問(2)〜複素数平面乗の正三角形の頂点を求める

単元:
#大学入試過去問(数学)#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
複素数平面上の3点$\mathrm{P}(z), \mathrm{Q}(-1),\mathrm{R}(\sqrt3-1-i)$が正三角形をなすとき、複素数$z$を求めよ。
この動画を見る
複素数平面上の3点$\mathrm{P}(z), \mathrm{Q}(-1),\mathrm{R}(\sqrt3-1-i)$が正三角形をなすとき、複素数$z$を求めよ。
福田のおもしろ数学197〜正五角形の辺、対角線の積の値
単元:
#数Ⅰ#複素数平面#図形と計量#三角比への応用(正弦・余弦・面積)#図形への応用#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
半径$1$の円に内接する正五角形$\mathrm{ABCDE}$について$\mathrm{AB}\cdot\mathrm{AC}\cdot\mathrm{AD}\cdot\mathrm{AE}$を求めよ。
この動画を見る
半径$1$の円に内接する正五角形$\mathrm{ABCDE}$について$\mathrm{AB}\cdot\mathrm{AC}\cdot\mathrm{AD}\cdot\mathrm{AE}$を求めよ。
頭の体操に 四天王寺
単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
数学を数楽に
問題文全文(内容文):
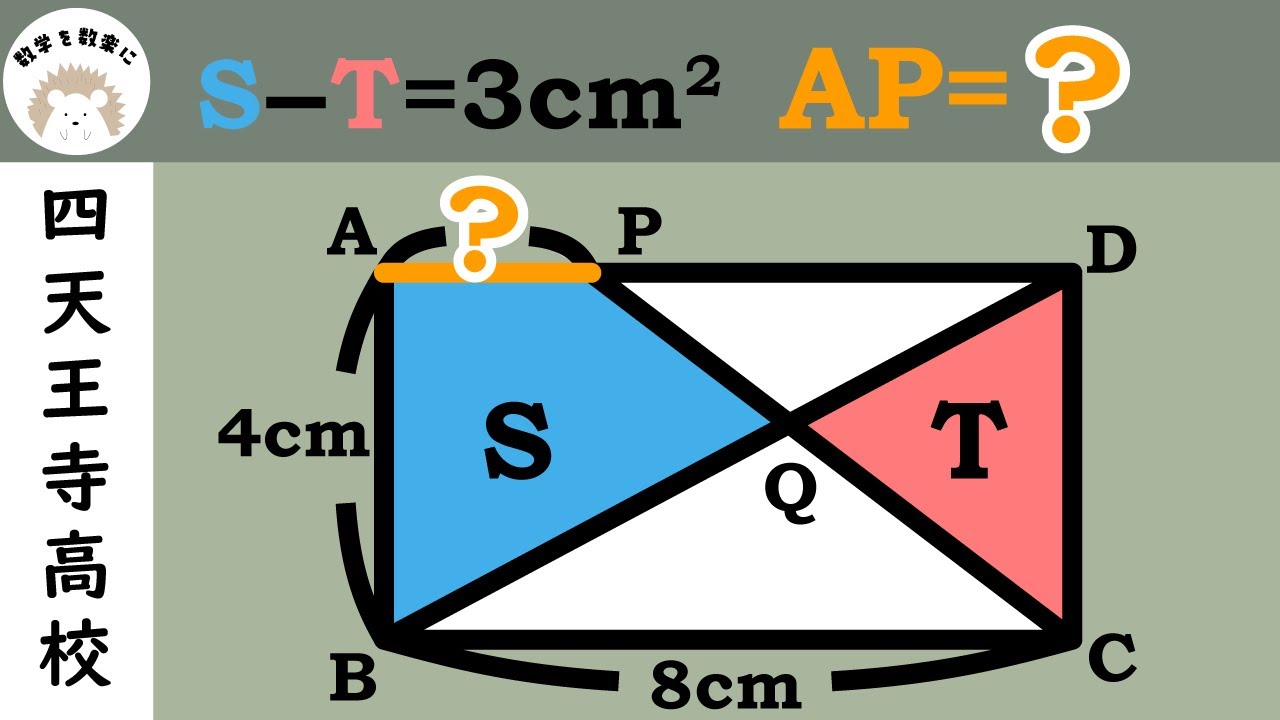
$S-T=3\,\rm{cm}^2$
$AP=?$
*図は動画内参照
四天王寺高等学校
この動画を見る
$S-T=3\,\rm{cm}^2$
$AP=?$
*図は動画内参照
四天王寺高等学校
福田の数学〜東京大学2018年理系第5問〜複素数平面上の点の軌跡

単元:
#大学入試過去問(数学)#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
複素数平面上の原点を中心とする半径 1 の円を C とする。
点 P(z) は C 上にあり、点 A(I) とは異なるとする。
点 P における円 C の接線に関して、点 A と対称な点を Q(u) とする。
$\omega=\displaystyle \frac{1}{1-u}$とおき$\omega$と共役な複素数を$\overline{ \omega }$で表す。
(1)uと$\displaystyle \frac{\overline{ \omega }}{\omega}$をzについての整数として表し、絶対値の値$\displaystyle \frac{\vert \omega+\overline{ \omega }-1 \vert}{\vert \omega \vert}$を求めよ。
(2)Cのうち実部が$\frac{1}{2}$以下の複素数平面で表される部分をCとする。点P(z)がC’上を動くときの点R($\omega$)の軌跡を求めよ。
$\omega=x+yi$(x,yは実数)とおく。
2018東大理系過去問
この動画を見る
複素数平面上の原点を中心とする半径 1 の円を C とする。
点 P(z) は C 上にあり、点 A(I) とは異なるとする。
点 P における円 C の接線に関して、点 A と対称な点を Q(u) とする。
$\omega=\displaystyle \frac{1}{1-u}$とおき$\omega$と共役な複素数を$\overline{ \omega }$で表す。
(1)uと$\displaystyle \frac{\overline{ \omega }}{\omega}$をzについての整数として表し、絶対値の値$\displaystyle \frac{\vert \omega+\overline{ \omega }-1 \vert}{\vert \omega \vert}$を求めよ。
(2)Cのうち実部が$\frac{1}{2}$以下の複素数平面で表される部分をCとする。点P(z)がC’上を動くときの点R($\omega$)の軌跡を求めよ。
$\omega=x+yi$(x,yは実数)とおく。
2018東大理系過去問
数学どうにかしたい人へ

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#図形の性質#式と証明#複素数と方程式#平面上のベクトル#空間ベクトル#平面上の曲線#複素数平面#図形と計量#データの分析#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#一次不等式(不等式・絶対値のある方程式・不等式)#集合と命題(集合・命題と条件・背理法)#2次方程式と2次不等式#2次関数とグラフ#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#データの分析#整数の性質#場合の数#確率#三角形の辺の比(内分・外分・二等分線)#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#図形と方程式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#円と方程式#軌跡と領域#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数列#確率分布と統計的な推測#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#数列とその和(等差・等比・階差・Σ)#漸化式#数学的帰納法#確率分布#統計的な推測#関数と極限#微分とその応用#積分とその応用#2次曲線#複素数平面#図形への応用#関数(分数関数・無理関数・逆関数と合成関数)#数列の極限#関数の極限#微分法#色々な関数の導関数#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#不定積分#定積分#面積・体積・長さ・速度#空間における垂直と平行と多面体(オイラーの法則)#不定積分・定積分#面積、体積#媒介変数表示と極座標#速度と近似式#数学(高校生)#数B#数C#数Ⅲ
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
数学が共通テストのみの人の勉強法紹介動画です
この動画を見る
数学が共通テストのみの人の勉強法紹介動画です
自治医大 三次方程式の解

単元:
#数Ⅱ#複素数と方程式#複素数平面#複素数#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
2023自治医科大学過去問題
kは実数
$x^3-6x^2+kx-7 = 0$
の3つの解は複素数平面で1辺の長さが$\sqrt{3}$の正三角形の頂点となる
kの値
この動画を見る
2023自治医科大学過去問題
kは実数
$x^3-6x^2+kx-7 = 0$
の3つの解は複素数平面で1辺の長さが$\sqrt{3}$の正三角形の頂点となる
kの値
福田の数学〜筑波大学2023年理系第6問〜複素数平面上の点の軌跡とアポロニウスの円

単元:
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#軌跡と領域#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{6}$ $i$を虚数単位とする。複素数平面に関する以下の問いに答えよ。
(1)等式|$z$+2|=2|$z$-1| を満たす点$z$の全体が表す図形は円であることを示し、その中心と半径を求めよ。
(2)等式
$\left\{|z+2|-2|z-1|\right\}$$|z+6i|$=$3\left\{|z+2|-2|z-1|\right\}$$|z-2i|$
を満たす点$z$の全体が表す図形をSとする。このときSを複素数平面上に図示せよ。
(3)点$z$が(2)における図形S上を動くとき、$w$=$\frac{1}{z}$ で定義される点$w$が描く図形を複素数平面上に図示せよ。
2023筑波大学理系過去問
この動画を見る
$\Large\boxed{6}$ $i$を虚数単位とする。複素数平面に関する以下の問いに答えよ。
(1)等式|$z$+2|=2|$z$-1| を満たす点$z$の全体が表す図形は円であることを示し、その中心と半径を求めよ。
(2)等式
$\left\{|z+2|-2|z-1|\right\}$$|z+6i|$=$3\left\{|z+2|-2|z-1|\right\}$$|z-2i|$
を満たす点$z$の全体が表す図形をSとする。このときSを複素数平面上に図示せよ。
(3)点$z$が(2)における図形S上を動くとき、$w$=$\frac{1}{z}$ で定義される点$w$が描く図形を複素数平面上に図示せよ。
2023筑波大学理系過去問
【数Ⅲ】複素数平面:複素数で表された方程式が示す図形とは?

単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の方程式を満たす点Z全体が表す図形を答えよ。
(1)$\vert \bar{z} - i \vert = 1$
(2)$\vert z - 3 + i\vert = \vert z + 1\vert $
(3)$\vert z - i\vert =2\vert z - 1\vert$
この動画を見る
次の方程式を満たす点Z全体が表す図形を答えよ。
(1)$\vert \bar{z} - i \vert = 1$
(2)$\vert z - 3 + i\vert = \vert z + 1\vert $
(3)$\vert z - i\vert =2\vert z - 1\vert$
産業医科大 三角比の計算

単元:
#数Ⅰ#大学入試過去問(数学)#複素数平面#図形と計量#三角比(三角比・拡張・相互関係・単位円)#図形への応用#学校別大学入試過去問解説(数学)#数学(高校生)#数C#産業医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\cos\dfrac{2}{7}\pi+\cos\dfrac{4}{7}\pi+\cos\dfrac{8}{7}\pi=?$
$\sin\dfrac{2}{7}\pi+\sin\dfrac{4}{7}\pi+\sin\dfrac{8}{7}\pi=?$
これらを求めよ。
産業医科大過去問
この動画を見る
$\cos\dfrac{2}{7}\pi+\cos\dfrac{4}{7}\pi+\cos\dfrac{8}{7}\pi=?$
$\sin\dfrac{2}{7}\pi+\sin\dfrac{4}{7}\pi+\sin\dfrac{8}{7}\pi=?$
これらを求めよ。
産業医科大過去問
福田の数学〜慶應義塾大学2023年医学部第4問PART1〜円に内接する円の性質
単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#複素数平面#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#円と方程式#微分とその応用#複素数平面#図形への応用#微分法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
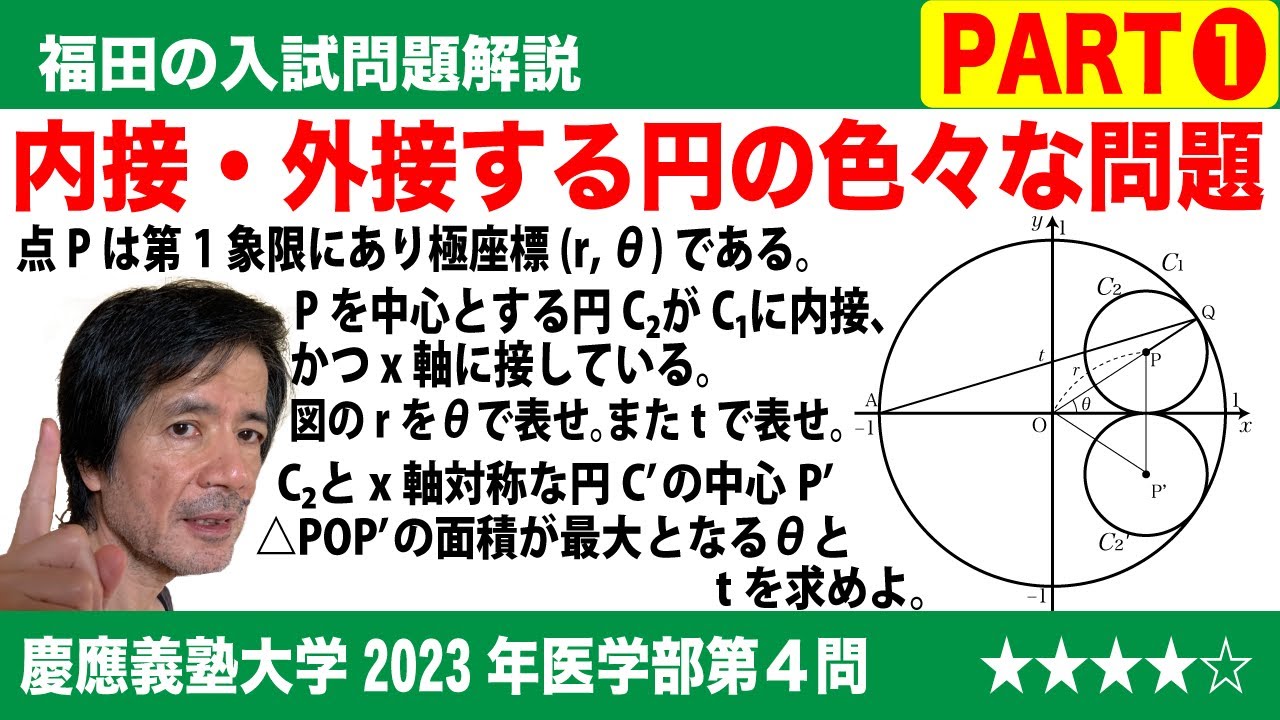
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
福田の数学〜早稲田大学2023年理工学部第4問〜複素数平面上の点の軌跡

単元:
#大学入試過去問(数学)#複素数平面#微分とその応用#複素数平面#図形への応用#色々な関数の導関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 複素数平面上に2点A(1), B($\sqrt 3 i$)がある。ただし、$i$は虚数単位である。
複素数zに対し$w$=$\frac{3}{z}$で表される点$w$を考える。以下の問いに答えよ。
(1)z=1, $\frac{1+\sqrt 3i}{2}$, $\sqrt 3 i$のときのwをそれぞれ計算せよ。
(2)実数tに対し、z=(1-t)+t$\sqrt 3 i$とする。$\alpha$=$\frac{3-\sqrt 3 i}{2}$について、$\alpha z$の実部を求め、さらに($w-\alpha$)($\bar{w-\alpha}$)を求めよ。
(3)wと原点を結んでできる線分Lを考える。zが線分AB上を動くとき、線分Lが通過する範囲を図示し、その面積を求めよ。
この動画を見る
$\Large\boxed{4}$ 複素数平面上に2点A(1), B($\sqrt 3 i$)がある。ただし、$i$は虚数単位である。
複素数zに対し$w$=$\frac{3}{z}$で表される点$w$を考える。以下の問いに答えよ。
(1)z=1, $\frac{1+\sqrt 3i}{2}$, $\sqrt 3 i$のときのwをそれぞれ計算せよ。
(2)実数tに対し、z=(1-t)+t$\sqrt 3 i$とする。$\alpha$=$\frac{3-\sqrt 3 i}{2}$について、$\alpha z$の実部を求め、さらに($w-\alpha$)($\bar{w-\alpha}$)を求めよ。
(3)wと原点を結んでできる線分Lを考える。zが線分AB上を動くとき、線分Lが通過する範囲を図示し、その面積を求めよ。
福田の数学〜北海道大学2023年理系第1問〜複素数平面上の図形の列

単元:
#大学入試過去問(数学)#複素数平面#関数と極限#複素数平面#図形への応用#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 複素数平面上における図形$C_1$, $C_2$, ...,$C_n$, ...は次の条件(A)と(B)を満たすとする。ただし、$i$は虚数単位とする。
(A)$C_1$は原点Oを中心とする半径2の円である。
(B)自然数nに対して、zが$C_n$上を動くとき2w=z+1+$i$で定まるwの描く図形が$C_{n+1}$である。
(1)すべての自然数nに対して、$C_n$は円であることを示し、その中心を表す複素数$\alpha_n$と半径$r_n$を求めよ。
(2)$C_n$上の点とOとの距離の最小値を$d_n$とする。このとき、$d_n$を求めよ。
また、$\displaystyle\lim_{n \to \infty}d_n$を求めよ。
2023北海道大学理系過去問
この動画を見る
$\Large\boxed{1}$ 複素数平面上における図形$C_1$, $C_2$, ...,$C_n$, ...は次の条件(A)と(B)を満たすとする。ただし、$i$は虚数単位とする。
(A)$C_1$は原点Oを中心とする半径2の円である。
(B)自然数nに対して、zが$C_n$上を動くとき2w=z+1+$i$で定まるwの描く図形が$C_{n+1}$である。
(1)すべての自然数nに対して、$C_n$は円であることを示し、その中心を表す複素数$\alpha_n$と半径$r_n$を求めよ。
(2)$C_n$上の点とOとの距離の最小値を$d_n$とする。このとき、$d_n$を求めよ。
また、$\displaystyle\lim_{n \to \infty}d_n$を求めよ。
2023北海道大学理系過去問
複素数平面の基本⑬3点が一直線上にあるとき、なす角が垂直のときを考える

複素数平面の基本⑫半直線のなす角を考える

複素数平面の基本⑨垂直二等分線を考える

慈恵医大 複素数の基本問題

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東京慈恵会医科大学#東京慈恵会医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha=\cos\dfrac{2}{7}\pi+i\sin\dfrac{2}{7}\pi$
(1)$\alpha^7,\displaystyle \sum_{k=0}^6 {\alpha}_{k}$の値を求めよ.
(2)$\beta=\alpha^3+\alpha^5+\alpha^6$とするとき,$\beta+\bar{\beta},\beta\bar{\beta}$の値を求めよ.
(3)$\beta=a+bi,b$の正負を判定し$a,b$の値を求めよ.
慈恵医大過去問
この動画を見る
$\alpha=\cos\dfrac{2}{7}\pi+i\sin\dfrac{2}{7}\pi$
(1)$\alpha^7,\displaystyle \sum_{k=0}^6 {\alpha}_{k}$の値を求めよ.
(2)$\beta=\alpha^3+\alpha^5+\alpha^6$とするとき,$\beta+\bar{\beta},\beta\bar{\beta}$の値を求めよ.
(3)$\beta=a+bi,b$の正負を判定し$a,b$の値を求めよ.
慈恵医大過去問
