 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
福田の1.5倍速演習〜合格する重要問題004〜東北大学2015年理系数学第1問

単元:
#大学入試過去問(数学)#平面上の曲線#2次曲線#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#東北大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
xy平面において、次の式が表す曲線をCとする。
$x^2+4y^2=1,x \gt 0, y \gt 0$
PをC上の点とする。PでCに接する直線をlとし、Pを通りlと垂直な直線を
mとして、x軸とy軸とmで囲まれてできる三角形の面積をSとする。PがC
上の点全体をうごくとき、Sの最大値とその時のPの座標を求めよ。
2015東北大学理系過去問
この動画を見る
xy平面において、次の式が表す曲線をCとする。
$x^2+4y^2=1,x \gt 0, y \gt 0$
PをC上の点とする。PでCに接する直線をlとし、Pを通りlと垂直な直線を
mとして、x軸とy軸とmで囲まれてできる三角形の面積をSとする。PがC
上の点全体をうごくとき、Sの最大値とその時のPの座標を求めよ。
2015東北大学理系過去問
座標平面と確率
単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
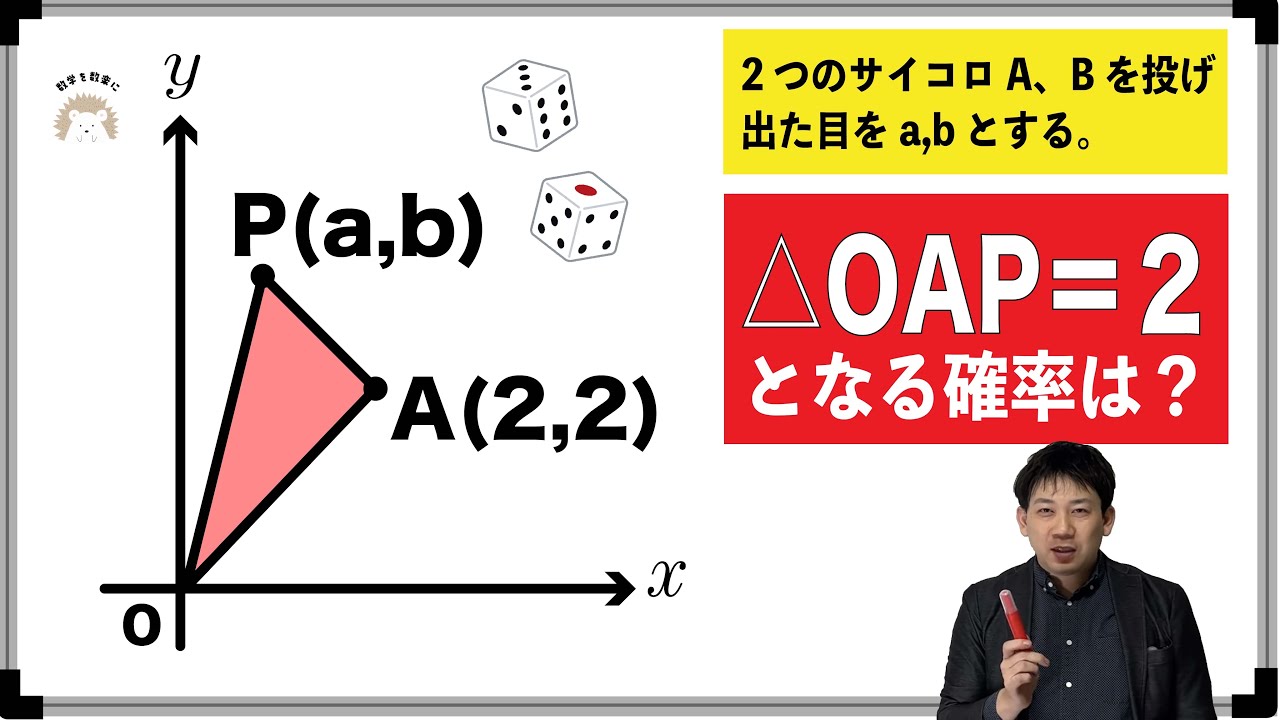
2つのサイコロA,Bを投げ出た目をa,bとする。
△OAP=2となる確率は?
*図は動画内参照
この動画を見る
2つのサイコロA,Bを投げ出た目をa,bとする。
△OAP=2となる確率は?
*図は動画内参照
大学入試問題#372「初手が命」 兵庫県立大学2015 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#兵庫県立大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{3}}\displaystyle \frac{dx}{\cos^4x}$
出典:2015年兵庫県立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{3}}\displaystyle \frac{dx}{\cos^4x}$
出典:2015年兵庫県立大学 入試問題
Factorizationよどみなく因数分解してくれ!

素数に関する問題 国学院高校
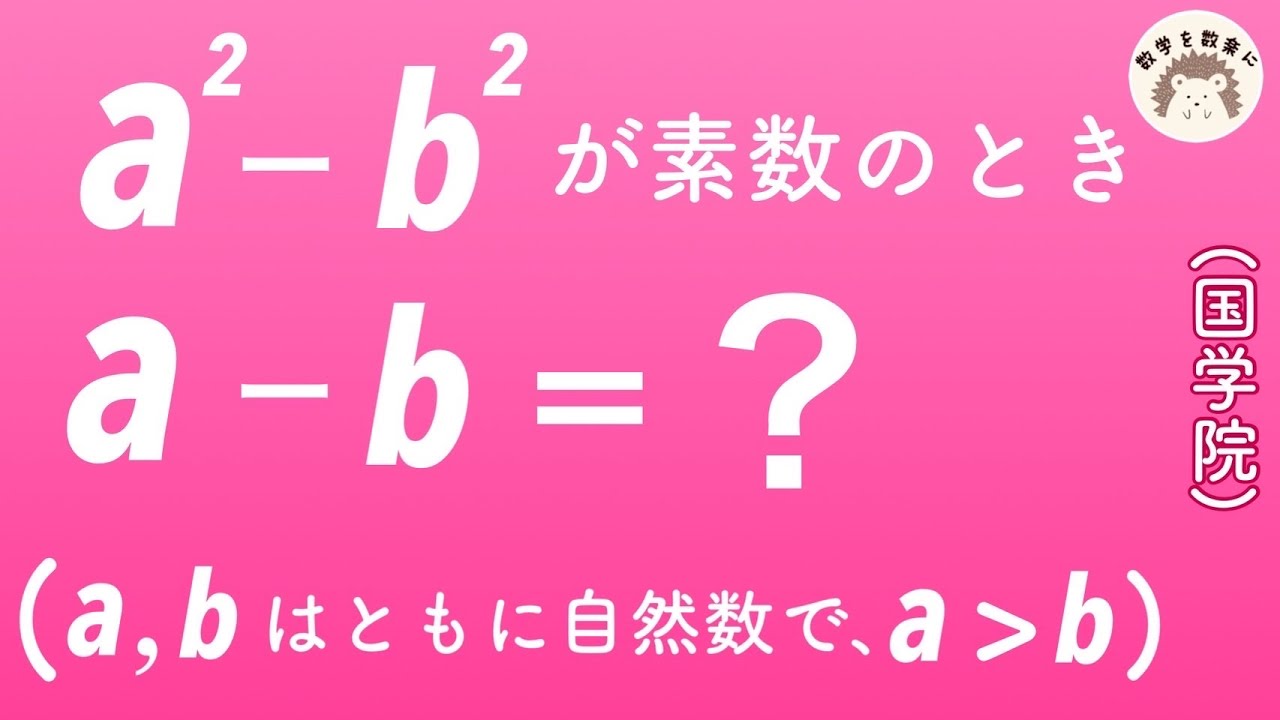
単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^2-b^2$が素数のとき
a-b=?
(a,bはともに自然数で、a>b)
國學院高等学校
この動画を見る
$a^2-b^2$が素数のとき
a-b=?
(a,bはともに自然数で、a>b)
國學院高等学校
【ひとまず解答してみよう…!】整数:慶応義塾高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2つの自然数$m,n$は$2^m-1=(2n+1)(2n+3)$を満たす.
$m=6$のとき,$n$の値を求めよ.
慶應義塾高校過去問
この動画を見る
2つの自然数$m,n$は$2^m-1=(2n+1)(2n+3)$を満たす.
$m=6$のとき,$n$の値を求めよ.
慶應義塾高校過去問
福田の1.5倍速演習〜合格する重要問題003〜北海道大学2015年文系数学第4問〜隣り合う順列、隣り合わない順列

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
福田次郎
問題文全文(内容文):
ジョーカーを除く1組52枚のトランプのカードを1列に並べる思考を考える。
(1)番号7のカードが4枚連続して並ぶ確率を求めよ。
(2)番号7のカードが2枚ずつ隣り合い、4枚連続しては並ばない確率を求めよ。
8人の人が一列に並ぶとき、
(1)A,B,Cの3人が連続して並ぶ場合の数を求めよ。
(2)A,B,Cの3人が隣りあわないように並ぶ場合の数を求めよ。
2015北海道大学文系過去問
この動画を見る
ジョーカーを除く1組52枚のトランプのカードを1列に並べる思考を考える。
(1)番号7のカードが4枚連続して並ぶ確率を求めよ。
(2)番号7のカードが2枚ずつ隣り合い、4枚連続しては並ばない確率を求めよ。
8人の人が一列に並ぶとき、
(1)A,B,Cの3人が連続して並ぶ場合の数を求めよ。
(2)A,B,Cの3人が隣りあわないように並ぶ場合の数を求めよ。
2015北海道大学文系過去問
大学入試問題#371「少し変わった置換積分」 京都大学 改 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{2}{\sqrt{ 3 }}}^{2}\displaystyle \frac{dx}{x\sqrt{ x^2-1 }}$
出典:京都大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{2}{\sqrt{ 3 }}}^{2}\displaystyle \frac{dx}{x\sqrt{ x^2-1 }}$
出典:京都大学 入試問題
三乗根の方程式

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt[3]{4-x}+\sqrt[3]{x-300}=-2$
これを解け.
この動画を見る
$\sqrt[3]{4-x}+\sqrt[3]{x-300}=-2$
これを解け.
本気で「数学」をデキるようにしたい人だけが見る動画。難問をスラスラ解けるようにするための勉強法、問題集・参考書紹介

単元:
#数学検定・数学甲子園・数学オリンピック等#その他#勉強法#数学(高校生)
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
本気で「数学」をデキるようにしたい人に贈る動画です
難問をスラスラ解けるようにするための勉強法、問題集・参考書紹介
この動画を見る
本気で「数学」をデキるようにしたい人に贈る動画です
難問をスラスラ解けるようにするための勉強法、問題集・参考書紹介
2020年度第4回K塾記述高2模試全問解説 #shorts #K塾模試 #りすうこべつチャンネル

京大の整数問題!〇〇に注目!【京都大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
二つの奇数$a,b$に対して,$m=11a+b,n=3a+b$とおく。$m,n$がともに平方数であることはないことを証明せよ。
京都大過去問
この動画を見る
二つの奇数$a,b$に対して,$m=11a+b,n=3a+b$とおく。$m,n$がともに平方数であることはないことを証明せよ。
京都大過去問
【大学受験数学】本気で「数学」をデキるようになる勉強法、問題集・参考書紹介

単元:
#その他#勉強法#数学(高校生)
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
【大学受験数学】本気で「数学」をデキるようになる勉強法、問題集・参考書紹介
この動画を見る
【大学受験数学】本気で「数学」をデキるようになる勉強法、問題集・参考書紹介
放物線と直線
単元:
#数学(中学生)#数Ⅱ#図形と方程式#点と直線#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
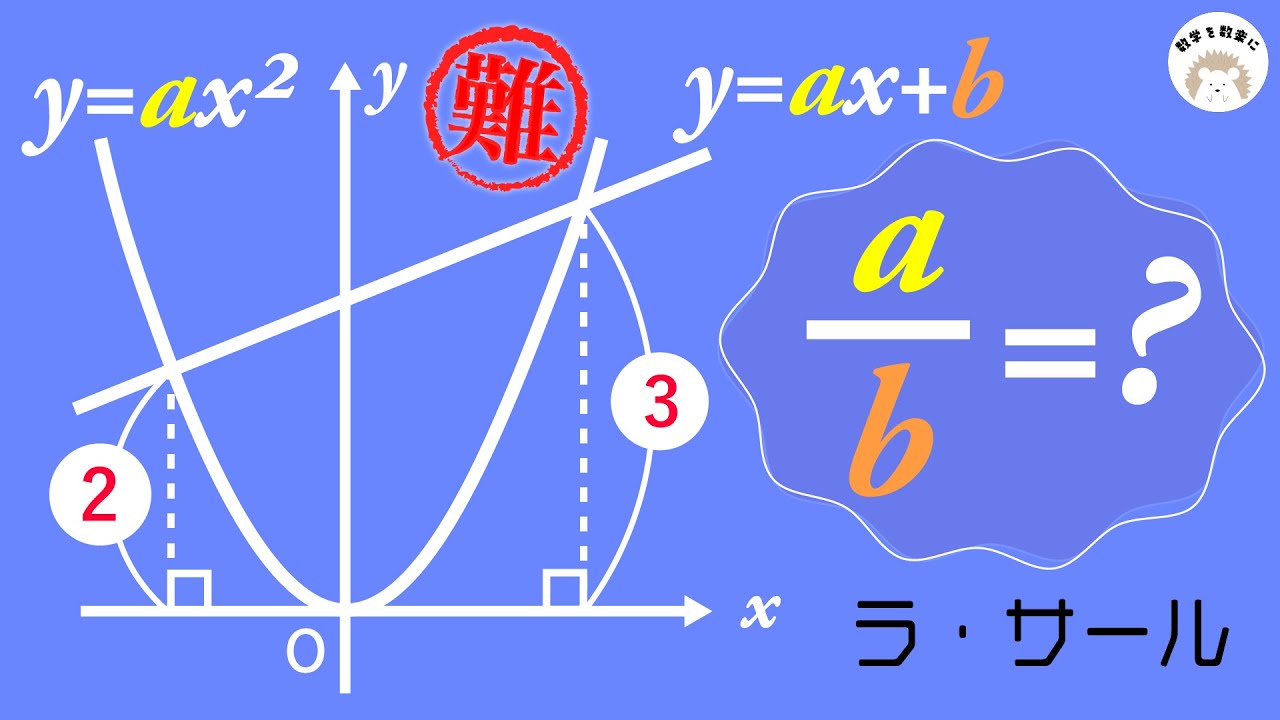
$\frac{a}{b}=?$
*図は動画内参照
ラ・サール高等学校
この動画を見る
$\frac{a}{b}=?$
*図は動画内参照
ラ・サール高等学校
【苦手な人6分時間をください!!】必要十分条件を解説!〔現役塾講師解説、数学〕

福田の1.5倍速演習〜合格する重要問題002〜京都大学2015年理系数学第1問〜回転体の体積

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
2つの関数$y = \sin(x+\frac{\pi}{8})$と$y=\sin2x$のグラフの$0\leqq x\leqq \frac{\pi}{2}$の部分で囲まれ
る領域を、x軸のまわりに1回転させてできる立体の体積を求めよ。
ただし、$x=0$と$x=\frac{\pi}{2}$は領域を囲む線とは考えない。
2015京都大学理系過去問
この動画を見る
2つの関数$y = \sin(x+\frac{\pi}{8})$と$y=\sin2x$のグラフの$0\leqq x\leqq \frac{\pi}{2}$の部分で囲まれ
る領域を、x軸のまわりに1回転させてできる立体の体積を求めよ。
ただし、$x=0$と$x=\frac{\pi}{2}$は領域を囲む線とは考えない。
2015京都大学理系過去問
京大の整数問題!〇〇に注目!【京都大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
2つの奇数a,bに対して、$m=11a+b,n=3a+b$とおく。
$m,n$が平方数でないことを証明しなさい。
京都大過去問
この動画を見る
2つの奇数a,bに対して、$m=11a+b,n=3a+b$とおく。
$m,n$が平方数でないことを証明しなさい。
京都大過去問
大学入試問題#370「初手は好み」 滋賀医科大学2012 #定積分
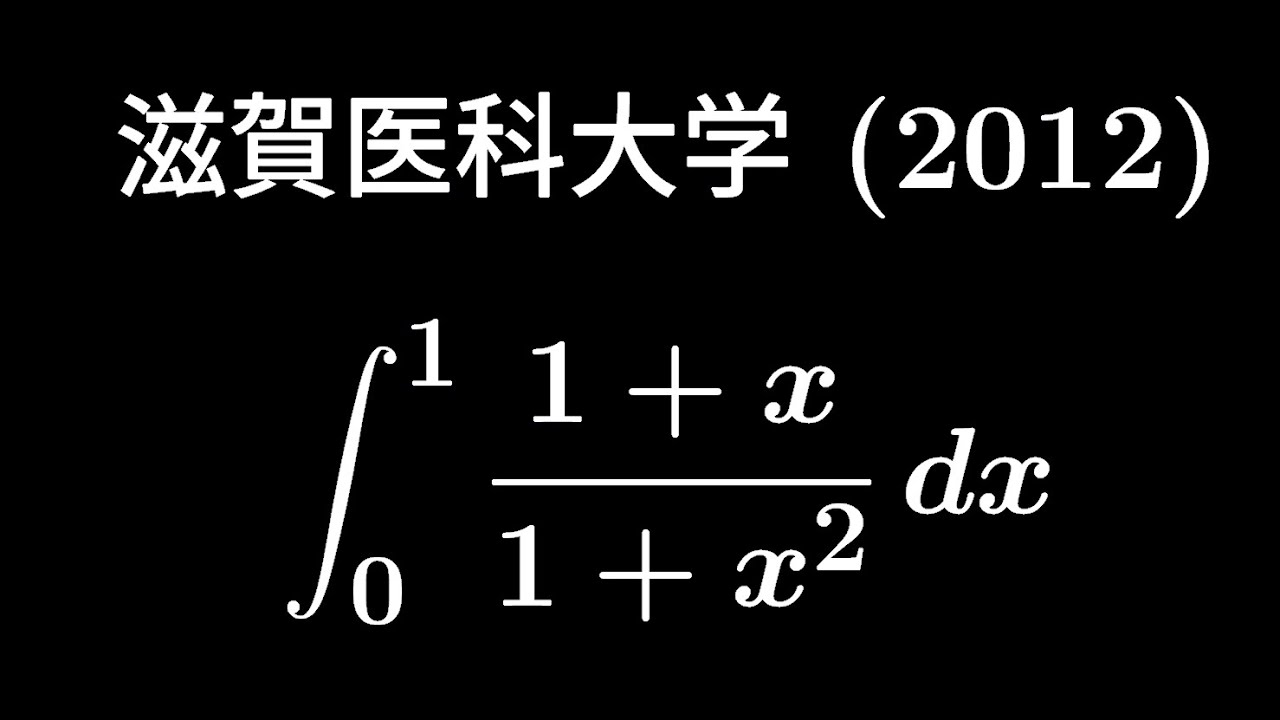
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#滋賀医科大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{1+x}{1+x^2}dx$
出典:2012年滋賀医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{1+x}{1+x^2}dx$
出典:2012年滋賀医科大学 入試問題
ナイスな整数問題だよ

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^3+y^3+3xy=17$をみたす整数x,yの組をすべて求めよ.
この動画を見る
$x^3+y^3+3xy=17$をみたす整数x,yの組をすべて求めよ.
二次方程式 国学院高校
単元:
#数学(中学生)#数Ⅰ#2次関数#2次方程式と2次不等式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a+b=-6$ , $ab = 5$のとき方程式$(x+a)(x+b)=0$を解け
國學院高等学校
この動画を見る
$a+b=-6$ , $ab = 5$のとき方程式$(x+a)(x+b)=0$を解け
國學院高等学校
福田の1.5倍速演習〜合格する重要問題001〜東京大学2015年理系問題1〜放物線の通過範囲

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
問題文全文(内容文):
正の実数aに対して、座標平面上で次の放物線を考える。
$C:\ y=ax^2+\frac{1-4a^2}{4a}$aが正の実数全体を動くとき、Cの通過する領域を図示せよ。
2015東京大学理系過去問
この動画を見る
正の実数aに対して、座標平面上で次の放物線を考える。
$C:\ y=ax^2+\frac{1-4a^2}{4a}$aが正の実数全体を動くとき、Cの通過する領域を図示せよ。
2015東京大学理系過去問
大学入試問題#369「2種類準備しました」 広島市立大学2014 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{\cos\ x}{\cos^2x+2\sin\ x-2}dx$
出典:2014年広島市立大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{\cos\ x}{\cos^2x+2\sin\ x-2}dx$
出典:2014年広島市立大学 入試問題
手を動かすだけの指数方程式
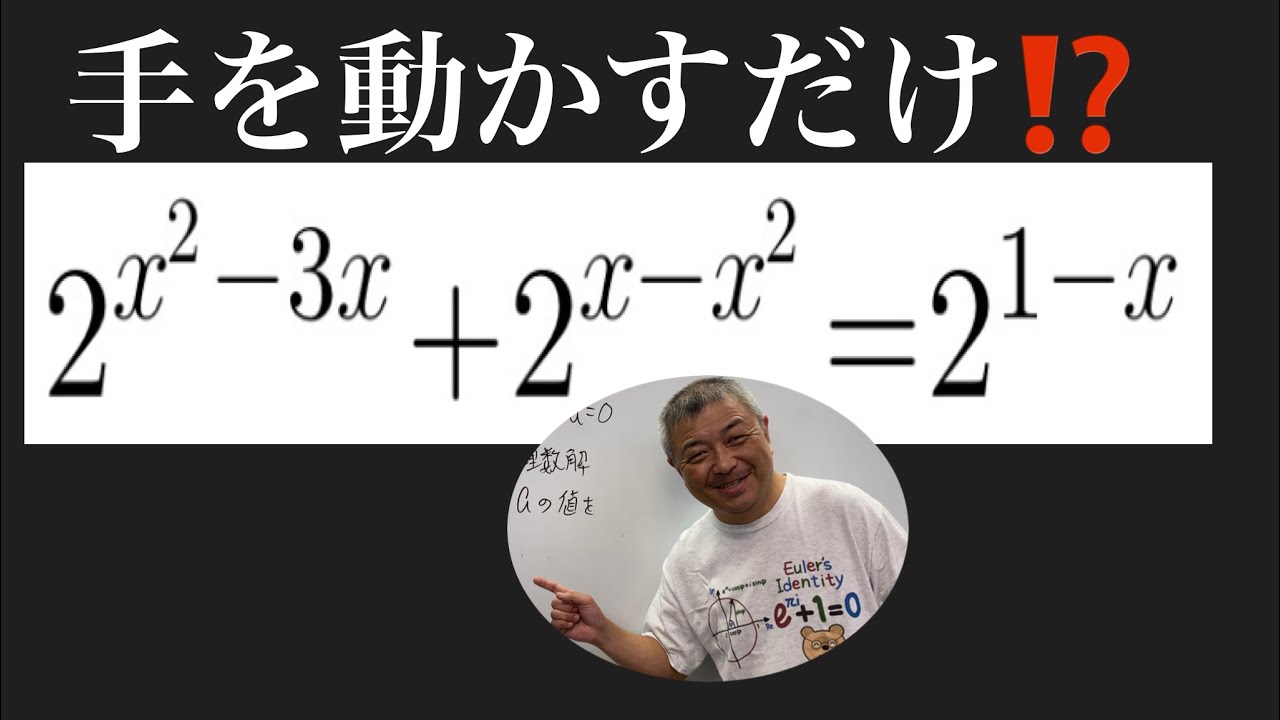
単元:
#数Ⅱ#指数関数と対数関数#指数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 2^{x^2-3x}+2^{x-x^2}=2^{1-x}$
これを解け.
この動画を見る
$ 2^{x^2-3x}+2^{x-x^2}=2^{1-x}$
これを解け.
見た目は難問!?直角三角形に関する問題
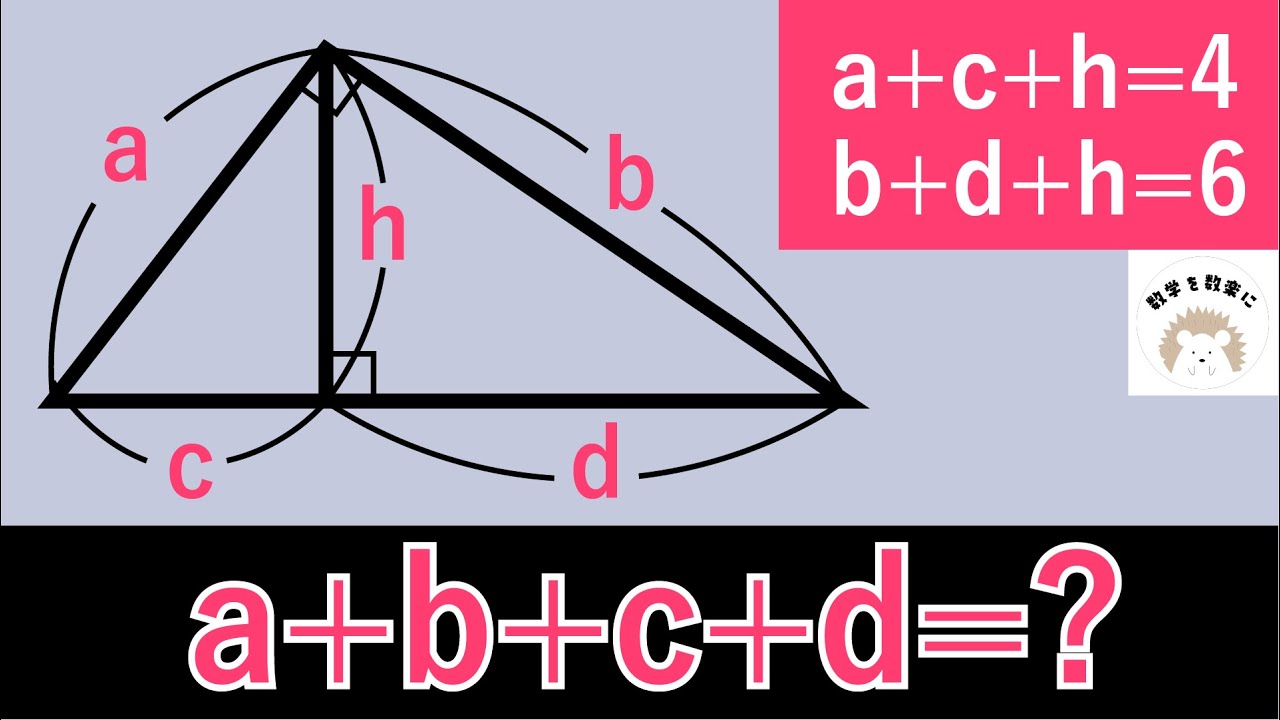
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a+c+h = 4
b+d+h = 6
a+b+c+d =?
*図は動画内参照
この動画を見る
a+c+h = 4
b+d+h = 6
a+b+c+d =?
*図は動画内参照
【数Ⅲ】三角関数・指数・対数の微分公式【合成関数との合せ技】

福田の数学〜東京理科大学2022年理工学部第3問〜接線と法線と囲まれる面積
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
関数f(x)を次で定める。
$f(x)=\frac{1}{x}\ \ (x \gt 0)$
座標平面上の曲線y=f(x)をCとする。C上の点$P(2,\ \frac{1}{2})$と、正の定数tに対して
y軸上の点$A(0,\ -t)$をとる。点Aと点Pを通る直線を$l_1$とする。
(1)直線$l_1$を表す方程式を、tを用いて表せ。
(2)C上の点PにおけるCの法線とy軸の交点を$(0,\ -t_0)$とおく。$t_o$を求めよ。
上の(2)で求めたt_0に対してt \lt t_0とする。点Pを通り、直線$l_1$に垂直な直線を
$l_2$とする。$l_2$とCの交点のうち、点Pと異なる点をQとおく。
(3)点Qの座標を、tを用いて表せ。
最後に$t=\frac{3}{2}$の時を考える。
(4)点Qを通るCの接線を$l_3$とする。このとき、2つの直線$l_1,l_3$および曲線Cで
囲まれた部分の面積を求めよ。
2022東京理科大学理工学部過去問
この動画を見る
関数f(x)を次で定める。
$f(x)=\frac{1}{x}\ \ (x \gt 0)$
座標平面上の曲線y=f(x)をCとする。C上の点$P(2,\ \frac{1}{2})$と、正の定数tに対して
y軸上の点$A(0,\ -t)$をとる。点Aと点Pを通る直線を$l_1$とする。
(1)直線$l_1$を表す方程式を、tを用いて表せ。
(2)C上の点PにおけるCの法線とy軸の交点を$(0,\ -t_0)$とおく。$t_o$を求めよ。
上の(2)で求めたt_0に対してt \lt t_0とする。点Pを通り、直線$l_1$に垂直な直線を
$l_2$とする。$l_2$とCの交点のうち、点Pと異なる点をQとおく。
(3)点Qの座標を、tを用いて表せ。
最後に$t=\frac{3}{2}$の時を考える。
(4)点Qを通るCの接線を$l_3$とする。このとき、2つの直線$l_1,l_3$および曲線Cで
囲まれた部分の面積を求めよ。
2022東京理科大学理工学部過去問
大学入試問題#368「よくみる積分」 防衛医科大学校2014 #不定積分
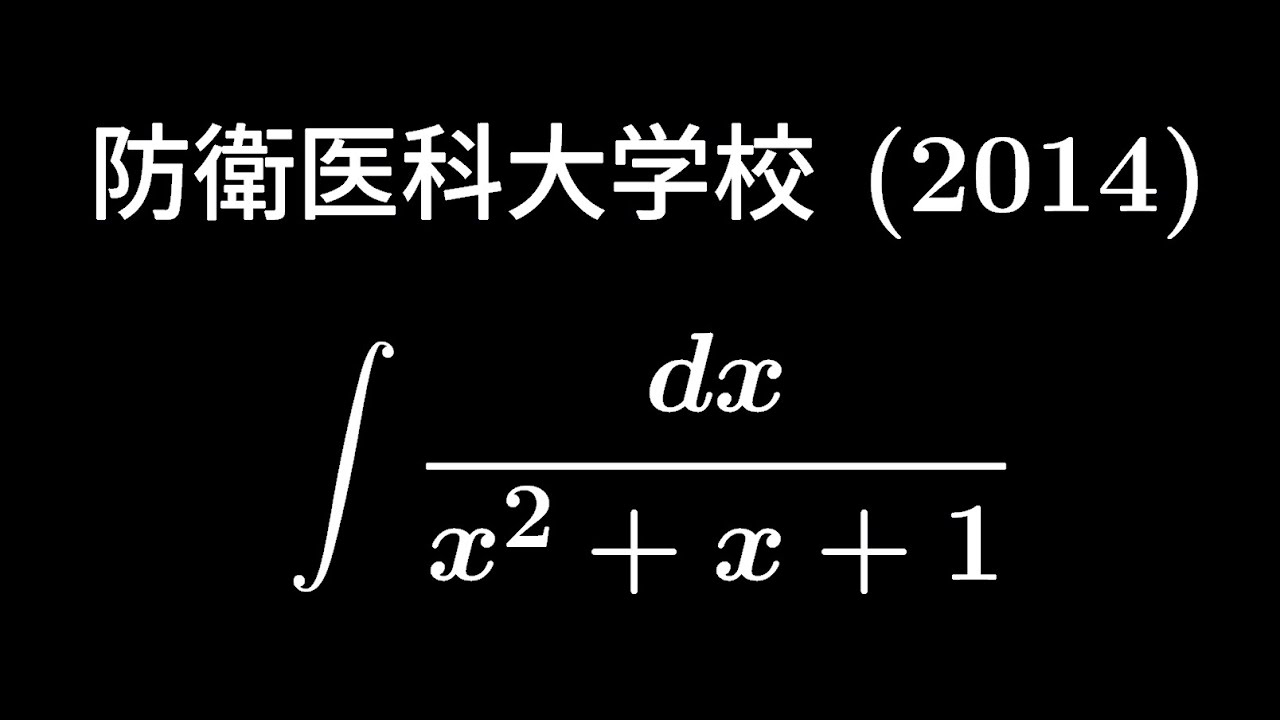
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#防衛医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{dx}{x^2+x+1}$
出典:2014年防衛医科大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{x^2+x+1}$
出典:2014年防衛医科大学 入試問題
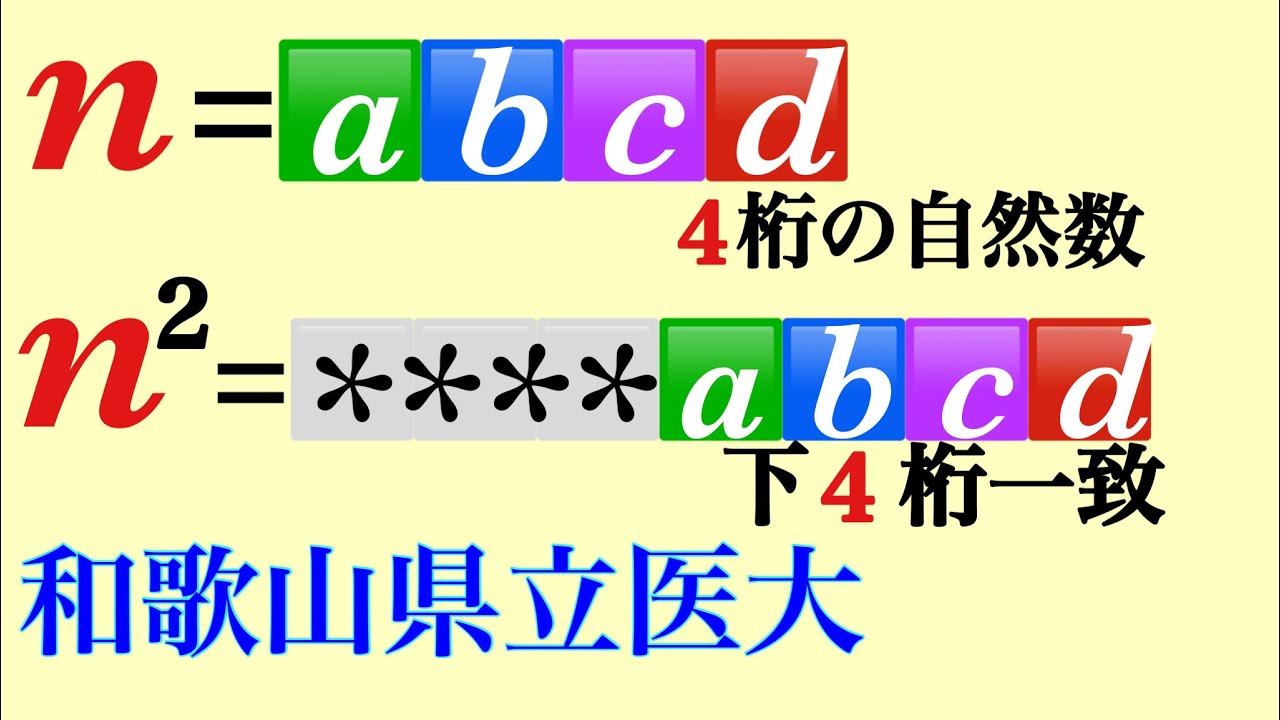
和歌山県立医大ナイスな整数問題
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
nは4桁の自然数$n^2$の下4桁がnとするとき,nをすべて求めよ.
和歌山県立医大過去問
この動画を見る
nは4桁の自然数$n^2$の下4桁がnとするとき,nをすべて求めよ.
和歌山県立医大過去問
【工夫あり】これが本当に京大の入試問題?絶対値を含んだ積分【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
定積分$\displaystyle \int_{-1}^{1}\left| x^2-\dfrac{1}{2}x-\dfrac{1}{2} \right | dx$を求めよ。
京都大過去問
この動画を見る
定積分$\displaystyle \int_{-1}^{1}\left| x^2-\dfrac{1}{2}x-\dfrac{1}{2} \right | dx$を求めよ。
京都大過去問
宝くじと隕石が当たる確率は?

