 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
福田の数学〜中央大学2024経済学部第1問(3)〜パスワードで無事にログインできる確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
あるWebサイトにログインするには4桁の暗証番号を入力しなければならないが、それを忘れてしまった。覚えているのは、各桁の数は5以上ですべて異なる数であり、末尾の2桁は$78$か$87$のどちらかということだけである。このWebサイトでは暗証番号は3回まで入力することができるが、記憶に当てはまる班員台で手当たり次第に入力して無事にログインできる確率を求めよ。
この動画を見る
あるWebサイトにログインするには4桁の暗証番号を入力しなければならないが、それを忘れてしまった。覚えているのは、各桁の数は5以上ですべて異なる数であり、末尾の2桁は$78$か$87$のどちらかということだけである。このWebサイトでは暗証番号は3回まで入力することができるが、記憶に当てはまる班員台で手当たり次第に入力して無事にログインできる確率を求めよ。
#高専数学_5#不定積分#元高専教員

単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
下記の不定積分を解け。
$\displaystyle \int x log (x+1)$ $dx$
この動画を見る
下記の不定積分を解け。
$\displaystyle \int x log (x+1)$ $dx$
#千葉大学2020#不定積分#ますただ
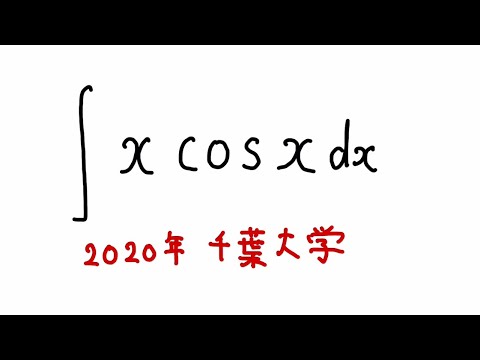
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int x\cos x$ $dx$
出典:2024年千葉大学
この動画を見る
$\displaystyle \int x\cos x$ $dx$
出典:2024年千葉大学
福田のおもしろ数学218〜不動点と合成関数の作る方程式の解

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$f(x)=x^2+1$のとき、方程式$f(f(x))=x$を満たす$x$をすべて求めよ。
この動画を見る
$f(x)=x^2+1$のとき、方程式$f(f(x))=x$を満たす$x$をすべて求めよ。
大学入試問題#897「解法の迷走」 #北海道大学(2024)

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \frac{x^2-x+1}{x^2+x+1}$
が整数となるような実数$x$をすべて求めよ。
出典:2024年北海道大学後期
この動画を見る
$\displaystyle \frac{x^2-x+1}{x^2+x+1}$
が整数となるような実数$x$をすべて求めよ。
出典:2024年北海道大学後期
指数方程式 (高校数学)
福田の数学〜中央大学2024経済学部第1問(2)〜集合の要素の個数

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$1$から$1000$までの整数全体の集合を$U$とする。$U$の部分集合$A,B$をそれぞれ$A=\{x|xは5の倍数\},B=\{x|xは7の倍数\}$とするとき、$\overline A \cap \overline B$の要素の個数$n(\overline A \cap \overline B)$を求めよ。
この動画を見る
$1$から$1000$までの整数全体の集合を$U$とする。$U$の部分集合$A,B$をそれぞれ$A=\{x|xは5の倍数\},B=\{x|xは7の倍数\}$とするとき、$\overline A \cap \overline B$の要素の個数$n(\overline A \cap \overline B)$を求めよ。
#高専_4#不定積分#元高専教員

単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け。
$\displaystyle \int \displaystyle \frac{(log t)^2}{t} dt$
この動画を見る
以下の不定積分を解け。
$\displaystyle \int \displaystyle \frac{(log t)^2}{t} dt$
【数学】計算ミスを撲滅する5つのライフハック

【数学】中高一貫校用問題集数式・関数編:2次関数の決定

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#TK数学#TK数学問題集3(数式・関数編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の問いに答えよ。
(1)$x^2$の係数が2で、そのグラフが点(1,3)を通り、頂点が直線$y=2x-3$上にあるような2次関数を求めよ。
(2)2次関数$y=x^2-2ax+b$のグラフが点(1,3)を通り、頂点が直線$y=x-10$上にあるとき、定数a,bの値を求めよ。
(3)2次関数$y=2x^2+ax+b$のグラフが点(3,5)を通り、頂点が直線$y=2x-5$上にあるとき、定数a,bの値を求めよ。
この動画を見る
次の問いに答えよ。
(1)$x^2$の係数が2で、そのグラフが点(1,3)を通り、頂点が直線$y=2x-3$上にあるような2次関数を求めよ。
(2)2次関数$y=x^2-2ax+b$のグラフが点(1,3)を通り、頂点が直線$y=x-10$上にあるとき、定数a,bの値を求めよ。
(3)2次関数$y=2x^2+ax+b$のグラフが点(3,5)を通り、頂点が直線$y=2x-5$上にあるとき、定数a,bの値を求めよ。
#高専_3#定積分#元高専教員

単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{1} (e^x-e^{-x})^2(e^x+e^{-x}) dx$
この動画を見る
$\displaystyle \int_{-1}^{1} (e^x-e^{-x})^2(e^x+e^{-x}) dx$
福田のおもしろ数学217〜ルートの中の巨大な数の分数を計算しよう

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\sqrt{\dfrac{1111111088888889}{123456787654321}}$を計算して下さい
この動画を見る
$\sqrt{\dfrac{1111111088888889}{123456787654321}}$を計算して下さい
大学入試問題#896「難関大学ではたまにでる?」 #北海道大学(2024)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
ますただ
問題文全文(内容文):
関数$f_1(x),f_2(x),f_3(x),…$を次の関係式で定める。
$f_1(x)=3x$
$f_{n+1}(x)=(n+2)x^{n+1}+(\displaystyle \int_{0}^{1} f_n(t) dt)x$
関数$f_n(x)$を$x$と$n$の式で表せ。$(n=1,2,3,…)$
出典:2024年北海道大学
この動画を見る
関数$f_1(x),f_2(x),f_3(x),…$を次の関係式で定める。
$f_1(x)=3x$
$f_{n+1}(x)=(n+2)x^{n+1}+(\displaystyle \int_{0}^{1} f_n(t) dt)x$
関数$f_n(x)$を$x$と$n$の式で表せ。$(n=1,2,3,…)$
出典:2024年北海道大学
福田の数学〜中央大学2024経済学部第1問(1)〜絶対値の付いた2次不等式の解

#高専_2#定積分

単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int (1-\sin^3x)\cos x$ $dx$
この動画を見る
$\displaystyle \int (1-\sin^3x)\cos x$ $dx$
【分かりやすく順を追って…!】整数:福岡大学附属大濠高等学校~全国入試問題解法
単元:
#整数の性質#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
二つの正の整数を $m,n$とする。
$1 < \sqrt m < 2$, $5 < \sqrt n < 6 $ のとき、$ m + n $ で作られる素数は $\Box$ 通りある。
この動画を見る
二つの正の整数を $m,n$とする。
$1 < \sqrt m < 2$, $5 < \sqrt n < 6 $ のとき、$ m + n $ で作られる素数は $\Box$ 通りある。
まず二乗したものを求める

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^2=2+\sqrt{3} \\
b^2=2-\sqrt{3}
\end{array}
\right.
\end{eqnarray}
$
のとき、$ab$の値を求めよ
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^2=2+\sqrt{3} \\
b^2=2-\sqrt{3}
\end{array}
\right.
\end{eqnarray}
$
のとき、$ab$の値を求めよ
微分法と積分法 数Ⅱ定積分:1/6公式の使い方【烈's study!がていねいに解説】

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\displaystyle \int_{α}^{ β } (x-α)(x-β)dx=-\dfrac{1}{6}(β-α)^3$を用いて、次の定積分を求めよ。
(1)$\displaystyle \int_{-1}^{ 2 } (x^2-x-2)dx$
(2)$\displaystyle \int_{1-\sqrt{2} }^{1+\sqrt{2}} (x^2-2x-1)dx$
(3)$\displaystyle \int_{3}^{ 4 } (14x-24-2x^2)dx$
この動画を見る
$\displaystyle \int_{α}^{ β } (x-α)(x-β)dx=-\dfrac{1}{6}(β-α)^3$を用いて、次の定積分を求めよ。
(1)$\displaystyle \int_{-1}^{ 2 } (x^2-x-2)dx$
(2)$\displaystyle \int_{1-\sqrt{2} }^{1+\sqrt{2}} (x^2-2x-1)dx$
(3)$\displaystyle \int_{3}^{ 4 } (14x-24-2x^2)dx$
#高専#不定積分-1

単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ 4-x^2 }} dx$
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ 4-x^2 }} dx$
大学入試問題#895「2番だけで良い大問」 #福井大学医学部(2015) #数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#福井大学#数B
指導講師:
ますただ
問題文全文(内容文):
$a_1=2$
$3a_{n+1}-4a_n+1=0$
1.数列{$a_n$}の一般項を求めよ。
2.$\displaystyle \frac{a_{n+1}}{a_n}$の小数部分を$b_n$とし、数列{$b_n$}の一般項を求めよ。
3.$\displaystyle \sum_{k=1}^n \displaystyle \frac{1}{b_k}$を求めよ。
出典:2015年福井大学医学部
この動画を見る
$a_1=2$
$3a_{n+1}-4a_n+1=0$
1.数列{$a_n$}の一般項を求めよ。
2.$\displaystyle \frac{a_{n+1}}{a_n}$の小数部分を$b_n$とし、数列{$b_n$}の一般項を求めよ。
3.$\displaystyle \sum_{k=1}^n \displaystyle \frac{1}{b_k}$を求めよ。
出典:2015年福井大学医学部
連立方程式 2通りで解説!! コメント欄に訂正あり。

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
次の連立方程式を解け
$\begin{eqnarray}
\left\{
\begin{array}{l}
xy=2 \\
yz=6 \\
zx=3
\end{array}
\right.
\end{eqnarray}$
この動画を見る
次の連立方程式を解け
$\begin{eqnarray}
\left\{
\begin{array}{l}
xy=2 \\
yz=6 \\
zx=3
\end{array}
\right.
\end{eqnarray}$
福田の数学〜筑波大学2024理系第6問〜純虚数となる条件と複素数平面上の点

単元:
#数Ⅱ#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
定数$\alpha$は実数でない複素数とする。以下の問いに答えよ。
(1) $\dfrac{\alpha - | \alpha|}{\alpha + | \alpha|} $は純虚数であることを示せ。
(2) 純虚数$\beta$で$\dfrac{\beta - | \alpha|}{\alpha + | \alpha|}$が純虚数となるものがただ1つ存在することを示せ。
(3) 複素数$z$を$\dfrac{z - | \alpha|}{\alpha + | \alpha|}$が純虚数となるように動かすとき、$|z|$が最小となる$z$を$\alpha$を用いて示せ。
この動画を見る
定数$\alpha$は実数でない複素数とする。以下の問いに答えよ。
(1) $\dfrac{\alpha - | \alpha|}{\alpha + | \alpha|} $は純虚数であることを示せ。
(2) 純虚数$\beta$で$\dfrac{\beta - | \alpha|}{\alpha + | \alpha|}$が純虚数となるものがただ1つ存在することを示せ。
(3) 複素数$z$を$\dfrac{z - | \alpha|}{\alpha + | \alpha|}$が純虚数となるように動かすとき、$|z|$が最小となる$z$を$\alpha$を用いて示せ。
#千葉大学2024#定積分
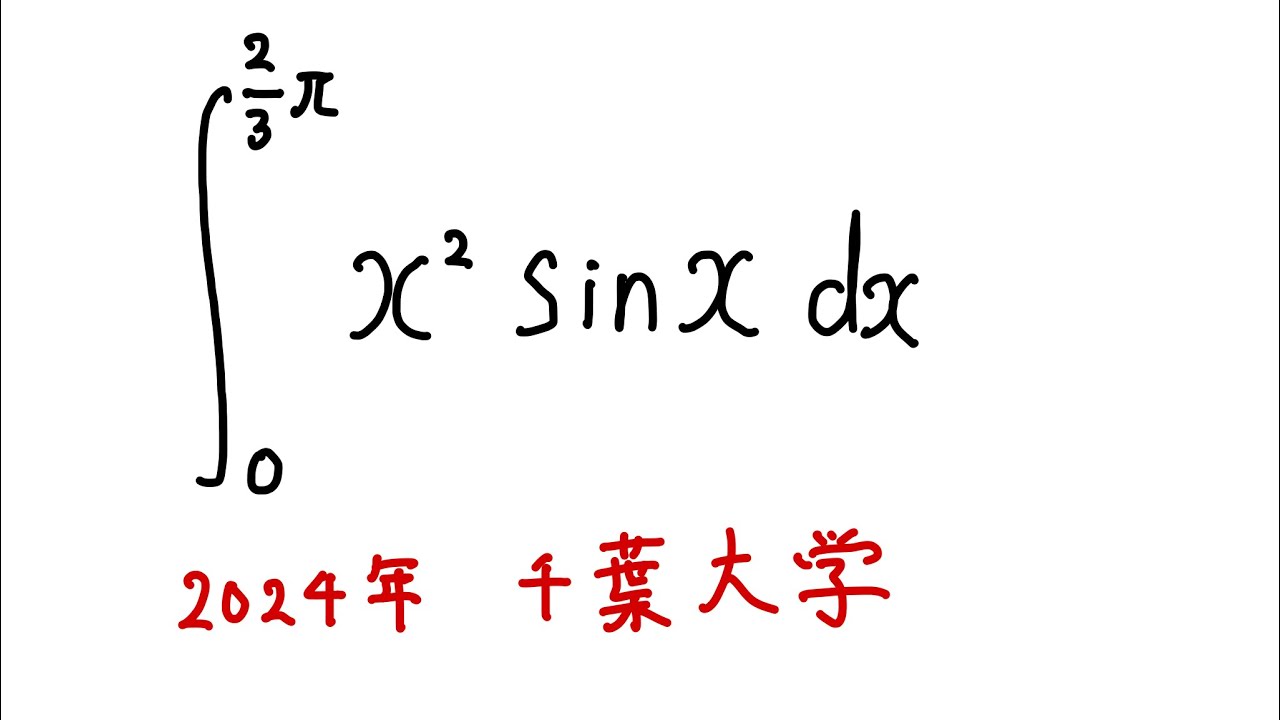
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{2}{3}\pi} x^2\sin x$ $dx$
出典:2024年千葉大学
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{2}{3}\pi} x^2\sin x$ $dx$
出典:2024年千葉大学
【数学】いわゆる「難問・奇問」も勉強するべきか?

単元:
#その他#勉強法#その他#勉強法#数学(高校生)
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
【数学】いわゆる「難問・奇問」の勉強を解説していきます。
この動画を見る
【数学】いわゆる「難問・奇問」の勉強を解説していきます。
#千葉大学2023#定積分#ますただ
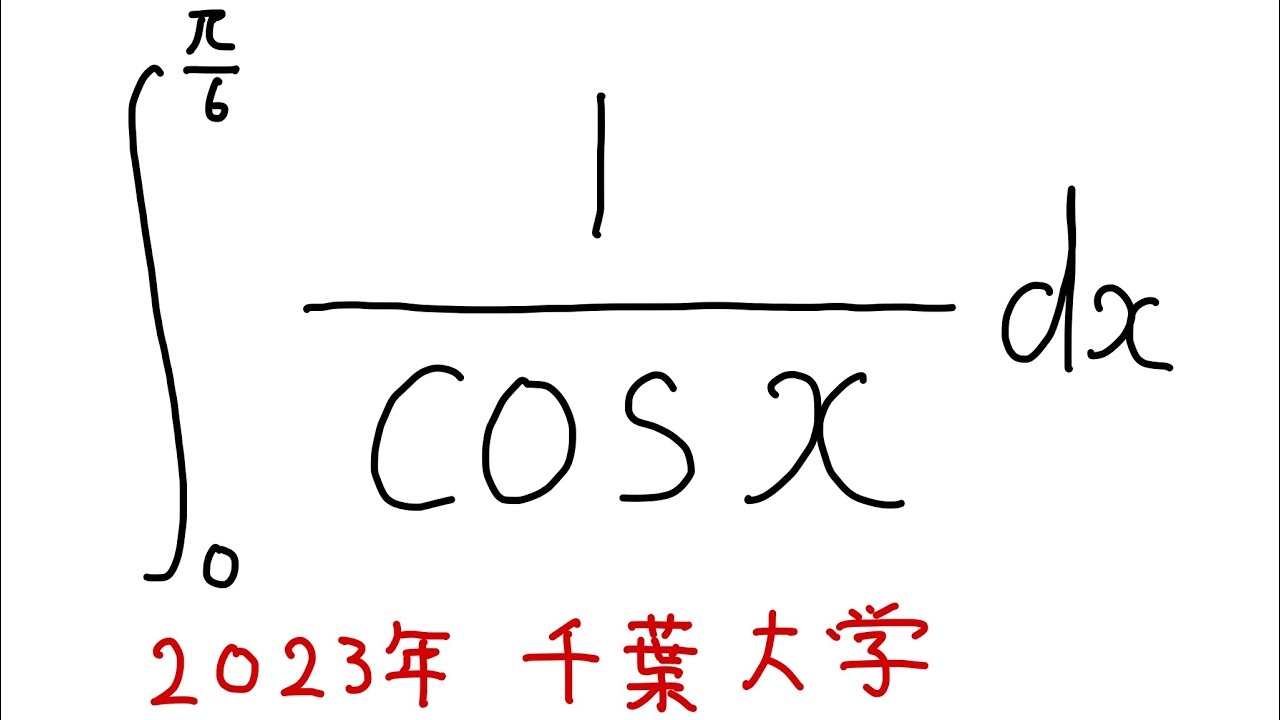
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{1}{\cos x} dx$
出典:2023年千葉大学
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{1}{\cos x} dx$
出典:2023年千葉大学
福田のおもしろ数学215〜三平方の定理が成り立つ左辺の二項のどちらか一方は4の倍数である証明

単元:
#数A#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
正の数$x,y$が$x^2+y^2=z^2$を満たすとき、$x$または$y$は$4$の倍数となることを証明してください。
この動画を見る
正の数$x,y$が$x^2+y^2=z^2$を満たすとき、$x$または$y$は$4$の倍数となることを証明してください。
最大値=❓ 分数関数 (高校数学)

福田の数学〜筑波大学2024理系第5問〜極値をもつかもたないかを考える

単元:
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$a$と$b$は実数の定数とする。関数
$f(x)=(1-2x^2)cos2x+2xsin2x+acos^2x+b\displaystyle \int_{0}^{x } tsin2t dt$
について、以下の問いに答えよ。
(1) $a=8 \pi ^2, \ b=-4 \pi$のとき、$0
(2) 次の条件(B)を満たす$a,b$を求めよ。
(B) $0
この動画を見る
$a$と$b$は実数の定数とする。関数
$f(x)=(1-2x^2)cos2x+2xsin2x+acos^2x+b\displaystyle \int_{0}^{x } tsin2t dt$
について、以下の問いに答えよ。
(1) $a=8 \pi ^2, \ b=-4 \pi$のとき、$0
(2) 次の条件(B)を満たす$a,b$を求めよ。
(B) $0
#千葉大学2023#定積分
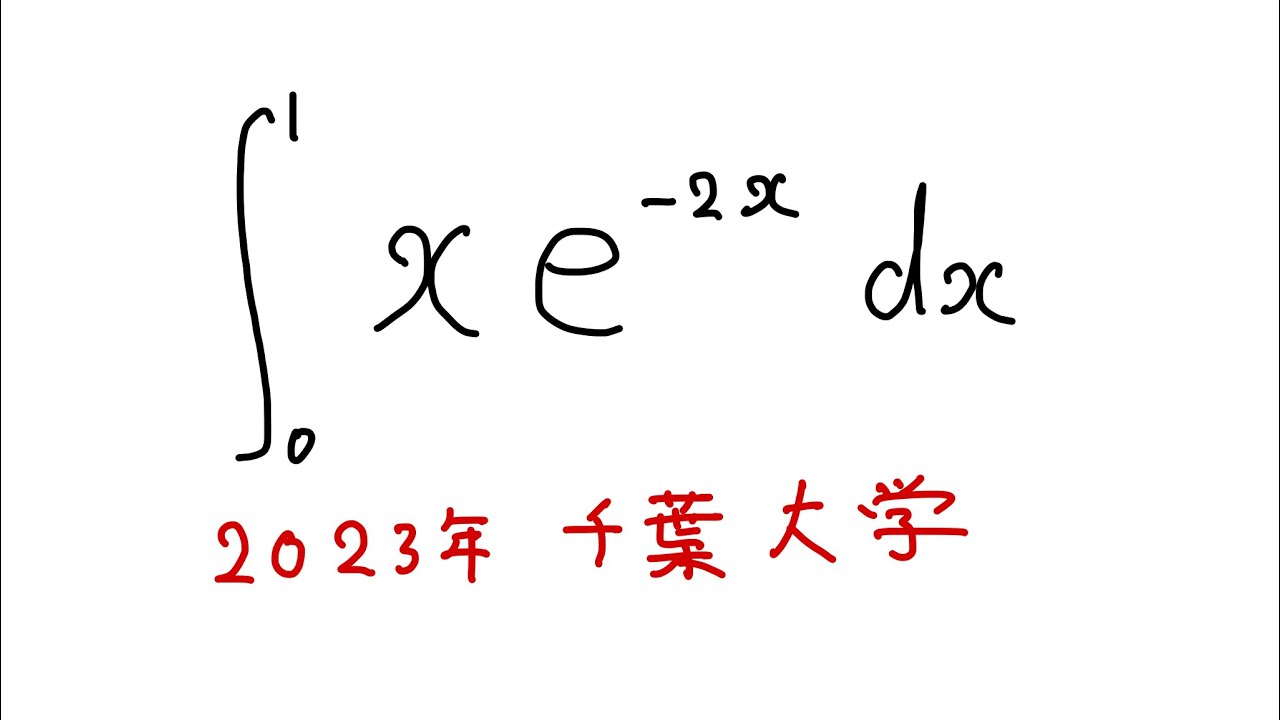
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
下記の定積分を解け
$\displaystyle \int_{0}^{1} xe^{-2x} dx$
出典:2023年千葉大学
この動画を見る
下記の定積分を解け
$\displaystyle \int_{0}^{1} xe^{-2x} dx$
出典:2023年千葉大学
#広島市立大学#不定積分#ますただ
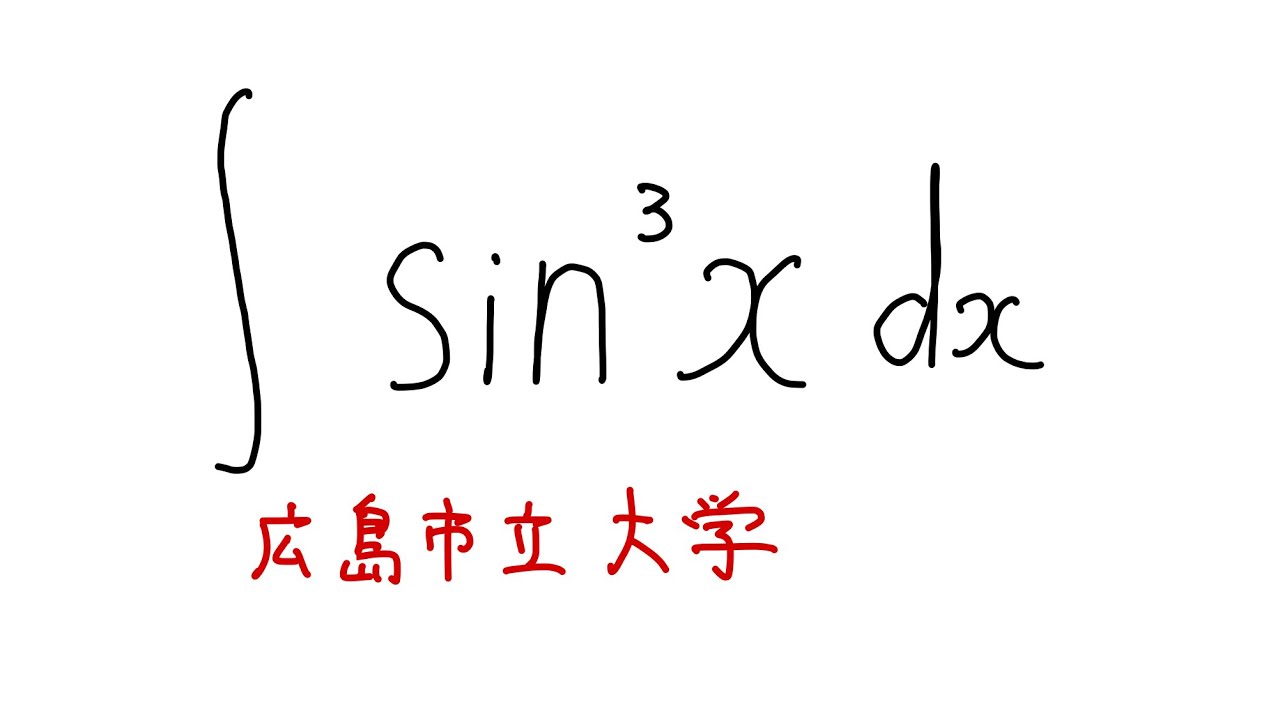
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \sin^3 x$ $dx$
広島市立大過去問
この動画を見る
$\displaystyle \int \sin^3 x$ $dx$
広島市立大過去問
