 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
高校入試だけど多項定理 江戸川学園取手

1次関数の文章題の解き方

この問題解ける?

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
問題
縦の長さが$15m$、横の長さが$18m$の長方形の土地があります。
これに下の図のように、縦と横に同じ幅の道をつくり、
残りを花壇にします。
花畑の面積を$180m^3$になるようにするには、
道場を何mにすればよいでしょうか。
図は動画内参照
この動画を見る
問題
縦の長さが$15m$、横の長さが$18m$の長方形の土地があります。
これに下の図のように、縦と横に同じ幅の道をつくり、
残りを花壇にします。
花畑の面積を$180m^3$になるようにするには、
道場を何mにすればよいでしょうか。
図は動画内参照
6つの小さい円と大きい円 2024城北高校

【総集編】1次関数の問題演習まとめ

【中学数学】方程式の裏技3選~意外と知らない技~【中1数学】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
【中学数学】方程式の裏技3選~意外と知らない技~【中1数学】を解説していきます。
この動画を見る
【中学数学】方程式の裏技3選~意外と知らない技~【中1数学】を解説していきます。
このスマートに問題解ける?

【総集編】1次関数の基礎授業まとめ

shape problems : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
単元:
#数学(中学生)#中3数学#三平方の定理#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
半径が$1$cm, $2$cm, $3$cmの同心円。
半径$3$cmの円の弦が、半径$1$cmの円と点Rで接している。
弦の実線部分PQの長さは$\fbox{$\hskip5em\Rule{0pt}{0.8em}{0em}$}$cmである。
この動画を見る
半径が$1$cm, $2$cm, $3$cmの同心円。
半径$3$cmの円の弦が、半径$1$cmの円と点Rで接している。
弦の実線部分PQの長さは$\fbox{$\hskip5em\Rule{0pt}{0.8em}{0em}$}$cmである。
2次関数を通る直線の式の求め方

これどうやって解く?
単元:
#数学(中学生)#中3数学#2次関数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
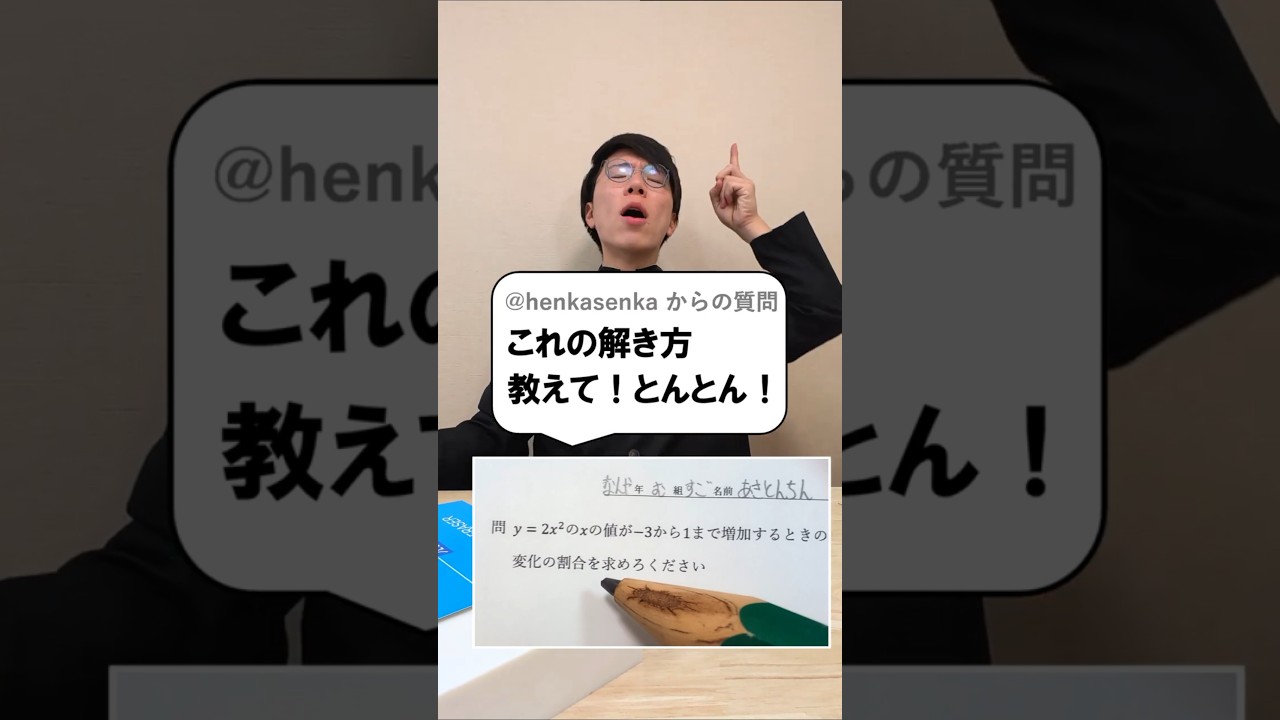
$y=2x^2$の4$x$の値が$-3$から$1$まで増加するときの
変化の割合を求めなさい。
この動画を見る
$y=2x^2$の4$x$の値が$-3$から$1$まで増加するときの
変化の割合を求めなさい。
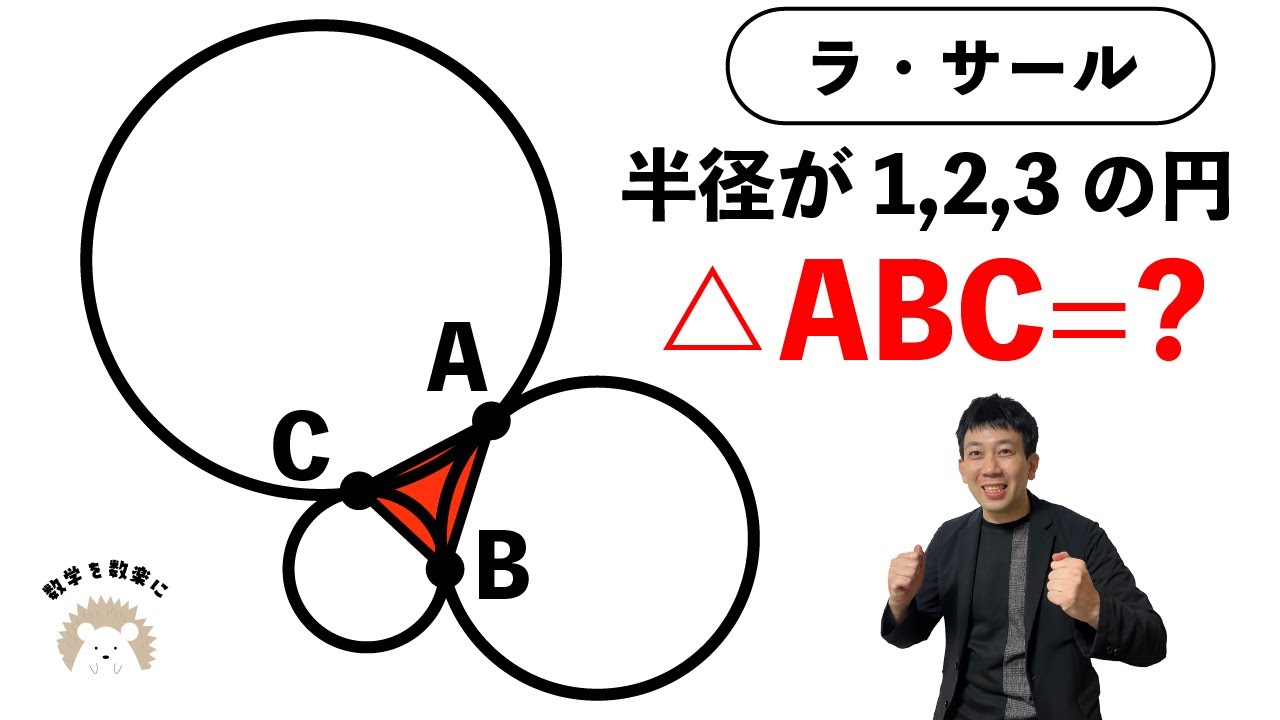
3つの円と三角形の面積 ラ・サール
方程式の裏技3選

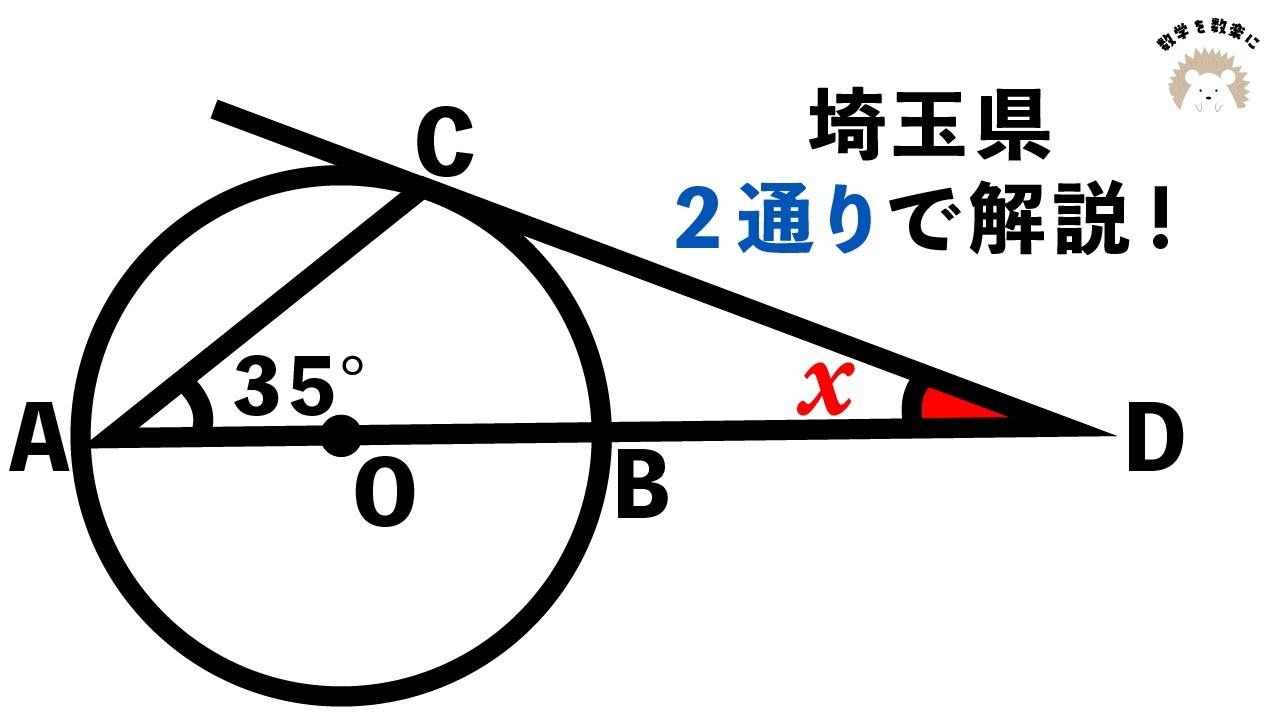
円と接線 2通りで解説
1次関数の特徴と例題

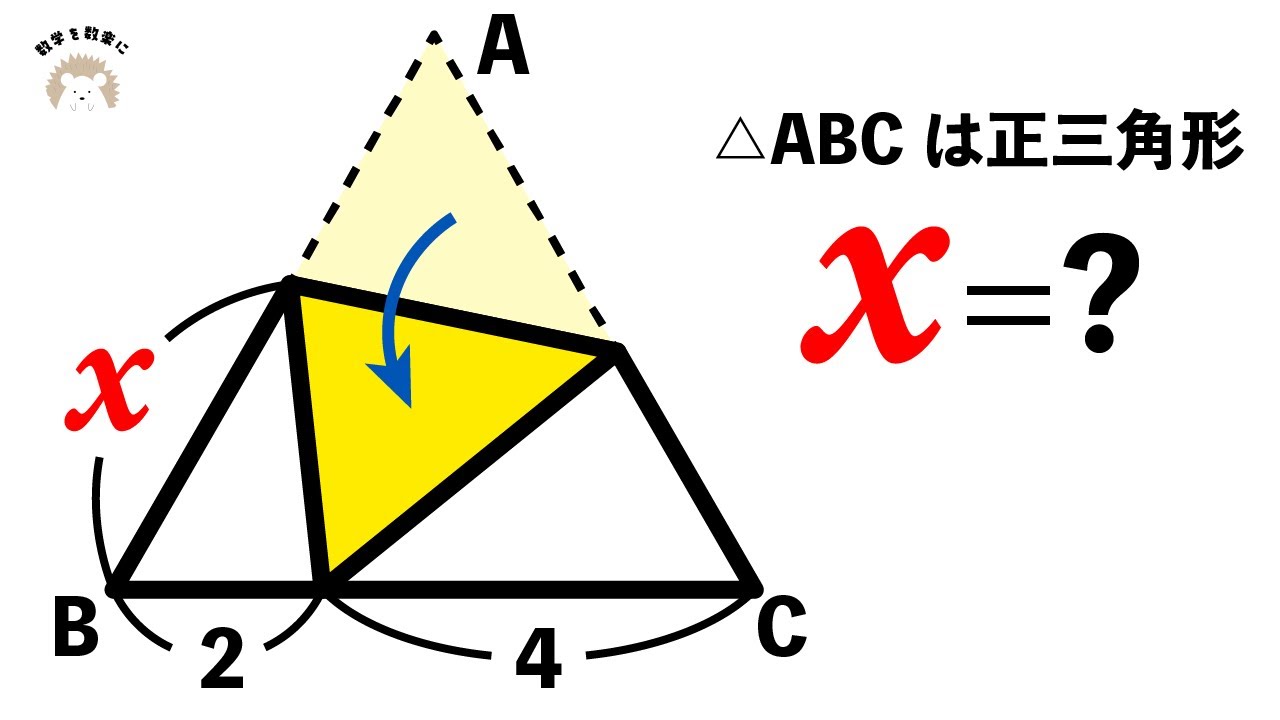
正三角形の折り返し
中学数学の重要度ランキング
ギザギザの土地をきれいに分けられる?

単元:
#数学(中学生)#中2数学
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
A地点には共通の井戸がある。この井戸を境界線上に置き、
ギザギザの土地をきれいに分けられる?
この動画を見る
A地点には共通の井戸がある。この井戸を境界線上に置き、
ギザギザの土地をきれいに分けられる?
これ解ける?

equation : Shirotan's cute kawaii math show #高校受験 #数学 #京大数学 #勉強 #小学生テスト #高校入試 #ライブ #長方形

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
x²-4y²-10x+25=0
x²+x-6-2xy+4y=0
上記が成り立つx,yの組をすべて求めよ。
この動画を見る
x²-4y²-10x+25=0
x²+x-6-2xy+4y=0
上記が成り立つx,yの組をすべて求めよ。
【近道は…!】因数分解:法政大学高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
(x+2)(x-3)-4(x+1)-14を因数分解しなさい。
この動画を見る
(x+2)(x-3)-4(x+1)-14を因数分解しなさい。
【高校受験対策】数学-関数33

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
問題文全文(内容文):
右の図で、直線①、直線②、直線③の式は、
それぞれ$y = 2x + 1 ,\quad y =\dfrac{1}{2}x - 2,\quad y=ax+b(a,bは定数,a \lt 0)$である。
点Aは直線①と直線③の交点で、座標は(3,7)である。
点Bは、直線①と直線②の交点である。
点Cは直線②と直線③の交点である。 次の各問に答えよ。
問1 直線②と$x$軸の交点を$D$とし、線分$OD$の中点を$E$とする。
$y$軸上に点$F$を$AF+FE$の長さが最も短くなるようにとるとき、
点$F$の座標を求めなさい。
問2 $x$軸上の$x \lt 0$に対応する部分に点$G$を、
$△ABC$の面積と$△GBC$の面積が等しくなるようにとるとき、点$G$の$x$座標を求めよ。
問3点$B$から直線③に垂線をひき、直線③との交点を$H$とする。
$AH=CH$となるとき、点$c$の$x$座標を$t$とし、
方程式をつくって点$c$の座標を求めよ。
図は動画内参照
この動画を見る
右の図で、直線①、直線②、直線③の式は、
それぞれ$y = 2x + 1 ,\quad y =\dfrac{1}{2}x - 2,\quad y=ax+b(a,bは定数,a \lt 0)$である。
点Aは直線①と直線③の交点で、座標は(3,7)である。
点Bは、直線①と直線②の交点である。
点Cは直線②と直線③の交点である。 次の各問に答えよ。
問1 直線②と$x$軸の交点を$D$とし、線分$OD$の中点を$E$とする。
$y$軸上に点$F$を$AF+FE$の長さが最も短くなるようにとるとき、
点$F$の座標を求めなさい。
問2 $x$軸上の$x \lt 0$に対応する部分に点$G$を、
$△ABC$の面積と$△GBC$の面積が等しくなるようにとるとき、点$G$の$x$座標を求めよ。
問3点$B$から直線③に垂線をひき、直線③との交点を$H$とする。
$AH=CH$となるとき、点$c$の$x$座標を$t$とし、
方程式をつくって点$c$の座標を求めよ。
図は動画内参照
【一度まともに解きたい…!】:文字式~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
12x^2-7x-12=0のとき、(12x^2-7x)√(12x^2-7x-13)の値を求めなさい。
この動画を見る
12x^2-7x-12=0のとき、(12x^2-7x)√(12x^2-7x-13)の値を求めなさい。
【理論?ひらめき…!?】因数分解:中央大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
a^2+b^2-c^2+2ab-2c-1を因数分解しなさい。
この動画を見る
a^2+b^2-c^2+2ab-2c-1を因数分解しなさい。
function : Shirotan's cute kawaii math show

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
x^2-□x+14が(x-a)(x-b)の形に因数分解できる。
a,b:いずれも自然数。
□に当てはまる自然数を2つ書け。
この動画を見る
x^2-□x+14が(x-a)(x-b)の形に因数分解できる。
a,b:いずれも自然数。
□に当てはまる自然数を2つ書け。
mathematical formula : Shirotan's cute kawaii math show

単元:
#数学(中学生)#中1数学#中3数学#平方根#文字と式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
a=2(√13-2)の整数部分b,小数部分cとする。
この時、(a+3b+1)(c+1)の値を求めよ
この動画を見る
a=2(√13-2)の整数部分b,小数部分cとする。
この時、(a+3b+1)(c+1)の値を求めよ
【見た目よりカンタン…!】文字式:日本大学第三高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#中3数学#平方根#文字と式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
x=√6,y=√2のとき
√(x-y)/√(x+y) - √(x+y)/√(x-y)
この式の値を求めなさい
この動画を見る
x=√6,y=√2のとき
√(x-y)/√(x+y) - √(x+y)/√(x-y)
この式の値を求めなさい
【数式に翻訳せよ…!】整数:新潟県~全国入試問題解法
単元:
#数学(中学生)#整数の性質#高校入試過去問(数学)#新潟県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ある連続する自然数n,mについて、以下が成立するとき(n,m)を求めよ$
$n*m+55=n+m$
この動画を見る
$ある連続する自然数n,mについて、以下が成立するとき(n,m)を求めよ$
$n*m+55=n+m$
【別解もあるから…!】因数分解:和洋国府台女子高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
x²-xy-3x+3yを因数分解せよ
この動画を見る
x²-xy-3x+3yを因数分解せよ
苦手意識を持たない…!】二次方程式:東京都立西高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
3(x+1)²=(x-2)(x-1)-2 を解け
この動画を見る
3(x+1)²=(x-2)(x-1)-2 を解け
