中３数学
中３数学
【中学数学】三平方の定理の応用～正三角形の面積の公式を導こう～【中３数学】
【とても大切な解法…！】二次方程式：中央大学附属高等学校～全国入試解法
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#２次方程式#高校入試過去問(数学)#中央大学附属高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
2次方程式 $3\left(x+1\right)^2=2\left(x+1\right)\left(x-6\right)-\left(x+1\right)\left(x-1\right)\;$を解きなさい。
この動画を見る
2次方程式 $3\left(x+1\right)^2=2\left(x+1\right)\left(x-6\right)-\left(x+1\right)\left(x-1\right)\;$を解きなさい。
これ裏技？
単元：
#数学(中学生)#中３数学#２次方程式
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
2次関数上の2点を通る直線の方程式を素早く求める方法についての動画です。
この動画を見る
2次関数上の2点を通る直線の方程式を素早く求める方法についての動画です。
【うまいやり方とは…！】二次方程式：東京都立新宿高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#２次方程式#高校入試過去問(数学)#東京都立新宿高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$x^2+ax+b=0\;$の解が1と2であるとき、
$\displaystyle\frac{\left(a+b\right)\left(2a+b\right)}{\left(a+b+2\right)\left(2a+b+2\right)}\;$の値を求めよ。
この動画を見る
$x^2+ax+b=0\;$の解が1と2であるとき、
$\displaystyle\frac{\left(a+b\right)\left(2a+b\right)}{\left(a+b+2\right)\left(2a+b+2\right)}\;$の値を求めよ。
【中学数学】三平方の定理～平面図形への応用～【中３数学】
単元：
#数学(中学生)#中３数学#三平方の定理
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
(1) 2点A(2,3), B(5,7)の距離を求めよ
(2) 図におけるx（円の弦）の長さを求めよ
※図は動画内参照
この動画を見る
(1) 2点A(2,3), B(5,7)の距離を求めよ
(2) 図におけるx（円の弦）の長さを求めよ
※図は動画内参照
【分かる人だけ…！】二次方程式：早稲田大学系属早稲田実業学校高等部～全国入試問題解法
単元：
#数学(中学生)#２次方程式#高校入試過去問(数学)#早稲田大学系属早稲田実業学校高等部
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$3x^2-4x-2=0$の2つの解を$a,b$とするとき, $(3a^2-4a+2)(6b^2-8b)$の値を求めよ
この動画を見る
$3x^2-4x-2=0$の2つの解を$a,b$とするとき, $(3a^2-4a+2)(6b^2-8b)$の値を求めよ
【どれも大切…！】二次方程式：慶応義塾高等学校～全国入試問題解法
単元：
#数学(中学生)#２次方程式#高校入試過去問(数学)#慶應義塾高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$2x^2+10\sqrt{2}x+9=0$の解を求めよ。
この動画を見る
$2x^2+10\sqrt{2}x+9=0$の解を求めよ。
解の公式を忘れてしまったときの対処法
square root : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
単元：
#数学(中学生)#平方根#高校入試過去問(数学)#城北高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$(3-2\sqrt{2})^{2023}\times(3+2\sqrt{2})^{2024}\times(2-\sqrt{2})$を計算せよ。
この動画を見る
$(3-2\sqrt{2})^{2023}\times(3+2\sqrt{2})^{2024}\times(2-\sqrt{2})$を計算せよ。
【中学数学】相似な図形の面積比と体積比～分かりやすく～【中３数学】
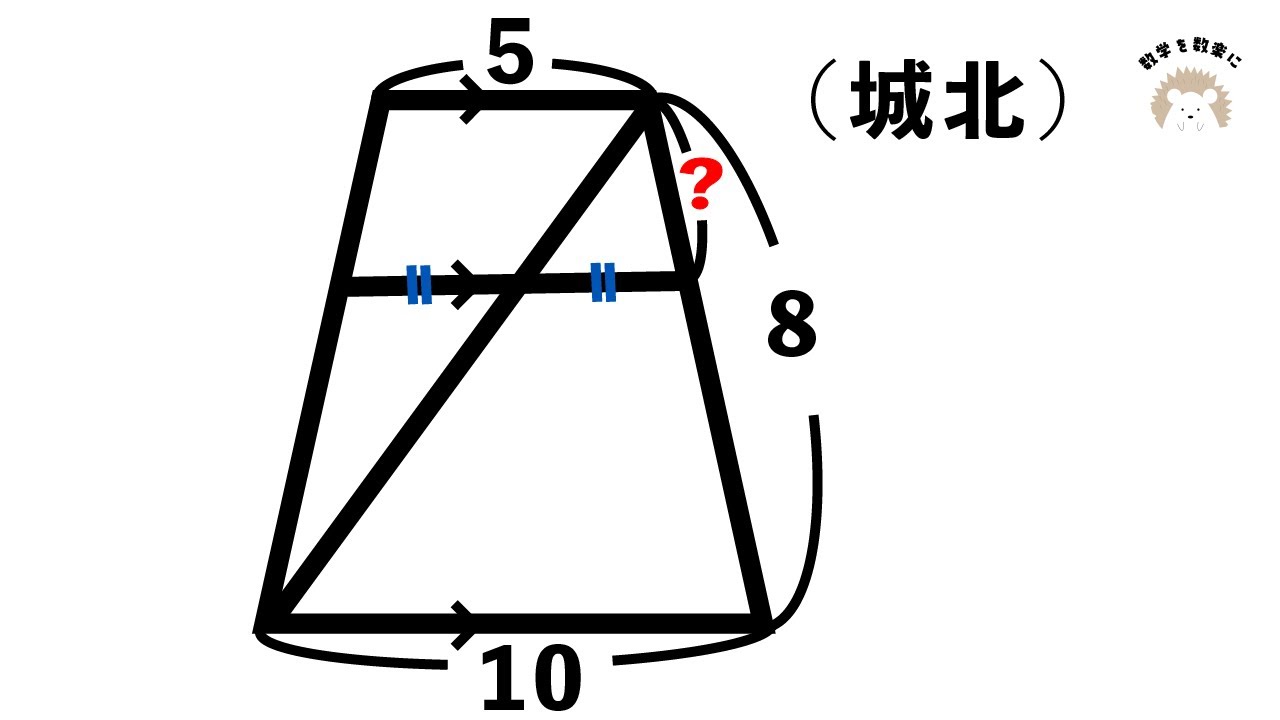
台形 城北高校
【目がくらむ…！】因数分解：中央大学附属高等学校～全国入試問題解法
単元：
#数学(中学生)#式の計算（展開、因数分解）#高校入試過去問(数学)#中央大学附属高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$7a^2x^3y^3-42a^2x^2y^4+56a^2xy^5$を因数分解しなさい。
この動画を見る
$7a^2x^3y^3-42a^2x^2y^4+56a^2xy^5$を因数分解しなさい。
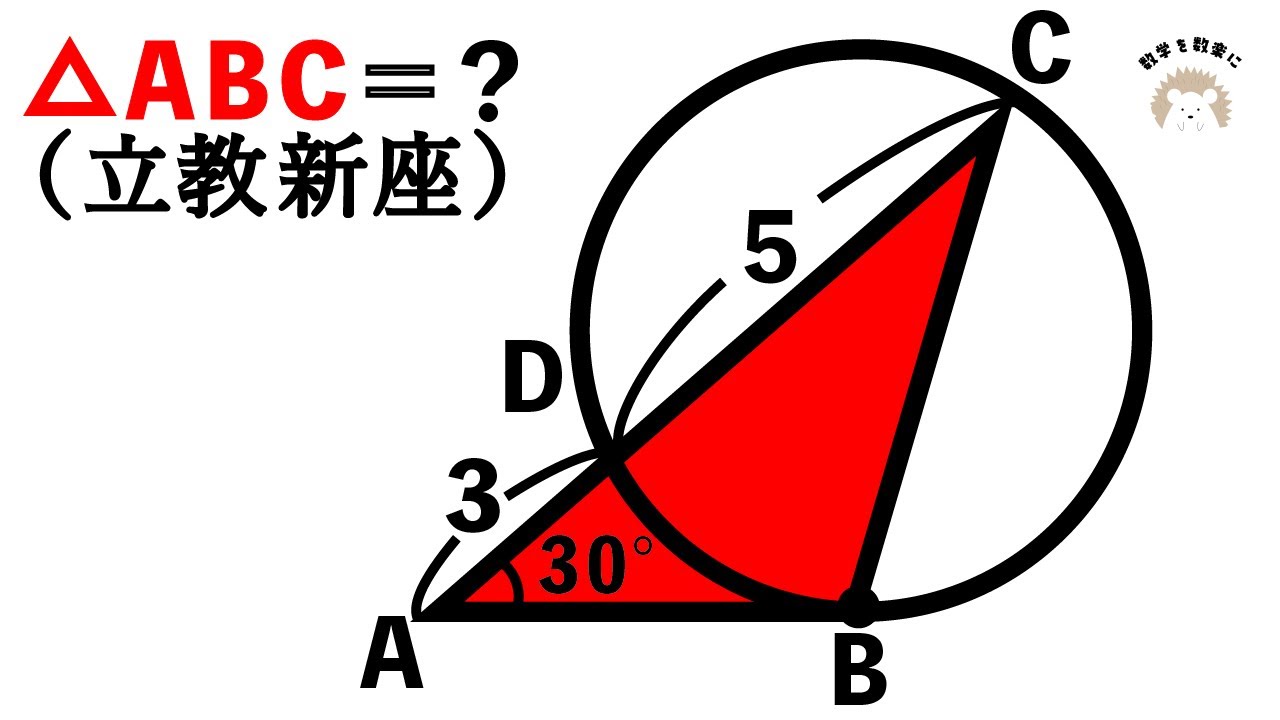
円と接線と三角形 立教新座
2021素因数分解できる？
８９９９９を素因数分解せよ 朋優学院
【そのやり方以外に…！】因数分解：日本大学習志野高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)#日本大学習志野高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
\( (x^2+2x-5)^2-4(x^2+2x-5)-60\)
を因数分解しなさい
この動画を見る
\( (x^2+2x-5)^2-4(x^2+2x-5)-60\)
を因数分解しなさい
5で割った余り 法政大学高校
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)#法政大学高等学校
指導講師：
数学を数楽に
問題文全文(内容文)：
$2023^{3}+2024^{4}を5で割ったときの余りは？$
この動画を見る
$2023^{3}+2024^{4}を5で割ったときの余りは？$
5で割った余り 法政大学高校
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)#法政大学高等学校
指導講師：
数学を数楽に
問題文全文(内容文)：
$2023^{3}+2024^{4}$
を5で割った時の余りは？
この動画を見る
$2023^{3}+2024^{4}$
を5で割った時の余りは？
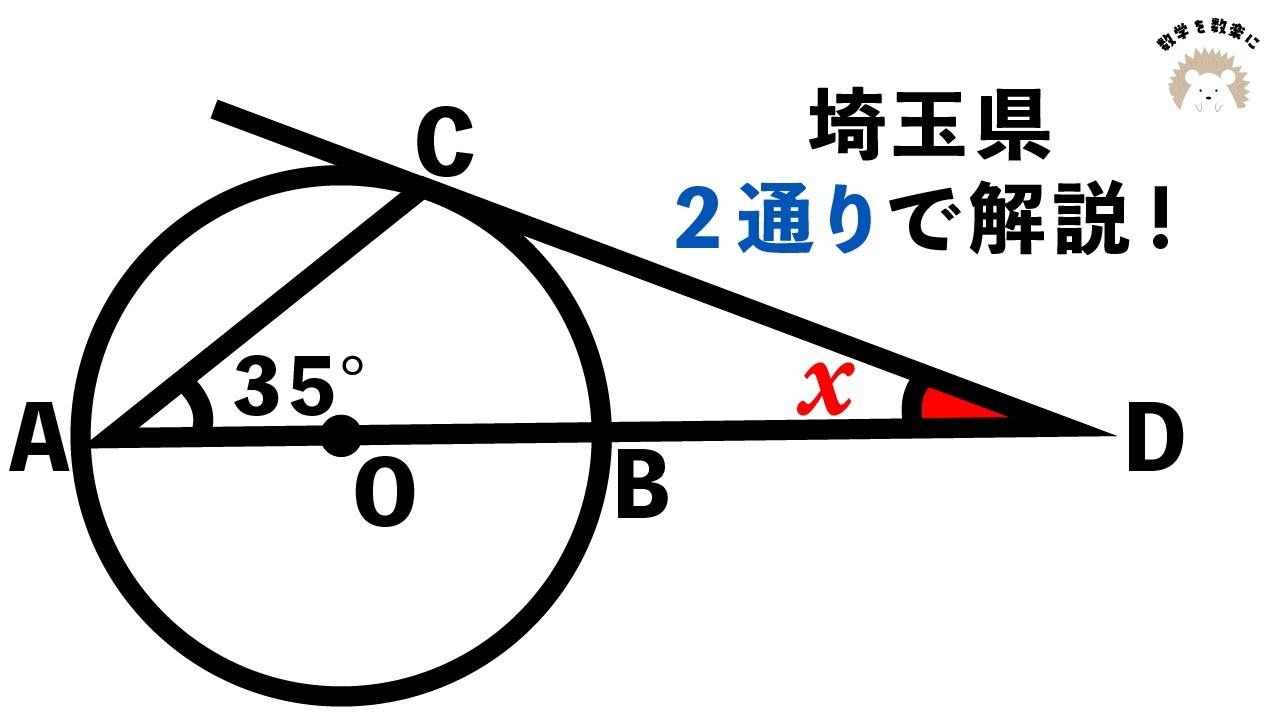
円と接線 2通りで解説 埼玉県
integer problems : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)#立教新座高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$\displaystyle \frac{24}{a^2+4a+3}\;$が自然数となるような整数$a\;$は何個ありますか。
※$a^2+4a+3\;$は0ではない。
この動画を見る
$\displaystyle \frac{24}{a^2+4a+3}\;$が自然数となるような整数$a\;$は何個ありますか。
※$a^2+4a+3\;$は0ではない。
三角形に内接する正方形 明大明治
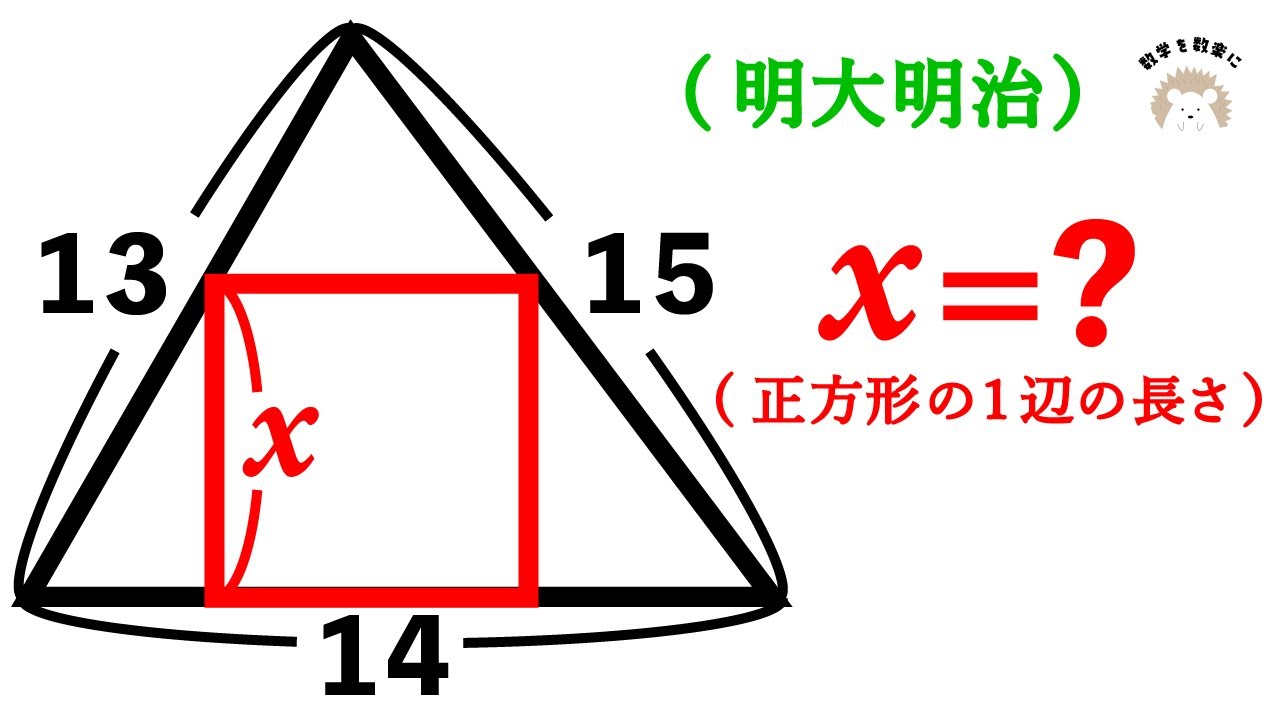
三角形に内接する正方形 明大明治
単元：
#数学(中学生)#中１数学#中２数学#中３数学#相似な図形#平面図形#三角形と四角形#高校入試過去問(数学)#明治大学付属明治高等学校
指導講師：
数学を数楽に
問題文全文(内容文)：
x=?(正方形の1辺の長さ)
この動画を見る
x=?(正方形の1辺の長さ)
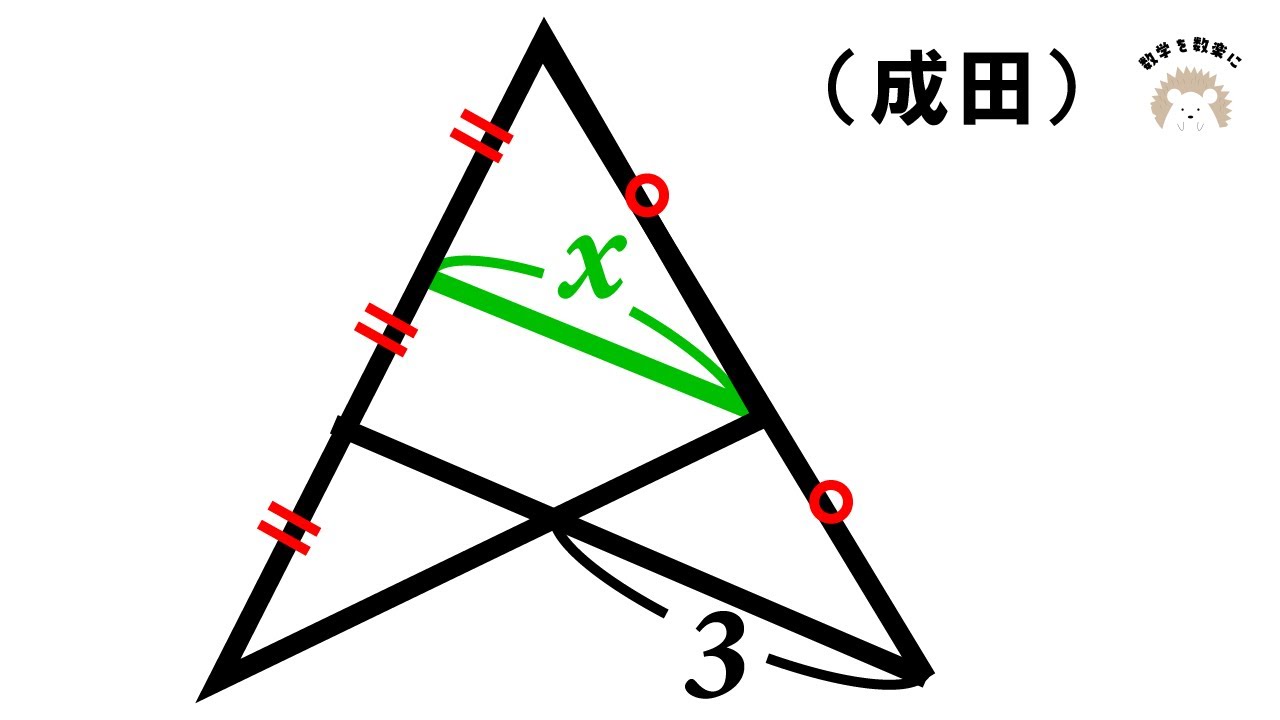
平面図形 成田高校
【ひるまず慌てず…！】文字式：西大和学園高校～全国入試問題解法
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#平方根#高校入試過去問(数学)#西大和学園高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$\displaystyle\frac{\sqrt{y}}{\sqrt{x}}-\frac{\sqrt{x}}{\sqrt{y}}=3\;$を満たすとき$(x,y\;$:正の数$)$、
$\displaystyle\frac{5x^2-54xy+5y^2}{xy}$の値を求めよ。
この動画を見る
$\displaystyle\frac{\sqrt{y}}{\sqrt{x}}-\frac{\sqrt{x}}{\sqrt{y}}=3\;$を満たすとき$(x,y\;$:正の数$)$、
$\displaystyle\frac{5x^2-54xy+5y^2}{xy}$の値を求めよ。
ルートが入っている二次方程式 広尾学園
単元：
#数学(中学生)#中３数学#２次方程式#高校入試過去問(数学)#広尾学園高等学校
指導講師：
数学を数楽に
問題文全文(内容文)：
方程式を解け
$x^2-\sqrt{2}(1+\sqrt{5})x+2\sqrt{5}=0$
この動画を見る
方程式を解け
$x^2-\sqrt{2}(1+\sqrt{5})x+2\sqrt{5}=0$
【初見では固まる…！】平方根：関西学院高等部～全国入試問題解法
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)#関西学院高等部
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$\sqrt{12-2\sqrt{35}}\;$を簡単にせよ。
この動画を見る
$\sqrt{12-2\sqrt{35}}\;$を簡単にせよ。
二次方程式の応用 三田学園
単元：
#数学(中学生)#中３数学#２次方程式#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
次の２つの２次方程式の共通な解が
$x=-2$だけになるとき、
a,bの値を求めよ
$x^2-(b+2)x-b^2=0$
$x^2+ax+2b=0$
この動画を見る
次の２つの２次方程式の共通な解が
$x=-2$だけになるとき、
a,bの値を求めよ
$x^2-(b+2)x-b^2=0$
$x^2+ax+2b=0$
equation : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#平方根#２次方程式#高校入試過去問(数学)#渋谷教育学園幕張高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$\left(x+\sqrt{3}+\sqrt{5}\right)^2-3\sqrt{5}\left(x-2\sqrt{5}+\sqrt{3}\right)-35=0\;$を計算しなさい。
この動画を見る
$\left(x+\sqrt{3}+\sqrt{5}\right)^2-3\sqrt{5}\left(x-2\sqrt{5}+\sqrt{3}\right)-35=0\;$を計算しなさい。
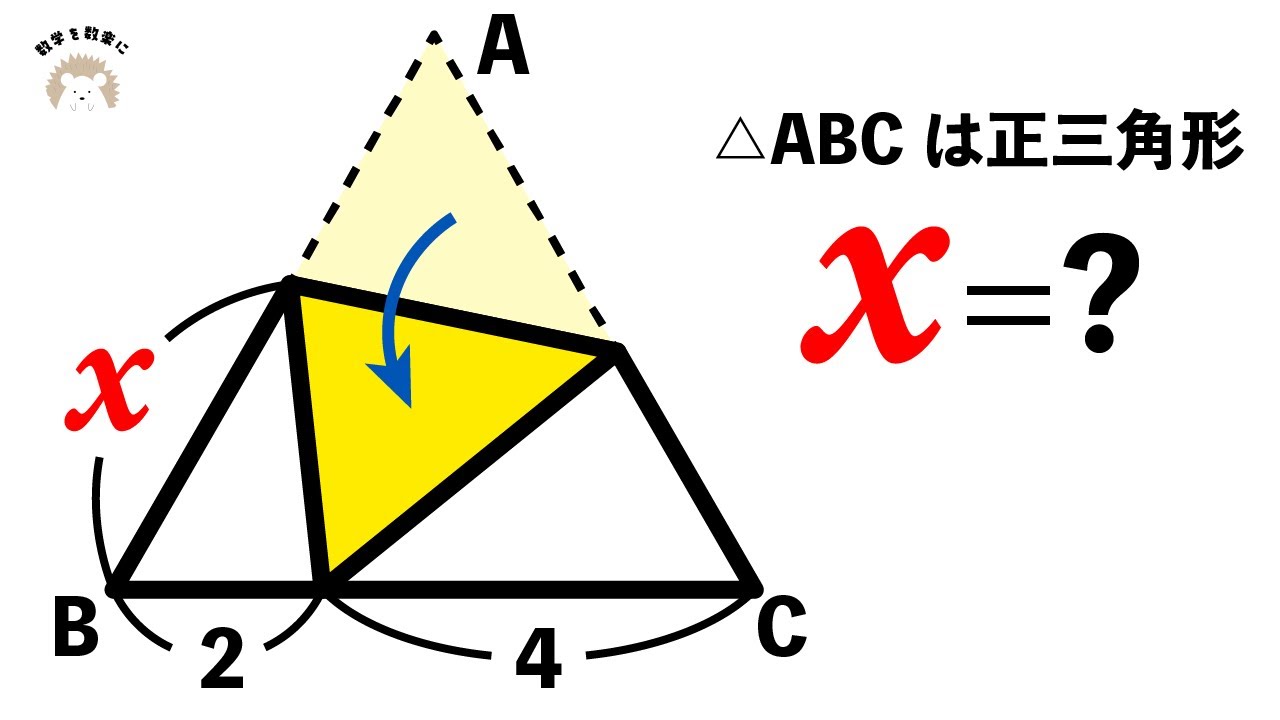
正三角形の折り返し
【工夫のポイントは…！】平方根：お茶の水女子大学附属高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#平方根#高校入試過去問(数学)#お茶の水女子大学附属高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
次の式を計算し、簡単にしなさい。
$\left(\displaystyle\frac{\sqrt{3}}{\sqrt{5}-2}-\frac{4\sqrt{3}}{3-\sqrt{5}}\right)^7\times\left(-\sqrt{\displaystyle\frac{1}{9}}\right)^6$
この動画を見る
次の式を計算し、簡単にしなさい。
$\left(\displaystyle\frac{\sqrt{3}}{\sqrt{5}-2}-\frac{4\sqrt{3}}{3-\sqrt{5}}\right)^7\times\left(-\sqrt{\displaystyle\frac{1}{9}}\right)^6$