 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
【中学数学】円周角の定理の問題~2024年度埼玉県公立高校入試大問1(10)~【高校受験】

単元:
#数学(中学生)#中3数学#円#高校入試過去問(数学)#埼玉県高等学校
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
図のように、円周の長さを10等分する点A~Jがあります。
△AEHと△BEHをつくり、辺AEと辺BEとの交点をKとするとき、
∠AKHの大きさxを求めよ。
※図は動画内参照
この動画を見る
図のように、円周の長さを10等分する点A~Jがあります。
△AEHと△BEHをつくり、辺AEと辺BEとの交点をKとするとき、
∠AKHの大きさxを求めよ。
※図は動画内参照
平方根の計算
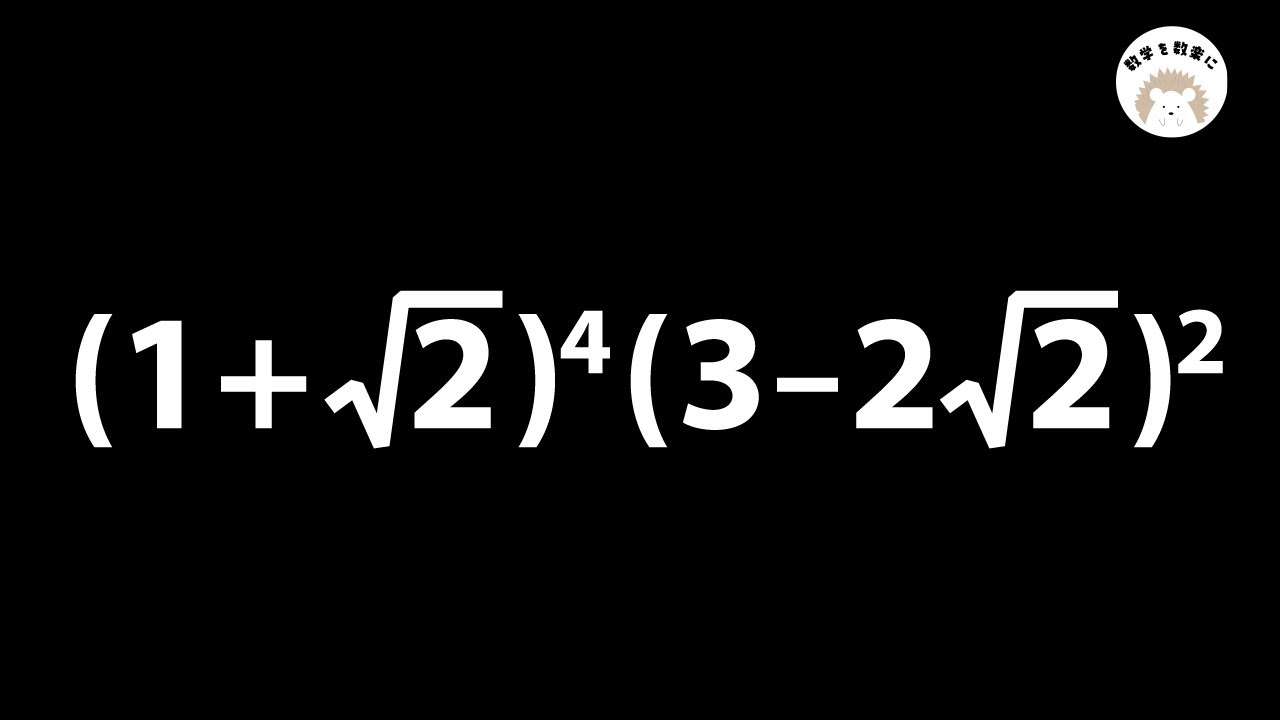
【何個知ってる?】受験生が覚えてたらお得な公式

【試される思考…!】整数:日本大学第二高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#日本大学第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$【a】は自然数aを5で割った余りを表す。$
$このとき次の値を求めよ$
$【1^2】+【2^2】+【3^2】+...+【100^2】$
この動画を見る
$【a】は自然数aを5で割った余りを表す。$
$このとき次の値を求めよ$
$【1^2】+【2^2】+【3^2】+...+【100^2】$
【問題文が全て…!】二次方程式:桐朋高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#桐朋高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ax^2+2a^2x-6=0$
$x=3が解であるとき、定数aの値を全て求めよ$
この動画を見る
$ax^2+2a^2x-6=0$
$x=3が解であるとき、定数aの値を全て求めよ$
【中学数学】標本調査の問題演習~応用問題~ 8-1.5【中3数学】

単元:
#数学(中学生)#中3数学#標本調査
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1)
黒ごまがたくさん入った袋がある。何粒の黒ごまが入っているか調べるため、白ごま50粒を黒ごまの入っている袋に入れてよく混ぜ、30粒のごまを無作為に取り出したところ、そのうちの3粒が白ごまだった。袋の中の黒ごまはおよそ何粒と考えれるか答えなさい。
(2)
下の表は、ある中学生150人の中から44人を無作為に抽出して、平日1日に何時間くらいYouTubeを見るかアンケートをとって調べた結果である。次の問に答えなさい。
\begin{array}{|c|c|c|c|c|c|}
\hline
時間&見ない&1時間未満&1時間以上2時間未満&2時間以上3時間未満&3時間以上\\
\hline
人数&3&5&22&10&4\\
\hline
\end{array}
(a)この調査の母集団と標本は?
(b)中学生150人のうち、テレビを見る時間が「1時間以上2時間未満」なのは、およそ何人と考えられるか答えなさい。
この動画を見る
(1)
黒ごまがたくさん入った袋がある。何粒の黒ごまが入っているか調べるため、白ごま50粒を黒ごまの入っている袋に入れてよく混ぜ、30粒のごまを無作為に取り出したところ、そのうちの3粒が白ごまだった。袋の中の黒ごまはおよそ何粒と考えれるか答えなさい。
(2)
下の表は、ある中学生150人の中から44人を無作為に抽出して、平日1日に何時間くらいYouTubeを見るかアンケートをとって調べた結果である。次の問に答えなさい。
\begin{array}{|c|c|c|c|c|c|}
\hline
時間&見ない&1時間未満&1時間以上2時間未満&2時間以上3時間未満&3時間以上\\
\hline
人数&3&5&22&10&4\\
\hline
\end{array}
(a)この調査の母集団と標本は?
(b)中学生150人のうち、テレビを見る時間が「1時間以上2時間未満」なのは、およそ何人と考えられるか答えなさい。
【どちらで解く…!】平方根:巣鴨高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#巣鴨高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$(\frac{\sqrt{5}+\sqrt{2}}{\sqrt{7}})^2+(\frac{\sqrt{5}-\sqrt{2}}{\sqrt{7}})^2$を計算しなさい
この動画を見る
$(\frac{\sqrt{5}+\sqrt{2}}{\sqrt{7}})^2+(\frac{\sqrt{5}-\sqrt{2}}{\sqrt{7}})^2$を計算しなさい
【中学数学】標本調査の問題演習~標準問題~【中3数学】

単元:
#数学(中学生)#中3数学#統計的な推測#標本調査
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1)
白と黒の玉が合わせて500個入った袋がある。
この袋の中から30個を無作為に取り出すと、そのうちの12個が白い玉だった。袋の中の白い球はおよそ何個と表されるか?
(2)
池にいる魚の数を調べる。
1度20匹捕まえて印をつけ池に戻し
1週間後、今度は60匹の魚を捕まえたところ
そのうち4匹の魚に印がついていました。
この池には何匹の魚がいると考えられる?
この動画を見る
(1)
白と黒の玉が合わせて500個入った袋がある。
この袋の中から30個を無作為に取り出すと、そのうちの12個が白い玉だった。袋の中の白い球はおよそ何個と表されるか?
(2)
池にいる魚の数を調べる。
1度20匹捕まえて印をつけ池に戻し
1週間後、今度は60匹の魚を捕まえたところ
そのうち4匹の魚に印がついていました。
この池には何匹の魚がいると考えられる?
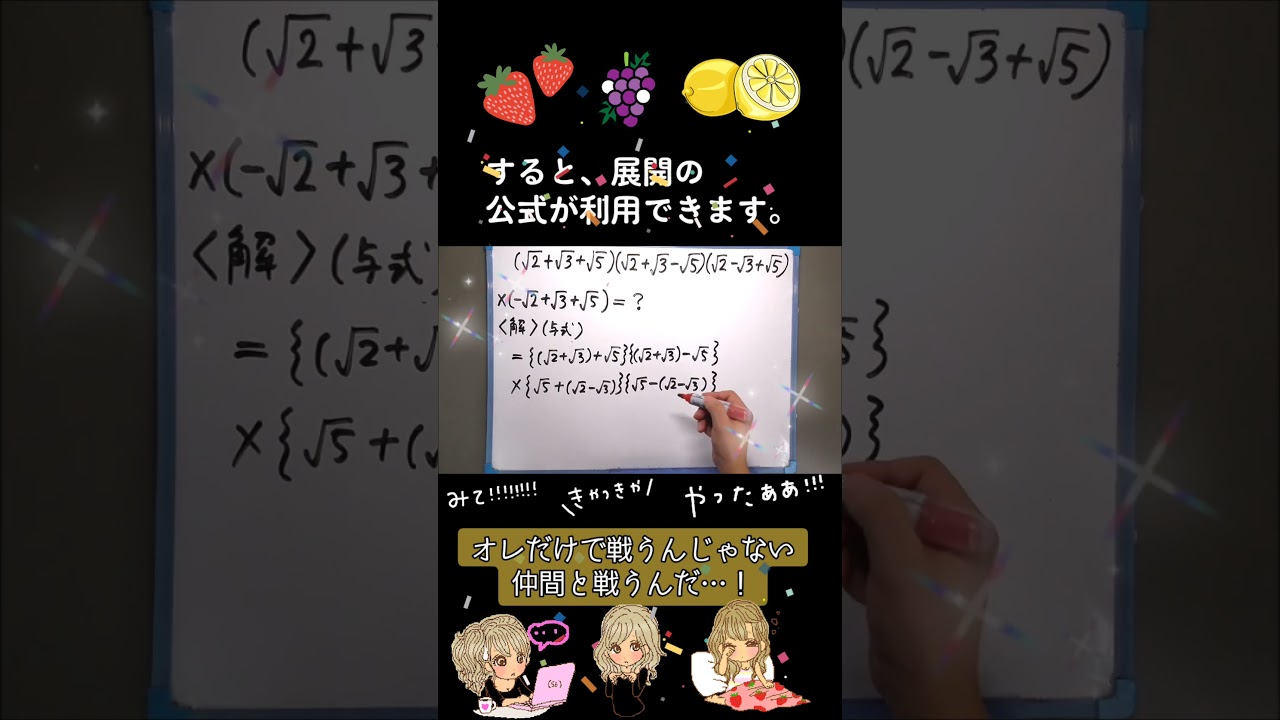
square root : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study #test
単元:
#数学(中学生)#中3数学#数と式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$(\sqtr{2}+\sqrt{3}+\sqrt{5})(\sqtr{2}+\sqrt{3}-\sqrt{5})×(\sqtr{2}-\sqrt{3}+\sqrt{5})(-\sqtr{2}+\sqrt{3}+\sqrt{5})=\boxed{ }$
この動画を見る
$(\sqtr{2}+\sqrt{3}+\sqrt{5})(\sqtr{2}+\sqrt{3}-\sqrt{5})×(\sqtr{2}-\sqrt{3}+\sqrt{5})(-\sqtr{2}+\sqrt{3}+\sqrt{5})=\boxed{ }$
2次方程式のこれ解ける?

単元:
#数学(中学生)#中3数学#2次方程式#数Ⅰ#2次関数#2次方程式と2次不等式#高校入試過去問(数学)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
aを定数とする。xの2次方程式
$3(x+a)^2 = (2a^2+1)(x+a)+x^2-2ax-3a^2$
が解を1つしかもたないようなaの値を全て求めよ。(灘高校 2024)
この動画を見る
aを定数とする。xの2次方程式
$3(x+a)^2 = (2a^2+1)(x+a)+x^2-2ax-3a^2$
が解を1つしかもたないようなaの値を全て求めよ。(灘高校 2024)
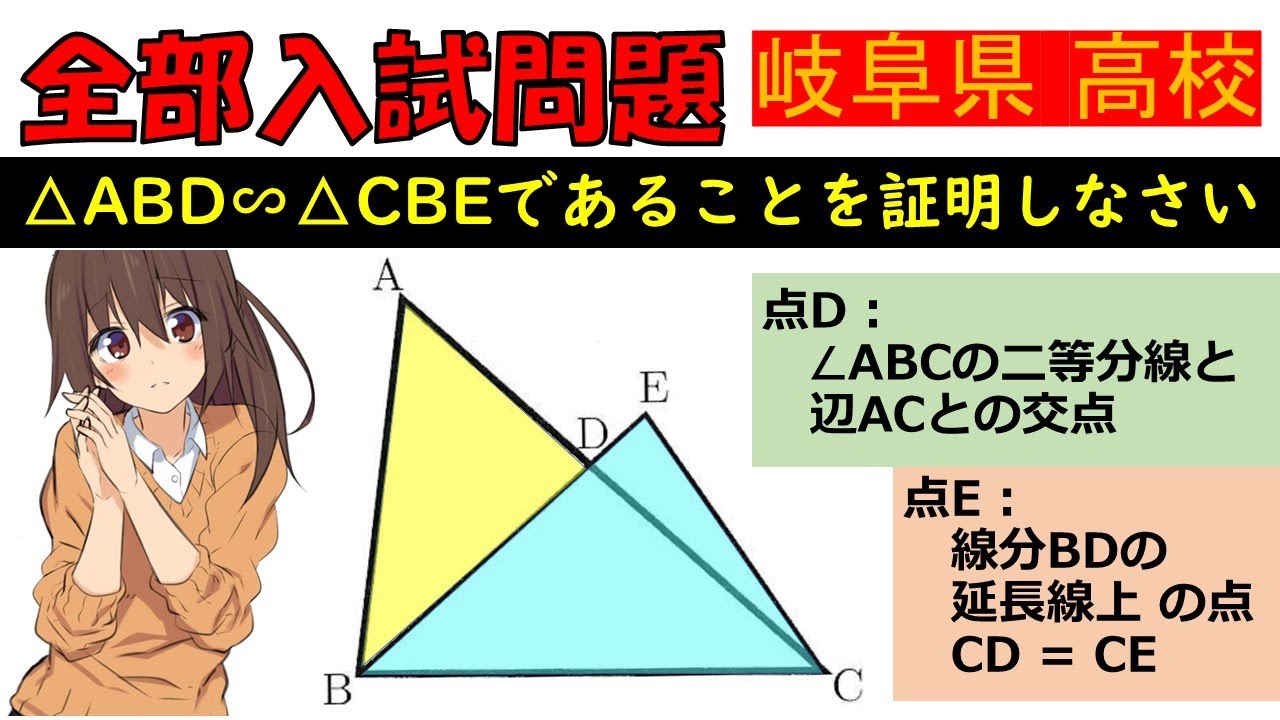
【重要な図形…!】図形:岐阜県~全国入試問題解法
単元:
#数学(中学生)#中1数学#中3数学#相似な図形#平面図形#高校入試過去問(数学)#岐阜県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\triangle ABD \backsim \triangle CBE であることを証明しなさい$
$点D : \angle ABCの二等分線と辺ACとの交点$
$点E : 線分BDの延長線上の点CD =CE$
この動画を見る
$\triangle ABD \backsim \triangle CBE であることを証明しなさい$
$点D : \angle ABCの二等分線と辺ACとの交点$
$点E : 線分BDの延長線上の点CD =CE$
【さらに発展的解法…!】整数:東京都立産業技術高等専門学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#東京都立産業技術高等専門学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$a^2bcの約数は何個あるか。$
$a,b,cは素数で a \lt b \lt cである$
この動画を見る
$a^2bcの約数は何個あるか。$
$a,b,cは素数で a \lt b \lt cである$
integer problems : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study

単元:
#高校入試過去問(数学)#立命館高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$2104^2を11で割った余りを求めなさい$
この動画を見る
$2104^2を11で割った余りを求めなさい$
【数式に翻訳せよ…!】整数:新潟県~全国入試問題解法
factorization : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study #test
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$(x-3)(x-1)(x+5)(x+7)-960 を因数分解せよ$
この動画を見る
$(x-3)(x-1)(x+5)(x+7)-960 を因数分解せよ$
【会話文形式が楽しい…!】図形:早稲田大学系属早稲田実業学校高等部~全国入試問題解法
【会話文形式が楽しい…!】図形:早稲田大学系属早稲田実業学校高等部~全国入試問題解法
【正解を導くことが第一…!】連立方程式:東京都立新宿高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#東京都立新宿高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
0.25x + y = 0.75 \\
\frac{x-2y}{5} = \frac{21}{25}
\end{array}
\right.
\end{eqnarray}$
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
0.25x + y = 0.75 \\
\frac{x-2y}{5} = \frac{21}{25}
\end{array}
\right.
\end{eqnarray}$
【正解を導くことが第一…!】連立方程式:東京都立新宿高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学
指導講師:
問題文全文(内容文):
連立方程式
\begin{align}
\left\{
\begin{array}{l}
0.25x + y = 0.75 \\
\displaystyle\frac{x - 2y}{5} = \frac{21}{25}
\end{array}
\right.
\end{align}
この動画を見る
連立方程式
\begin{align}
\left\{
\begin{array}{l}
0.25x + y = 0.75 \\
\displaystyle\frac{x - 2y}{5} = \frac{21}{25}
\end{array}
\right.
\end{align}
"2025"を含む予想問題(5):入試予想問題~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
問題文全文(内容文):
"2025"を含む入試予想問題
$\left( \frac{\sqrt{2025} + \sqrt{1975}}{\sqrt{2}} \right)^2 - (\sqrt{2025} + \sqrt{1975}) \times (\sqrt{2025} - \sqrt{1975}) + \left( \frac{\sqrt{225} - \sqrt{1975}}{\sqrt{2}} \right)^2$
この動画を見る
"2025"を含む入試予想問題
$\left( \frac{\sqrt{2025} + \sqrt{1975}}{\sqrt{2}} \right)^2 - (\sqrt{2025} + \sqrt{1975}) \times (\sqrt{2025} - \sqrt{1975}) + \left( \frac{\sqrt{225} - \sqrt{1975}}{\sqrt{2}} \right)^2$
equation : Shirotan's cute kawaii math show #Math #exam #questions #study #test
単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
問題文全文(内容文):
x,yについての連立方程式
\begin{equation}
\left\{ \,
\begin{aligned}
\frac{3}{3x-4y} - \frac{4}{4x+3y} = 8 \\
\frac{1}{3x-4y} + \frac{2}{4x+3y} = 6
\end{aligned}
\right.
\end{equation}
この動画を見る
x,yについての連立方程式
\begin{equation}
\left\{ \,
\begin{aligned}
\frac{3}{3x-4y} - \frac{4}{4x+3y} = 8 \\
\frac{1}{3x-4y} + \frac{2}{4x+3y} = 6
\end{aligned}
\right.
\end{equation}
"2025"を含む予想問題(4):入試予想問題~全国入試問題解法
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x = \sqrt{2025}のとき$
$x^2 - 87x + 1890$を求めよ
この動画を見る
$x = \sqrt{2025}のとき$
$x^2 - 87x + 1890$を求めよ
【話題】三角形の面積を求めよ

単元:
#数学(中学生)#中1数学#中2数学#中3数学#その他#その他
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
辺BCの長さは12㎝です。
三角形ABCの面積は?
この動画を見る
辺BCの長さは12㎝です。
三角形ABCの面積は?
角度を求めるこの問題できる?

"2025"を含む予想問題(1):入試予想問題~全国入試問題解法
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$2025×2024-2024×2023$
$+2025×2026-2026×2027$
この動画を見る
$2025×2024-2024×2023$
$+2025×2026-2026×2027$
"2025"を含む問題予想《考察編》:入試予想問題~全国入試問題解法
【中学数学】標本調査と全数調査の違い~分かりやすく丁寧に~ 8-1【中3数学】

単元:
#数学(中学生)#中3数学#標本調査
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
次のア~オの調査で全数調査に適しているものと標本調査に適しているものを答えなさい
ア. 学校での健康診断 イ. 空港での手荷物検査 ウ. 国勢調査 エ. 不良品の調査 オ. テレビの視聴率
この動画を見る
次のア~オの調査で全数調査に適しているものと標本調査に適しているものを答えなさい
ア. 学校での健康診断 イ. 空港での手荷物検査 ウ. 国勢調査 エ. 不良品の調査 オ. テレビの視聴率
【ひらめきか論理性か…!】整数:慶応義塾女子高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#慶應義塾女子高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$a^2 + b^2 - 2a - 4b = 20$$が成り立つような自然数a,bの組を全て求めなさい。$
この動画を見る
$a^2 + b^2 - 2a - 4b = 20$$が成り立つような自然数a,bの組を全て求めなさい。$
【定石が唯一ではない…!】因数分解:國學院大學久我山高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#高校入試過去問(数学)#数学(高校生)#國學院大學久我山高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x^2-4y^2+8y-4$
$を因数分解せよ。$
この動画を見る
$x^2-4y^2+8y-4$
$を因数分解せよ。$
【ひらめきと経験と…!】図形:慶応義塾高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\triangle ABCにおいて、AB=AC,BC=2,\angle BAC=36^{ \circ }$
$のとき、ABの長さを求めよ。$
この動画を見る
$\triangle ABCにおいて、AB=AC,BC=2,\angle BAC=36^{ \circ }$
$のとき、ABの長さを求めよ。$
