4S数学
4S数学
【数A】【場合の数と確率】円順列基本 ※問題文は概要欄
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#場合の数と確率#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
・大人2人と子供8人が円形のテーブルに着席するとき、次のような並び方は何通りあるか。
(1)大人2人が隣り合う。
(2)大人2人が向かい合う。
・男子4人、女子4人が手をつないで輪を作るとき、次のような並び方は何通りあるか。
(1)女子4人が続いて並ぶ。
(2)男女が交互に並ぶ。
・8人の中から選ばれた5人が円形上に並ぶとき、並び方は何通りあるか。
この動画を見る
・大人2人と子供8人が円形のテーブルに着席するとき、次のような並び方は何通りあるか。
(1)大人2人が隣り合う。
(2)大人2人が向かい合う。
・男子4人、女子4人が手をつないで輪を作るとき、次のような並び方は何通りあるか。
(1)女子4人が続いて並ぶ。
(2)男女が交互に並ぶ。
・8人の中から選ばれた5人が円形上に並ぶとき、並び方は何通りあるか。
【数A】【場合の数と確率】並び替え基本2 ※問題文は概要欄
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#場合の数と確率#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
・「equations」という単語の文字をすべて使って順列を作るとき、次の問いに答えよ。
(1)少なくとも一端に子音の文字がくるものは何通りあるか。
(2)eとaの間に文字が2つあるものは何通りあるか。
・A,B,C,D,E,Fの6文字をすべて使ってできる順列を、ABCDEFを1番目として自書式に並べるとき、次の問いに答えよ。
(1)140番目の文字列を求めよ。
(2)FBCDAEは何番目の文字列か。
この動画を見る
・「equations」という単語の文字をすべて使って順列を作るとき、次の問いに答えよ。
(1)少なくとも一端に子音の文字がくるものは何通りあるか。
(2)eとaの間に文字が2つあるものは何通りあるか。
・A,B,C,D,E,Fの6文字をすべて使ってできる順列を、ABCDEFを1番目として自書式に並べるとき、次の問いに答えよ。
(1)140番目の文字列を求めよ。
(2)FBCDAEは何番目の文字列か。
【数A】【場合の数と確率】並び替え基本1 ※問題文は概要欄
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#場合の数と確率#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
・6個の数字1,2,3,4,5,6から異なる4種の数字を使って4桁の整数を作るとき、次のような整数は何個あるか。
(1)4300より大きい整数
(2)5000より大きい整数
・女子5人、男子3人が1列に並ぶとき、次の並び方は何通りあるか。
(1)女子5人が続いて並ぶ。
(2)女子5人、男子3人がそれぞれ続いて並ぶ。
(3)両端が男子である。
(4)どの男子も隣合わない。
・男子4人、女子4人が男女交互に1列に並ぶ方法は何通りあるか。
この動画を見る
・6個の数字1,2,3,4,5,6から異なる4種の数字を使って4桁の整数を作るとき、次のような整数は何個あるか。
(1)4300より大きい整数
(2)5000より大きい整数
・女子5人、男子3人が1列に並ぶとき、次の並び方は何通りあるか。
(1)女子5人が続いて並ぶ。
(2)女子5人、男子3人がそれぞれ続いて並ぶ。
(3)両端が男子である。
(4)どの男子も隣合わない。
・男子4人、女子4人が男女交互に1列に並ぶ方法は何通りあるか。
【数A】【場合の数と確率】組み合わせ考え方の基本 ※問題文は概要欄
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#場合の数と確率#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
・5人乗りの車に5人が乗車してドライブをするとき、乗り方は何通りあるか。次の各場合について求めよ。
(1)5人全員が運転免許を持っている場合
(2)5人のうち3人だけが運転免許を持っている場合
・6個の数字0,1,2,3,4,5を使ってできる、次のような整数は何個あるか。ただし、同じ数字は2度以上使わないこととする。
(1)6桁の整数
(2)6桁の整数で5の倍数
・5個の数字0,1,2,3,4を使ってできる3桁の整数のうち、次のような整数は何個あるか。ただし、同じ数字は2度以上使わないものとする。
(1)偶数
(2)3の倍数
この動画を見る
・5人乗りの車に5人が乗車してドライブをするとき、乗り方は何通りあるか。次の各場合について求めよ。
(1)5人全員が運転免許を持っている場合
(2)5人のうち3人だけが運転免許を持っている場合
・6個の数字0,1,2,3,4,5を使ってできる、次のような整数は何個あるか。ただし、同じ数字は2度以上使わないこととする。
(1)6桁の整数
(2)6桁の整数で5の倍数
・5個の数字0,1,2,3,4を使ってできる3桁の整数のうち、次のような整数は何個あるか。ただし、同じ数字は2度以上使わないものとする。
(1)偶数
(2)3の倍数
【数Ⅲ】【微分とその応用】微分計算の基本2 ※問題文は概要欄
単元：
#微分とその応用#微分法#数学(高校生)#数Ⅲ
教材：
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師：
理数個別チャンネル
問題文全文(内容文)：
すべての実数に対して 1+2x-3x²≦f(x)≦1+2x+3x² が成り立つようなf(x)がある。このときf'(0)を求めよ。
この動画を見る
すべての実数に対して 1+2x-3x²≦f(x)≦1+2x+3x² が成り立つようなf(x)がある。このときf'(0)を求めよ。
【数Ⅲ】【微分とその応用】色々な関数の微分1 ※問題文は概要欄
単元：
#微分とその応用#色々な関数の導関数#数Ⅲ
教材：
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の関数を微分せよ
y= sin²3x
y= sin⁵x+cos5x
y= sin⁴xcos⁴x
y= √（1+sin²x)
y= sin√（x²+x+1)
y= (tanx + 1/tanx)²
y= cosx/(1-sinx)
y= (1-sinx) / (1+cosx)
次の極限値を求めよ
lim_(x→a) (sinx - sina) / sin(x-a)
lim_(x→a) (x²sina - a²sinx) / (x-a)
次の関数を微分せよ。ただしa,bは定数で、a＞0,a≠0 とする。
y= e^(-2x) sin2x
y= 10^sinx
y= log_x(a)
y= log(logx)
y= log_a(sinx)
y= log(1-cosx)
y= log_a(x+√（x²-a²）
y= log ((x²-b) / (x²+b))
この動画を見る
次の関数を微分せよ
y= sin²3x
y= sin⁵x+cos5x
y= sin⁴xcos⁴x
y= √（1+sin²x)
y= sin√（x²+x+1)
y= (tanx + 1/tanx)²
y= cosx/(1-sinx)
y= (1-sinx) / (1+cosx)
次の極限値を求めよ
lim_(x→a) (sinx - sina) / sin(x-a)
lim_(x→a) (x²sina - a²sinx) / (x-a)
次の関数を微分せよ。ただしa,bは定数で、a＞0,a≠0 とする。
y= e^(-2x) sin2x
y= 10^sinx
y= log_x(a)
y= log(logx)
y= log_a(sinx)
y= log(1-cosx)
y= log_a(x+√（x²-a²）
y= log ((x²-b) / (x²+b))
【数Ⅰ】【図形と計量】測量の応用2 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
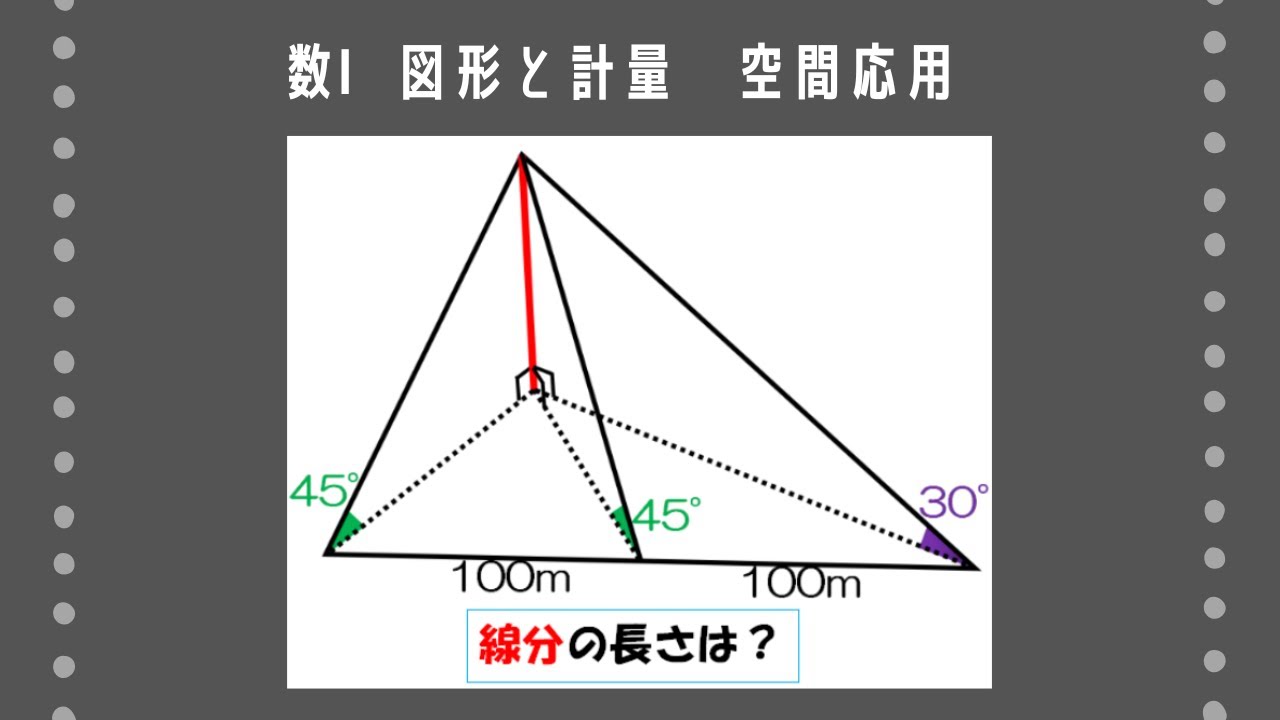
右の図のように1つの直線上にならぶ水平面上の3点A、B、Cから山頂Dの仰角を測ると、それぞれ45°、45°、30°であったという。AB=100m、BC=100mであるとき、山の高さDHを求めよ。
この動画を見る
右の図のように1つの直線上にならぶ水平面上の3点A、B、Cから山頂Dの仰角を測ると、それぞれ45°、45°、30°であったという。AB=100m、BC=100mであるとき、山の高さDHを求めよ。
【数Ⅰ】【図形と計量】測量の応用1 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
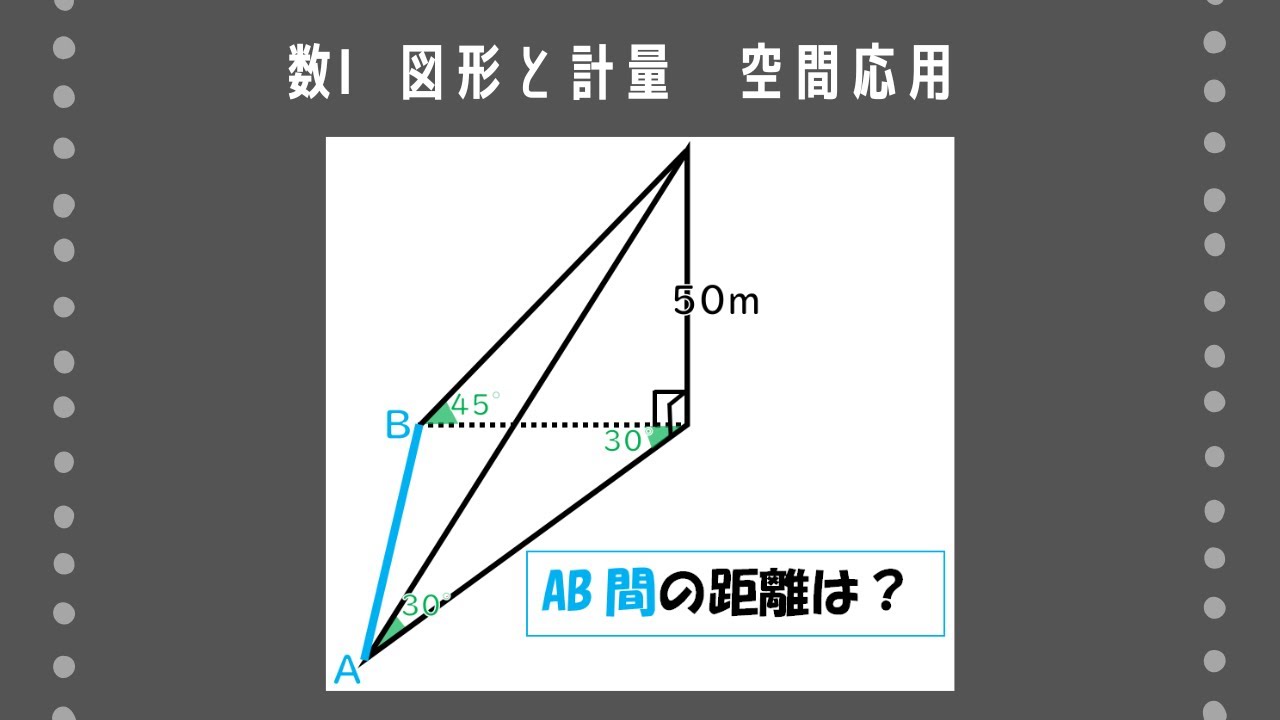
高さ50mの塔が立っている地点Hと同じ標高の地点Aから、塔の先端Pを見たところ、仰角が30°であった。また、Hと同じ標高の地点BからPを見たところ、仰角が45°で、∠BHA=30°であった。2地点A、B間の距離を求めよ。
この動画を見る
高さ50mの塔が立っている地点Hと同じ標高の地点Aから、塔の先端Pを見たところ、仰角が30°であった。また、Hと同じ標高の地点BからPを見たところ、仰角が45°で、∠BHA=30°であった。2地点A、B間の距離を求めよ。
【数Ⅰ】【図形と計量】球2 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
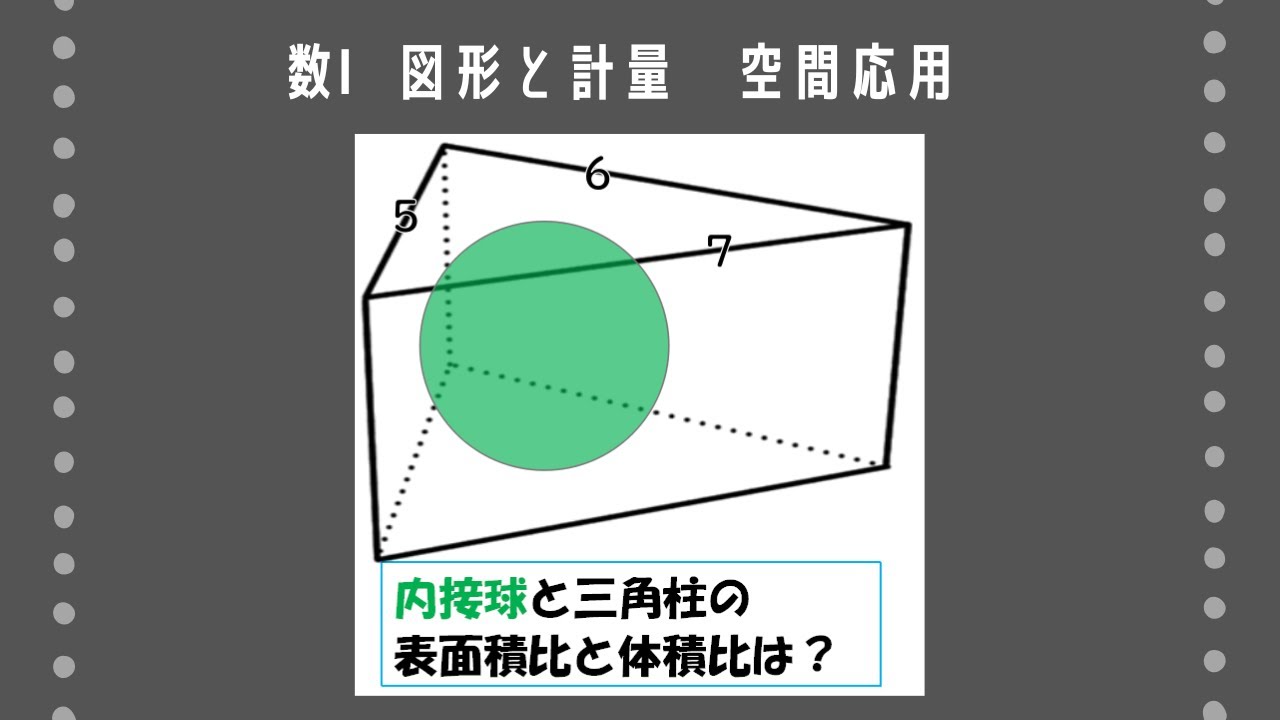
右の図のように、3辺の長さが5、6、7である三角形を底面とする三角柱に、三角柱の高さと同じ直径の球が内接している。
(1)球の表面積と体積を求めよ。
(2)三角柱の表面積と体積を求めよ。
(3)球と三角柱の表面積の比を求めよ。
(4)球と三角柱の体積比は、球と三角柱の表面積の比に等しいことを示せ。
※図は動画内参照
この動画を見る
右の図のように、3辺の長さが5、6、7である三角形を底面とする三角柱に、三角柱の高さと同じ直径の球が内接している。
(1)球の表面積と体積を求めよ。
(2)三角柱の表面積と体積を求めよ。
(3)球と三角柱の表面積の比を求めよ。
(4)球と三角柱の体積比は、球と三角柱の表面積の比に等しいことを示せ。
※図は動画内参照
【数Ⅰ】【図形と計量】球1 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
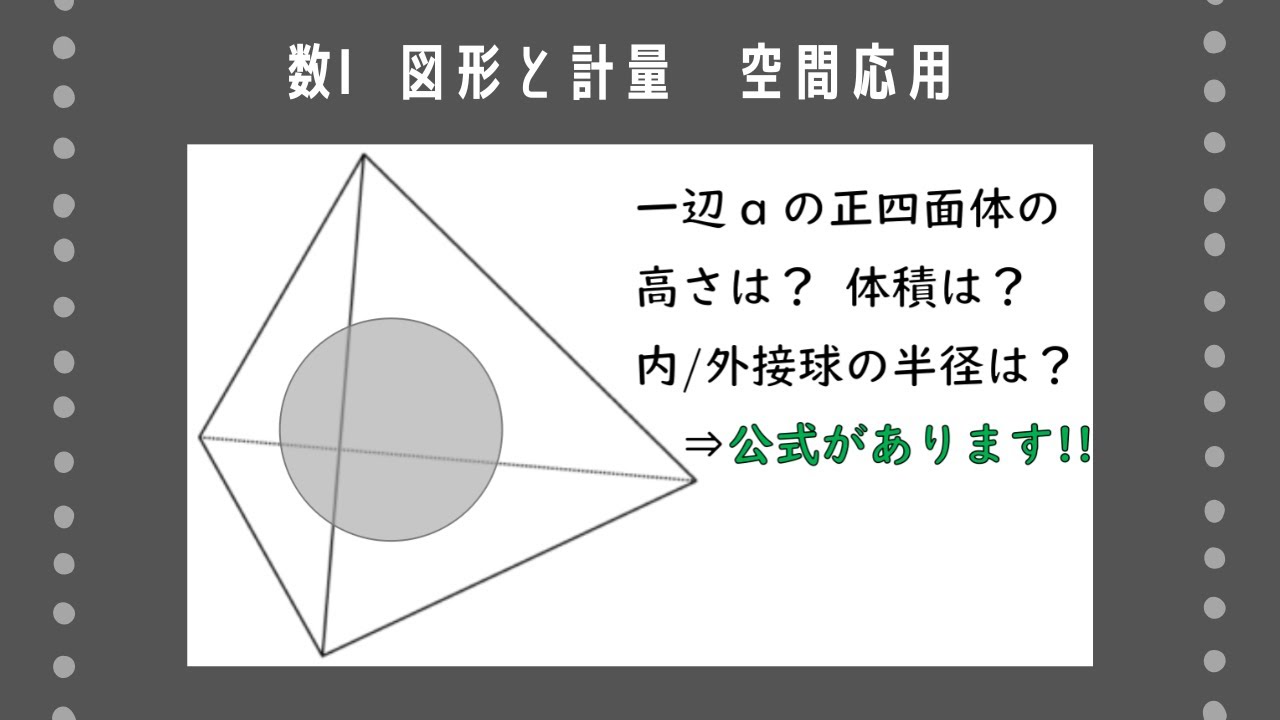
1辺の長さが3の正四面体ABCDに内接する球の中心をOとする。次の問いに答えよ。
(1)四面体OBCDの体積$V$を求めよ。
(2)球の半径$r$、表面積、体積を求めよ。
この動画を見る
1辺の長さが3の正四面体ABCDに内接する球の中心をOとする。次の問いに答えよ。
(1)四面体OBCDの体積$V$を求めよ。
(2)球の半径$r$、表面積、体積を求めよ。
【数Ⅰ】【図形と計量】空間の応用2 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
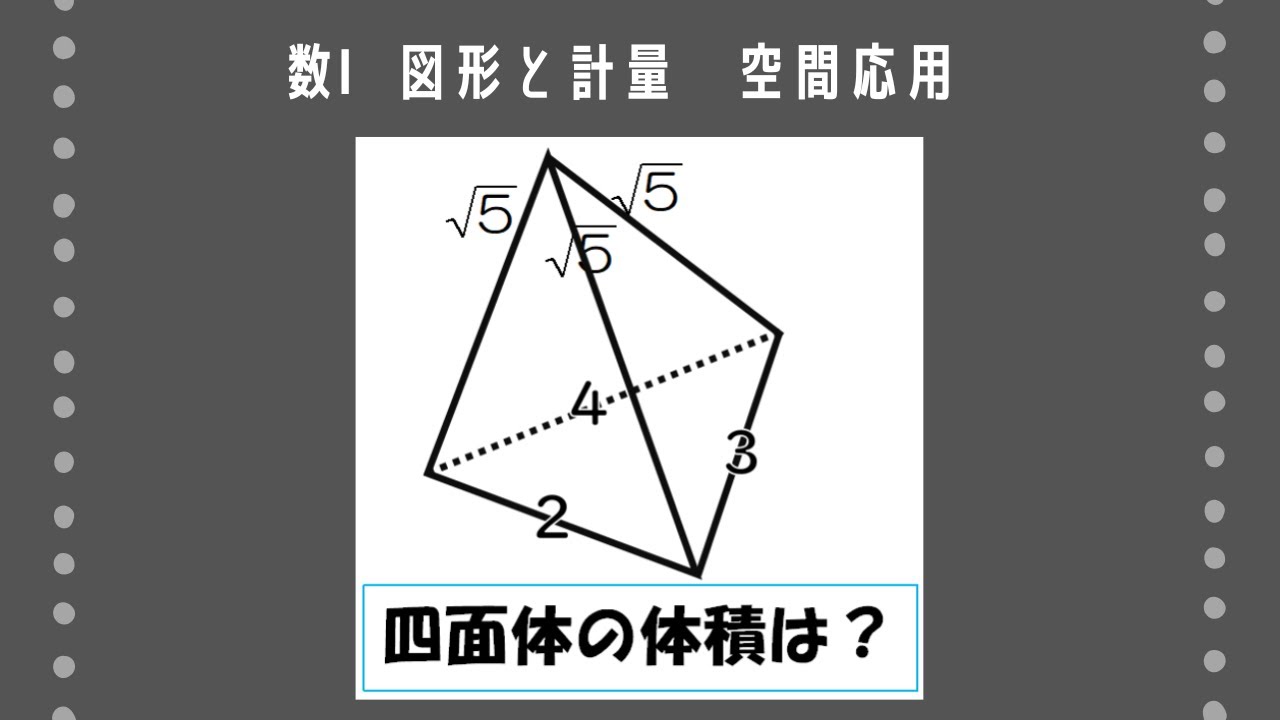
$\rm PA＝PB=PC=\sqrt5,AB=3,BC=3,CA=4$である三角錐PABCの体積を求めよ。
この動画を見る
$\rm PA＝PB=PC=\sqrt5,AB=3,BC=3,CA=4$である三角錐PABCの体積を求めよ。
【数Ⅰ】【図形と計量】空間の応用1 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
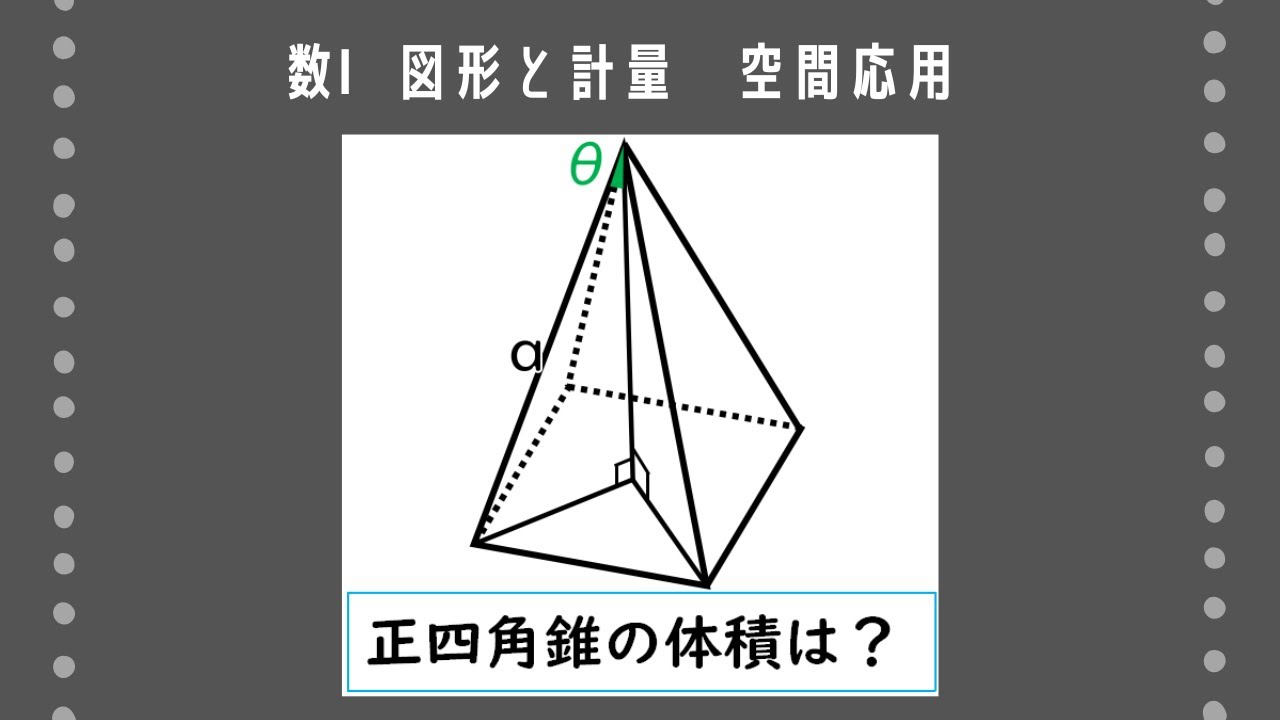
図のような正四角錐$\rm PABCD$において、頂点$\rm P$から正方形$\rm ABCD$に下ろした垂線を$\rm PH$とする。$\rm PA=a,\angle APH=\theta$であるとき、正四角錐の体積を求めよ。
この動画を見る
図のような正四角錐$\rm PABCD$において、頂点$\rm P$から正方形$\rm ABCD$に下ろした垂線を$\rm PH$とする。$\rm PA=a,\angle APH=\theta$であるとき、正四角錐の体積を求めよ。
【数Ⅰ】【図形と計量】空間の基本2 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
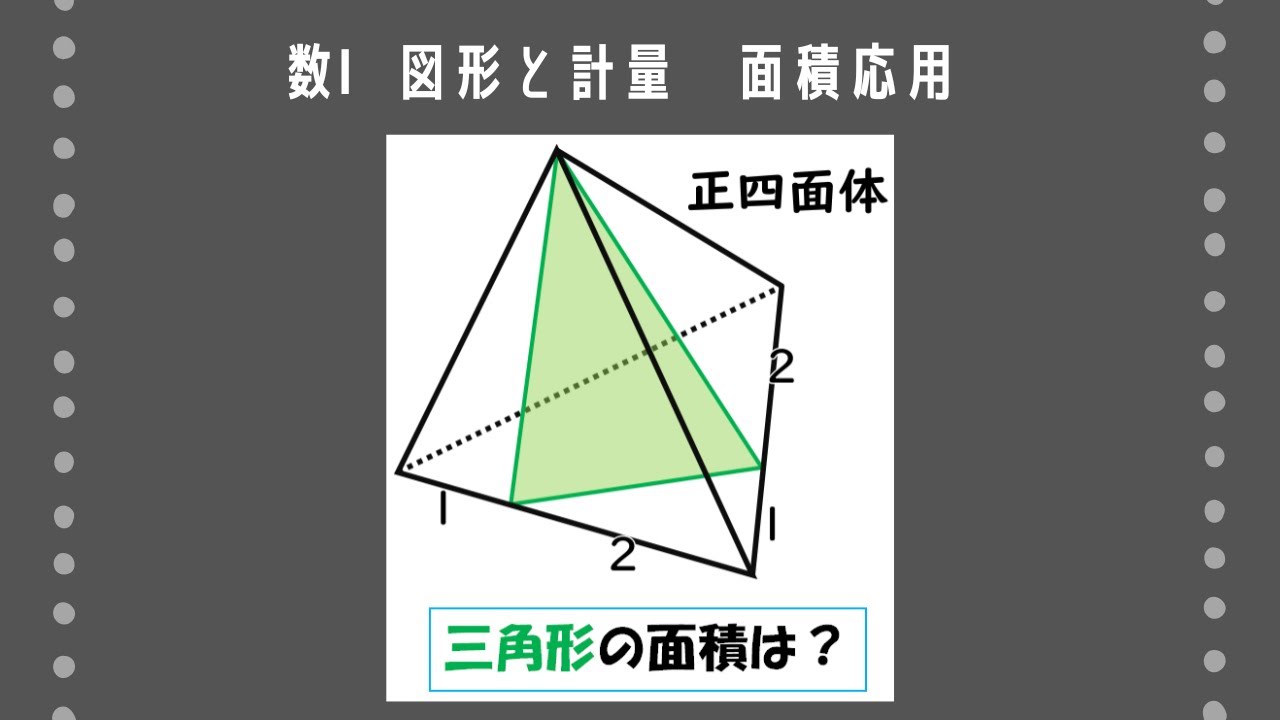
1辺の長さが3の正四面体$\rm ABCD$において、辺$\rm BC,CD$を$1:2$に分ける点を、それぞれ$\rm P,Q$とする。このとき、次のものを求めよ。
(1)$\rm AP,AQ,PQ$の長さ (2)$\cos \angle \rm PAQ$の値 (3)$\rm \triangle APQ$の面積
この動画を見る
1辺の長さが3の正四面体$\rm ABCD$において、辺$\rm BC,CD$を$1:2$に分ける点を、それぞれ$\rm P,Q$とする。このとき、次のものを求めよ。
(1)$\rm AP,AQ,PQ$の長さ (2)$\cos \angle \rm PAQ$の値 (3)$\rm \triangle APQ$の面積
【数Ⅰ】【図形と計量】空間の基本3 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
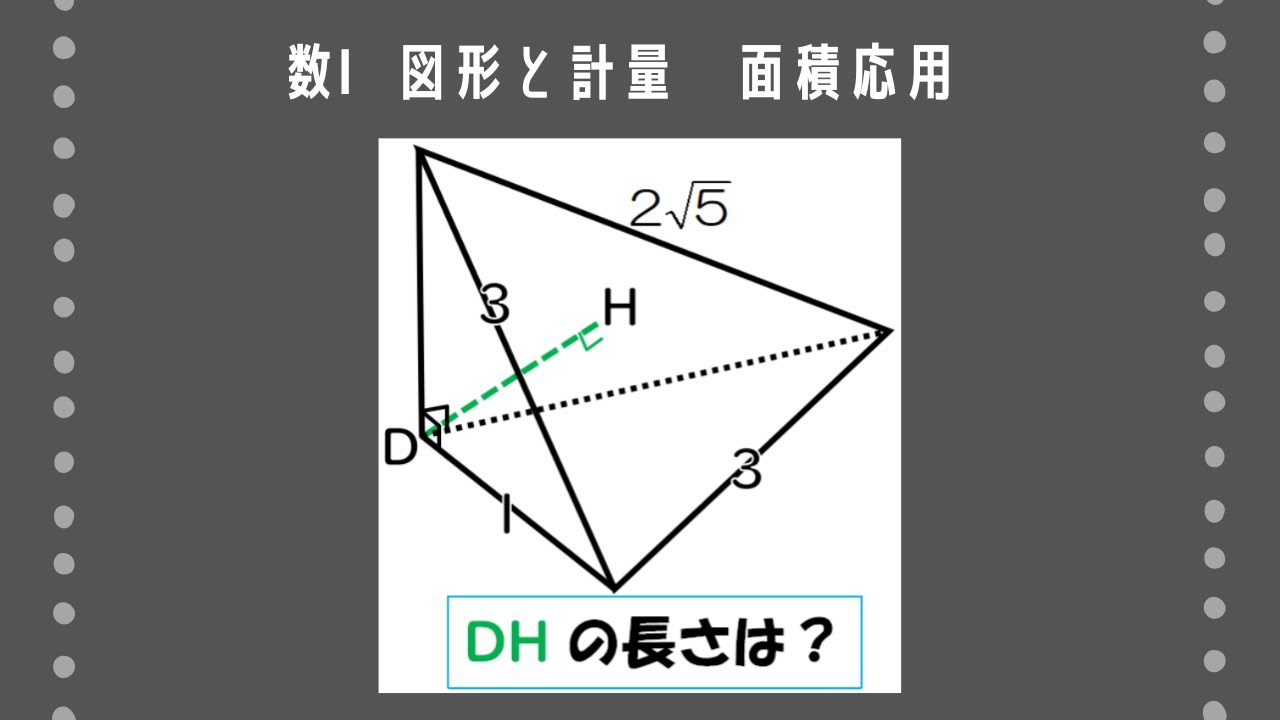
四面体$\rm ABCD$において、$\rm AB=BC=3,CA=2\sqrt5,BD=1,\angle ADB=\angle ADC=90^{\circ}$であるとき、次のものを求めよ。
(1)$\rm CD$の長さ (2)四面体$\rm ABCD$の体積 (3)$\triangle \rm ABC$の面積 (4)頂点$\rm D$から平面
この動画を見る
四面体$\rm ABCD$において、$\rm AB=BC=3,CA=2\sqrt5,BD=1,\angle ADB=\angle ADC=90^{\circ}$であるとき、次のものを求めよ。
(1)$\rm CD$の長さ (2)四面体$\rm ABCD$の体積 (3)$\triangle \rm ABC$の面積 (4)頂点$\rm D$から平面
【数Ⅰ】【図形と計量】空間の基本1 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
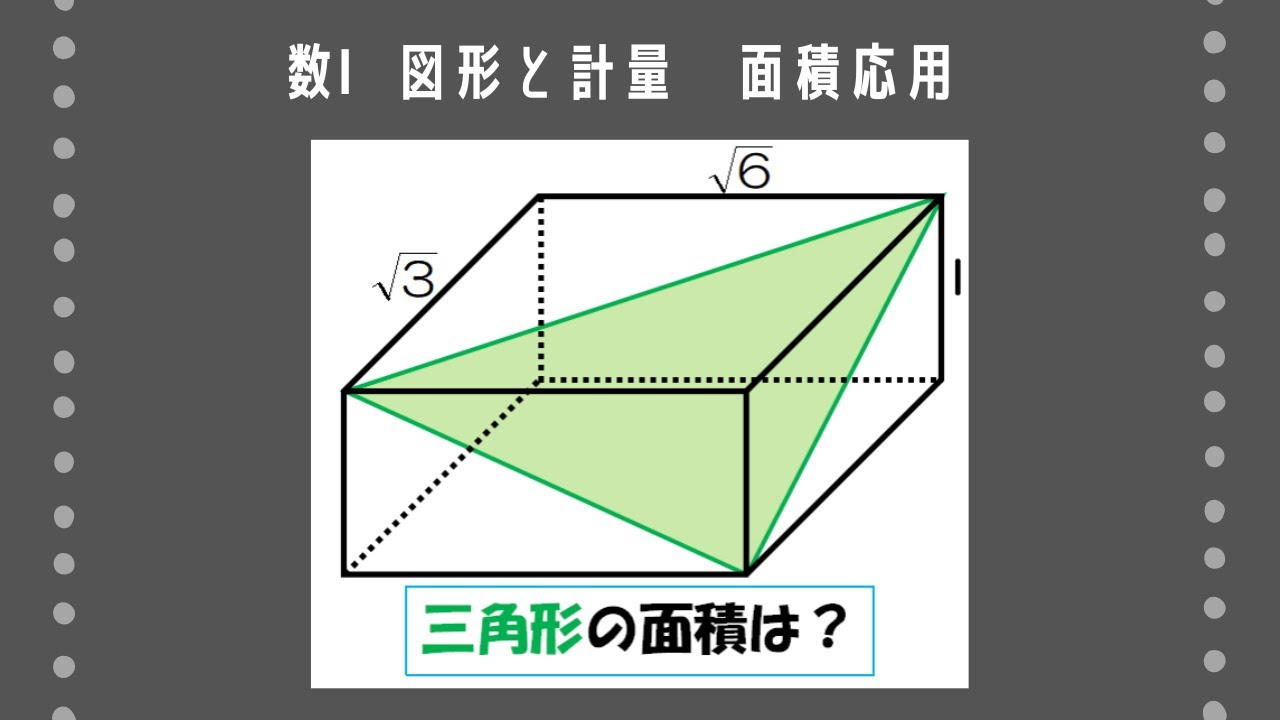
右の図のような$\rm AB=\sqrt6,AD=\sqrt3,AE=1$である直方体$\rm ABCD-EFGH$がある。このとき、次のものを求めよ。
(1)$\rm\angle ACF$の大きさ
(2)$\rm \triangle ACF$の面積
この動画を見る
右の図のような$\rm AB=\sqrt6,AD=\sqrt3,AE=1$である直方体$\rm ABCD-EFGH$がある。このとき、次のものを求めよ。
(1)$\rm\angle ACF$の大きさ
(2)$\rm \triangle ACF$の面積
【数Ⅰ】【図形と計量】面積応用10 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
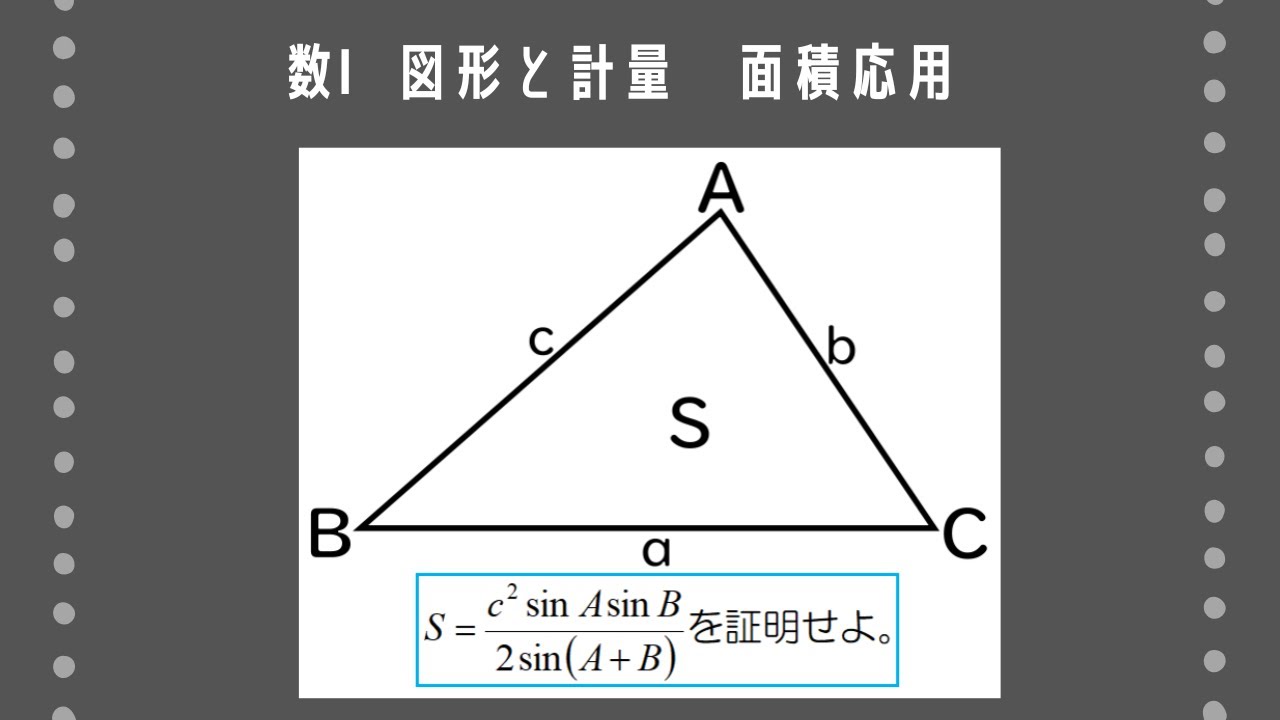
1辺$c$と2つの角$\rm A,B$が与えられた$rm\triangle ABC$の面積を$S$とするとき、次の問いに答えよ。
(1)$a$を$c,\rm A,B$で表せ。 (2)$S=\dfrac{c^2\rm\sin A\sin B}{2\sin\rm(A+B)}$を証明せよ。
この動画を見る
1辺$c$と2つの角$\rm A,B$が与えられた$rm\triangle ABC$の面積を$S$とするとき、次の問いに答えよ。
(1)$a$を$c,\rm A,B$で表せ。 (2)$S=\dfrac{c^2\rm\sin A\sin B}{2\sin\rm(A+B)}$を証明せよ。
【数Ⅰ】【図形と計量】面積応用9 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
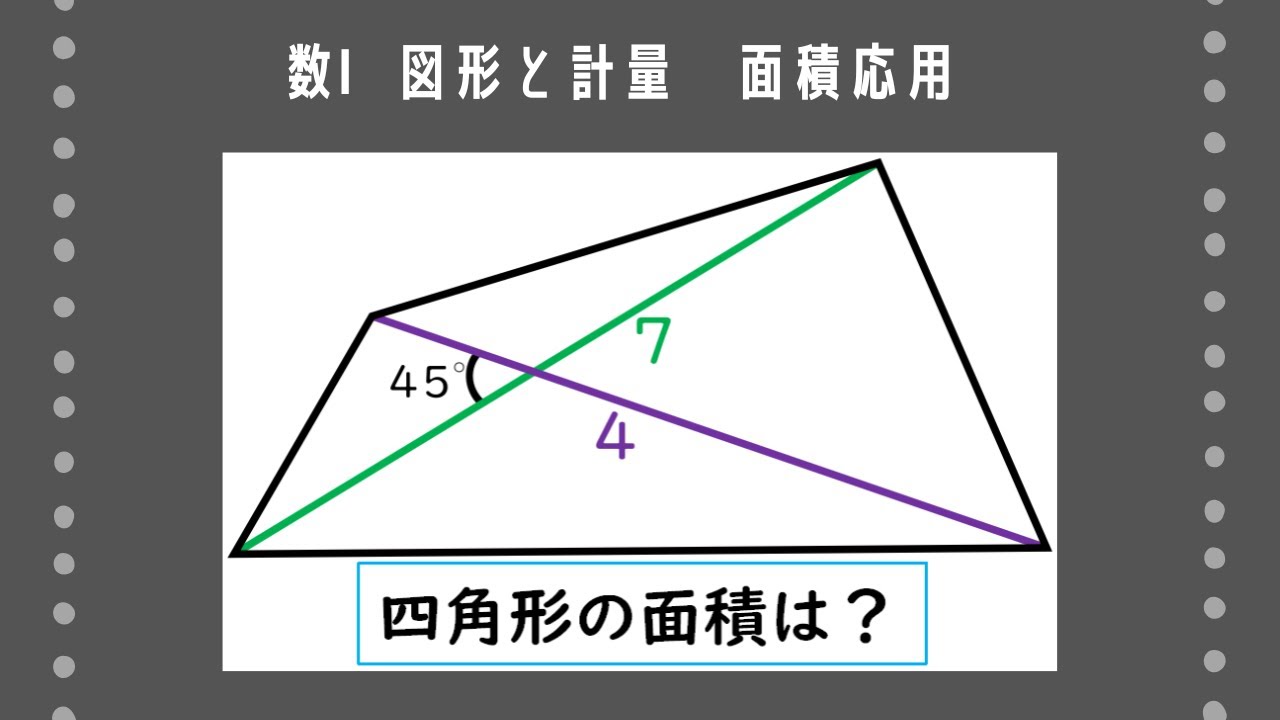
四角形$\rm ABCD$の2つの対角線$\rm AC,BD$の交点を$\rm O$とする。$\rm AC=4,BD=7,\angle AOB=45^{\circ}$であるとき、四角形$\rm ABCD$の面積$S$を求めよ。
この動画を見る
四角形$\rm ABCD$の2つの対角線$\rm AC,BD$の交点を$\rm O$とする。$\rm AC=4,BD=7,\angle AOB=45^{\circ}$であるとき、四角形$\rm ABCD$の面積$S$を求めよ。
【数Ⅰ】【図形と計量】面積応用8 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
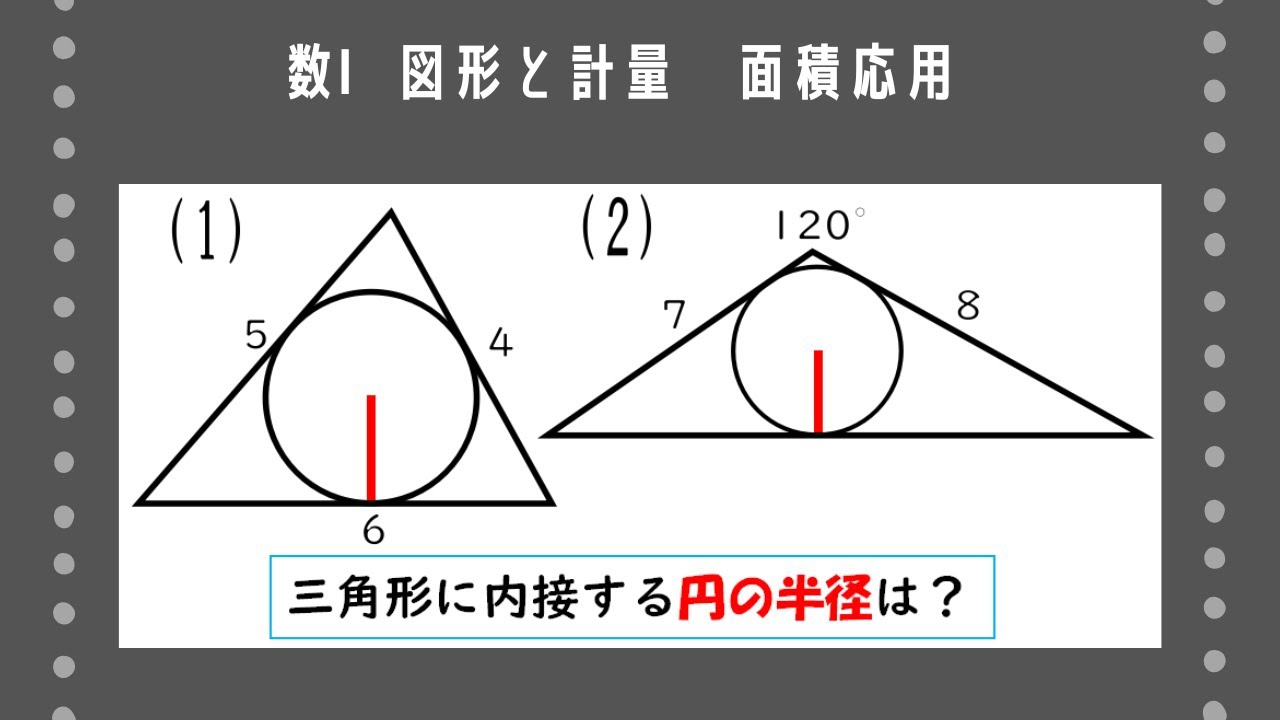
次のような$\rm \triangle ABC$に内接する円の半径$r$を求めよ。
(1)$a=4,b=5,c=6$ (2)${\rm A=120^{\circ}},b=7,c=8$
この動画を見る
次のような$\rm \triangle ABC$に内接する円の半径$r$を求めよ。
(1)$a=4,b=5,c=6$ (2)${\rm A=120^{\circ}},b=7,c=8$
【数Ⅰ】【図形と計量】面積応用3 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
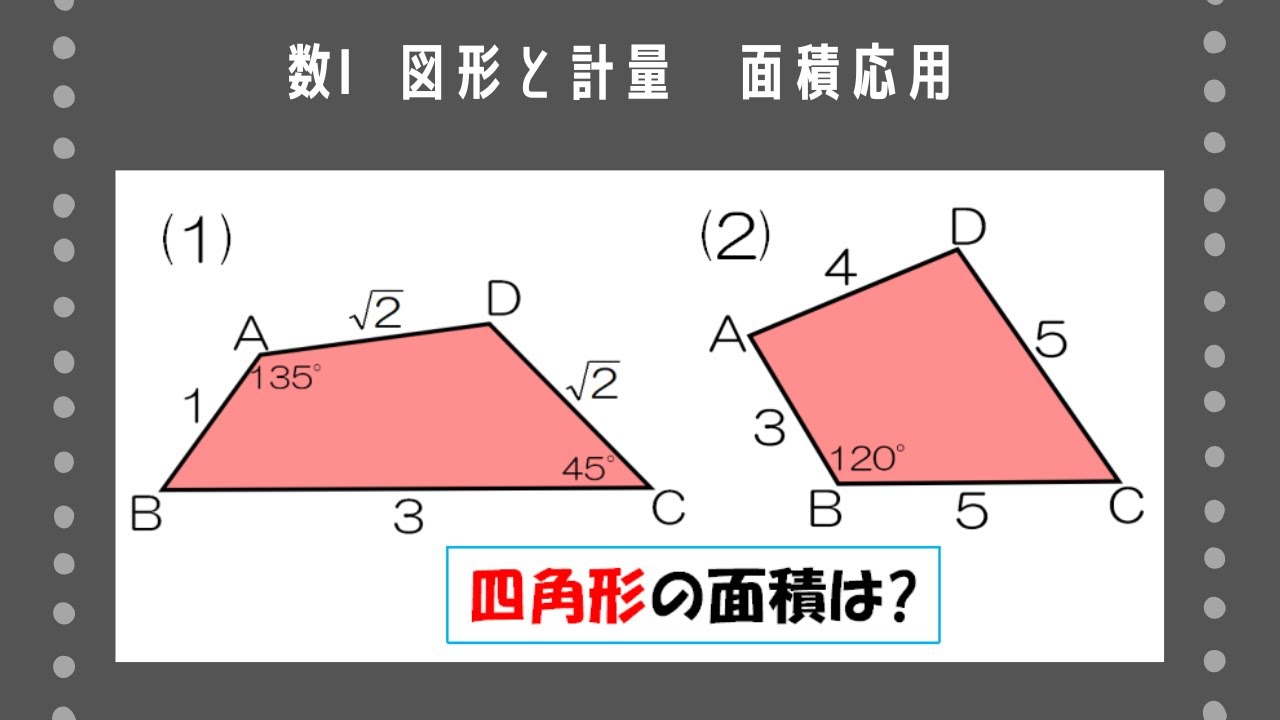
次のような四角形ABCDの面積を求めよ。
(1)∠A=135°、∠C=45°、AB=1、BC=3、CD=$\sqrt{2}$、DA=$\sqrt{2}$
(2)∠B=120°、AB=3、BC=5、CD=5、DA=4
この動画を見る
次のような四角形ABCDの面積を求めよ。
(1)∠A=135°、∠C=45°、AB=1、BC=3、CD=$\sqrt{2}$、DA=$\sqrt{2}$
(2)∠B=120°、AB=3、BC=5、CD=5、DA=4
【数Ⅰ】【図形と計量】面積応用7 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
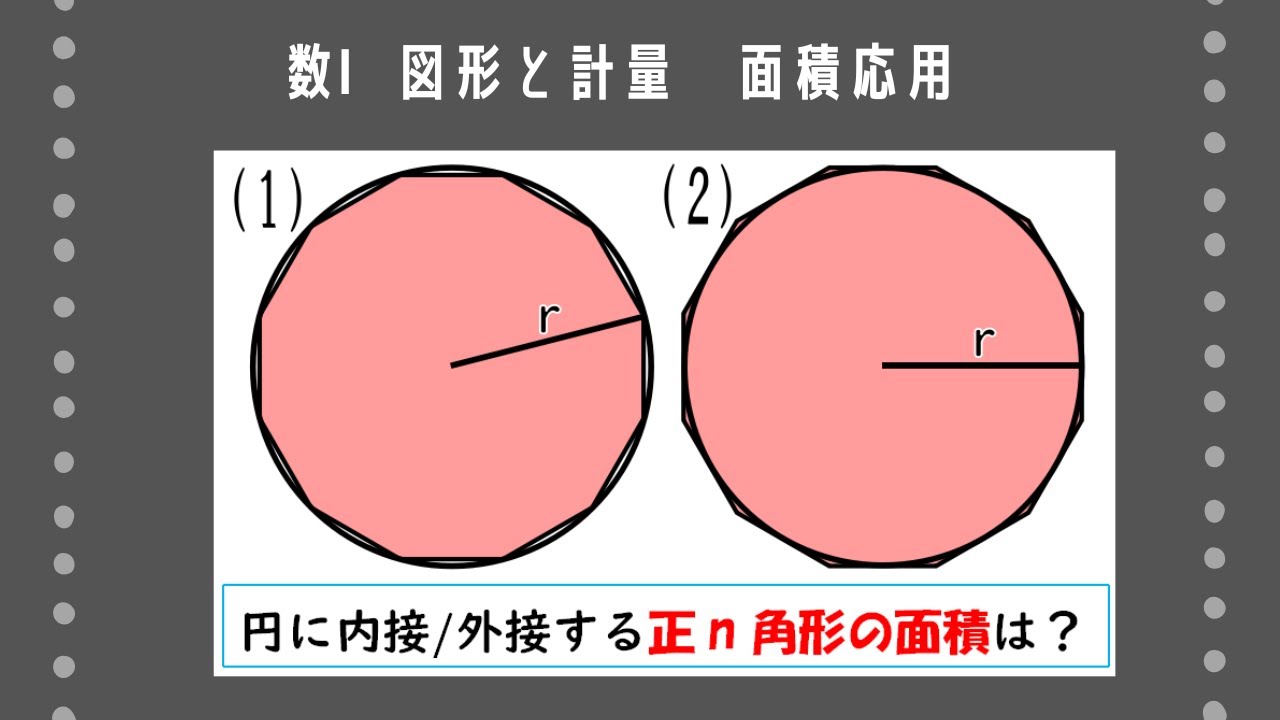
半径$r$の円に内接する正$n$角形の面積、および外接する正$n$角形の面積を、それぞれ$r$と$n$を用いて求めよ。
この動画を見る
半径$r$の円に内接する正$n$角形の面積、および外接する正$n$角形の面積を、それぞれ$r$と$n$を用いて求めよ。
【数Ⅰ】【図形と計量】面積応用2 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
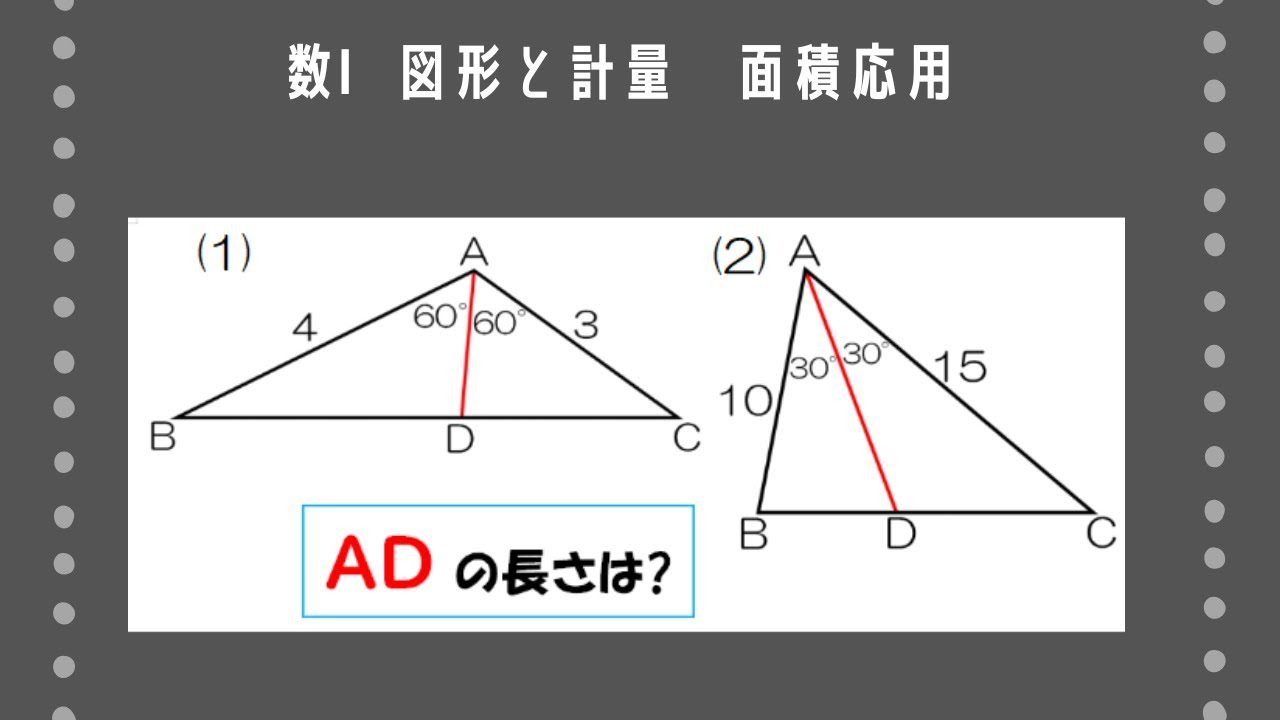
次のような△ABCについて、∠Aの二等分線と辺BCの交点をDとするとき、線分ADの長さを求めよ。
(1)AB=4、AC=3、A=120°
(2)AB=10、AC=15、A=60°
この動画を見る
次のような△ABCについて、∠Aの二等分線と辺BCの交点をDとするとき、線分ADの長さを求めよ。
(1)AB=4、AC=3、A=120°
(2)AB=10、AC=15、A=60°
【数Ⅰ】【図形と計量】面積応用6 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
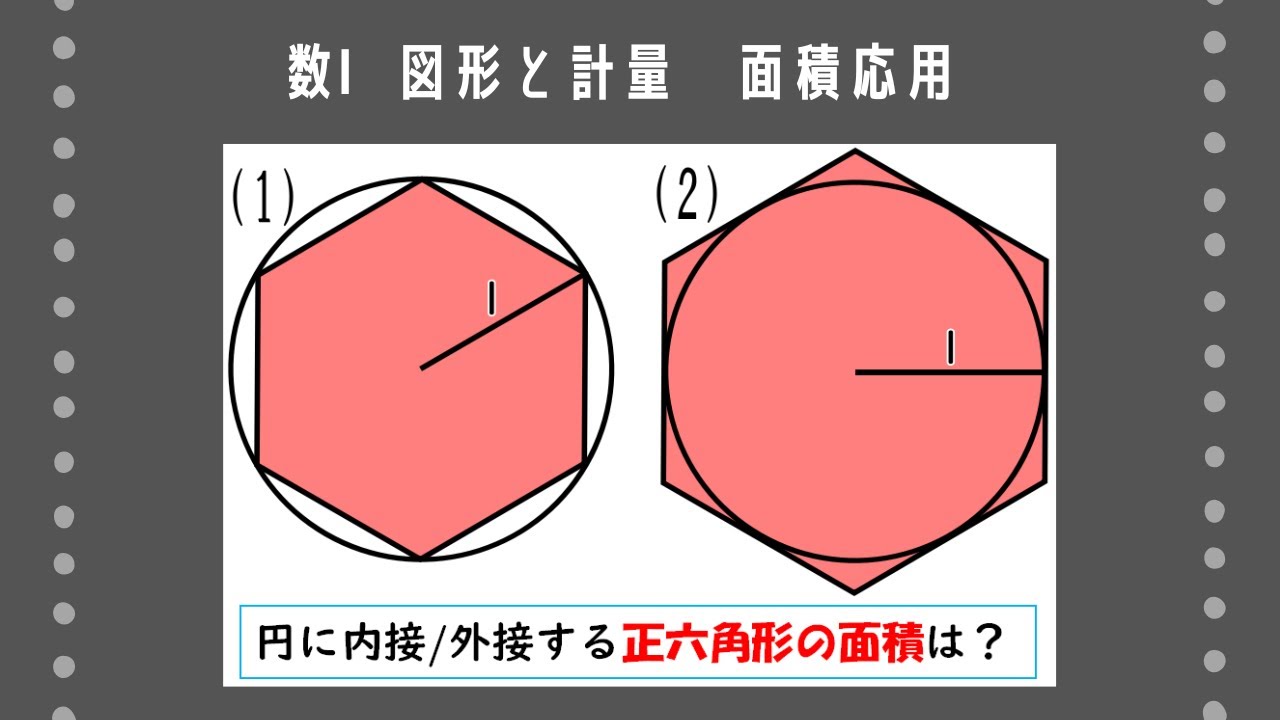
(1)半径1の円に内接する正六角形の面積を求めよ。
(2)半径1の円に外接する正六角形の面積を求めよ。
この動画を見る
(1)半径1の円に内接する正六角形の面積を求めよ。
(2)半径1の円に外接する正六角形の面積を求めよ。
【数Ⅰ】【図形と計量】面積応用5 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
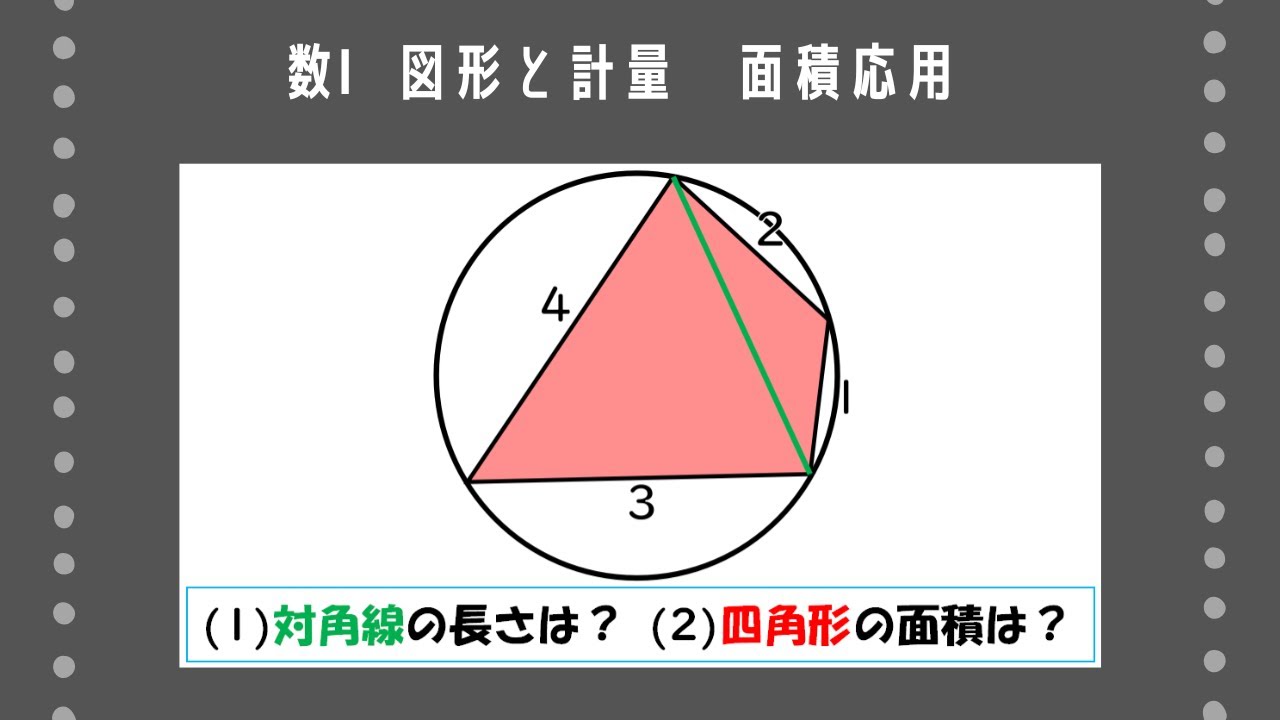
円に内接する四角形$\rm ABCD$において、$\rm AB=4,BC=3,CD=1,DA=2$とするとき、次のものを求めよ。
(1)対角線$\rm AC$の長さ
(2)四角形$\rm ABCD$の面積
この動画を見る
円に内接する四角形$\rm ABCD$において、$\rm AB=4,BC=3,CD=1,DA=2$とするとき、次のものを求めよ。
(1)対角線$\rm AC$の長さ
(2)四角形$\rm ABCD$の面積
【数Ⅰ】【図形と計量】面積応用4 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
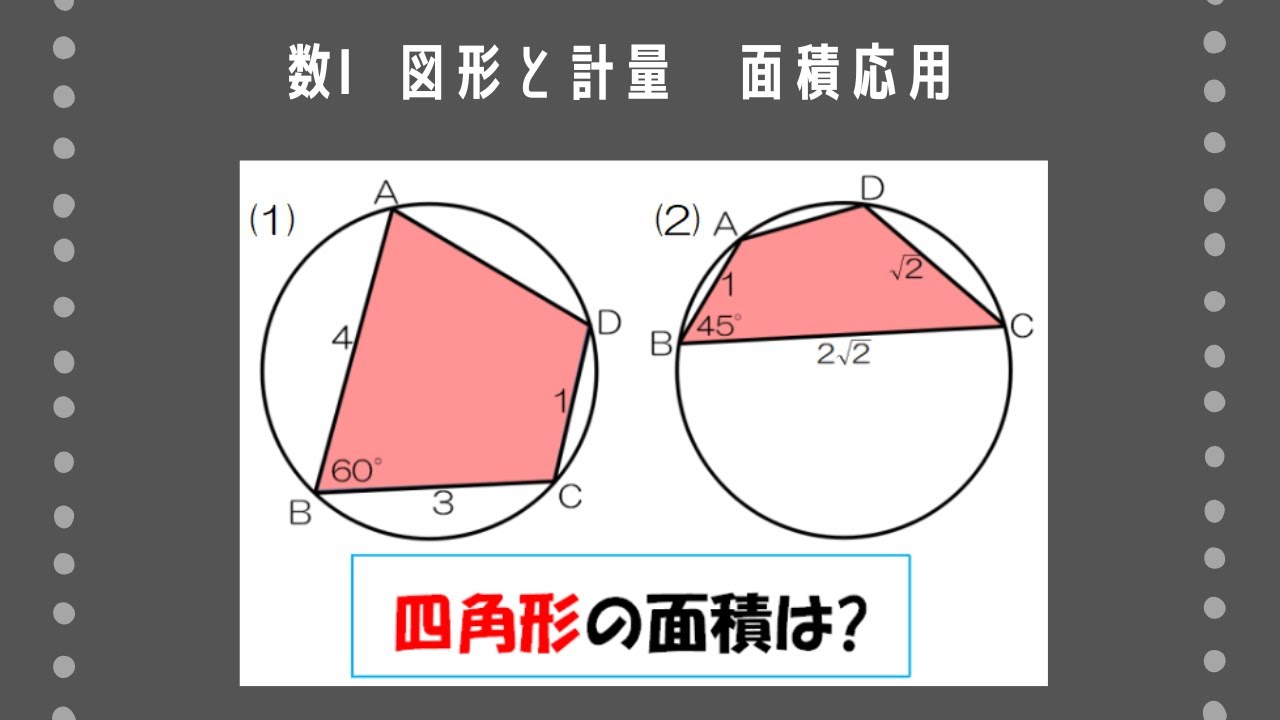
次のような四角形$\rm ABCD$の面積を求めよ。
(1)円に内接し、$\rm AB=4,BC=3,CD=1,\angle B=60^{\circ}$
(2)円に内接し、$\rm AB=1,BC=2\sqrt2,CD=\sqrt2,\angle B=45^{\circ}$
この動画を見る
次のような四角形$\rm ABCD$の面積を求めよ。
(1)円に内接し、$\rm AB=4,BC=3,CD=1,\angle B=60^{\circ}$
(2)円に内接し、$\rm AB=1,BC=2\sqrt2,CD=\sqrt2,\angle B=45^{\circ}$
【数Ⅰ】【図形と計量】面積応用1 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
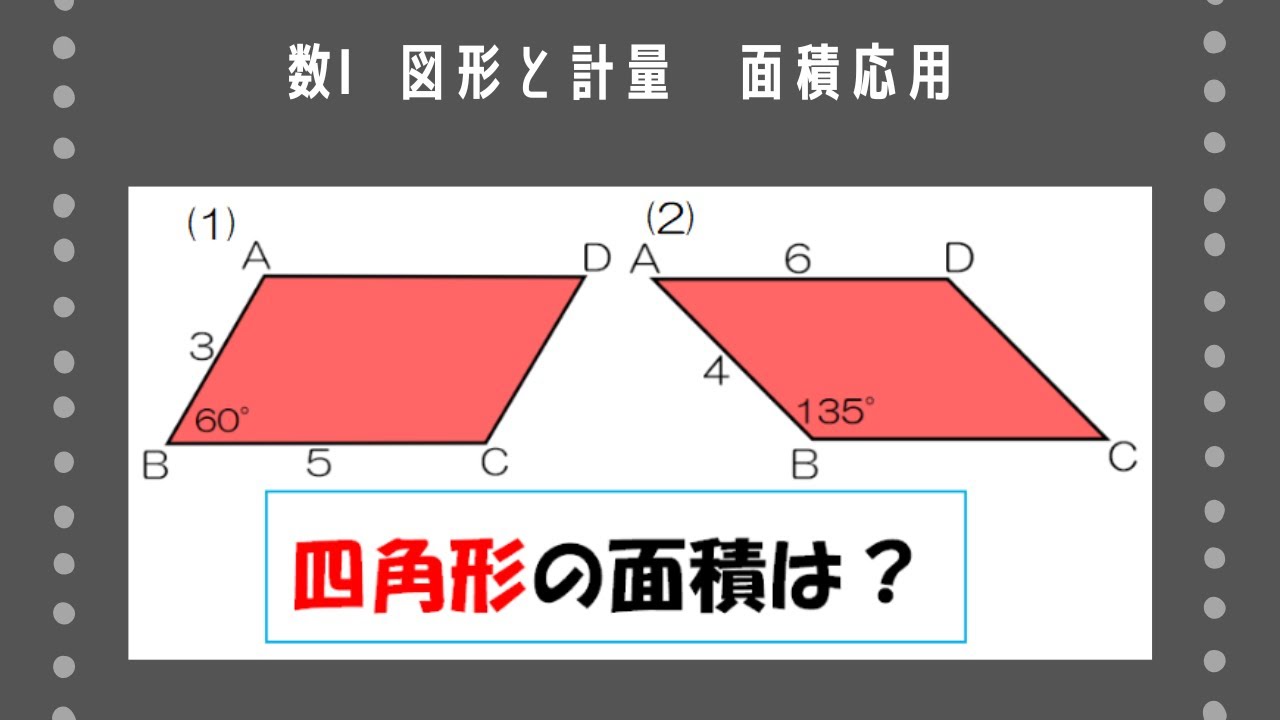
次のような平行四辺形ABCDの面積を求めよ。
(1)AB=3、BC=5、∠ABC=60°
(2)AB=4、AD=6、∠ABC=135°
この動画を見る
次のような平行四辺形ABCDの面積を求めよ。
(1)AB=3、BC=5、∠ABC=60°
(2)AB=4、AD=6、∠ABC=135°
【数Ⅰ】【図形と計量】正弦定理と余弦定理の応用3 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
図を利用して、sin105°とcos105°の値を求めよ。
この動画を見る
図を利用して、sin105°とcos105°の値を求めよ。
【数Ⅰ】【図形と計量】正弦定理と余弦定理の応用2 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
2地点P、Q間の距離を求めるために、1つの直線上にある3地点A、B、Cをとったら、AB=400m、BC=$100\sqrt{3}$m、∠QAB=30°、∠PBA=∠QBC=75°、∠PCB=45°であった。P、Q間の距離を求めよ。
この動画を見る
2地点P、Q間の距離を求めるために、1つの直線上にある3地点A、B、Cをとったら、AB=400m、BC=$100\sqrt{3}$m、∠QAB=30°、∠PBA=∠QBC=75°、∠PCB=45°であった。P、Q間の距離を求めよ。
【数Ⅰ】【図形と計量】正弦定理と余弦定理の応用1 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
△ABCにおいて、辺BCの中点をM、辺BCを1:2に分ける点をDとする。a=6、b=5、c=7のとき、AM、ADの長さを求めよ。
この動画を見る
△ABCにおいて、辺BCの中点をM、辺BCを1:2に分ける点をDとする。a=6、b=5、c=7のとき、AM、ADの長さを求めよ。
【数C】【平面上のベクトル】ベクトルの成分5 ※問題文は概要欄
単元：
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材：
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$\vec{ a }=(3 ,1)$ ,$\vec{ b }=(1 ,2)$ のとし、$\vec{ c }=\vec{ a }+t\vec{ b }$ (tは実数)とする。
(1) $| \vec{ c } |=\sqrt{15}$ のとき、tの値を求めよ。
(2) $| \vec{ c } |$の最小値と、そのときのtの値を求めよ。
この動画を見る
$\vec{ a }=(3 ,1)$ ,$\vec{ b }=(1 ,2)$ のとし、$\vec{ c }=\vec{ a }+t\vec{ b }$ (tは実数)とする。
(1) $| \vec{ c } |=\sqrt{15}$ のとき、tの値を求めよ。
(2) $| \vec{ c } |$の最小値と、そのときのtの値を求めよ。
【数C】【平面上のベクトル】ベクトルの成分4 ※問題文は概要欄
単元：
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材：
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$\vec{ a }=(2 ,2)$ ,$\vec{ b }=(3 ,1)$ のとき､$\vec{ x }-\vec{ b }$ が $\vec{ a }$に平行で､
かつ $| \vec{ x }+\vec{ b } |=4$ となるような$\vec{ x }$ を成分表示せよ｡
この動画を見る
$\vec{ a }=(2 ,2)$ ,$\vec{ b }=(3 ,1)$ のとき､$\vec{ x }-\vec{ b }$ が $\vec{ a }$に平行で､
かつ $| \vec{ x }+\vec{ b } |=4$ となるような$\vec{ x }$ を成分表示せよ｡