数学・算数の楽しさを思い出した / Ken
数学・算数の楽しさを思い出した / Ken
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
高校の時に唯一好きだった教科の数学。 その延長で、大学は某大学の数学科に進学。
社会人になり、数学から離れていたが、仕事で数学に触れる機会があり、再度その面白さに魅了されました。
数学・算数の成績が上がるような動画や数学・算数が好きになるような動画配信をしています。
本職はエンジニア。
数学成績アップのための問題解説 ・面白い算数・数学の問題解説 ・入試問題の問題解説 ・高校数学・中学数学の解説を配信中！
難易度表記のあるレベルのわかりやすい動画内容が魅力。難関大学の過去問を中心に数学解説動画を展開中。
【Study With Me】一緒に勉強しよう！【BGMあり】(2023/10/21)
7を書く回数？どのように考えますか？【早稲田大学】【数学 入試問題】
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
1から$10^{5}$=100000までのすべての整数を、順に十進法で書いたとすると、
数字を全部で何回書いたことになるか？答えよ.
早稲田大過去問
この動画を見る
1から$10^{5}$=100000までのすべての整数を、順に十進法で書いたとすると、
数字を全部で何回書いたことになるか？答えよ.
早稲田大過去問
早稲田の恒等式！この形は〇〇したくなりますよね【早稲田大学】【数学 入試問題】
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#微分法と積分法#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
正の整数$m$,定数関数でない整式$P(x)$である.
$\displaystyle\int_{0}^{x} {P(t)}^m dt=P(x^3)-P(0)$
$P(x)$を求めよ.
早稲田大過去問
この動画を見る
正の整数$m$,定数関数でない整式$P(x)$である.
$\displaystyle\int_{0}^{x} {P(t)}^m dt=P(x^3)-P(0)$
$P(x)$を求めよ.
早稲田大過去問
早稲田の整数問題！標準的なレベルなのでいい練習になります【早稲田大学】【数学 入試問題】
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
次の条件を満たす正の整数の組(a,b,n)は？である。
ｎ≧2，bは素数,$a^{2}$=$b^{n}$+225
早稲田大過去問
この動画を見る
次の条件を満たす正の整数の組(a,b,n)は？である。
ｎ≧2，bは素数,$a^{2}$=$b^{n}$+225
早稲田大過去問
【算数練習】5 （”大人”は頭の体操） ”平均”
単元：
#算数(中学受験)#文章題#平均算・過不足算・差集め算・消去算
指導講師：
数学・算数の楽しさを思い出した / Ken算数・数学ちゃんねる
問題文全文(内容文)：
重さ275g、302g、280gの 3個のリンゴがあります。
1個平均何gか求めよ。
この動画を見る
重さ275g、302g、280gの 3個のリンゴがあります。
1個平均何gか求めよ。
整数問題！問題文でかなり範囲が絞られている！？さらに候補を絞り込もう！【一橋大学】【数学 入試問題】
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
nを2以上20以下の整数、kを1以上n-1以下の整数とする。
${}_{n+1} \mathrm{ C }_{k+1}$＝$2({}_n \mathrm{ C }_{k-1}＋{}_n \mathrm{ C }_{k＋1})$
が成り立つような整数の組(n,k)を求めよ。
一橋大過去問
この動画を見る
nを2以上20以下の整数、kを1以上n-1以下の整数とする。
${}_{n+1} \mathrm{ C }_{k+1}$＝$2({}_n \mathrm{ C }_{k-1}＋{}_n \mathrm{ C }_{k＋1})$
が成り立つような整数の組(n,k)を求めよ。
一橋大過去問
整数問題が苦手な人は要チェック！絶対に取りたい整数問題【関西医科大学】【数学 入試問題】
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
( 1) (a + 1)(a - 1)(b + 1)(b - 1) - 4ab を因数分解せよ。
( 2) (a + 1)(a - 1)(b + 1)(b - 1) = 4ab を満たす整数a,bの組で、 a < b の条件を満たすものは
？組あり、そのなかでa,bのどちらも正の整数となる組(a,b) は ？である 。
(2023年 関西医科大学)
この動画を見る
( 1) (a + 1)(a - 1)(b + 1)(b - 1) - 4ab を因数分解せよ。
( 2) (a + 1)(a - 1)(b + 1)(b - 1) = 4ab を満たす整数a,bの組で、 a < b の条件を満たすものは
？組あり、そのなかでa,bのどちらも正の整数となる組(a,b) は ？である 。
(2023年 関西医科大学)
【整数問題】考えられる候補は何パターンだろうか【慶應義塾大学】【数学 入試問題】
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$6a^{3}+11a^{2}b^{2}c+3ab^{3}c$=6270を満たす(a,b,c)の組をすべて求めよ。
ただし、a,b,cはそれぞれ2以上の整数とする。
慶應義塾大過去問
この動画を見る
$6a^{3}+11a^{2}b^{2}c+3ab^{3}c$=6270を満たす(a,b,c)の組をすべて求めよ。
ただし、a,b,cはそれぞれ2以上の整数とする。
慶應義塾大過去問
【ガチ良問】素数が絡んだ整数問題の難問です【数学】
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
pを素数,kを自然数とする。
$12p^{2}+12p+1=k^{2}$を満たすようなpの値を求めよ。
この動画を見る
pを素数,kを自然数とする。
$12p^{2}+12p+1=k^{2}$を満たすようなpの値を求めよ。
微分の超頻出の問題！どこで最大値を取るかしっかり考えよう【大阪大学】【数学 入試問題】
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#微分法と積分法#対数関数#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
正の実数a,xに対して,
y=$(\log_{\frac{1}{2}}x)^{3}$+$a(\log_{\sqrt{ 2 } } x)(\log_{4} x^{3})$とする。
(1)t=$\log_{ 2 } x$とするとき,yをa,tを用いて表せ。
(2)xが$\dfrac{1}{2}$≦x≦8の範囲を動くとき,yの最大値Mをaを用いて表せ。
大阪大過去問
この動画を見る
正の実数a,xに対して,
y=$(\log_{\frac{1}{2}}x)^{3}$+$a(\log_{\sqrt{ 2 } } x)(\log_{4} x^{3})$とする。
(1)t=$\log_{ 2 } x$とするとき,yをa,tを用いて表せ。
(2)xが$\dfrac{1}{2}$≦x≦8の範囲を動くとき,yの最大値Mをaを用いて表せ。
大阪大過去問
意外と差がつく？しっかりと取りたい問題です【大阪大学】【数学 入試問題】
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#三角関数#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
a,bを実数とする。θについての方程式$\cos 2θ=a\ sin θ+b$が実数解をもつような点(a,b)の存在範囲を座標平面上に図示せよ。
大阪大過去問
この動画を見る
a,bを実数とする。θについての方程式$\cos 2θ=a\ sin θ+b$が実数解をもつような点(a,b)の存在範囲を座標平面上に図示せよ。
大阪大過去問
【数Ⅲ】東大の文系の問題を微分で解いてみた【東京大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#微分とその応用#微分法#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
kを正の実数とし,二次方程式$x^{2}+x-k=0$の二つの実数解を、$\alpha,\beta$とする。
$kがk＞2$の範囲を動くとき,
$\displaystyle \frac{\alpha^{3}}{1-\beta}+\displaystyle \frac{\beta^{3}}{1-\alpha}$の最小値を求めよ。
東大過去問
この動画を見る
kを正の実数とし,二次方程式$x^{2}+x-k=0$の二つの実数解を、$\alpha,\beta$とする。
$kがk＞2$の範囲を動くとき,
$\displaystyle \frac{\alpha^{3}}{1-\beta}+\displaystyle \frac{\beta^{3}}{1-\alpha}$の最小値を求めよ。
東大過去問
【２通りで解説】微分禁止！問題文から「あれ」を使う匂いがぷんぷんします【東京大学】【数学 入試問題】
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
kを正の実数とし,二次方程式$x^{2}+x-k=0$の二つの実数解を、$\alpha,\beta$とする。
$kがk＞2$の範囲を動くとき,
$\displaystyle \frac{\alpha^{3}}{1-\beta}+\displaystyle \frac{\beta^{3}}{1-\alpha}$
の最小値を求めよ。
東大過去問
この動画を見る
kを正の実数とし,二次方程式$x^{2}+x-k=0$の二つの実数解を、$\alpha,\beta$とする。
$kがk＞2$の範囲を動くとき,
$\displaystyle \frac{\alpha^{3}}{1-\beta}+\displaystyle \frac{\beta^{3}}{1-\alpha}$
の最小値を求めよ。
東大過去問
【別解あり】2023年京大の三角関数！円に内接する多角形は頻出です【京都大学】【数学 入試問題】
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
(1)$\cos 2θと\cos 3θを\cos θ$の式として表せ。
(2)半径1の円に内接する正五角形の一辺の長さが1.15より大きいか否かを理由をつけて判定せよ。
京都大過去問
この動画を見る
(1)$\cos 2θと\cos 3θを\cos θ$の式として表せ。
(2)半径1の円に内接する正五角形の一辺の長さが1.15より大きいか否かを理由をつけて判定せよ。
京都大過去問
2023年京大の漸化式！典型的なパターンが詰まった問題です【京都大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
{${ a_n}$}は次の条件を満たしている。
${ a_1}=3$、${ a_n}=\displaystyle \frac{{ S_n}}{n}+(n-1)・2^{ｎ}(n=2,3,4…)$
ただし,${ S_n}={ a_1}+{ a_2}+･･･+{ a_n}$である。このとき、数列{${ a_n}$}の一般項を求めよ。
京都大過去問
この動画を見る
{${ a_n}$}は次の条件を満たしている。
${ a_1}=3$、${ a_n}=\displaystyle \frac{{ S_n}}{n}+(n-1)・2^{ｎ}(n=2,3,4…)$
ただし,${ S_n}={ a_1}+{ a_2}+･･･+{ a_n}$である。このとき、数列{${ a_n}$}の一般項を求めよ。
京都大過去問
2023年京大の解説！回転体の体積の難問です【京都大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
○を原点とするxyz空間において、点Pと点Qは次の3つの条件(a), (b), (c)を満たしている。
(a) 点Pはx軸上にある。
(b) 点Qはyz平面上にある。
(c) 線分OPと線分OQの長さの和は1である。
点Pと点Qが条件(a), (b), (c)を満たしながらくまなく動くとき、線分PQが通過してできる立体 の体積を求めよ。
京都大過去問
この動画を見る
○を原点とするxyz空間において、点Pと点Qは次の3つの条件(a), (b), (c)を満たしている。
(a) 点Pはx軸上にある。
(b) 点Qはyz平面上にある。
(c) 線分OPと線分OQの長さの和は1である。
点Pと点Qが条件(a), (b), (c)を満たしながらくまなく動くとき、線分PQが通過してできる立体 の体積を求めよ。
京都大過去問
【高校数学】気持ちいい計算問題！ずばずば消えて残るのはたったのこれだけ！？ #Shorts
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$\displaystyle \frac{\sqrt{2}-\sqrt{1}}{\sqrt[4]{2}+\sqrt[4]{1}}$+$\displaystyle \frac{\sqrt{3}-\sqrt{2}}{\sqrt[4]{3}+\sqrt[4]{2}}$+･･････+$\displaystyle \frac{\sqrt{20}-\sqrt{19}}{\sqrt[4]{20}+\sqrt[4]{19}}$
気持ちよい計算問題です。
この動画を見る
$\displaystyle \frac{\sqrt{2}-\sqrt{1}}{\sqrt[4]{2}+\sqrt[4]{1}}$+$\displaystyle \frac{\sqrt{3}-\sqrt{2}}{\sqrt[4]{3}+\sqrt[4]{2}}$+･･････+$\displaystyle \frac{\sqrt{20}-\sqrt{19}}{\sqrt[4]{20}+\sqrt[4]{19}}$
気持ちよい計算問題です。
【算数】良問！この面積求めることできる？【中学受験】
単元：
#算数(中学受験)#平面図形#角度と面積
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
四角形ABCDは長方形である。
このとき、四角形AFCEの面積を求めよ。
この動画を見る
四角形ABCDは長方形である。
このとき、四角形AFCEの面積を求めよ。
きょ、京大！？絶対に落としてはいけない2023年度の確率の問題【京都大学】【数学 入試問題】
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$n$を自然数とする。一個のさいころを$n$回投げ、出た目を順に$X_{1},X_{2}……,X_{n}$とし、$n$個の数の積$X_{1},X_{2}……,X_{n}$を$Y$とする。
(1)$Y$が5で割り切れる確率を求めよ。
京都大過去問
この動画を見る
$n$を自然数とする。一個のさいころを$n$回投げ、出た目を順に$X_{1},X_{2}……,X_{n}$とし、$n$個の数の積$X_{1},X_{2}……,X_{n}$を$Y$とする。
(1)$Y$が5で割り切れる確率を求めよ。
京都大過去問
なんでこれが正解になるの？２乗の計算のテクニック #Shorts #裏技
単元：
#その他#その他#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
次の解を求めよ。
(1)$988^{2}$
(2)$993^{2}$
(3)$9991^{2}$
この動画を見る
次の解を求めよ。
(1)$988^{2}$
(2)$993^{2}$
(3)$9991^{2}$
場合分けは何パターン？多くの絶対値を含んだ問題【京都大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
nは整数
｜n-1｜+｜n-2｜+...+｜n-100｜の最小値を求めよ
京都大学1961年過去問
この動画を見る
nは整数
｜n-1｜+｜n-2｜+...+｜n-100｜の最小値を求めよ
京都大学1961年過去問
場合分けは何パターン？多くの絶対値を含んだ問題【京都大学】【数学 入試問題】
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$n$が整数であるとき$S=\vert n-1 \vert+\vert n-2 \vert+……+\vert n-100 \vert$の最小値を求めよ。
また、そのときの$n$の値を求めよ。
京都大学1961年過去問
この動画を見る
$n$が整数であるとき$S=\vert n-1 \vert+\vert n-2 \vert+……+\vert n-100 \vert$の最小値を求めよ。
また、そのときの$n$の値を求めよ。
京都大学1961年過去問
【裏技】２乗の計算！一瞬で求める方法（100より小さい数） #Shorts
2023年京大の空間ベクトル！ベクトルが苦手な人も絶対に取りたい問題【京都大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数C
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
空間内の4点$O、A、B、C$は同一平面上にないとする。点$D,P,O$を次のように定める。
点$D$は$\overrightarrow{OD}=\overrightarrow{OA}+\overrightarrow{2OB}+\overrightarrow{3OC}$を満 たし、点Pは線分$OA$を1: 2に内分し、点Qは線分$OB$の中点である。
さらに、直線$OD$上の点$R$を $OC$が交点を持つように定める。
このとき、線分$OR$の長さと線分$RD$の長さの比$OR: RD$を求めよ。
2023京都大過去問
この動画を見る
空間内の4点$O、A、B、C$は同一平面上にないとする。点$D,P,O$を次のように定める。
点$D$は$\overrightarrow{OD}=\overrightarrow{OA}+\overrightarrow{2OB}+\overrightarrow{3OC}$を満 たし、点Pは線分$OA$を1: 2に内分し、点Qは線分$OB$の中点である。
さらに、直線$OD$上の点$R$を $OC$が交点を持つように定める。
このとき、線分$OR$の長さと線分$RD$の長さの比$OR: RD$を求めよ。
2023京都大過去問
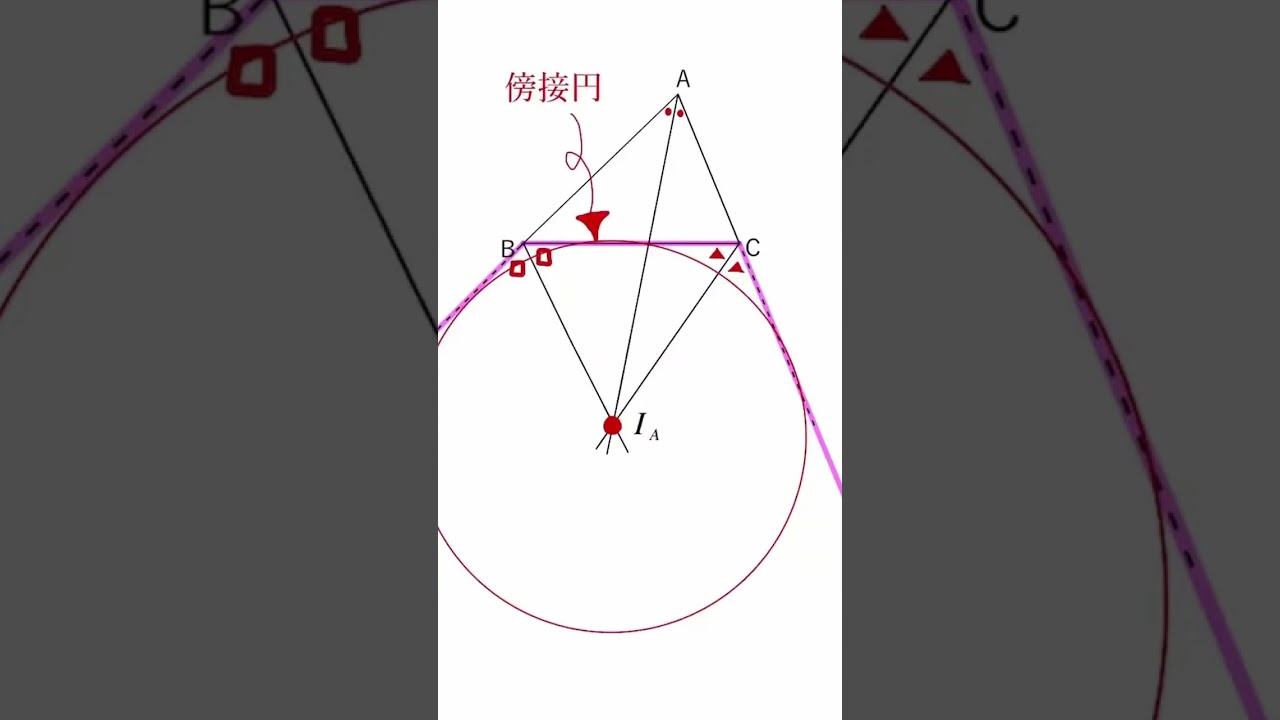
忘れがち！？三角形の傍心ってなに？ #Shorts
単元：
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
三角形の傍心に関して解説していきます。
この動画を見る
三角形の傍心に関して解説していきます。
2023年東工大の整数問題！86400！？大きい値をどう扱うか【東京工業大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$(x^3-x)^2(y^3-y)=86400$を満たす整数の組(x,y)を求めよ
東工大過去問
この動画を見る
$(x^3-x)^2(y^3-y)=86400$を満たす整数の組(x,y)を求めよ
東工大過去問
2023年東工大の整数問題！86400！？大きい値をどう扱うか【東京工業大学】【数学 入試問題】
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
方程式 $(x^{3}-x)^{2}(y^{3}-y)$=86400
を満たす整数の組$(x,y)$をすべて求めよ。
この動画を見る
方程式 $(x^{3}-x)^{2}(y^{3}-y)$=86400
を満たす整数の組$(x,y)$をすべて求めよ。
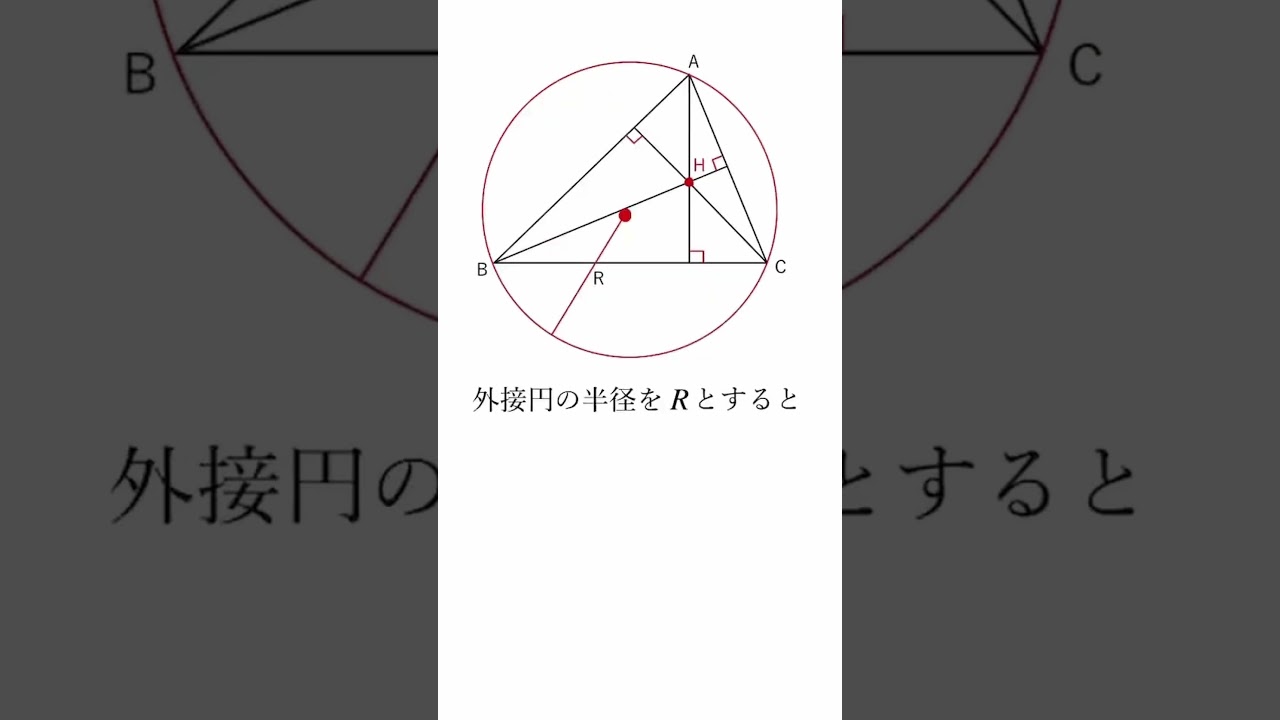
【まとめ】三角形の垂心の特徴をまとめてみた！ #Shorts
単元：
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
三角形の垂心の特徴について解説していきます。
この動画を見る
三角形の垂心の特徴について解説していきます。
【積分】2023年京大数学！絶対に落としてはいけない問題です【京都大学】【数学 入試問題】
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
定積分 $\displaystyle \int_{1}^{4}\sqrt{x}\log(x^{2})dx$の値を求めよ。
京都大過去問
この動画を見る
定積分 $\displaystyle \int_{1}^{4}\sqrt{x}\log(x^{2})dx$の値を求めよ。
京都大過去問
【重要】頻出の三角形の内心の特徴をまとめてみた #Shorts
単元：
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
三角形の内心に関して解説していきます。
この動画を見る
三角形の内心に関して解説していきます。