ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
大学入試問題をベースに数学の動画を作成しています。大学過去問を多数解説しています。
頻繁に更新していますので是非ご視聴ください！
職業：数学者
職歴：高校非常勤（院生時代）、高専、大学 准教授
趣味：
①将棋 棋力は将棋ウォーズ４段、将棋倶楽部２４はR２０００前後（小学校５，６年のころに頑張ってました）
②麻雀 アカウントは消えましたが、無課金で天鵬で７段まで上がりました。
③ソフトテニス 中学から大学まで、１０年間部活でやっていました。大学時代は４年になってもリーグにでていました。
#宮崎大学(2016)
単元：
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
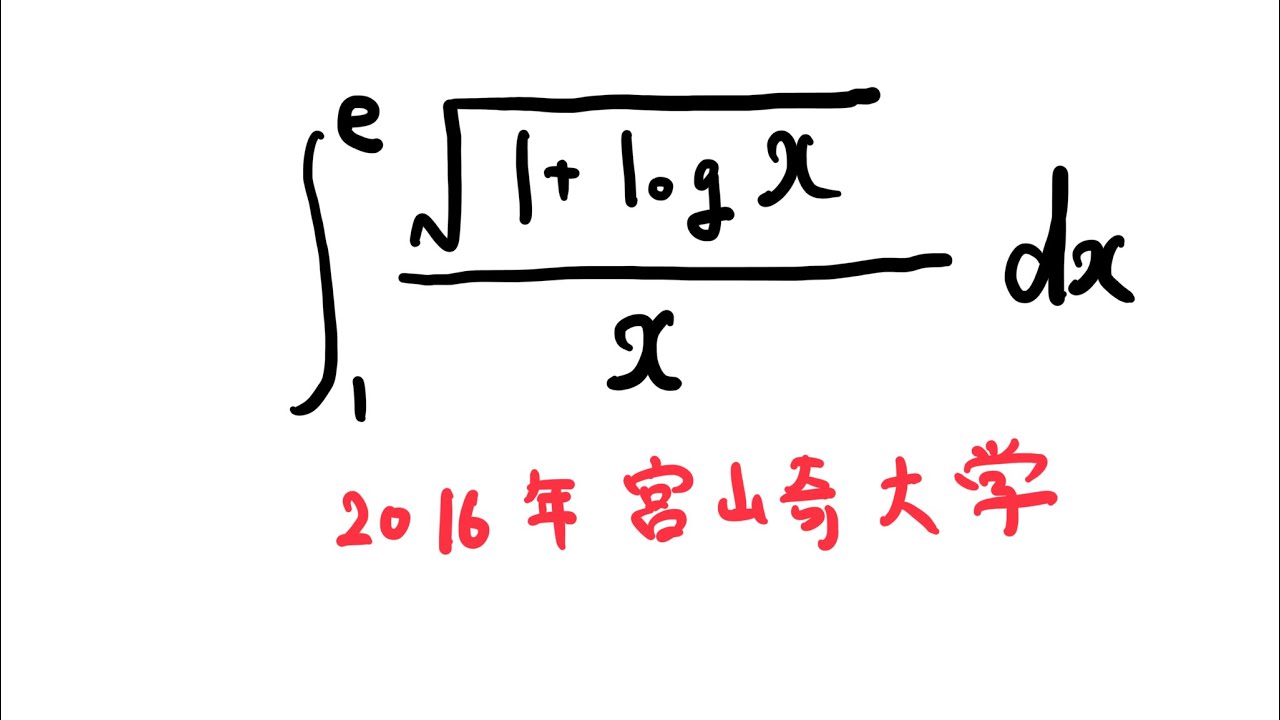
$\displaystyle \int_{1}^{e} \displaystyle \frac{\sqrt{ 1+log\ x }}{x} dx$
出典：2016年宮崎大学
この動画を見る
$\displaystyle \int_{1}^{e} \displaystyle \frac{\sqrt{ 1+log\ x }}{x} dx$
出典：2016年宮崎大学
#電気通信大学(2013) #極限 #Shorts
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to 1 } \displaystyle \frac{3^{1-x}-1}{x-1}$
出典：2013年電気通信大学
この動画を見る
$\displaystyle \lim_{ x \to 1 } \displaystyle \frac{3^{1-x}-1}{x-1}$
出典：2013年電気通信大学
大学入試問題#836「このタイプの問題ばかり探していますw」 #長崎大学(2024) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#長崎大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-1}^{1} \displaystyle \frac{x^2-x^4}{1+e^x}dx$
出典：2024年長崎大学
この動画を見る
$\displaystyle \int_{-1}^{1} \displaystyle \frac{x^2-x^4}{1+e^x}dx$
出典：2024年長崎大学
#電気通信大学(2014) #定積分 #Shorts
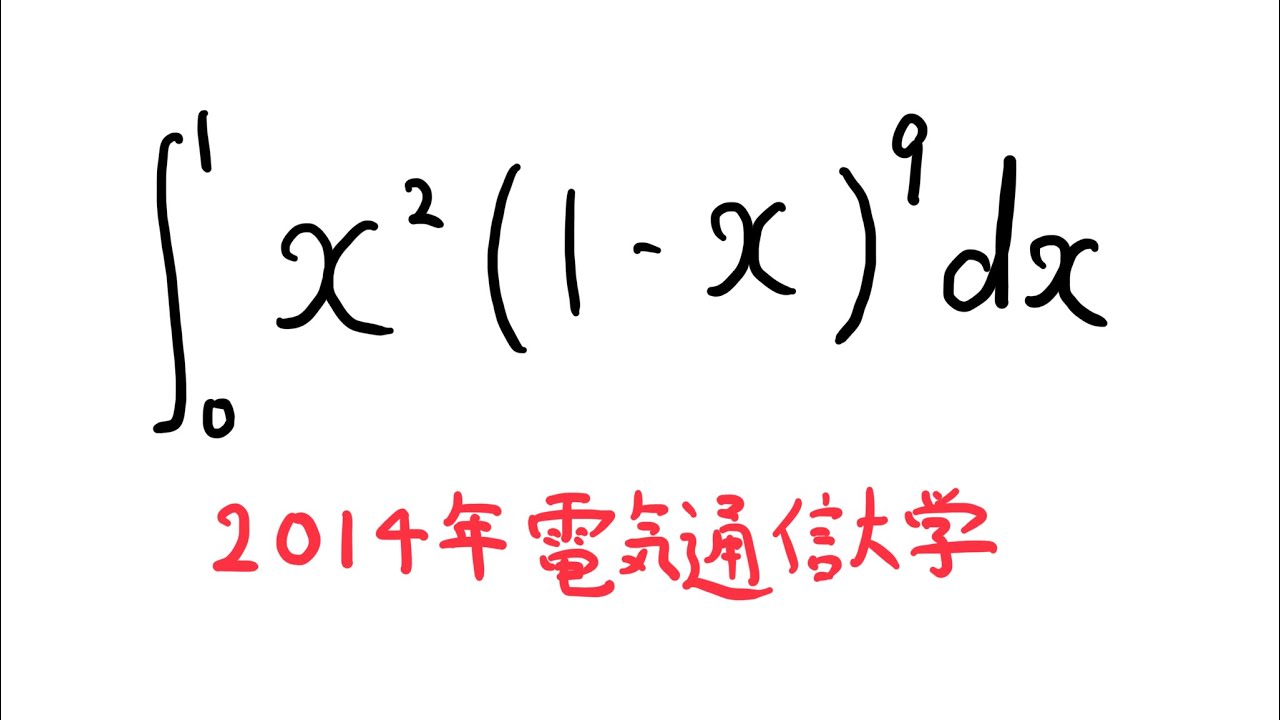
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} x^2(1-x)^9 \ dx$
出典：2014年電気通信大学
この動画を見る
$\displaystyle \int_{0}^{1} x^2(1-x)^9 \ dx$
出典：2014年電気通信大学
#宮崎大学(2023) #不定積分 #Shorts
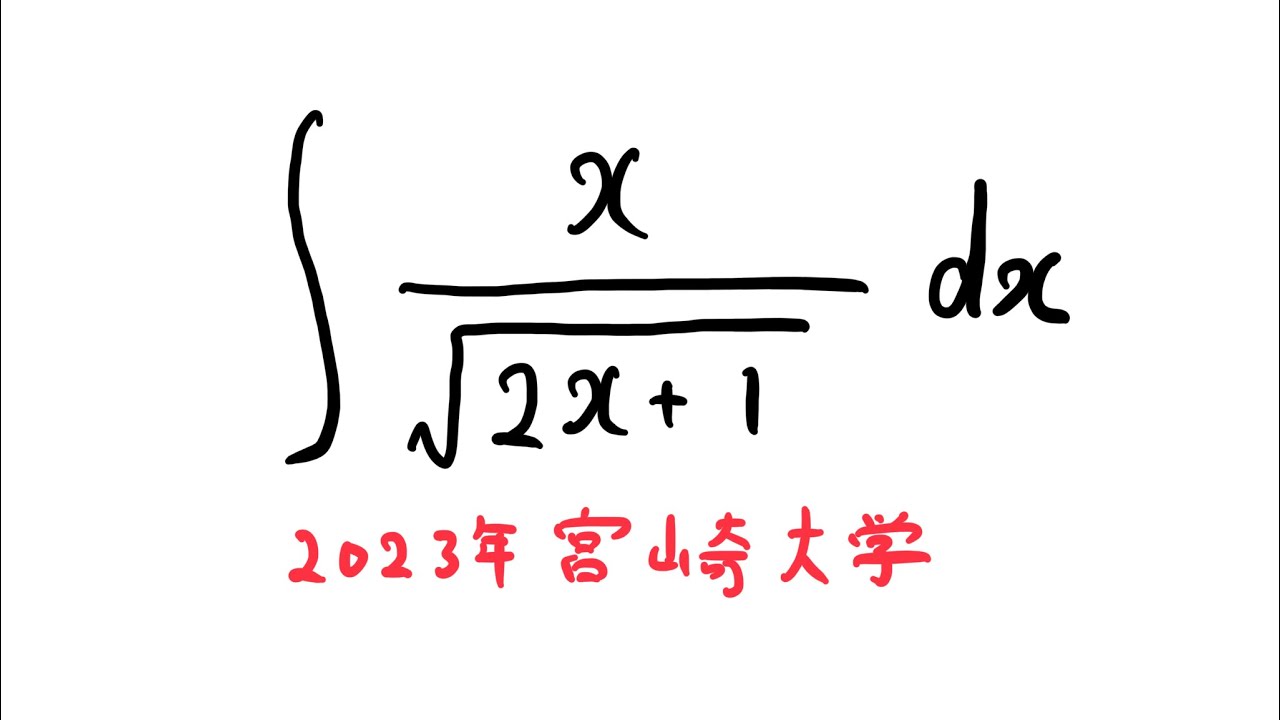
単元：
#大学入試過去問(数学)#宮崎大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ 2x+1 }}dx$
出典：2023年宮崎大学
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ 2x+1 }}dx$
出典：2023年宮崎大学
大学入試問題#835「初見は厳しいかも」 #岩手大学(2014) #級数
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#岩手大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \sum_{n=1}^\infty \displaystyle \frac{1}{(n+2)(n+3)(n+4)}$
出典：2014年岩手大学 入試問題
この動画を見る
$\displaystyle \sum_{n=1}^\infty \displaystyle \frac{1}{(n+2)(n+3)(n+4)}$
出典：2014年岩手大学 入試問題
#電気通信大学(2017) #区分求積法 #Shorts
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師：
ますただ
問題文全文(内容文)：
以下の区分求積法を解け
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{k}{4n^2-3k^2}$
出典：2017年電気通信大学
この動画を見る
以下の区分求積法を解け
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{k}{4n^2-3k^2}$
出典：2017年電気通信大学
大学入試問題#833「計算力大事！」 #筑波大学(2023) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学
指導講師：
ますただ
問題文全文(内容文)：
関数$f(x)$の導関数$g(x)$は定数$k( \neq 0)$を用いて次式で与えられる。
$g(x)=\displaystyle \frac{e^{kx}-e^{kx}}{2}$
次の問いに答えよ。
１．$f(0)=0$であるとき$f(x)$を求めよ。
２．$p$は定数とする。
$\displaystyle \int_{0}^{p} \displaystyle \frac{1}{\sqrt{ 1+\{g(x)\} }}g'(x) \ dx$を求めよ
出典：2023年筑波大学 入試問題
この動画を見る
関数$f(x)$の導関数$g(x)$は定数$k( \neq 0)$を用いて次式で与えられる。
$g(x)=\displaystyle \frac{e^{kx}-e^{kx}}{2}$
次の問いに答えよ。
１．$f(0)=0$であるとき$f(x)$を求めよ。
２．$p$は定数とする。
$\displaystyle \int_{0}^{p} \displaystyle \frac{1}{\sqrt{ 1+\{g(x)\} }}g'(x) \ dx$を求めよ
出典：2023年筑波大学 入試問題
#岩手大学(2013) #不定積分 #Shorts
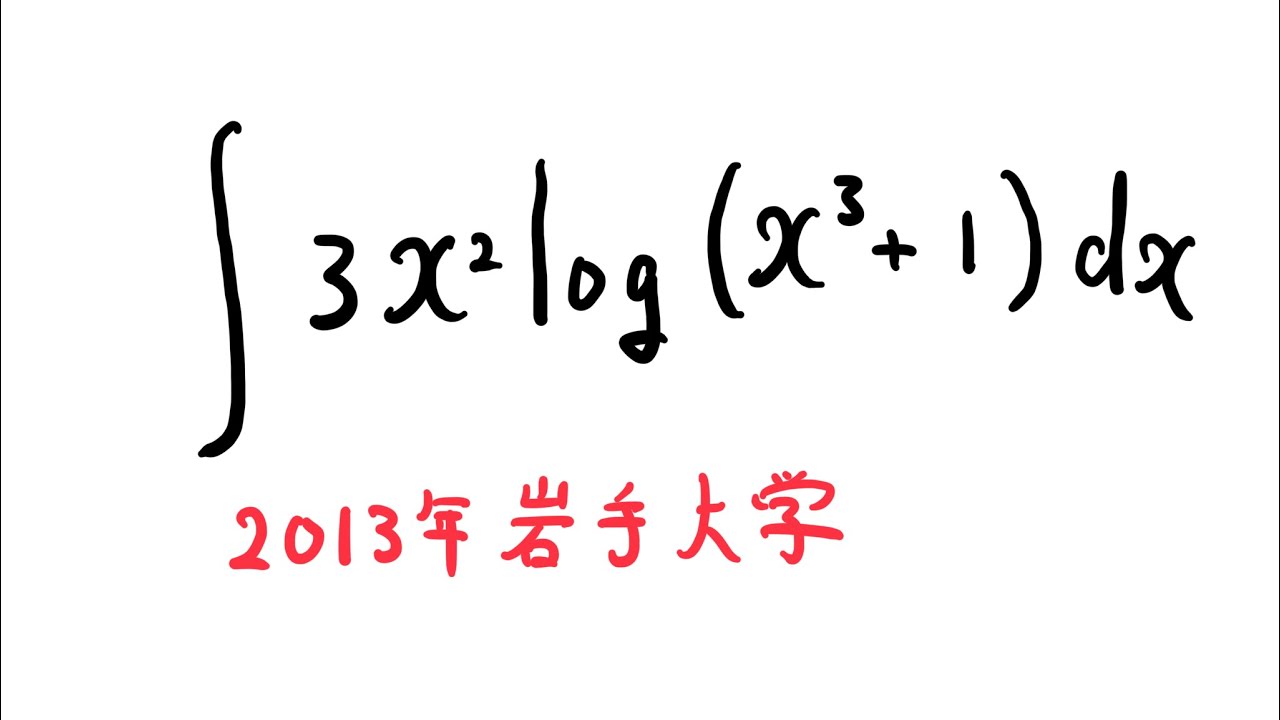
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#岩手大学#大阪市立大学
指導講師：
ますただ
問題文全文(内容文)：
以下の不定積分を解け。
$\displaystyle \int 3x^2 log(x^3+1)dx$
出典：2013年岩手大学
この動画を見る
以下の不定積分を解け。
$\displaystyle \int 3x^2 log(x^3+1)dx$
出典：2013年岩手大学
#電気通信大学(2023) #不定積分 #Shorts
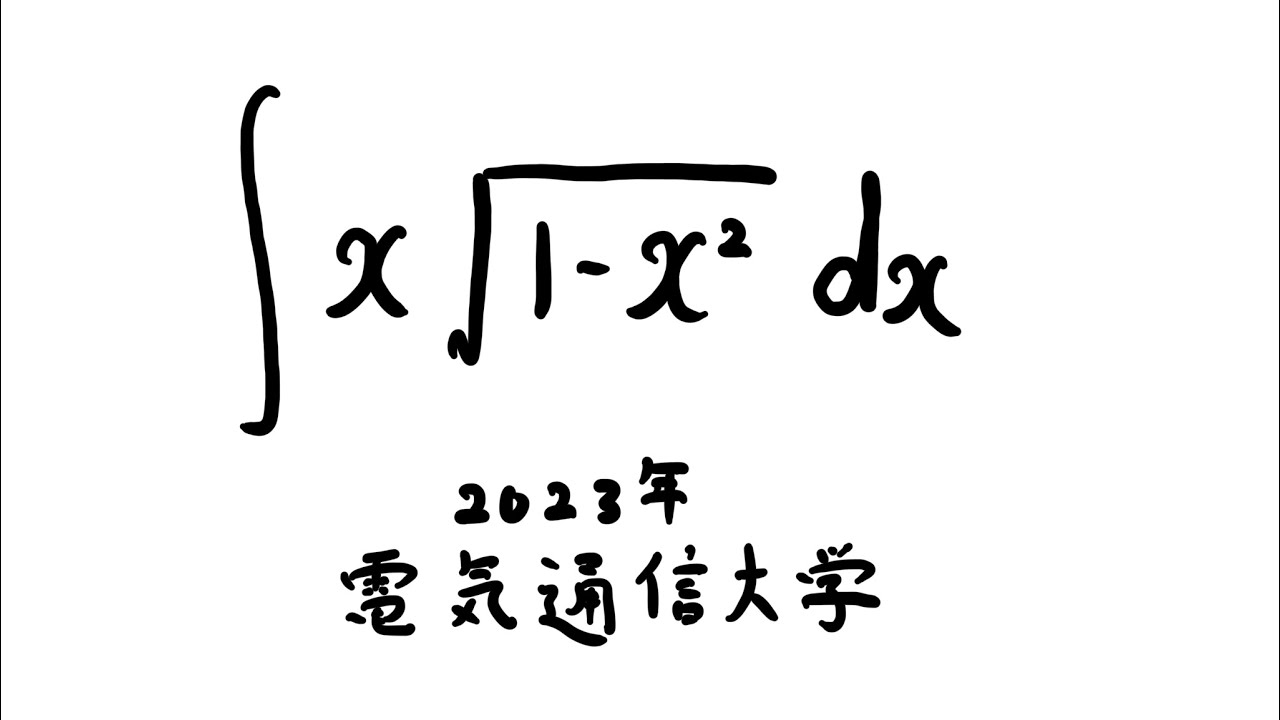
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
以下の不定積分を解け。
$\displaystyle \int x\sqrt{ 1-x^2 } \ dx$
出典：2023年電気通信大学
この動画を見る
以下の不定積分を解け。
$\displaystyle \int x\sqrt{ 1-x^2 } \ dx$
出典：2023年電気通信大学
大学入試問題#834「置換一択！？」 #弘前大学(2022) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学
指導講師：
ますただ
問題文全文(内容文)：
以下の定積分を解け。
$\displaystyle \int_{\sqrt{ 3 }}^{2} (3x-1)\sqrt{ 4-x^2 }\ dx$
出典：2022年広前大学 入試問題
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{\sqrt{ 3 }}^{2} (3x-1)\sqrt{ 4-x^2 }\ dx$
出典：2022年広前大学 入試問題
#電気通信大学(2023) #定積分 #Shorts
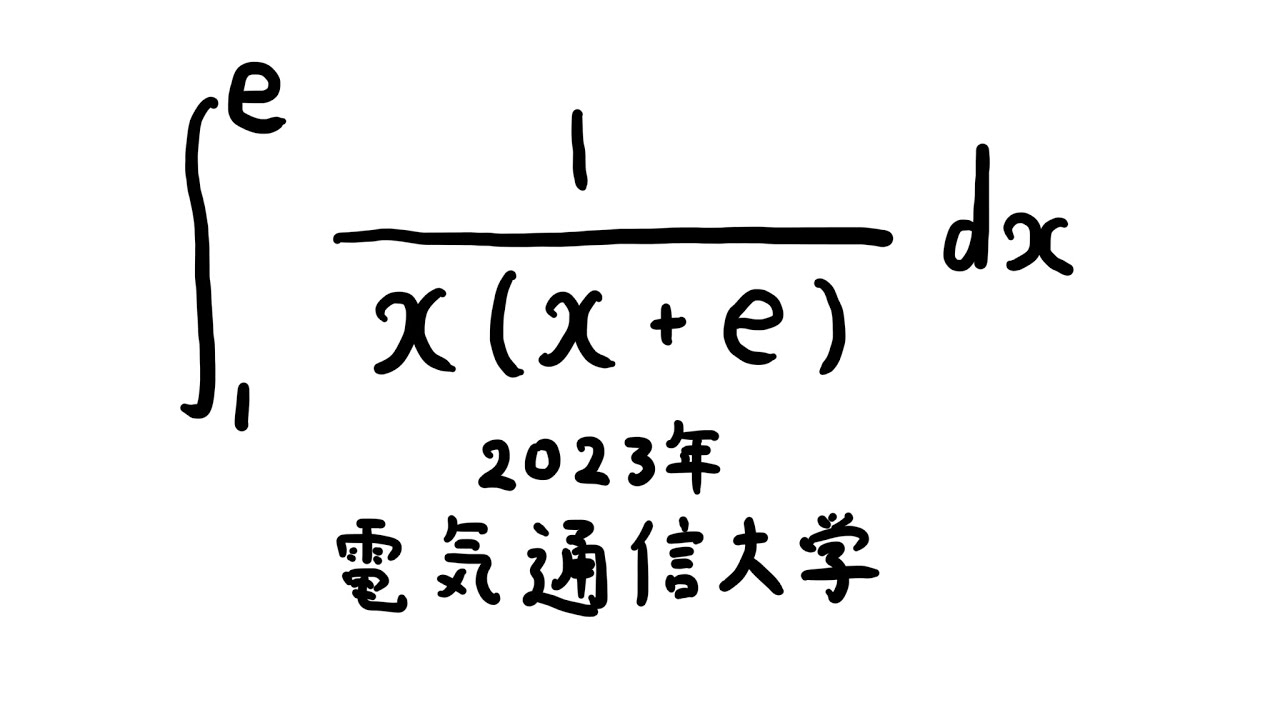
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
以下の定積分を解け。
$\displaystyle \int_{1}^{e} \displaystyle \frac{1}{x(x+e)} dx$
出典：2023年電気通信大学
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{1}^{e} \displaystyle \frac{1}{x(x+e)} dx$
出典：2023年電気通信大学
#筑波大学(1996) #極限 #Shorts
単元：
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to \infty } (\sqrt{ x^2+x+1 }-x)$
出典：1996年筑波大学
この動画を見る
$\displaystyle \lim_{ x \to \infty } (\sqrt{ x^2+x+1 }-x)$
出典：1996年筑波大学
大学入試問題#832「これは落としたくない」 #岩手大学(2011) #極限
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#岩手大学
指導講師：
ますただ
問題文全文(内容文)：
関数$f(x)=\displaystyle \int_{0}^{x} \displaystyle \frac{6}{t^2+7t+10} dt$について$\displaystyle \lim_{ x \to \infty } f(x)$を求めよ。
出典：2011年岩手大学
この動画を見る
関数$f(x)=\displaystyle \int_{0}^{x} \displaystyle \frac{6}{t^2+7t+10} dt$について$\displaystyle \lim_{ x \to \infty } f(x)$を求めよ。
出典：2011年岩手大学
#電気通信大学(2023) #不定積分 #Shorts
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
以下の不定積分を解け。
$\displaystyle \int \displaystyle \frac{x^3}{\sqrt{ 1-x^2 }} dx$
出典：2023年電気通信大学
この動画を見る
以下の不定積分を解け。
$\displaystyle \int \displaystyle \frac{x^3}{\sqrt{ 1-x^2 }} dx$
出典：2023年電気通信大学
大学入試問題#831「教科書の章末問題」 #山形大学(2010) #三角関数
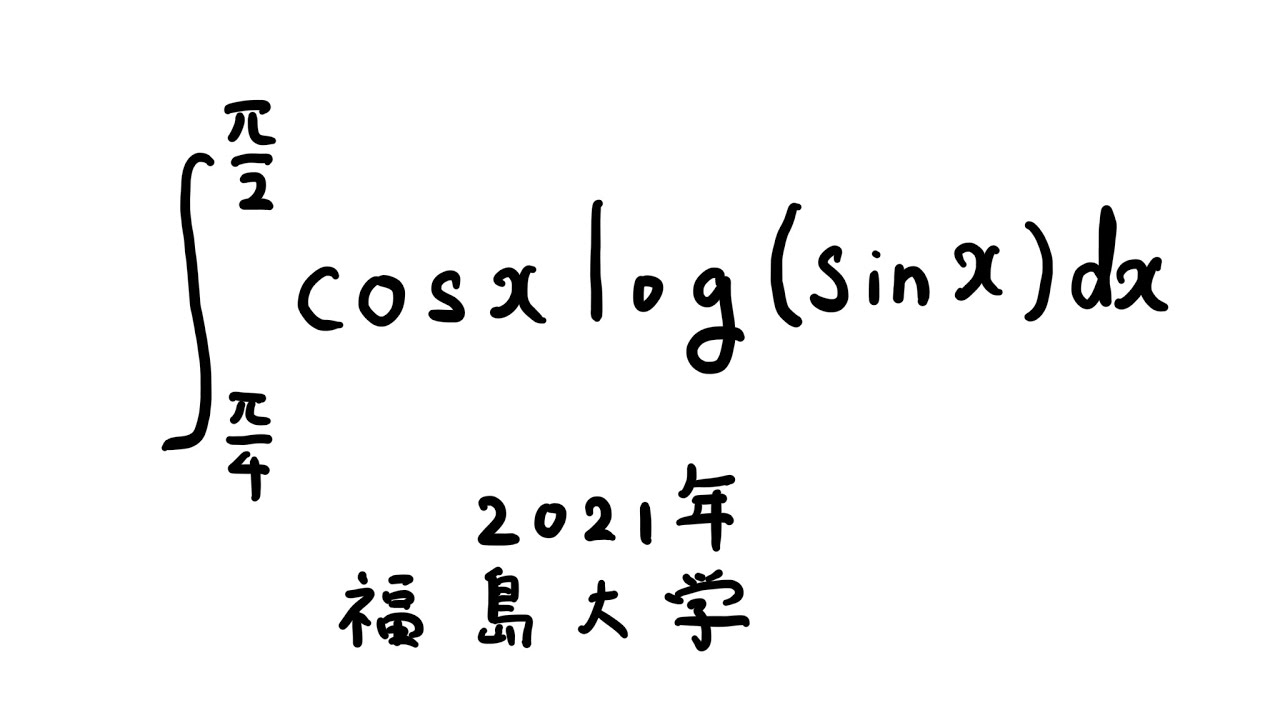
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#山形大学
指導講師：
ますただ
問題文全文(内容文)：
$\sin\displaystyle \frac{19}{12}\pi$の値を求めよ
出典：2010年山形大学
この動画を見る
$\sin\displaystyle \frac{19}{12}\pi$の値を求めよ
出典：2010年山形大学
#福島大学(2021) #定積分 #Shorts
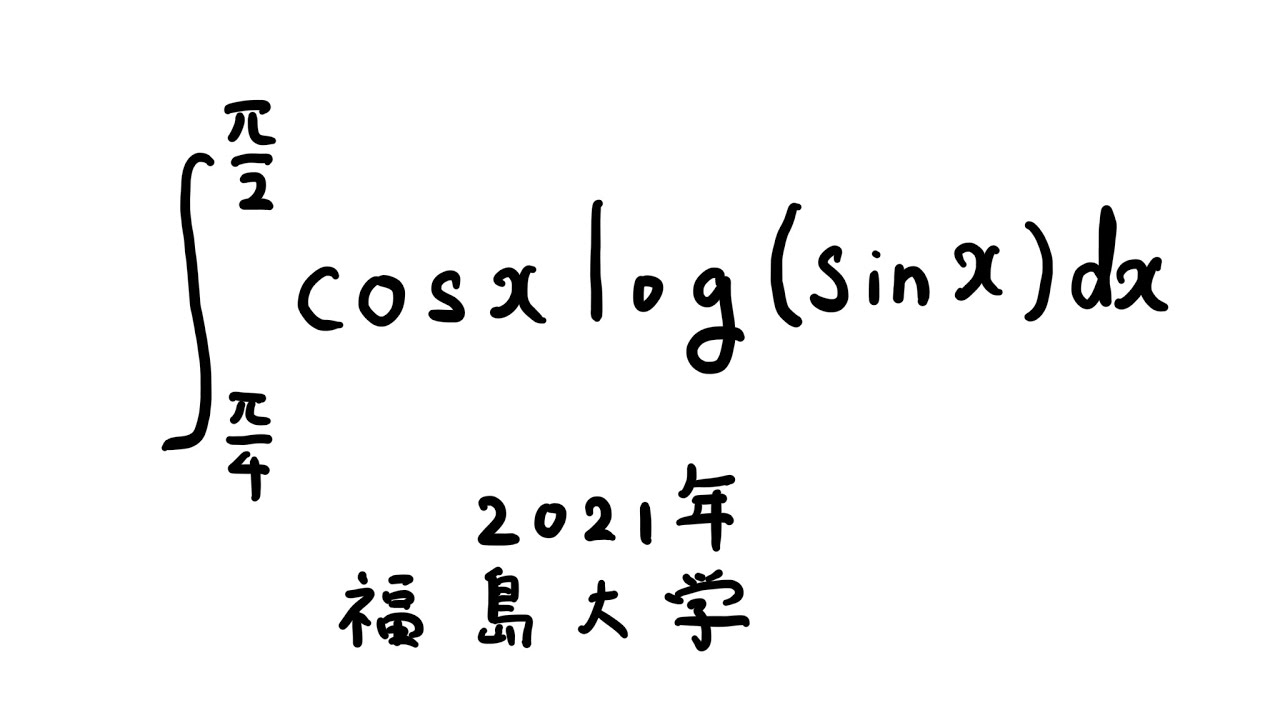
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#福島大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \cos\ x\ log(\sin\ x) dx$
出典：2021年福島大学
この動画を見る
$\displaystyle \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \cos\ x\ log(\sin\ x) dx$
出典：2021年福島大学
#岩手大学(2015) #定積分 #Shorts
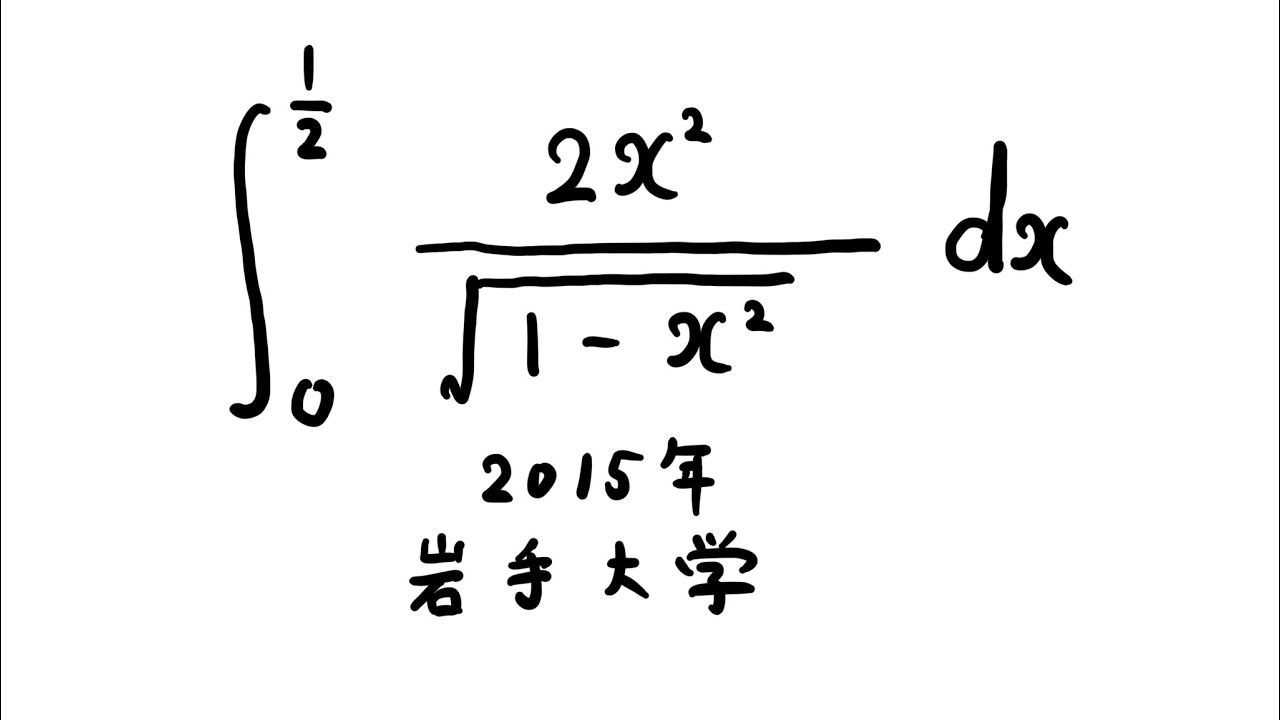
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#岩手大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{1}{2}} \displaystyle \frac{2x^2}{\sqrt{ 1-x^2 }} dx$
出典：2015年岩手大学
この動画を見る
$\displaystyle \int_{0}^{\frac{1}{2}} \displaystyle \frac{2x^2}{\sqrt{ 1-x^2 }} dx$
出典：2015年岩手大学
大学入試問題#830「たまには、こんな問題でも」 #筑波大学(2016) #極限
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\cos4x-2\cos\ 2x+1}{x^2}$
出典：2016年筑波大学
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\cos4x-2\cos\ 2x+1}{x^2}$
出典：2016年筑波大学
#上智大学(2005) #Shorts
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$f(x)=x^2+x+2\displaystyle \int_{0}^{1} f(t) dt$を満たす関数$f(x)$を求めよ
出典：2005年上智大学
この動画を見る
$f(x)=x^2+x+2\displaystyle \int_{0}^{1} f(t) dt$を満たす関数$f(x)$を求めよ
出典：2005年上智大学
#福島大学(2020) #不定積分 #Shorts
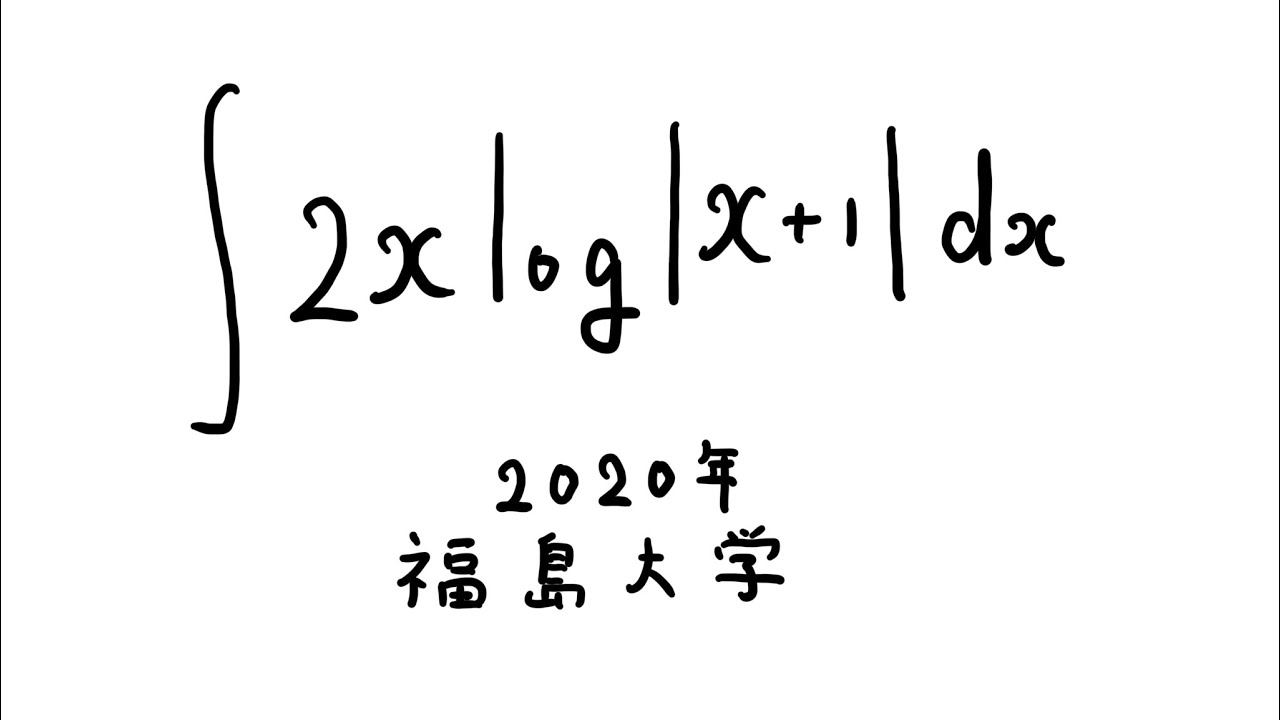
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int 2\ x\ log|x+1|dx$
出典：2020年福島大学
この動画を見る
$\displaystyle \int 2\ x\ log|x+1|dx$
出典：2020年福島大学
大学入試問題#829「綺麗な詰将棋！」 #筑波大学(2016) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} \displaystyle \frac{x-1}{x^3+1} dx$
出典：2016年筑波大学
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{x-1}{x^3+1} dx$
出典：2016年筑波大学
#立教大学(2010) #定積分 #Shorts
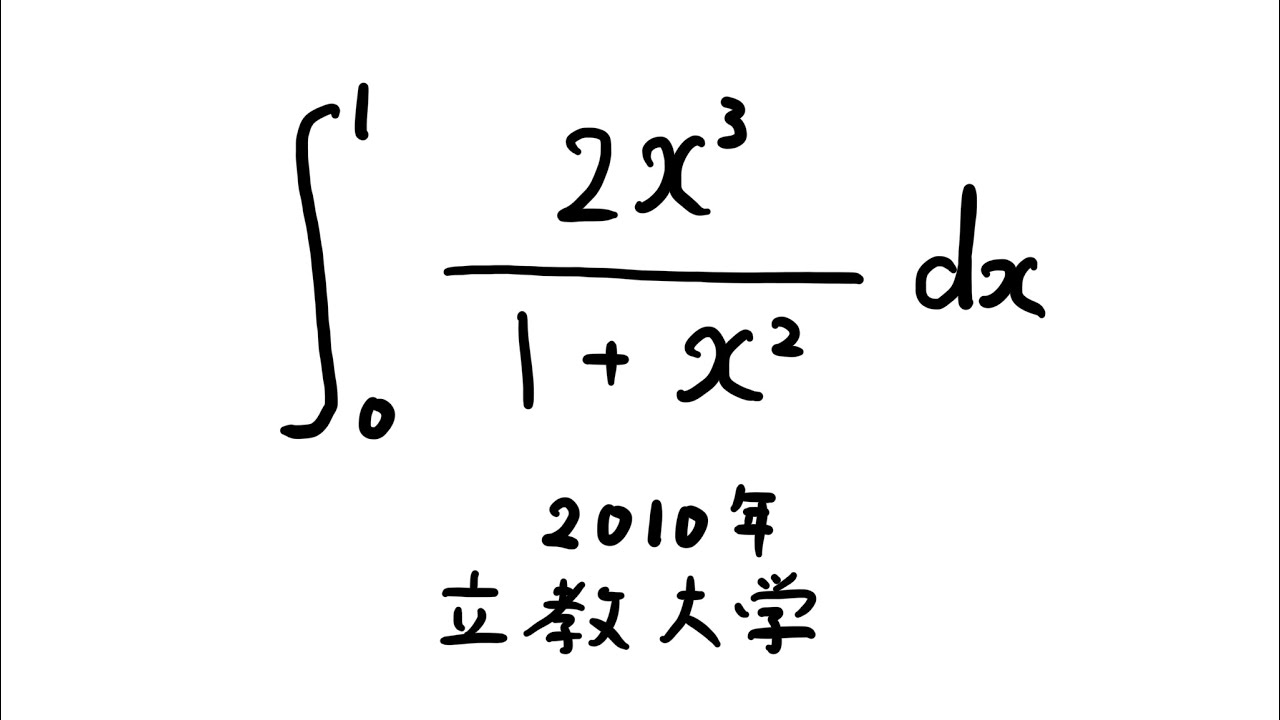
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} \displaystyle \frac{2x^3}{1+x^2} dx$
出典：2010年立教大学
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{2x^3}{1+x^2} dx$
出典：2010年立教大学
#岩手大学(2019) #定積分 #Shorts
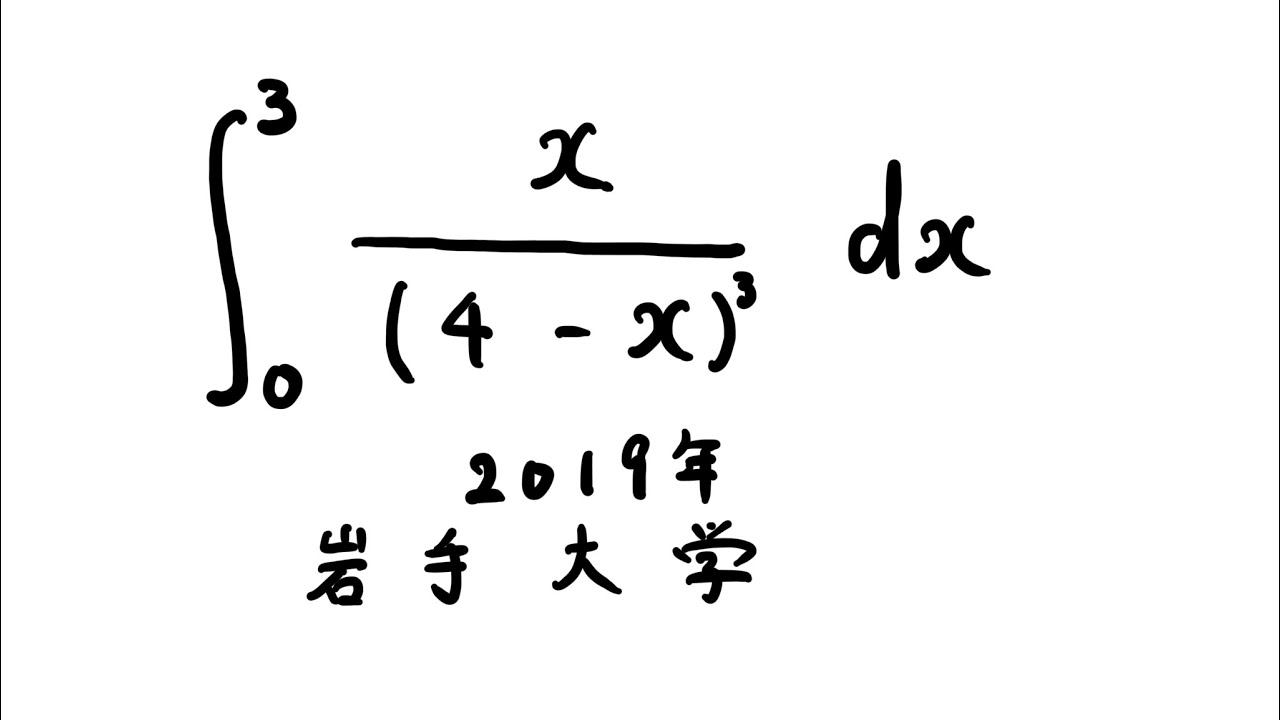
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#岩手大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{3} \displaystyle \frac{x}{(4-x)^3} dx$
出典：2019年岩手大学
この動画を見る
$\displaystyle \int_{0}^{3} \displaystyle \frac{x}{(4-x)^3} dx$
出典：2019年岩手大学
大学入試問題#828「式変形難しめの良問！」 #久留米大学医学部(2024) #数列
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#久留米大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \sum_{k=1}^n \displaystyle \frac{3k+5}{(3k-1)(3k+2)2^{k+1}}$
出典：2024年久留米大学医学部
この動画を見る
$\displaystyle \sum_{k=1}^n \displaystyle \frac{3k+5}{(3k-1)(3k+2)2^{k+1}}$
出典：2024年久留米大学医学部
#東京都市大学(2010) #不定積分 #Shorts
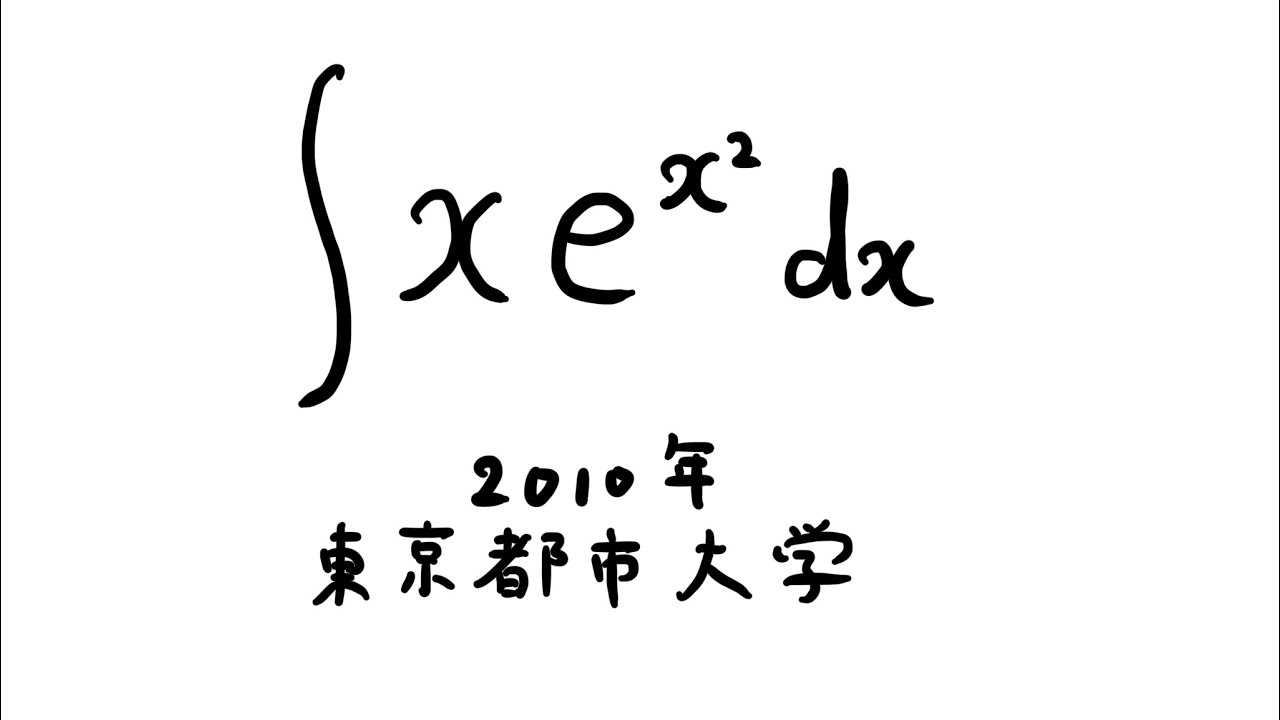
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int xe^{x^2} dx$
出典：2010年東京都市大学
この動画を見る
$\displaystyle \int xe^{x^2} dx$
出典：2010年東京都市大学
#岩手大学(2019) #極限 #Shorts
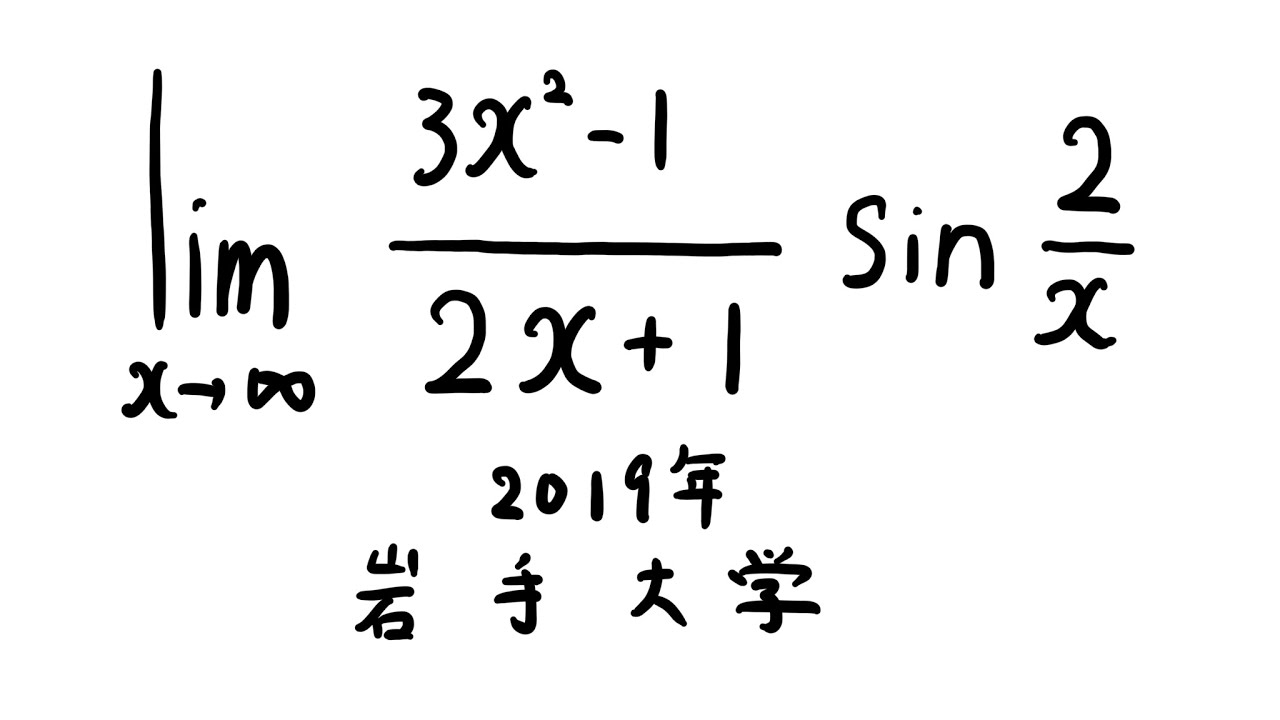
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#岩手大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{3x^2-1}{2x+1}\sin\displaystyle \frac{2}{x}$
出典：2019年岩手大学
この動画を見る
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{3x^2-1}{2x+1}\sin\displaystyle \frac{2}{x}$
出典：2019年岩手大学
大学入試問題#827「とりま絶対値はずそ：0≦t≦π/2」 #筑波大学(2020) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{2}} |\sin\ x-\sin\ t\ |\ dx$
出典：2020年筑波大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} |\sin\ x-\sin\ t\ |\ dx$
出典：2020年筑波大学
#岩手大学(2018) #定積分 #Shorts
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#岩手大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{e} x^3log\ x\ dx$
出典：2018年岩手大学
この動画を見る
$\displaystyle \int_{1}^{e} x^3log\ x\ dx$
出典：2018年岩手大学
#筑波大学(2016) #定積分 #Shorts
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \tan^3x\ dx$
出典：2016年筑波大学
この動画を見る
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \tan^3x\ dx$
出典：2016年筑波大学