 めいちゃんねる
めいちゃんねる
 めいちゃんねる
めいちゃんねる
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
016計算問題の集まりは著作物になるか #shorts
単元:
#情報Ⅰ(高校生)#情報社会#知的財産権の扱い
指導講師:
めいちゃんねる
問題文全文(内容文):
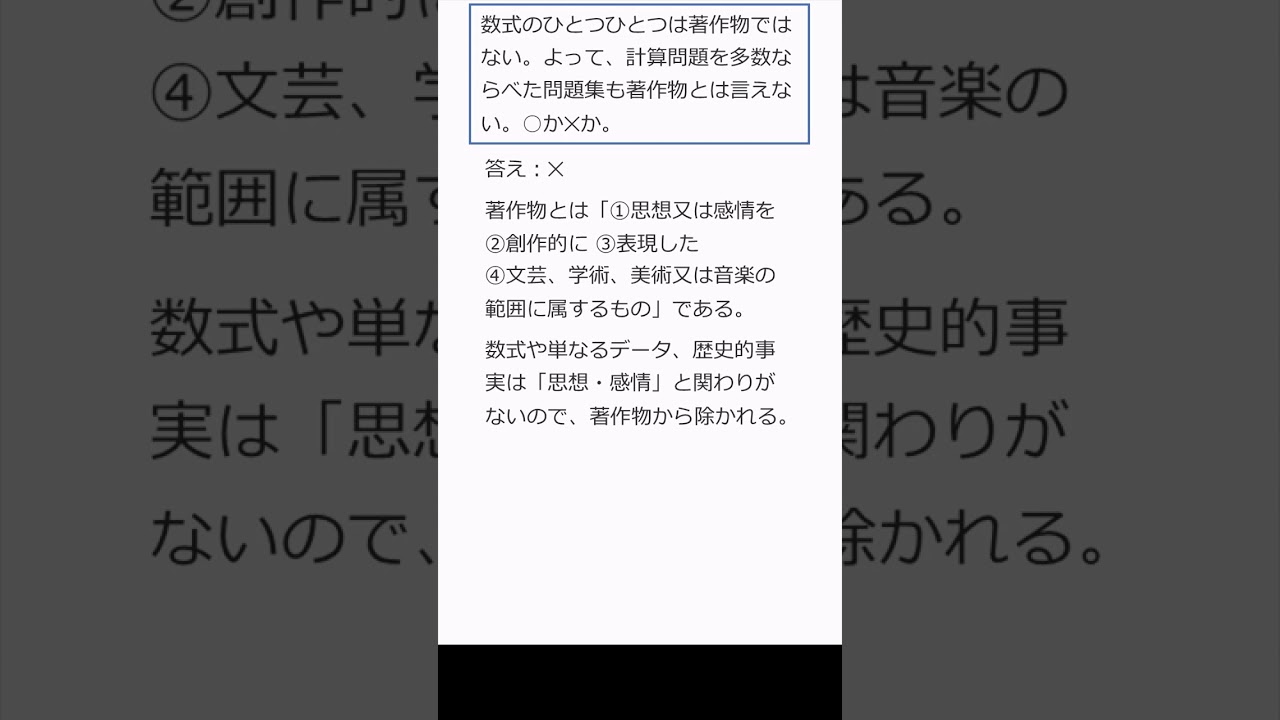
$ 数字のひとつひとつは著作物ではない.$
$ よって,計算問題を多数ならべた問題集も著作物とは言えない.これは正しいか?$
この動画を見る
$ 数字のひとつひとつは著作物ではない.$
$ よって,計算問題を多数ならべた問題集も著作物とは言えない.これは正しいか?$
015 世界観と著作権 #shorts

単元:
#情報Ⅰ(高校生)#情報社会#知的財産権の扱い
指導講師:
めいちゃんねる
問題文全文(内容文):
$ 特定の果物を食べることで異能を得たキャラクターたちが,$
$ 隠された遺産を巡ってバトルするという有名漫画の世界観を模倣した作品を作成した.$
$ これは著作権を侵害している.これは正しいか?$
この動画を見る
$ 特定の果物を食べることで異能を得たキャラクターたちが,$
$ 隠された遺産を巡ってバトルするという有名漫画の世界観を模倣した作品を作成した.$
$ これは著作権を侵害している.これは正しいか?$
014 2次的著作物の著作権はだれにあるか #shorts
単元:
#情報Ⅰ(高校生)#情報社会#知的財産権の扱い
指導講師:
めいちゃんねる
問題文全文(内容文):
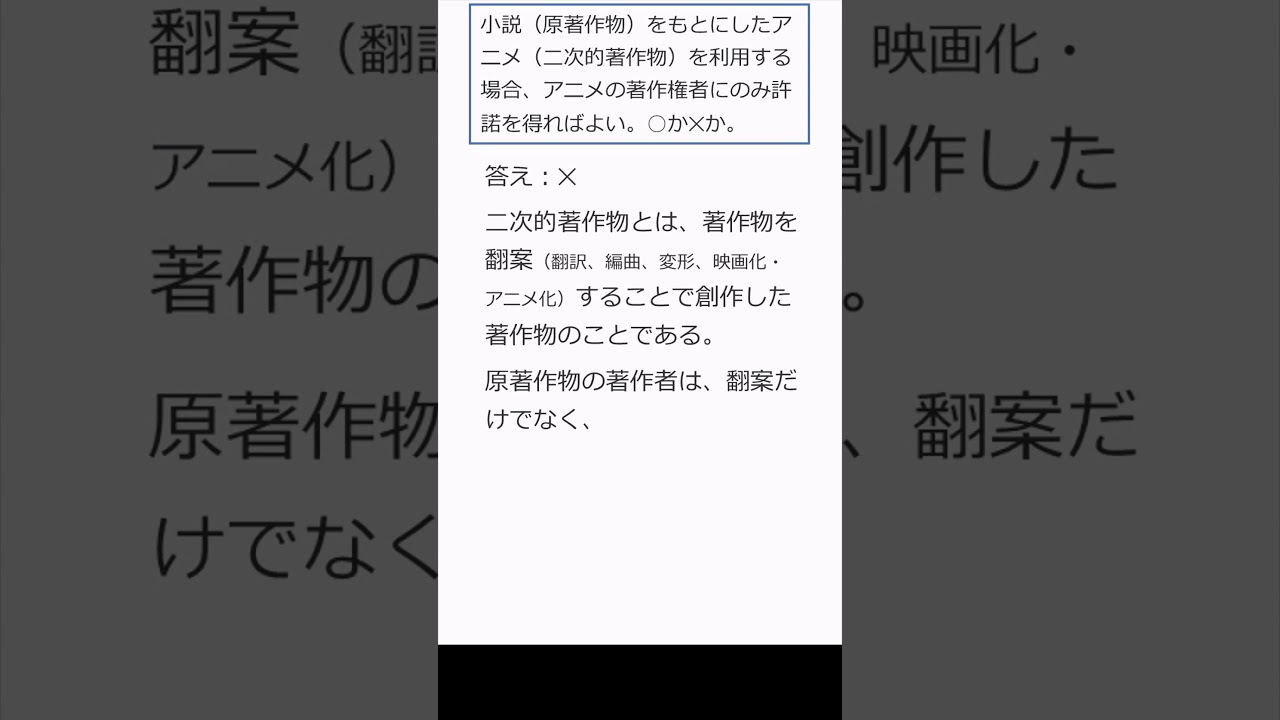
$ 小説(原著作物)をもとにしたアニメ(二次的著作物)を利用する場合,$
$ アニメの著作権者にのみ許諾を得ればよい.これは正しいか?$
この動画を見る
$ 小説(原著作物)をもとにしたアニメ(二次的著作物)を利用する場合,$
$ アニメの著作権者にのみ許諾を得ればよい.これは正しいか?$
013 引用できる条件 #shorts
単元:
#情報Ⅰ(高校生)#情報社会#知的財産権の扱い
指導講師:
めいちゃんねる
問題文全文(内容文):
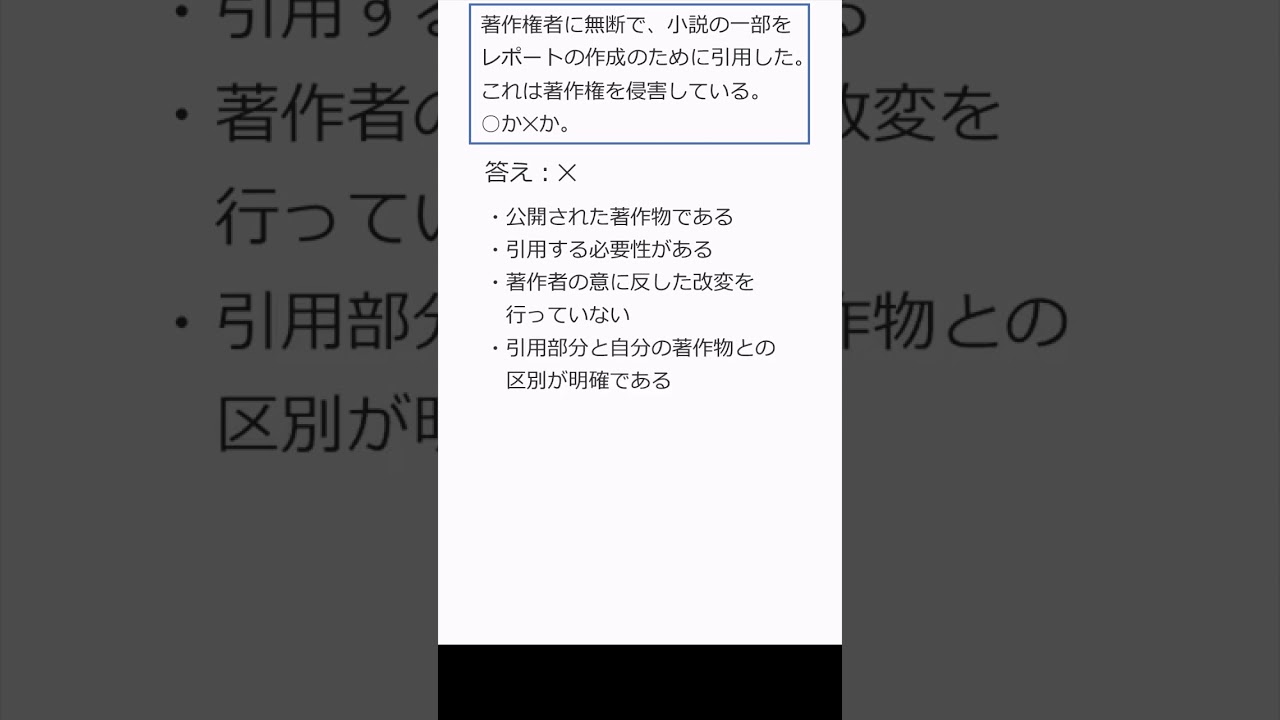
$ 著作権者に無断で,小説の一部をレポート作成のために引用した.$
$ これは著作権を侵害している.これは正しいか?$
この動画を見る
$ 著作権者に無断で,小説の一部をレポート作成のために引用した.$
$ これは著作権を侵害している.これは正しいか?$
012 文化祭でライブをするときの著作権 #shorts
単元:
#情報Ⅰ(高校生)#情報社会#知的財産権の扱い
指導講師:
めいちゃんねる
問題文全文(内容文):
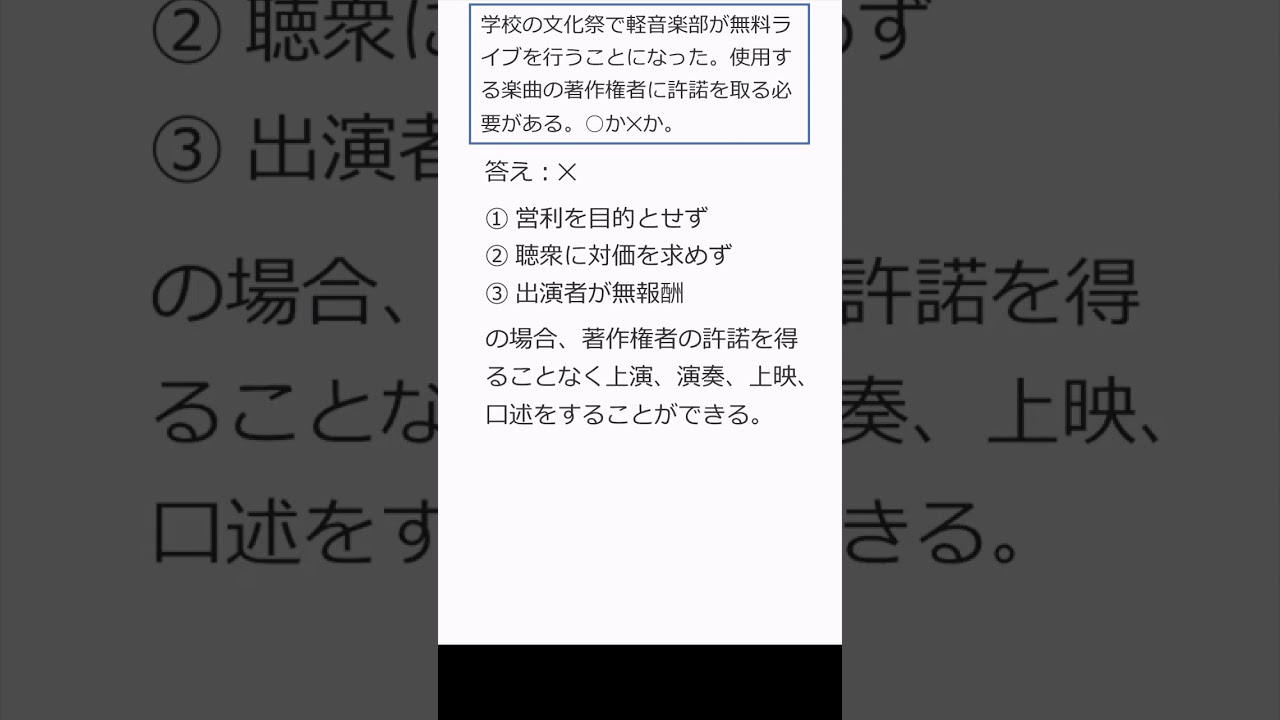
$ 学校の文化祭で軽音楽部が無料ライブを行うことになった.$
$ 使用する楽曲の著作権者に許諾を取る必要がある.これは正しいか?$
この動画を見る
$ 学校の文化祭で軽音楽部が無料ライブを行うことになった.$
$ 使用する楽曲の著作権者に許諾を取る必要がある.これは正しいか?$
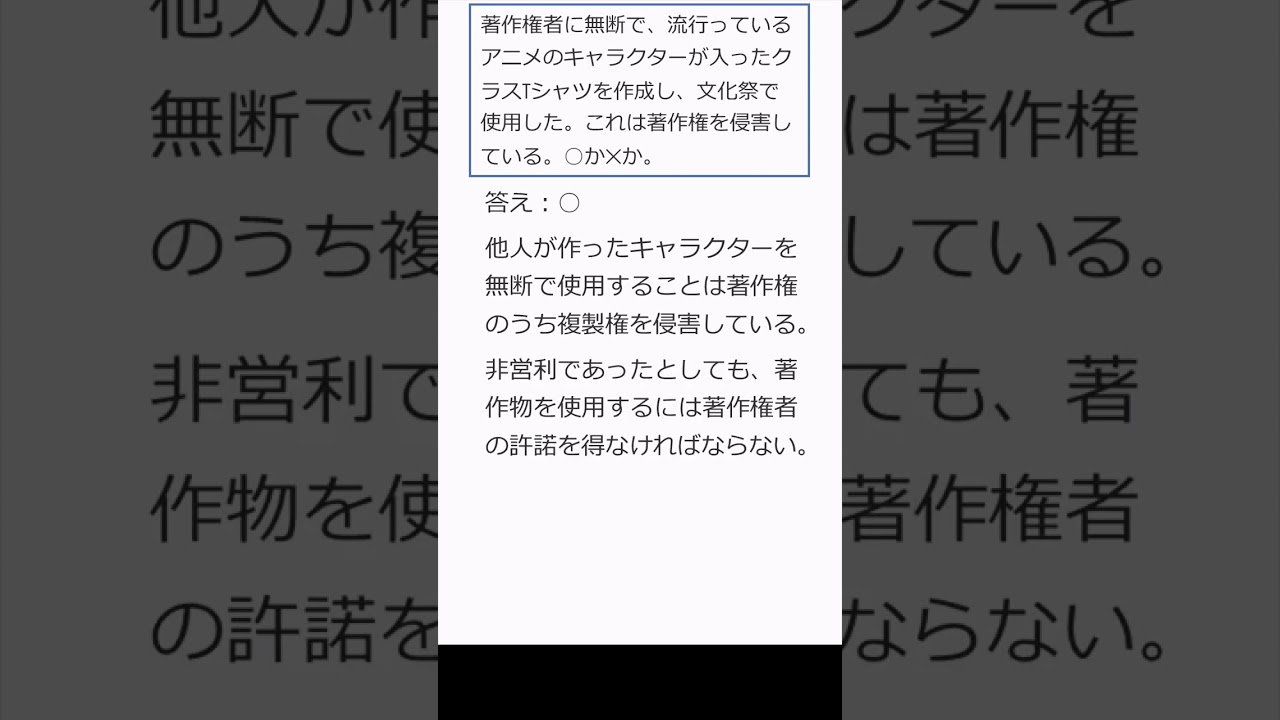
011 文化祭のクラスTシャツと著作権 #shorts
単元:
#情報Ⅰ(高校生)#情報社会#知的財産権の扱い
指導講師:
めいちゃんねる
問題文全文(内容文):
$ 著作権者に無断で,流行っているアニメのキャラクターが入ったクラスTシャツを作成し,$
$ 文化祭で使用した.これは著作権を侵害している.これは正しいか?$
この動画を見る
$ 著作権者に無断で,流行っているアニメのキャラクターが入ったクラスTシャツを作成し,$
$ 文化祭で使用した.これは著作権を侵害している.これは正しいか?$
010 著作権の取得方法 #shorts

単元:
#情報Ⅰ(高校生)#情報社会#知的財産権の扱い
指導講師:
めいちゃんねる
問題文全文(内容文):
$ 特許庁への届け出がない作品については著作権を行使することができない.$
$ これは正しいか?$
この動画を見る
$ 特許庁への届け出がない作品については著作権を行使することができない.$
$ これは正しいか?$
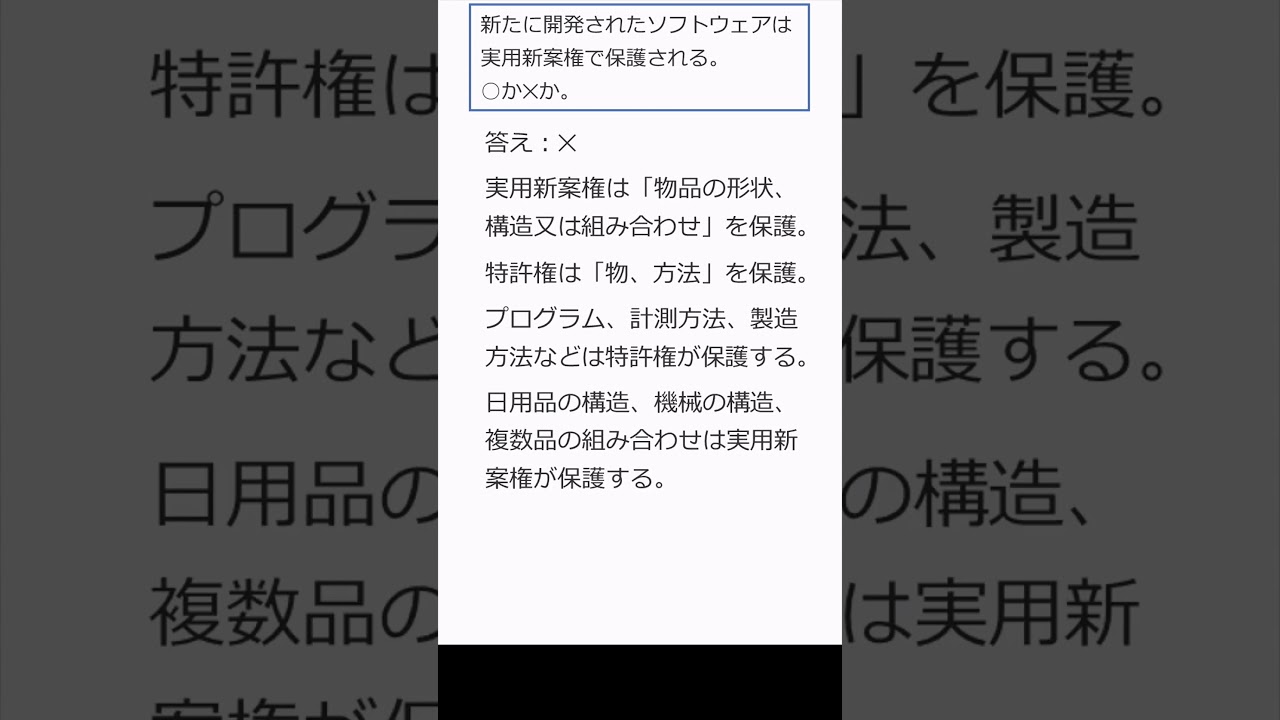
009 ソフトウェアは実用新案権?特許権? #shorts
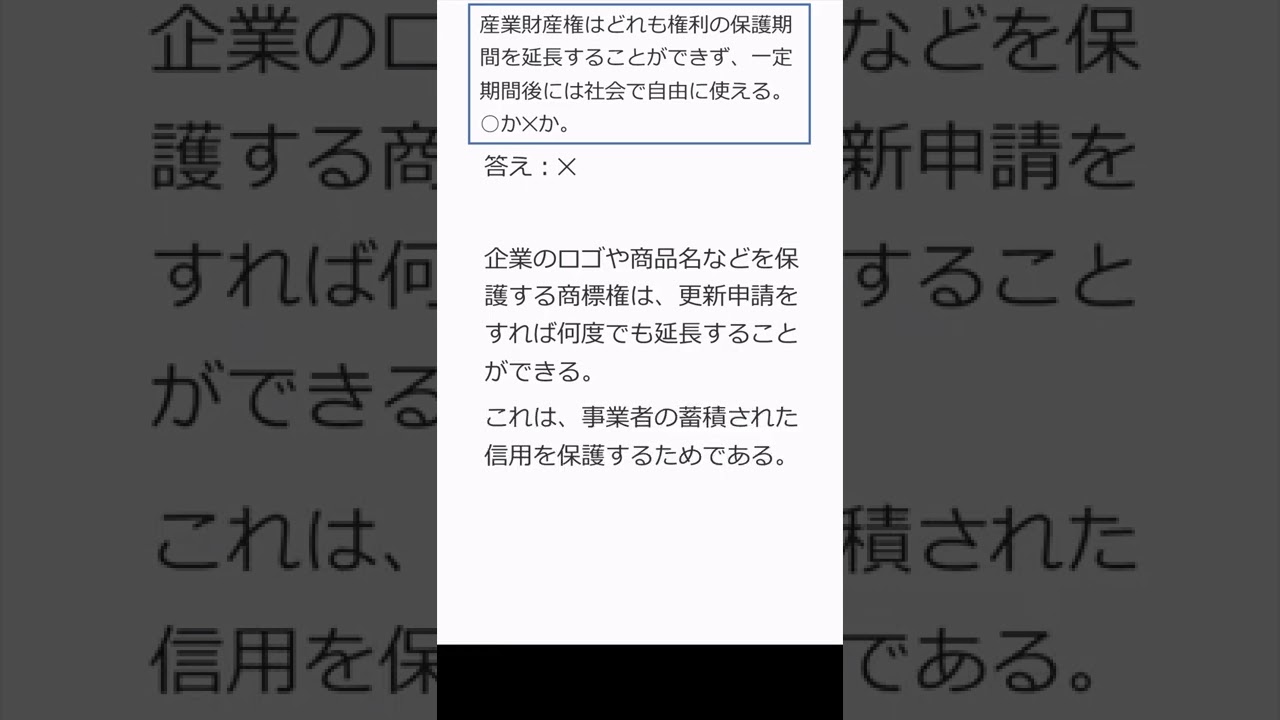
008 産業財産権の保護期間 #shorts
単元:
#情報Ⅰ(高校生)#情報社会#知的財産権の扱い
指導講師:
めいちゃんねる
問題文全文(内容文):
$ 産業財産権はどれも権利の保護期間を延長することができず,$
$ 一定期間後には社会で自由に使える.これは正しいか?$
この動画を見る
$ 産業財産権はどれも権利の保護期間を延長することができず,$
$ 一定期間後には社会で自由に使える.これは正しいか?$
【数Ⅲ】陰関数のグラフ【対称性を使って最低限の労力でグラフを描く】

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
めいちゃんねる
問題文全文(内容文):
$ (1)y^2=x^2(4-x^2)のグラフを描け.$
$ (2)y^2=x^2(4-x^2)をyについて解け.$
この動画を見る
$ (1)y^2=x^2(4-x^2)のグラフを描け.$
$ (2)y^2=x^2(4-x^2)をyについて解け.$
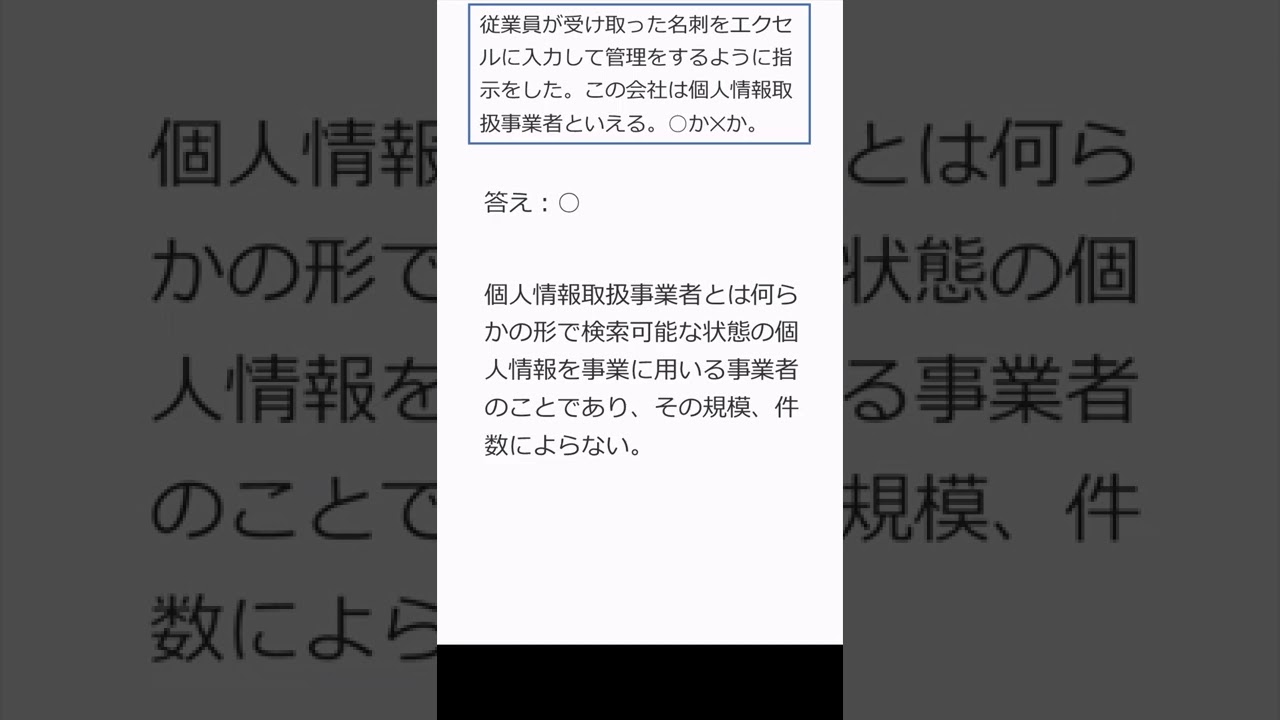
007 従業員が受け取った名刺の個人情報 #shorts
単元:
#情報Ⅰ(高校生)#情報社会#情報セキュリティと法規
指導講師:
めいちゃんねる
問題文全文(内容文):
$ 従業員が受け取った名刺をエクセルに入力して管理をするように指示した.$
$ この会社は個人情報取扱事業者といえる.これは正しいか?$
この動画を見る
$ 従業員が受け取った名刺をエクセルに入力して管理をするように指示した.$
$ この会社は個人情報取扱事業者といえる.これは正しいか?$
006 匿名化された個人情報 #shorts
単元:
#情報Ⅰ(高校生)#情報社会#問題解決#情報セキュリティと法規#知的財産権の扱い#データの収集と整理#データの扱いと処理
指導講師:
めいちゃんねる
問題文全文(内容文):
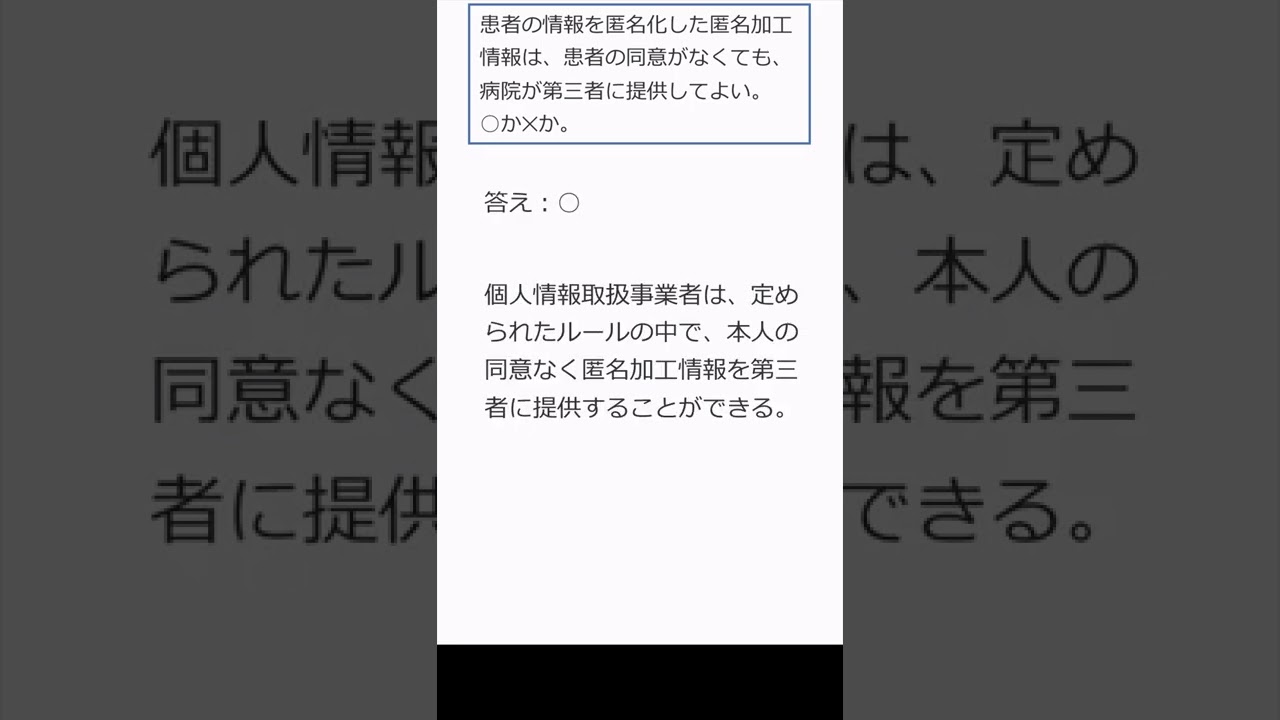
$ 患者の情報を匿名化した匿名加工情報は,患者の同意がなくても,病院が第三者に提供してよい.$
$ これは正しいか?$
この動画を見る
$ 患者の情報を匿名化した匿名加工情報は,患者の同意がなくても,病院が第三者に提供してよい.$
$ これは正しいか?$
005 年賀状と個人情報保護法 #shorts
単元:
#情報Ⅰ(高校生)#情報社会#情報セキュリティと法規#知的財産権の扱い
指導講師:
めいちゃんねる
問題文全文(内容文):
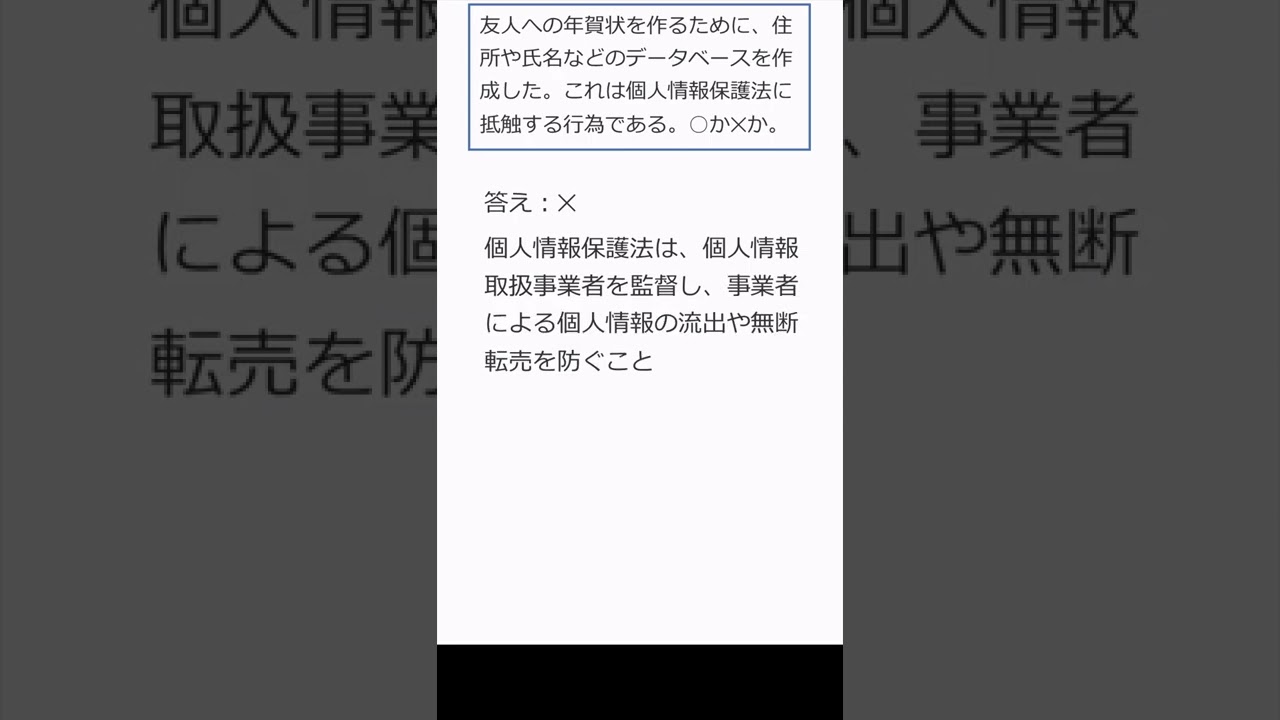
$ 友人への年賀状を作るために,住所や氏名などのデーターベースを作成した.$
$ これは個人情報保護法に抵触する行為である.これは正しいか?$
この動画を見る
$ 友人への年賀状を作るために,住所や氏名などのデーターベースを作成した.$
$ これは個人情報保護法に抵触する行為である.これは正しいか?$
004 拾ったメモとサイバー犯罪 #shorts
単元:
#情報Ⅰ(高校生)#情報社会#情報セキュリティと法規
指導講師:
めいちゃんねる
問題文全文(内容文):
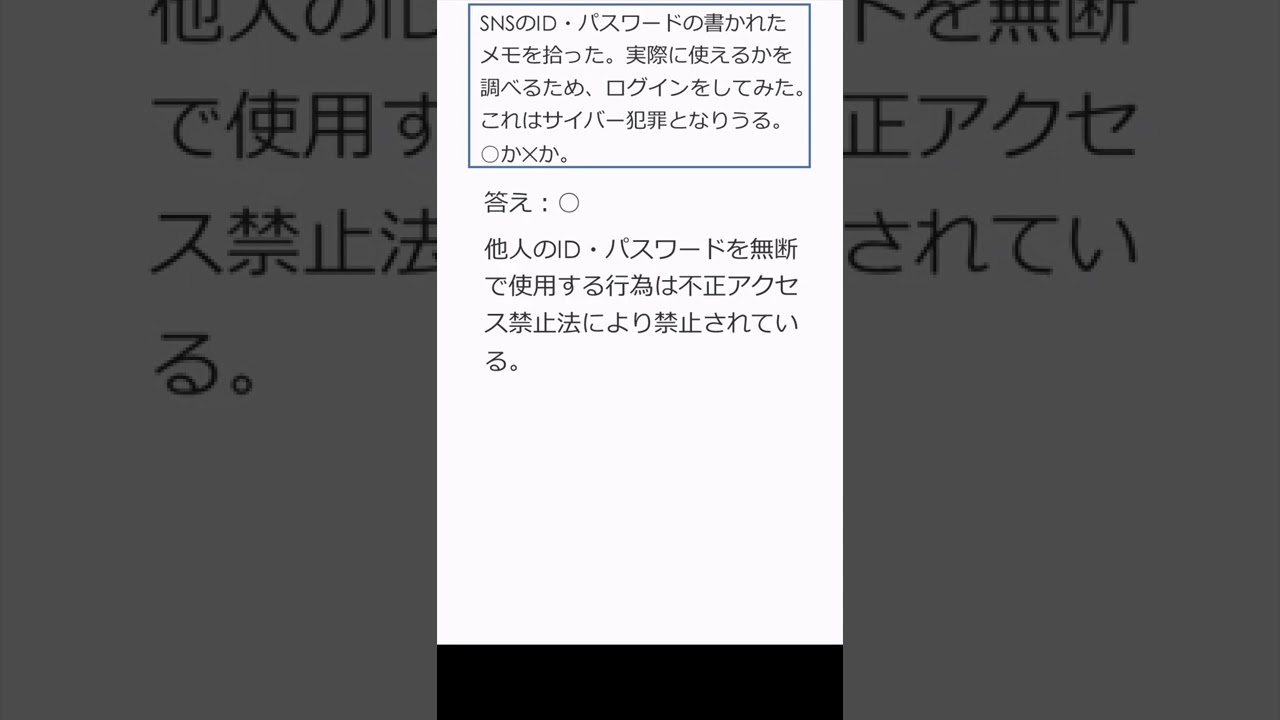
$ SNSのID・パスワードの書かれたメモを拾った.$
$ 実際に使えるかを調べるため,ログインをしてみた.$
$ これはサイバー犯罪となりうる.これは正しいか?$
この動画を見る
$ SNSのID・パスワードの書かれたメモを拾った.$
$ 実際に使えるかを調べるため,ログインをしてみた.$
$ これはサイバー犯罪となりうる.これは正しいか?$
003 アイドルの自作冊子とパブリシティ権 #shorts
単元:
#情報Ⅰ(高校生)#情報社会#情報セキュリティと法規#知的財産権の扱い
指導講師:
めいちゃんねる
問題文全文(内容文):
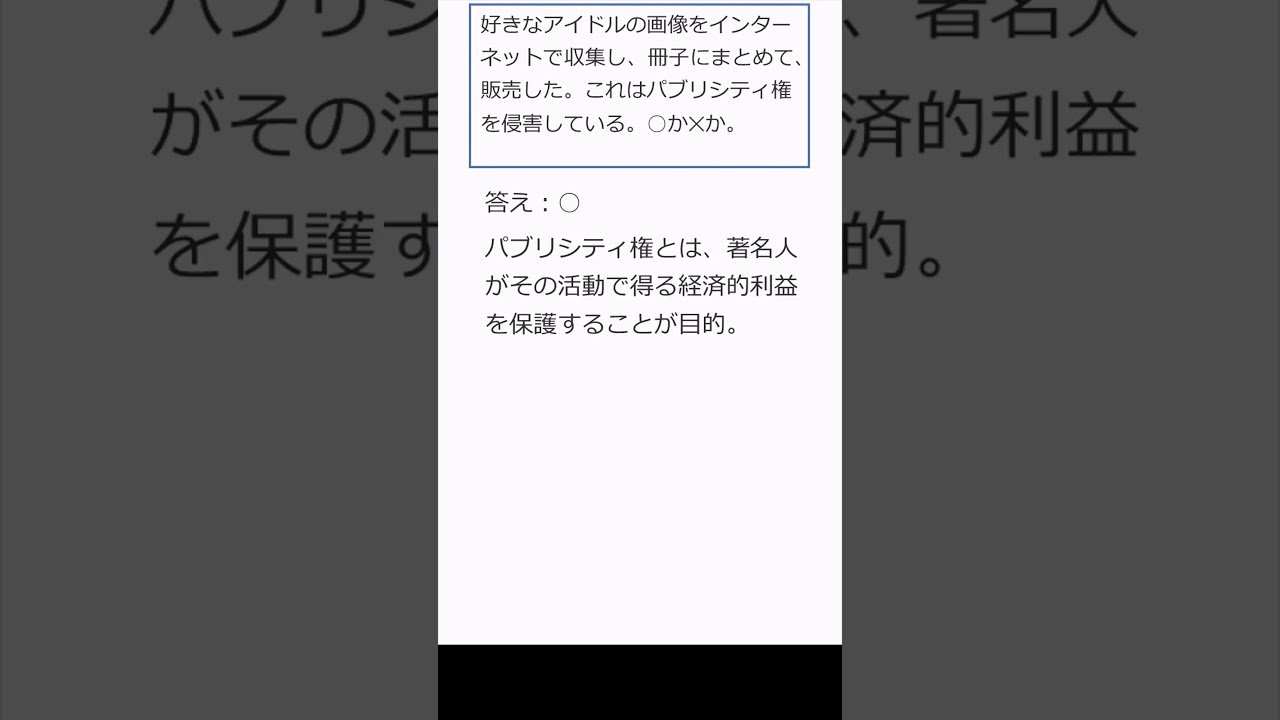
$ 好きなアイドルの画像をインターネットで収集し,$
$ 冊子にまとめて販売した.これはパブリシティ権を侵害している.これは正しいか?$
この動画を見る
$ 好きなアイドルの画像をインターネットで収集し,$
$ 冊子にまとめて販売した.これはパブリシティ権を侵害している.これは正しいか?$
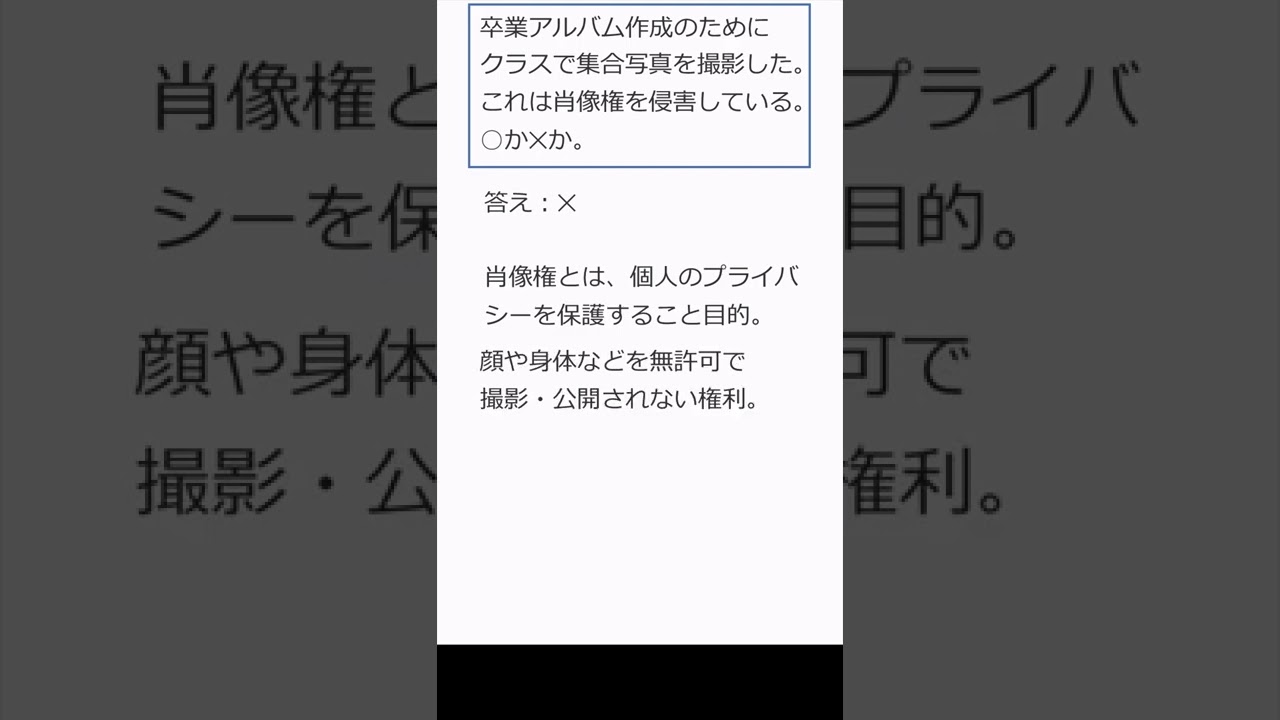
002 卒業アルバムと肖像権 #shorts
単元:
#情報Ⅰ(高校生)#情報社会#情報セキュリティと法規
指導講師:
めいちゃんねる
問題文全文(内容文):
$ 卒業アルバム作成のためにクラスで集合写真を撮影した. $
$ これは肖像権を侵害している.これは正しいか?$
この動画を見る
$ 卒業アルバム作成のためにクラスで集合写真を撮影した. $
$ これは肖像権を侵害している.これは正しいか?$
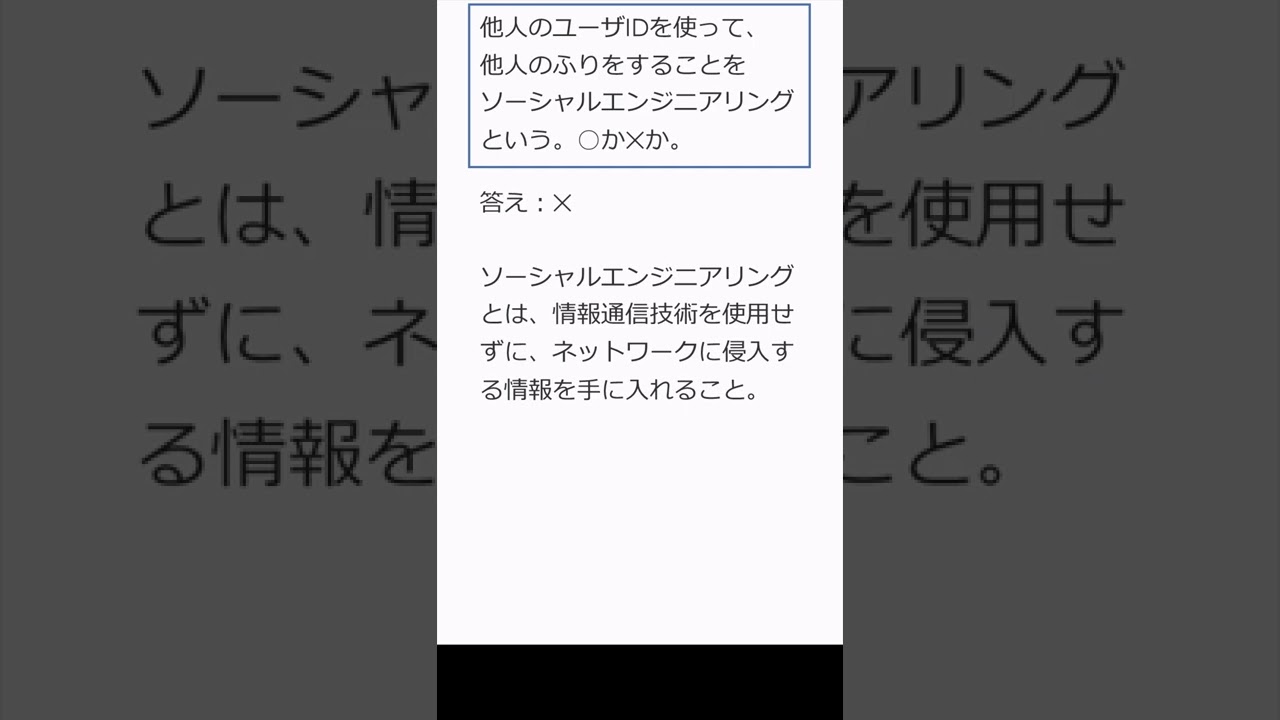
001 ソーシャルエンジニアリング #shorts
単元:
#情報Ⅰ(高校生)#情報社会#ネットワーク#情報セキュリティと法規#安全のための対策と技術
指導講師:
めいちゃんねる
問題文全文(内容文):
$ 他人のユーザーIDを使って,他人のふりをすることをソーシャルエンジニアリングという.$
$ これは正しいか? $
この動画を見る
$ 他人のユーザーIDを使って,他人のふりをすることをソーシャルエンジニアリングという.$
$ これは正しいか? $
【数Ⅲ】グラフを描く【チェックするべきポイントを押さえる】
単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
めいちゃんねる
問題文全文(内容文):
グラフを描くことに関して解説していきます.
この動画を見る
グラフを描くことに関して解説していきます.
【数Ⅲ】三角関数・指数・対数の微分公式【合成関数との合せ技】

【数Ⅲ】微分の公式 積・商・合成関数の微分【中身と外側を区別しよう】

【数学Ⅰ・新課程】仮説検定の考え方【確率的に正しさを証明する】

単元:
#数Ⅰ#確率#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$(1)ある企業の新商品について20人中15人が「よい」と回答した.$
$この商品は「よい」商品であるか,仮説検定の考え方を用いて考察せよ.$
$(2)A,B,C,D,E,Fの6人の候補者がいる.$
$100人中25人がAを支持していると答えた.$
$Aの支持者は多いと言えるか,仮説検定の考え方を用いて考察せよ.$
この動画を見る
$(1)ある企業の新商品について20人中15人が「よい」と回答した.$
$この商品は「よい」商品であるか,仮説検定の考え方を用いて考察せよ.$
$(2)A,B,C,D,E,Fの6人の候補者がいる.$
$100人中25人がAを支持していると答えた.$
$Aの支持者は多いと言えるか,仮説検定の考え方を用いて考察せよ.$
【数Ⅱ】積分で面積が求まる理由【面積を表すことが先、積分が後。区分求積法で積分を使わず面積を計算しよう】

【数Ⅱ】積分で定義された関数【積分区間を見て、計算結果を考えよう。】
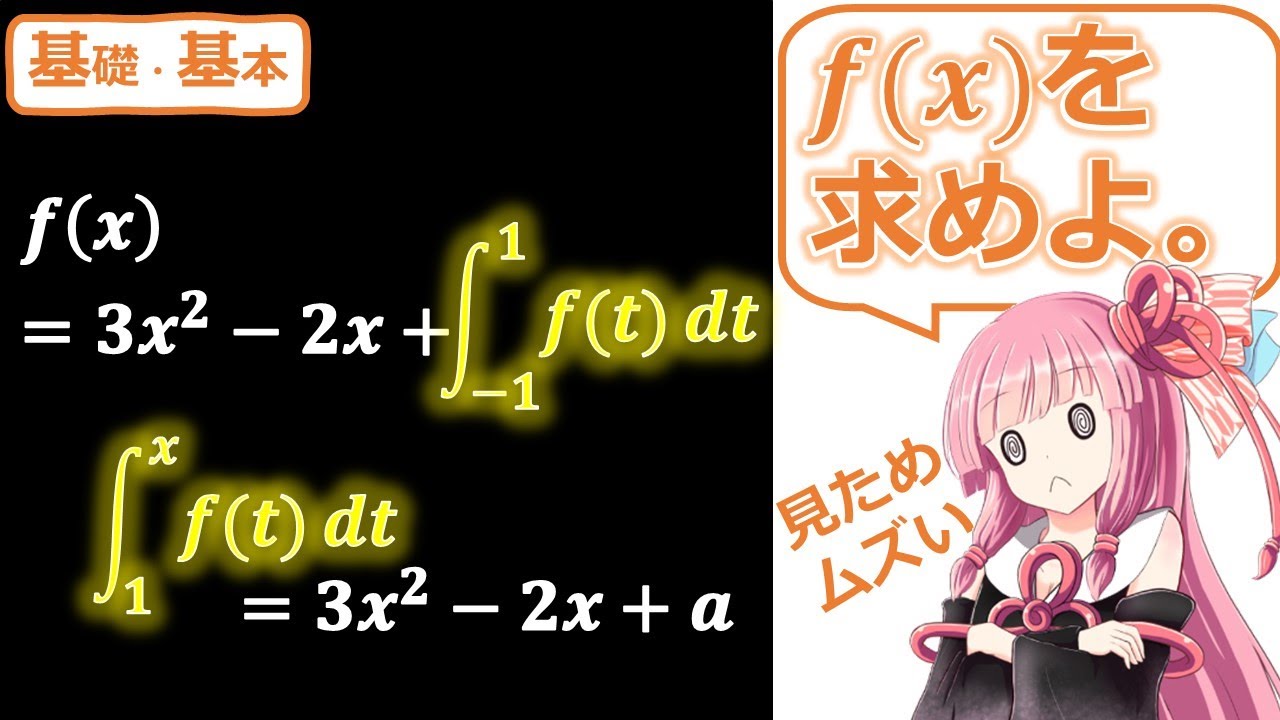
単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$(1)f(x)=3x^2-2x+ \displaystyle \int_{-1}^{1}f(t)dtを満たす関数f(x)を求めよ.$
$(2)f(x)=3x+\displaystyle \int_{0}^{1}(x+t)f(t)dtを満たす関数f(x)を求めよ.$
$(3)y=\displaystyle \int_{1}^{x}(t^2-2t-3)dtの極値を求めよ.$
$(4)\displaystyle \int_{1}^{x}f(t)dt=3x^2-2x+aを満たす関数f(x)と定数aを求めよ.$
この動画を見る
$(1)f(x)=3x^2-2x+ \displaystyle \int_{-1}^{1}f(t)dtを満たす関数f(x)を求めよ.$
$(2)f(x)=3x+\displaystyle \int_{0}^{1}(x+t)f(t)dtを満たす関数f(x)を求めよ.$
$(3)y=\displaystyle \int_{1}^{x}(t^2-2t-3)dtの極値を求めよ.$
$(4)\displaystyle \int_{1}^{x}f(t)dt=3x^2-2x+aを満たす関数f(x)と定数aを求めよ.$
【数Ⅱ】放物線と面積 1/3・1/6・1/12の公式を使いこなせ【定積分をせずに面積を求める】

単元:
#数Ⅱ#微分法と積分法#面積、体積#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$(1)y=x^2-2x+2とy=2x-1で囲われた図形の面積を求めよ.$
$(2)y=x^2-2x+2とy=-x^2+4x+2で囲われた図形の面積を求めよ.$
$(3)y= \vert x^2-1 \vertとx軸,x=0,x=2で囲われた図形の面積を求めよ.$
$(4)放物線C:y=x^2+3x+1上の点(-3,1)における接線と$
$放物線C,y軸で囲われた図形の面積を求めよ.$
$(5)放物線C:y=x^2-x+3と点A(1,-1)からこの放物線に引いた接線で$
$囲われた図形の面積を求めよ.$
この動画を見る
$(1)y=x^2-2x+2とy=2x-1で囲われた図形の面積を求めよ.$
$(2)y=x^2-2x+2とy=-x^2+4x+2で囲われた図形の面積を求めよ.$
$(3)y= \vert x^2-1 \vertとx軸,x=0,x=2で囲われた図形の面積を求めよ.$
$(4)放物線C:y=x^2+3x+1上の点(-3,1)における接線と$
$放物線C,y軸で囲われた図形の面積を求めよ.$
$(5)放物線C:y=x^2-x+3と点A(1,-1)からこの放物線に引いた接線で$
$囲われた図形の面積を求めよ.$
【数Ⅱ】積分をイチから理解。面積を求めよう【まずは計算方法をマスターする】

単元:
#数Ⅱ#微分法と積分法#面積、体積#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$(1)微分するとx^2+4x+3となる関数を求めよ.$
$(2)\displaystyle \int_{1}^{2} (x^2+4x+3)dxを計算せよ. $
$(3)y=x^2-4x+3とx軸で囲われた図形の面積を求めよ.$
$(4)y=x^3-5x^2+6xとx軸で囲われた2つの図形の面積の和を求めよ.$
この動画を見る
$(1)微分するとx^2+4x+3となる関数を求めよ.$
$(2)\displaystyle \int_{1}^{2} (x^2+4x+3)dxを計算せよ. $
$(3)y=x^2-4x+3とx軸で囲われた図形の面積を求めよ.$
$(4)y=x^3-5x^2+6xとx軸で囲われた2つの図形の面積の和を求めよ.$
【数Ⅱ】共通接線を求める【2つのグラフが接する・別々の接点をもつ】

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$(1)y=ax^2+3x-8,y=x^3+bxがx=2で接するような実数a,bを求めよ.$
$(2)y=x^2+2x+7,y=2x^2の共通接線の方程式を求めよ.$
この動画を見る
$(1)y=ax^2+3x-8,y=x^3+bxがx=2で接するような実数a,bを求めよ.$
$(2)y=x^2+2x+7,y=2x^2の共通接線の方程式を求めよ.$
【数Ⅱ】微分とグラフ【増減表で整理しよう。極値を持つ条件、正確に言えますか?】

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$(1)y=x^3-6x^2+9x+1のグラフを描け.$
$(2)y=3x^4-8x^3+6x^2のグラフを描け.$
$(3)y=x^3+kx^2+kx+2が極値を持つkの範囲を求めよ.$
この動画を見る
$(1)y=x^3-6x^2+9x+1のグラフを描け.$
$(2)y=3x^4-8x^3+6x^2のグラフを描け.$
$(3)y=x^3+kx^2+kx+2が極値を持つkの範囲を求めよ.$
【数Ⅱ】微分の定義と接線の方程式【接線の傾きがなんで微分で計算できるのか】

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$(1) y=x^2+2x+3のxが1から3まで変化するときの平均変化率を求めよ.$
$(2)y=x^2+2x+3のx=1における微分係数を求めよ.$
$(3)y=x^2+2x+3上の点(1,6)における接線を求めよ.$
$(4)y=x^2+2x+3のx=aにおける微分係数を求めよ.$
$(5)Y=X^2+2X+3に点(1,2)から引いた接線を求めよ.$
この動画を見る
$(1) y=x^2+2x+3のxが1から3まで変化するときの平均変化率を求めよ.$
$(2)y=x^2+2x+3のx=1における微分係数を求めよ.$
$(3)y=x^2+2x+3上の点(1,6)における接線を求めよ.$
$(4)y=x^2+2x+3のx=aにおける微分係数を求めよ.$
$(5)Y=X^2+2X+3に点(1,2)から引いた接線を求めよ.$
【数Ⅱ】常用対数の使い方【対数ってなんのためにあるの? 人類の計算力に革命を与えた技 桁数問題から罹患者数の増え方、複利計算をマスターしよう】

【数Ⅱ】対数のグラフと不等式【底に注意してグラフを描こう。指数関数と全く同じ!?】




