鈴木貫太郎
鈴木貫太郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
指数法則の話がしたいだけの動画
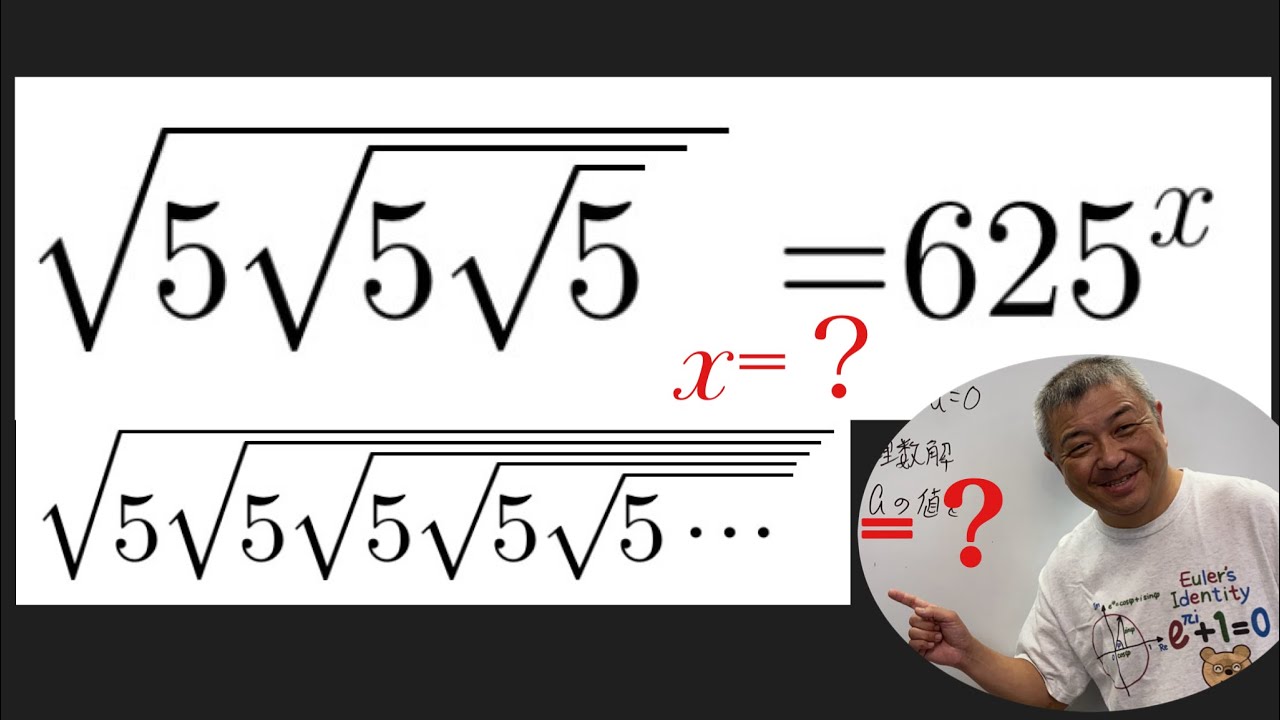
5次式の因数分解
これもオイラーの公式っていうんだ！
単元：
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\displaystyle \prod_{n=1}^\infty cos(\frac x{2^n}) = cos\frac x{2}cos\frac x{4} cos\frac x{8} \cdots $
$cos\frac x{2^n} = \frac {sinx}x $
これを証明せよ.
この動画を見る
$\displaystyle \prod_{n=1}^\infty cos(\frac x{2^n}) = cos\frac x{2}cos\frac x{4} cos\frac x{8} \cdots $
$cos\frac x{2^n} = \frac {sinx}x $
これを証明せよ.
４次関数の最小値
効率よく解を絞り込め
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$9a^2-4b^2=2160$
を満たす整数、a,bの組をすべて求めよ.
この動画を見る
$9a^2-4b^2=2160$
を満たす整数、a,bの組をすべて求めよ.
出題者の想定した解法０人の問題・難問ではありません（慶應・理工）
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
係数を整数とする多項式を$f(x)$とする
任意の整数m,nにおいて$f(m+n)-f(n)$はmの倍数であることを証明せよ
慶應・理工過去問
この動画を見る
係数を整数とする多項式を$f(x)$とする
任意の整数m,nにおいて$f(m+n)-f(n)$はmの倍数であることを証明せよ
慶應・理工過去問
連立方程式をあれで解こう
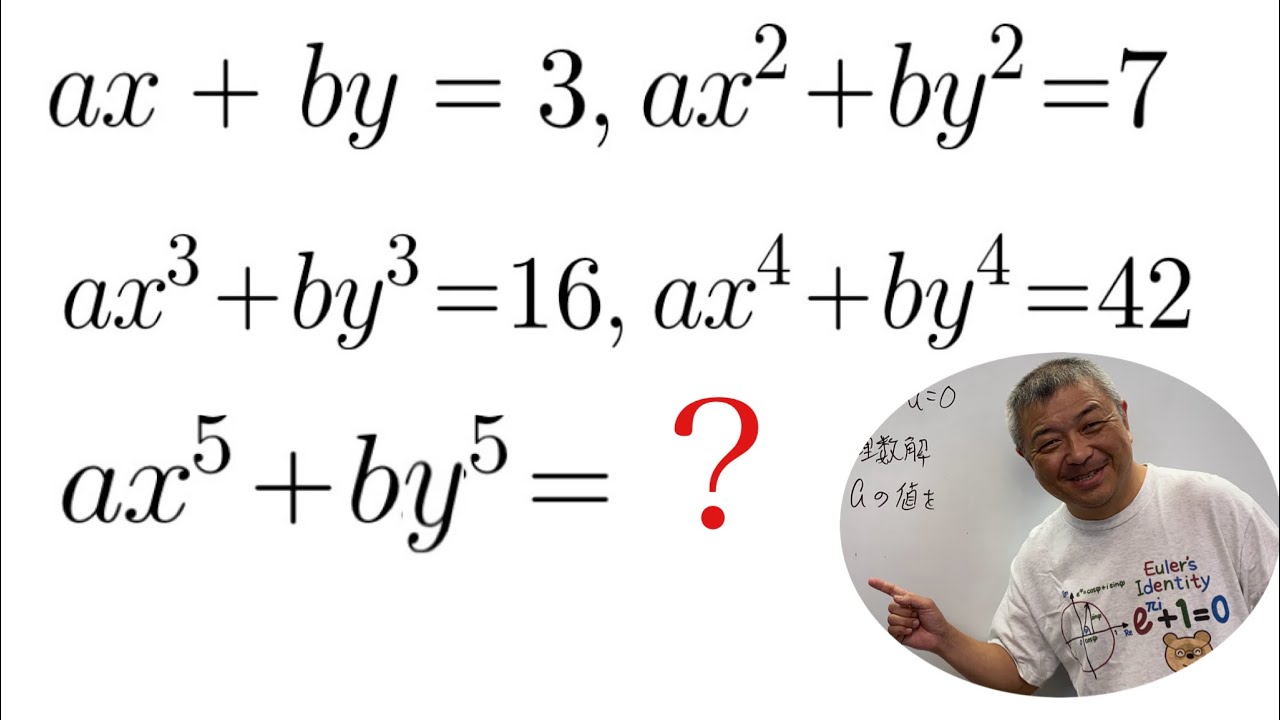
単元：
#大学入試過去問(数学)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ax+by = 3$
$ax^2+by^2 = 7$
$ax^3+by^3 = 16$
$ax^4+by^4 = 42$
$ax^5 +by^5 = ? $
この動画を見る
$ax+by = 3$
$ax^2+by^2 = 7$
$ax^3+by^3 = 16$
$ax^4+by^4 = 42$
$ax^5 +by^5 = ? $
式の値
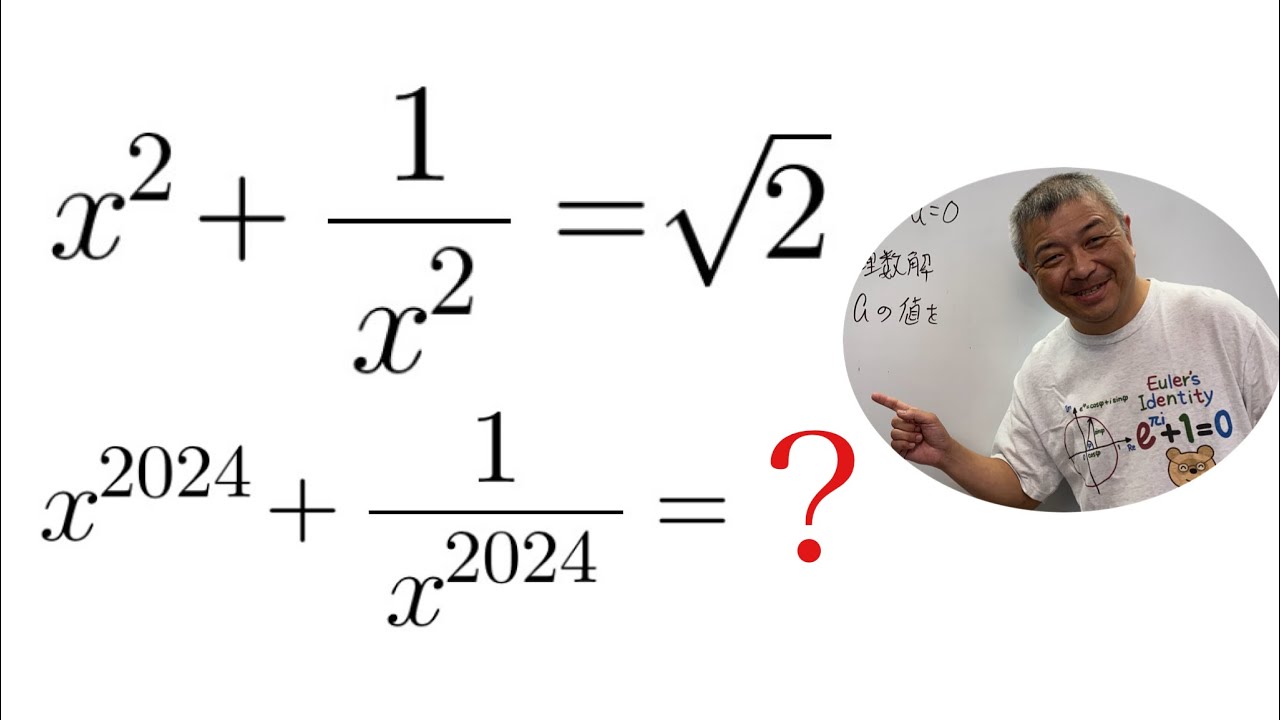
単元：
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x^2+\frac 1{x^2} = \sqrt2$
$x^{2024} + \frac 1{x^{2024}} = ?$
この動画を見る
$x^2+\frac 1{x^2} = \sqrt2$
$x^{2024} + \frac 1{x^{2024}} = ?$
連立方程式
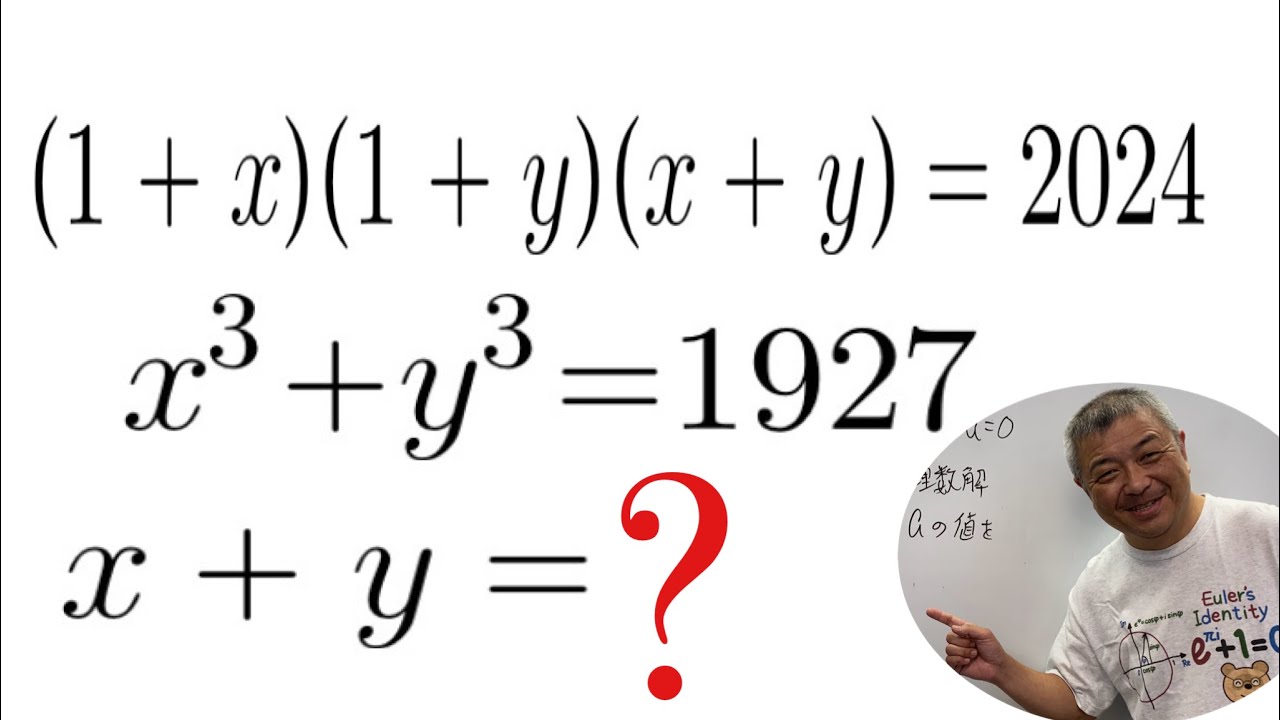
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$
\begin{cases}
(1+x)(1+y)(x+y) =2024 \\
x^3 +y^3 =1927
\end{cases}
$
$x+y=?$
この動画を見る
$
\begin{cases}
(1+x)(1+y)(x+y) =2024 \\
x^3 +y^3 =1927
\end{cases}
$
$x+y=?$
連立方程式
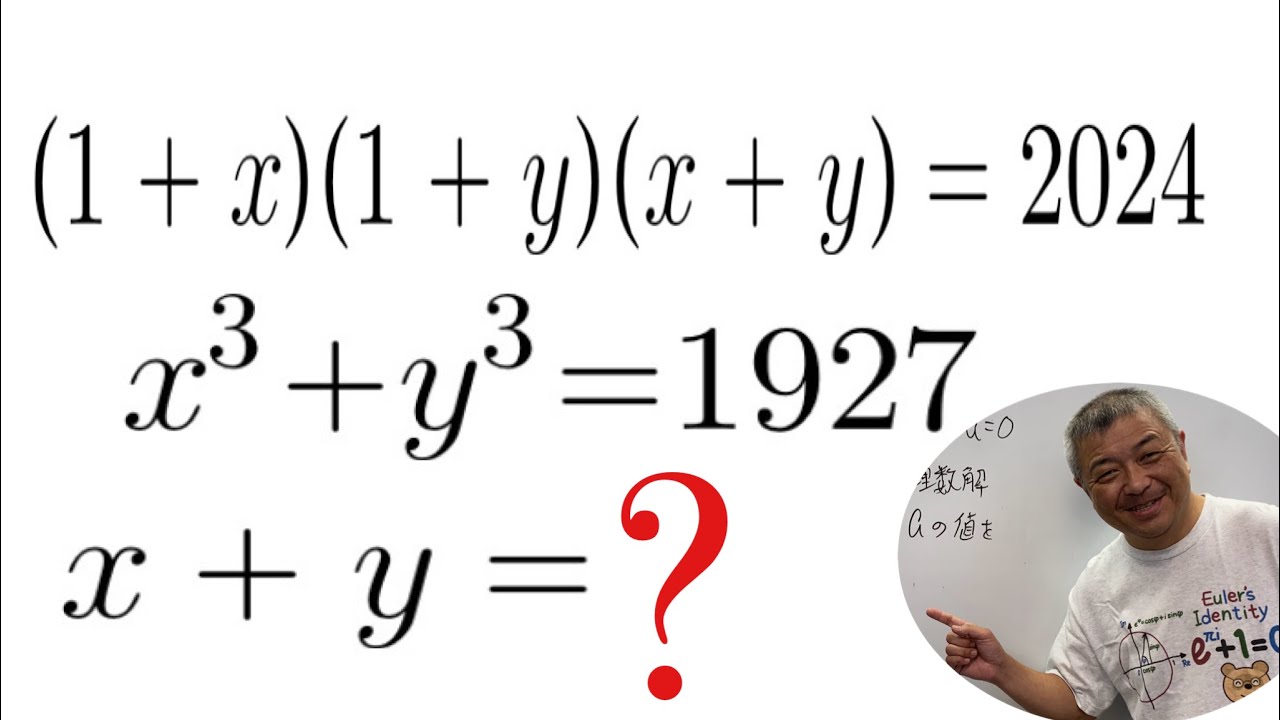
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\begin{eqnarray}
\left\{
\begin{array}{l}
(1+x)(1+y)(x+y)=2024 \\
x^3+y^3=1927
\end{array}
\right.
\end{eqnarray}$
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
(1+x)(1+y)(x+y)=2024 \\
x^3+y^3=1927
\end{array}
\right.
\end{eqnarray}$
微分の基本問題（落とし穴注意）
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$
f(x)=x^4-8x^3+18kx^2
$
が極大値をもたないkの範囲
この動画を見る
$
f(x)=x^4-8x^3+18kx^2
$
が極大値をもたないkの範囲
バングラデシュ数学オリンピック
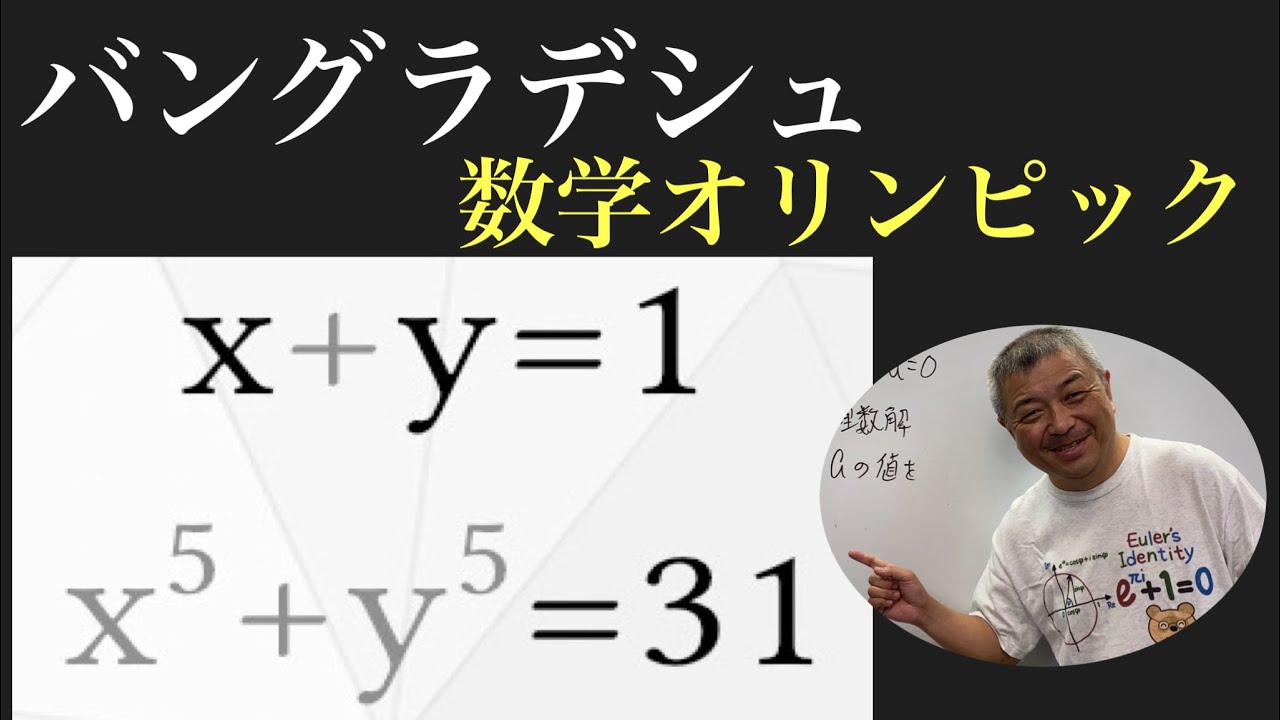
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学オリンピック#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$
\begin{cases}
x+y = 1 \\
x^5+y^5 = 31
\end{cases}
$
バングラデシュ数学オリンピック過去問
この動画を見る
$
\begin{cases}
x+y = 1 \\
x^5+y^5 = 31
\end{cases}
$
バングラデシュ数学オリンピック過去問
バングラデシュ数学オリンピック
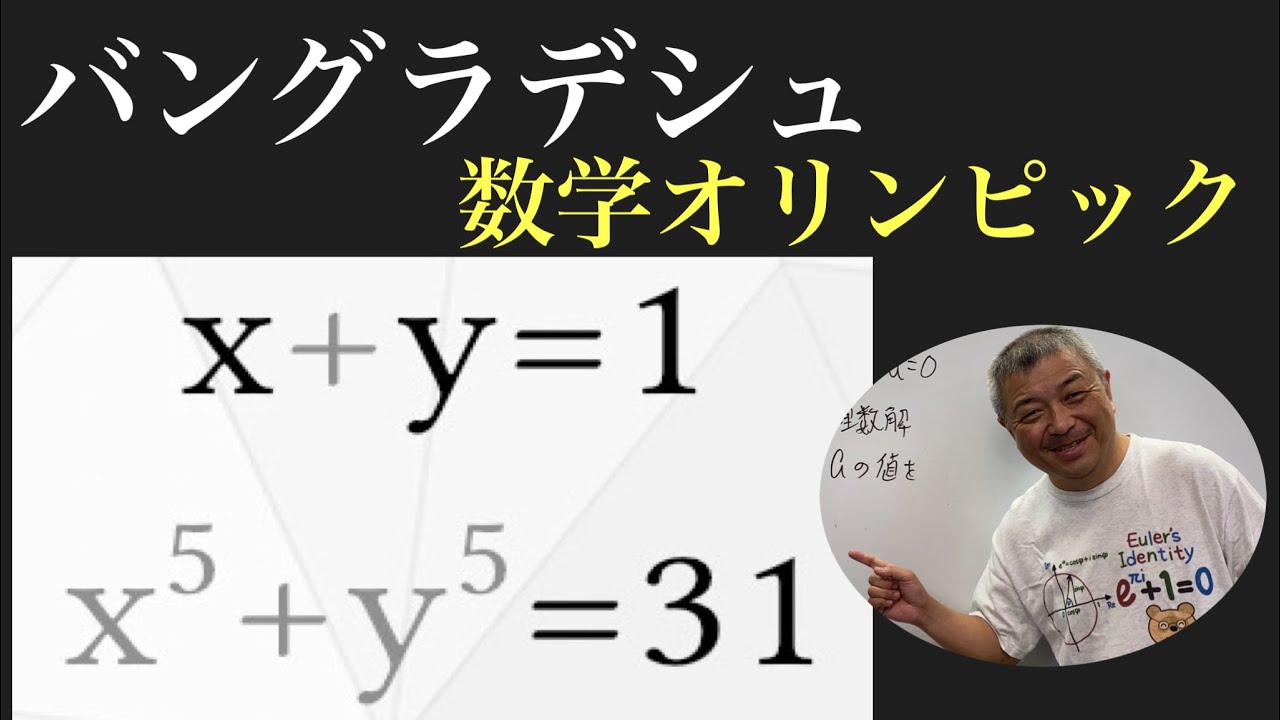
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=1 \\
x^5+y^5=31
\end{array}
\right.
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=1 \\
x^5+y^5=31
\end{array}
\right.
\end{eqnarray}
$
7の2024乗の下４桁
4次方程式
例のアレ
単元：
#数列とその和（等差・等比・階差・Σ）
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\displaystyle \frac{1}{1×2×3×4}＋\displaystyle \frac{1}{2×3×4×5}+\displaystyle \frac{1}{3×4×5×6}$$＋…+\displaystyle \frac{1}{6×7×8×9}＋\displaystyle \frac{1}{7×8×9×10}$
この動画を見る
$\displaystyle \frac{1}{1×2×3×4}＋\displaystyle \frac{1}{2×3×4×5}+\displaystyle \frac{1}{3×4×5×6}$$＋…+\displaystyle \frac{1}{6×7×8×9}＋\displaystyle \frac{1}{7×8×9×10}$
自作問題・良問（自画自賛）
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
ｎは自然数
$4^{7n－3}＋5^{2n＋3}$
は必ずある素数をもつ
ある素数を求めよ
$4^{n+1}＋5^{2n-1}$
は21の倍数であることを証明しなさい
この動画を見る
ｎは自然数
$4^{7n－3}＋5^{2n＋3}$
は必ずある素数をもつ
ある素数を求めよ
$4^{n+1}＋5^{2n-1}$
は21の倍数であることを証明しなさい
因数分解
対数方程式 京都産業大
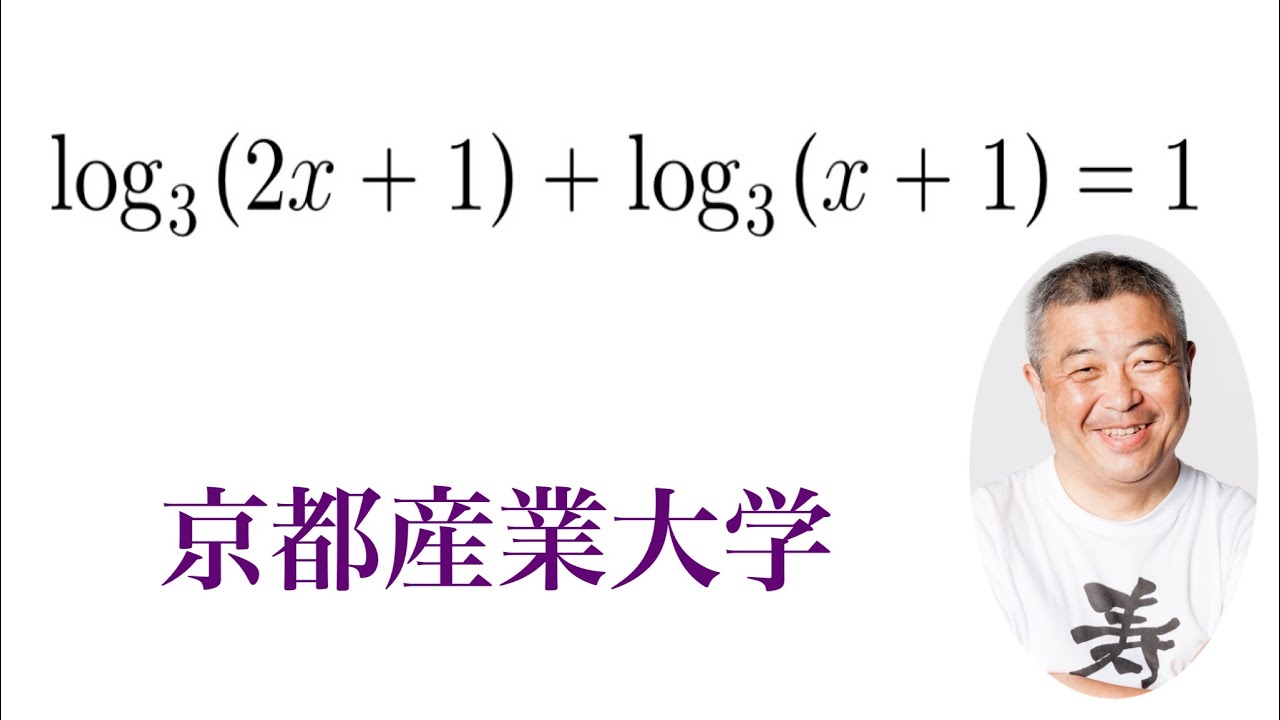
単元：
#対数関数
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\log_{3} {(2x+1)}＋\log_{3} {(x+1)}$＝1
これの実数解を求めよ。
京都産業大過去問
この動画を見る
$\log_{3} {(2x+1)}＋\log_{3} {(x+1)}$＝1
これの実数解を求めよ。
京都産業大過去問
確率の基本問題
見掛け倒しの対数方程式
久留米大（医）虚数係数の三次方程式
単元：
#複素数と方程式
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x^{3}＋(3+bi)x^{2}＋(3k+2i)x+1+ki$=0
kは実数であり、上の3次方程式は負の実数解を持つ
解を求めよ.
久留米大(医)過去問
この動画を見る
$x^{3}＋(3+bi)x^{2}＋(3k+2i)x+1+ki$=0
kは実数であり、上の3次方程式は負の実数解を持つ
解を求めよ.
久留米大(医)過去問
反省して数字を変えてみた
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$5^{2024}$÷1000
あまりを求めよ
$2^{2024}$÷196
あまりを求めよ
この動画を見る
$5^{2024}$÷1000
あまりを求めよ
$2^{2024}$÷196
あまりを求めよ
割り算の復習をしよう
素因数分解
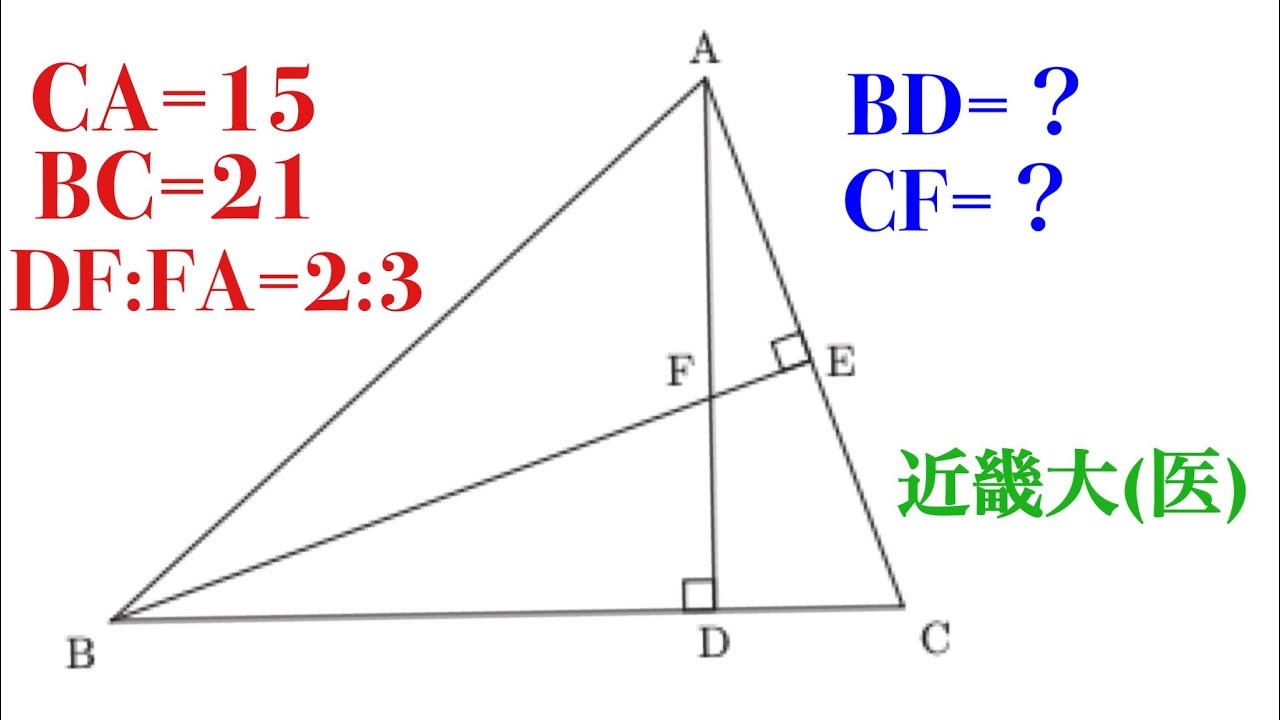
近畿大（医）メネラウスの定理の証明もやるよ
単元：
#数A#大学入試過去問(数学)#図形の性質#学校別大学入試過去問解説(数学)#近畿大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
BC=21 DF:FA=2:3のとき、CFは？
近畿大(医)過去問
この動画を見る
BC=21 DF:FA=2:3のとき、CFは？
近畿大(医)過去問
連続する2つの整数の積で表せ
近畿大（医）お知らせもあるよ
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#近畿大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\log_{10} 5$
の小数第二位を求めよ
この動画を見る
$\log_{10} 5$
の小数第二位を求めよ
ミスリードに気をつけろ！久留米大（医）
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
(1)$\displaystyle \frac{3}{2\sqrt13-7}$
整数部分と小数部分を求めよ
(2)$\displaystyle \frac{2}{a-\sqrt7}$
整数部分が5である。整数aを求めよ
久留米大(医)過去問
この動画を見る
(1)$\displaystyle \frac{3}{2\sqrt13-7}$
整数部分と小数部分を求めよ
(2)$\displaystyle \frac{2}{a-\sqrt7}$
整数部分が5である。整数aを求めよ
久留米大(医)過去問
整数問題 あれを使えばスッキリ解決
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
a,bが互いに素ならば、abとa²-b²も互いに素であることを示せ
この動画を見る
a,bが互いに素ならば、abとa²-b²も互いに素であることを示せ