 京都大学
京都大学
 京都大学
京都大学
【n進法】同じ桁数になるようなもの?【京都大学】

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
ある自然数を八進法、九進法、十進法でそれぞれ表したとき、桁数がすべて同じになった。このような自然数で最大のものを求めよ。ただし、必要なら次を用いてよい。
0.3010<log₁₀2<0.3011 , 0.4771<log₁₀3<0.4772
この動画を見る
ある自然数を八進法、九進法、十進法でそれぞれ表したとき、桁数がすべて同じになった。このような自然数で最大のものを求めよ。ただし、必要なら次を用いてよい。
0.3010<log₁₀2<0.3011 , 0.4771<log₁₀3<0.4772
福田の数学〜京都大学2025文系第5問〜平面が定点を通ることの証明

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#平面上のベクトル#恒等式・等式・不等式の証明#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{5}$
座標空間の$4$点$O,A,B,C$同一平面上にないとする。
$s,t,u$は$0$でない実数とする。
直線$OA$上の点$L$、直線$OB$の点$M$、直線$OC$上の点$N$を
$\overrightarrow{ OL }=s\overrightarrow{ OA},\quad \overrightarrow{ OM }=t\overrightarrow{ OB},\quad \overrightarrow{ ON }=u\overrightarrow{ OC }$
が成り立つようにとる。
$s,t,u$が$\dfrac{1}{s}+\dfrac{2}{t}+\dfrac{3}{u}=4$を満たす範囲で
あらゆる値をとるとき、
$3$点$L,M,N$の定める平面$LMN$は、
$s,t,u$の値に無関係な一定の点を通ることを示せ。
$2025$年京都大学文系過去問題
この動画を見る
$\boxed{5}$
座標空間の$4$点$O,A,B,C$同一平面上にないとする。
$s,t,u$は$0$でない実数とする。
直線$OA$上の点$L$、直線$OB$の点$M$、直線$OC$上の点$N$を
$\overrightarrow{ OL }=s\overrightarrow{ OA},\quad \overrightarrow{ OM }=t\overrightarrow{ OB},\quad \overrightarrow{ ON }=u\overrightarrow{ OC }$
が成り立つようにとる。
$s,t,u$が$\dfrac{1}{s}+\dfrac{2}{t}+\dfrac{3}{u}=4$を満たす範囲で
あらゆる値をとるとき、
$3$点$L,M,N$の定める平面$LMN$は、
$s,t,u$の値に無関係な一定の点を通ることを示せ。
$2025$年京都大学文系過去問題
福田の数学〜京都大学2025文系第3問〜確率漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
$n$は正の整数とする。
$1$枚の硬貨を投げ、
表が出たら$1$、裏が出たら$2$と記録する。
この試行を$n$回繰り返し、
記録された順に数字を左から
並べて$n$桁の数$X$を作る。
ただし、数の表し方は十進法とする。
このとき、$X$が$6$で割り切れる確率を求めよ。
$2025$年京都大学文系過去問題
この動画を見る
$\boxed{3}$
$n$は正の整数とする。
$1$枚の硬貨を投げ、
表が出たら$1$、裏が出たら$2$と記録する。
この試行を$n$回繰り返し、
記録された順に数字を左から
並べて$n$桁の数$X$を作る。
ただし、数の表し方は十進法とする。
このとき、$X$が$6$で割り切れる確率を求めよ。
$2025$年京都大学文系過去問題
福田の数学〜京都大学2025文系第2問〜恒等式

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
実数$a,b$についての次の条件(*)を考える。
(*)ある実数係数の$2$次式$f(x)$と、
ある実数$c$に対して、
$x$についての恒等式
$\dfrac{1}{8}x^4+ax^3+bx^2=f(f(x))+c \cdots ①$
が成り立つ。
この条件(*)を満たす点$(a,b)$全体の集合を
座標平面上に図示せよ。
$2025$年京都大学文系過去問題
この動画を見る
$\boxed{2}$
実数$a,b$についての次の条件(*)を考える。
(*)ある実数係数の$2$次式$f(x)$と、
ある実数$c$に対して、
$x$についての恒等式
$\dfrac{1}{8}x^4+ax^3+bx^2=f(f(x))+c \cdots ①$
が成り立つ。
この条件(*)を満たす点$(a,b)$全体の集合を
座標平面上に図示せよ。
$2025$年京都大学文系過去問題
福田の数学〜京都大学2025文系第1問(2)〜整数の割り算で割り切れる条件

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(2)$n^4+6n^2+23$が$n^2+n+3$で
割り切れるような正の整数$n$をすべて求めよ。
$2025$年京都大学文系過去問題
この動画を見る
$\boxed{1}$
(2)$n^4+6n^2+23$が$n^2+n+3$で
割り切れるような正の整数$n$をすべて求めよ。
$2025$年京都大学文系過去問題
福田の数学〜京都大学2025文系第1問(1)〜指数・対数の計算

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
$x,y,z$は実数で
$2025^x=3^y=5^z$を満たすとする。
このとき、
$2xy+4xz-yz=0$であることを示せ。
$2025$年京都大学文系過去問題
この動画を見る
$\boxed{1}$
$x,y,z$は実数で
$2025^x=3^y=5^z$を満たすとする。
このとき、
$2xy+4xz-yz=0$であることを示せ。
$2025$年京都大学文系過去問題
福田の数学〜京都大学2025理系第6問〜確率確率漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{6}$
$n$は$2$以上の整数とする。
$1$枚の硬貨を続けて$n$回投げる。
このとき、$k$回目$(1\leqq l \leqq n)$に表が出たら
$X_k=1$、裏が出たら$X_k=0$として、
$X_1,X_2,\cdots ,X_n$を定める。
$Y_n=\displaystyle \sum_{k-2}^{n} X_{k-1}X_k$とするとき、
$Y_n$が奇数である確率$p_n$を求めよ。
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{6}$
$n$は$2$以上の整数とする。
$1$枚の硬貨を続けて$n$回投げる。
このとき、$k$回目$(1\leqq l \leqq n)$に表が出たら
$X_k=1$、裏が出たら$X_k=0$として、
$X_1,X_2,\cdots ,X_n$を定める。
$Y_n=\displaystyle \sum_{k-2}^{n} X_{k-1}X_k$とするとき、
$Y_n$が奇数である確率$p_n$を求めよ。
$2025$年京都大学理系過去問題
福田の数学〜京都大学2025理系第5問〜媒介変数表示で表された曲線

単元:
#大学入試過去問(数学)#平面上の曲線#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#京都大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{5}$
$\theta$は実数とする。
$xyz$空間の$2$点
$A\left(0,0,\dfrac{\sqrt2}{4}\right),P\left(\cos\theta,\sin\theta,\dfrac{1}{2}\cos\theta\right)$を
通る直線$AP$が$xy$平面と交わるとき、
その交点を$Q$とする。
$\theta$が$-\dfrac{\pi}{4}\lt \theta \lt \dfrac{\pi}{4}$の範囲を動くときの
点$Q$の軌跡を求め、その軌跡を$xy$平面上に図示せよ。
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{5}$
$\theta$は実数とする。
$xyz$空間の$2$点
$A\left(0,0,\dfrac{\sqrt2}{4}\right),P\left(\cos\theta,\sin\theta,\dfrac{1}{2}\cos\theta\right)$を
通る直線$AP$が$xy$平面と交わるとき、
その交点を$Q$とする。
$\theta$が$-\dfrac{\pi}{4}\lt \theta \lt \dfrac{\pi}{4}$の範囲を動くときの
点$Q$の軌跡を求め、その軌跡を$xy$平面上に図示せよ。
$2025$年京都大学理系過去問題
福田の数学〜京都大学2025理系第4問〜平面が定点を通過する条件

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
座標空間の$4$点$O,A,B,C$は同一平面上にないとする。
$s,t,u$は$0$でない実数とする。
直線$OA$上の点$L$、
直線$OB$上の点$M$、直線$OC$上の点$N$を
$\overrightarrow{ OL }=s\overrightarrow{ OA },\overrightarrow{ OM }=t\overrightarrow{ OB },\overrightarrow{ ON }=u\overrightarrow{ OC }$が
成り立つようにとる。
(1)$s,t,u$が$\dfrac{1}{s}+\dfrac{2}{t}+\dfrac{3}{u}=4$を満たす範囲で
あらゆる値をとるとき、
$3$点$L,M,N$の定める平面$LMN$は、
$s,t,u$の値に無関係な一定の点$P$を通ることを示せ。
さらに、そのような点$P$はただ一つに定まることを示せ。
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{4}$
座標空間の$4$点$O,A,B,C$は同一平面上にないとする。
$s,t,u$は$0$でない実数とする。
直線$OA$上の点$L$、
直線$OB$上の点$M$、直線$OC$上の点$N$を
$\overrightarrow{ OL }=s\overrightarrow{ OA },\overrightarrow{ OM }=t\overrightarrow{ OB },\overrightarrow{ ON }=u\overrightarrow{ OC }$が
成り立つようにとる。
(1)$s,t,u$が$\dfrac{1}{s}+\dfrac{2}{t}+\dfrac{3}{u}=4$を満たす範囲で
あらゆる値をとるとき、
$3$点$L,M,N$の定める平面$LMN$は、
$s,t,u$の値に無関係な一定の点$P$を通ることを示せ。
さらに、そのような点$P$はただ一つに定まることを示せ。
$2025$年京都大学理系過去問題
福田の数学〜京都大学2025理系第2問〜不定方程式で表された数の最小値

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
正の整数$x,y,z$を用いて
$N=9z^2=x^6+y^4$
と表される正の整数$N$の最小値を求めよ。
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{2}$
正の整数$x,y,z$を用いて
$N=9z^2=x^6+y^4$
と表される正の整数$N$の最小値を求めよ。
$2025$年京都大学理系過去問題
福田の数学〜京都大学2025理系第1問(2−2)〜定積分の計算
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
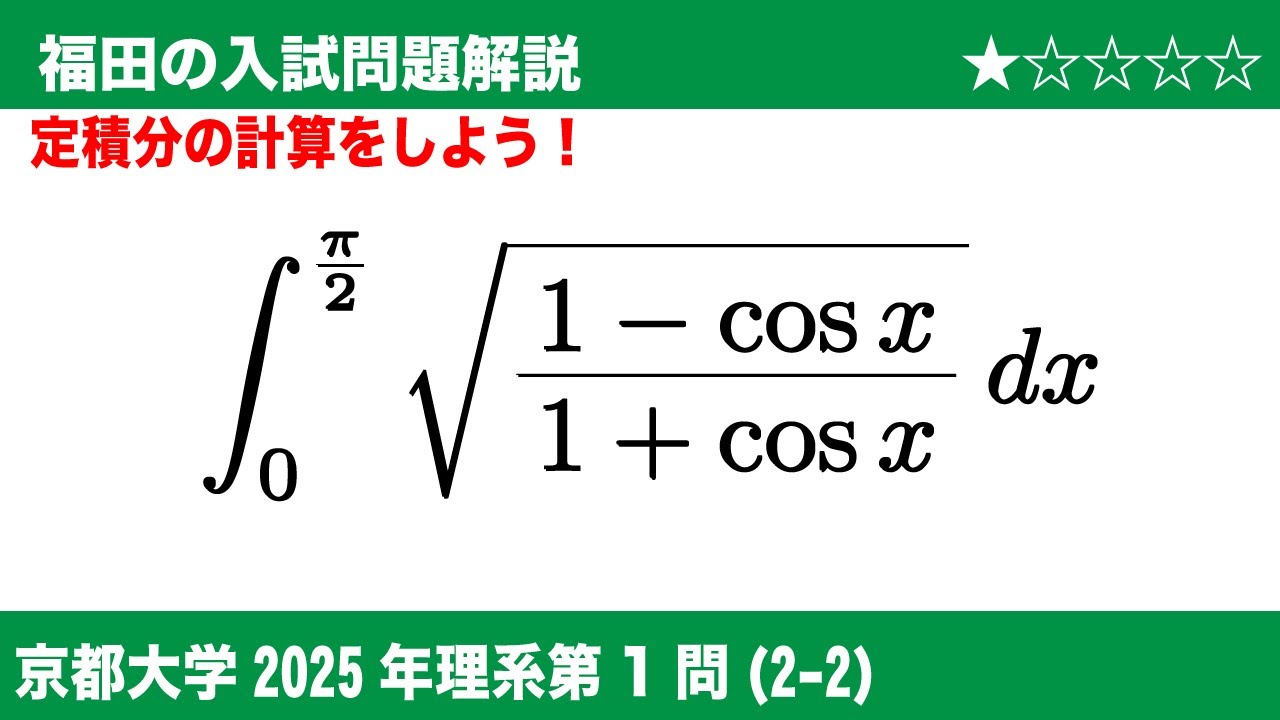
(2-2)次の定積分の値を求めよ。
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{\dfrac{1-\cos x}{1+\cos x}}dx$
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{1}$
(2-2)次の定積分の値を求めよ。
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{\dfrac{1-\cos x}{1+\cos x}}dx$
$2025$年京都大学理系過去問題
福田の数学〜京都大学2025理系第1問(2−1)〜定積分の計算
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
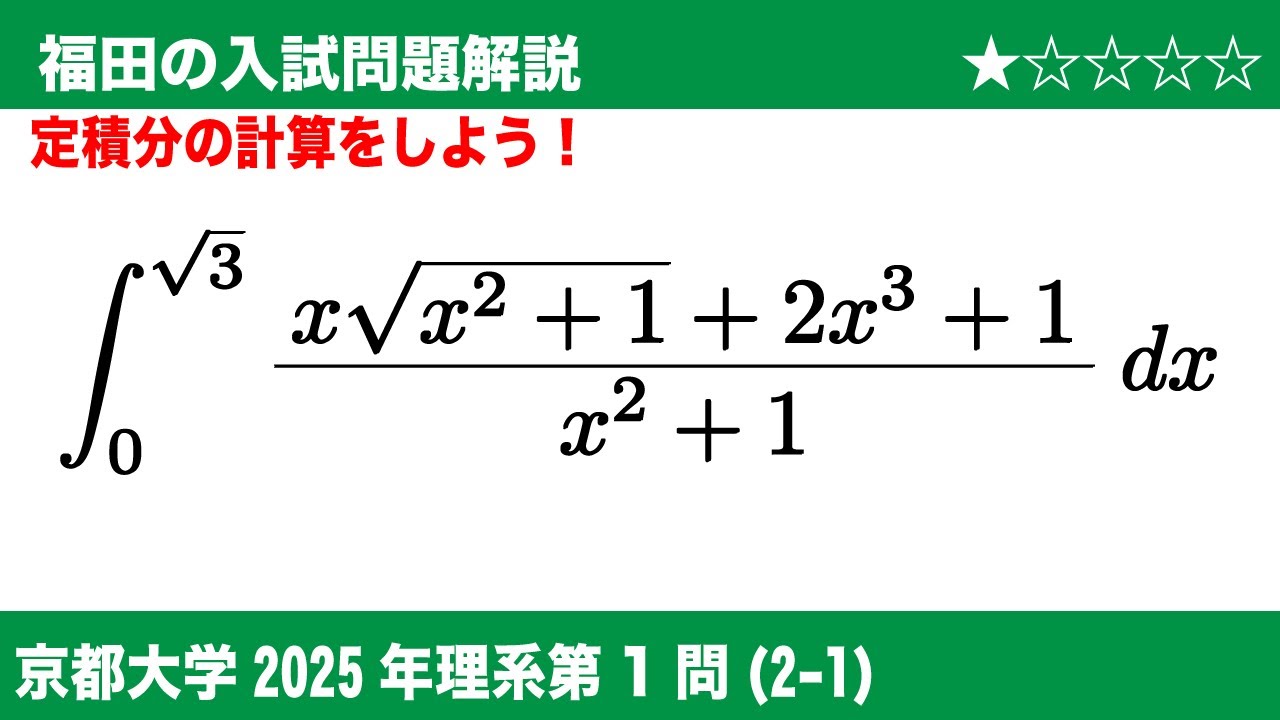
(2-1)次の定積分の値を求めよ。
$\displaystyle \int_{0}^{\sqrt3} \dfrac{x\sqrt{x^2+1}+2x^3+1}{x^2+1}dx$
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{1}$
(2-1)次の定積分の値を求めよ。
$\displaystyle \int_{0}^{\sqrt3} \dfrac{x\sqrt{x^2+1}+2x^3+1}{x^2+1}dx$
$2025$年京都大学理系過去問題
福田の数学〜京都大学2025理系第1問(1)〜複素数の絶対値の取り得る値の最大最小

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(1)$i$は虚数単位とする。
複素数$z$が、
絶対値が$2$である複素数全体を動くとき、
$\left \vert z-\dfrac{i}{z}\right \vert$
の最大値と最小値を求めよ。
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{1}$
(1)$i$は虚数単位とする。
複素数$z$が、
絶対値が$2$である複素数全体を動くとき、
$\left \vert z-\dfrac{i}{z}\right \vert$
の最大値と最小値を求めよ。
$2025$年京都大学理系過去問題
【高校数学】京都大学の定積分の問題は半角の公式で攻略できた!

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
■【京都大学 2025】
次の定積分の値を求めよ。
$\displaystyle \int_0^{\frac{π}{2}}\sqrt{\frac{1-cosx}{1+cosx}}dx$
この動画を見る
■【京都大学 2025】
次の定積分の値を求めよ。
$\displaystyle \int_0^{\frac{π}{2}}\sqrt{\frac{1-cosx}{1+cosx}}dx$
【高校数学】京都大学の定積分の問題はとにかく基本に忠実に!

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
【京都大学 2025】
次の定積分の値を求めよ。
$\displaystyle \int _0^\sqrt{3}\frac{x\sqrt{x^2+1}+2x^3+1}{x^2+1}dx$
この動画を見る
【京都大学 2025】
次の定積分の値を求めよ。
$\displaystyle \int _0^\sqrt{3}\frac{x\sqrt{x^2+1}+2x^3+1}{x^2+1}dx$
素数を扱う整数問題の良問!分からなければ実験あるのみ!【京都大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
f(x)=x³+2x²+2
|f(n)|と|f(n+1)|が素数となる整数nをすべて求めよ。
この動画を見る
f(x)=x³+2x²+2
|f(n)|と|f(n+1)|が素数となる整数nをすべて求めよ。
京大!?教科書レベル!?解けますよね?【京都大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
8.94^18の整数部分は何桁か。また、最高位からの2桁の数字を求めよ。例えば、12345.6789の最高位の2桁は12を指す。
ただし、0.951<log10_8.94<0.952, 0.113<log10_1.3<0.114, 0.146<log10_1.4<0.147 であることは用いてよい。
この動画を見る
8.94^18の整数部分は何桁か。また、最高位からの2桁の数字を求めよ。例えば、12345.6789の最高位の2桁は12を指す。
ただし、0.951<log10_8.94<0.952, 0.113<log10_1.3<0.114, 0.146<log10_1.4<0.147 であることは用いてよい。
京大の三角関数!18度系の三角比はどう扱う? #Shorts #ずんだもん #勉強 #数学

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
半径1の円に内接する正五角形の一辺の長さが1.15より大きいか否かを理由を付けて判定せよ。
この動画を見る
半径1の円に内接する正五角形の一辺の長さが1.15より大きいか否かを理由を付けて判定せよ。
二次関数とて侮ることなかれ。難問です【京都大学】【数学 入試問題】

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
aを正の定数とする。次の関数の最大値を求めよ。
f(x)=|x²-(ax+3a²/4)|+ax+3a²/4 (-1<=x<=1)
この動画を見る
aを正の定数とする。次の関数の最大値を求めよ。
f(x)=|x²-(ax+3a²/4)|+ax+3a²/4 (-1<=x<=1)
疲労を求める?京大数学を2通りで解説!【京都大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
Aが毎時akmの一定の速さで、ある地点から出発し、lkm進んだのち、Bが同一地点を出発し、同一の路をへて一定の速さでAを追う。BがAに追いつくまでの疲労を最小にするには、どんな速さで進めばよいか。ただし、疲労は速さの二乗と時間とに比例するものとする。
この動画を見る
Aが毎時akmの一定の速さで、ある地点から出発し、lkm進んだのち、Bが同一地点を出発し、同一の路をへて一定の速さでAを追う。BがAに追いつくまでの疲労を最小にするには、どんな速さで進めばよいか。ただし、疲労は速さの二乗と時間とに比例するものとする。
京大の不等式の証明問題!3通りで解いてみました【京都大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
0<x(1-x²)√x/2が成り立つことを証明せよ。
この動画を見る
0<x(1-x²)√x/2が成り立つことを証明せよ。
気付けば一瞬!内心が絡んだ京大のベクトル!【京都大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
⊿ABCの内心をPとする。PA+PB+PC=0が成り立っているとき、この三角形は正三角形であることを示せ。
この動画を見る
⊿ABCの内心をPとする。PA+PB+PC=0が成り立っているとき、この三角形は正三角形であることを示せ。
落とせないベクトル!京大でもびびる必要なし!【京都大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数C
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
三角形ABCと点Pに対して、次の二つの条件は同値であることを証明せよ。
(i) 点Pは三角形ABCの内部(周は除く)にある
(ii)正の数a,b,cがあって、aPA+bPB+cPC=0が成り立つ。
この動画を見る
三角形ABCと点Pに対して、次の二つの条件は同値であることを証明せよ。
(i) 点Pは三角形ABCの内部(周は除く)にある
(ii)正の数a,b,cがあって、aPA+bPB+cPC=0が成り立つ。
相加平均相乗平均の関係を使えそうだけど、どう使う!?京大の証明!どう解く? #Shorts #ずんだもん #勉強 #数学

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
a,b,cを正の数とする。
2((a+b)/2 -√ab)<=3((a+b+c)/3 -³√abc)
を証明せよ。
この動画を見る
a,b,cを正の数とする。
2((a+b)/2 -√ab)<=3((a+b+c)/3 -³√abc)
を証明せよ。
n進法って対策してない人が多いから差がつく!京大の入試問題!どう解く? #Shorts #ずんだもん #勉強

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
nを4以上の自然数とする。
2,12,1331がすべてn進法で表記されているとして
2¹²=1331
が成り立っている。このときnはいくつか。十進法で答えよ。
この動画を見る
nを4以上の自然数とする。
2,12,1331がすべてn進法で表記されているとして
2¹²=1331
が成り立っている。このときnはいくつか。十進法で答えよ。
100個の絶対値の合計!?どう解く? #Shorts #ずんだもん #勉強

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
nが整数であるとき、S=|n-1|+|n-2|+・・・+|n-100|の最小値を求めよ。
この動画を見る
nが整数であるとき、S=|n-1|+|n-2|+・・・+|n-100|の最小値を求めよ。
高校2年生から京大に挑戦!積分習いたての人にも解ける問題【京都大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
2x, 5-x, 2のうち最小の数をf(x)とし、g(x)=xf(x)とおく。y=g(x)とx軸で囲まれた部分の面積は?
この動画を見る
2x, 5-x, 2のうち最小の数をf(x)とし、g(x)=xf(x)とおく。y=g(x)とx軸で囲まれた部分の面積は?
この式はあれしかない!!どう解く?

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
多項式(x^100+1)^100+(x^2+1)^100+1は多項式x^2+x+1で割り切れるか。
この動画を見る
多項式(x^100+1)^100+(x^2+1)^100+1は多項式x^2+x+1で割り切れるか。
【高校数学】京大の整数問題!どう解く?

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
pを3以上の素数とする。4個の整数a,b,c,dが次の3条件
a+b+c+d=0
ad-bc-+p=0
a≧b≧c≧d
を満たすとき、a,b,c,dをpで表せ。
この動画を見る
pを3以上の素数とする。4個の整数a,b,c,dが次の3条件
a+b+c+d=0
ad-bc-+p=0
a≧b≧c≧d
を満たすとき、a,b,c,dをpで表せ。
差がつく!素数を扱う整数問題!【京都大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
pを3以上の素数とする。4個の整数a,b,c,dが次の3条件
a+b+c+d=0,ad-bc+p=0,a≧b≧c≧d
を満たすとき、a,b,c,dをpで表せ。
この動画を見る
pを3以上の素数とする。4個の整数a,b,c,dが次の3条件
a+b+c+d=0,ad-bc+p=0,a≧b≧c≧d
を満たすとき、a,b,c,dをpで表せ。
