東京理科大学
東京理科大学
福田の数学〜東京理科大学2024創域理工学部第3問〜関数の増減と変曲点と体積面積
単元：
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$関数$f(x)$を
$f(x)=\frac{logx}{\sqrt{x}} (x\gt 0)$
と定める。ただし、logは自然対数とする。
(1)導関数$f'(x)$と第2次導関数$f''(x)$をそれぞれ求めよ。
座標平面上の曲線$y=f(x)(x \gt 0)$を$C$とおき、$C$の交点を$P$とおく。$C$と$x$軸の交点を$Q$とする。$C$と直線$PQ$で囲まれた部分を$A$とし、$A$を$x$軸の周りに1回転して得られる回転体の体積を$V$とする。
(2)$P$の座標を求めよ。
(3)$V$を求めよ。
(4)$A$の面積を求めよ。
この動画を見る
$\boxed{3}$関数$f(x)$を
$f(x)=\frac{logx}{\sqrt{x}} (x\gt 0)$
と定める。ただし、logは自然対数とする。
(1)導関数$f'(x)$と第2次導関数$f''(x)$をそれぞれ求めよ。
座標平面上の曲線$y=f(x)(x \gt 0)$を$C$とおき、$C$の交点を$P$とおく。$C$と$x$軸の交点を$Q$とする。$C$と直線$PQ$で囲まれた部分を$A$とし、$A$を$x$軸の周りに1回転して得られる回転体の体積を$V$とする。
(2)$P$の座標を求めよ。
(3)$V$を求めよ。
(4)$A$の面積を求めよ。
福田の数学〜東京理科大学2024創域理工学部第1問(3)〜条件を満たす点の個数
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a,b$を正の実数とする。座標平面上に点$\textrm{A}(a,1)$をとり、自然数$n=1,2,3,\cdots$に対して点$\textrm{P}_n(n,0)$をとる。集合$U$を次で定める。
$U=\{n|n$は自然数かつ2点$\textrm{A}, \textrm{P}_n$間の距離は$b$以下$\}$
(a) $a=2$とする。$b=1$のとき、$U$の要素の個数は？また、$b=\sqrt{3}$のとき、$U$の要素の個数は？
(b) $a=\dfrac72$とする。$b=\sqrt2$のとき、$U$の要素の個数は？また、$b=2\sqrt2$のとき、$U$の要素の個数は？
(c) $b=2$のとき、$U$の要素の個数が2個となる正の整数$a$は？また、$b=5$のとき、$U$の要素の個数が9個となる最小の正の整数$a$は？
この動画を見る
$a,b$を正の実数とする。座標平面上に点$\textrm{A}(a,1)$をとり、自然数$n=1,2,3,\cdots$に対して点$\textrm{P}_n(n,0)$をとる。集合$U$を次で定める。
$U=\{n|n$は自然数かつ2点$\textrm{A}, \textrm{P}_n$間の距離は$b$以下$\}$
(a) $a=2$とする。$b=1$のとき、$U$の要素の個数は？また、$b=\sqrt{3}$のとき、$U$の要素の個数は？
(b) $a=\dfrac72$とする。$b=\sqrt2$のとき、$U$の要素の個数は？また、$b=2\sqrt2$のとき、$U$の要素の個数は？
(c) $b=2$のとき、$U$の要素の個数が2個となる正の整数$a$は？また、$b=5$のとき、$U$の要素の個数が9個となる最小の正の整数$a$は？
福田の数学〜東京理科大学2024創域理工学部第1問(2)〜三角不等式の解法
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#加法定理とその応用#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}(2)0 \leqq θ \lt 2π$のとき、次の不等式を解こう。
$sin2θ \gt 2cos(θ+\frac{π}{6})+\frac{\sqrt{3}}{2}・・・③$
$a=cosθ,b=sinθ$とおくと、次の不等式$③$は
$\boxed{キ}ab-\boxed{ク}\sqrt{\boxed{ケ}}a+\boxed{コ}b-\sqrt{2}\gt0 ・・・④$
となる。不等式$④$の左辺は
$(\boxed{サ}a+\boxed{シ})(\boxed{ス}b-\sqrt{セ})$
と因数分解できる。これより、不等式$③$の解は
$\frac{π}{\boxed{ソ}} \lt θ \lt \frac{\boxed{タ}}{\boxed{チ}}π$または$\frac{\boxed{ツ}}{\boxed{テ}}π \lt θ \lt\frac{\boxed{ト}}{\boxed{ナ}}π$
と求まる。
この動画を見る
$\boxed{1}(2)0 \leqq θ \lt 2π$のとき、次の不等式を解こう。
$sin2θ \gt 2cos(θ+\frac{π}{6})+\frac{\sqrt{3}}{2}・・・③$
$a=cosθ,b=sinθ$とおくと、次の不等式$③$は
$\boxed{キ}ab-\boxed{ク}\sqrt{\boxed{ケ}}a+\boxed{コ}b-\sqrt{2}\gt0 ・・・④$
となる。不等式$④$の左辺は
$(\boxed{サ}a+\boxed{シ})(\boxed{ス}b-\sqrt{セ})$
と因数分解できる。これより、不等式$③$の解は
$\frac{π}{\boxed{ソ}} \lt θ \lt \frac{\boxed{タ}}{\boxed{チ}}π$または$\frac{\boxed{ツ}}{\boxed{テ}}π \lt θ \lt\frac{\boxed{ト}}{\boxed{ナ}}π$
と求まる。
福田の数学〜東京理科大学2024創域理工学部第1問(1)〜複素数と三角形の外接円
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}(1)a$を正の実数とする。$x$についての方程式
$(x^2+ax+2)(x^2-ax-1)=0・・・①$
が異なる2つの実数解と異なる2つの虚数解をもつのは
$\boxed{ア} \lt a \lt \boxed{イ}\sqrt{\boxed{ウ}}・・・②$
のときである。
以下では、$a$は不等式$②$を満たす最大の整数とし、$i$は虚数単位とする。このとき、複素数平面上において、方程式$①$の異なる2つの虚数解と$3+i$を頂点とする三角形の面積は$\boxed{エ}$であり、この三角形の外接円を複素数zの方程式で表すと
$|x-\boxed{オ}|=\sqrt{\boxed{カ}}$
である。
この動画を見る
$\boxed{1}(1)a$を正の実数とする。$x$についての方程式
$(x^2+ax+2)(x^2-ax-1)=0・・・①$
が異なる2つの実数解と異なる2つの虚数解をもつのは
$\boxed{ア} \lt a \lt \boxed{イ}\sqrt{\boxed{ウ}}・・・②$
のときである。
以下では、$a$は不等式$②$を満たす最大の整数とし、$i$は虚数単位とする。このとき、複素数平面上において、方程式$①$の異なる2つの虚数解と$3+i$を頂点とする三角形の面積は$\boxed{エ}$であり、この三角形の外接円を複素数zの方程式で表すと
$|x-\boxed{オ}|=\sqrt{\boxed{カ}}$
である。
大学入試問題#902「いやーこれはしんどかった」 #東京理科大学(2010)
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
点$(x,y)$は$x^2+y^2=1$を満たしているとき
$\displaystyle \frac{2x+y+1}{3x+y+5}$の最大値と最小値を求めよ。
出典：2010年東京理科大学
この動画を見る
点$(x,y)$は$x^2+y^2=1$を満たしているとき
$\displaystyle \frac{2x+y+1}{3x+y+5}$の最大値と最小値を求めよ。
出典：2010年東京理科大学
#東京理科大学2023#定積分#ますただ
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#東京理科大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\sqrt{ e }} \displaystyle \frac{e}{x^2+e} dx$
出典：2023年東京理科大学
この動画を見る
$\displaystyle \int_{0}^{\sqrt{ e }} \displaystyle \frac{e}{x^2+e} dx$
出典：2023年東京理科大学
大学入試問題#884「ミスれん」 #東京理科大学(2022) #定積分
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#東京理科大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} \displaystyle \frac{x-4}{2x^2+5x+2}$ $dx$
出典：2022年東京理科大学
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{x-4}{2x^2+5x+2}$ $dx$
出典：2022年東京理科大学
大学入試問題#873「コメント欄が賑わいそう」 #東京理科大学(2022) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{4} \displaystyle \frac{2}{(x+1)(x+2)(x+3)} dx$
出典：2022年東京理科大学 大学入試問題
この動画を見る
$\displaystyle \int_{0}^{4} \displaystyle \frac{2}{(x+1)(x+2)(x+3)} dx$
出典：2022年東京理科大学 大学入試問題
大学入試問題#763「読みの入った式変形」 東京理科大学理学部(2003) #複素数
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$0 \lt t \lt 2\pi$とする
$z=\displaystyle \frac{1+\cos\ t+i\ \sin\ t}{1-\cos\ t-i\ \sin\ t}$
（1）$0 \lt t \lt \pi$における$z$の偏角を弧度法で表せ
（2）$\displaystyle \int_{\frac{\pi}{2}}^{\pi} |z|dt$を求めよ。
出典：2003年東京理科大学理学部 入試問題
この動画を見る
$0 \lt t \lt 2\pi$とする
$z=\displaystyle \frac{1+\cos\ t+i\ \sin\ t}{1-\cos\ t-i\ \sin\ t}$
（1）$0 \lt t \lt \pi$における$z$の偏角を弧度法で表せ
（2）$\displaystyle \int_{\frac{\pi}{2}}^{\pi} |z|dt$を求めよ。
出典：2003年東京理科大学理学部 入試問題
大学入試問題#762「再生回数は、期待できない」 東京理科大学工学部(2003) #曲線の長さ
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
曲線$y=(2x+1)\sqrt{ 2x+1 }$の区間$0 \leq x \leq \displaystyle \frac{1}{3}$にある部分の長さを求めよ。
出典：2003年東京理科大学工学部 入試問題
この動画を見る
曲線$y=(2x+1)\sqrt{ 2x+1 }$の区間$0 \leq x \leq \displaystyle \frac{1}{3}$にある部分の長さを求めよ。
出典：2003年東京理科大学工学部 入試問題
大学入試問題#761「微積の入試勉強は、まずこれから！」 東京理科大学理学部(2002) #微積
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
関数$F(x)$を
$F(x)=\displaystyle \int_{0}^{x} (\sin\ t+\cos\ t)^2 dt$と定める。
$F(x),\displaystyle \lim_{ x \to \infty } \displaystyle \frac{F(x)}{x},\displaystyle \lim_{ x \to 0 } \displaystyle \frac{F(x)}{x}$を求めよ。
出典：2002年東京理科大学理学部 入試問題
この動画を見る
関数$F(x)$を
$F(x)=\displaystyle \int_{0}^{x} (\sin\ t+\cos\ t)^2 dt$と定める。
$F(x),\displaystyle \lim_{ x \to \infty } \displaystyle \frac{F(x)}{x},\displaystyle \lim_{ x \to 0 } \displaystyle \frac{F(x)}{x}$を求めよ。
出典：2002年東京理科大学理学部 入試問題
大学入試問題#760「ほぼ一直線」 東京理科大学(2003) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
定積分
$I=\displaystyle \int_{1}^{4} t^2\sin(\displaystyle \frac{\pi}{4}t\sqrt{ t })\ dt$を求めよ。
出典：2003年東京理科大学 入試問題
この動画を見る
定積分
$I=\displaystyle \int_{1}^{4} t^2\sin(\displaystyle \frac{\pi}{4}t\sqrt{ t })\ dt$を求めよ。
出典：2003年東京理科大学 入試問題
大学入試問題#759「サムネみすった」 東京理科大学(2002) #定積分
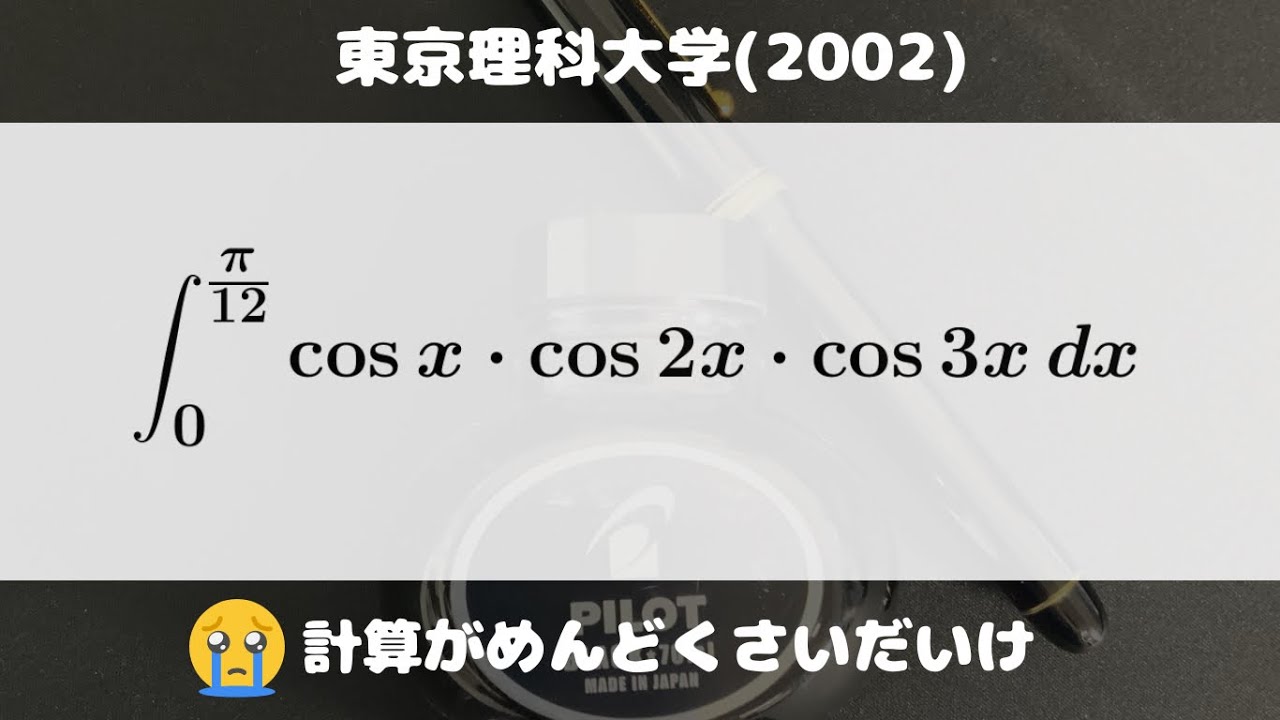
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{12}} \cos\ x・\cos\ 2x・\cos\ 3x\ dx$
出典：2002年東京理科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{12}} \cos\ x・\cos\ 2x・\cos\ 3x\ dx$
出典：2002年東京理科大学 入試問題
大学入試問題#758 「ミスりようがない。」 東京理科大学理学部(2002) #方程式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
方程式$(x+2)(x+3)(x-4)(x-5)=44$を解け。
出典：2002年東京理科大学理学部 入試問題
この動画を見る
方程式$(x+2)(x+3)(x-4)(x-5)=44$を解け。
出典：2002年東京理科大学理学部 入試問題
大学入試問題#757「綺麗な基本問題」 東京理科大学(2001) #積分方程式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
関数$f(x)=1+\displaystyle \frac{1}{2}ce^{-x}$において、定数$c$は
$c=\displaystyle \int_{0}^{\frac{\pi}{2}} e^t f(t)\sin\ t\ dt$を満たす。
このとき、$c$の値を求めよ。
出典：2001年東京理科大学工学部 入試問題
この動画を見る
関数$f(x)=1+\displaystyle \frac{1}{2}ce^{-x}$において、定数$c$は
$c=\displaystyle \int_{0}^{\frac{\pi}{2}} e^t f(t)\sin\ t\ dt$を満たす。
このとき、$c$の値を求めよ。
出典：2001年東京理科大学工学部 入試問題
大学入試問題#753「普通に超良問」 東京理科大学理工学部(1999) #積分方程式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$f(2x)=\displaystyle \int_{0}^{\pi} f(t) dt+K\ x\ \cos\ x$
$f'(\pi)=\displaystyle \frac{\pi}{2}$
を満たすとき、定数$K$の値と、関数$f(x)$を求めよ。
出典：1999年東京理科大学理工学部 入試問題
この動画を見る
$f(2x)=\displaystyle \int_{0}^{\pi} f(t) dt+K\ x\ \cos\ x$
$f'(\pi)=\displaystyle \frac{\pi}{2}$
を満たすとき、定数$K$の値と、関数$f(x)$を求めよ。
出典：1999年東京理科大学理工学部 入試問題
大学入試問題#750「超良問！」 東京理科大学工学部(2001) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{4}} \displaystyle \frac{e^{\tan\ x}}{\cos^4x} dx$
出典：2001年東京理科大学工学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}} \displaystyle \frac{e^{\tan\ x}}{\cos^4x} dx$
出典：2001年東京理科大学工学部 入試問題
大学入試問題#749「まあミスれん」 東京理科大学(2000) #不定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int e^{\sqrt[ 3 ]{ x }} dx$
出典：2000年東京理科大学工学部 入試問題
この動画を見る
$\displaystyle \int e^{\sqrt[ 3 ]{ x }} dx$
出典：2000年東京理科大学工学部 入試問題
大学入試問題#746「慣れれば瞬間部分積分！？」 東京理科大学(2024) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{3}^{5} (x-3)^3(5-x)^5 dx$
出典：2024年東京理科大学 入試問題
この動画を見る
$\displaystyle \int_{3}^{5} (x-3)^3(5-x)^5 dx$
出典：2024年東京理科大学 入試問題
大学入試問題#741「頭のラジオ体操」 東京理科大学(2009) 数列
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$b_1=\displaystyle \frac{1}{2},$
$b_{n+1}=-3b_n+\displaystyle \frac{2n^2-6n-17}{n^2+3n+2}$を満たす数列$\{b_n\}$の一般項を求めよ。
出典：2009年東京理科大学全学部 入試問題
この動画を見る
$b_1=\displaystyle \frac{1}{2},$
$b_{n+1}=-3b_n+\displaystyle \frac{2n^2-6n-17}{n^2+3n+2}$を満たす数列$\{b_n\}$の一般項を求めよ。
出典：2009年東京理科大学全学部 入試問題
大学入試問題#711「この問題好きすぎ（笑）」 東京理科大学(2013) 極限
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n^2} \sqrt[ n ]{ {}_{ 4n }P_{2n} }$
出典：2013年トウキョウ理科大学入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n^2} \sqrt[ n ]{ {}_{ 4n }P_{2n} }$
出典：2013年トウキョウ理科大学入試問題
大学入試問題#709「ちょっと大変」 東京理科大学(2012)整数問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$k,l,m,n$は自然数とする。
条件$k・l・m・n=k+l+m+n,$
$k \leq l \leq m \leq n$を満たす組$(k,l,m,n)$をすべて求めよ
出典：2012年東京理科大学 入試問題
この動画を見る
$k,l,m,n$は自然数とする。
条件$k・l・m・n=k+l+m+n,$
$k \leq l \leq m \leq n$を満たす組$(k,l,m,n)$をすべて求めよ
出典：2012年東京理科大学 入試問題
大学入試問題#708「数検1級１次でもみたことある」 東京理科大学(2013) 極限
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n}\sqrt[ n ]{ {}_{ 2n } P_n }$
出典：2013年東京理科大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n}\sqrt[ n ]{ {}_{ 2n } P_n }$
出典：2013年東京理科大学 入試問題
大学入試問題#704 東京理科大学(2013) #定積分 #Shorts
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\pi} x\ \sin\displaystyle \frac{x}{3} dx$
出典：2013年東京理科大学
この動画を見る
$\displaystyle \int_{0}^{\pi} x\ \sin\displaystyle \frac{x}{3} dx$
出典：2013年東京理科大学
大学入試問題#703「まあ落としたくない」 東京理科大学(2014) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{4} \displaystyle \frac{x}{\sqrt{ 2x+1 }} dx$
出典：2014年東京理科大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{4} \displaystyle \frac{x}{\sqrt{ 2x+1 }} dx$
出典：2014年東京理科大学 入試問題
大学入試問題#702「落としたくない」 東京理科大学(2013) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} \displaystyle \frac{x}{\sqrt{ x }+1} dx$
出典：2013年東京理科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{x}{\sqrt{ x }+1} dx$
出典：2013年東京理科大学 入試問題
大学入試問題#681「綺麗な良問」 東京理科大学(2016) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{4}} \displaystyle \frac{\sin\ 4x}{\sqrt{ 1+\sin^2x }} dx$
出典：2016年東京理科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}} \displaystyle \frac{\sin\ 4x}{\sqrt{ 1+\sin^2x }} dx$
出典：2016年東京理科大学 入試問題
大学入試問題#680「よく見る形」 東京理科大学(2015) 極限
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to \infty } (\displaystyle \frac{x+3}{x-3})^x$
出典：2015年東京理科大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to \infty } (\displaystyle \frac{x+3}{x-3})^x$
出典：2015年東京理科大学 入試問題
大学入試問題#678「基本問題」 東京理科大学(2016) 不定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{x^3}{\sqrt{ 2x^2+3 }} dx$
出典：2016年東京理科大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{x^3}{\sqrt{ 2x^2+3 }} dx$
出典：2016年東京理科大学 入試問題
大学入試問題#676「たぶん良い問題」 東京理科大学(2017) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} \displaystyle \frac{4x+1}{x^4+2x^3+x+2}dx$
出典：2017年東京理科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{4x+1}{x^4+2x^3+x+2}dx$
出典：2017年東京理科大学 入試問題