 数と式
数と式
 数と式
数と式
式の値 高校数学

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
abc=1のとき
$\frac{1}{ab+a+1} +\frac{1}{bc+b+1} + \frac{1}{ca+c+1}$
の値を求めよ
この動画を見る
abc=1のとき
$\frac{1}{ab+a+1} +\frac{1}{bc+b+1} + \frac{1}{ca+c+1}$
の値を求めよ
東京医科大 楽ちん問題
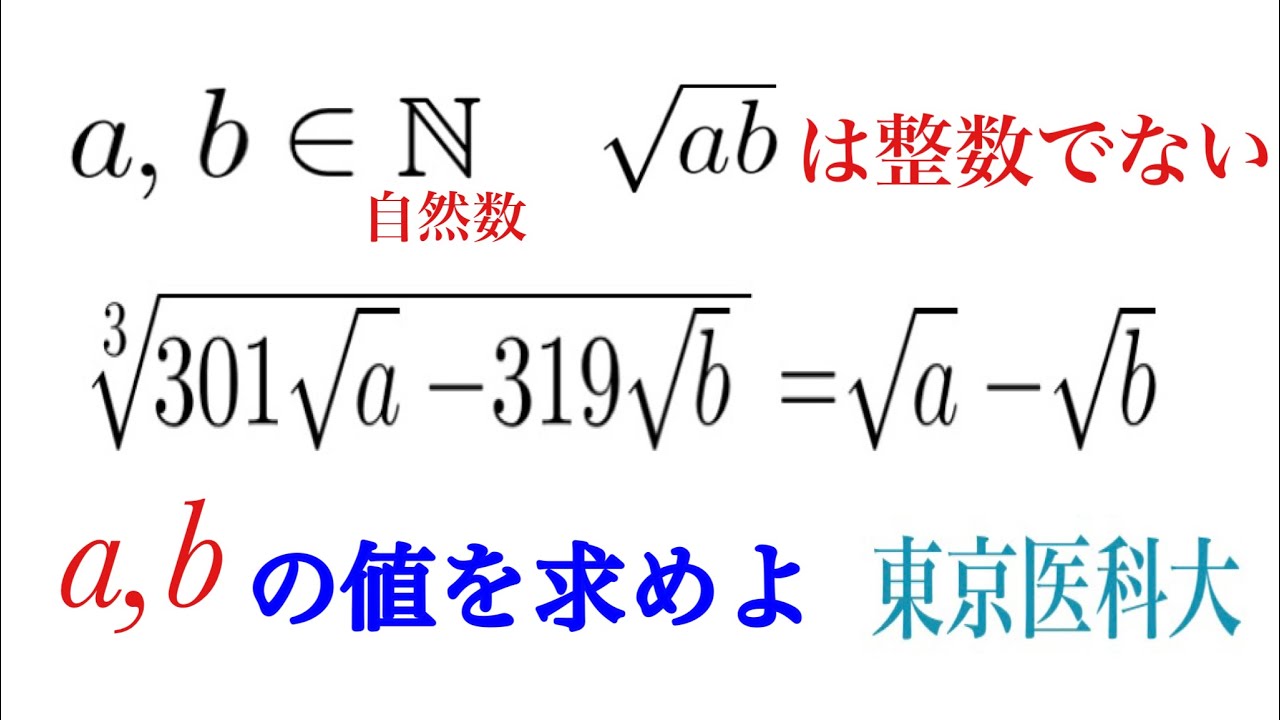
単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)#東京医科大学#東京医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b$は自然数であり、$\sqrt{ab}$は整数でないとき、
$\sqrt[3]{301\sqrt{a}-319\sqrt{b}}=\sqrt{a}-\sqrt{b}$
をみたす$a,b$を求めよ。
この動画を見る
$a,b$は自然数であり、$\sqrt{ab}$は整数でないとき、
$\sqrt[3]{301\sqrt{a}-319\sqrt{b}}=\sqrt{a}-\sqrt{b}$
をみたす$a,b$を求めよ。
x3乗=1
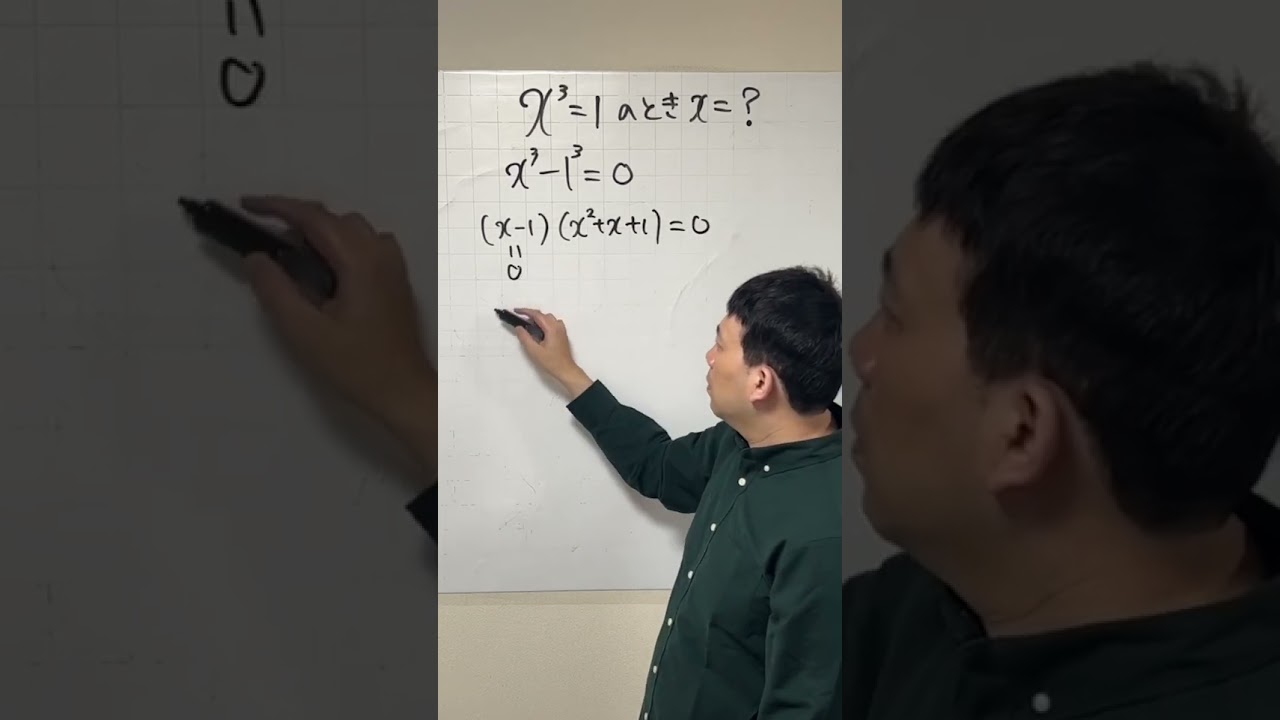
マイナス乗とは?2分の1乗とは?基本から丁寧に解説
2乗➖2乗は○と○の積を使ってもいいけどさ 大阪教育大附属平野

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$340^2-337^2-3^2$
大阪教育大学附属高等学校平野校舎
2022
この動画を見る
$340^2-337^2-3^2$
大阪教育大学附属高等学校平野校舎
2022
部分分数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1}{2} + \frac{1}{6} + \frac{1}{12} +\frac{1}{20}$
この動画を見る
$\frac{1}{2} + \frac{1}{6} + \frac{1}{12} +\frac{1}{20}$
【ホーン・フィールドがていねいに解説】数と式 4S数学問題集数Ⅰ 83,84,85 1次不等式の利用2
単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題83
1個800円の品物がある。入会金500円を払って会員になると、この品物を6%引きで買うことができる。入会して品物を買う場合、何個以上買えば入会しないで買うより安くなるか。ただし、消費税は考えないものとする。
問題84
13%と5%の食塩水を混ぜて400gの食塩水を作った。その濃度が10%以上であるとき、混ぜた5%の食塩水は何g以下か。
問題85
ある高等学校の1年全員が長いすに座っていくとき、1脚に6人ずつ座っていくと15人が座れなくなる。また、1脚に7人ずつ座っていくと、使わない長いすが3脚できる。長いすの数は何脚以上何脚以下か。
この動画を見る
問題83
1個800円の品物がある。入会金500円を払って会員になると、この品物を6%引きで買うことができる。入会して品物を買う場合、何個以上買えば入会しないで買うより安くなるか。ただし、消費税は考えないものとする。
問題84
13%と5%の食塩水を混ぜて400gの食塩水を作った。その濃度が10%以上であるとき、混ぜた5%の食塩水は何g以下か。
問題85
ある高等学校の1年全員が長いすに座っていくとき、1脚に6人ずつ座っていくと15人が座れなくなる。また、1脚に7人ずつ座っていくと、使わない長いすが3脚できる。長いすの数は何脚以上何脚以下か。
場合分け不要!!絶対値を含む不等式

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
(1) $|x-1|<2$
(2) $|x-1|<2x$
不等式を解け
この動画を見る
(1) $|x-1|<2$
(2) $|x-1|<2x$
不等式を解け
難しい因数分解やろうぜ【高校数学】

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
難しい因数分解
(1)$a(l^2-c^2)+l(c^2-a^2)+c(a^2-l^2)$
(2)$a^2(b+c)+b^2(c+a)+c^2(a+b)+2abc$
(3)$2x^2+5xy+2y^2-x+y-1$
(4)$a(b^2-c^2)+b(c^2-a^2)+c(a^2-b^2)$
(5)$x^2-y^2-zx+yz$
(6)$a(b+c)^2+b(c+a)^2+c(a+b)^2-4abc$
この動画を見る
難しい因数分解
(1)$a(l^2-c^2)+l(c^2-a^2)+c(a^2-l^2)$
(2)$a^2(b+c)+b^2(c+a)+c^2(a+b)+2abc$
(3)$2x^2+5xy+2y^2-x+y-1$
(4)$a(b^2-c^2)+b(c^2-a^2)+c(a^2-b^2)$
(5)$x^2-y^2-zx+yz$
(6)$a(b+c)^2+b(c+a)^2+c(a+b)^2-4abc$
【スムーズに!スマートに!】一次方程式:関西大倉高等学校~全国入試問題解法

単元:
#数学(中学生)#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#高校入試過去問(数学)#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
方程式$ 3-\dfrac{x-5}{12}=0.25(3x+2)$を解け.
関西大倉高校過去問
この動画を見る
方程式$ 3-\dfrac{x-5}{12}=0.25(3x+2)$を解け.
関西大倉高校過去問
筆算不要!!

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt {999 \times 997 +1}$
この動画を見る
$\sqrt {999 \times 997 +1}$
式の値 早稲田実業

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^2 - b^2 -a -b = 0$のとき
$a^2+b^2-2ab-a+b=?$
(a>0,b>0)
早稲田実業学校
この動画を見る
$a^2 - b^2 -a -b = 0$のとき
$a^2+b^2-2ab-a+b=?$
(a>0,b>0)
早稲田実業学校
絶対値を含む方程式
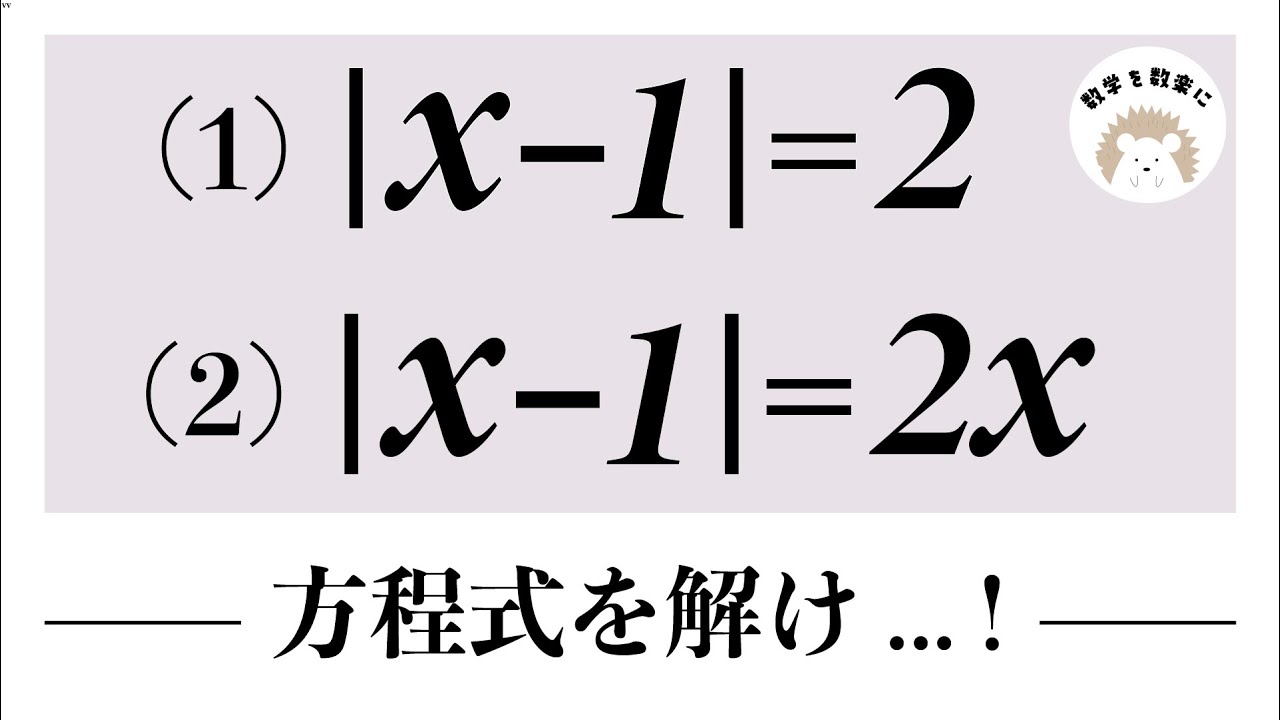
単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
(1)|x-1|=2
(2)|x-1|=2x
方程式を解け
この動画を見る
(1)|x-1|=2
(2)|x-1|=2x
方程式を解け
6乗−6乗の因数分解

ハートで分けろ 高校数学 式の値
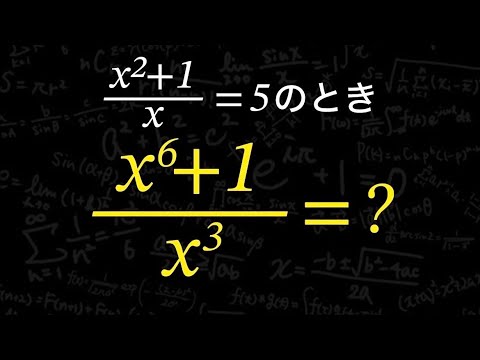
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{x^2+1}{x}=5$のとき
$\frac{x^6+1}{x^3}=?$
この動画を見る
$\frac{x^2+1}{x}=5$のとき
$\frac{x^6+1}{x^3}=?$
工夫して解こうよ!平方根の計算

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{(\sqrt 3 + 1)^2}{\sqrt 2} + \frac{(\sqrt 6 - \sqrt 2 )^2}{2 \sqrt 2}$
滝高等学校
この動画を見る
$\frac{(\sqrt 3 + 1)^2}{\sqrt 2} + \frac{(\sqrt 6 - \sqrt 2 )^2}{2 \sqrt 2}$
滝高等学校
2024を素因数分解

福田の数学〜慶應義塾大学2023年看護医療学部第2問(2)〜ルートが自然数になる条件

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ (2)$n$を自然数とする。$\sqrt{\frac{200}{\sqrt n}}$が自然数となるような$n$をすべて求めると$n$=$\boxed{\ \ サ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{2}$ (2)$n$を自然数とする。$\sqrt{\frac{200}{\sqrt n}}$が自然数となるような$n$をすべて求めると$n$=$\boxed{\ \ サ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
2=3
数と式 真偽の調べ方【いつものシミズ君がていねいに解説】

単元:
#数Ⅰ#数と式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
a,bは実数とする。次の命題の真偽を求めよ。
(1)$ab=0$ならば$a^2+b^2=0$である。
(2)$a^2=4$ならば$\vert a+1\vert \geqq 1$である。
(3)$ab$が有理数であるならば、a、bはともに有理数である。
(4)$a+b、ab$がともに有理数ならば、a、bはともに有理数である。
全体集合を$U$とし、条件$p、q$を満たす全体の集合を、それぞれ$P.Q$とする。
命題$p$(補集合)⇒$q$が真であるとき、$P、Q$について常に成り立つ事をすべて選べ。
①$P=Q$
②$Q⊂P$
③$Q$(補集合)$⊂P$
④$P⊂Q$(補集合)
⑤$P∪Q$(補集合)$=P$
⑥$P∪Q$(補集合)$=Q$(補集合)
⑦$P∩Q=∅$
⑧$P∪Q=U$
この動画を見る
a,bは実数とする。次の命題の真偽を求めよ。
(1)$ab=0$ならば$a^2+b^2=0$である。
(2)$a^2=4$ならば$\vert a+1\vert \geqq 1$である。
(3)$ab$が有理数であるならば、a、bはともに有理数である。
(4)$a+b、ab$がともに有理数ならば、a、bはともに有理数である。
全体集合を$U$とし、条件$p、q$を満たす全体の集合を、それぞれ$P.Q$とする。
命題$p$(補集合)⇒$q$が真であるとき、$P、Q$について常に成り立つ事をすべて選べ。
①$P=Q$
②$Q⊂P$
③$Q$(補集合)$⊂P$
④$P⊂Q$(補集合)
⑤$P∪Q$(補集合)$=P$
⑥$P∪Q$(補集合)$=Q$(補集合)
⑦$P∩Q=∅$
⑧$P∪Q=U$
数と式 集合の考え方【いつものシミズ君がていねいに解説】

単元:
#数Ⅰ#数と式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$U={1,2,3,4,5,6,7,8,9}$を全体集合とする。$U$の部分集合A、Bについて
$A∩B={2}$ $A$(補集合)$∩B={4,6,8}$ $A$(補集合)$∩B$(補集合)$={1.9}$
であるとき、次の$∩$を求めよ。
(1)$A∪B$
(2)$B$
(3)$A∩B$(補集合)
$U={x|1≦x≦10、xは整数}$を全体集合とする。$U$の部分集合
$A={1,2,3,4,8},B={3,4,5,6},C{2,3,6,7}$
について、次の集合を求めよ。
(1)$A∩B∩C$
(2)$A∪B∪C$
(3)$A∩B∩C$(補集合)
(4)$A$(補集合)$∩B∩C$(補集合)
(5)$(A∩B∩C)$(補集合)
(6)$(A∪C)∩B$(補集合)
$A={1、3、3a-2}$, $B={-5、a+2、a^2-2a+1}$,$A∩B={1、4}$のとき
定数aの値と和集合$A∪B$を求めよ。
この動画を見る
$U={1,2,3,4,5,6,7,8,9}$を全体集合とする。$U$の部分集合A、Bについて
$A∩B={2}$ $A$(補集合)$∩B={4,6,8}$ $A$(補集合)$∩B$(補集合)$={1.9}$
であるとき、次の$∩$を求めよ。
(1)$A∪B$
(2)$B$
(3)$A∩B$(補集合)
$U={x|1≦x≦10、xは整数}$を全体集合とする。$U$の部分集合
$A={1,2,3,4,8},B={3,4,5,6},C{2,3,6,7}$
について、次の集合を求めよ。
(1)$A∩B∩C$
(2)$A∪B∪C$
(3)$A∩B∩C$(補集合)
(4)$A$(補集合)$∩B∩C$(補集合)
(5)$(A∩B∩C)$(補集合)
(6)$(A∪C)∩B$(補集合)
$A={1、3、3a-2}$, $B={-5、a+2、a^2-2a+1}$,$A∩B={1、4}$のとき
定数aの値と和集合$A∪B$を求めよ。
計算が面白い問題 大阪教育大附属池田

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
18のすべての正の約数の正の平方根の和は$(1+\sqrt 2)x$という式で表される。
x=?
大阪教育大学附属高等学校平野校舎
この動画を見る
18のすべての正の約数の正の平方根の和は$(1+\sqrt 2)x$という式で表される。
x=?
大阪教育大学附属高等学校平野校舎
数と式 式の展開②【化学のタカシーがていねいに解説】

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
展開せよ
$(a+1)^3$ $(x+3y)^3$
$(2a-1)^3$ $(-3a+2b)^3$
展開せよ
$(a+5)(a^2-5a+25)$
$(3-a)(9+3a+a^2)$
$(2x+y)(4x^2-2xy+y^2)$
$(3a-2b)(9a^2+6ab+4b^2)$
計算せよ
$(x-1)(x-3)(x+1)(x+3)$ $(x+2)(x+5)(x-4)(x-1)$
$(a-b)(a+b)(a+b)(a+b)$ $(2x-y)^3(2x+y)^3$
$(a+b)^2(a-b)^2(a+ab+b)^2(a-ab+b)^2$
$(x+2)(x-2)(x^2+2x+4)(x^2-2x+4)$
$(a+b+c)^2+(a+b-c)^2+(b+c-a)^2+(c+a-b)^2$
この動画を見る
展開せよ
$(a+1)^3$ $(x+3y)^3$
$(2a-1)^3$ $(-3a+2b)^3$
展開せよ
$(a+5)(a^2-5a+25)$
$(3-a)(9+3a+a^2)$
$(2x+y)(4x^2-2xy+y^2)$
$(3a-2b)(9a^2+6ab+4b^2)$
計算せよ
$(x-1)(x-3)(x+1)(x+3)$ $(x+2)(x+5)(x-4)(x-1)$
$(a-b)(a+b)(a+b)(a+b)$ $(2x-y)^3(2x+y)^3$
$(a+b)^2(a-b)^2(a+ab+b)^2(a-ab+b)^2$
$(x+2)(x-2)(x^2+2x+4)(x^2-2x+4)$
$(a+b+c)^2+(a+b-c)^2+(b+c-a)^2+(c+a-b)^2$
数と式 式の展開①【化学のタカシーがていねいに解説】

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
[ ]内の文字について降べきの順に整理せよ
$ax^2+bx-x^4+ax^2-ab [x]$
$2x^2+y^2-3xy-2y^2+3y+4xy-x^2-2x-5 [y]$
$ax^3+a^2x-2x^2-a^3-3ax^3+4a^3 [a]$
$a^2b+b^3+abc-a^2c-ac^2+bc^2-ab^2+c^3 [a]$
ある多項式から$3x^2-xy+2y^2$を引くところ
を誤って加えたため,答えが$2x^2+xy-y^2$
となった。正しい答えを求めよ
次の式を展開した時の[ ]内の項の係数を
求めよ
$(5a^3-3a^2b+7ab^2-2b^3)(3a^2+2ab-3b^2)[a^2b^3][a^3b^2]$
$(x+2y-z)(3x+4y+2z)(-x+y-3z)[xy^2][xyz]$
この動画を見る
[ ]内の文字について降べきの順に整理せよ
$ax^2+bx-x^4+ax^2-ab [x]$
$2x^2+y^2-3xy-2y^2+3y+4xy-x^2-2x-5 [y]$
$ax^3+a^2x-2x^2-a^3-3ax^3+4a^3 [a]$
$a^2b+b^3+abc-a^2c-ac^2+bc^2-ab^2+c^3 [a]$
ある多項式から$3x^2-xy+2y^2$を引くところ
を誤って加えたため,答えが$2x^2+xy-y^2$
となった。正しい答えを求めよ
次の式を展開した時の[ ]内の項の係数を
求めよ
$(5a^3-3a^2b+7ab^2-2b^3)(3a^2+2ab-3b^2)[a^2b^3][a^3b^2]$
$(x+2y-z)(3x+4y+2z)(-x+y-3z)[xy^2][xyz]$
シンガポール数学オリンピック整数問題の基本
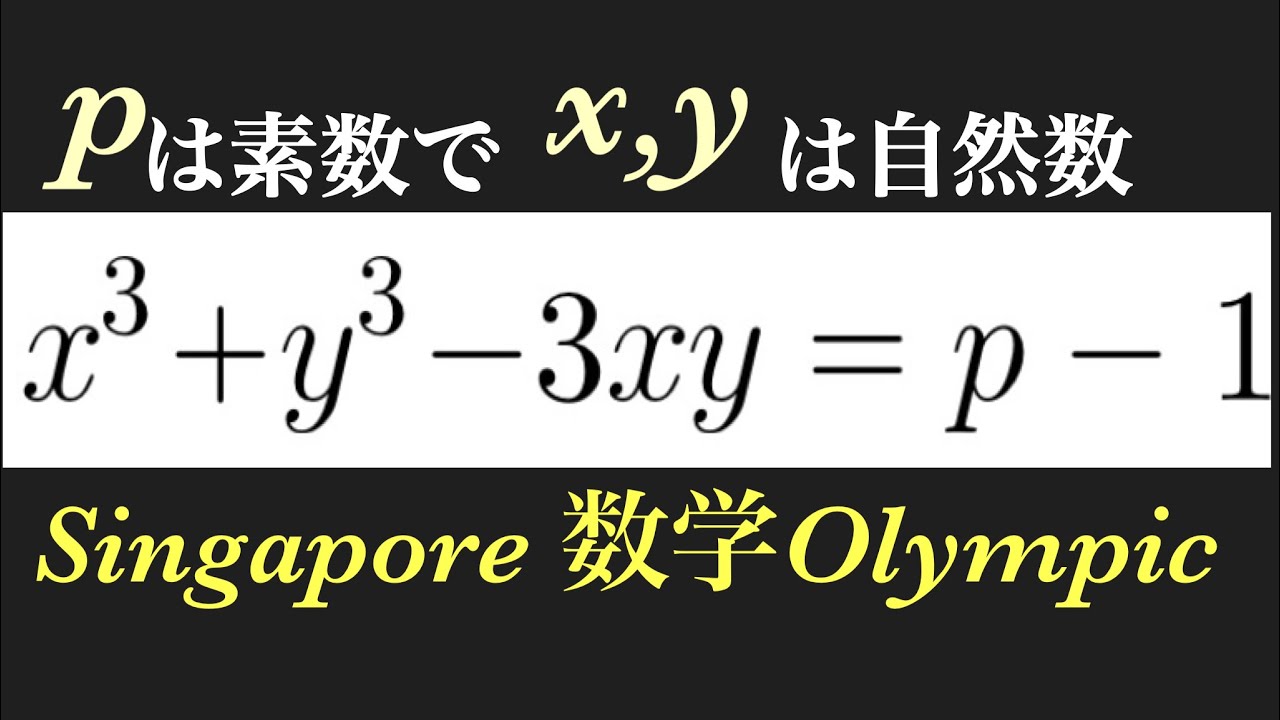
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$P$は素数であり,$x,y$を自然数としたとき,
$x^3+y^3-3xy=p-1$をみたす$(x,y)$をすべて求めよ.
シンガポール数学オリンピック過去問
この動画を見る
$P$は素数であり,$x,y$を自然数としたとき,
$x^3+y^3-3xy=p-1$をみたす$(x,y)$をすべて求めよ.
シンガポール数学オリンピック過去問
対数と不等式

単元:
#数Ⅰ#数Ⅱ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\dfrac{k-1}{k}\lt \log_{10}7 \lt \dfrac{k}{k+1}$
自然数kを求めよ.
この動画を見る
$\dfrac{k-1}{k}\lt \log_{10}7 \lt \dfrac{k}{k+1}$
自然数kを求めよ.
神戸大 不等式の証明

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#一次不等式(不等式・絶対値のある方程式・不等式)#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)$\dfrac{y}{x}+\dfrac{x}{y}\geqq 2$を示せ.等号成立するか?
(2)n個の正実数$a_1・・・・a_n\left(a_1+・・・a_n\right)\left(\dfrac{1}{a_1}+・・・・+\dfrac{1}{a_n}\right)\geqq n^2$
を示せ。等号成立はするか?
この動画を見る
(1)$\dfrac{y}{x}+\dfrac{x}{y}\geqq 2$を示せ.等号成立するか?
(2)n個の正実数$a_1・・・・a_n\left(a_1+・・・a_n\right)\left(\dfrac{1}{a_1}+・・・・+\dfrac{1}{a_n}\right)\geqq n^2$
を示せ。等号成立はするか?
数と式 1次不等式の利用【ホーン・フィールドがていねいに解説】

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のものを求めよ。
(1)不等式$5(x-3)\lt -2(x-14)$を満たす最大の整数x
(2)不等式$\dfrac{x}{2}+\dfrac{4}{3}\geqq x-\dfrac{2}{3}$を満たす自然数xの個数
不等式$2x-3gt a+8x$について、次の問いに答えよ。
(1)解が$x\lt 1$となるように、定数aの値を定めよ。
(2)解が$x=0$を含むように、定数aの値の範囲を定めよ。
(3)この不等式を満たすxのうち、最大の整数が0となるように、定数aの値の範囲を定めよ。
aを定数とするとき、次の方程式、不等式を解け。
(1)$ax=1$
(2)$ax\leqq 2$
(3)$ax+6\gt 3x+2a$
この動画を見る
次のものを求めよ。
(1)不等式$5(x-3)\lt -2(x-14)$を満たす最大の整数x
(2)不等式$\dfrac{x}{2}+\dfrac{4}{3}\geqq x-\dfrac{2}{3}$を満たす自然数xの個数
不等式$2x-3gt a+8x$について、次の問いに答えよ。
(1)解が$x\lt 1$となるように、定数aの値を定めよ。
(2)解が$x=0$を含むように、定数aの値の範囲を定めよ。
(3)この不等式を満たすxのうち、最大の整数が0となるように、定数aの値の範囲を定めよ。
aを定数とするとき、次の方程式、不等式を解け。
(1)$ax=1$
(2)$ax\leqq 2$
(3)$ax+6\gt 3x+2a$
ただの因数分解だよ

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
次の式は整数の範囲で因数分解できることが分かっています.
$2x^2-2519376x-3^10$
$(2^{\Box}x-3^{\Box})(2^{\Box}x+3^{\Box})
\Box$ に0以上の整数を入れなさい.
この動画を見る
次の式は整数の範囲で因数分解できることが分かっています.
$2x^2-2519376x-3^10$
$(2^{\Box}x-3^{\Box})(2^{\Box}x+3^{\Box})
\Box$ に0以上の整数を入れなさい.
これって高校範囲なのでは? 埼玉県
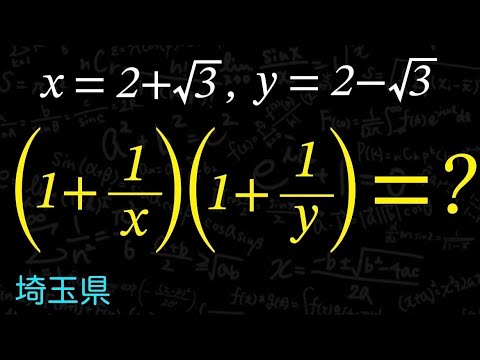
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=2+\sqrt 3,y=2- \sqrt 3$
$(1+\frac{1}{x})(1+\frac{1}{y})=?$
埼玉県
この動画を見る
$x=2+\sqrt 3,y=2- \sqrt 3$
$(1+\frac{1}{x})(1+\frac{1}{y})=?$
埼玉県
