 2次関数
2次関数
 2次関数
2次関数
【短時間でマスター!!】2次関数のグラフの書き方を解説!〔現役塾講師解説、数学〕

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学1A
2次関数のグラフの書き方について解説します。
$y=x^2-6x+3$
$y=-2x^2+8x-3$
この動画を見る
数学1A
2次関数のグラフの書き方について解説します。
$y=x^2-6x+3$
$y=-2x^2+8x-3$
【短時間でマスター!!】平方完成の解き方を解説!〔現役塾講師解説、数学〕

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学1A
平方完成の解き方について解説します。
$y=x^2-6x+3$
$y=-2x^2+8x-3$
この動画を見る
数学1A
平方完成の解き方について解説します。
$y=x^2-6x+3$
$y=-2x^2+8x-3$
中学生にとっては激ムズすぎる 仙台育英(改)

単元:
#数学(中学生)#数Ⅰ#2次関数#2次方程式と2次不等式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式$2x^2-mx-m=0$の解の1つが1よりも大きいとき、mの値の範囲を求めよ。
(仙台育英学園高等学校 誘導省略)
この動画を見る
2次方程式$2x^2-mx-m=0$の解の1つが1よりも大きいとき、mの値の範囲を求めよ。
(仙台育英学園高等学校 誘導省略)
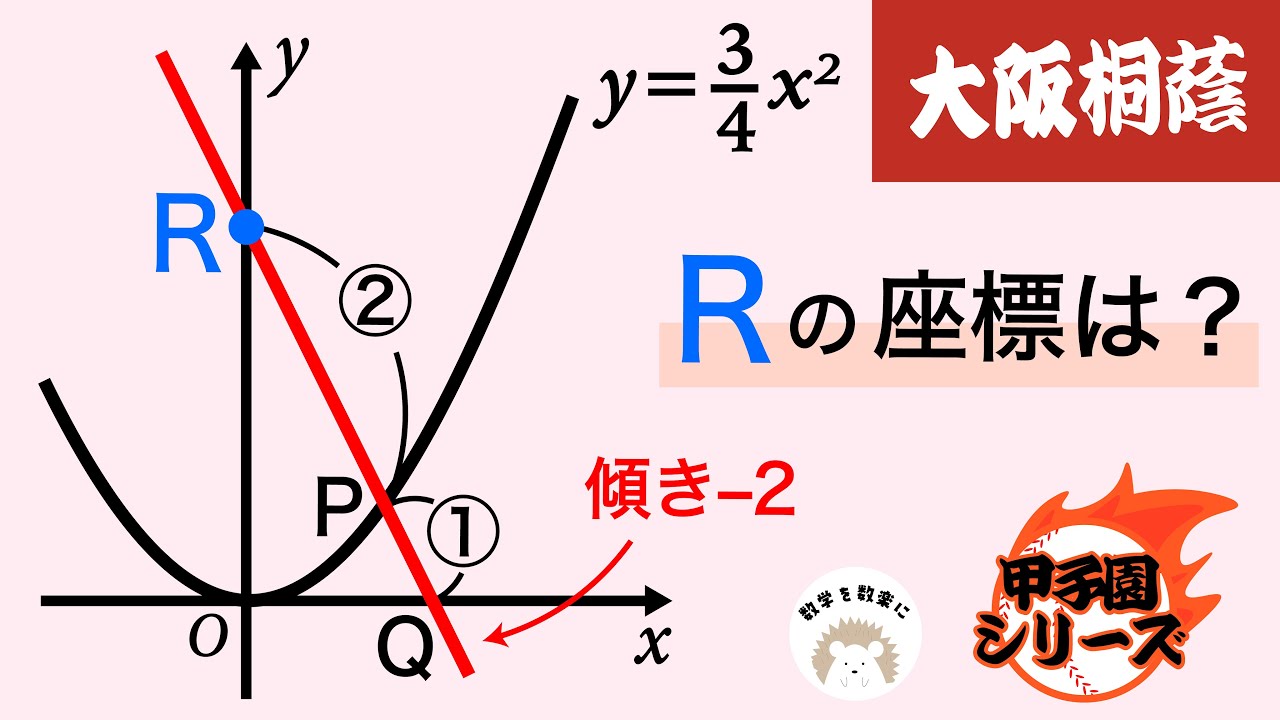
放物線と比 大阪桐蔭
単元:
#数学(中学生)#数Ⅰ#数Ⅱ#2次関数#三角関数#三角関数とグラフ#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
Rの座標は?
*図は動画内参照
大阪桐蔭高等学校
この動画を見る
Rの座標は?
*図は動画内参照
大阪桐蔭高等学校
福田の数学〜早稲田大学2022年人間科学部第5問〜2次関数の区間の動く最大最小

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#面積、体積#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{5}}$aを実数とする。関数
$f(x)=-x^2+6x(a-2 \leqq x \leqq a)$
の最大値をg(a)、最小値をh(a)とする。このとき、
$ab$平面において$b=g(a)$のグラフとa軸によって囲まれる部分の面積は$\boxed{\ \ ア\ \ }$であり、
ab平面において$b=h(a)$のグラフとa軸によって囲まれる部分の面積は$\boxed{\ \ イ\ \ }$である。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{5}}$aを実数とする。関数
$f(x)=-x^2+6x(a-2 \leqq x \leqq a)$
の最大値をg(a)、最小値をh(a)とする。このとき、
$ab$平面において$b=g(a)$のグラフとa軸によって囲まれる部分の面積は$\boxed{\ \ ア\ \ }$であり、
ab平面において$b=h(a)$のグラフとa軸によって囲まれる部分の面積は$\boxed{\ \ イ\ \ }$である。
2022早稲田大学人間科学部過去問
福田の数学〜早稲田大学2022年人間科学部第1問(2)〜2次関数のグラフの位置から係数決定

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(2)2次関数$y=ax^2+bx+c$の係数$a,b,c$は次の条件をともに満たすとする。
条件1.$a,b,c$は互いに異なる。
条件2. -3以上5以下の整数である。
この2次関数のグラフが、原点を通り、かつ、頂点が第1象限または第3象限
にあるような$a,b,c$の組は全部で$\boxed{\ \ イ\ \ }$組ある。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{1}}$(2)2次関数$y=ax^2+bx+c$の係数$a,b,c$は次の条件をともに満たすとする。
条件1.$a,b,c$は互いに異なる。
条件2. -3以上5以下の整数である。
この2次関数のグラフが、原点を通り、かつ、頂点が第1象限または第3象限
にあるような$a,b,c$の組は全部で$\boxed{\ \ イ\ \ }$組ある。
2022早稲田大学人間科学部過去問
福田の数学〜早稲田大学2022年理工学部第2問〜条件を満たすm個の2次関数の積でできる2m次方程式の異なる解の総和

単元:
#数Ⅰ#数A#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{2}}\ p,q$を相異なる素数とする。次の3条件を満たすxの2次式f(x)を考える。
・係数はすべて整数1で$x^2$の係数は1である。
・$f(1)=pq$である。
・方程式$f(x)=0$は整数解をもつ。
以下の問いに答えよ。
(1)$f(x)$をすべて求めよ。
(2)(1)で求めたものを$f_1(x),f_2(x),\ldots,f_m(x)$とする。2m次方程式
$f_1(x)×f_2(x)×\ldots×f_m(x)=0$
の相異なる解の総和は$p,q$によらないことを示せ。
2022早稲田大学理工学部過去問
この動画を見る
${\large\boxed{2}}\ p,q$を相異なる素数とする。次の3条件を満たすxの2次式f(x)を考える。
・係数はすべて整数1で$x^2$の係数は1である。
・$f(1)=pq$である。
・方程式$f(x)=0$は整数解をもつ。
以下の問いに答えよ。
(1)$f(x)$をすべて求めよ。
(2)(1)で求めたものを$f_1(x),f_2(x),\ldots,f_m(x)$とする。2m次方程式
$f_1(x)×f_2(x)×\ldots×f_m(x)=0$
の相異なる解の総和は$p,q$によらないことを示せ。
2022早稲田大学理工学部過去問
【わかりやすく】2次関数の最大最小「範囲が動く場合」(高校数学Ⅰ)

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
関数$y=x^2-2x+3(0 \leqq x \leqq a)$について、次の問いに答えよ。
ただし、$a \gt 0$
(1)最大値を求めよ
(2)最小値を求めよ
この動画を見る
関数$y=x^2-2x+3(0 \leqq x \leqq a)$について、次の問いに答えよ。
ただし、$a \gt 0$
(1)最大値を求めよ
(2)最小値を求めよ
【わかりやすく解説】定義域が定められている2次関数の最大最小(数学Ⅰ)

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の定義域における関数$y=-x^2-2x+1$の最大値、最小値を求めよ。
(1)$-3 \leqq x \leqq 0$
(2)$1 \leqq x \leqq 2$
(3)$-2 \leqq x \leqq -1$
この動画を見る
次の定義域における関数$y=-x^2-2x+1$の最大値、最小値を求めよ。
(1)$-3 \leqq x \leqq 0$
(2)$1 \leqq x \leqq 2$
(3)$-2 \leqq x \leqq -1$
【基礎から解説】2次関数の最大・最小の基本を解説!(数学Ⅰ)

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の2次関数の最大値・最小値を求めよ。
(1)
$y=2x^2+8x+5$
(2)
$y=-\displaystyle \frac{1}{2}x^2+x-1$
この動画を見る
次の2次関数の最大値・最小値を求めよ。
(1)
$y=2x^2+8x+5$
(2)
$y=-\displaystyle \frac{1}{2}x^2+x-1$
x,yの2次式の値の範囲

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#2次関数とグラフ#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
x,yは実数とする.
$x^2+2y^2-4y=2$を満たすとき,
$x+4y^2-8y$の値の範囲を求めよ.
この動画を見る
x,yは実数とする.
$x^2+2y^2-4y=2$を満たすとき,
$x+4y^2-8y$の値の範囲を求めよ.
福田の数学〜慶應義塾大学2022年商学部第3問〜絶対値の付いた2次関数のグラフと直線の共有点と面積

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#2次関数#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$mを実数とし、関数$y=|x^2-5x+4|$のグラフをC、直線$y=mx$を$l$とする。
(1)グラフCと直線lの共有点の個数は
$\boxed{\ \ アイ\ \ } \lt m \lt \boxed{\ \ ウ\ \ }$のとき0個
$m=\boxed{\ \ エオ\ \ }$のとき1個
$m \lt \boxed{\ \ カキ\ \ },\ m=\boxed{\ \ ク\ \ }$,または$m \gt \boxed{\ \ ケ\ \ }$のとき2個
$m=\boxed{\ \ コ\ \ }$のとき3個
$\boxed{\ \ サ\ \ } \lt m \lt \boxed{\ \ シ\ \ }$のとき4個
以下、グラフCと直線lの共有点の個数が3個の場合を考え、
グラフCと直線lの共有点を、x座標が小さい順にP,Q,Rとする。
(2)3点P,Q,Rのx座標は、順に$\boxed{\ \ ス\ \ }-\sqrt{\boxed{\ \ セ\ \ }},\ \boxed{\ \ ソ\ \ },\ \boxed{\ \ タ\ \ }+\sqrt{\boxed{\ \ チ\ \ }}$である。
(3)グラフCと線分QRで囲まれた部分の面積は$\frac{-\ \boxed{\ \ ツ\ \ }+\boxed{\ \ テト\ \ }\sqrt{\boxed{\ \ ナ\ \ }}}{\boxed{\ \ ニ\ \ }}$である。
2022慶應義塾大学商学部過去問
この動画を見る
${\Large\boxed{3}}$mを実数とし、関数$y=|x^2-5x+4|$のグラフをC、直線$y=mx$を$l$とする。
(1)グラフCと直線lの共有点の個数は
$\boxed{\ \ アイ\ \ } \lt m \lt \boxed{\ \ ウ\ \ }$のとき0個
$m=\boxed{\ \ エオ\ \ }$のとき1個
$m \lt \boxed{\ \ カキ\ \ },\ m=\boxed{\ \ ク\ \ }$,または$m \gt \boxed{\ \ ケ\ \ }$のとき2個
$m=\boxed{\ \ コ\ \ }$のとき3個
$\boxed{\ \ サ\ \ } \lt m \lt \boxed{\ \ シ\ \ }$のとき4個
以下、グラフCと直線lの共有点の個数が3個の場合を考え、
グラフCと直線lの共有点を、x座標が小さい順にP,Q,Rとする。
(2)3点P,Q,Rのx座標は、順に$\boxed{\ \ ス\ \ }-\sqrt{\boxed{\ \ セ\ \ }},\ \boxed{\ \ ソ\ \ },\ \boxed{\ \ タ\ \ }+\sqrt{\boxed{\ \ チ\ \ }}$である。
(3)グラフCと線分QRで囲まれた部分の面積は$\frac{-\ \boxed{\ \ ツ\ \ }+\boxed{\ \ テト\ \ }\sqrt{\boxed{\ \ ナ\ \ }}}{\boxed{\ \ ニ\ \ }}$である。
2022慶應義塾大学商学部過去問
福田の数学〜慶應義塾大学2022年経済学部第5問〜指数対数の性質と格子点と2次関数の最大

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{5}}$aを2以上の整数、pを整数とし、$s=2^{2p+1}$とおく。実数$x,y$が等式
$2^{a+1}\log_23^x+2x\log_2(\frac{1}{3})^x=\log_s9^y$
を満たすとき、yをxの関数として表したものを$y=f(x)$とする。
(1)対数の記号を使わずに、$f(x)$を$a,p$およびxを用いて表せ。
(2)$a=2,\ p=0$とする。このとき、$n \leqq f(m)$を満たし、かつ、$m+n$が正となる
ような整数の組(m,n)の個数を求めよ。
(3)$y=f(x)(0 \leqq x \leqq 2^{a+1})$の最大値が$2^{3a}$以下となるような整数pの
最大値と最小値を、それぞれaを用いて表せ。
2022慶應義塾大学経済学部過去問
この動画を見る
${\Large\boxed{5}}$aを2以上の整数、pを整数とし、$s=2^{2p+1}$とおく。実数$x,y$が等式
$2^{a+1}\log_23^x+2x\log_2(\frac{1}{3})^x=\log_s9^y$
を満たすとき、yをxの関数として表したものを$y=f(x)$とする。
(1)対数の記号を使わずに、$f(x)$を$a,p$およびxを用いて表せ。
(2)$a=2,\ p=0$とする。このとき、$n \leqq f(m)$を満たし、かつ、$m+n$が正となる
ような整数の組(m,n)の個数を求めよ。
(3)$y=f(x)(0 \leqq x \leqq 2^{a+1})$の最大値が$2^{3a}$以下となるような整数pの
最大値と最小値を、それぞれaを用いて表せ。
2022慶應義塾大学経済学部過去問
破れたページは何ページ目?

単元:
#数Ⅰ#数と式#2次関数#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1枚だけページが破れた本があります。
破れていないページの番号を合計すると15000になる
破れたページは何ページ目ですか?
この動画を見る
1枚だけページが破れた本があります。
破れていないページの番号を合計すると15000になる
破れたページは何ページ目ですか?
よく出る問題!放物線と直線が接するということは?【数学 入試問題】【京都大学】

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#2次関数とグラフ#図形と方程式#点と直線#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
放物線$y=ax^2+bx+c$が3直線$y=x,y=2x-1,y=3x-3$のすべてと接するとき、$a,b,c$の値を求めよ。
京都大過去問
この動画を見る
放物線$y=ax^2+bx+c$が3直線$y=x,y=2x-1,y=3x-3$のすべてと接するとき、$a,b,c$の値を求めよ。
京都大過去問
【数Ⅰ】絶対値付きの不等式【場合分けしなくても解ける!? 裏技的解法も】

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$(1)\vert x \vert \lt 3を解け.$
$(2)\vert 2x-1 \vert \lt x+4を解け.$
この動画を見る
$(1)\vert x \vert \lt 3を解け.$
$(2)\vert 2x-1 \vert \lt x+4を解け.$
【裏技】2次方程式の裏技

福田の数学〜九州大学2022年文系第1問〜絶対値の付いた放物線と直線で囲まれた面積

単元:
#数Ⅱ#大学入試過去問(数学)#2次関数#微分法と積分法#解と判別式・解と係数の関係#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#九州大学
指導講師:
福田次郎
問題文全文(内容文):
aを$-3 \lt a \lt 13$を満たす実数とし、次の曲線Cと直線lが接しているとする。
$C:y=|x^2+(3-a)x-3a|, l:y=-x+13$
以下の問いに答えよ。
(1)aの値を求めよ。
(2)曲線Cと直線lで囲まれた2つの図形のうち、点(a,0)が境界線上にある図形の面積を求めよ。
2022九州大学文系過去問
この動画を見る
aを$-3 \lt a \lt 13$を満たす実数とし、次の曲線Cと直線lが接しているとする。
$C:y=|x^2+(3-a)x-3a|, l:y=-x+13$
以下の問いに答えよ。
(1)aの値を求めよ。
(2)曲線Cと直線lで囲まれた2つの図形のうち、点(a,0)が境界線上にある図形の面積を求めよ。
2022九州大学文系過去問
サクッとスッキリ

単元:
#2次方程式と2次不等式
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
a+\dfrac{1}{c}=1 \\
b+\dfrac{1}{a}=1\\
c+\dfrac{1}{b}=5 \\
\end{array}
\right.
\end{eqnarray}$
$abc$はいくつか?
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
a+\dfrac{1}{c}=1 \\
b+\dfrac{1}{a}=1\\
c+\dfrac{1}{b}=5 \\
\end{array}
\right.
\end{eqnarray}$
$abc$はいくつか?
【数Ⅰ】絶対値が2つある方程式【見た目より難しい!?丁寧に場合分けをしよう】

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$ \vert x+2 \vert + \vert 2x-3 \vert =6を解け.$
この動画を見る
$ \vert x+2 \vert + \vert 2x-3 \vert =6を解け.$
【数Ⅰ】絶対値付きの方程式【絶対値ってなに? 場合分けってなんでするの?】

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$ (1)\vert 2x-1 \vert =3を解け.$
$ (2)\vert x-1 \vert =2x+4を解け.$
この動画を見る
$ (1)\vert 2x-1 \vert =3を解け.$
$ (2)\vert x-1 \vert =2x+4を解け.$
因数分解や解の公式が不要な新しい解き方~2次関数・2次方程式~

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\displaystyle
(1)\,x^2-2x-24=0
$
$\displaystyle
(2)\,3x^2-7x-6=0
$
この動画を見る
$\displaystyle
(1)\,x^2-2x-24=0
$
$\displaystyle
(2)\,3x^2-7x-6=0
$
一文字削除からの判別式【2014年早稲田大学】

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#2次関数#式の計算(整式・展開・因数分解)#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
実数$a,b,c$が
$a+b+c=8,a^2+b^2+c^2=32$
を満たす時、実数$c$の最大値を求めよ。
2014早稲田大過去問
この動画を見る
実数$a,b,c$が
$a+b+c=8,a^2+b^2+c^2=32$
を満たす時、実数$c$の最大値を求めよ。
2014早稲田大過去問
福田の数学〜東京工業大学2022年理系第1問〜2次方程式の解の存在範囲

単元:
#大学入試過去問(数学)#2次関数#複素数平面#2次方程式と2次不等式#図形への応用#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
a,bを実数とし、$f(z)=z^2+az+b$ とする。a,bが
$|a| \leqq 1, |b| \leqq 1$
を満たしながら動くとき、$f(z)=0$を満たす複素数zが取りうる値の範囲を
複素平面上に図示せよ。
2022東京工業大学理系過去問
この動画を見る
a,bを実数とし、$f(z)=z^2+az+b$ とする。a,bが
$|a| \leqq 1, |b| \leqq 1$
を満たしながら動くとき、$f(z)=0$を満たす複素数zが取りうる値の範囲を
複素平面上に図示せよ。
2022東京工業大学理系過去問
福田の入試問題解説〜東京大学2022年文系第1問〜放物線と接線

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
a,bを実数とする。座標平面上の放物線$y=x^2+ax+b$をCとおく。
Cは、原点で垂直に交わる2本の接線$l_1,l_2$を持つとする。
ただし、Cと$l_1$の接点$P_1$のx座標は、Cと$l_2$の接点$P_2$のx座標より小さいとする。
(1)bをaで表せ。またaの値は全ての実数をとりうることを示せ。
(2)i=1,2に対し、円$D_i$を、放物線Cの軸上に中心を持ち、点$P_i$で$l_i$
と接するものと定める。$D_2$の半径が$D_1$の半径の2倍となるとき、aの値を求めよ。
2022東京大学文系過去問
この動画を見る
a,bを実数とする。座標平面上の放物線$y=x^2+ax+b$をCとおく。
Cは、原点で垂直に交わる2本の接線$l_1,l_2$を持つとする。
ただし、Cと$l_1$の接点$P_1$のx座標は、Cと$l_2$の接点$P_2$のx座標より小さいとする。
(1)bをaで表せ。またaの値は全ての実数をとりうることを示せ。
(2)i=1,2に対し、円$D_i$を、放物線Cの軸上に中心を持ち、点$P_i$で$l_i$
と接するものと定める。$D_2$の半径が$D_1$の半径の2倍となるとき、aの値を求めよ。
2022東京大学文系過去問
これは有名?

連立2元9次方程式
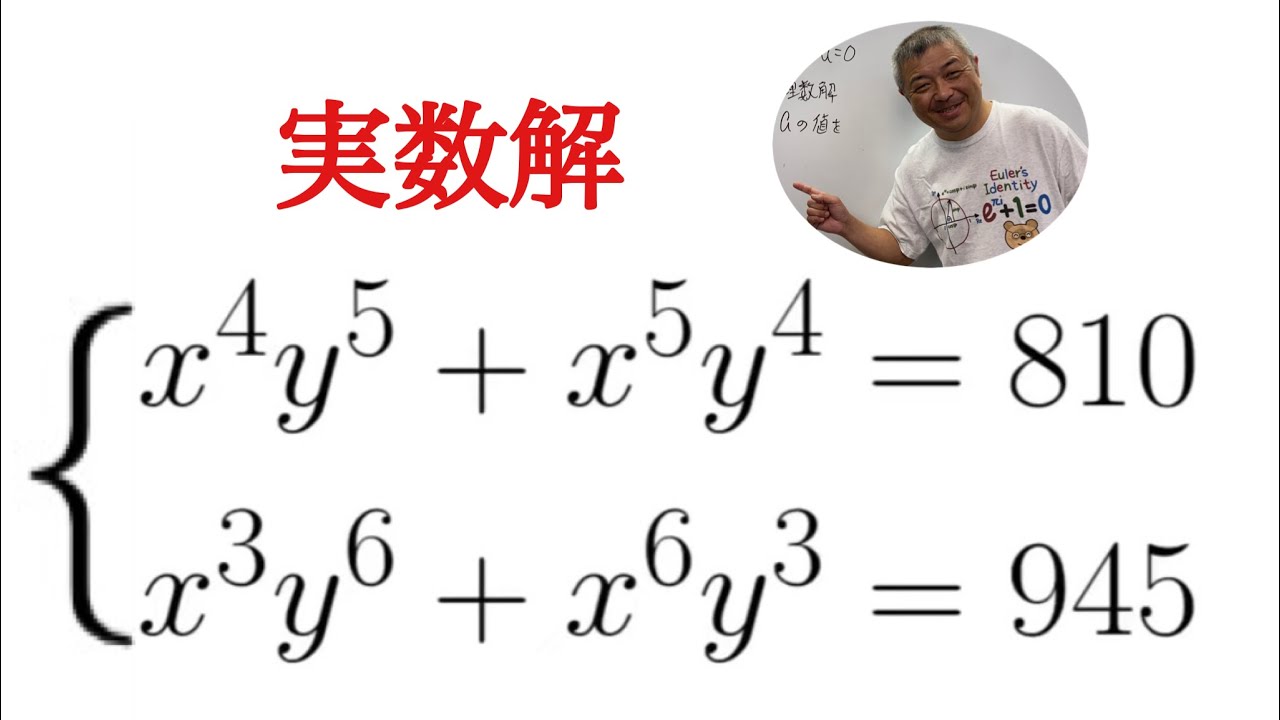
単元:
#数Ⅰ#数Ⅱ#数と式#2次関数#複素数と方程式#式の計算(整式・展開・因数分解)#2次方程式と2次不等式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x^4y^5+x^5y^4=810 \\
x^3y^6+x^6y^3=945
\end{array}
\right.
\end{eqnarray}$
実数解を求めよ.
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x^4y^5+x^5y^4=810 \\
x^3y^6+x^6y^3=945
\end{array}
\right.
\end{eqnarray}$
実数解を求めよ.
ざ・息抜き

単元:
#数Ⅰ#数Ⅱ#2次関数#2次方程式と2次不等式#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt{2022}x^{\log_{2022}x}=x^2$の解の積の下3桁を求めよ.
この動画を見る
$ \sqrt{2022}x^{\log_{2022}x}=x^2$の解の積の下3桁を求めよ.
福田の入試問題解説〜北海道大学2022年理系第1問〜絶対値の付いた2次関数の最小値(難)

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#2次関数#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#2次関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
福田次郎
問題文全文(内容文):
$0 \leqq a \leqq b \leqq 1$を満たすa,bに対し、関数
$f(x)=|x(x-1)|+|(x-a)(x-b)|$
を考える。xが実数の範囲を動くとき、$f(x)$は最小値mをもつとする。
(1)$x \lt 0$および$x \gt 1$では$f(x) \gt m$となることを示せ。
(2)$m=f(0)$または$m=f(1)$であることを示せ。
(3)$a,b$が$0 \leqq a \leqq b \leqq 1$を満たして動くとき、mの最大値を求めよ。
2022北海道大学理系過去問
この動画を見る
$0 \leqq a \leqq b \leqq 1$を満たすa,bに対し、関数
$f(x)=|x(x-1)|+|(x-a)(x-b)|$
を考える。xが実数の範囲を動くとき、$f(x)$は最小値mをもつとする。
(1)$x \lt 0$および$x \gt 1$では$f(x) \gt m$となることを示せ。
(2)$m=f(0)$または$m=f(1)$であることを示せ。
(3)$a,b$が$0 \leqq a \leqq b \leqq 1$を満たして動くとき、mの最大値を求めよ。
2022北海道大学理系過去問
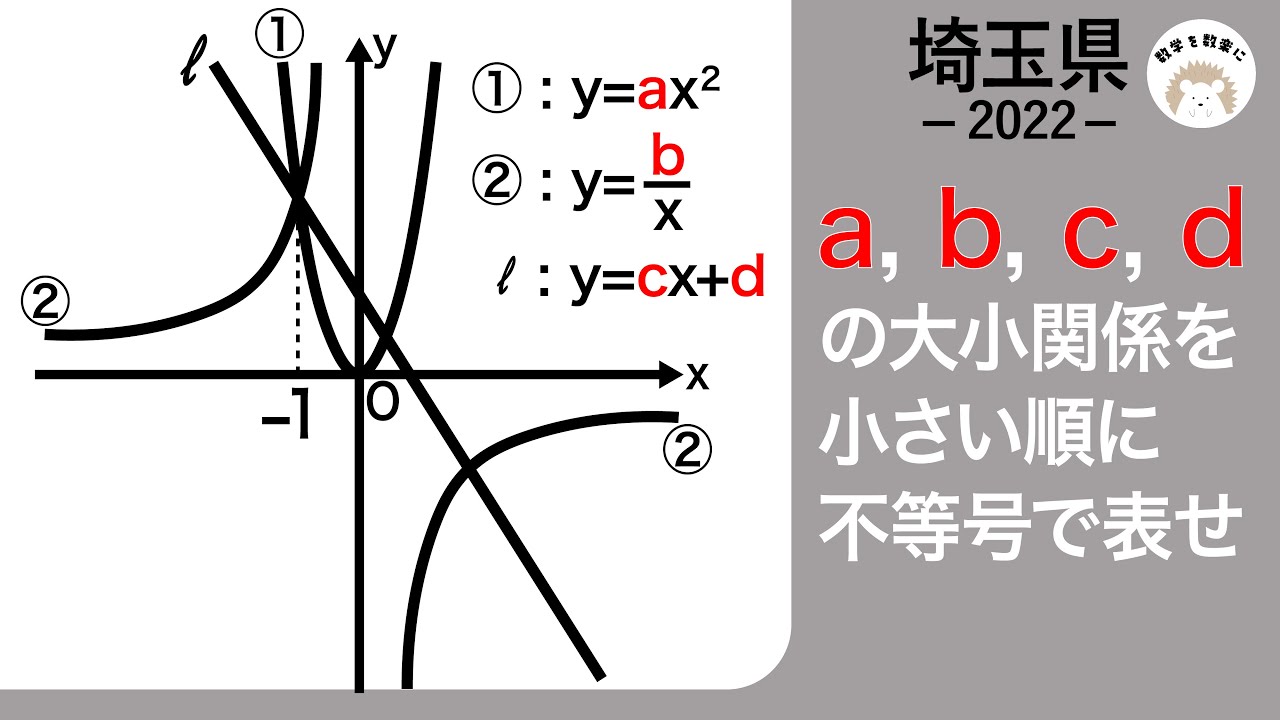
埼玉県 令和4年度 数学 関数 2022 入試問題100題解説74問目!
単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
①:$y=ax^2$
②:$y=\frac{b}{x}$
l :$y=cx+d$
a,b,c,dの大小関係を小さい順に不等号で表せ
*図は動画内参照
2022埼玉県
この動画を見る
①:$y=ax^2$
②:$y=\frac{b}{x}$
l :$y=cx+d$
a,b,c,dの大小関係を小さい順に不等号で表せ
*図は動画内参照
2022埼玉県
