 図形と計量
図形と計量
 図形と計量
図形と計量
【数Ⅰ】【図形と計量】面積応用3 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
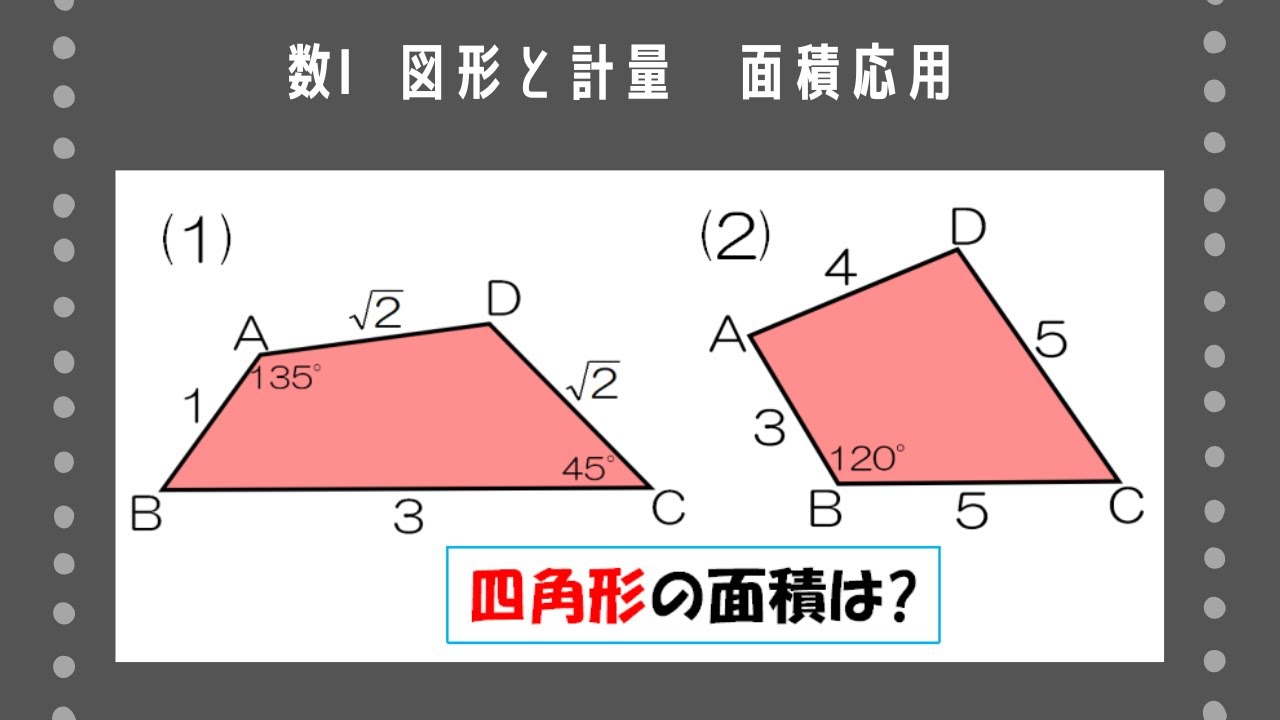
次のような四角形ABCDの面積を求めよ。
(1)∠A=135°、∠C=45°、AB=1、BC=3、CD=$\sqrt{2}$、DA=$\sqrt{2}$
(2)∠B=120°、AB=3、BC=5、CD=5、DA=4
この動画を見る
次のような四角形ABCDの面積を求めよ。
(1)∠A=135°、∠C=45°、AB=1、BC=3、CD=$\sqrt{2}$、DA=$\sqrt{2}$
(2)∠B=120°、AB=3、BC=5、CD=5、DA=4
【数Ⅰ】【図形と計量】面積応用7 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
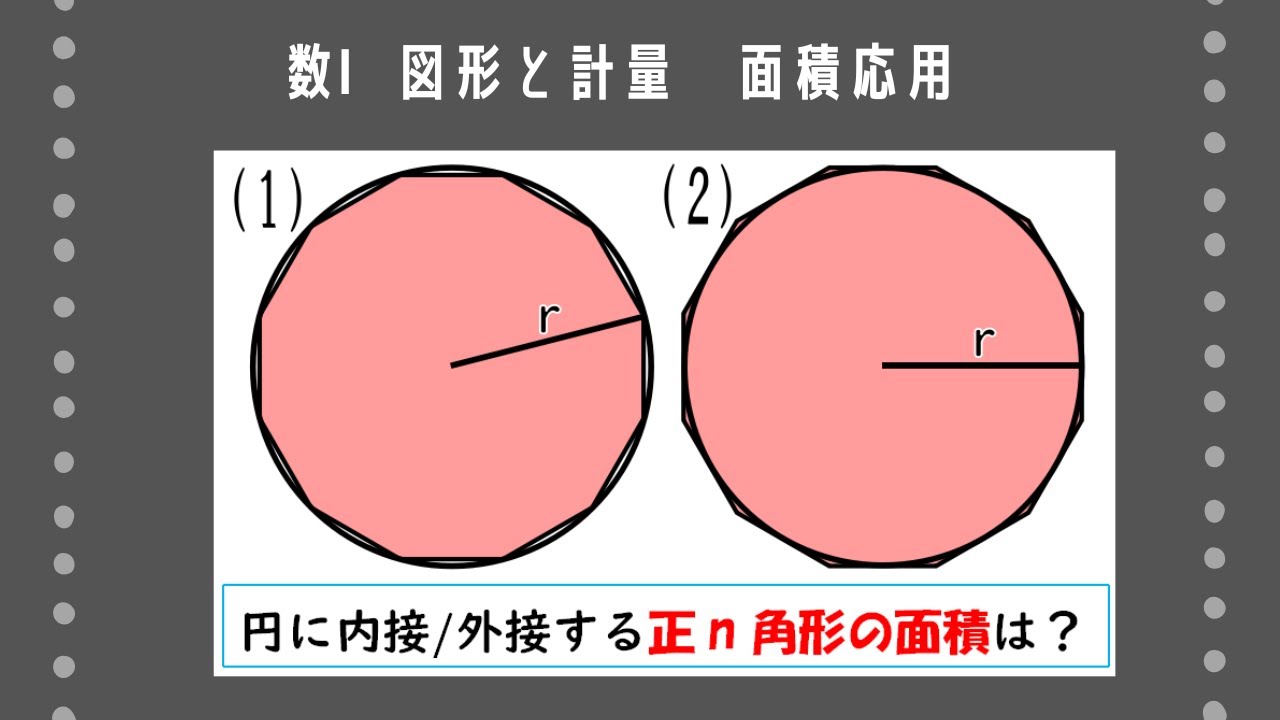
半径$r$の円に内接する正$n$角形の面積、および外接する正$n$角形の面積を、それぞれ$r$と$n$を用いて求めよ。
この動画を見る
半径$r$の円に内接する正$n$角形の面積、および外接する正$n$角形の面積を、それぞれ$r$と$n$を用いて求めよ。
【数Ⅰ】【図形と計量】面積応用2 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
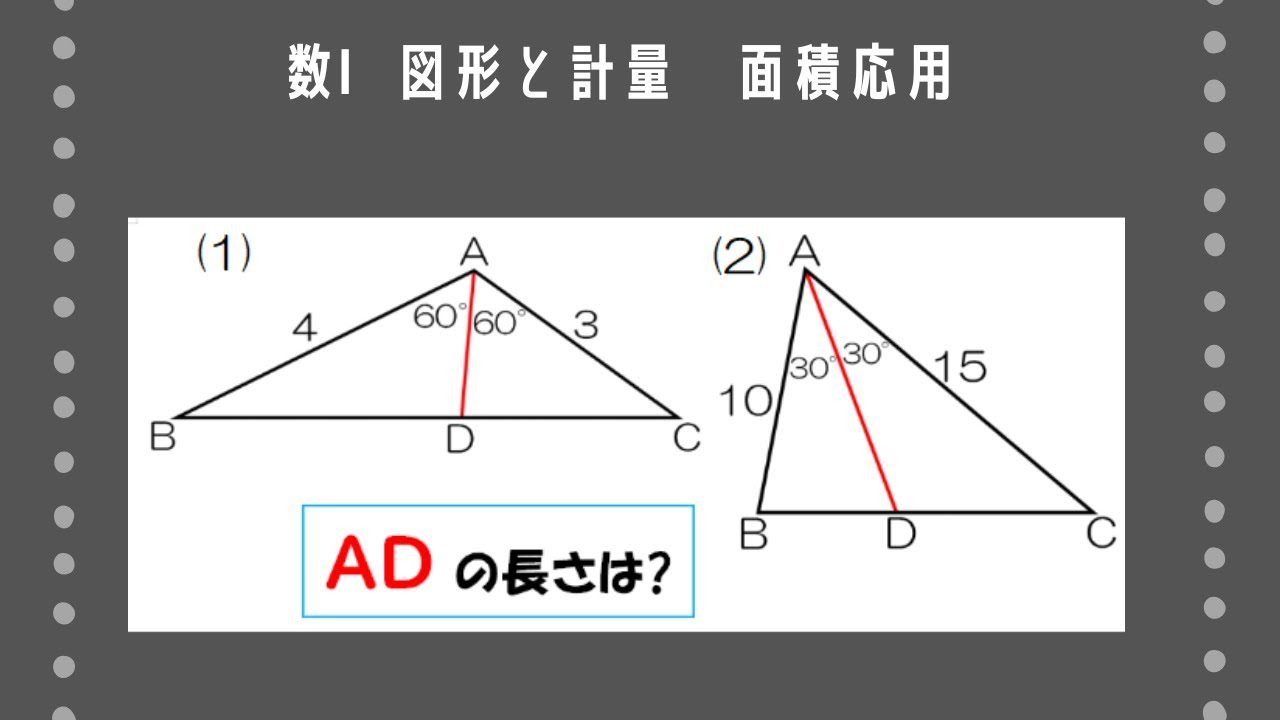
次のような△ABCについて、∠Aの二等分線と辺BCの交点をDとするとき、線分ADの長さを求めよ。
(1)AB=4、AC=3、A=120°
(2)AB=10、AC=15、A=60°
この動画を見る
次のような△ABCについて、∠Aの二等分線と辺BCの交点をDとするとき、線分ADの長さを求めよ。
(1)AB=4、AC=3、A=120°
(2)AB=10、AC=15、A=60°
【数Ⅰ】【図形と計量】面積応用6 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
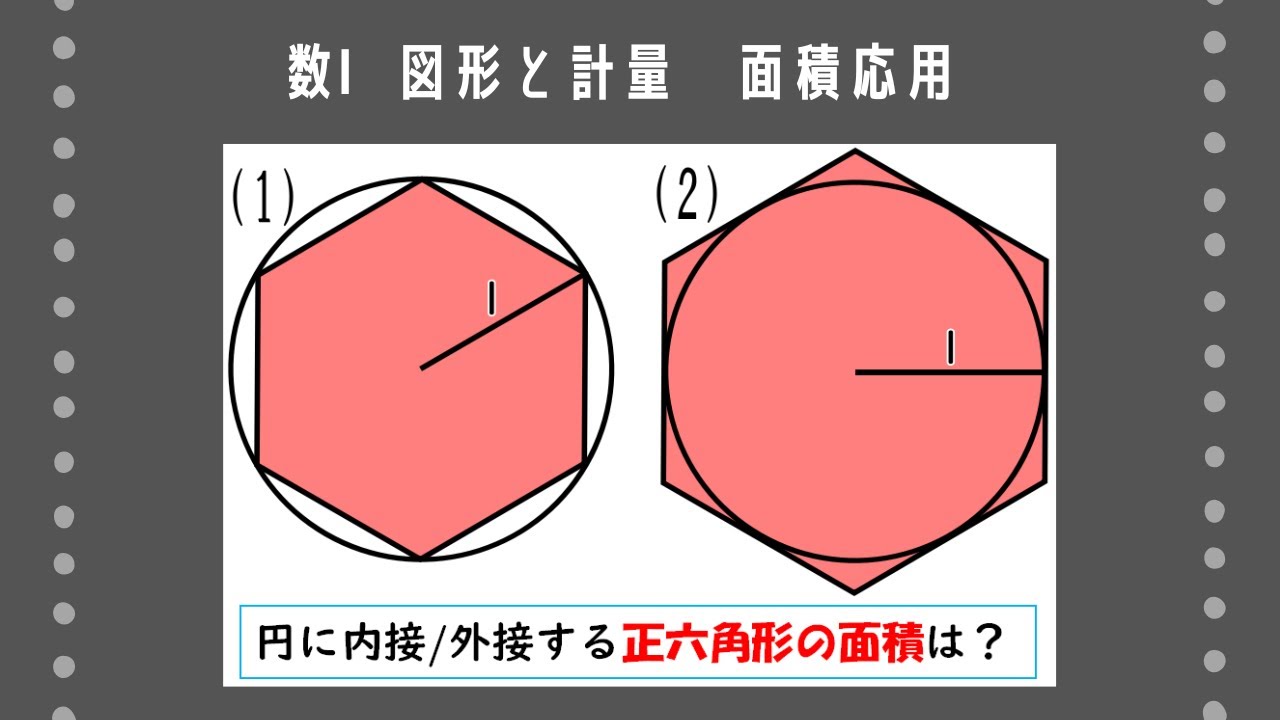
(1)半径1の円に内接する正六角形の面積を求めよ。
(2)半径1の円に外接する正六角形の面積を求めよ。
この動画を見る
(1)半径1の円に内接する正六角形の面積を求めよ。
(2)半径1の円に外接する正六角形の面積を求めよ。
【数Ⅰ】【図形と計量】面積応用5 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
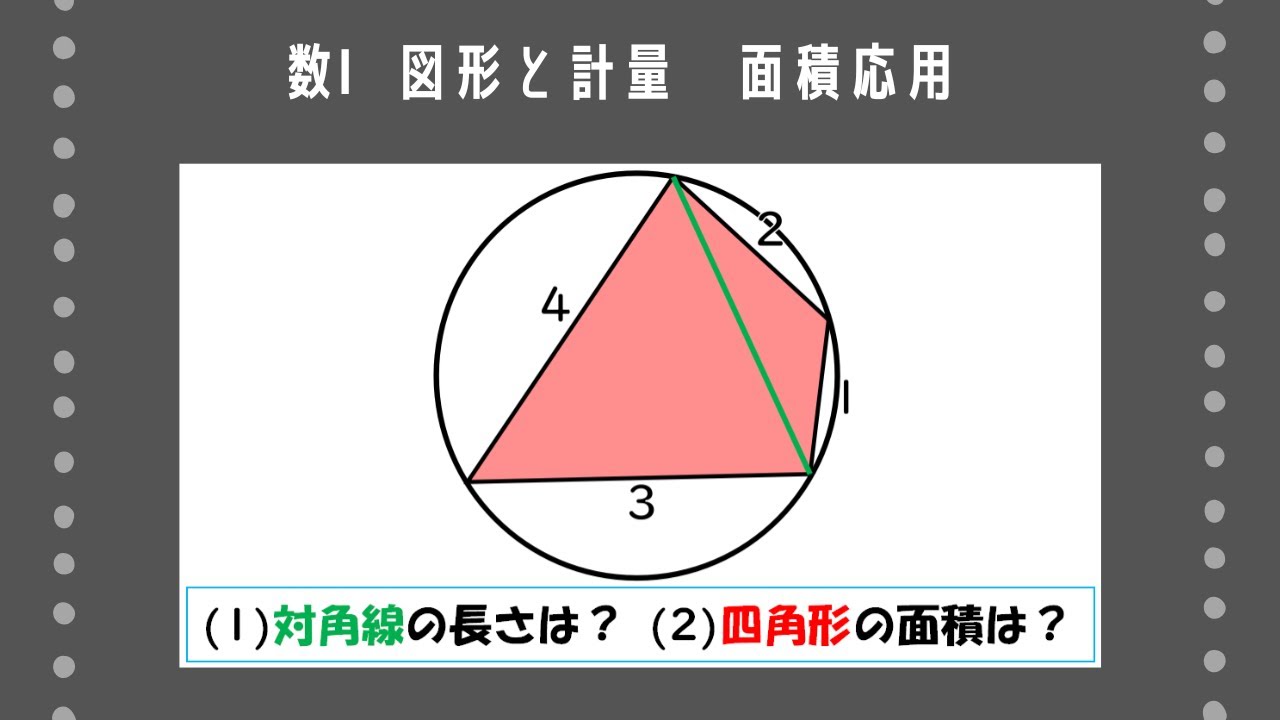
円に内接する四角形$\rm ABCD$において、$\rm AB=4,BC=3,CD=1,DA=2$とするとき、次のものを求めよ。
(1)対角線$\rm AC$の長さ
(2)四角形$\rm ABCD$の面積
この動画を見る
円に内接する四角形$\rm ABCD$において、$\rm AB=4,BC=3,CD=1,DA=2$とするとき、次のものを求めよ。
(1)対角線$\rm AC$の長さ
(2)四角形$\rm ABCD$の面積
【数Ⅰ】【図形と計量】面積応用4 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
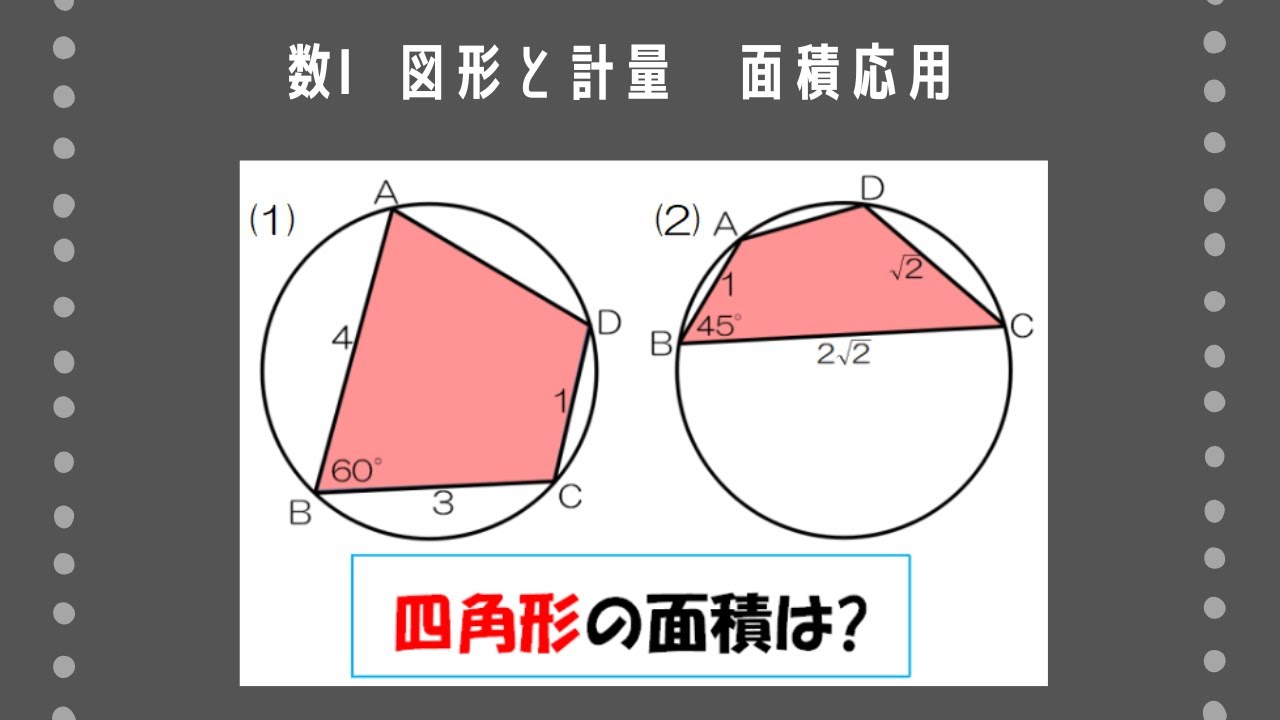
次のような四角形$\rm ABCD$の面積を求めよ。
(1)円に内接し、$\rm AB=4,BC=3,CD=1,\angle B=60^{\circ}$
(2)円に内接し、$\rm AB=1,BC=2\sqrt2,CD=\sqrt2,\angle B=45^{\circ}$
この動画を見る
次のような四角形$\rm ABCD$の面積を求めよ。
(1)円に内接し、$\rm AB=4,BC=3,CD=1,\angle B=60^{\circ}$
(2)円に内接し、$\rm AB=1,BC=2\sqrt2,CD=\sqrt2,\angle B=45^{\circ}$
【数Ⅰ】【図形と計量】面積応用1 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
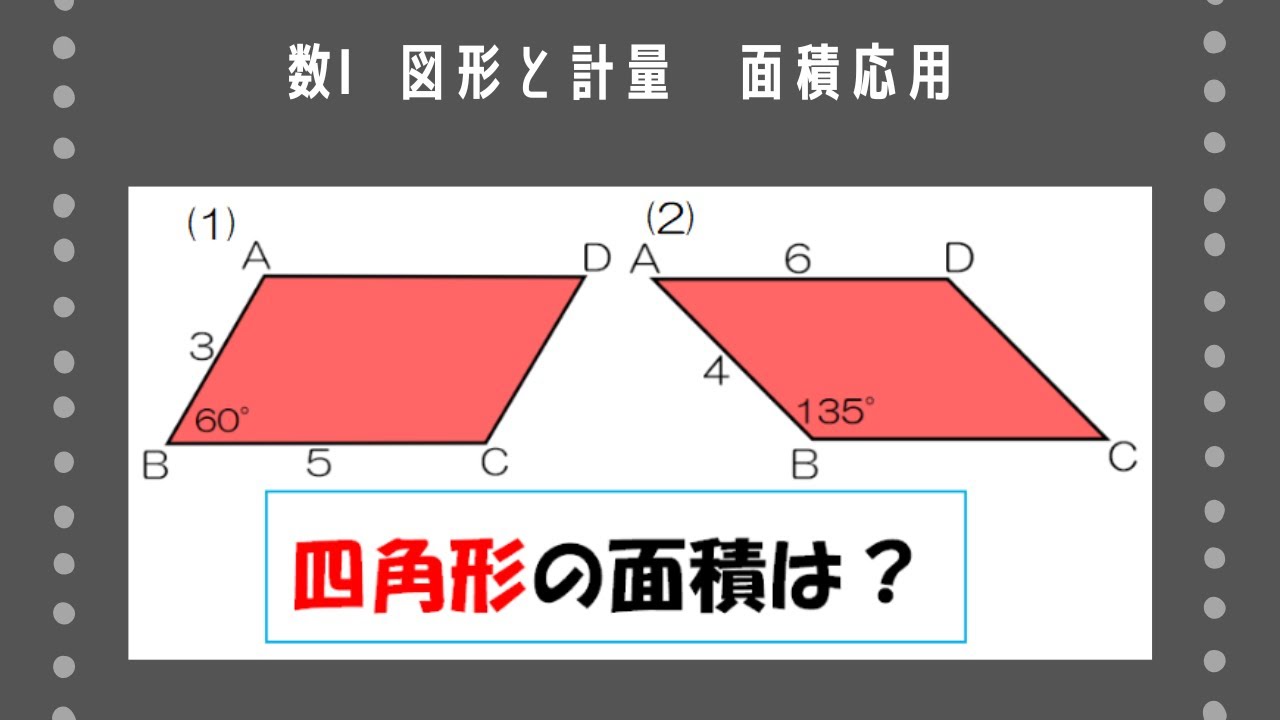
次のような平行四辺形ABCDの面積を求めよ。
(1)AB=3、BC=5、∠ABC=60°
(2)AB=4、AD=6、∠ABC=135°
この動画を見る
次のような平行四辺形ABCDの面積を求めよ。
(1)AB=3、BC=5、∠ABC=60°
(2)AB=4、AD=6、∠ABC=135°
【数Ⅰ】【図形と計量】正弦定理と余弦定理の応用3 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
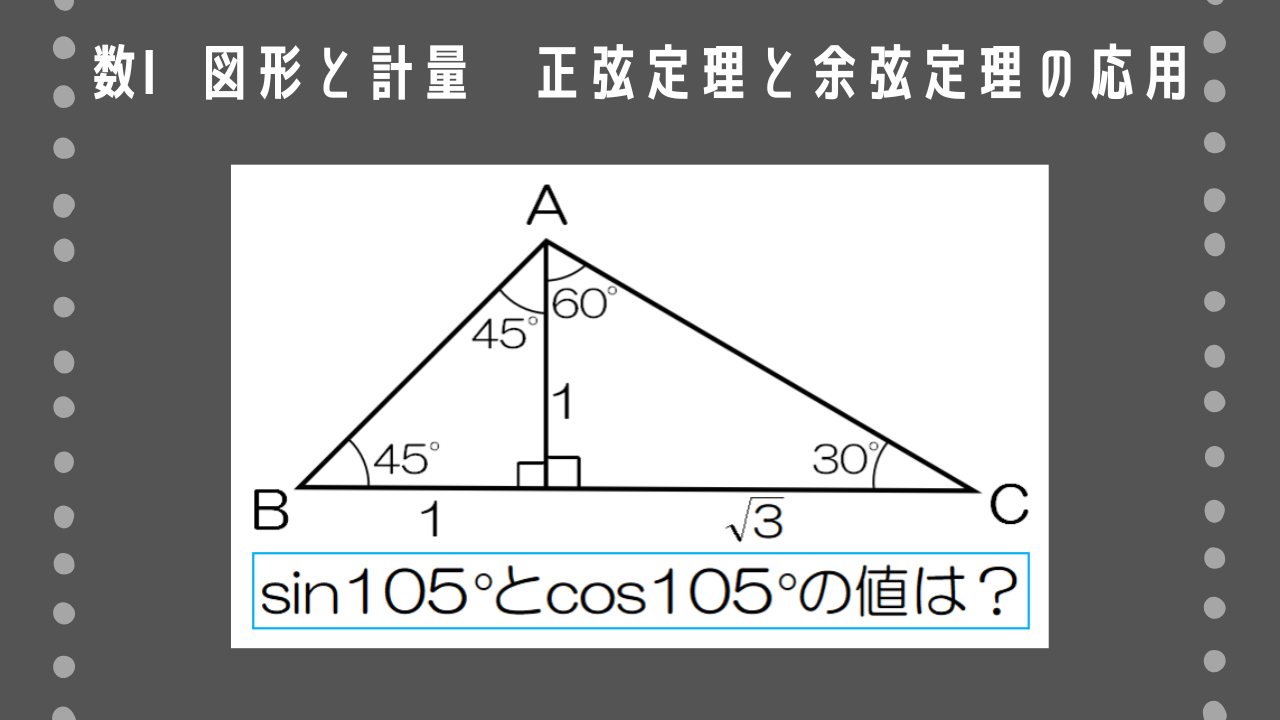
図を利用して、sin105°とcos105°の値を求めよ。
この動画を見る
図を利用して、sin105°とcos105°の値を求めよ。
【数Ⅰ】【図形と計量】正弦定理と余弦定理の応用2 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
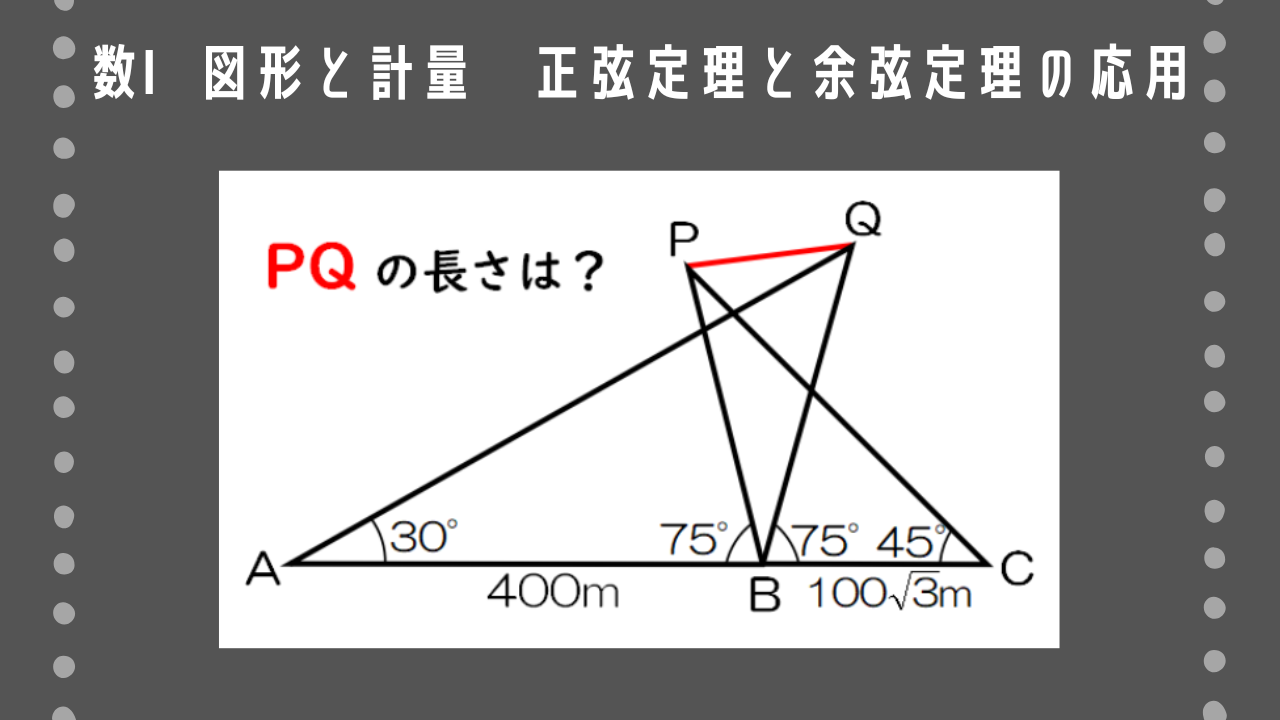
2地点P、Q間の距離を求めるために、1つの直線上にある3地点A、B、Cをとったら、AB=400m、BC=$100\sqrt{3}$m、∠QAB=30°、∠PBA=∠QBC=75°、∠PCB=45°であった。P、Q間の距離を求めよ。
この動画を見る
2地点P、Q間の距離を求めるために、1つの直線上にある3地点A、B、Cをとったら、AB=400m、BC=$100\sqrt{3}$m、∠QAB=30°、∠PBA=∠QBC=75°、∠PCB=45°であった。P、Q間の距離を求めよ。
【数Ⅰ】【図形と計量】正弦定理と余弦定理の応用1 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
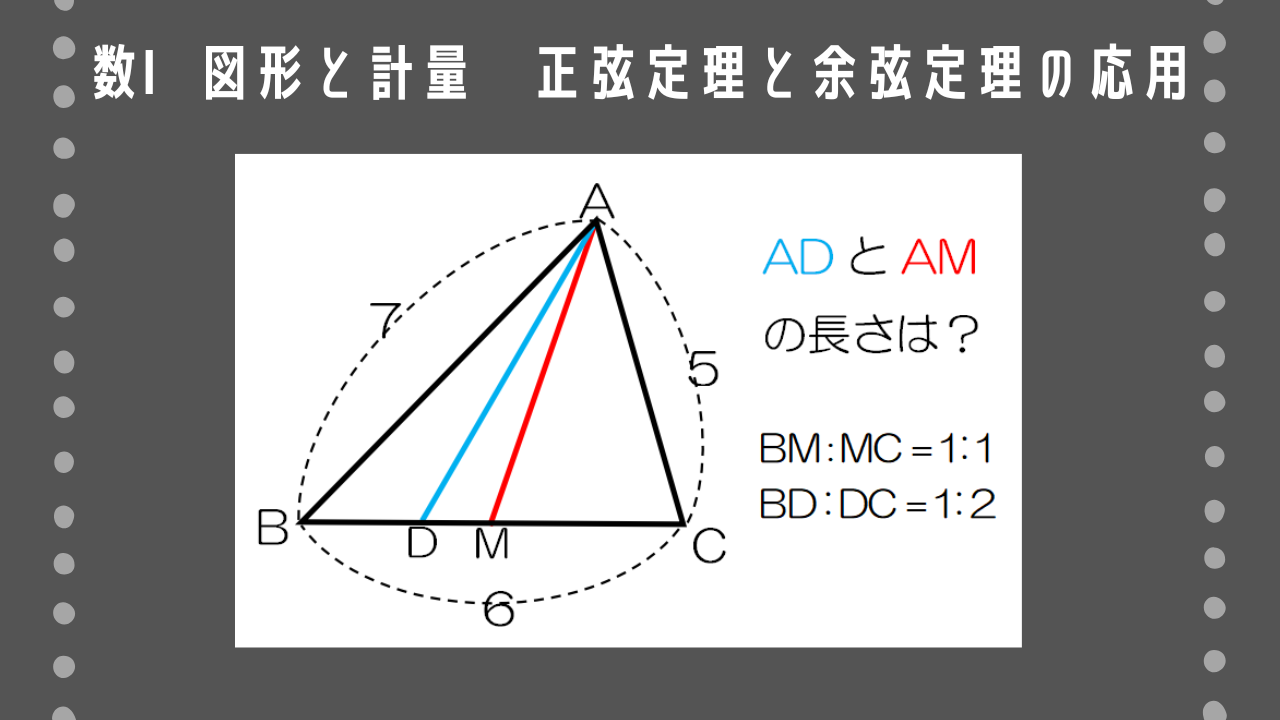
△ABCにおいて、辺BCの中点をM、辺BCを1:2に分ける点をDとする。a=6、b=5、c=7のとき、AM、ADの長さを求めよ。
この動画を見る
△ABCにおいて、辺BCの中点をM、辺BCを1:2に分ける点をDとする。a=6、b=5、c=7のとき、AM、ADの長さを求めよ。
【数Ⅰ】【図形と計量】正弦、余弦定理応用2 ※問題文は概要欄

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$△ABC$において,
$\dfrac{\sin A}{13}=\dfrac{\sin B}{8}=\dfrac{\sin C}{7}$
が成り立つとき,次のものを求めよ。
(1) 最も大きい角の大きさ (2) 最も小さい角の正接
この動画を見る
$△ABC$において,
$\dfrac{\sin A}{13}=\dfrac{\sin B}{8}=\dfrac{\sin C}{7}$
が成り立つとき,次のものを求めよ。
(1) 最も大きい角の大きさ (2) 最も小さい角の正接
【数Ⅰ】【図形と計量】正弦、余弦定理応用1 ※問題文は概要欄

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$△ABC$において,$a:b=(1+\sqrt{3}):2$,外接円の半径 $R=1$,$C=60°$のとき,$a,b,c,A,B$を求めよ。
この動画を見る
$△ABC$において,$a:b=(1+\sqrt{3}):2$,外接円の半径 $R=1$,$C=60°$のとき,$a,b,c,A,B$を求めよ。
【数Ⅰ】【図形と計量】余弦定理応用4 ※問題文は概要欄

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$△ABC$において,次のものを求めよ。
(1) $\sin A: \sin B:\sin C=5:8:7$ のとき,$\cos C,C$
(2) $(b+c):(c+a):(a+b)=4:5:6$のとき$A$
(3) $A:B:C=5:4:8$のとき $A, B, C, b:c$
この動画を見る
$△ABC$において,次のものを求めよ。
(1) $\sin A: \sin B:\sin C=5:8:7$ のとき,$\cos C,C$
(2) $(b+c):(c+a):(a+b)=4:5:6$のとき$A$
(3) $A:B:C=5:4:8$のとき $A, B, C, b:c$
【数Ⅰ】【図形と計量】余弦定理の利用 ※問題文は概要欄

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
△ABCにおいて,c²=a²+b²-abのとき,Cを求めよ。更に,a=3,c=√7のとき,bを求めよ。
この動画を見る
△ABCにおいて,c²=a²+b²-abのとき,Cを求めよ。更に,a=3,c=√7のとき,bを求めよ。
【数Ⅰ】【図形と計量】平行四辺形 ※問題文は概要欄

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
平行四辺形ABCDにおいて,AB=3,AD=5,∠B=60°のとき,対角線AC,BDの長さを求めよ。
この動画を見る
平行四辺形ABCDにおいて,AB=3,AD=5,∠B=60°のとき,対角線AC,BDの長さを求めよ。
【数Ⅰ】【図形と計量】余弦定理応用3 ※問題文は概要欄

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\triangle \mathrm{ABC}$において、$a=2,b=\sqrt{6},c=\sqrt{3}-1,A=45 ^\circ$のとき、次の問いに答えよ。
(1) 正弦定理を用いて、$\sin B$ の値を求めよ。
(2) (1)の$\sin B$ の値から、$B$ の候補として$2$ つ考えられるが、そのうち$1$ つは不適である。その理由を説明せよ。
この動画を見る
$\triangle \mathrm{ABC}$において、$a=2,b=\sqrt{6},c=\sqrt{3}-1,A=45 ^\circ$のとき、次の問いに答えよ。
(1) 正弦定理を用いて、$\sin B$ の値を求めよ。
(2) (1)の$\sin B$ の値から、$B$ の候補として$2$ つ考えられるが、そのうち$1$ つは不適である。その理由を説明せよ。
【数Ⅰ】【図形と計量】余弦定理応用2 ※問題文は概要欄

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
a=4,b=5,c=6 である△ABCにおいて,最も大きい角の余弦を求めよ。また,余弦が最も大きい角はどの角か。
この動画を見る
a=4,b=5,c=6 である△ABCにおいて,最も大きい角の余弦を求めよ。また,余弦が最も大きい角はどの角か。
【数Ⅰ】【図形と計量】余弦定理応用1 ※問題文は概要欄

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の各場合について,△ABC の残りの辺の長さと角の大きさを求めよ。
(1) b=3,c=√3,B=60°
(2) b=2√3,c=2,C=30°
この動画を見る
次の各場合について,△ABC の残りの辺の長さと角の大きさを求めよ。
(1) b=3,c=√3,B=60°
(2) b=2√3,c=2,C=30°
【数Ⅰ】【図形と計量】余弦定理を使った証明 ※問題文は概要欄

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
△ABC において,次のことが成り立つことを正弦定理を利用して証明せよ。
b<c⇒B<C
この動画を見る
△ABC において,次のことが成り立つことを正弦定理を利用して証明せよ。
b<c⇒B<C
【数Ⅰ】【図形と計量】三角比の値 ※問題文は概要欄

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$0°\leqq\theta\leqq 180°$とする。$\sin\theta-\cos\theta=\dfrac{1}{3}$のとき,$\sin\theta\cos\theta$の値を求めよ。
この動画を見る
$0°\leqq\theta\leqq 180°$とする。$\sin\theta-\cos\theta=\dfrac{1}{3}$のとき,$\sin\theta\cos\theta$の値を求めよ。
【数Ⅰ】【図形と計量】三角比の値域 ※問題文は概要欄

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の式のとりうる値の範囲を求めよ。(1)~(4)では$0°\leqq\theta\leqq 180°$とする。
(1) $sin\theta+2$ (2) $2\cos\theta$ (3) $2\sin\theta-1$ (4) $-3\cos\theta+1$ (5) $2\tan\theta+1$ ($0°\leqq0\leqq 60°$)
(6)$\tan\theta+1$ ($30°\leqq 0\lt 90°$)
この動画を見る
次の式のとりうる値の範囲を求めよ。(1)~(4)では$0°\leqq\theta\leqq 180°$とする。
(1) $sin\theta+2$ (2) $2\cos\theta$ (3) $2\sin\theta-1$ (4) $-3\cos\theta+1$ (5) $2\tan\theta+1$ ($0°\leqq0\leqq 60°$)
(6)$\tan\theta+1$ ($30°\leqq 0\lt 90°$)
【数Ⅰ】【図形と計量】三角比の変換応用 ※問題文は概要欄

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の式の値を簡単にせよ。
(1) sin10°cos80°-sin100°cos170°
(2) 1/(1+sin²20°)-tan²110°
(3) sin²(180°-θ)+sin²(90°-θ)+sin²(90°+θ)+cos²(90°-θ)
この動画を見る
次の式の値を簡単にせよ。
(1) sin10°cos80°-sin100°cos170°
(2) 1/(1+sin²20°)-tan²110°
(3) sin²(180°-θ)+sin²(90°-θ)+sin²(90°+θ)+cos²(90°-θ)
【数Ⅰ】【図形と計量】2直線のなす角 ※問題文は概要欄

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の2直線のなす鋭角θを求めよ。
(1) $y=-\sqrt{3}x, y=-x$
(2) $y=-\frac{1}{\sqrt{3}}x, y=x$
この動画を見る
次の2直線のなす鋭角θを求めよ。
(1) $y=-\sqrt{3}x, y=-x$
(2) $y=-\frac{1}{\sqrt{3}}x, y=x$
【数Ⅰ】【図形と計量】三角比大小比較 ※問題文は概要欄

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の三角比の値を,小さい方から順に並べよ。ただし,三角比の表は用いないものとする。
cos10°,sin40°,cos80°,sin110°,sin130°,sin160°
この動画を見る
次の三角比の値を,小さい方から順に並べよ。ただし,三角比の表は用いないものとする。
cos10°,sin40°,cos80°,sin110°,sin130°,sin160°
shape problems : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study

単元:
#数学(中学生)#中1数学#数Ⅰ#図形と計量#角度と面積#平面図形#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$lとmが平行のとき\angle{x}の大きさを求めよ$
$図は動画参照$
この動画を見る
$lとmが平行のとき\angle{x}の大きさを求めよ$
$図は動画参照$
高校1年生から早稲田に挑戦!三角比の難問!【早稲田大学】【数学 入試問題】

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
m,nを正の整数とする。半径1の円に内接する△ABCが
sinA=m/17,sinB=n/17,sin²C=sin²A+sin²B
を満たすとき△ABCの内接円の半径を求めよ。
この動画を見る
m,nを正の整数とする。半径1の円に内接する△ABCが
sinA=m/17,sinB=n/17,sin²C=sin²A+sin²B
を満たすとき△ABCの内接円の半径を求めよ。
京大の三角関数!18度系の三角比はどう扱う? #Shorts #ずんだもん #勉強 #数学

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
半径1の円に内接する正五角形の一辺の長さが1.15より大きいか否かを理由を付けて判定せよ。
この動画を見る
半径1の円に内接する正五角形の一辺の長さが1.15より大きいか否かを理由を付けて判定せよ。
【数Ⅰ】【図形と計量】三角比の相互関係式の使い方2 ※問題文は概要欄

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\sin\theta-\cos\theta$を$\sin\theta$だけを用いた式で表せ。また,$\cos\theta$だけを用いた式で表せ。
この動画を見る
$\sin\theta-\cos\theta$を$\sin\theta$だけを用いた式で表せ。また,$\cos\theta$だけを用いた式で表せ。
【数Ⅰ】【図形と計量】三角比の相互関係式の使い方1 ※問題文は概要欄

単元:
#数Ⅰ#図形と計量#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の式の値を求めよ。
(1)$ (\sin\theta+\cos\theta)²+(\sin\theta-\cos\theta)²$
(2) $(1-\sin\theta)(1+\sin\theta)-\frac{1}{1+\tan^2\theta}$
この動画を見る
次の式の値を求めよ。
(1)$ (\sin\theta+\cos\theta)²+(\sin\theta-\cos\theta)²$
(2) $(1-\sin\theta)(1+\sin\theta)-\frac{1}{1+\tan^2\theta}$
【数Ⅰ】【図形と計量】有名角以外を含む三角比の計算 ※問題文は概要欄

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の式の値を求めよ。
(1) $\sin^2 40°+\sin^2 50°$
(2) $\tan35°\tan55°+\tan15°\tan75°$
(3) $(\sin70°+\sin20°)^2-2\tan70°\cos^2 50°$
この動画を見る
次の式の値を求めよ。
(1) $\sin^2 40°+\sin^2 50°$
(2) $\tan35°\tan55°+\tan15°\tan75°$
(3) $(\sin70°+\sin20°)^2-2\tan70°\cos^2 50°$
