 図形の性質
図形の性質
 図形の性質
図形の性質
練習問題24 兵庫県教採練習問題 14番 面積

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{14}$
$c:y=x\sin x \ (0\leqq x\leqq 2\pi)$
第4象限にある$C$上の点の接線$\ell$は原点を通る.
$c$と$\ell$で囲まれた面積$S$を求めよ.
この動画を見る
$\boxed{14}$
$c:y=x\sin x \ (0\leqq x\leqq 2\pi)$
第4象限にある$C$上の点の接線$\ell$は原点を通る.
$c$と$\ell$で囲まれた面積$S$を求めよ.
気付くの難しめ 西大和学園2021
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
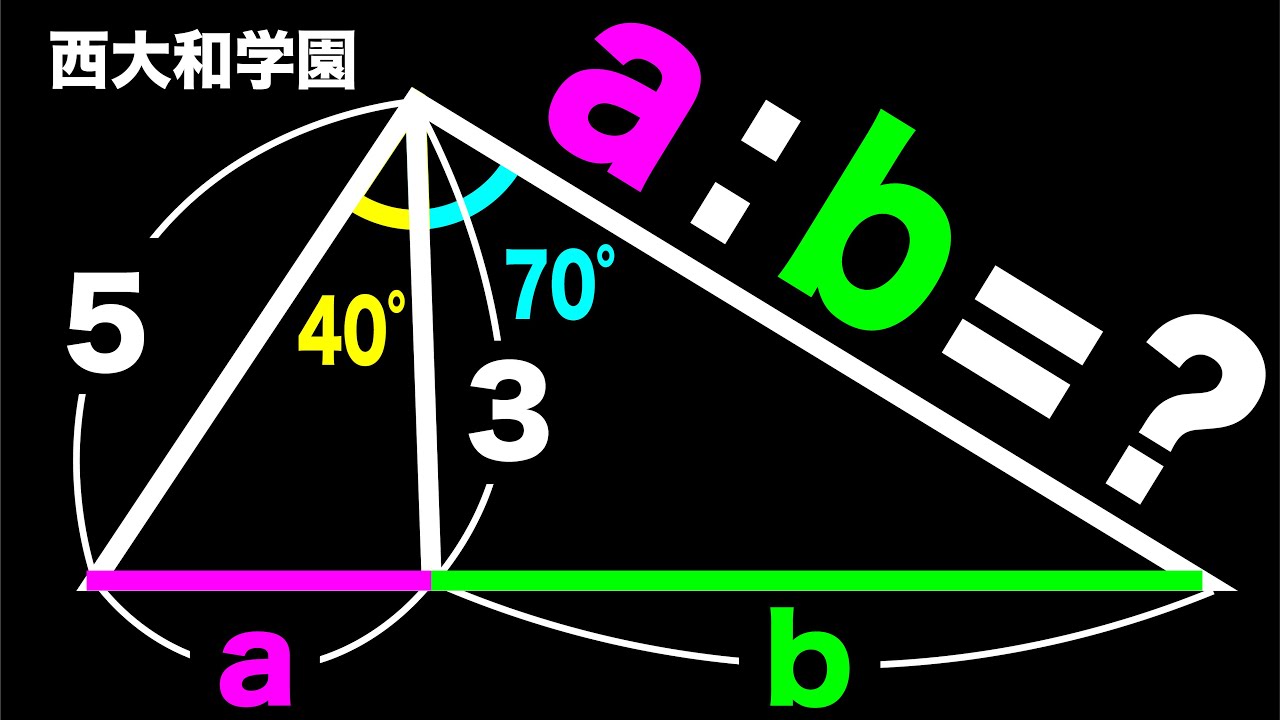
a:b=?
*図は動画内参照
西大和学園高等学校
この動画を見る
a:b=?
*図は動画内参照
西大和学園高等学校
3つの並んだ合同な正三角形

単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
1つの正三角形の面積=18
斜線部の面積は?
*図は動画内参照
この動画を見る
1つの正三角形の面積=18
斜線部の面積は?
*図は動画内参照
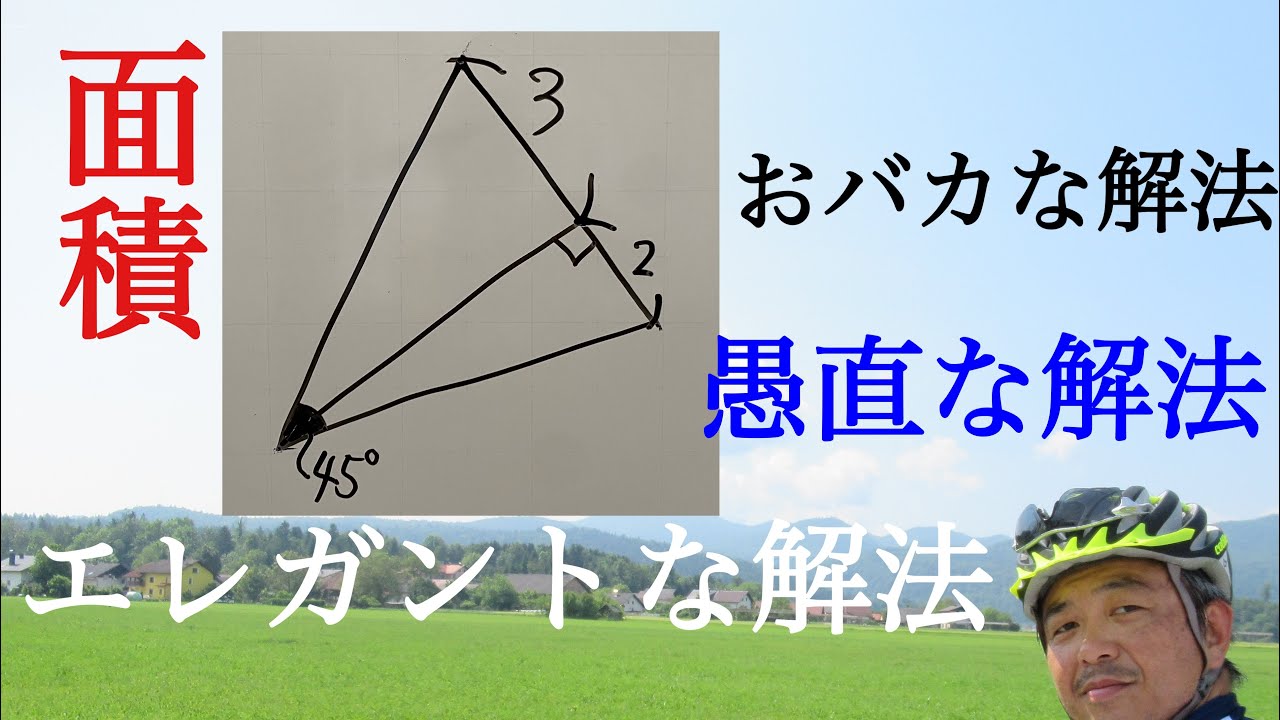
三角形の面積 おバカな解法・愚直な解法・エレガントな解法
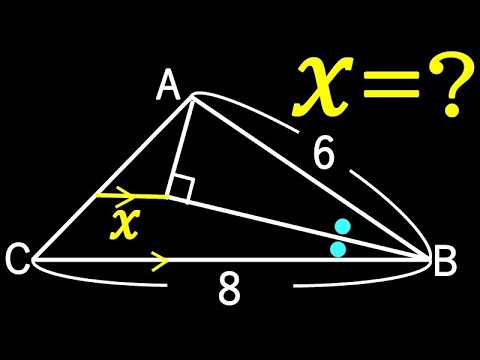
角の二等分線+垂直=❓
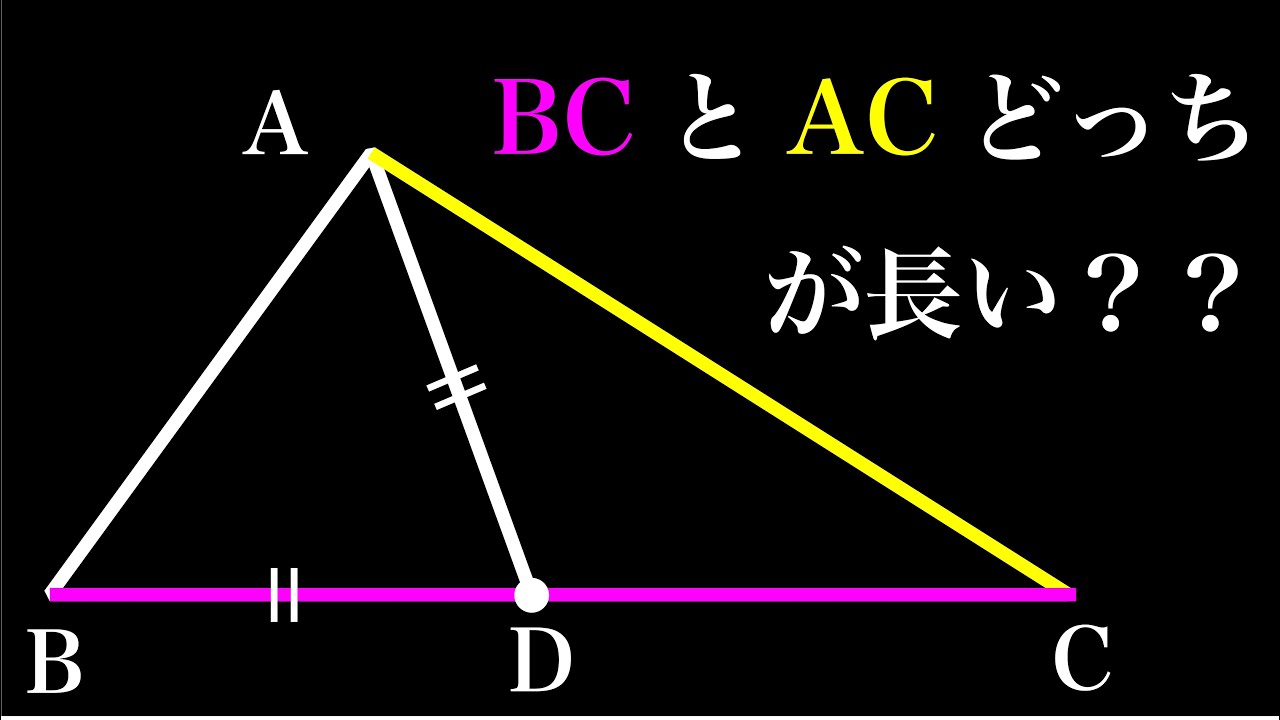
どっちが長い?? 広島県(改)
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
BCとACどっちが長い?
*図は動画内参照
広島県(改)
この動画を見る
BCとACどっちが長い?
*図は動画内参照
広島県(改)
0.2秒で答えが出る⁉️半円の面積の和

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
大円の半径を1とする.
2つの半円の面積の和を求めよ.
この動画を見る
大円の半径を1とする.
2つの半円の面積の和を求めよ.
気づけば一瞬!!角の和 東北学院
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
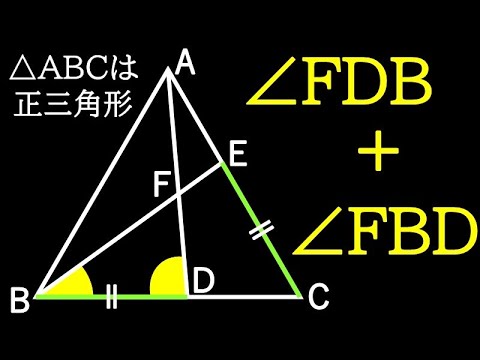
△ABCは正三角形
○+✖=?
*図は動画内参照
東北学院高等学校
この動画を見る
△ABCは正三角形
○+✖=?
*図は動画内参照
東北学院高等学校
気づけば一瞬!!長方形の面積=❓
単元:
#数学(中学生)#中2数学#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#三角形と四角形#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
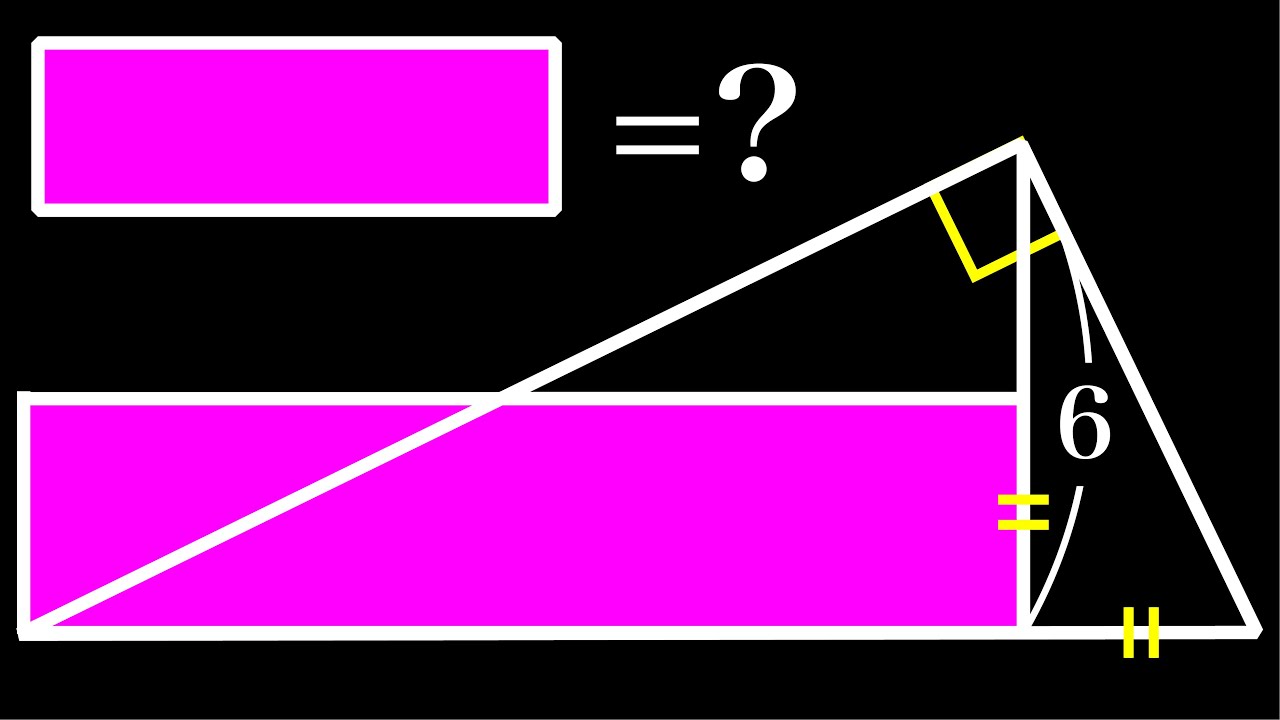
長方形の面積=?
*図は動画内参照
この動画を見る
長方形の面積=?
*図は動画内参照
❤️ (❤️は面積です)
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#平面図形#角度と面積#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
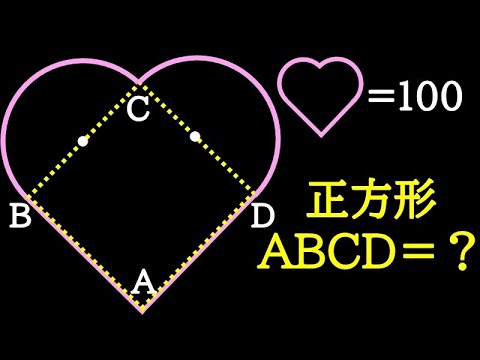
♡=100のとき正方形ABCD=?
*図は動画内参照
この動画を見る
♡=100のとき正方形ABCD=?
*図は動画内参照
長方形の分割 江戸川学園取手
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
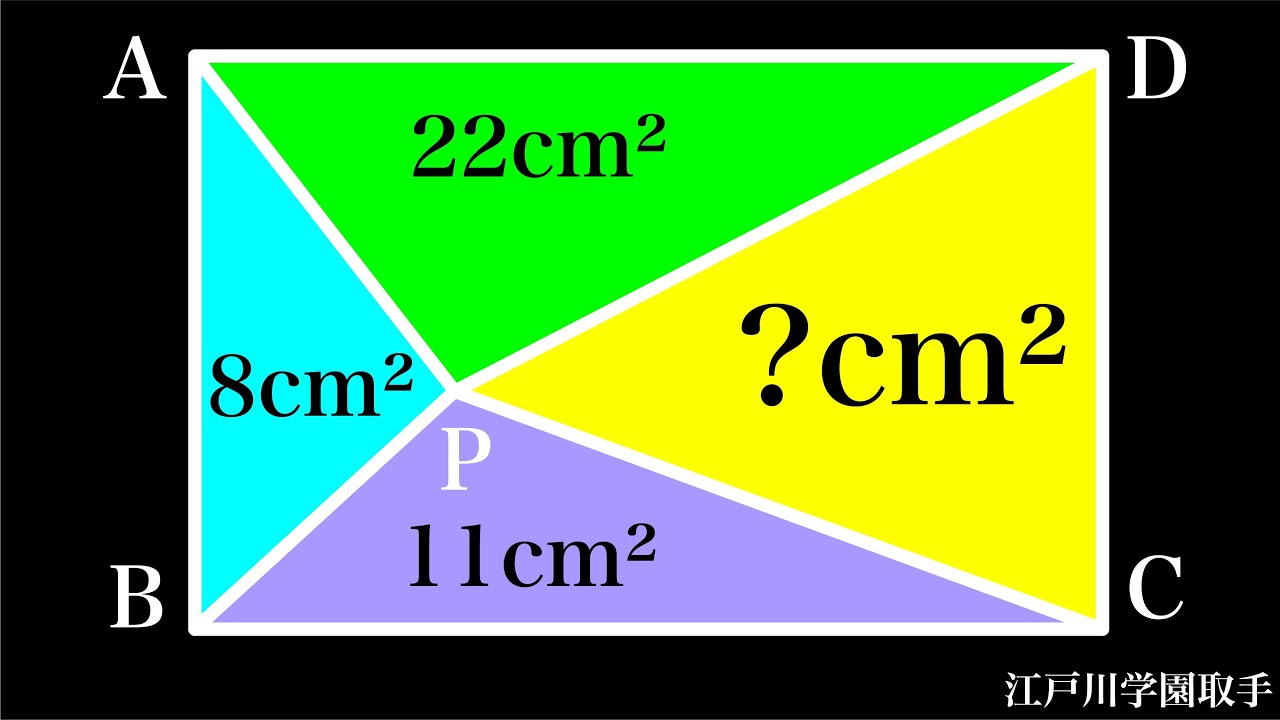
三角形CDPの面積=?
*図は動画内参照
この動画を見る
三角形CDPの面積=?
*図は動画内参照
三平方の定理不要!! B

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABC=?
*図は動画内参照
鎌倉学園高等学校
この動画を見る
△ABC=?
*図は動画内参照
鎌倉学園高等学校
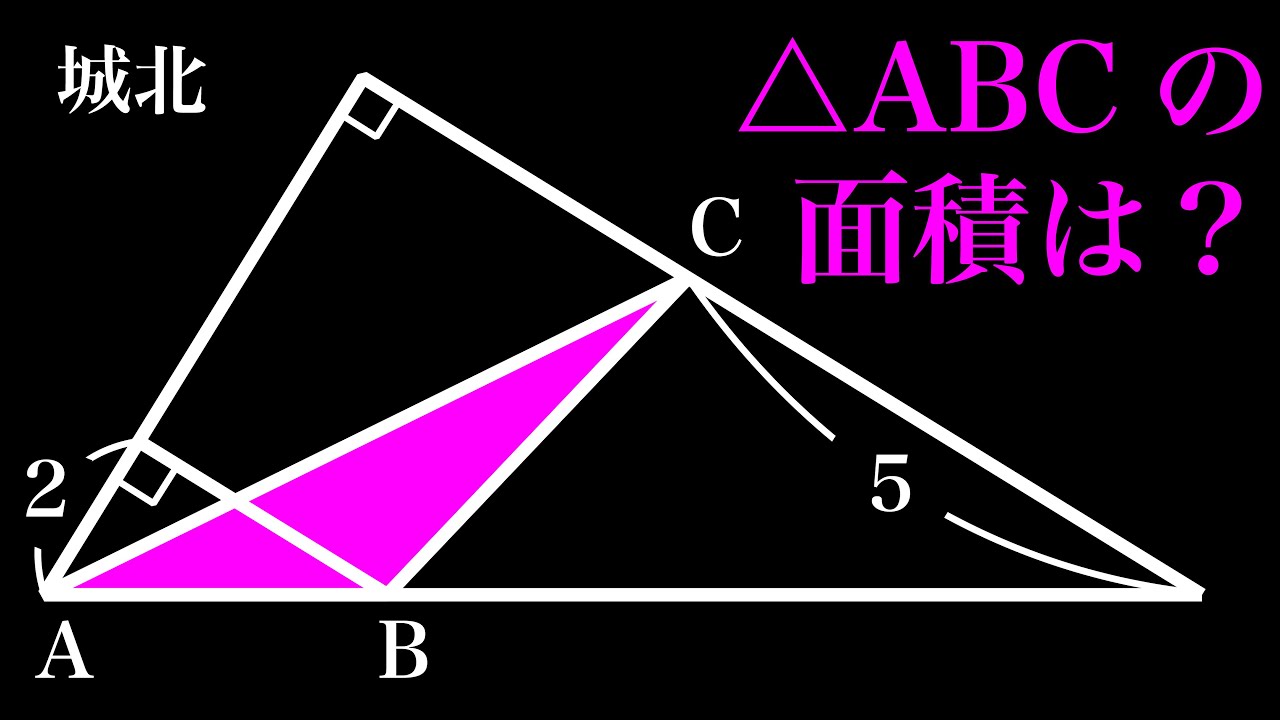
3通りで解説しました (城北)
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABCの面積=?
*図は動画内参照
城北高等学校
この動画を見る
△ABCの面積=?
*図は動画内参照
城北高等学校
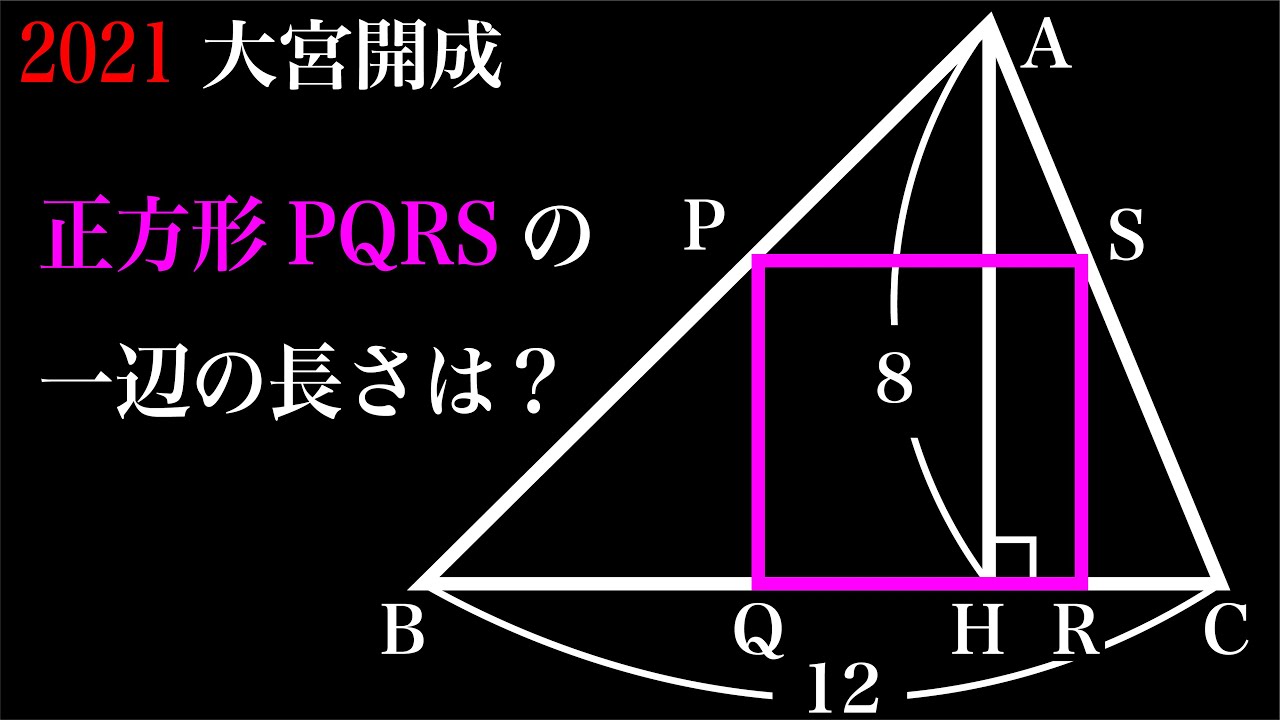
三角形に内接する正方形 B
単元:
#数学(中学生)#中2数学#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#三角形と四角形#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正方形PQRSの1辺の長さ=?
*図は動画内参照
2021大宮開成高等学校
この動画を見る
正方形PQRSの1辺の長さ=?
*図は動画内参照
2021大宮開成高等学校
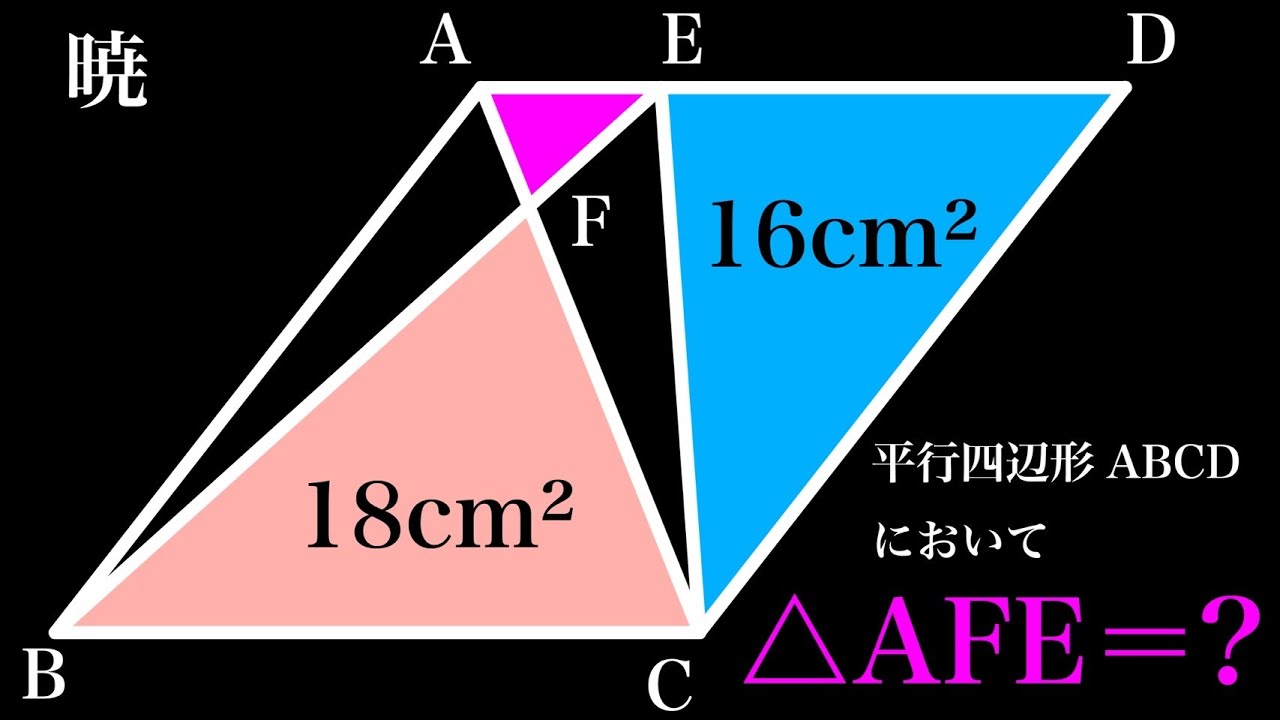
パズル的な問題!! B
単元:
#数学(中学生)#中2数学#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#三角形と四角形#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
平行四辺形ABCDにおいて
△AFEの面積=?
*図は動画内参照
暁高等学校
この動画を見る
平行四辺形ABCDにおいて
△AFEの面積=?
*図は動画内参照
暁高等学校
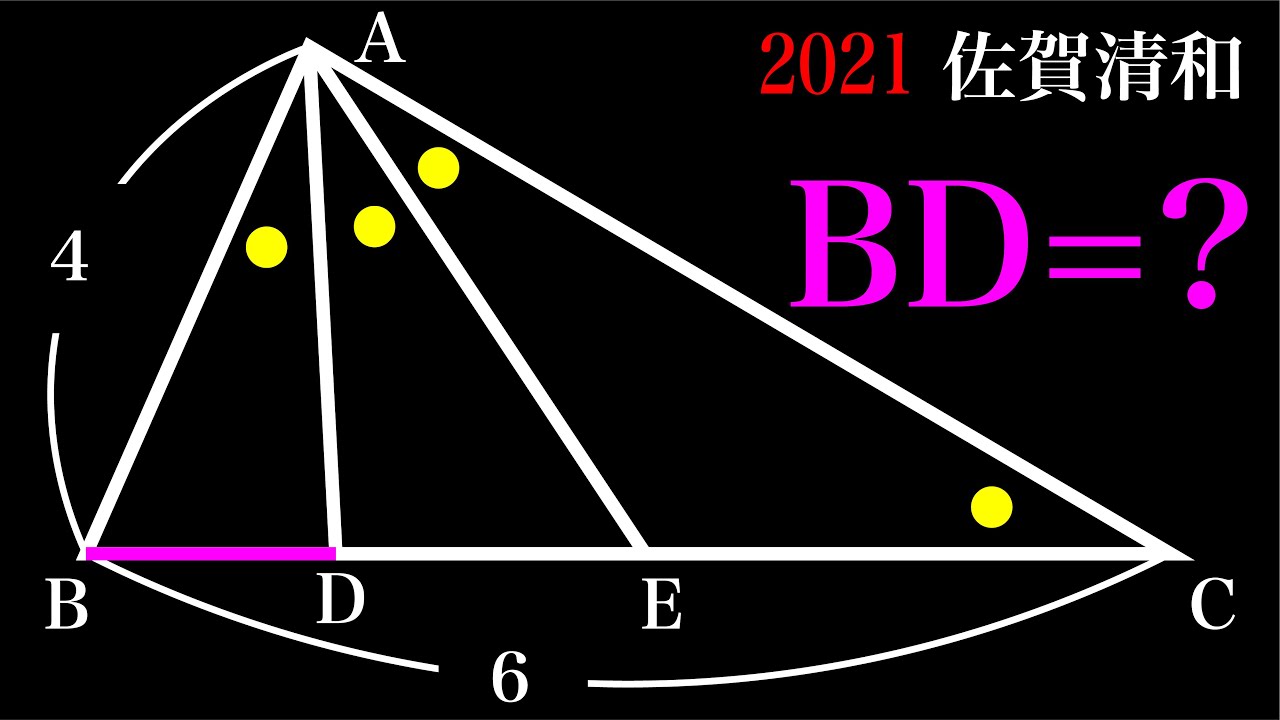
角の三等分!!2通りで解説 B
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
BD=?
*図は動画内参照
2021佐賀清和高等学校
この動画を見る
BD=?
*図は動画内参照
2021佐賀清和高等学校
円周の長さ 円の面積 文字式 A

単元:
#数学(中学生)#中1数学#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#文字と式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
周の長さがaの円の面積をaで表せ。
大阪教育大学附属高等学校天王寺校舎
この動画を見る
周の長さがaの円の面積をaで表せ。
大阪教育大学附属高等学校天王寺校舎
12京都府採用試験(数学:2番 接線の個数)

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{2}$
点$(a,0)$から$y=\dfrac{1}{x^2+x+1}$に異なる2本の接線を
ひくことができるような$a$の範囲を求めよ.
この動画を見る
$\boxed{2}$
点$(a,0)$から$y=\dfrac{1}{x^2+x+1}$に異なる2本の接線を
ひくことができるような$a$の範囲を求めよ.
とある奈良県教員採用試験の問題(数学:接線の数)

単元:
#数A#数Ⅱ#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#微分法と積分法#接線と増減表・最大値・最小値#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
点$P(a,0)$を通り,
曲線$y=\dfrac{x}{\log_x}\ (x\gt 1)$に接する直線が
2本引けるように$a$の値の範囲を求めよ.
この動画を見る
点$P(a,0)$を通り,
曲線$y=\dfrac{x}{\log_x}\ (x\gt 1)$に接する直線が
2本引けるように$a$の値の範囲を求めよ.
軌跡 C 2021久留米大附設
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
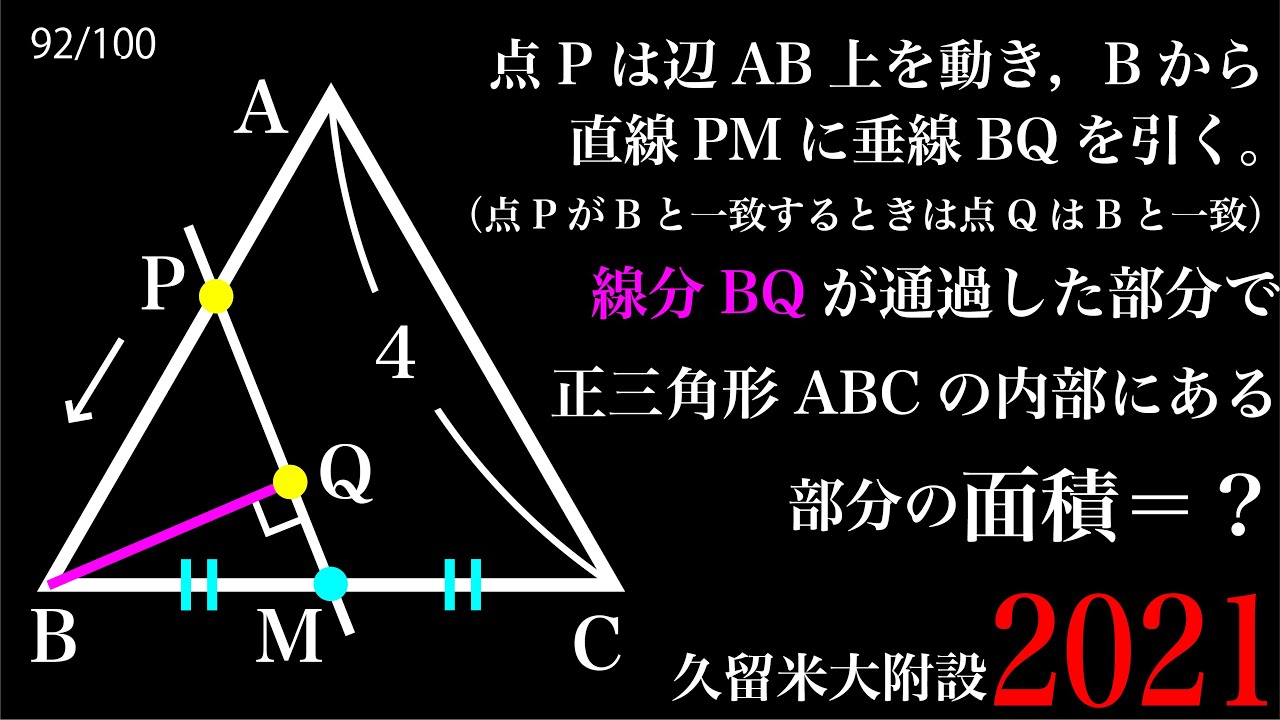
点Pは辺AB上を動き、Bから直線PMに垂線BQを引く。
(点PがBと一致するときは点QはBと一致するとする)
線分BQが通過した部分で正三角形ABCの内部にある部分の面積=?
(2021久留米大学附設高等学校)
この動画を見る
点Pは辺AB上を動き、Bから直線PMに垂線BQを引く。
(点PがBと一致するときは点QはBと一致するとする)
線分BQが通過した部分で正三角形ABCの内部にある部分の面積=?
(2021久留米大学附設高等学校)
軌跡その2 C
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
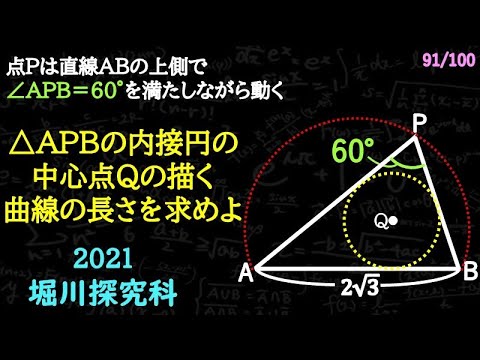
点Pが$\angle APB = 60°$をみたしながら動く
(ただし点Pは直線ABの上側)
△APBの内接円の中心点Qの描く曲線の長さを求めよ
*図は動画内参照
(2021京都市立堀川高校探究科)
この動画を見る
点Pが$\angle APB = 60°$をみたしながら動く
(ただし点Pは直線ABの上側)
△APBの内接円の中心点Qの描く曲線の長さを求めよ
*図は動画内参照
(2021京都市立堀川高校探究科)
軌跡その1 B
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
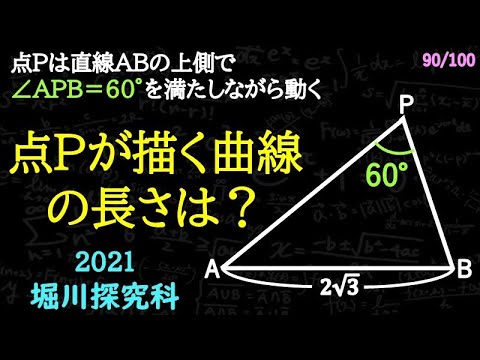
点Pが$\angle APB = 60°$を満たしながら動く。
(ただし、点Pは直線ABの上側)
点Pがえがく曲線の長さは??
*図は動画内参照
京都市立堀川高校探究科
この動画を見る
点Pが$\angle APB = 60°$を満たしながら動く。
(ただし、点Pは直線ABの上側)
点Pがえがく曲線の長さは??
*図は動画内参照
京都市立堀川高校探究科
小学生は求められない!角度 2021明大中野A
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
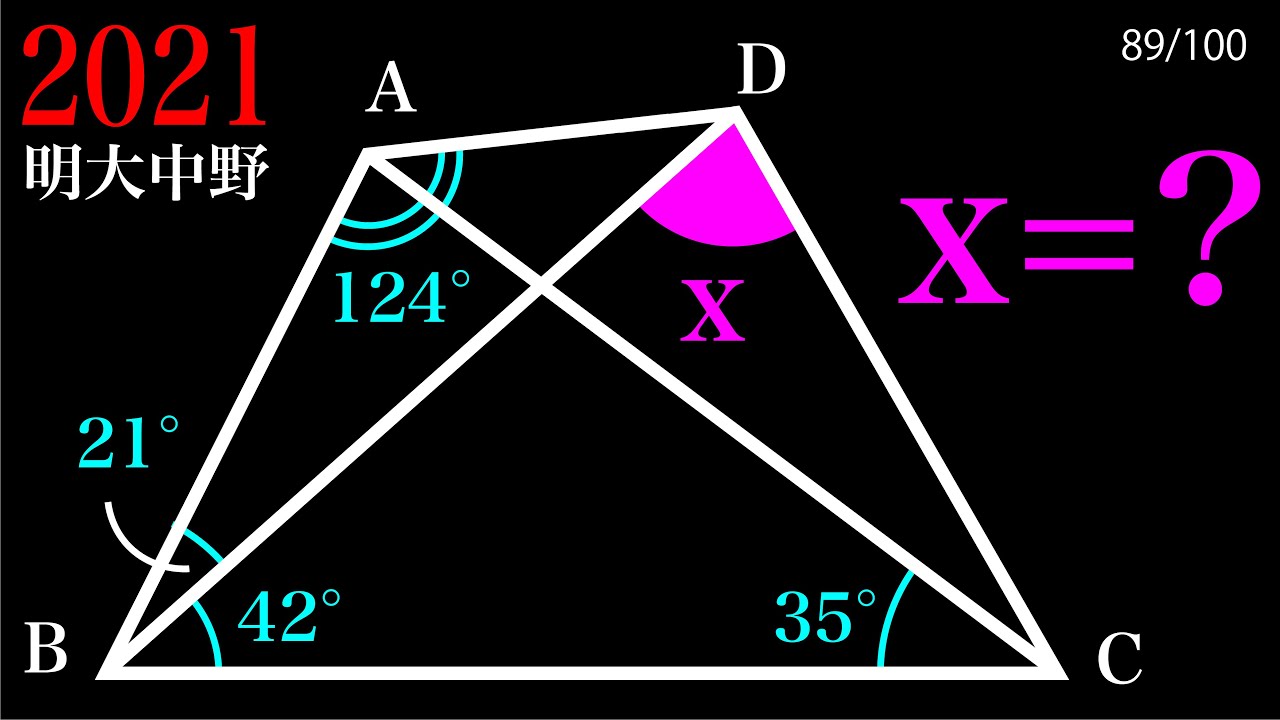
$\angle x =?$
*図は動画内参照
2021明治大学付属中野高等学校
この動画を見る
$\angle x =?$
*図は動画内参照
2021明治大学付属中野高等学校
難C(むずかしー) 円に外接する正八角形 2021中大横浜

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
円の面積=?
*図は動画内参照
2021中央大学附属横浜高等学校
この動画を見る
円の面積=?
*図は動画内参照
2021中央大学附属横浜高等学校
正六角形と円 A 中大横浜 2021

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正六角形の周の長さは?
*図は動画内参照
2021中央大学附属横浜高等学校
この動画を見る
正六角形の周の長さは?
*図は動画内参照
2021中央大学附属横浜高等学校
ピザを切れ!! B 中大横浜2021

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正八角形の面積=?
*図は動画内参照
2021中央大学附属横浜高等学校
この動画を見る
正八角形の面積=?
*図は動画内参照
2021中央大学附属横浜高等学校
気付くか、気付かないか 2021 埼玉県 B

2つの三角形の関係に注目!! B 2021 慶應義塾
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
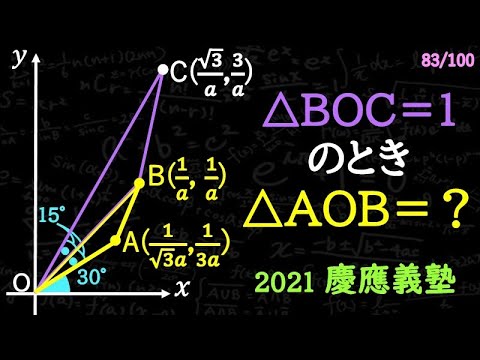
△BOC=1のとき△AOBの面積=?
*図は動画内参照
2021慶應義塾高等学校
この動画を見る
△BOC=1のとき△AOBの面積=?
*図は動画内参照
2021慶應義塾高等学校
2通りで解説!! 都立青山 B

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
DP=?
*図は動画内参照
2021東京都立青山高等学校
この動画を見る
DP=?
*図は動画内参照
2021東京都立青山高等学校
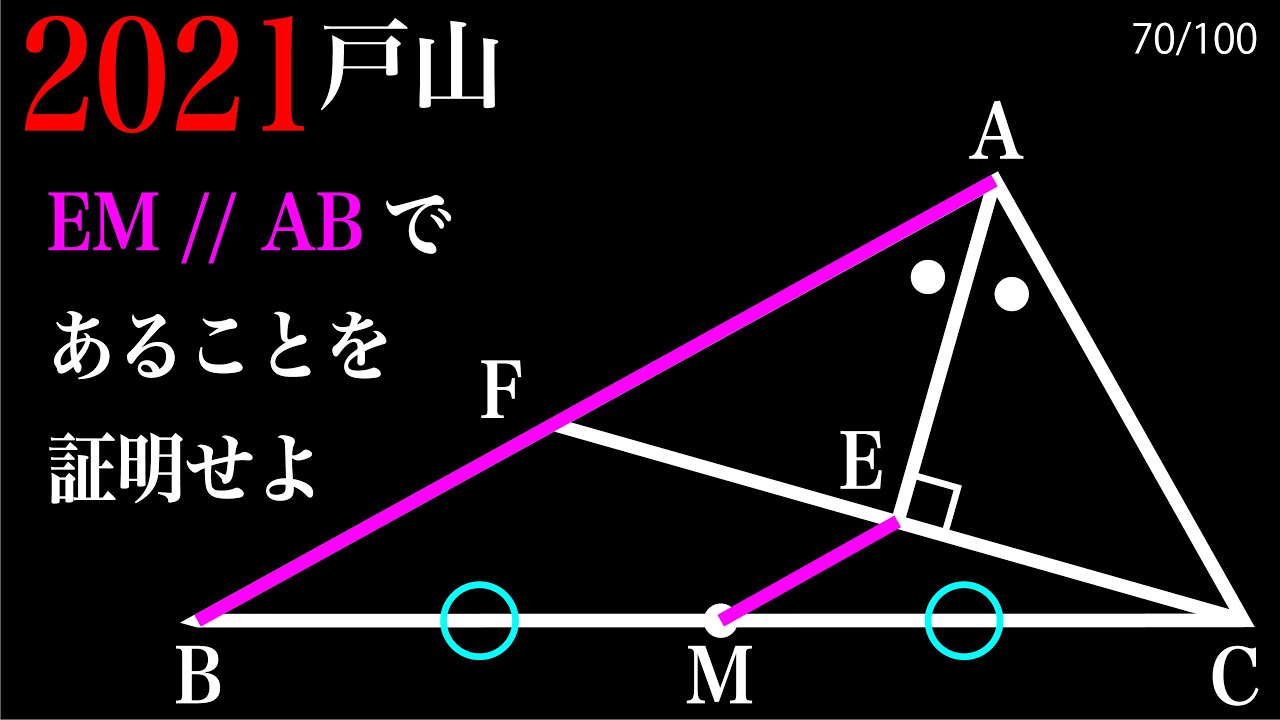
平行であることの証明 2021 戸山(改) A
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
EM//ABを示せ
*図は動画内参照
2021戸山高等学校
この動画を見る
EM//ABを示せ
*図は動画内参照
2021戸山高等学校
