 図形の性質
図形の性質
 図形の性質
図形の性質
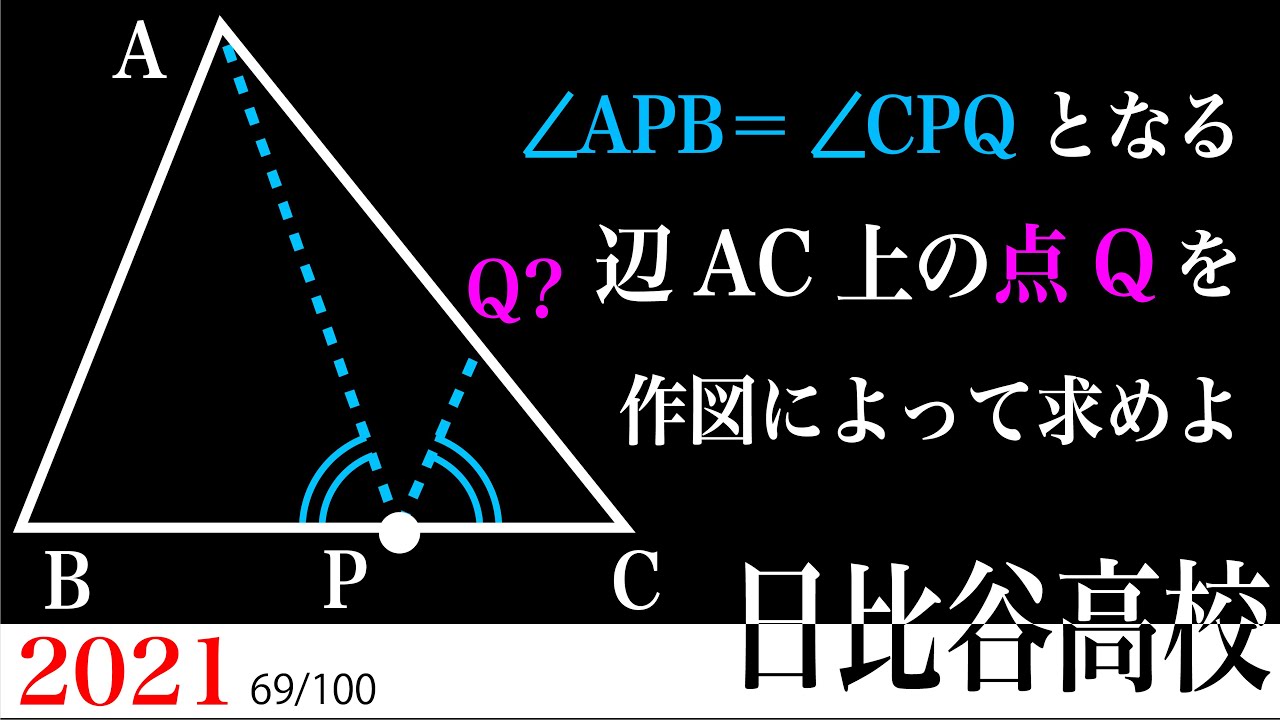
角度が等しい作図 2021 日比谷 B
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle APB = \angle CPQ$となる辺AC上の点Qを作図によって求めよ。
*図は動画内参照
2021日比谷高等学校
この動画を見る
$\angle APB = \angle CPQ$となる辺AC上の点Qを作図によって求めよ。
*図は動画内参照
2021日比谷高等学校
四面体の体積(垂線はどこに落ちる??)慶應義塾 2021 C

単元:
#数学(中学生)#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
体積=?
*図は動画内参照
2021慶應義塾高等学校
この動画を見る
体積=?
*図は動画内参照
2021慶應義塾高等学校
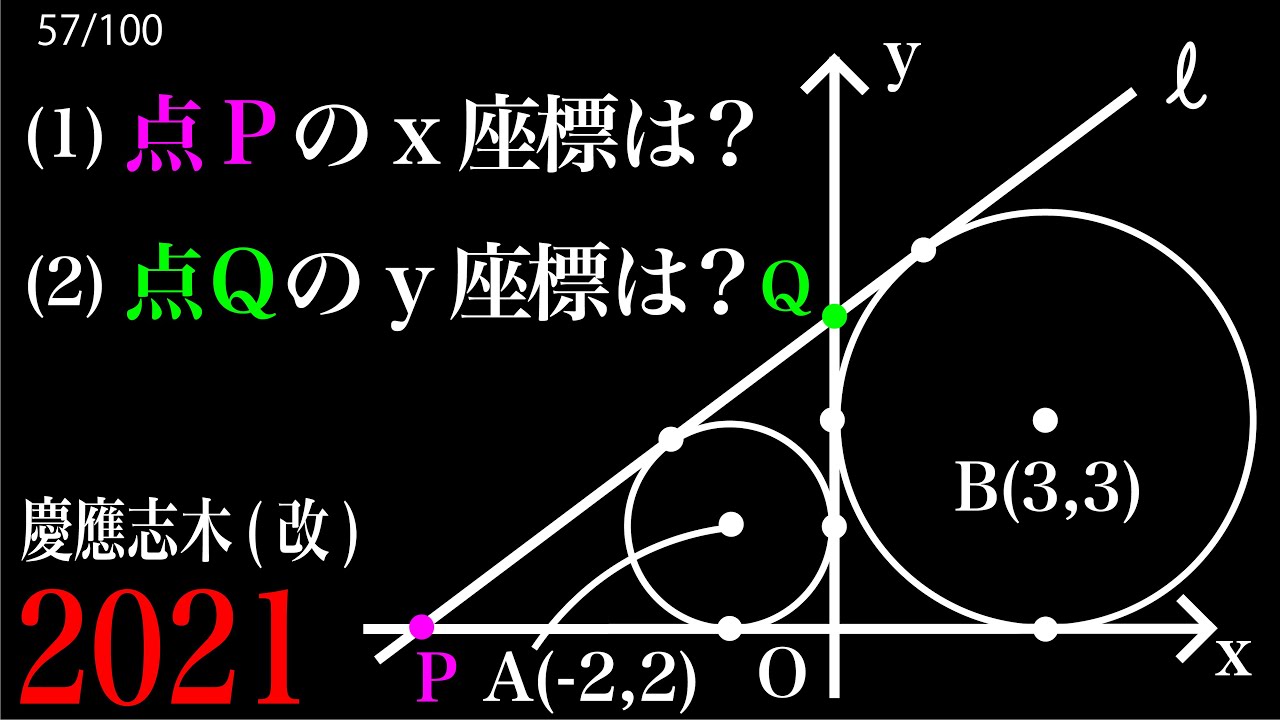
内接円 傍接円 関数 B 慶應志木2021
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
(1)点Pのx座標は?
(2)点Qのy座標は?
*図は動画内参照
2021慶應義塾志木高等学校
この動画を見る
(1)点Pのx座標は?
(2)点Qのy座標は?
*図は動画内参照
2021慶應義塾志木高等学校
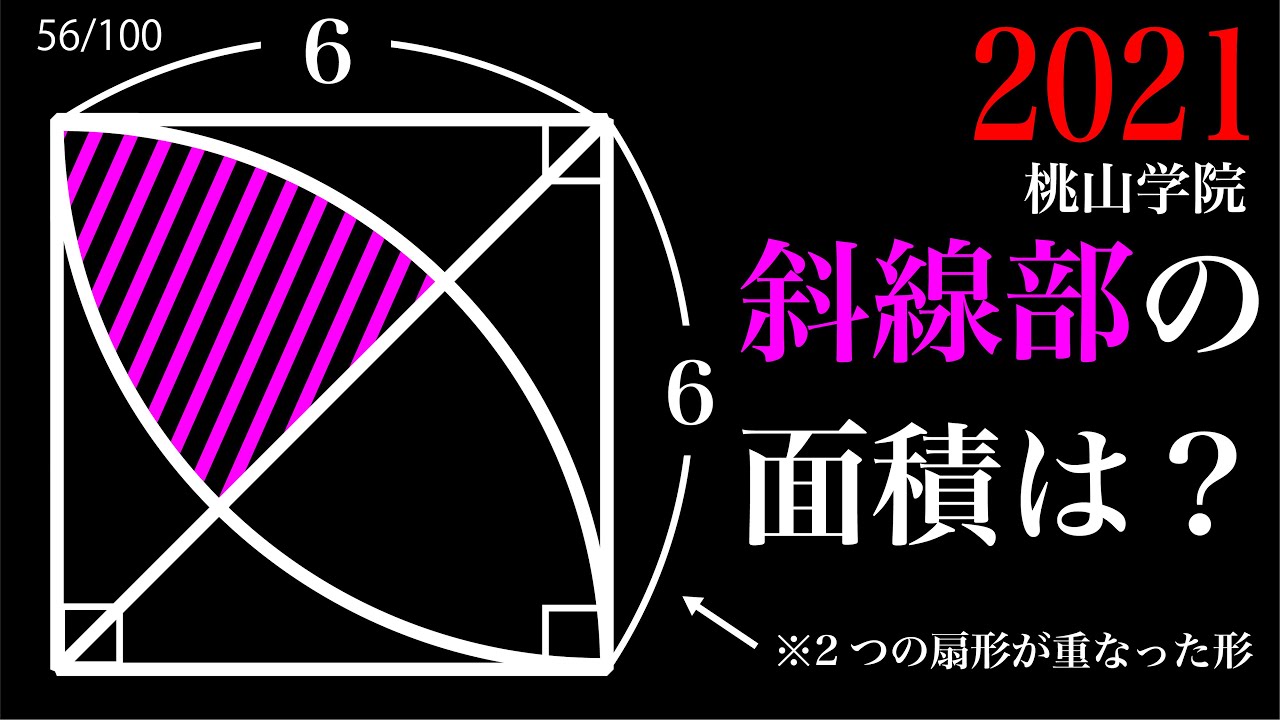
葉っぱの半分 桃山学院 A
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
斜線部の面積=?
*図は動画内参照
2021桃山学院高等学校
この動画を見る
斜線部の面積=?
*図は動画内参照
2021桃山学院高等学校
各辺の垂直二等分線の交点が一致することの証明 慶応志木 2021 C

単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
下の図において点Pから辺BCに下した垂線と辺BCとの交点をQとするとき
点Qは辺BCの中点であることを示せ。
(各辺の垂直二等分線の交点一致の証明)
*図は動画内参照
2021慶應義塾志木高等学校
この動画を見る
下の図において点Pから辺BCに下した垂線と辺BCとの交点をQとするとき
点Qは辺BCの中点であることを示せ。
(各辺の垂直二等分線の交点一致の証明)
*図は動画内参照
2021慶應義塾志木高等学校
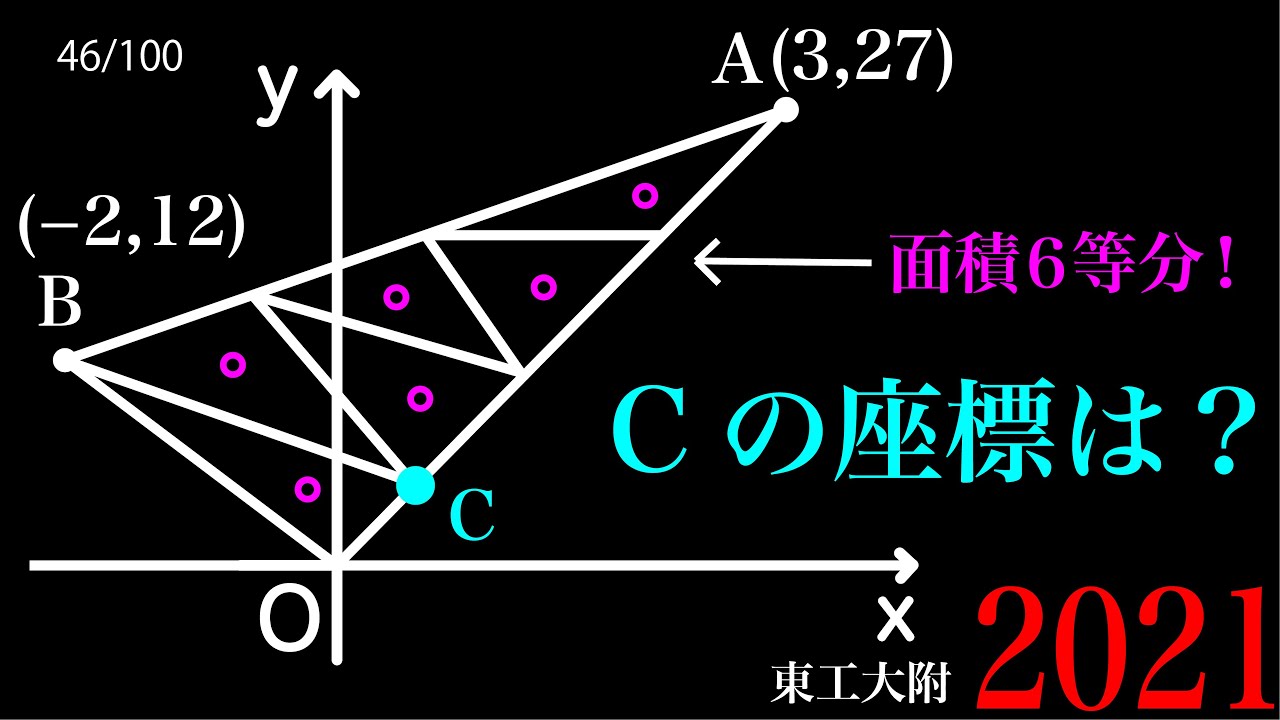
関数と図形 東工大附属(改) B
単元:
#数学(中学生)#数Ⅰ#数A#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
面積6等分
Cの座標は?
*図は動画内参照
2021東京工業大学附属科学技術高等学校
この動画を見る
面積6等分
Cの座標は?
*図は動画内参照
2021東京工業大学附属科学技術高等学校
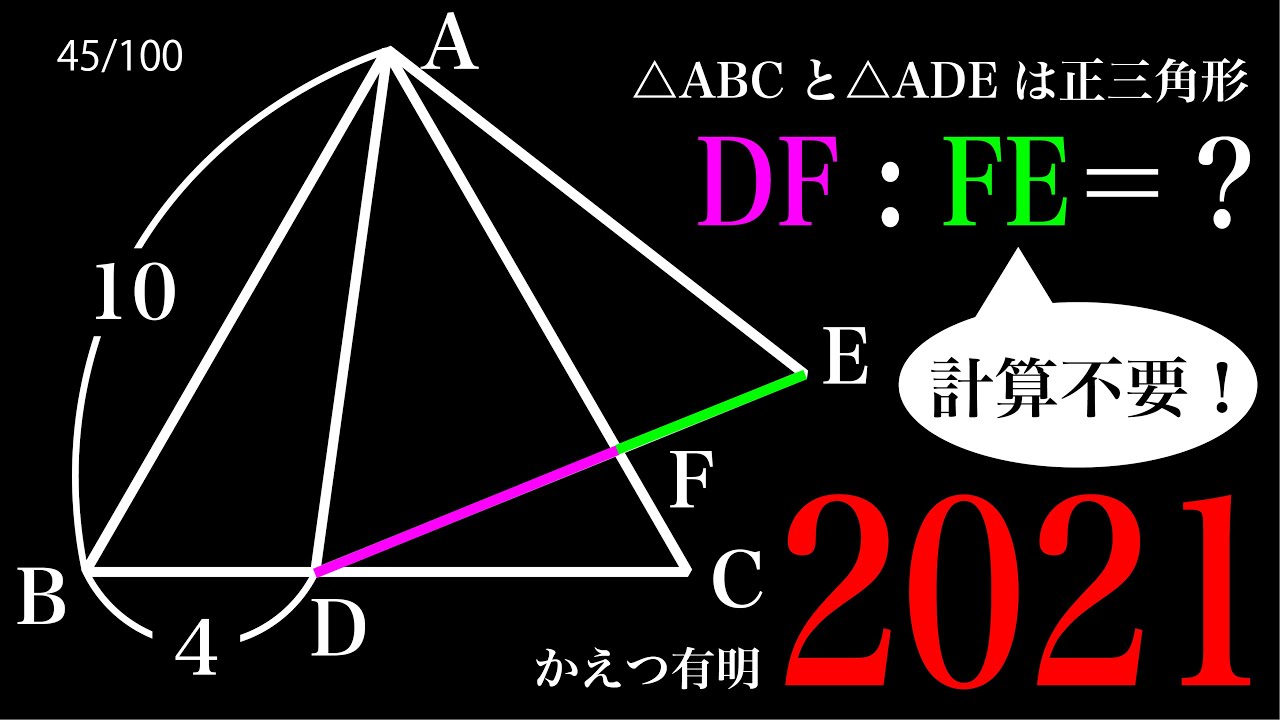
計算不要 正三角形2こ 2021かえつ有明 C
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABC、△ADEは正三角形
DF:FE=?
*図は動画内参照
2021かえつ有明高等学校
この動画を見る
△ABC、△ADEは正三角形
DF:FE=?
*図は動画内参照
2021かえつ有明高等学校
2021神奈川県 解き方2通り! 正三角形2つ B

単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABCと△DEFは正三角形
△ABCと△DEFの面積比=12:7
AD=?(AD<DB))
*図は動画内参照
2021神奈川県
この動画を見る
△ABCと△DEFは正三角形
△ABCと△DEFの面積比=12:7
AD=?(AD<DB))
*図は動画内参照
2021神奈川県
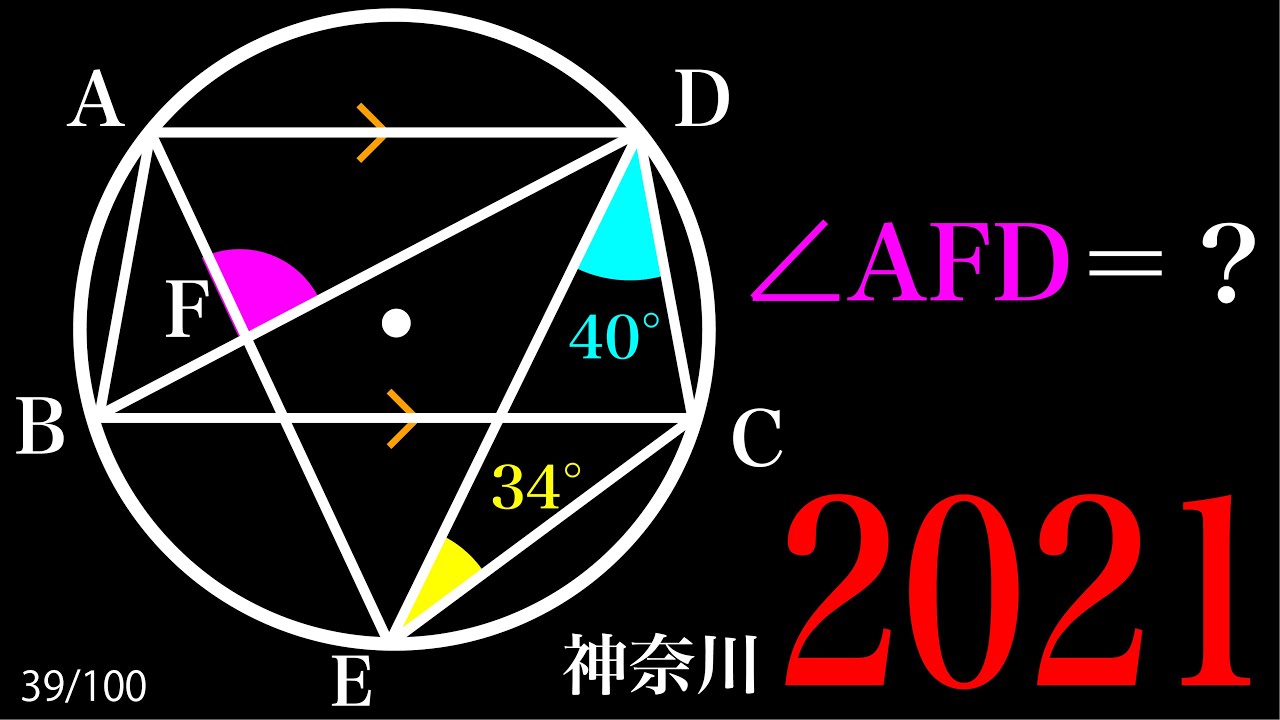
2021 神奈川県 円周角 A
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle AFD=?$
*図は動画内参照
2021神奈川県
この動画を見る
$\angle AFD=?$
*図は動画内参照
2021神奈川県
こういう問題が好き 城北 円周角 B

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\stackrel{\huge\frown}{AB} : \stackrel{\huge\frown}{CD} =?$
*図は動画内参照
2021城北高等学校
この動画を見る
$\stackrel{\huge\frown}{AB} : \stackrel{\huge\frown}{CD} =?$
*図は動画内参照
2021城北高等学校
2021 筑波大学附属駒場 15°75°90°の直角三角形の面積

単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABC=?
*図は動画内参照
2021筑波大学附属駒場高等学校
この動画を見る
△ABC=?
*図は動画内参照
2021筑波大学附属駒場高等学校
出てきた答えについて考える 錦城 A

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
斜線部の面積=?
*図は動画内参照
2021錦城高等学校
この動画を見る
斜線部の面積=?
*図は動画内参照
2021錦城高等学校
慶應女子2021 関数 B

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABCの内接円の半径r=?
*図は動画内参照
2021慶應義塾女子高等学校
この動画を見る
△ABCの内接円の半径r=?
*図は動画内参照
2021慶應義塾女子高等学校
2021順天堂(医)正五角形・簡単作図法も

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
1辺の長さが1の正五角形の
①外接円の面積を求めよ.
②正五角形の面積を求めよ.
2021順天堂(医)
この動画を見る
1辺の長さが1の正五角形の
①外接円の面積を求めよ.
②正五角形の面積を求めよ.
2021順天堂(医)
正方形と円 2021 愛知高校

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
斜線部の面積=x
正方形の面積をxで表せ。
*図は動画内参照
2021愛知高等学校
この動画を見る
斜線部の面積=x
正方形の面積をxで表せ。
*図は動画内参照
2021愛知高等学校
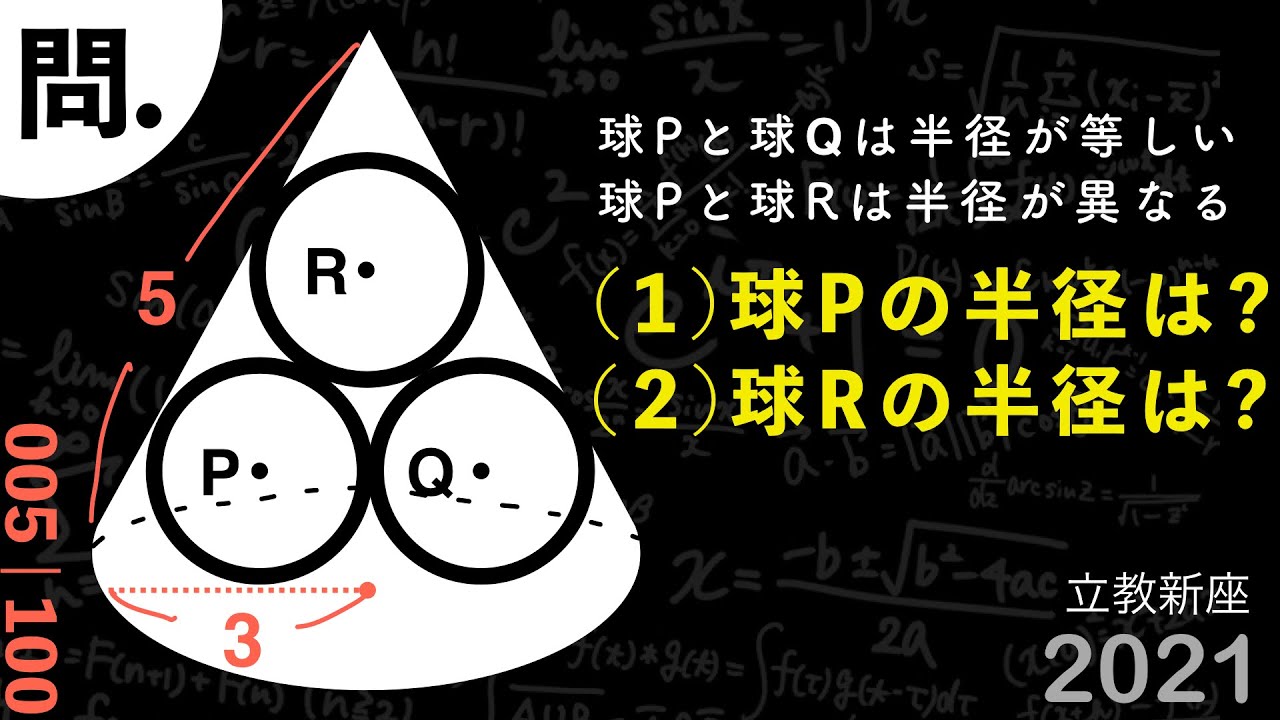
円錐と内接球3つ D 立教新座(改)2021
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
球Pと球Qは半径が等しい
球Pと球Rは半径が異なる
(1)球Pの半径は?
(2)球Rの半径は?
*図は動画内参照
2021立教新座高等学校(改)
この動画を見る
球Pと球Qは半径が等しい
球Pと球Rは半径が異なる
(1)球Pの半径は?
(2)球Rの半径は?
*図は動画内参照
2021立教新座高等学校(改)
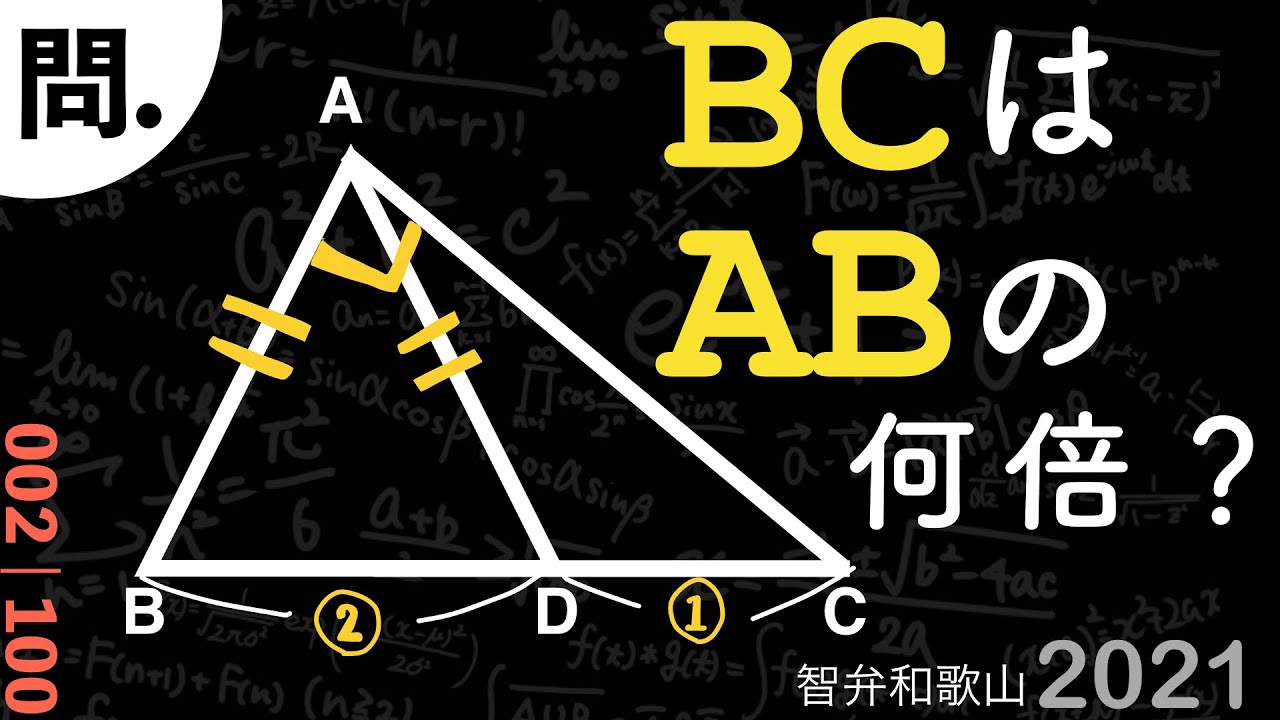
2021 智弁和歌山 B
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
BCはABの何倍?
*図は動画内参照
2021智辯学園和歌山高等学校
この動画を見る
BCはABの何倍?
*図は動画内参照
2021智辯学園和歌山高等学校
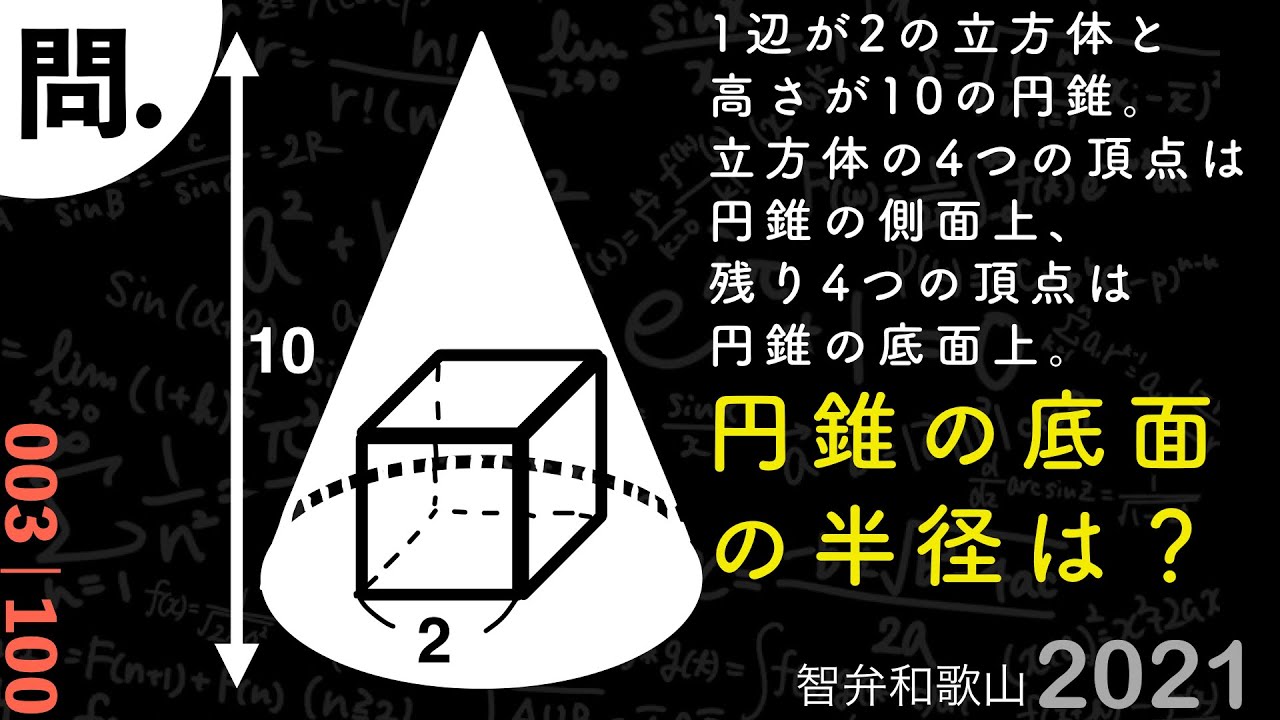
円錐に内接する立方体 智弁和歌山(改) B
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#立体図形#立体図形その他#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
円錐の底面の半径は?
*図は動画内参照
2021智辯学園和歌山高等学校(改)
この動画を見る
円錐の底面の半径は?
*図は動画内参照
2021智辯学園和歌山高等学校(改)
難易度MAX 2021ラ・サール最後の問題 D

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
半径1の2つの円が重ならないように正方形内を動く。
円の中心P,Qが存在しうる範囲の面積を求めよ。
*図は動画内参照
2021ラ・サール高等学校
この動画を見る
半径1の2つの円が重ならないように正方形内を動く。
円の中心P,Qが存在しうる範囲の面積を求めよ。
*図は動画内参照
2021ラ・サール高等学校
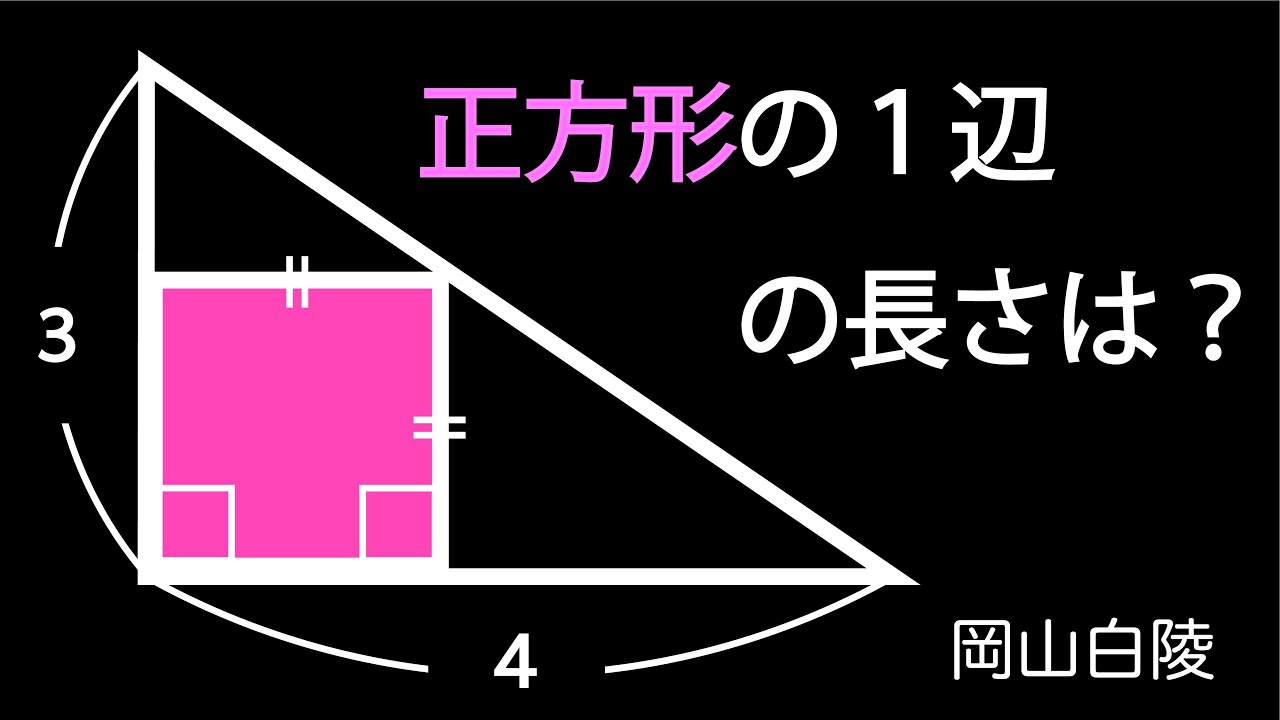
直角三角形の中の正方形 A 解き方2通り 岡山白陵
単元:
#数学(中学生)#中2数学#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#三角形と四角形#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正方形の1辺の長さは?
*図は動画内参照
岡山白陵高等学校
この動画を見る
正方形の1辺の長さは?
*図は動画内参照
岡山白陵高等学校
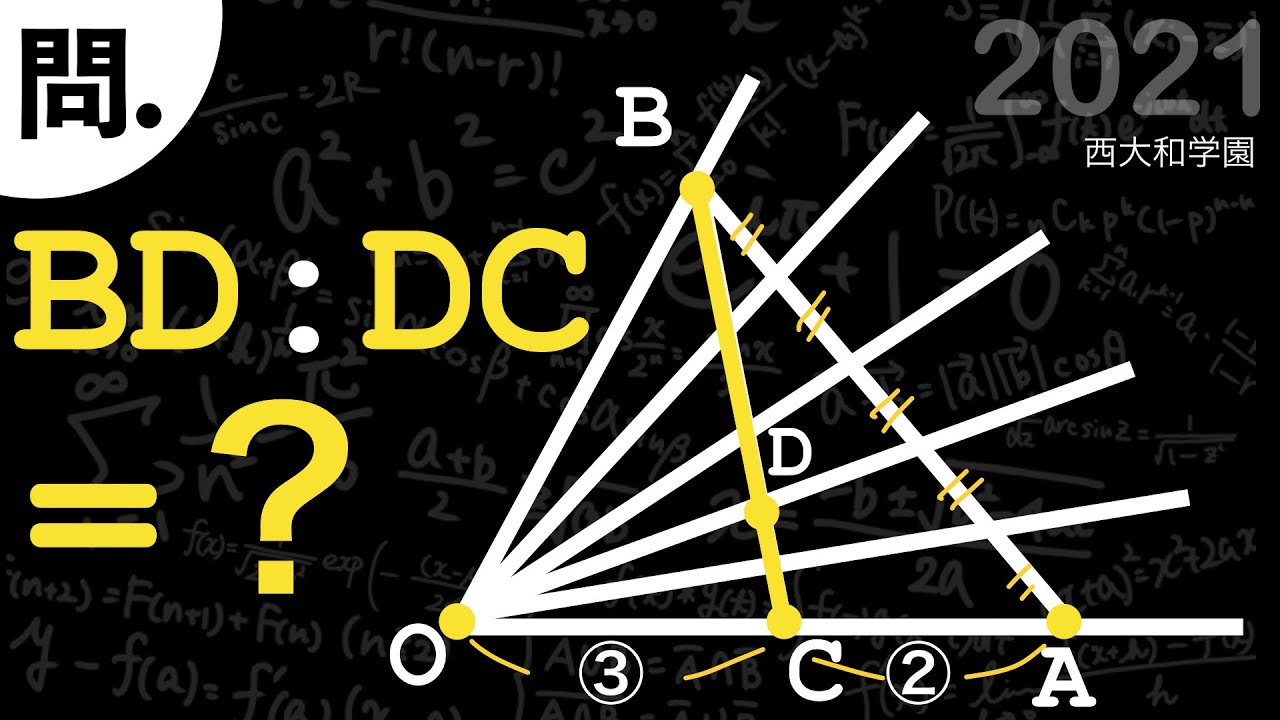
気がつけば爽快!! B
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
BD:DC=?
*図は動画内参照
2021西大和学園高等学校
この動画を見る
BD:DC=?
*図は動画内参照
2021西大和学園高等学校
受験生必見!!円と相似

単元:
#数学(中学生)#中3数学#数A#図形の性質#相似な図形#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
円と相似まとめ
*図は動画内参照
この動画を見る
円と相似まとめ
*図は動画内参照
共通テスト2021年数学詳しい解説〜共通テスト2021年IA第5問〜平面幾何

単元:
#数A#大学入試過去問(数学)#図形の性質#三角形の辺の比(内分・外分・二等分線)#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large第5問}$
$\triangle ABC$において、$AB=3$, $BC=4$, $AC=5$とする。
$\angle BAC$の二等分線と辺$BC$との交点を$D$とすると
$BD=\displaystyle \frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$, $AD=\displaystyle \frac{\boxed{\ \ ウ\ \ }\sqrt{\boxed{\ \ エ\ \ }}}{\boxed{\ \ オ\ \ }}$
である。
また、$\angle BAC$の二等分線と$\triangle ABC$の外接円$O$との交点で点$A$とは異なる
点を$E$とする。$\triangle AEC$に着目すると
$AE=\boxed{\ \ カ\ \ }\sqrt{\boxed{\ \ キ\ \ }}$
である。
$\triangle ABC$の2辺$AB$と$AC$の両方に接し、外接円$O$に内接する円の中心を
$P$とする。円$P$の半径を$r$とする。さらに、円$P$と外接円$O$との接点を
$F$とし、直線$PF$と外接円$O$との交点で点$F$とは異なる点を$G$とする。
このとき
$AP=\sqrt{\boxed{\ \ ク\ \ }}\ r$, $PG=\boxed{\ \ ケ\ \ }-r$
と表せる。したがって、方べきの定理により$r=\displaystyle \frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$である。
$\triangle ABC$の内心を$Q$とする。内接円$Q$の半径は$\boxed{\ \ シ\ \ }$で、$AQ=\sqrt{\boxed{\ \ ス\ \ }}$
である。また、円$P$と辺$AB$との接点を$H$とすると、$AH=\displaystyle \frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソ\ \ }}$である。
以上から、点$H$に関する次の$(\textrm{a}),(\textrm{b})$の正誤の組合せとして正しいもの
は$\boxed{\boxed{\ \ タ\ \ }}$である。
$(\textrm{a})$点$H$は3点$B,D,Q$を通る円の周上にある。
$(\textrm{b})$点$H$は3点$B,E,Q$を通る円の周上にある。
$\boxed{\boxed{\ \ タ\ \ }}$の解答群
(※選択肢は動画参照)
2021共通テスト過去問
この動画を見る
${\large第5問}$
$\triangle ABC$において、$AB=3$, $BC=4$, $AC=5$とする。
$\angle BAC$の二等分線と辺$BC$との交点を$D$とすると
$BD=\displaystyle \frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$, $AD=\displaystyle \frac{\boxed{\ \ ウ\ \ }\sqrt{\boxed{\ \ エ\ \ }}}{\boxed{\ \ オ\ \ }}$
である。
また、$\angle BAC$の二等分線と$\triangle ABC$の外接円$O$との交点で点$A$とは異なる
点を$E$とする。$\triangle AEC$に着目すると
$AE=\boxed{\ \ カ\ \ }\sqrt{\boxed{\ \ キ\ \ }}$
である。
$\triangle ABC$の2辺$AB$と$AC$の両方に接し、外接円$O$に内接する円の中心を
$P$とする。円$P$の半径を$r$とする。さらに、円$P$と外接円$O$との接点を
$F$とし、直線$PF$と外接円$O$との交点で点$F$とは異なる点を$G$とする。
このとき
$AP=\sqrt{\boxed{\ \ ク\ \ }}\ r$, $PG=\boxed{\ \ ケ\ \ }-r$
と表せる。したがって、方べきの定理により$r=\displaystyle \frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$である。
$\triangle ABC$の内心を$Q$とする。内接円$Q$の半径は$\boxed{\ \ シ\ \ }$で、$AQ=\sqrt{\boxed{\ \ ス\ \ }}$
である。また、円$P$と辺$AB$との接点を$H$とすると、$AH=\displaystyle \frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソ\ \ }}$である。
以上から、点$H$に関する次の$(\textrm{a}),(\textrm{b})$の正誤の組合せとして正しいもの
は$\boxed{\boxed{\ \ タ\ \ }}$である。
$(\textrm{a})$点$H$は3点$B,D,Q$を通る円の周上にある。
$(\textrm{b})$点$H$は3点$B,E,Q$を通る円の周上にある。
$\boxed{\boxed{\ \ タ\ \ }}$の解答群
(※選択肢は動画参照)
2021共通テスト過去問
円錐台 内接球 2021 C

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
球を除いた体積=?
*図は動画内参照
2021専修大学松戸高等学校
この動画を見る
球を除いた体積=?
*図は動画内参照
2021専修大学松戸高等学校
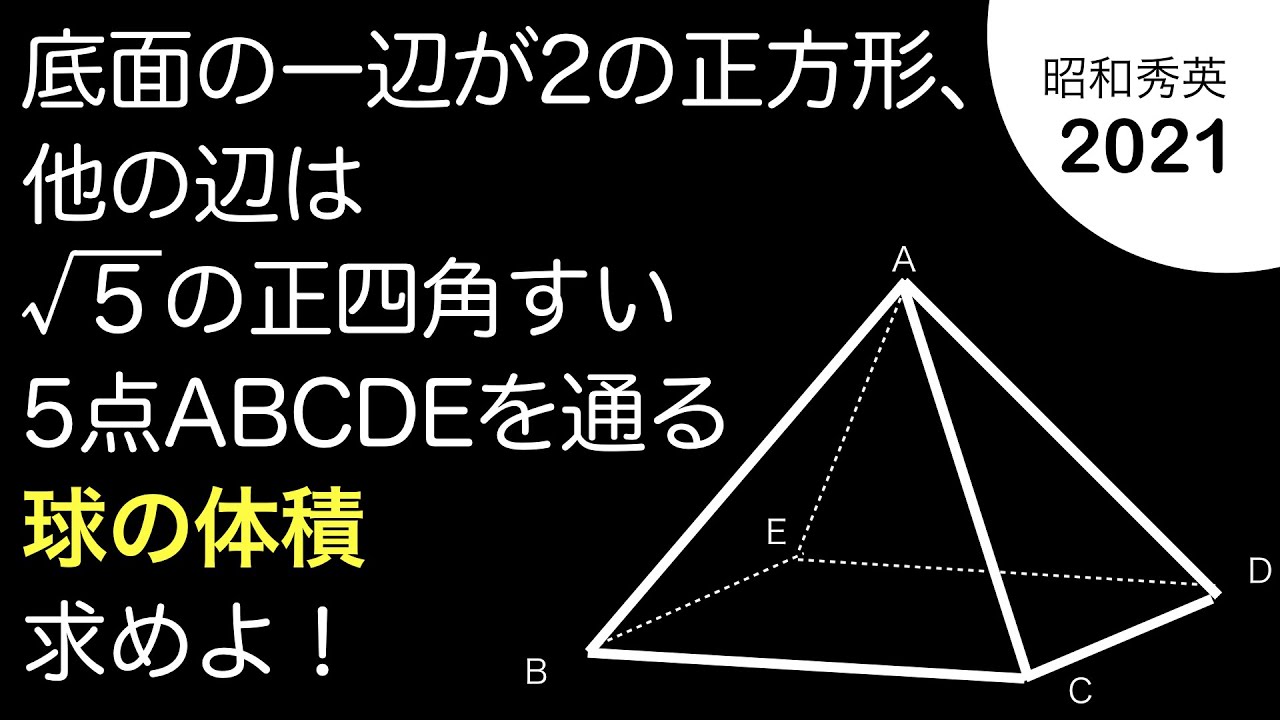
2021昭和秀英 正四角錐の外接球
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
底面の一辺が2の正方形、他の辺は$\sqrt 5$の正四角すい
5点ABCDEを通る球の体積を求めよ。
*図は動画内参照
2021昭和学院秀英高等学校
この動画を見る
底面の一辺が2の正方形、他の辺は$\sqrt 5$の正四角すい
5点ABCDEを通る球の体積を求めよ。
*図は動画内参照
2021昭和学院秀英高等学校
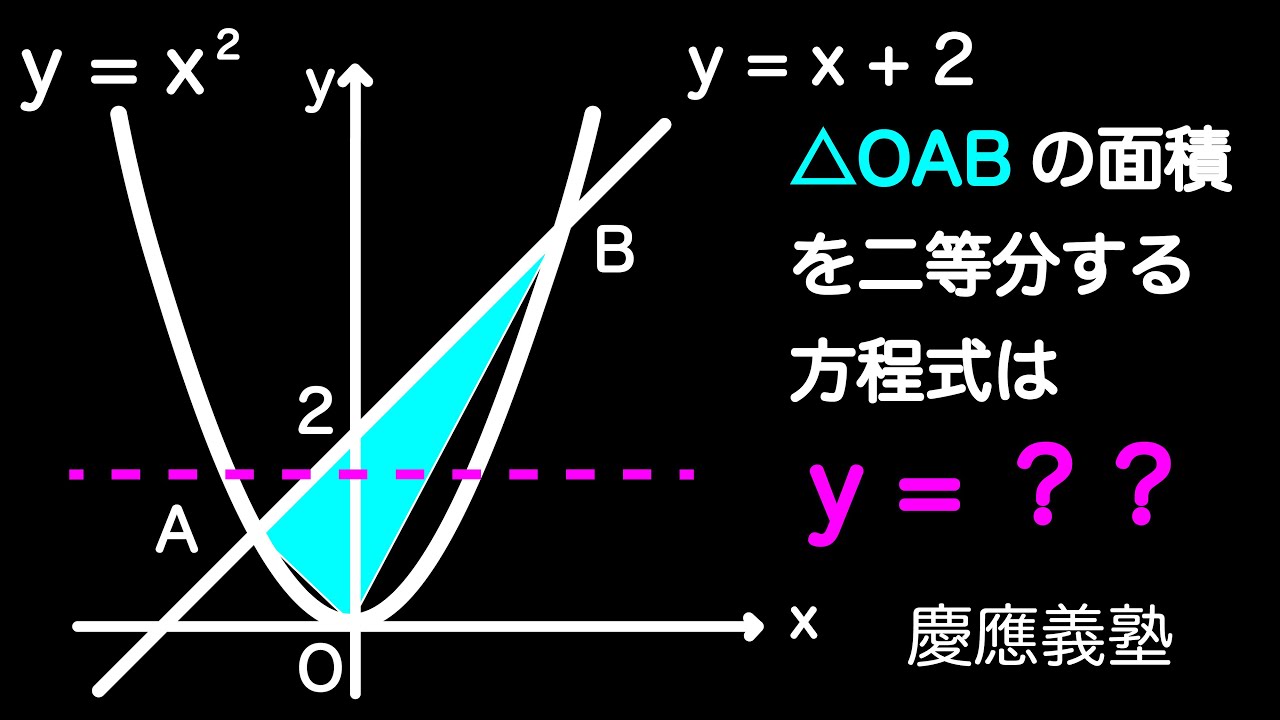
瞬殺!!三角形の面積二等分 慶應義塾
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△OABの面積を二等分するx軸に平行な直線の式を求めよ。
*図は動画内参照
慶應義塾高等学校
この動画を見る
△OABの面積を二等分するx軸に平行な直線の式を求めよ。
*図は動画内参照
慶應義塾高等学校
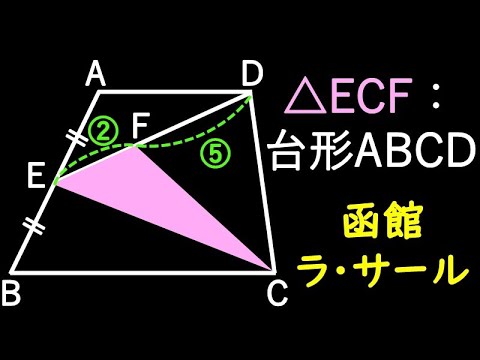
函館ラ・サール 面積比
単元:
#数学(中学生)#中2数学#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#三角形と四角形#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△ECF:台形ABCD=?
*図は動画内参照
函館ラ・サール高等学校
この動画を見る
△ECF:台形ABCD=?
*図は動画内参照
函館ラ・サール高等学校
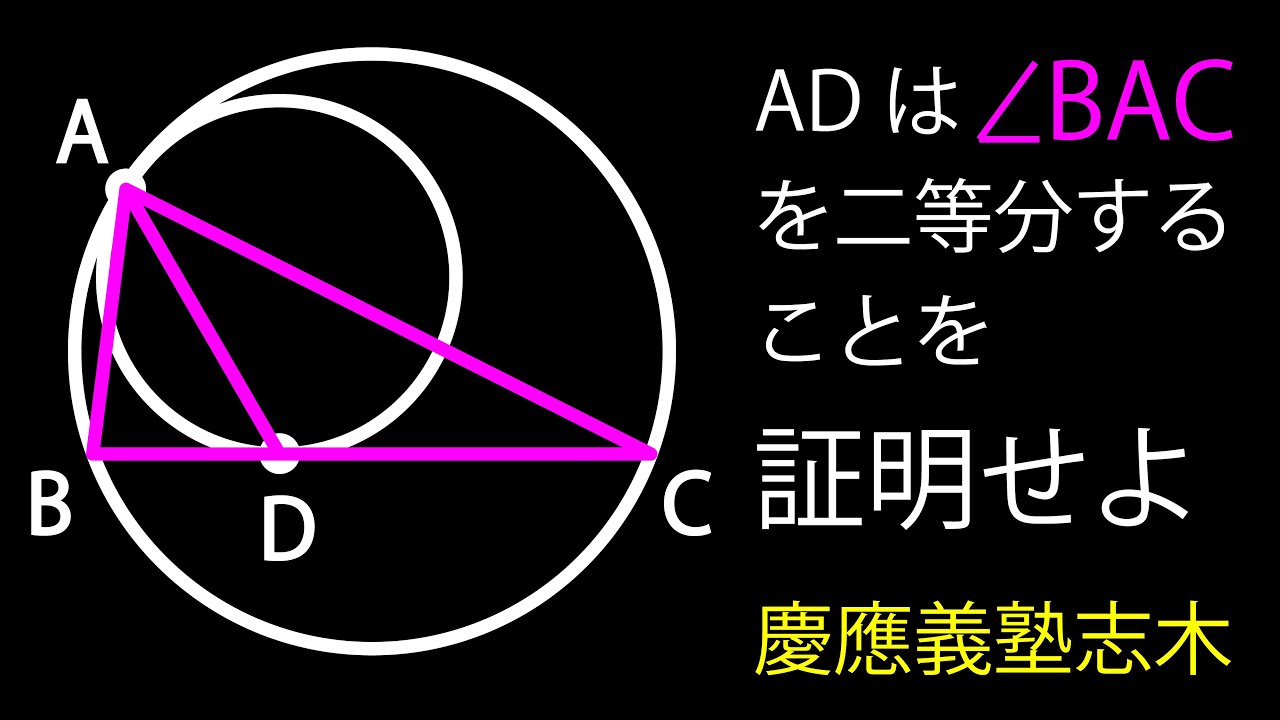
二つの円 角の二等分線 C
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
ADは$\angle BAC$を二等分することを示せ
*図は動画内参照
慶應義塾志木高等学校
この動画を見る
ADは$\angle BAC$を二等分することを示せ
*図は動画内参照
慶應義塾志木高等学校
バーゼル問題 出題されてから91年後にオイラーが解決

単元:
#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$n\to \infty$とする.
$\dfrac{1}{1^2}+\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+・・・・+\dfrac{1}{n^2}=\dfrac{\boxed{?}}{6}$
この動画を見る
これを解け.$n\to \infty$とする.
$\dfrac{1}{1^2}+\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+・・・・+\dfrac{1}{n^2}=\dfrac{\boxed{?}}{6}$
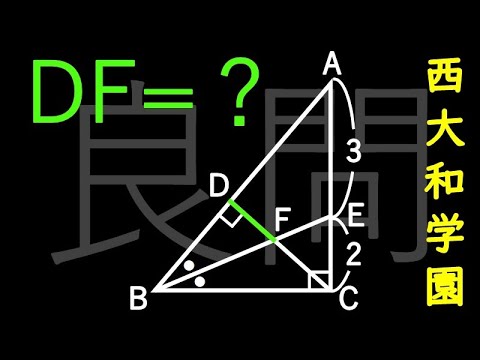
三平方の定理不要! 西大和学園 B
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
DF=?
*図は動画内参照
西大和学園高等学校
この動画を見る
DF=?
*図は動画内参照
西大和学園高等学校
