 図形と方程式
図形と方程式
 図形と方程式
図形と方程式
【短時間でマスター!!】直線の方程式(平行と垂直)の求め方を解説!〔現役講師解説、数学〕

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学2B
直線の方程式
並行と垂直の条件
①点$(1,-3)$を通り、直線$4x+5y=2$に平行な直線
②点$(0,1)$を通り、直線$y=-3x-1$に垂直な直線
この動画を見る
数学2B
直線の方程式
並行と垂直の条件
①点$(1,-3)$を通り、直線$4x+5y=2$に平行な直線
②点$(0,1)$を通り、直線$y=-3x-1$に垂直な直線
大学入試問題#614「これは、時間内で解くのは大変かもしれない」 立命館大学(2023) #曲線の長さ

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#学校別大学入試過去問解説(数学)#数学(高校生)#立命館大学
指導講師:
ますただ
問題文全文(内容文):
次の曲線の長さ$L$を求めよ。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\cos^4\theta \\
y=\sin^4\theta
\end{array}
\right.
\end{eqnarray}$
$(0 \leqq \theta \leqq \displaystyle \frac{\pi}{2})$
出典:2023年立命館大学 入試問題
この動画を見る
次の曲線の長さ$L$を求めよ。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\cos^4\theta \\
y=\sin^4\theta
\end{array}
\right.
\end{eqnarray}$
$(0 \leqq \theta \leqq \displaystyle \frac{\pi}{2})$
出典:2023年立命館大学 入試問題
【短時間でマスター!!】円の方程式(中心と半径)の求め方を解説!〔現役講師解説、数学〕

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学2B
円の方程式
中心と半径の求め方について解説します。
次の方程式はどのような図形を表すか。
①$x^2+y^2+2y-3=0$
②$x^2+y^2+4x-6y-4=0$
この動画を見る
数学2B
円の方程式
中心と半径の求め方について解説します。
次の方程式はどのような図形を表すか。
①$x^2+y^2+2y-3=0$
②$x^2+y^2+4x-6y-4=0$
内角と外角 愛工大名電(愛知県)

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正n角形の頂点における内角の大きさが外角の大きさより90°大きいときnの値を求めよ。
愛知工業大学名電高等学校
この動画を見る
正n角形の頂点における内角の大きさが外角の大きさより90°大きいときnの値を求めよ。
愛知工業大学名電高等学校
サッカーボールの頂点の個数は? 共栄学園(東東京)

単元:
#数Ⅱ#点と直線#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
12個の正五角形と20個の正六角形の合わせて32面からなる多面体
どの頂点にも1個の正五角形と2個の正六角形の面が集まっている
この多面体の頂点の個数は?
共栄学園高等学校
この動画を見る
12個の正五角形と20個の正六角形の合わせて32面からなる多面体
どの頂点にも1個の正五角形と2個の正六角形の面が集まっている
この多面体の頂点の個数は?
共栄学園高等学校
【数学】2022年度 第2回 K塾記述高2模試 全問解説(ベクトルはおまけ)、※修正箇所:問1(1)(概要欄へ)

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#図形の性質#複素数と方程式#図形と計量#式の計算(整式・展開・因数分解)#一次不等式(不等式・絶対値のある方程式・不等式)#2次方程式と2次不等式#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#確率#図形と方程式#三角関数#複素数#三角関数とグラフ#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
2022年度第2回全統記述高2模試全問解説動画です!
この動画を見る
2022年度第2回全統記述高2模試全問解説動画です!
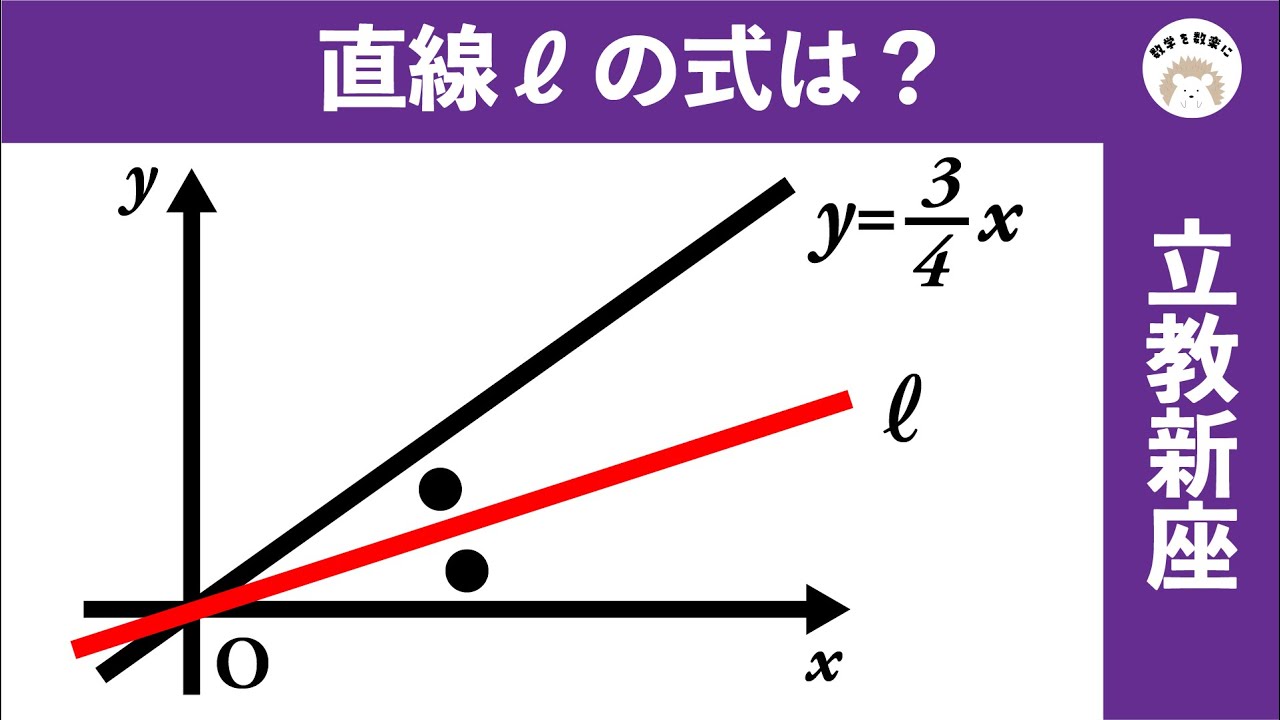
内角を二等分する直線の式 立教新座
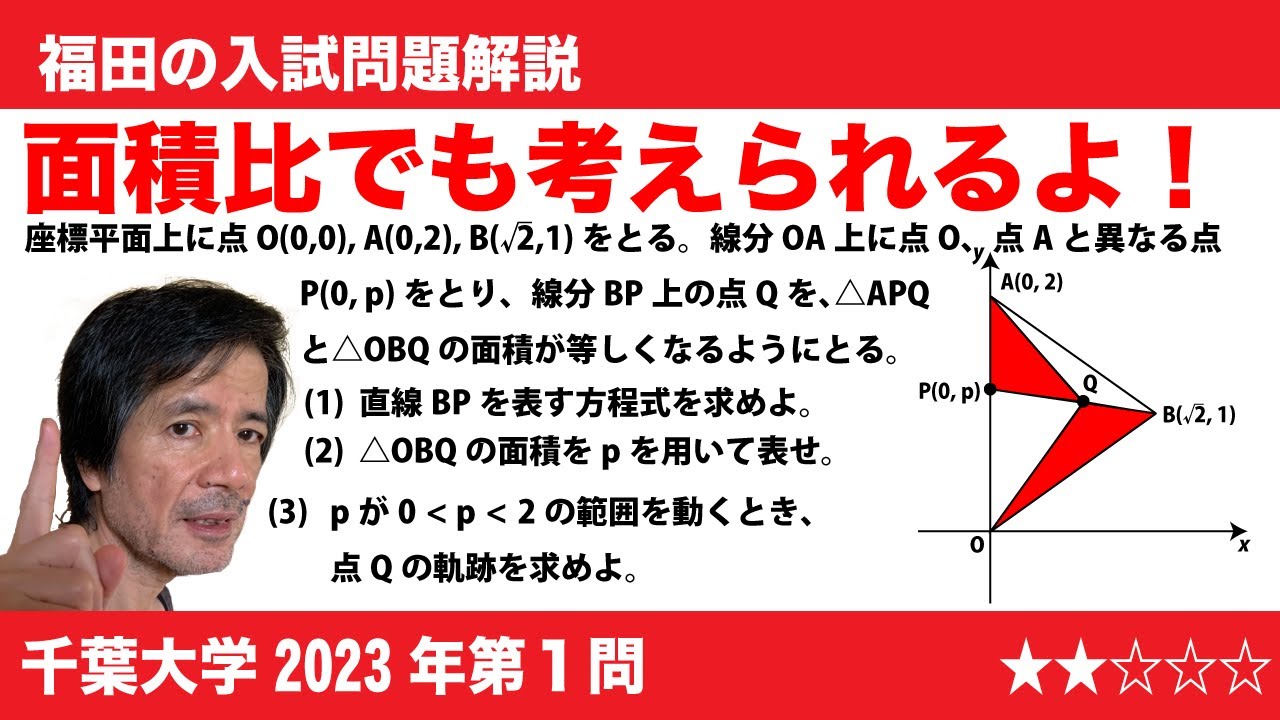
福田の数学〜千葉大学2023年第1問〜三角形の面積と軌跡
単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 座標平面上に点O(0,0), A(0,2), B($\sqrt 2$, 1)をとる。線分OA上に点O、点Aと異なる点P(0,$p$)をとり、線分BP上の点Qを、$\triangle$APQと$\triangle$OBQの面積が等しくなるようにとる。
(1)直線BPを表す方程式を求めよ。
(2)$\triangle$OBQの面積を$p$を用いて表せ。
(3)$p$が0<$p$<2の範囲を動くとき、点Qの軌跡を求めよ。
この動画を見る
$\Large\boxed{1}$ 座標平面上に点O(0,0), A(0,2), B($\sqrt 2$, 1)をとる。線分OA上に点O、点Aと異なる点P(0,$p$)をとり、線分BP上の点Qを、$\triangle$APQと$\triangle$OBQの面積が等しくなるようにとる。
(1)直線BPを表す方程式を求めよ。
(2)$\triangle$OBQの面積を$p$を用いて表せ。
(3)$p$が0<$p$<2の範囲を動くとき、点Qの軌跡を求めよ。
福田の数学〜立教大学2023年経済学部第3問〜放物線と直線で囲まれた図形の面積
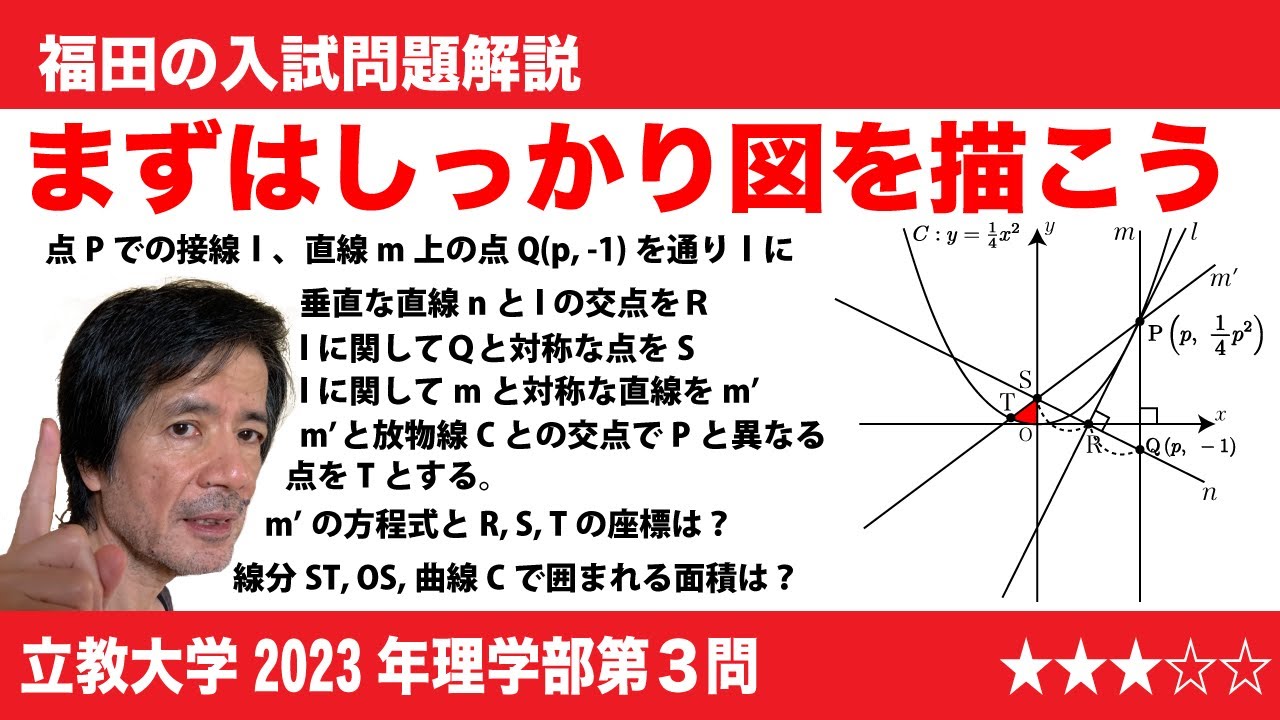
単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#点と直線#学校別大学入試過去問解説(数学)#面積、体積#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ pを正の実数とする。Oを原点とする座標平面上の放物線C:$y$=$\frac{1}{4}x^2$上の点P$\left(p, \frac{1}{4}p^2\right)$における接線を$l$、Pを通り$x$軸に垂直な直線を$m$とする。また、$m$上の点Q$\left(p, -1\right)$を通り$l$に垂直な直線を$n$とし、$l$と$n$の交点をRとする。さらに、$l$に関してQと対称な点をSとする。このとき、次の問いに答えよ。
(1)$l$の方程式を$p$を用いて表せ。
(2)$n$の方程式およびRの座標をそれぞれ$p$を用いて表せ。
(3)Sの座標を求めよ。
(4)$l$を対象軸として、$l$に関して$m$と対称な直線$m'$の方程式を$p$を用いて表せ。
また、$m'$とCの交点のうちPと異なる点をTとするとき、Tの$x$座標を$p$を用いて表せ。
(5)(4)のTに対して、線分ST、線分OSおよびCで囲まれた部分の面積を$p$を用いて表せ。
この動画を見る
$\Large\boxed{3}$ pを正の実数とする。Oを原点とする座標平面上の放物線C:$y$=$\frac{1}{4}x^2$上の点P$\left(p, \frac{1}{4}p^2\right)$における接線を$l$、Pを通り$x$軸に垂直な直線を$m$とする。また、$m$上の点Q$\left(p, -1\right)$を通り$l$に垂直な直線を$n$とし、$l$と$n$の交点をRとする。さらに、$l$に関してQと対称な点をSとする。このとき、次の問いに答えよ。
(1)$l$の方程式を$p$を用いて表せ。
(2)$n$の方程式およびRの座標をそれぞれ$p$を用いて表せ。
(3)Sの座標を求めよ。
(4)$l$を対象軸として、$l$に関して$m$と対称な直線$m'$の方程式を$p$を用いて表せ。
また、$m'$とCの交点のうちPと異なる点をTとするとき、Tの$x$座標を$p$を用いて表せ。
(5)(4)のTに対して、線分ST、線分OSおよびCで囲まれた部分の面積を$p$を用いて表せ。
【数Ⅱ】間違えやすい? 点と直線の距離の公式の覚え方

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
点と直線の距離の公式がどっちだっけ…となったとき、そんなときのための講義です。
この動画を見る
点と直線の距離の公式がどっちだっけ…となったとき、そんなときのための講義です。
慶應義塾大 直線の傾き

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2016慶応義塾大学過去問題
aは整数、aの値は?
$f(x)=x^3-x^2-x+c$
$A(0,f(x)),B(a,f(a))$
直線ABと$x=\frac{a}{3}$におけるf(x)の接線が直交する。
この動画を見る
2016慶応義塾大学過去問題
aは整数、aの値は?
$f(x)=x^3-x^2-x+c$
$A(0,f(x)),B(a,f(a))$
直線ABと$x=\frac{a}{3}$におけるf(x)の接線が直交する。
福田の数学〜筑波大学2023年理系第6問〜複素数平面上の点の軌跡とアポロニウスの円

単元:
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#軌跡と領域#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{6}$ $i$を虚数単位とする。複素数平面に関する以下の問いに答えよ。
(1)等式|$z$+2|=2|$z$-1| を満たす点$z$の全体が表す図形は円であることを示し、その中心と半径を求めよ。
(2)等式
$\left\{|z+2|-2|z-1|\right\}$$|z+6i|$=$3\left\{|z+2|-2|z-1|\right\}$$|z-2i|$
を満たす点$z$の全体が表す図形をSとする。このときSを複素数平面上に図示せよ。
(3)点$z$が(2)における図形S上を動くとき、$w$=$\frac{1}{z}$ で定義される点$w$が描く図形を複素数平面上に図示せよ。
2023筑波大学理系過去問
この動画を見る
$\Large\boxed{6}$ $i$を虚数単位とする。複素数平面に関する以下の問いに答えよ。
(1)等式|$z$+2|=2|$z$-1| を満たす点$z$の全体が表す図形は円であることを示し、その中心と半径を求めよ。
(2)等式
$\left\{|z+2|-2|z-1|\right\}$$|z+6i|$=$3\left\{|z+2|-2|z-1|\right\}$$|z-2i|$
を満たす点$z$の全体が表す図形をSとする。このときSを複素数平面上に図示せよ。
(3)点$z$が(2)における図形S上を動くとき、$w$=$\frac{1}{z}$ で定義される点$w$が描く図形を複素数平面上に図示せよ。
2023筑波大学理系過去問
福田の数学〜筑波大学2023年理系第1問〜3次関数の接線と三角形の面積

単元:
#大学入試過去問(数学)#図形と方程式#微分法と積分法#点と直線#平均変化率・極限・導関数#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#筑波大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 曲線C:$y$=$x$-$x^3$上の点A(1, 0)における接線を$l$とし、Cと$l$の共有点のうちAとは異なる点をBとする。また、-2<$t$<1とし、C上の点P($t$, $t$-$t^3$)をとる。さらに、三角形ABPの面積を$S(t)$とする。
(1)点Bの座標を求めよ。
(2)$S(t)$を求めよ。
(3)$t$が-2<$t$<1の範囲を動くとき、$S(t)$の最大値を求めよ。
2023筑波大学理系過去問
この動画を見る
$\Large\boxed{1}$ 曲線C:$y$=$x$-$x^3$上の点A(1, 0)における接線を$l$とし、Cと$l$の共有点のうちAとは異なる点をBとする。また、-2<$t$<1とし、C上の点P($t$, $t$-$t^3$)をとる。さらに、三角形ABPの面積を$S(t)$とする。
(1)点Bの座標を求めよ。
(2)$S(t)$を求めよ。
(3)$t$が-2<$t$<1の範囲を動くとき、$S(t)$の最大値を求めよ。
2023筑波大学理系過去問
福田の数学〜神戸大学2023年文系第3問〜2つの円の位置関係と共通弦

単元:
#大学入試過去問(数学)#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#筑波大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ aを正の実数とする。2つの円
$C_1$:$x^2$+$y^2$=$a$, $C_2$:$x^2$+$y^2$-$6x$-$4y$+3=0
が異なる2点A, Bで交わっているとする。直線ABが$x$軸および$y$軸と交わる点をそれぞれ($p$, 0), (0, $q$)とするとき、以下の問いに答えよ。
(1)$a$のとりうる値の範囲を求めよ。
(2)$p$, $q$の値を$a$を用いて表せ。
(3)$p$, $q$の値が共に整数となるような$a$の値をすべて求めよ。
2023筑波大学理系過去問
この動画を見る
$\Large\boxed{3}$ aを正の実数とする。2つの円
$C_1$:$x^2$+$y^2$=$a$, $C_2$:$x^2$+$y^2$-$6x$-$4y$+3=0
が異なる2点A, Bで交わっているとする。直線ABが$x$軸および$y$軸と交わる点をそれぞれ($p$, 0), (0, $q$)とするとき、以下の問いに答えよ。
(1)$a$のとりうる値の範囲を求めよ。
(2)$p$, $q$の値を$a$を用いて表せ。
(3)$p$, $q$の値が共に整数となるような$a$の値をすべて求めよ。
2023筑波大学理系過去問
福田の数学〜東北大学2023年文系第4問〜線分の通過範囲の面積
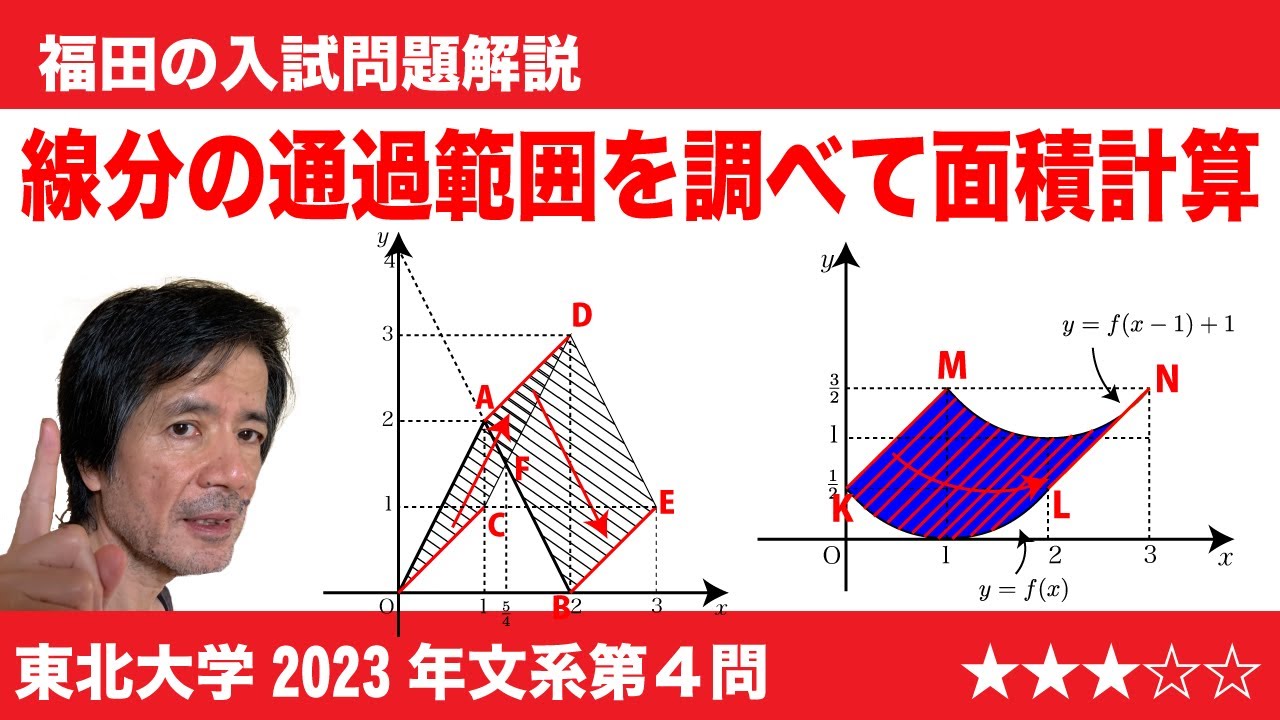
単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#東北大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 関数f(x)に対して、座標平面上の2つの点P(x, f(x)), Q(x+1, f(x)+1)を考える。実数xが0≦x≦2の範囲を動くとき、線分PQがつうかしてできる図形の面積をSとおく。以下の問いに答えよ。
(1)関数f(x)=-2|x-1|+2に 対して、Sの値を求めよ。
(2)関数f(x)=$\frac{1}{2}(x-1)^2$ に対して、曲線y=f(x)の接線で、傾きが1のものの方程式を求めよ。
(3)設問(2)の関数f(x)=$\frac{1}{2}(x-1)^2$ に対して、Sの値を求めよ。
2023東北大学文系過去問
この動画を見る
$\Large\boxed{4}$ 関数f(x)に対して、座標平面上の2つの点P(x, f(x)), Q(x+1, f(x)+1)を考える。実数xが0≦x≦2の範囲を動くとき、線分PQがつうかしてできる図形の面積をSとおく。以下の問いに答えよ。
(1)関数f(x)=-2|x-1|+2に 対して、Sの値を求めよ。
(2)関数f(x)=$\frac{1}{2}(x-1)^2$ に対して、曲線y=f(x)の接線で、傾きが1のものの方程式を求めよ。
(3)設問(2)の関数f(x)=$\frac{1}{2}(x-1)^2$ に対して、Sの値を求めよ。
2023東北大学文系過去問
福田の数学〜東北大学2023年理系第2問〜三角方程式の解の個数とその極限

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#三角関数#円と方程式#三角関数とグラフ#関数と極限#微分とその応用#関数の極限#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 関数f(x)=$\sin3x$+$\sin x$について、以下の問いに答えよ。
(1)f(x)=0 を満たす正の実数$x$のうち、最小のものを求めよ。
(2)正の整数$m$に対して、f(x)=0を満たす正の実数$x$のうち、$m$以下のものの個数を$p(m)$とする。極限値$\displaystyle\lim_{m \to \infty}\frac{p(m)}{m}$ を求めよ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{2}$ 関数f(x)=$\sin3x$+$\sin x$について、以下の問いに答えよ。
(1)f(x)=0 を満たす正の実数$x$のうち、最小のものを求めよ。
(2)正の整数$m$に対して、f(x)=0を満たす正の実数$x$のうち、$m$以下のものの個数を$p(m)$とする。極限値$\displaystyle\lim_{m \to \infty}\frac{p(m)}{m}$ を求めよ。
2023東北大学理系過去問
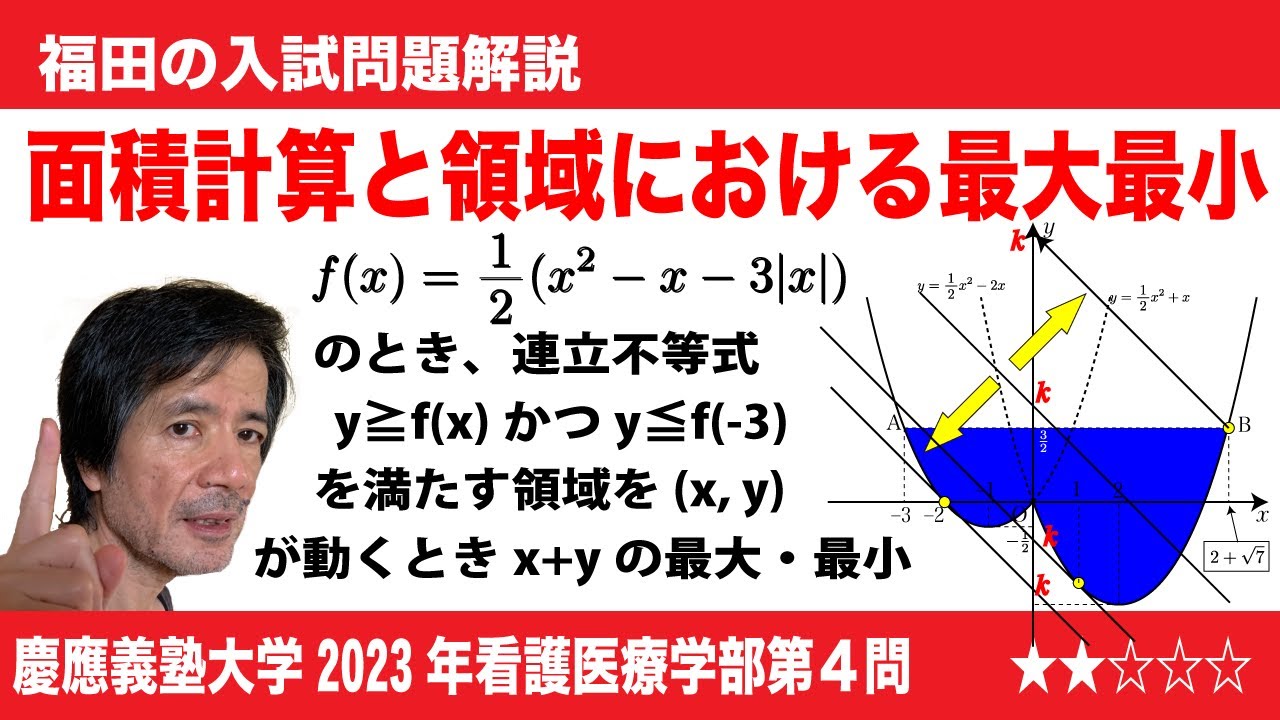
福田の数学〜慶應義塾大学2023年看護医療学部第4問〜絶対値の付いた関数と領域における最大最小
単元:
#大学入試過去問(数学)#図形と方程式#軌跡と領域#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 関数f(x)をf(x)=$\frac{1}{2}$($x^2$-$x$-3|$x$|)で定める。以下に答えなさい。
(1)y=f(x)のグラフをかきなさい。
(2)曲線y=f(x)上の点A(-3, f(-3))を通り、点Aにおける接線に垂直な直線lの方程式はy=$\boxed{\ \ ニ\ \ }$である。また、曲線と直線lは2つの共有点をもつが点Aとは異なる共有点の座標は$\boxed{\ \ ヌ\ \ }$である。さらに、曲線y=f(x)と直線lで囲まれた図形の面積は$\boxed{\ \ ネ\ \ }$である。
(3)連立不等式y≧f(x), y≦f(-3)の表す領域をDとする。点(x,y)がこの領域Dを動くとき、x+yは(x,y)=$\boxed{\ \ ノ\ \ }$のとき最大値$\boxed{\ \ ハ\ \ }$をとり、
(x,y)=$\boxed{\ \ ヒ\ \ }$のうち最小値$\boxed{\ \ フ\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{4}$ 関数f(x)をf(x)=$\frac{1}{2}$($x^2$-$x$-3|$x$|)で定める。以下に答えなさい。
(1)y=f(x)のグラフをかきなさい。
(2)曲線y=f(x)上の点A(-3, f(-3))を通り、点Aにおける接線に垂直な直線lの方程式はy=$\boxed{\ \ ニ\ \ }$である。また、曲線と直線lは2つの共有点をもつが点Aとは異なる共有点の座標は$\boxed{\ \ ヌ\ \ }$である。さらに、曲線y=f(x)と直線lで囲まれた図形の面積は$\boxed{\ \ ネ\ \ }$である。
(3)連立不等式y≧f(x), y≦f(-3)の表す領域をDとする。点(x,y)がこの領域Dを動くとき、x+yは(x,y)=$\boxed{\ \ ノ\ \ }$のとき最大値$\boxed{\ \ ハ\ \ }$をとり、
(x,y)=$\boxed{\ \ ヒ\ \ }$のうち最小値$\boxed{\ \ フ\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2023年看護医療学部第2問(1)〜三角方程式

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#三角関数#円と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ (1)0≦x≦π のとき、$\sqrt3\sin x$+$\cos x$=$\sqrt2$を解くと$x$=$\boxed{\ \ コ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{2}$ (1)0≦x≦π のとき、$\sqrt3\sin x$+$\cos x$=$\sqrt2$を解くと$x$=$\boxed{\ \ コ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
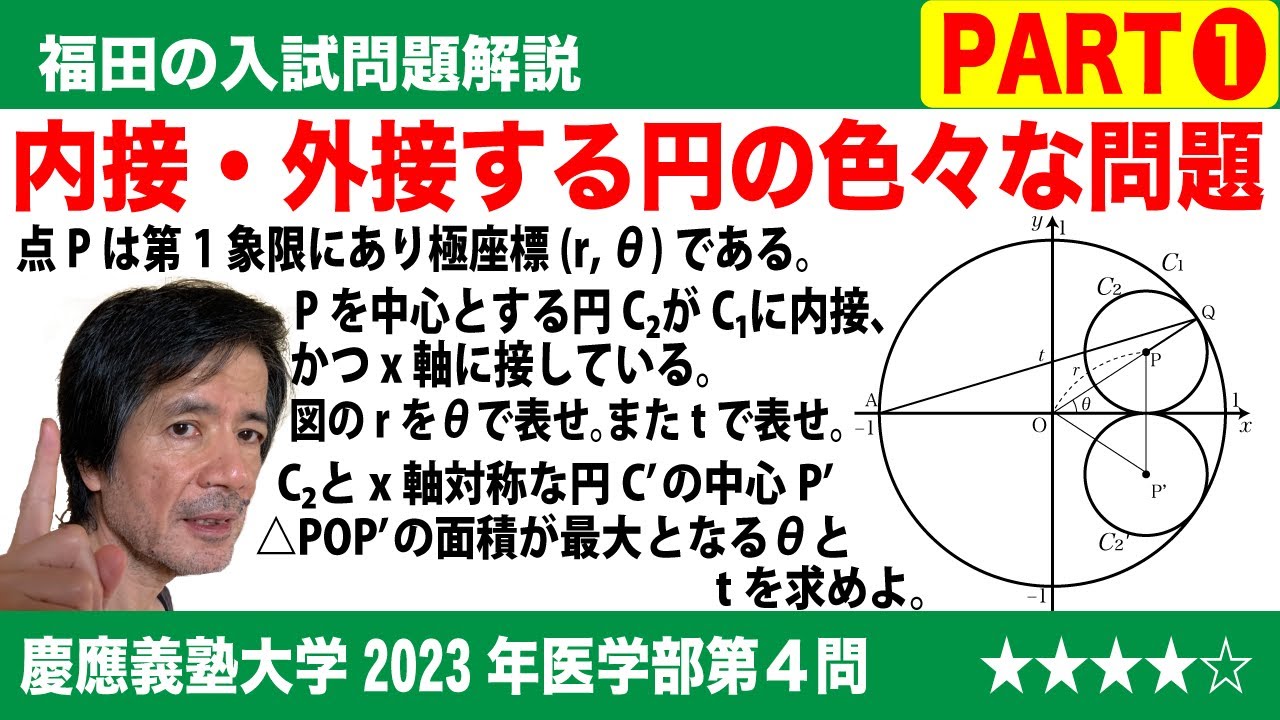
福田の数学〜慶應義塾大学2023年医学部第4問PART1〜円に内接する円の性質
単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#複素数平面#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#円と方程式#微分とその応用#複素数平面#図形への応用#微分法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2023年医学部第3問〜接線が作る三角形

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#三角形の辺の比(内分・外分・二等分線)#図形と方程式#微分法と積分法#軌跡と領域#接線と増減表・最大値・最小値#関数と極限#微分とその応用#積分とその応用#数列の極限#微分法#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 座標平面上の曲線y=$\frac{1}{x^2}$ (x $\ne$ 0)をCとする。$a_1$を正の実数とし、点$A_1$$\left(a_1, \frac{1}{a_1^2}\right)$におけるCの接線を$l_1$とする。$l_1$とCの交点で$A_1$と異なるものを$A_2$$\left(a_2, \frac{1}{a_2^2}\right)$とする。次に点$A_2$におけるCの接線を$l_2$とCの交点で$A_2$と異なるものを$A_3$$\left(a_3, \frac{1}{a_3^2}\right)$とする。以下、同様にしてn=3,4,5,...に対して、$A_n$$\left(a_n, \frac{1}{a_n^2}\right)$におけるCの接線を$l_n$とし、$l_n$とCの交点で$A_n$と異なるものを$A_{n+1}$$\left(a_{n+1}, \frac{1}{a_{n+1}^2}\right)$とする。
(1)$\frac{a_2}{a_1}$=$\boxed{\ \ あ\ \ }$であり、$\frac{a_3}{a_1}$=$\boxed{\ \ い\ \ }$である。
(2)$a_n$を$a_1$で表すと$a_n$=$\boxed{\ \ う\ \ }$である。無限級数$\displaystyle\sum_{n=1}^{\infty}a_n$の和をTを$a_1$を用いて表すとT=$\boxed{\ \ え\ \ }$である。
(3)$a_1$を正の実数すべてにわたって動かすとき、三角形$A_1A_2A_3$の重心が描く軌跡の方程式をy=f(x)の形で求めるとf(x)=$\boxed{\ \ お\ \ }$となる。
(4)三角形$A_1A_2A_3$が鋭角三角形になるための条件は$\boxed{\ \ か\ \ }$<$a_1$<$\boxed{\ \ き\ \ }$である。
(5)x軸上に2点$A'_1$($a_1$, 0), $A'_2$($a_2$, 0)をとり、台形$A_1A_2A'_2A'_1$の面積を$S_1$とする。また、点$A_1$から点$A_3$にいたる曲線Cの部分、および線分$A_3A_2$と$A_2A_1$で囲まれた図形の面積を$S_2$とする。このとき、$S_1$:$S_2$=$\boxed{\ \ く\ \ }$:$\boxed{\ \ け\ \ }$である。ただし、$\boxed{\ \ く\ \ }$と$\boxed{\ \ け\ \ }$は互いに素な自然数である。
2023慶應義塾大学医学部過去問
この動画を見る
$\Large\boxed{3}$ 座標平面上の曲線y=$\frac{1}{x^2}$ (x $\ne$ 0)をCとする。$a_1$を正の実数とし、点$A_1$$\left(a_1, \frac{1}{a_1^2}\right)$におけるCの接線を$l_1$とする。$l_1$とCの交点で$A_1$と異なるものを$A_2$$\left(a_2, \frac{1}{a_2^2}\right)$とする。次に点$A_2$におけるCの接線を$l_2$とCの交点で$A_2$と異なるものを$A_3$$\left(a_3, \frac{1}{a_3^2}\right)$とする。以下、同様にしてn=3,4,5,...に対して、$A_n$$\left(a_n, \frac{1}{a_n^2}\right)$におけるCの接線を$l_n$とし、$l_n$とCの交点で$A_n$と異なるものを$A_{n+1}$$\left(a_{n+1}, \frac{1}{a_{n+1}^2}\right)$とする。
(1)$\frac{a_2}{a_1}$=$\boxed{\ \ あ\ \ }$であり、$\frac{a_3}{a_1}$=$\boxed{\ \ い\ \ }$である。
(2)$a_n$を$a_1$で表すと$a_n$=$\boxed{\ \ う\ \ }$である。無限級数$\displaystyle\sum_{n=1}^{\infty}a_n$の和をTを$a_1$を用いて表すとT=$\boxed{\ \ え\ \ }$である。
(3)$a_1$を正の実数すべてにわたって動かすとき、三角形$A_1A_2A_3$の重心が描く軌跡の方程式をy=f(x)の形で求めるとf(x)=$\boxed{\ \ お\ \ }$となる。
(4)三角形$A_1A_2A_3$が鋭角三角形になるための条件は$\boxed{\ \ か\ \ }$<$a_1$<$\boxed{\ \ き\ \ }$である。
(5)x軸上に2点$A'_1$($a_1$, 0), $A'_2$($a_2$, 0)をとり、台形$A_1A_2A'_2A'_1$の面積を$S_1$とする。また、点$A_1$から点$A_3$にいたる曲線Cの部分、および線分$A_3A_2$と$A_2A_1$で囲まれた図形の面積を$S_2$とする。このとき、$S_1$:$S_2$=$\boxed{\ \ く\ \ }$:$\boxed{\ \ け\ \ }$である。ただし、$\boxed{\ \ く\ \ }$と$\boxed{\ \ け\ \ }$は互いに素な自然数である。
2023慶應義塾大学医学部過去問
福田の数学〜慶應義塾大学2023年医学部第1問(3)〜曲線と直線で囲まれた面積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#微分とその応用#積分とその応用#微分法#接線と法線・平均値の定理#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (3)曲線y=$x$$\log(x^2+1)$のx≧0の部分をCとすると、点(1, log2)におけるCの接線lの方程式はy=$\boxed{\ \ く\ \ }$である。
また、曲線Cと直線l、およびy軸で囲まれた図形の面積は$\boxed{\ \ け\ \ }$である。
2023慶應義塾大学医学部過去問
この動画を見る
$\Large\boxed{1}$ (3)曲線y=$x$$\log(x^2+1)$のx≧0の部分をCとすると、点(1, log2)におけるCの接線lの方程式はy=$\boxed{\ \ く\ \ }$である。
また、曲線Cと直線l、およびy軸で囲まれた図形の面積は$\boxed{\ \ け\ \ }$である。
2023慶應義塾大学医学部過去問
福田の数学〜慶應義塾大学2023年医学部第1問(1)〜図形の証明

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#式と証明#平面上のベクトル#図形と計量#三角比への応用(正弦・余弦・面積)#図形と方程式#恒等式・等式・不等式の証明#点と直線#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)三角形ABCにおいて辺BCを4:3に内分する点をDとするとき、等式
$\boxed{\ \ あ\ \ }$$AB^2$+$\boxed{\ \ い\ \ }$$AC^2$=$AD^2$+$\boxed{\ \ う\ \ }$$BD^2$
が成り立つ。
203慶應義塾大学医学部過去問
この動画を見る
$\Large\boxed{1}$ (1)三角形ABCにおいて辺BCを4:3に内分する点をDとするとき、等式
$\boxed{\ \ あ\ \ }$$AB^2$+$\boxed{\ \ い\ \ }$$AC^2$=$AD^2$+$\boxed{\ \ う\ \ }$$BD^2$
が成り立つ。
203慶應義塾大学医学部過去問
福田の数学〜慶應義塾大学2023年薬学部第2問〜対称式もどきの表す点の動く領域

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#軌跡と領域#学校別大学入試過去問解説(数学)#面積、体積#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 原点をOとするxy平面上に点A(1,-1)があり、点Bは$\overrightarrow{AB}$=(2$\cos\theta$, 2$\sin\theta$)(0≦θ≦2π)を満たす点である。Bの軌跡を境界線とする2つの領域のうち、点Aを含む領域を領域Cとする。ただし、領域Cは境界線を含む。
(1)点Bの軌跡の方程式は$\boxed{\ \ ナ\ \ }$である。
(2)点(x,y)がxy平面上のすべての点を動くとき、点(x-y,xy)がxy平面上で動く範囲は式$\boxed{\ \ ニ\ \ }$で表される領域である。
(3)点(x,y)が領域C上のすべての点を動くとき、点(x-y,xy)がxy平面上で動く領域を領域Dとする。
(i)領域Dを図示しなさい。ただし領域は斜線で示し、境界線となる式も図に記入すること。
(ii)領域Dの面積は$\boxed{\ \ ヌ\ \ }$である。
2023慶應義塾大学薬学部過去問
この動画を見る
$\Large\boxed{2}$ 原点をOとするxy平面上に点A(1,-1)があり、点Bは$\overrightarrow{AB}$=(2$\cos\theta$, 2$\sin\theta$)(0≦θ≦2π)を満たす点である。Bの軌跡を境界線とする2つの領域のうち、点Aを含む領域を領域Cとする。ただし、領域Cは境界線を含む。
(1)点Bの軌跡の方程式は$\boxed{\ \ ナ\ \ }$である。
(2)点(x,y)がxy平面上のすべての点を動くとき、点(x-y,xy)がxy平面上で動く範囲は式$\boxed{\ \ ニ\ \ }$で表される領域である。
(3)点(x,y)が領域C上のすべての点を動くとき、点(x-y,xy)がxy平面上で動く領域を領域Dとする。
(i)領域Dを図示しなさい。ただし領域は斜線で示し、境界線となる式も図に記入すること。
(ii)領域Dの面積は$\boxed{\ \ ヌ\ \ }$である。
2023慶應義塾大学薬学部過去問
福田の数学〜慶應義塾大学2023年薬学部第1問(4)〜球面上の3点が作る三角形

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#図形と計量#三角比(三角比・拡張・相互関係・単位円)#図形と方程式#円と方程式#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (4)座標空間に球面S:$(x-3)^2$+$(y+2)^2$+$(z-1)^2$=36 がある。球面Sが平面y=2 と交わってできる円をCとおく。
(i)円Cの中心の座標は$\boxed{\ \ ク\ \ }$であり、半径は$\boxed{\ \ ケ\ \ }$である。
(ii)円Cと平面x=3の交点をA,Bとし、AとB以外の球面S上の任意の点をPとする。三角形PABにおいて、辺PBを4:3に内分する点をD、線分ADを5:3に内分する点をMとし、直線PMと辺ABとの交点をEとする。このとき、AEの長さは$\boxed{\ \ コ\ \ }$である。ただし、Bのz座標はAのz座標よりも大きいとする。
2023慶應義塾大学薬学部過去問
この動画を見る
$\Large\boxed{1}$ (4)座標空間に球面S:$(x-3)^2$+$(y+2)^2$+$(z-1)^2$=36 がある。球面Sが平面y=2 と交わってできる円をCとおく。
(i)円Cの中心の座標は$\boxed{\ \ ク\ \ }$であり、半径は$\boxed{\ \ ケ\ \ }$である。
(ii)円Cと平面x=3の交点をA,Bとし、AとB以外の球面S上の任意の点をPとする。三角形PABにおいて、辺PBを4:3に内分する点をD、線分ADを5:3に内分する点をMとし、直線PMと辺ABとの交点をEとする。このとき、AEの長さは$\boxed{\ \ コ\ \ }$である。ただし、Bのz座標はAのz座標よりも大きいとする。
2023慶應義塾大学薬学部過去問
福田の数学〜慶應義塾大学2023年薬学部第1問(2)〜折れ線の最小と内接円の半径

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#三角関数#点と直線#加法定理とその応用#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (2)aは正の定数とする。原点をOとするxy平面上に直線l:y=$\frac{2}{3}$xと2点A(0,a), B(17,20)がある。直線l上にとった動点Pと2点A,Bそれぞれを線分で結び、2つの線分の長さの和AP+BPが最小となったとき、$\angle APO$=45°であった。AP+BPが最小であるとき、直線BPを表す方程式はy=$\boxed{\ \ ウ\ \ }$であり、三角形ABPの内接円の半径は$\boxed{\ \ エ\ \ }$である。
2023慶應義塾大学薬学部過去問
この動画を見る
$\Large\boxed{1}$ (2)aは正の定数とする。原点をOとするxy平面上に直線l:y=$\frac{2}{3}$xと2点A(0,a), B(17,20)がある。直線l上にとった動点Pと2点A,Bそれぞれを線分で結び、2つの線分の長さの和AP+BPが最小となったとき、$\angle APO$=45°であった。AP+BPが最小であるとき、直線BPを表す方程式はy=$\boxed{\ \ ウ\ \ }$であり、三角形ABPの内接円の半径は$\boxed{\ \ エ\ \ }$である。
2023慶應義塾大学薬学部過去問
福田の数学〜北海道大学2023年理系第5問〜中間値の定理と関数の増減PART1

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ a,bを$a^2$+$b^2$<1をみたす正の実数とする。また、座標平面上で原点を中心とする半径1の円をCとし、Cの内部にある2点A(a,0), B(0,b)を考える。
0<θ<$\frac{\pi}{2}$に対してC上の点P($\cos\theta$, $\sin\theta$)を考え、PにおけるCの接線に関してBと対称な点をDとおく。
(1)f(θ)=ab$\cos2\theta$+a$\sin\theta$-b$\cos\theta$とおく。方程式f(θ)=0の解が0<θ<$\frac{\pi}{2}$の範囲に少なくとも1つ存在することを示せ。
(2)Dの座標をa, $\theta$を用いて表せ。
(3)θが0<θ<$\frac{\pi}{2}$の範囲を動くとき、3点A,P,Dが同一直線上にあるようなθは少なくとも1つ存在することを示せ。また、このようなθはただ1つであることを示せ。
2023北海道大学理系過去問
この動画を見る
$\Large\boxed{5}$ a,bを$a^2$+$b^2$<1をみたす正の実数とする。また、座標平面上で原点を中心とする半径1の円をCとし、Cの内部にある2点A(a,0), B(0,b)を考える。
0<θ<$\frac{\pi}{2}$に対してC上の点P($\cos\theta$, $\sin\theta$)を考え、PにおけるCの接線に関してBと対称な点をDとおく。
(1)f(θ)=ab$\cos2\theta$+a$\sin\theta$-b$\cos\theta$とおく。方程式f(θ)=0の解が0<θ<$\frac{\pi}{2}$の範囲に少なくとも1つ存在することを示せ。
(2)Dの座標をa, $\theta$を用いて表せ。
(3)θが0<θ<$\frac{\pi}{2}$の範囲を動くとき、3点A,P,Dが同一直線上にあるようなθは少なくとも1つ存在することを示せ。また、このようなθはただ1つであることを示せ。
2023北海道大学理系過去問
福田の数学〜大阪大学2023年文系第1問〜三角方程式と解の存在範囲

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#2次関数とグラフ#図形と方程式#三角関数#円と方程式#三角関数とグラフ#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
a,bを実数とする。θについての方程式
$\cos 2θ =a\sin θ +b$
が実数解をもつような点(a,b)の存在範囲を座標平面上に図示せよ
2023大阪大学文系過去問
この動画を見る
a,bを実数とする。θについての方程式
$\cos 2θ =a\sin θ +b$
が実数解をもつような点(a,b)の存在範囲を座標平面上に図示せよ
2023大阪大学文系過去問
福田の数学〜大阪大学2023年理系第4問〜空間ベクトルと軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#空間ベクトル#図形と方程式#軌跡と領域#空間ベクトル#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
a,b を$a^2+b^2>1$かつ b≠0 をみたす実数の定数とする。
座標空間のA (a,0,b) と点 P(x, y, 0) をとる。
点O(0, 0, 0) を通り直線APと垂直な平面をαとし、平面と直線AP との交点をQとする。
$(\overrightarrow{ AP }・\overrightarrow{ AO })^2=|\overrightarrow{ AP }|^2|\overrightarrow{ AQ }|^2$が成り立つことを示せ。
$|\overrightarrow{ OQ }|^2=1$ をみたすように点P(x,y,0) が xy平面上を動くとき、点Pの軌跡を求めよ。
2023大阪大学理系過去問
この動画を見る
a,b を$a^2+b^2>1$かつ b≠0 をみたす実数の定数とする。
座標空間のA (a,0,b) と点 P(x, y, 0) をとる。
点O(0, 0, 0) を通り直線APと垂直な平面をαとし、平面と直線AP との交点をQとする。
$(\overrightarrow{ AP }・\overrightarrow{ AO })^2=|\overrightarrow{ AP }|^2|\overrightarrow{ AQ }|^2$が成り立つことを示せ。
$|\overrightarrow{ OQ }|^2=1$ をみたすように点P(x,y,0) が xy平面上を動くとき、点Pの軌跡を求めよ。
2023大阪大学理系過去問
福田の数学〜大阪大学2023年理系第3問〜三角方程式の解の個数

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#円と方程式#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ Pを座標平面上の点とし、点Pの座標を(a,b)とする。-π≦t≦πの範囲にある実数tのうち、曲線y=$\cos x$上の点(t, $\cos t$)における接線が点Pを通るという条件をみたすものの個数をN(P)とする。N(P)=4かつ0<a<πをみたすような点Pの存在範囲を座標平面上に図示せよ。
2023大阪大学理系過去問
この動画を見る
$\Large\boxed{3}$ Pを座標平面上の点とし、点Pの座標を(a,b)とする。-π≦t≦πの範囲にある実数tのうち、曲線y=$\cos x$上の点(t, $\cos t$)における接線が点Pを通るという条件をみたすものの個数をN(P)とする。N(P)=4かつ0<a<πをみたすような点Pの存在範囲を座標平面上に図示せよ。
2023大阪大学理系過去問
福田の数学〜大阪大学2023年理系第2問〜ベクトルと領域

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#図形と方程式#軌跡と領域#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 平面上の3点O,A,Bが
|2$\overrightarrow{OA}$+$\overrightarrow{OB}$|=|$\overrightarrow{OA}$+2$\overrightarrow{OB}$|=1 かつ (2$\overrightarrow{OA}$+$\overrightarrow{OB}$)・($\overrightarrow{OA}$+$\overrightarrow{OB}$)=$\displaystyle\frac{1}{3}$
を満たすとする。
(1)(2$\overrightarrow{OA}$+$\overrightarrow{OB}$)・($\overrightarrow{OA}$+2$\overrightarrow{OB}$)を求めよ。
(2)平面上の点Pが
|$\overrightarrow{OP}$ー($\overrightarrow{OA}$+$\overrightarrow{OB}$)|≦$\frac{1}{3}$ かつ $\overrightarrow{OP}$・(2$\overrightarrow{OA}$+$\overrightarrow{OB}$)≦$\frac{1}{3}$
を満たすように動くとき、|$\overrightarrow{OP}$|の最大値と最小値を求めよ。
2023大阪大学理系過去問
この動画を見る
$\Large\boxed{2}$ 平面上の3点O,A,Bが
|2$\overrightarrow{OA}$+$\overrightarrow{OB}$|=|$\overrightarrow{OA}$+2$\overrightarrow{OB}$|=1 かつ (2$\overrightarrow{OA}$+$\overrightarrow{OB}$)・($\overrightarrow{OA}$+$\overrightarrow{OB}$)=$\displaystyle\frac{1}{3}$
を満たすとする。
(1)(2$\overrightarrow{OA}$+$\overrightarrow{OB}$)・($\overrightarrow{OA}$+2$\overrightarrow{OB}$)を求めよ。
(2)平面上の点Pが
|$\overrightarrow{OP}$ー($\overrightarrow{OA}$+$\overrightarrow{OB}$)|≦$\frac{1}{3}$ かつ $\overrightarrow{OP}$・(2$\overrightarrow{OA}$+$\overrightarrow{OB}$)≦$\frac{1}{3}$
を満たすように動くとき、|$\overrightarrow{OP}$|の最大値と最小値を求めよ。
2023大阪大学理系過去問
