 対数関数
対数関数
 対数関数
対数関数
手を動かすだけの指数方程式
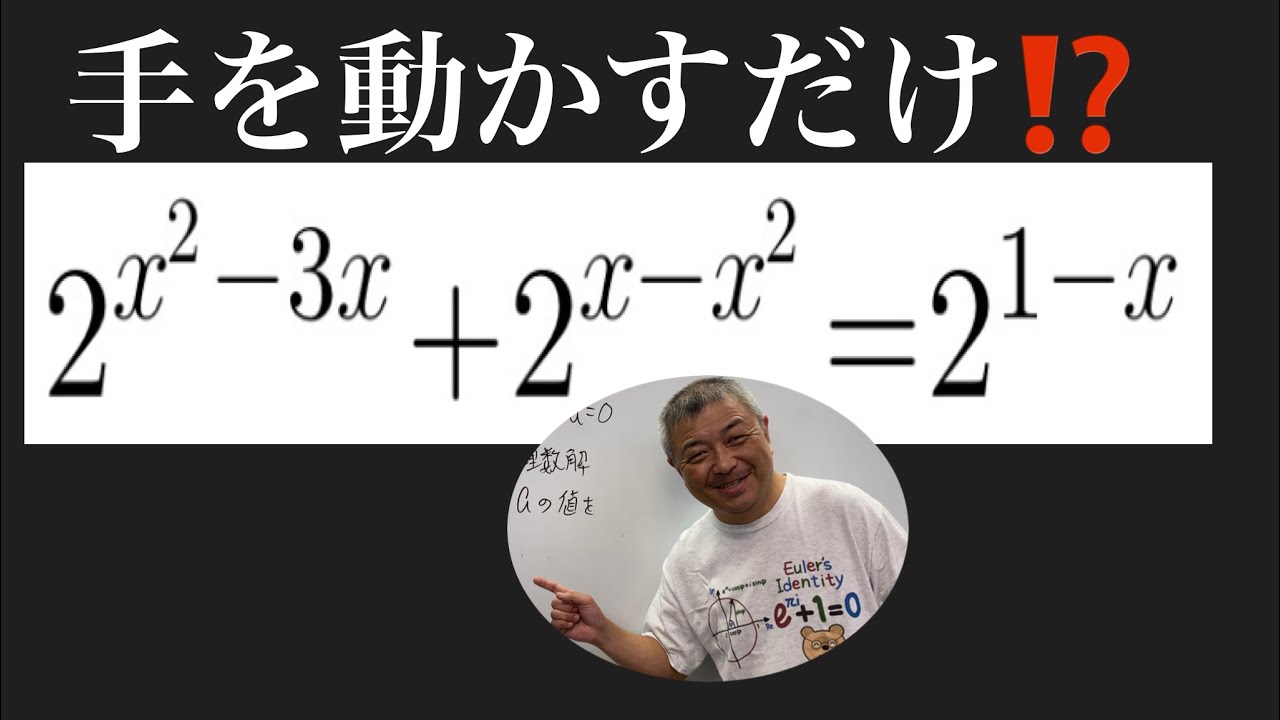
単元:
#数Ⅱ#指数関数と対数関数#指数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 2^{x^2-3x}+2^{x-x^2}=2^{1-x}$
これを解け.
この動画を見る
$ 2^{x^2-3x}+2^{x-x^2}=2^{1-x}$
これを解け.
どっちがでかい?かなりの大差じゃね?

福田の数学〜中央大学2022年経済学部第1問(4)〜常用対数と桁数

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(4)$15^{32}$は何桁の整数か。ただし、$\log_{10}2=0.3010,\log_{10}3=0.4471$とする。
2022中央大学経済学部過去問
この動画を見る
(4)$15^{32}$は何桁の整数か。ただし、$\log_{10}2=0.3010,\log_{10}3=0.4471$とする。
2022中央大学経済学部過去問
漸化式・対数の利用の融合問題 福井大

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#福井大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a_1=1,a_{n+1}=\dfrac{a_n}{a_n+3},a_{11}$は小数点以下0でない数が初めて表れるのは小数第何位?
福井大過去問
この動画を見る
$ a_1=1,a_{n+1}=\dfrac{a_n}{a_n+3},a_{11}$は小数点以下0でない数が初めて表れるのは小数第何位?
福井大過去問
どっちがでかい?

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ (2+3)(2^2+3^2)(2^4+3^4)(2^8+3^8)(2^{16}+3^{16})$
$(2^{32}+3^{32})$と,
$3^{64}$はどちらが大きいか?
この動画を見る
$ (2+3)(2^2+3^2)(2^4+3^4)(2^8+3^8)(2^{16}+3^{16})$
$(2^{32}+3^{32})$と,
$3^{64}$はどちらが大きいか?
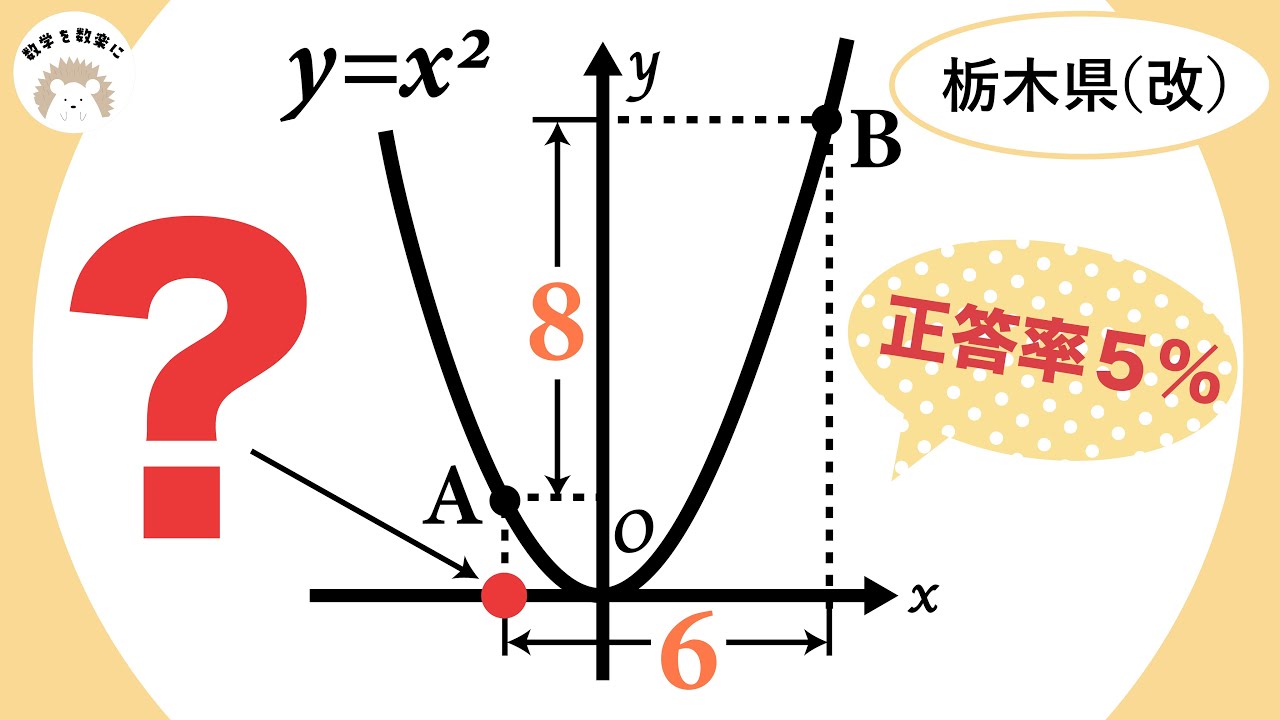
放物線 栃木県(改) 正答率5%!?
福田の数学〜立教大学2022年理学部第1問(1)〜対数方程式

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}(1)$実数$x$に関する方程式
$2\log(1-x)-\log(5-x)=\log 2$
を解くと$x=\boxed{ア}$である.
立教大学2022年理学部過去問
この動画を見る
$\boxed{1}(1)$実数$x$に関する方程式
$2\log(1-x)-\log(5-x)=\log 2$
を解くと$x=\boxed{ア}$である.
立教大学2022年理学部過去問
『log』の解説を30秒でします

早稲田(社)対数の基本

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \log_{10}2=0.3030,\log_{10}3$
$=0.4771,\log_{10}7=0.8451,7^{70}$
の上2桁の数を求めよ.
早稲田(社)過去問
この動画を見る
$ \log_{10}2=0.3030,\log_{10}3$
$=0.4771,\log_{10}7=0.8451,7^{70}$
の上2桁の数を求めよ.
早稲田(社)過去問
福田の数学〜明治大学2022年全学部統一入試12AB第1問(2)〜対数方程式と対称式

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#複素数と方程式#式の計算(整式・展開・因数分解)#指数関数と対数関数#剰余の定理・因数定理・組み立て除法と高次方程式#対数関数#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(2)1ではない正の実数$x,\ y$が次の条件を満たすとする。
$\left\{\begin{array}{1}
xy=\displaystyle\frac{1}{4}\\
\displaystyle\frac{1}{\log_2x}+\displaystyle\frac{1}{\log_2y}=\frac{8}{21}
\end{array}\right.$
このとき、$x+y=\frac{\boxed{\ \ キク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}}{\boxed{\ \ コサ\ \ }}$である。
2022明治大学全統過去問
この動画を見る
(2)1ではない正の実数$x,\ y$が次の条件を満たすとする。
$\left\{\begin{array}{1}
xy=\displaystyle\frac{1}{4}\\
\displaystyle\frac{1}{\log_2x}+\displaystyle\frac{1}{\log_2y}=\frac{8}{21}
\end{array}\right.$
このとき、$x+y=\frac{\boxed{\ \ キク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}}{\boxed{\ \ コサ\ \ }}$である。
2022明治大学全統過去問
対数の良問!何で2022を挟み込む?【京都大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$5.4<\log_4 2022<5.5$であることを示せ。
ただし,$0.301<\log_{10} 2<0.3011$であることは用いてよい。
京都大過去問
この動画を見る
$5.4<\log_4 2022<5.5$であることを示せ。
ただし,$0.301<\log_{10} 2<0.3011$であることは用いてよい。
京都大過去問
指数・対数の基本.2通りの解法(実質同じだけど)
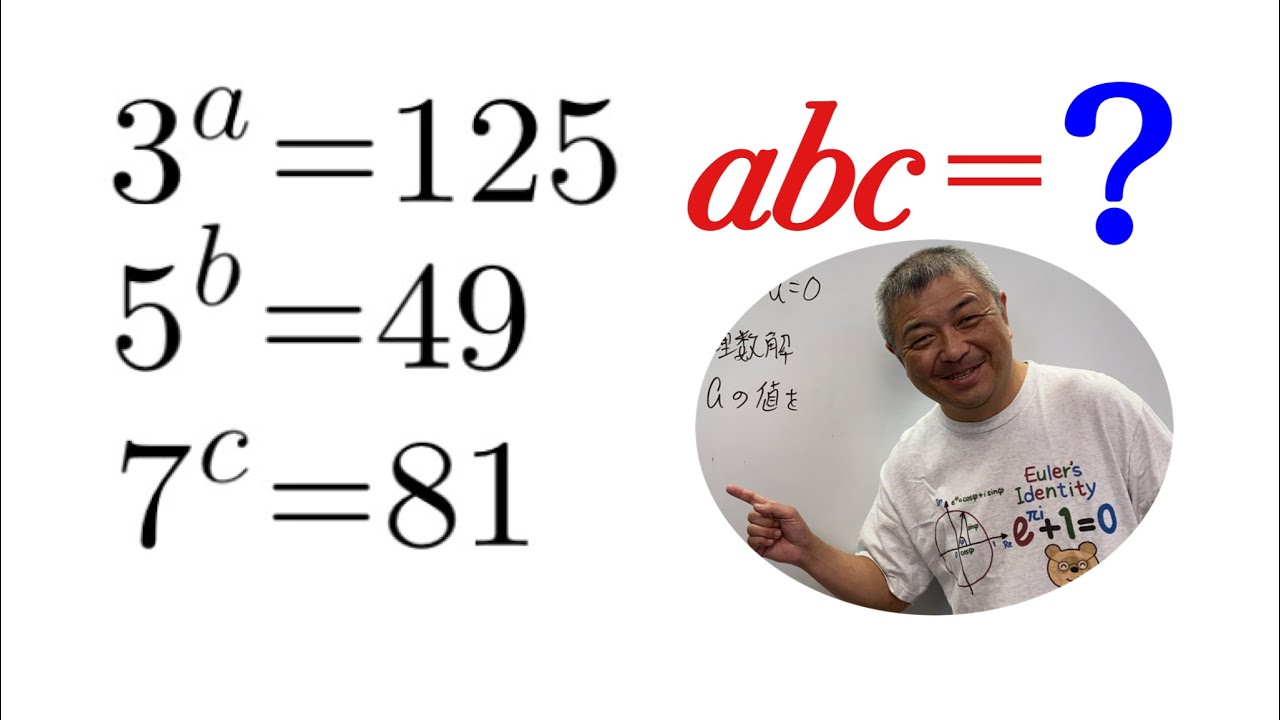
単元:
#数Ⅱ#指数関数と対数関数#指数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 3^a=125,5^b-49,7^c=81,abc=?$
これを解け.
この動画を見る
$ 3^a=125,5^b-49,7^c=81,abc=?$
これを解け.
対数の良問!値を上手く自分で評価できるかがポイント【大阪大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
自然数m,nと$0<a\dfrac{2}{3}$が成り立つことを示せ。
大阪大過去問
この動画を見る
自然数m,nと$0<a\dfrac{2}{3}$が成り立つことを示せ。
大阪大過去問
福田の数学〜早稲田大学2022年商学部第1問(1)〜漸化式の解法

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#数列#漸化式#数学的帰納法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(1)数列$\left\{a_n\right\}$が次の条件を満たしている。
$(\textrm{i})a_1=a_2=4$
$(\textrm{ii})a_{n+2}=a_n^{\log_2a_{n+1}} (n=1,2,3,\ldots)$
このとき、$\log_2(\log_2a_{10})=\boxed{\ \ ア\ \ }$である。
2022早稲田大学商学部過去問
この動画を見る
${\large\boxed{1}}$(1)数列$\left\{a_n\right\}$が次の条件を満たしている。
$(\textrm{i})a_1=a_2=4$
$(\textrm{ii})a_{n+2}=a_n^{\log_2a_{n+1}} (n=1,2,3,\ldots)$
このとき、$\log_2(\log_2a_{10})=\boxed{\ \ ア\ \ }$である。
2022早稲田大学商学部過去問
チリの大穴が地球を潰すまで計算した

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
チリの大穴の直径が25mだったのに1週間で2倍になりました。
直径が1週間で2倍になると仮定したときいつ地球は崩壊しますか。
この動画を見る
下記質問の解説動画です
チリの大穴の直径が25mだったのに1週間で2倍になりました。
直径が1週間で2倍になると仮定したときいつ地球は崩壊しますか。
【数学ネタ】近似値を信用しない人 #Shorts

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$2^{30}$の桁数を求めよ。
ただし、$\log_{10}2$=0.3010とする。
この動画を見る
$2^{30}$の桁数を求めよ。
ただし、$\log_{10}2$=0.3010とする。
【数Ⅱ】常用対数の使い方【対数ってなんのためにあるの? 人類の計算力に革命を与えた技 桁数問題から罹患者数の増え方、複利計算をマスターしよう】

【数Ⅱ】対数のグラフと不等式【底に注意してグラフを描こう。指数関数と全く同じ!?】

【誘導あり:概要欄】大学入試問題#256 神戸大学2012 #極限 #はさみうちの定理

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#対数関数#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$2 \leqq n$自然数
$S_n=\displaystyle \sum_{k=1}^{n^3-1}\displaystyle \frac{1}{k\ log\ k}$
(1)
$2 \leqq k$:自然数
$\displaystyle \frac{1}{(k+1)log(k+1)} \lt \displaystyle \int_{k}^{k+1}\displaystyle \frac{dx}{x\ log\ x} \lt \displaystyle \frac{1}{k\ log\ k}$
(2)
$\displaystyle \lim_{ n \to \infty }S_n$を求めよ。
出典:2012年神戸大学 入試問題
この動画を見る
$2 \leqq n$自然数
$S_n=\displaystyle \sum_{k=1}^{n^3-1}\displaystyle \frac{1}{k\ log\ k}$
(1)
$2 \leqq k$:自然数
$\displaystyle \frac{1}{(k+1)log(k+1)} \lt \displaystyle \int_{k}^{k+1}\displaystyle \frac{dx}{x\ log\ x} \lt \displaystyle \frac{1}{k\ log\ k}$
(2)
$\displaystyle \lim_{ n \to \infty }S_n$を求めよ。
出典:2012年神戸大学 入試問題
福田の数学〜慶應義塾大学2022年看護医療学部第1問(1)〜対数計算

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(1)$\log_3\sqrt6\ -\log_3\frac{2}{3}+\log_3\sqrt2\ $を有理数で表すと$\boxed{\ \ ア\ \ }$である。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{1}}$(1)$\log_3\sqrt6\ -\log_3\frac{2}{3}+\log_3\sqrt2\ $を有理数で表すと$\boxed{\ \ ア\ \ }$である。
2022慶應義塾大学看護医療学科過去問
大学入試問題#254 神戸大学2012 #定積分
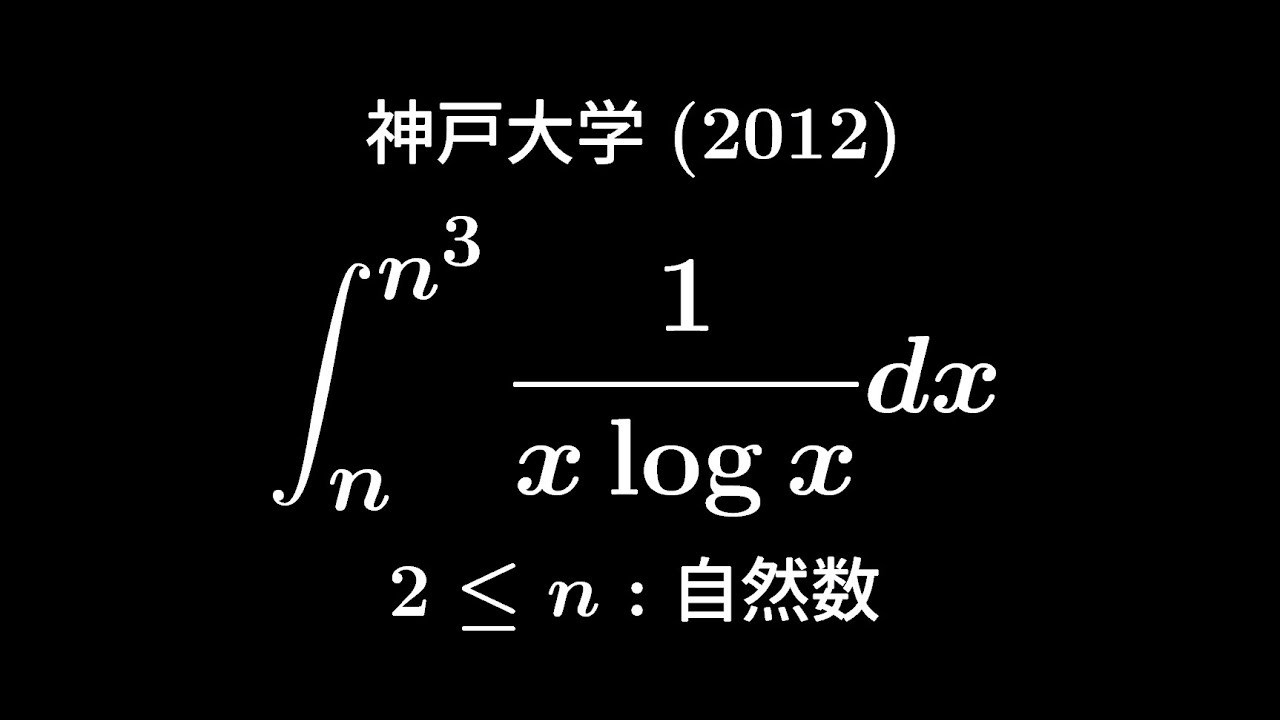
単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#積分とその応用#定積分#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$2 \leqq n$自然数
$\displaystyle \int_{n}^{n^3}\displaystyle \frac{dx}{x\ log\ x}$を計算せよ。
出典:2012年神戸大学 入試問題
この動画を見る
$2 \leqq n$自然数
$\displaystyle \int_{n}^{n^3}\displaystyle \frac{dx}{x\ log\ x}$を計算せよ。
出典:2012年神戸大学 入試問題
大学入試問題#252 茨城大学(2012) #定積分

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#指数関数と対数関数#対数関数#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{log2}e^{|x|}e^xdx$を計算せよ。
出典:2012年茨城大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{log2}e^{|x|}e^xdx$を計算せよ。
出典:2012年茨城大学 入試問題
【数Ⅱ】対数の定義と方程式【対数の意味とは。計算公式・底の変換公式を使いこなして対数方程式を解こう】

どうってことない計算

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \dfrac{1}{\log_2 10000}+\dfrac{1}{\log_5 10000}$
これを解け.
この動画を見る
$ \dfrac{1}{\log_2 10000}+\dfrac{1}{\log_5 10000}$
これを解け.
福田の入試問題解説〜慶應義塾大学2022年医学部第1問(3)〜集合と対数不等式

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(3)関数$f(x)=\log_{\frac{1}{3}}\sqrt{3x^3-2x^2}$と$g(x)=\log_9(3x^2-2)$の定義域をそれぞれ
集合A,Bで表すと、$A\cap B=\left\{x|xはx \gt \boxed{\ \ オ\ \ }$を満たす実数である。
実数xが集合$A\cap B$の要素であるとき、$f(x)+g(x) \lt 0$となるための条件は
$\boxed{\ \ オ\ \ } \lt x \lt \boxed{\ \ カ\ \ }$または$x \gt \boxed{\ \ キ\ \ }$となることである。
2022慶應義塾大学医学部過去問
この動画を見る
(3)関数$f(x)=\log_{\frac{1}{3}}\sqrt{3x^3-2x^2}$と$g(x)=\log_9(3x^2-2)$の定義域をそれぞれ
集合A,Bで表すと、$A\cap B=\left\{x|xはx \gt \boxed{\ \ オ\ \ }$を満たす実数である。
実数xが集合$A\cap B$の要素であるとき、$f(x)+g(x) \lt 0$となるための条件は
$\boxed{\ \ オ\ \ } \lt x \lt \boxed{\ \ カ\ \ }$または$x \gt \boxed{\ \ キ\ \ }$となることである。
2022慶應義塾大学医学部過去問
大学入試問題#227 琉球大学(2012) 方程式

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)#琉球大学
指導講師:
ますただ
問題文全文(内容文):
方程式
$log_5(1-4・5^x)=2x+1$を解け
出典:2012年琉球大学 入試問題
この動画を見る
方程式
$log_5(1-4・5^x)=2x+1$を解け
出典:2012年琉球大学 入試問題
早稲田の簡単すぎる問題!満点必須です【数学 入試問題】【早稲田大学】

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$x$が$\dfrac{1}{3}≦x≦9$の範囲を動くとき,関数 $f(x)=(\log_\frac{1}{3}9x)(log_\frac{1}{3}\dfrac{x}{3})$の最大値と最小値を求めよ。
早稲田大過去問
この動画を見る
$x$が$\dfrac{1}{3}≦x≦9$の範囲を動くとき,関数 $f(x)=(\log_\frac{1}{3}9x)(log_\frac{1}{3}\dfrac{x}{3})$の最大値と最小値を求めよ。
早稲田大過去問
対数を用いて桁数を求める良問【数学 入試問題】【東京理科大学】

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$\log_{10}2=0.3010,\log_{10}3=0.4771$とする。
2^{36}は$□$桁の整数である。$3^n$が$□$桁の整数となる。
最小の自然数$n$は$□$であり、$2^{36}+6・3^{□}$は$□$桁の整数である。
東京理科大過去問
この動画を見る
$\log_{10}2=0.3010,\log_{10}3=0.4771$とする。
2^{36}は$□$桁の整数である。$3^n$が$□$桁の整数となる。
最小の自然数$n$は$□$であり、$2^{36}+6・3^{□}$は$□$桁の整数である。
東京理科大過去問
解けるように作られた指数方程式

単元:
#数Ⅱ#複素数と方程式#指数関数と対数関数#剰余の定理・因数定理・組み立て除法と高次方程式#指数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x+y)^{x-y}=2 \\
2^{y-x},(x+y)=1
\end{array}
\right.
\end{eqnarray}$
これを解け.
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x+y)^{x-y}=2 \\
2^{y-x},(x+y)=1
\end{array}
\right.
\end{eqnarray}$
これを解け.
対数方程式

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \log_9a=\log_{12}b=\log_{16}(a+b),\dfrac{b}{a}$の値を求めよ.
この動画を見る
$ \log_9a=\log_{12}b=\log_{16}(a+b),\dfrac{b}{a}$の値を求めよ.
