 不定積分・定積分
不定積分・定積分
 不定積分・定積分
不定積分・定積分
#福島大学(2021) #定積分 #Shorts
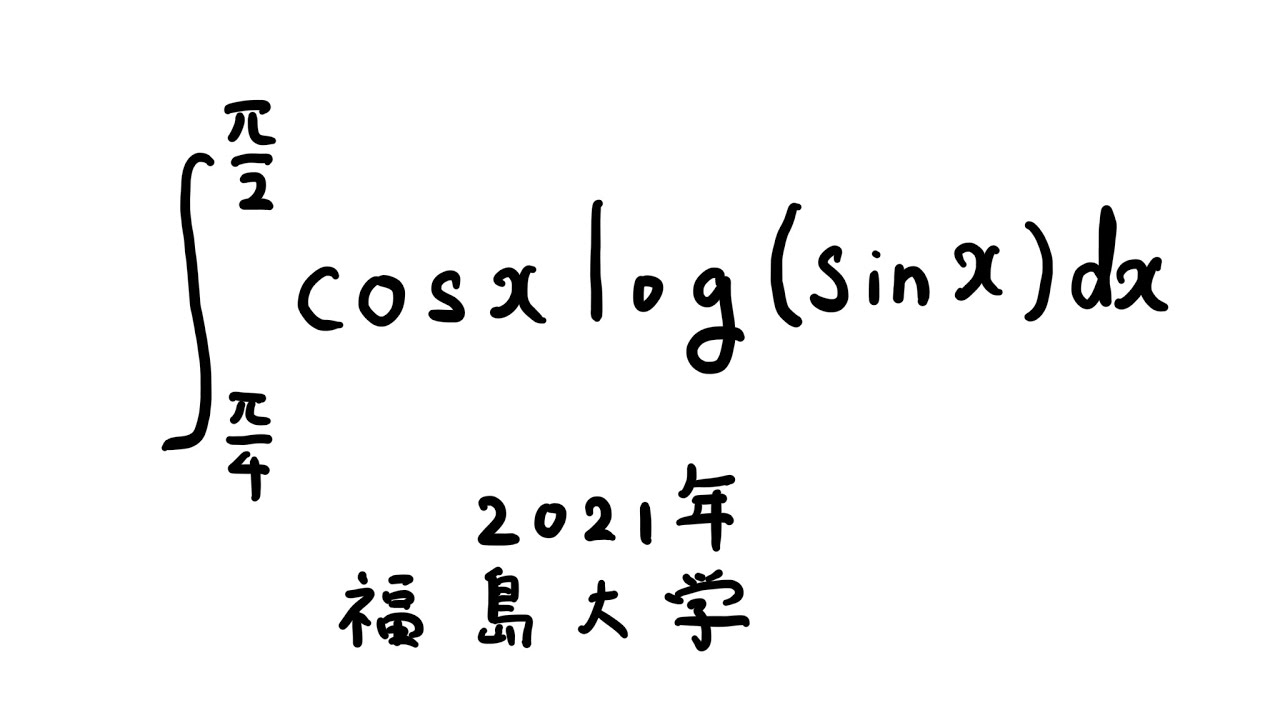
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#福島大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \cos\ x\ log(\sin\ x) dx$
出典:2021年福島大学
この動画を見る
$\displaystyle \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \cos\ x\ log(\sin\ x) dx$
出典:2021年福島大学
#筑波大学(2016) #定積分 #Shorts
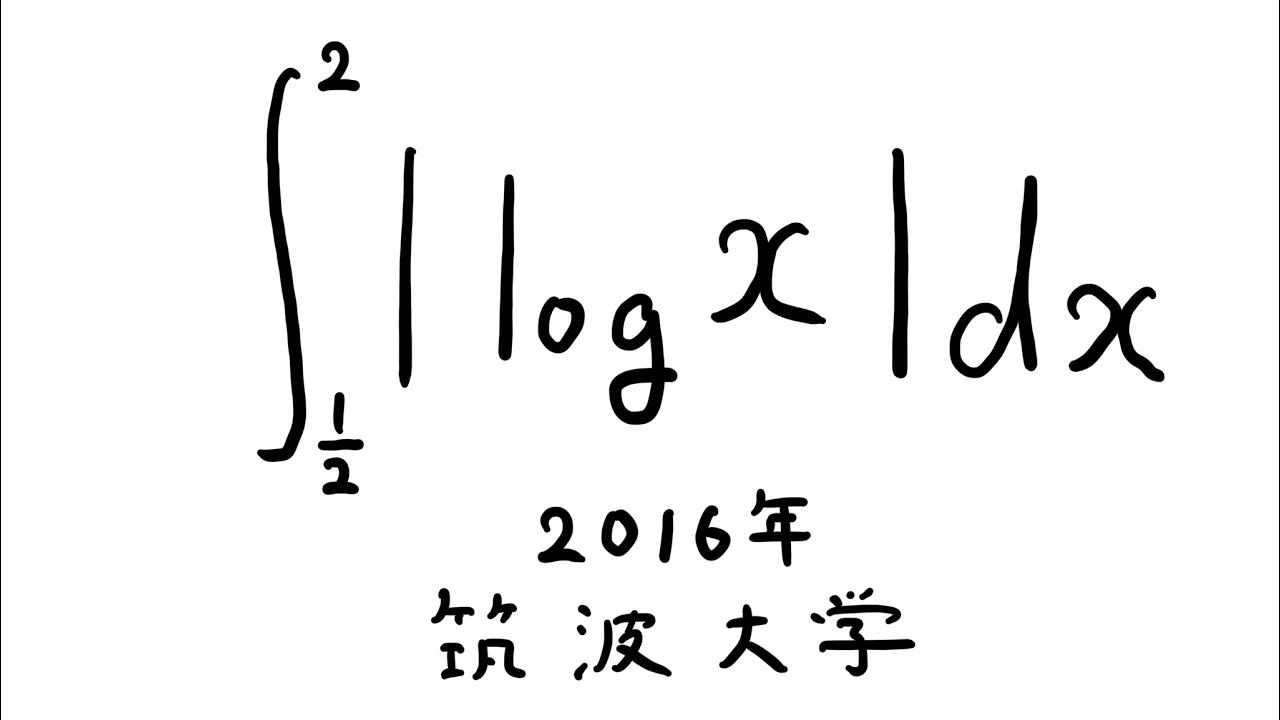
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{1}{2}}^{2} |log\ x| dx$
出典:2016年筑波大学
この動画を見る
$\displaystyle \int_{\frac{1}{2}}^{2} |log\ x| dx$
出典:2016年筑波大学
大学入試問題#825「まあまあ良問」 #茨城大学(2022) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-7}^{1}(2-x) \sqrt[ 3 ]{ 1-x }\ dx$
出典:2022年茨城大学
この動画を見る
$\displaystyle \int_{-7}^{1}(2-x) \sqrt[ 3 ]{ 1-x }\ dx$
出典:2022年茨城大学
#秋田大学(2019) #定積分 #Shorts
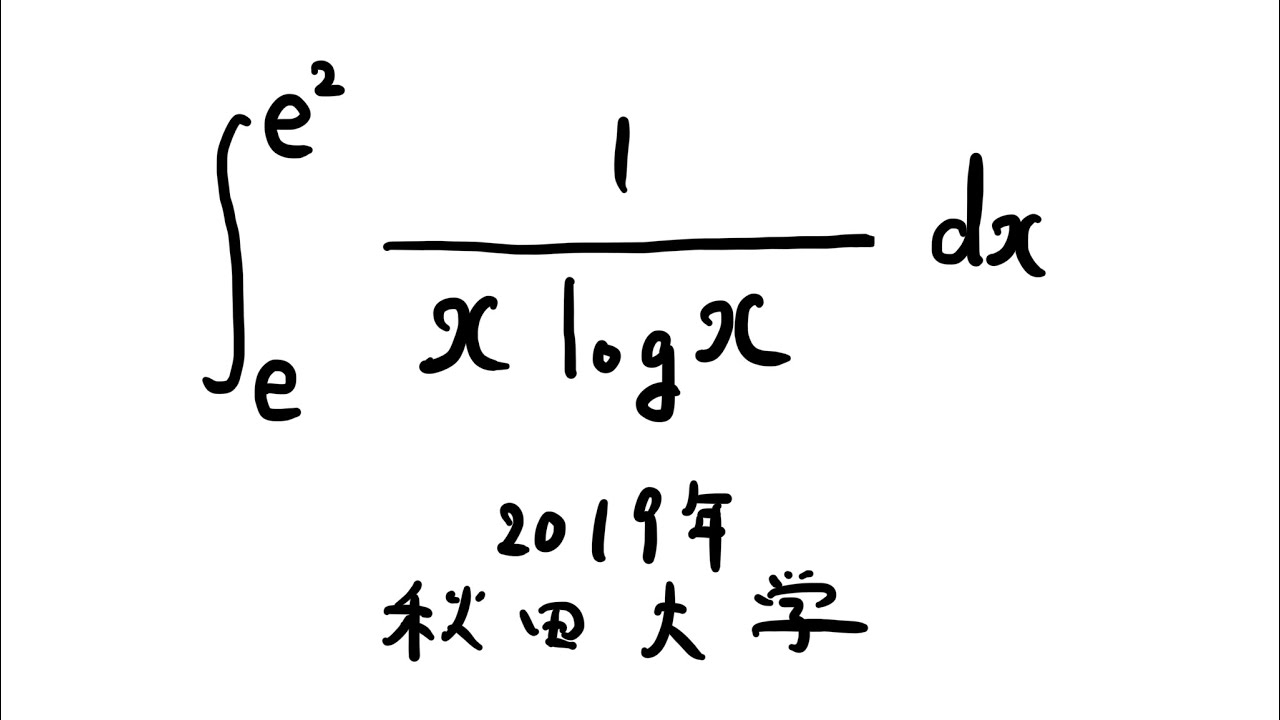
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#秋田大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{e}^{e^2} \displaystyle \frac{1}{x\ log\ x} dx$
出典:2019年秋田大学
この動画を見る
$\displaystyle \int_{e}^{e^2} \displaystyle \frac{1}{x\ log\ x} dx$
出典:2019年秋田大学
大学入試問題#824「たぶん良問」 #筑波大学(2022) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x^2-2x-2}{x^3-1} dx$
出典:2022年筑波大学
この動画を見る
$\displaystyle \int \displaystyle \frac{x^2-2x-2}{x^3-1} dx$
出典:2022年筑波大学
#茨城大学(2023) #定積分 #Shorts
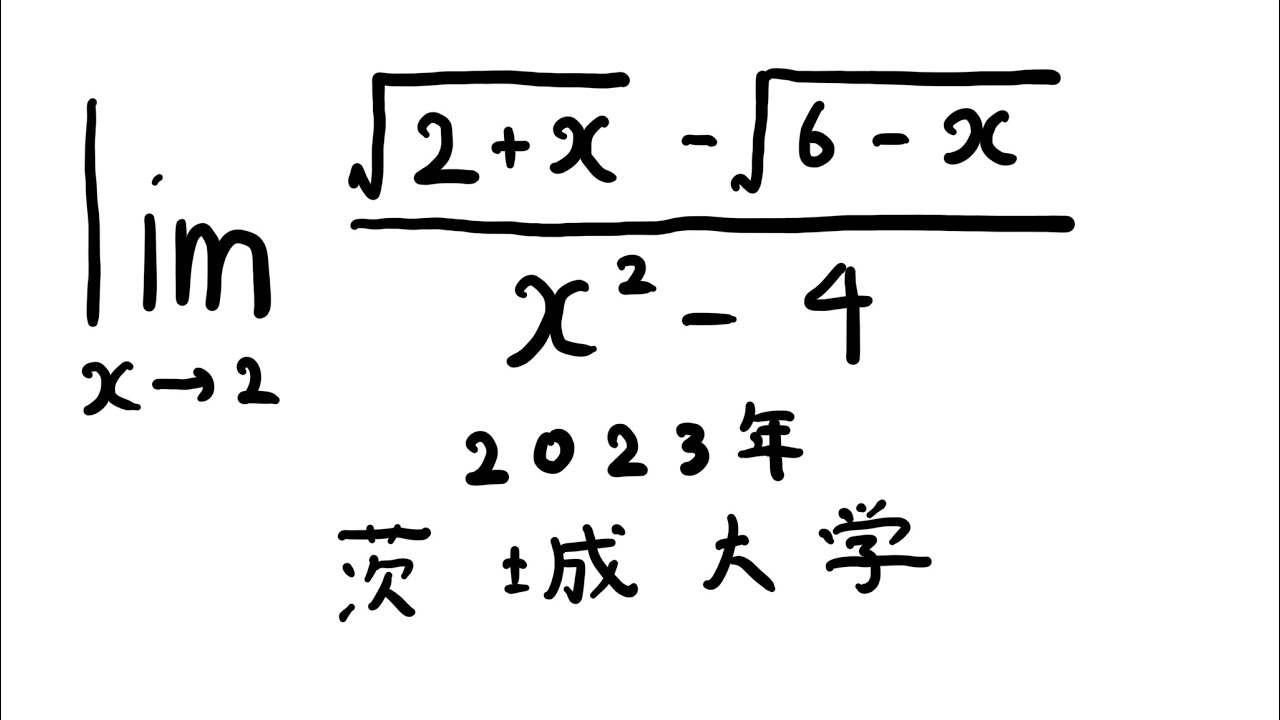
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 2 } \displaystyle \frac{\sqrt{ 2+x }-\sqrt{ 6-x }}{x^2-4}$
出典:2023年茨城大学
この動画を見る
$\displaystyle \lim_{ x \to 2 } \displaystyle \frac{\sqrt{ 2+x }-\sqrt{ 6-x }}{x^2-4}$
出典:2023年茨城大学
#茨城大学(2022) #定積分 #Shorts
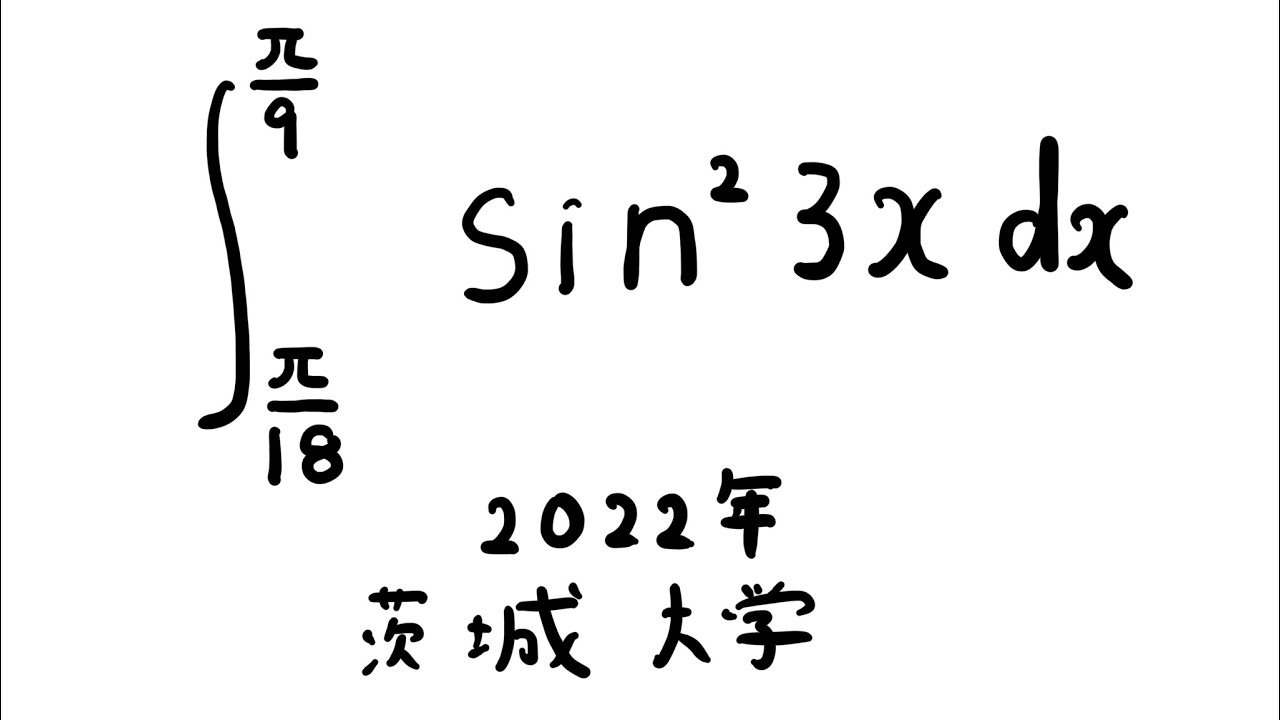
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{18}}^{\frac{\pi}{9}} \sin^23x\ dx$
出典:2022年茨城大学
この動画を見る
$\displaystyle \int_{\frac{\pi}{18}}^{\frac{\pi}{9}} \sin^23x\ dx$
出典:2022年茨城大学
大学入試問題#823「置換するかどうか」 #筑波大学(2019) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} (x+1)^2e-(x+1) dx$
出典:2019年筑波大学
この動画を見る
$\displaystyle \int_{0}^{1} (x+1)^2e-(x+1) dx$
出典:2019年筑波大学
#茨城大学(2022) #定積分 #Shorts
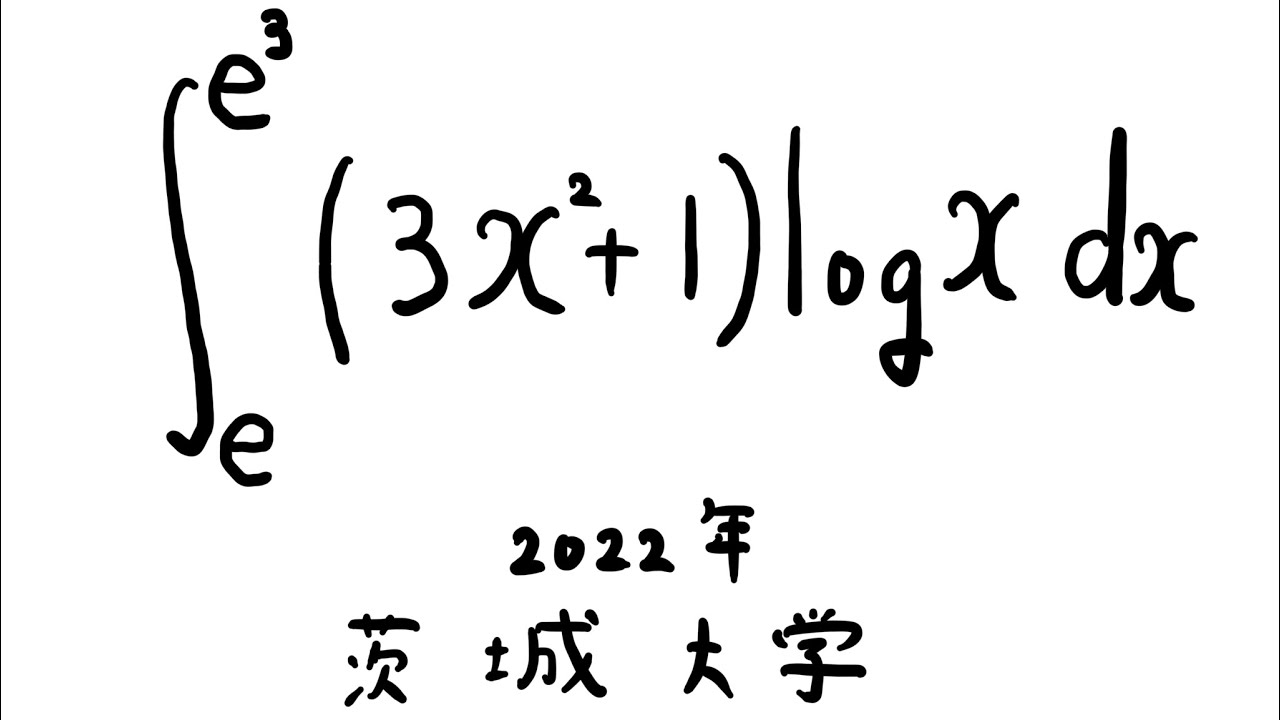
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{e}^{e^3} (3x^2+1)log\ x\ dx$
出典:2022年茨城大学
この動画を見る
$\displaystyle \int_{e}^{e^3} (3x^2+1)log\ x\ dx$
出典:2022年茨城大学
#茨城大学(2022) #定積分 #Shorts
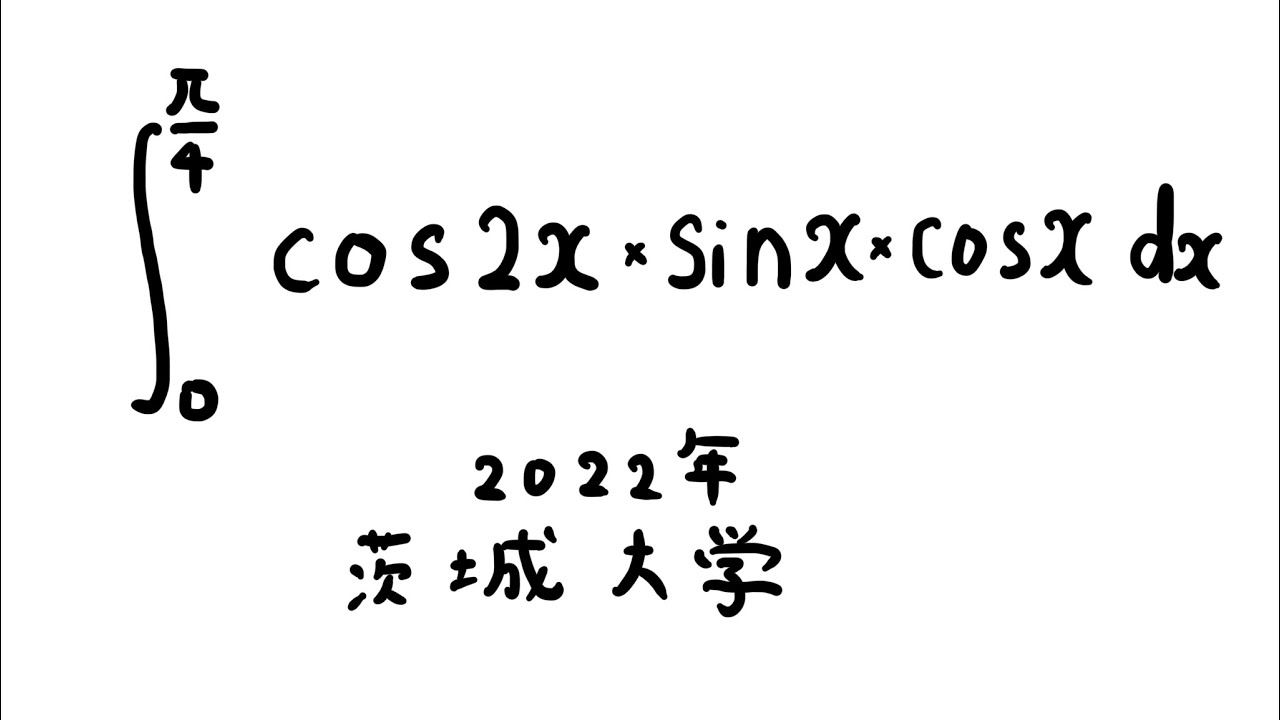
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}} \cos2x\times\sin\ x\ cos\ x\ dx$
出典:2022年茨城大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}} \cos2x\times\sin\ x\ cos\ x\ dx$
出典:2022年茨城大学
大学入試問題#822「これ、積分で出題されるんやー」 #筑波大学(2022) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int log(x+\sqrt{ x^2+1 }) dx$
出典:2022年筑波大学
この動画を見る
$\displaystyle \int log(x+\sqrt{ x^2+1 }) dx$
出典:2022年筑波大学
#茨城大学(2023) #定積分 #Shorts
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
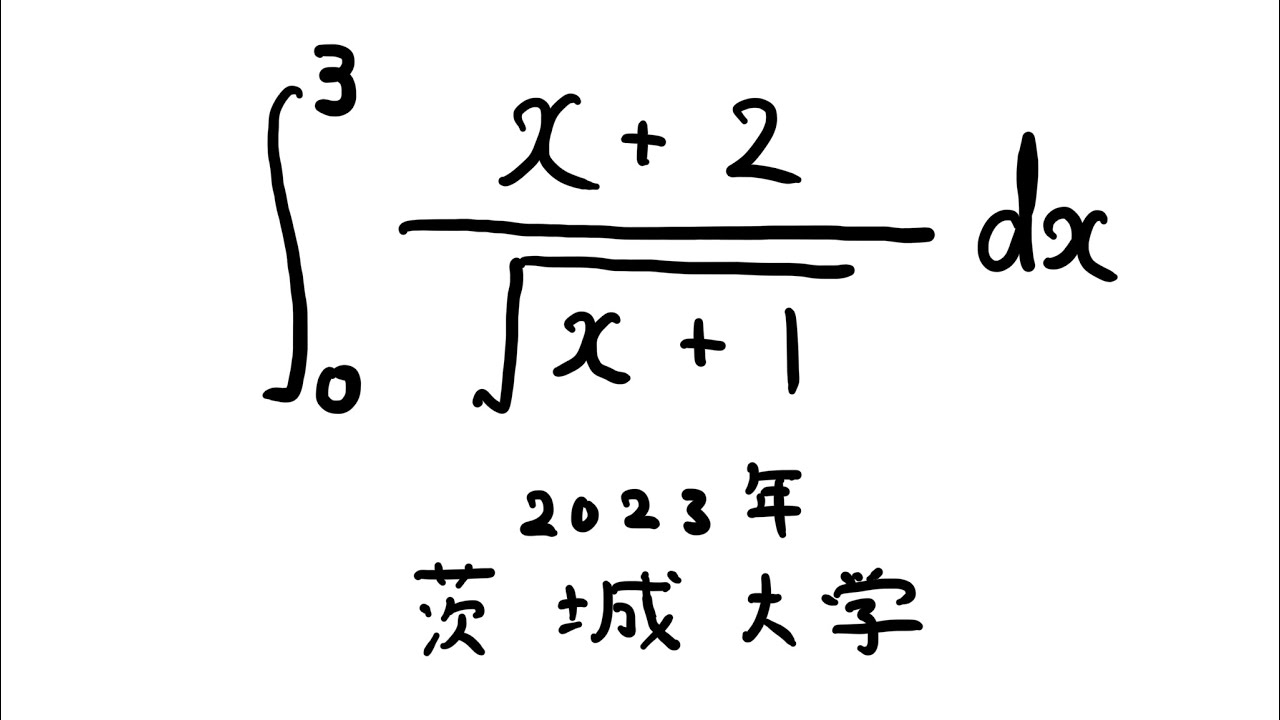
$\displaystyle \int_{0}^{3} \displaystyle \frac{x+2}{\sqrt{ x+1 }} dx$
出典:2023年茨城大学
この動画を見る
$\displaystyle \int_{0}^{3} \displaystyle \frac{x+2}{\sqrt{ x+1 }} dx$
出典:2023年茨城大学
#奈良教育大学(2008) #定積分 #Shorts
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#奈良教育大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
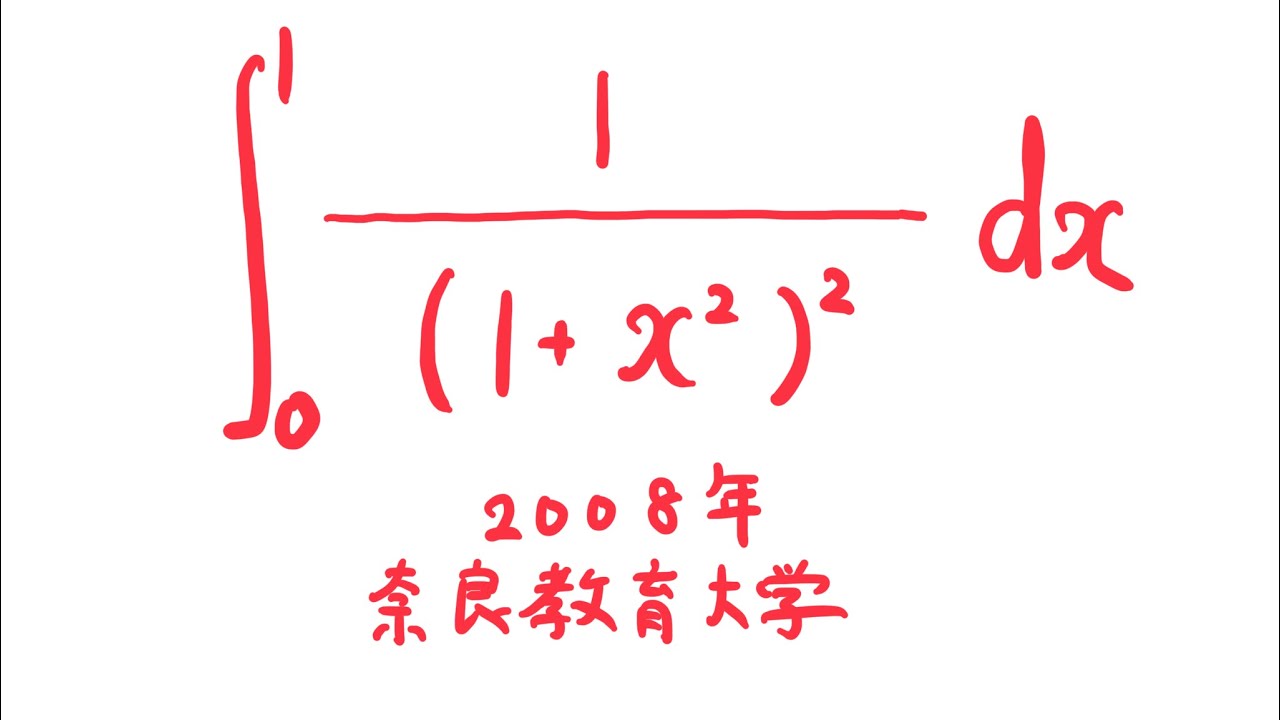
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{(1+x^2)^2} dx$
出典:2008年奈良教育大学
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{(1+x^2)^2} dx$
出典:2008年奈良教育大学
#筑波大学(2020) #定積分 #Shorts
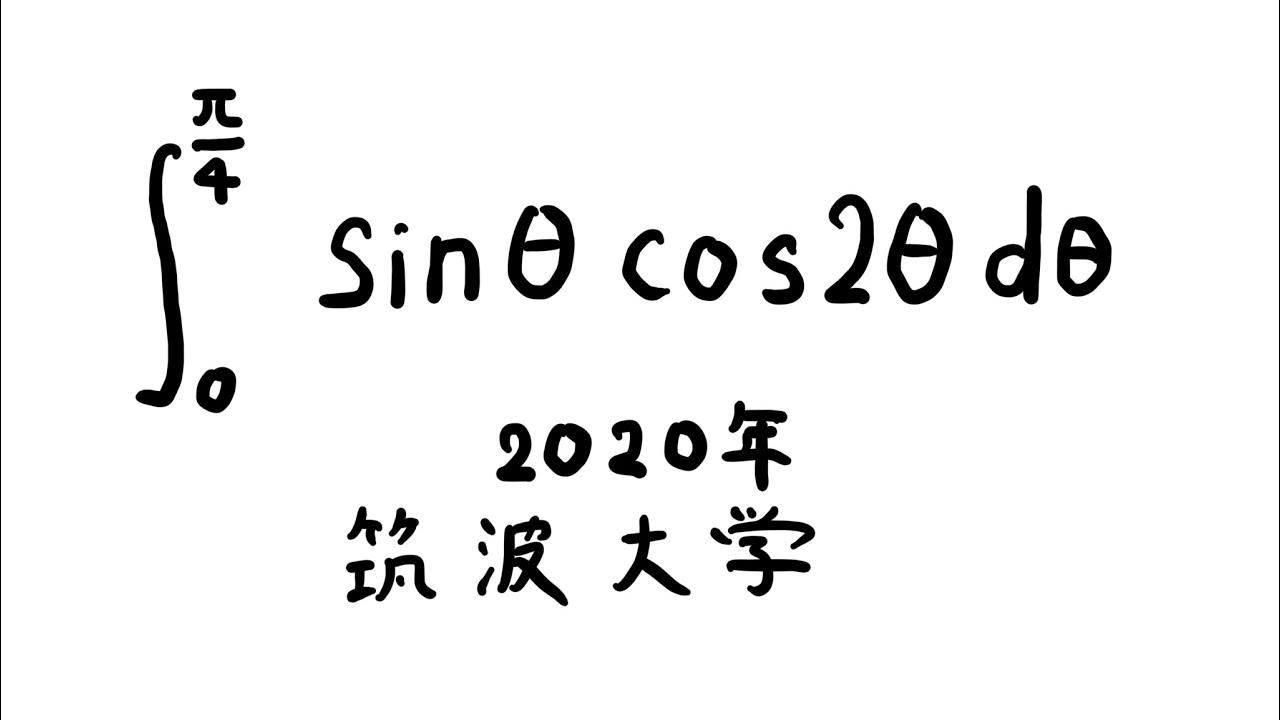
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}} \sin\theta\ \cos2\theta\ d\theta$
出典:2020年筑波大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}} \sin\theta\ \cos2\theta\ d\theta$
出典:2020年筑波大学
大学入試問題#821「王道問題」 #筑波大学(2022) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2} \displaystyle \frac{2x+3}{x^2+2x+4} dx$
出典:2022年筑波大学
この動画を見る
$\displaystyle \int_{0}^{2} \displaystyle \frac{2x+3}{x^2+2x+4} dx$
出典:2022年筑波大学
#茨城大学(2023) #定積分 #Shorts
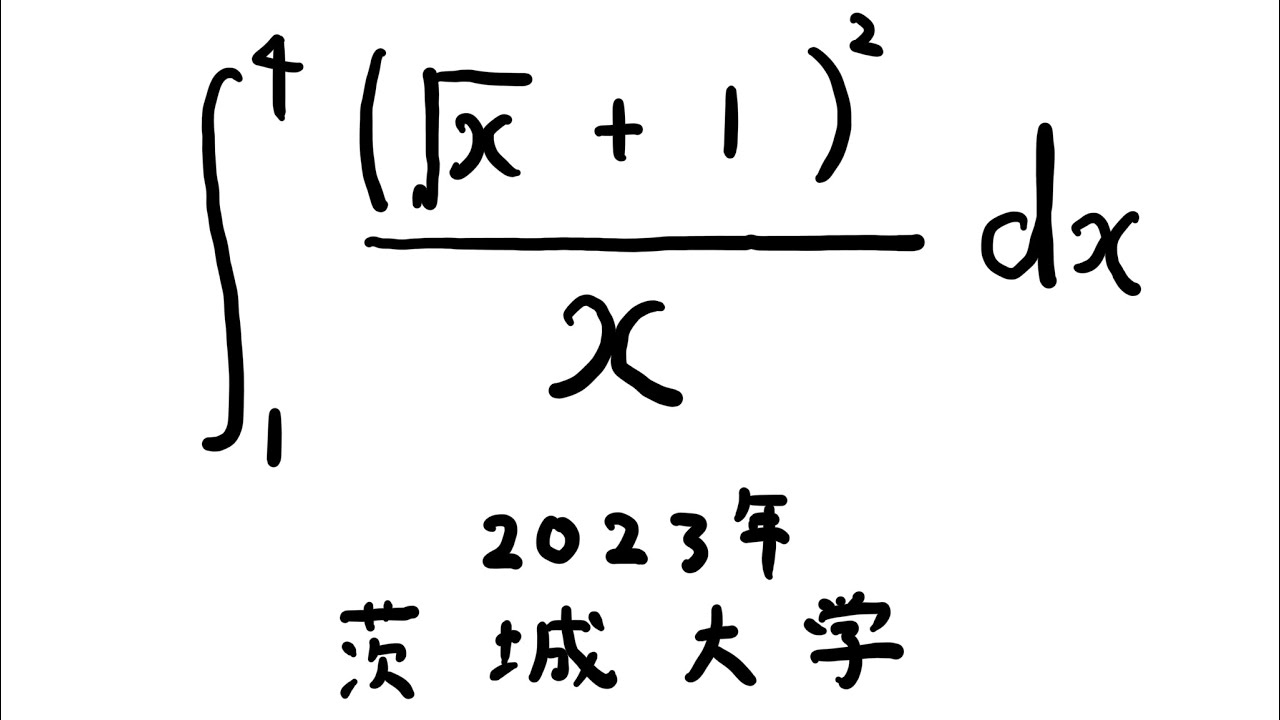
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{4} \displaystyle \frac{(\sqrt{ x }+1)^2}{x} dx$
出典:2023年茨城大学
この動画を見る
$\displaystyle \int_{1}^{4} \displaystyle \frac{(\sqrt{ x }+1)^2}{x} dx$
出典:2023年茨城大学
#奈良教育大学(2014) #定積分 #Shorts

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#奈良教育大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2} |e^x-e| dx$
出典:2014年奈良教育大学
この動画を見る
$\displaystyle \int_{0}^{2} |e^x-e| dx$
出典:2014年奈良教育大学
大学入試問題#820「初手は見えるが、次の手は?」 #奈良教育大学(2023) #定積分
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#奈良教育大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
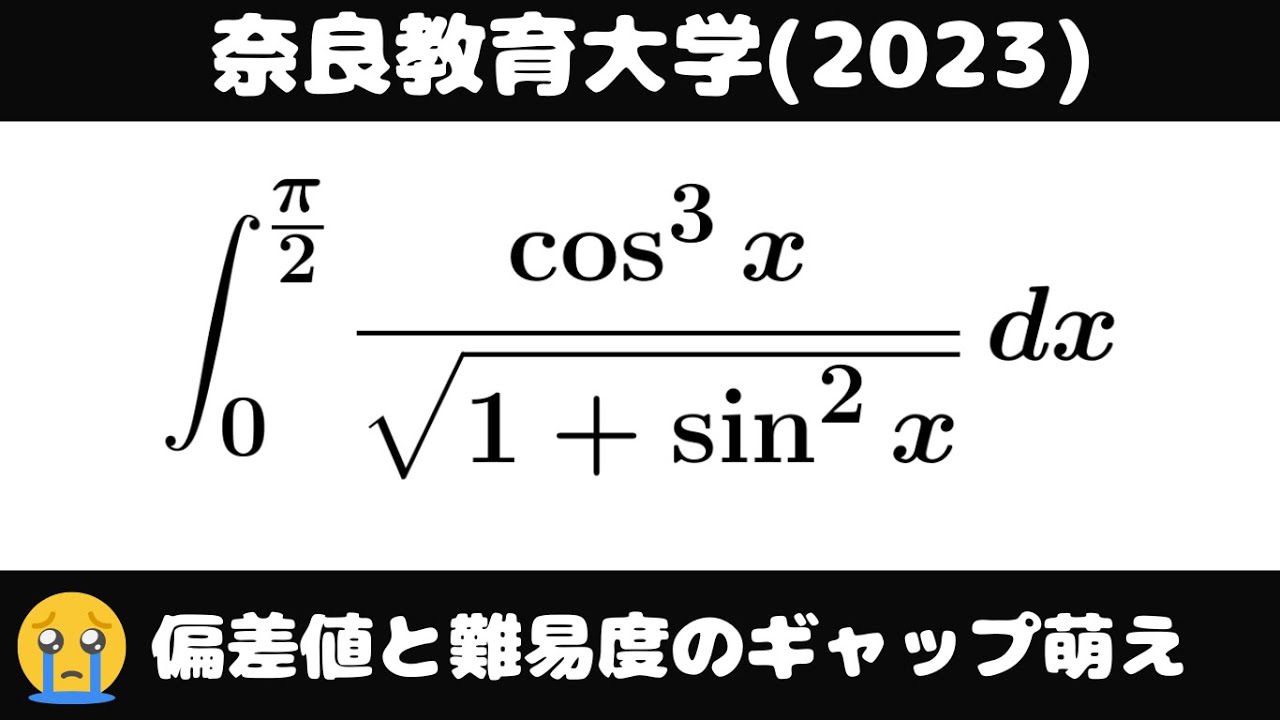
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\cos^3\ x}{\sqrt{ 1+\sin^2 }} dx$
出典:2023年奈良教育大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\cos^3\ x}{\sqrt{ 1+\sin^2 }} dx$
出典:2023年奈良教育大学 入試問題
福田の数学〜慶應義塾大学2024年商学部第1問(2)〜定積分で表された関数

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$
(2)等式 $f(x)$=$12x^2$+$\displaystyle 6x\int_0^1f(t)dt$+$\displaystyle 2\int_0^1tf(t)dt$ を満たす関数$f(x)$を求めよ。
この動画を見る
$\Large\boxed{1}$
(2)等式 $f(x)$=$12x^2$+$\displaystyle 6x\int_0^1f(t)dt$+$\displaystyle 2\int_0^1tf(t)dt$ を満たす関数$f(x)$を求めよ。
#茨城大学(2020) #定積分 #Shorts
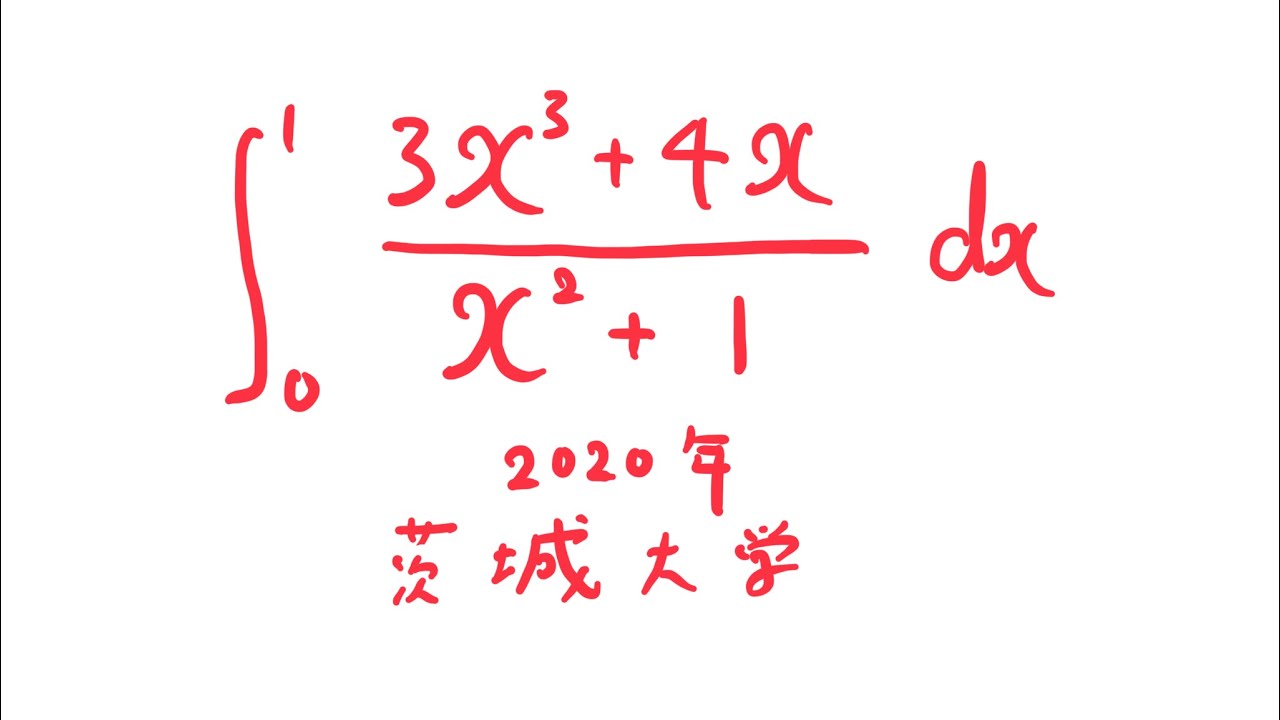
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{3x^3+4x}{x^2+1} dx$
出典:2020年茨城大学
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{3x^3+4x}{x^2+1} dx$
出典:2020年茨城大学
#筑波大学(2018) #定積分 #Shorts
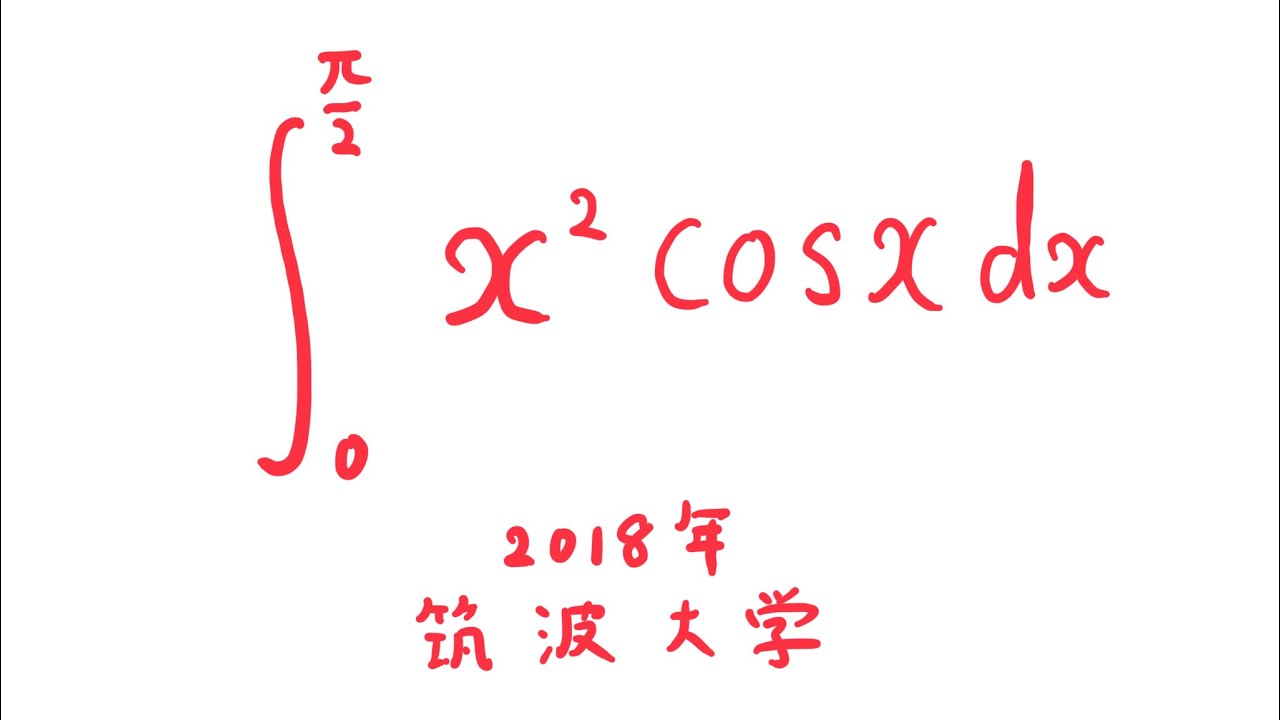
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} x^2\cos\ x\ dx$
出典:2018年筑波大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} x^2\cos\ x\ dx$
出典:2018年筑波大学
大学入試問題#819「楽に計算したい」 #奈良教育大学(2009) #積分方程式

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#奈良教育大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
次の等式を満たす関数$f(x)$を求めよ。
$f(x)=\cos\ x+2\displaystyle \int_{0}^{\frac{\pi}{2}} tf(t) \sin\ t\ dt$
出典:2009年奈良教育大学
この動画を見る
次の等式を満たす関数$f(x)$を求めよ。
$f(x)=\cos\ x+2\displaystyle \int_{0}^{\frac{\pi}{2}} tf(t) \sin\ t\ dt$
出典:2009年奈良教育大学
#筑波大学(2019) #定積分 #Shorts
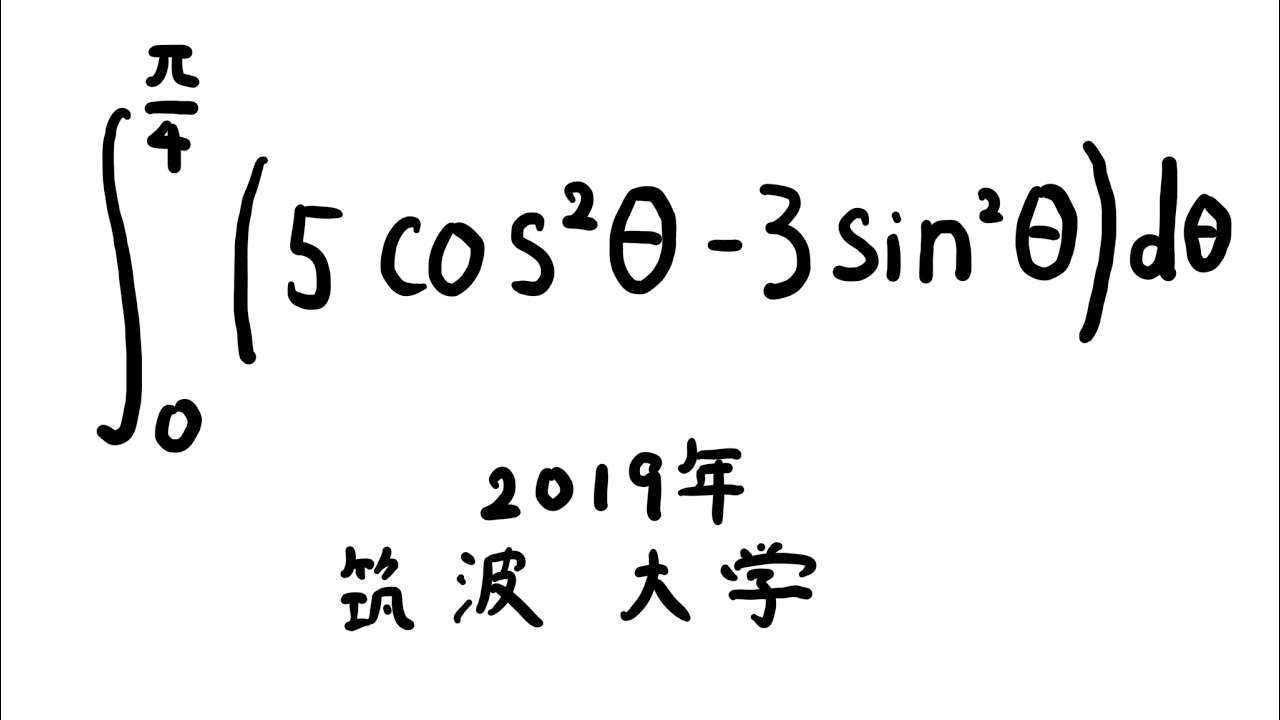
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}} (5\cos^2\theta-3\sin^2\theta)d\theta$
出典:2019年筑波大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}} (5\cos^2\theta-3\sin^2\theta)d\theta$
出典:2019年筑波大学
#筑波大学(2019) #定積分 #Shorts

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} xe^{2x} dx$
出典:2019年筑波大学
この動画を見る
$\displaystyle \int_{0}^{1} xe^{2x} dx$
出典:2019年筑波大学
#奈良教育大学(2014) #定積分 #Shorts
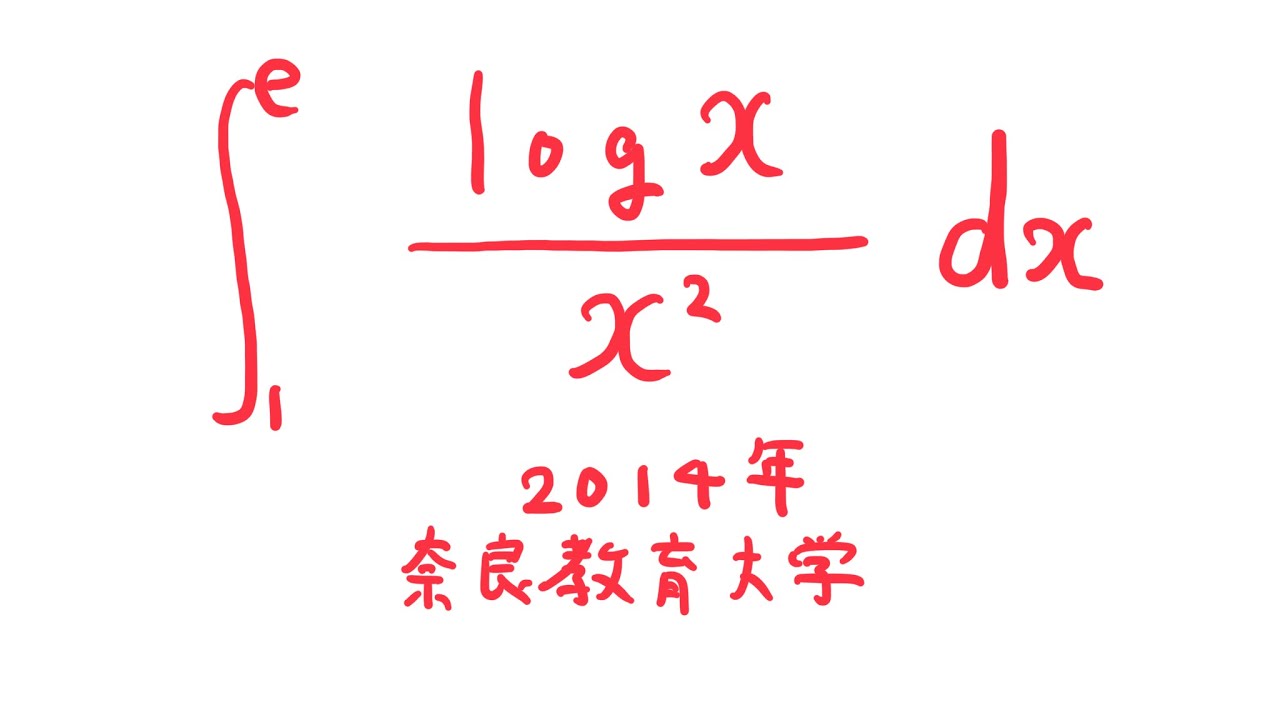
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#奈良教育大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e} \displaystyle \frac{log\ x}{x^2} dx$
出典:2014年奈良教育大学
この動画を見る
$\displaystyle \int_{1}^{e} \displaystyle \frac{log\ x}{x^2} dx$
出典:2014年奈良教育大学
大学入試問題#817「難易度の高い詰将棋!大局観が大事!」 #東京医科歯科大学(2024)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#東京医科歯科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\sin\ x}{1+\sqrt{ \sin\ 2x }} dx$
出典:2024年東京医科歯科大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\sin\ x}{1+\sqrt{ \sin\ 2x }} dx$
出典:2024年東京医科歯科大学
#上智大学(2016) #ウォリス積分 #定積分 #Shorts
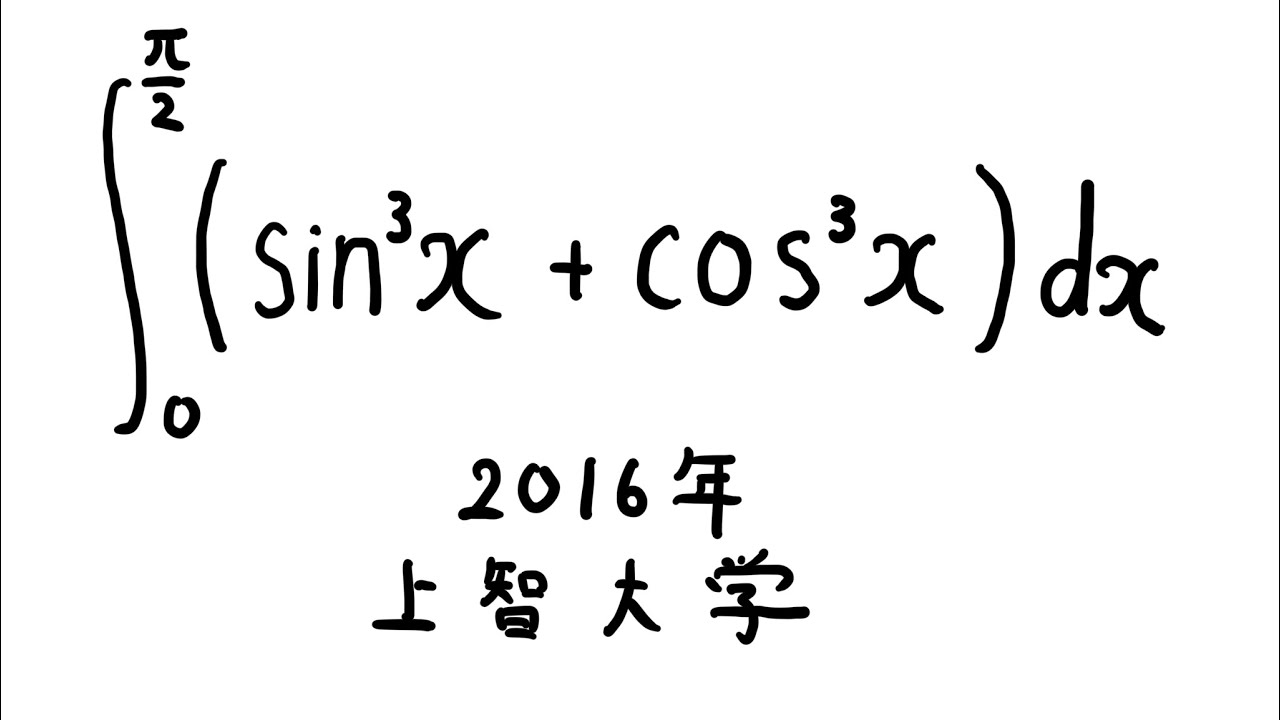
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#上智大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} (\sin^3x+\cos^3x) dx$
出典:2016年上智大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} (\sin^3x+\cos^3x) dx$
出典:2016年上智大学
#筑波大学(2018) #定積分 #Shorts
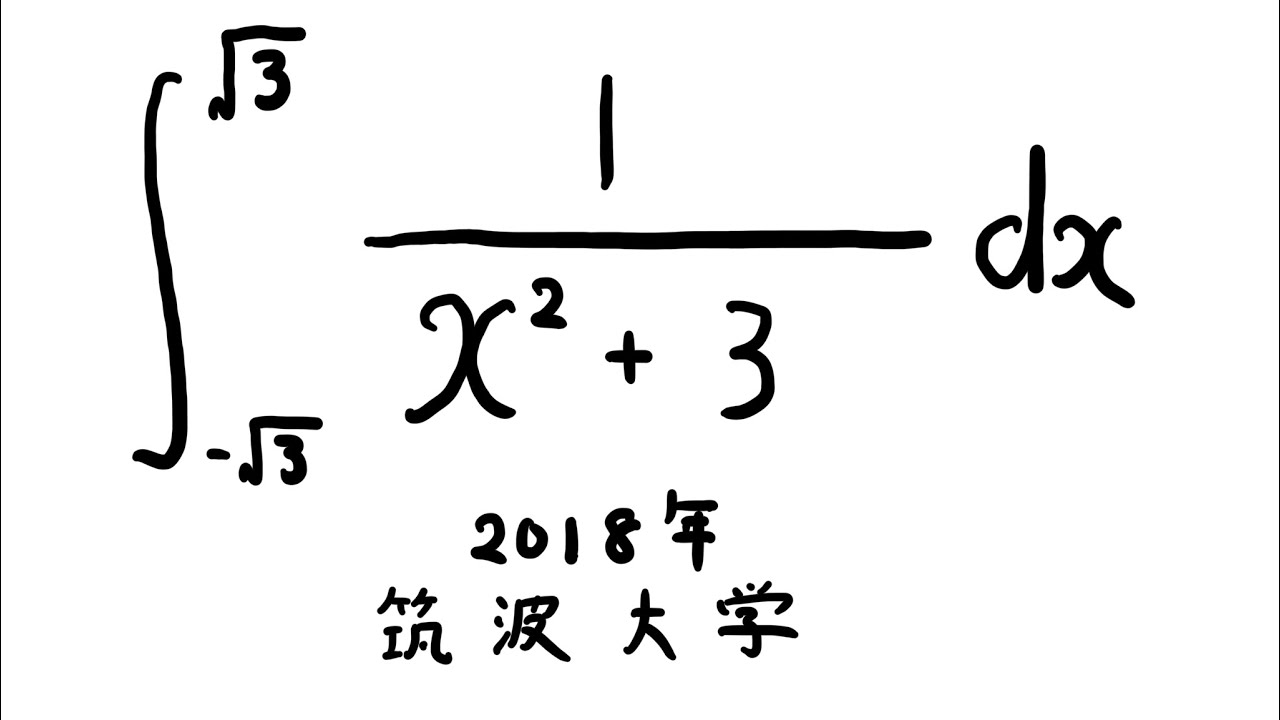
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\sqrt{ 3 }}^{\sqrt{ 3 }} \displaystyle \frac{1}{x^2+3} dx$
出典:2018年筑波大学
この動画を見る
$\displaystyle \int_{-\sqrt{ 3 }}^{\sqrt{ 3 }} \displaystyle \frac{1}{x^2+3} dx$
出典:2018年筑波大学
大学入試問題#803「マジで気合い!」 #大阪市立大学(2000) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#大阪市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{(1+x^2)^4} dx$
出典:2000年大阪市立大学
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{(1+x^2)^4} dx$
出典:2000年大阪市立大学
大学入試問題#799「もう詰んでます!」 #大阪公立大学(2024) #定積分 #King_property

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#大阪公立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\sqrt{ 3 }}^{\sqrt{ 3 }} \displaystyle \frac{log(1+x^2)}{1+e^x} dx$
出典:2024年大阪公立大学
この動画を見る
$\displaystyle \int_{-\sqrt{ 3 }}^{\sqrt{ 3 }} \displaystyle \frac{log(1+x^2)}{1+e^x} dx$
出典:2024年大阪公立大学
