 微分法と積分法
微分法と積分法
 微分法と積分法
微分法と積分法
#数検準1級1次-1 #定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{0}^{1} \displaystyle \frac{x}{x^4+2x^2+1} dx$
出典:数検準1級1次
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{0}^{1} \displaystyle \frac{x}{x^4+2x^2+1} dx$
出典:数検準1級1次
#数検準1級1次#6#極限
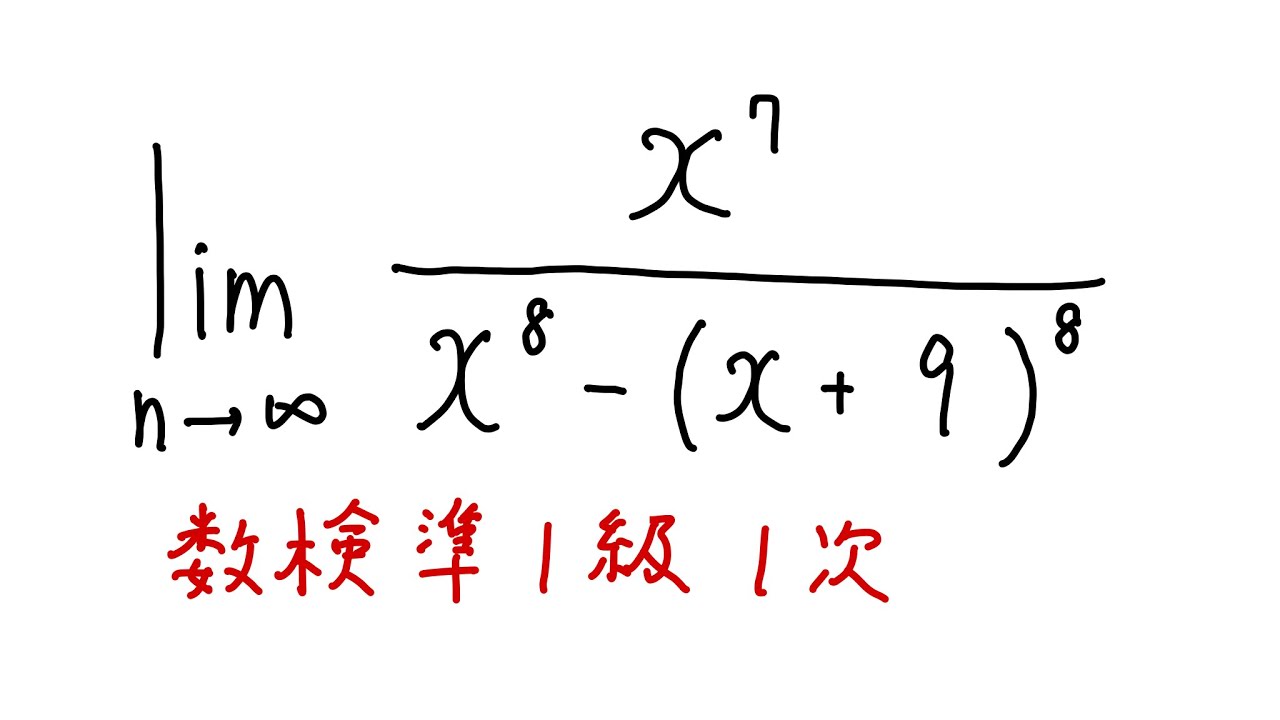
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{x^7}{x^8-(x+9)^8}$
出典:数検準1級1次
この動画を見る
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{x^7}{x^8-(x+9)^8}$
出典:数検準1級1次
#数検準1級1次過去問#極限#ますただ

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
以下の極限を解け。
$\displaystyle \lim_{ n \to \infty } \{2\sqrt{ n^2+4n }-\sqrt{ 4n^2+5n }\}$
出典:数検準1級1次
この動画を見る
以下の極限を解け。
$\displaystyle \lim_{ n \to \infty } \{2\sqrt{ n^2+4n }-\sqrt{ 4n^2+5n }\}$
出典:数検準1級1次
#数学検定準1級2次過去問#70「根性出すしかないんかなー」 #定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{x^4(1-x)^4}{1+x^2} dx$
出典:数検準1級2次
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{x^4(1-x)^4}{1+x^2} dx$
出典:数検準1級2次
#数検準1級1次#5#不定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ x+1 }} dx$
出典:数検準1級
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ x+1 }} dx$
出典:数検準1級
#東京理科大学2023#定積分#ますただ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#東京理科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\sqrt{ e }} \displaystyle \frac{e}{x^2+e} dx$
出典:2023年東京理科大学
この動画を見る
$\displaystyle \int_{0}^{\sqrt{ e }} \displaystyle \frac{e}{x^2+e} dx$
出典:2023年東京理科大学
福田のおもしろ数学207〜不等式の証明と図形的な意味

単元:
#数Ⅱ#微分法と積分法#面積・体積・長さ・速度#面積、体積#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a \geqq b \gt 0,n$ は正の整数とする。
$a^n-b^n \leqq \frac{n}{2}(a-b)(a^{n-1}+b^{n-1})$ であることを証明せよ。
この動画を見る
$a \geqq b \gt 0,n$ は正の整数とする。
$a^n-b^n \leqq \frac{n}{2}(a-b)(a^{n-1}+b^{n-1})$ であることを証明せよ。
#数検準1級-1#定積分#ますただ
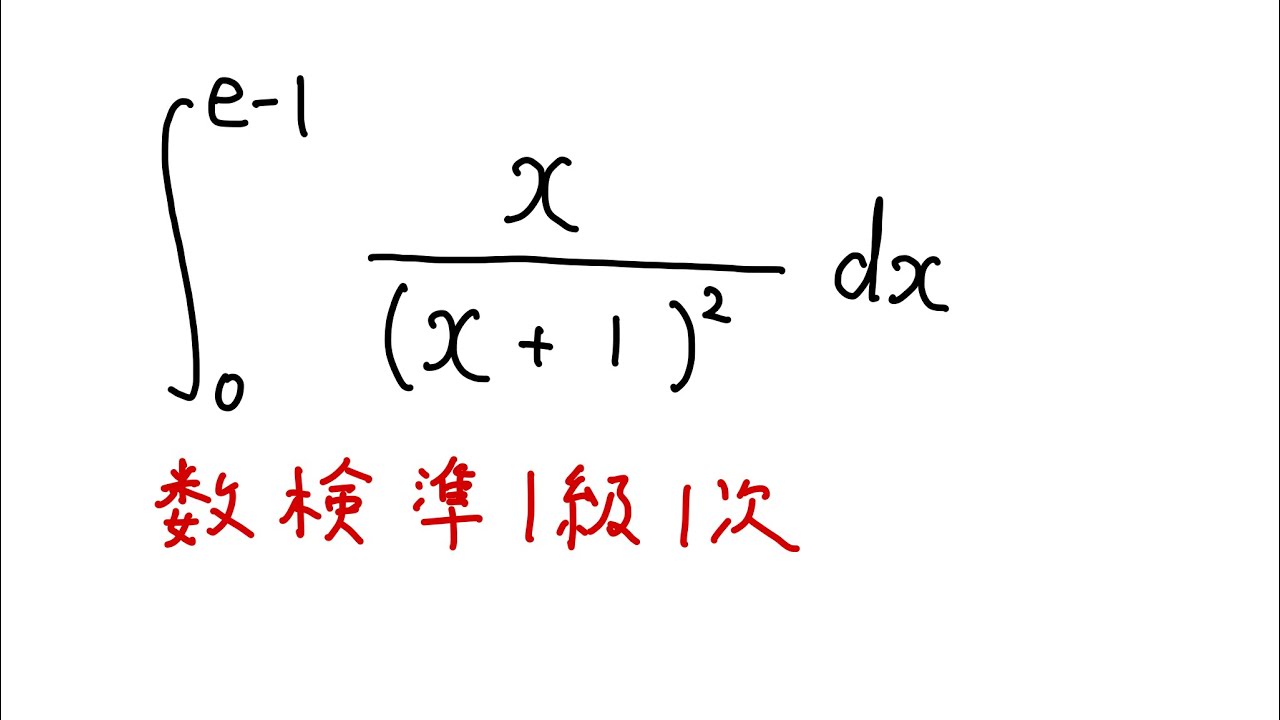
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{e-1} \displaystyle \frac{x}{(x+1)^2} dx$
出典:数検準1級1次
この動画を見る
$\displaystyle \int_{0}^{e-1} \displaystyle \frac{x}{(x+1)^2} dx$
出典:数検準1級1次
#数検準1級1次#極限#ますただ

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 3 } \displaystyle \frac{x-3}{\sqrt{ 3x+7 }-4}$
出典:数検準1級1次
この動画を見る
$\displaystyle \lim_{ x \to 3 } \displaystyle \frac{x-3}{\sqrt{ 3x+7 }-4}$
出典:数検準1級1次
#数学検定準1級2次過去問#69「展開が最短かも」 #定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} x^4(1-x)^4$ $dx$
出典:数検準1級1次
この動画を見る
$\displaystyle \int_{0}^{1} x^4(1-x)^4$ $dx$
出典:数検準1級1次
#数検準1級1次#定積分#ますただ
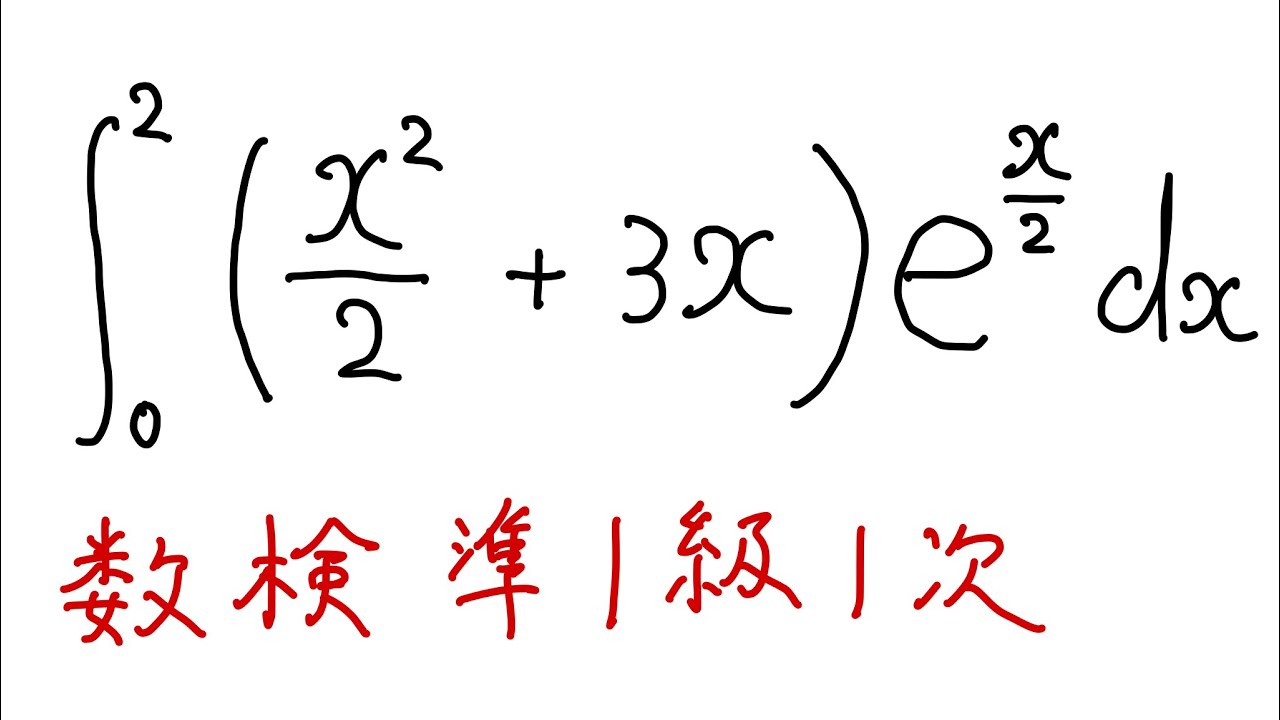
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2} (\displaystyle \frac{x^2}{2}+3x)e^{\frac{x}{2}}dx$
出典:
この動画を見る
$\displaystyle \int_{0}^{2} (\displaystyle \frac{x^2}{2}+3x)e^{\frac{x}{2}}dx$
出典:
#山梨大学2013#定積分#ますただ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#山梨大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-10}^{0} \displaystyle \frac{1}{(x+11)(x+12)}$ $dx$
出典:2013年山梨大学
この動画を見る
$\displaystyle \int_{-10}^{0} \displaystyle \frac{1}{(x+11)(x+12)}$ $dx$
出典:2013年山梨大学
#数検準1級1次過去問#定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{e^2-1} log(x+1)$ $dx$
出典:数検準1級1次
この動画を見る
$\displaystyle \int_{0}^{e^2-1} log(x+1)$ $dx$
出典:数検準1級1次
#福岡大学#不定積分#ますただ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#福岡大学
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ 2x+1 }}$ $dx$
出典:福岡大学
この動画を見る
以下の不定積分を解け
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ 2x+1 }}$ $dx$
出典:福岡大学
#福島大学2013#定積分#ますただ
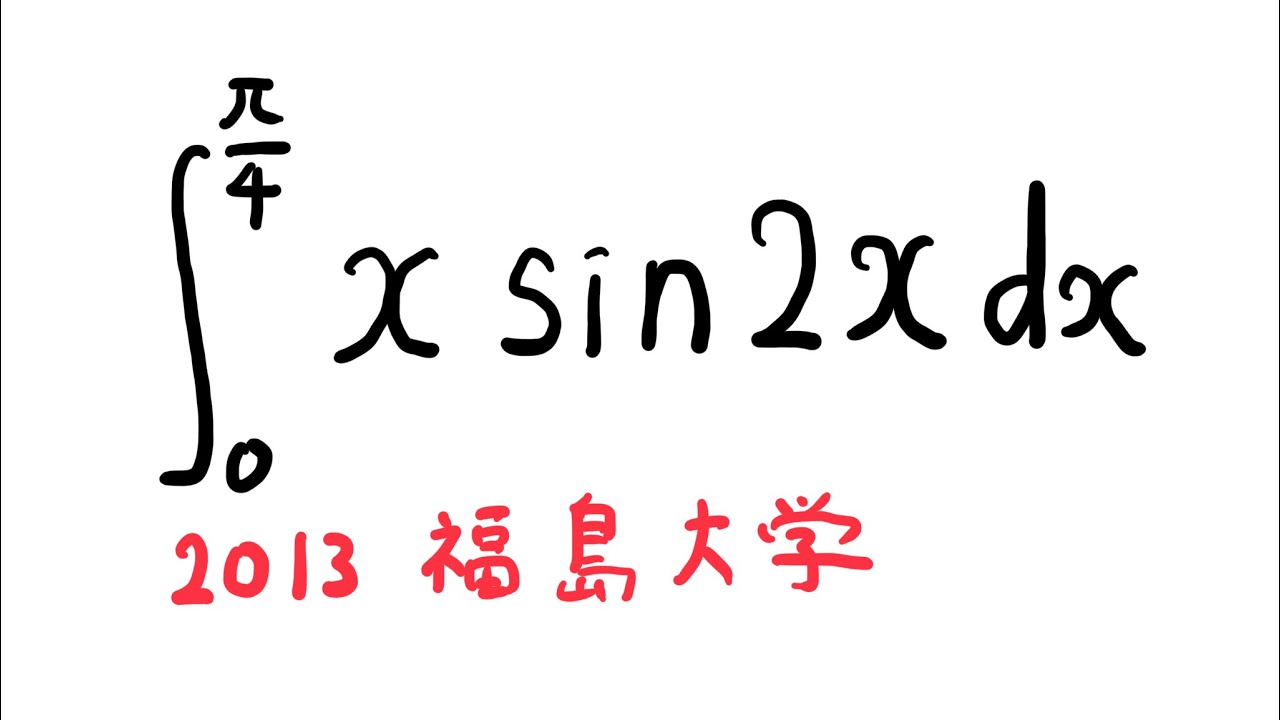
単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}} x$ $\sin2$ $x$ $dx$
出典:2013年福島大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}} x$ $\sin2$ $x$ $dx$
出典:2013年福島大学
#愛媛大学2014#極限#ますただ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#愛媛大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{(\sqrt{ x^2+x+4 }-\sqrt{ x^2+4 })\sin2x}{x^2}$
出典:2024年愛媛大学
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{(\sqrt{ x^2+x+4 }-\sqrt{ x^2+4 })\sin2x}{x^2}$
出典:2024年愛媛大学
大学入試問題#884「ミスれん」 #東京理科大学(2022) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#東京理科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{x-4}{2x^2+5x+2}$ $dx$
出典:2022年東京理科大学
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{x-4}{2x^2+5x+2}$ $dx$
出典:2022年東京理科大学
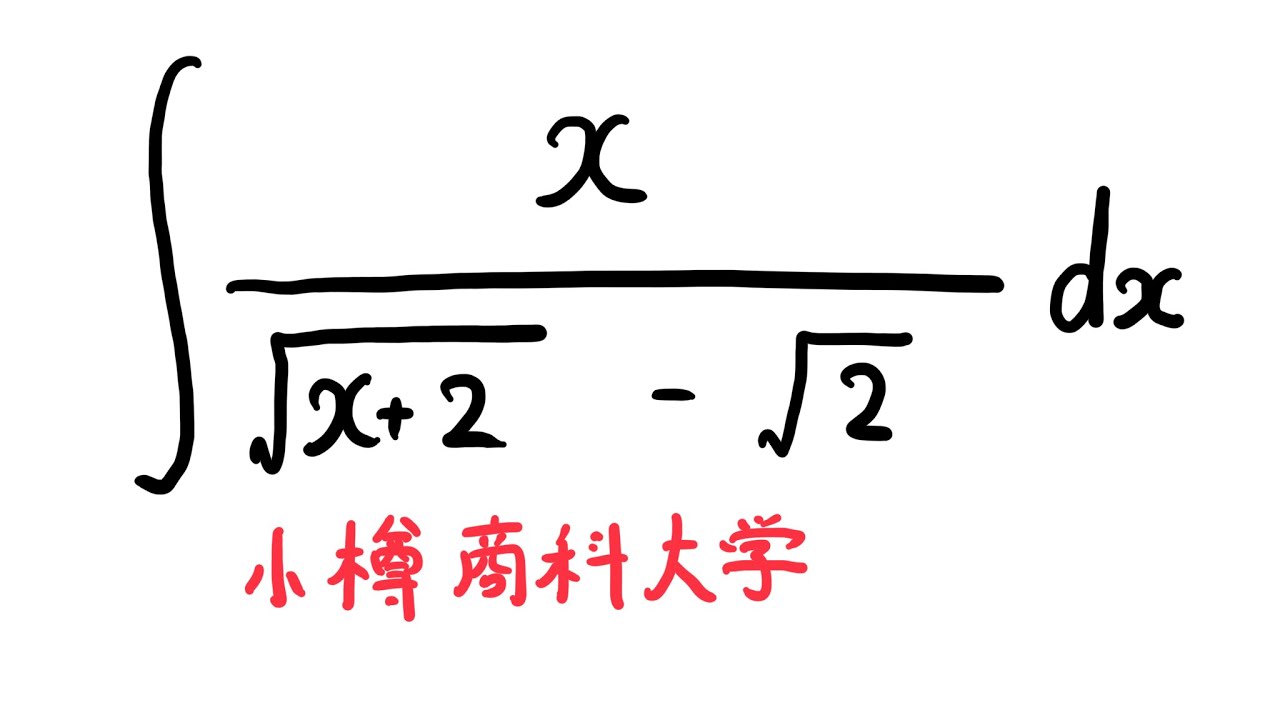
#小樽商科大学#不定積分#ますただ
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#小樽商科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ 2x+2}-\sqrt{ 2 }}$ $dx$
出典:小樽商科大学
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ 2x+2}-\sqrt{ 2 }}$ $dx$
出典:小樽商科大学
【高校数学】数Ⅱ:微分法と積分法:定積分の計算(同じ積分範囲)【NI・SHI・NOがていねいに解説】

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の定積分を求めよ。
$\displaystyle \int_{-2}^{3}(2x^2+4x-3)dx-2 \int_{-2}^{3}(x^2+4x+3)dx$
この動画を見る
次の定積分を求めよ。
$\displaystyle \int_{-2}^{3}(2x^2+4x-3)dx-2 \int_{-2}^{3}(x^2+4x+3)dx$
【高校数学】数Ⅱ:微分法と積分法:定積分の計算(同じ積分範囲)【NI・SHI・NOがていねいに解説】

単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
これを解け.
$\displaystyle \int_{-2}^{3}(2x^2+4x-3)dx-2 \displaystyle \int_{-2}^{3}(x^2+4x+3)dx$
この動画を見る
これを解け.
$\displaystyle \int_{-2}^{3}(2x^2+4x-3)dx-2 \displaystyle \int_{-2}^{3}(x^2+4x+3)dx$
福田の数学〜立教大学2024年経済学部第2問〜接線が作る三角形の面積の最小値

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$p,q$を正の定数とする。座標平面上に放物線$C:y=-x^2$がある。$C$上の点$\mathrm{P}(p,-p^2)$における$C$の接線を$l$,$\mathrm{Q}(q,-q^2)$における$C$の接線を$m$とする。また$l$と$m$の交点を$\mathrm{R}$とする。
(1) $l,m$の方程式をそれぞれ求めよ。
(2) $\mathrm{R}$の座標を$p,q$を用いて表せ。
(3) $\mathrm{Q}$と$l$の距離$d$を$p,q$を用いて表せ。
(4) 三角形$\mathrm{PQR}$の面積$S$を$p,q$を用いて表せ。
(5) $l$と$m$が直交するとき、$q$を$p$を用いて表せ。
(6) $l$と$m$が直交するとき、(4)の$S$の最小値を求めよ。また、そのときの$p$の値を求めよ。
この動画を見る
$p,q$を正の定数とする。座標平面上に放物線$C:y=-x^2$がある。$C$上の点$\mathrm{P}(p,-p^2)$における$C$の接線を$l$,$\mathrm{Q}(q,-q^2)$における$C$の接線を$m$とする。また$l$と$m$の交点を$\mathrm{R}$とする。
(1) $l,m$の方程式をそれぞれ求めよ。
(2) $\mathrm{R}$の座標を$p,q$を用いて表せ。
(3) $\mathrm{Q}$と$l$の距離$d$を$p,q$を用いて表せ。
(4) 三角形$\mathrm{PQR}$の面積$S$を$p,q$を用いて表せ。
(5) $l$と$m$が直交するとき、$q$を$p$を用いて表せ。
(6) $l$と$m$が直交するとき、(4)の$S$の最小値を求めよ。また、そのときの$p$の値を求めよ。
福田の数学〜立教大学2024年経済学部第1問(6)〜定積分で表された関数

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$0 \leqq x \leqq1$ の範囲において $f(x) \geqq 0$ である $2$ 次関数 $f(x) = ax^2+b$ は、等式
$\displaystyle f(x)(\int_0^1f(t)dt) = x^2+5$
を満たす。このとき、定数 $a,b$ は $a=\fbox{ケ}, b=\fbox{コ}$ である。
この動画を見る
$0 \leqq x \leqq1$ の範囲において $f(x) \geqq 0$ である $2$ 次関数 $f(x) = ax^2+b$ は、等式
$\displaystyle f(x)(\int_0^1f(t)dt) = x^2+5$
を満たす。このとき、定数 $a,b$ は $a=\fbox{ケ}, b=\fbox{コ}$ である。
#立教大学2012 #積分方程式

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#立教大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$f(x)=x^2+4x-\displaystyle \int_{0}^{1} f(x)$ $dt$を満たす関数$f(x)$を求めよ。
出典:2012年立教大学
この動画を見る
$f(x)=x^2+4x-\displaystyle \int_{0}^{1} f(x)$ $dt$を満たす関数$f(x)$を求めよ。
出典:2012年立教大学
福田の数学〜慶應義塾大学2024年経済学部第6問〜3次関数の増減と最大値と面積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{6}}$ $a$,$b$,$p$を実数とする。関数$f(x)$=$x^3$+$ax^2$+$bx$+17 は$x$=$p$で極大値、$x$=$-4p$で極小値をとり、$f(-2p)$=-17 を満たすとする。
(1)$a$,$b$,$p$の値、および$f(x)$の極大値$M$、極大値$m$を、それぞれ求めよ。
(2)(1)で求めた$a$,$b$および0≦$t$≦5 を満たす実数$t$に対して、区間0≦$x$≦$t$ における|$f(x)$|の最大値を$g(t)$とする。$t$の値について場合分けをして、それぞれの場合に$g(t)$を求めよ。
(3)(2)で求めた$g(t)$に対して、定積分$I$=$\displaystyle\int_0^5g(t)dt$ を求めよ。
この動画を見る
$\Large{\boxed{6}}$ $a$,$b$,$p$を実数とする。関数$f(x)$=$x^3$+$ax^2$+$bx$+17 は$x$=$p$で極大値、$x$=$-4p$で極小値をとり、$f(-2p)$=-17 を満たすとする。
(1)$a$,$b$,$p$の値、および$f(x)$の極大値$M$、極大値$m$を、それぞれ求めよ。
(2)(1)で求めた$a$,$b$および0≦$t$≦5 を満たす実数$t$に対して、区間0≦$x$≦$t$ における|$f(x)$|の最大値を$g(t)$とする。$t$の値について場合分けをして、それぞれの場合に$g(t)$を求めよ。
(3)(2)で求めた$g(t)$に対して、定積分$I$=$\displaystyle\int_0^5g(t)dt$ を求めよ。
【高校数学】数Ⅱ:微分法と積分法:定積分と面積:1/6公式を用いて曲線で囲まれた図形の面積を求める!【NI・SHI・NOがていねいに解説】

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#面積、体積#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の曲線または直線で囲まれた図形の面積Sを求めよ。
$y=x^2+3x,y=-x^2-x+6$
この動画を見る
次の曲線または直線で囲まれた図形の面積Sを求めよ。
$y=x^2+3x,y=-x^2-x+6$
【高校数学】数Ⅱ:微分法と積分法:定積分と面積:1/6公式を用いて面積を求める!【NI・SHI・NOがていねいに解説】

単元:
#数Ⅱ#微分法と積分法#面積、体積#数学(高校生)
教材:
#PRIME数学#PRIME数学Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の曲線または直線で囲まれた図形の面積$S$を求めよ。
$y=x^2-3x,y=2x$
この動画を見る
次の曲線または直線で囲まれた図形の面積$S$を求めよ。
$y=x^2-3x,y=2x$
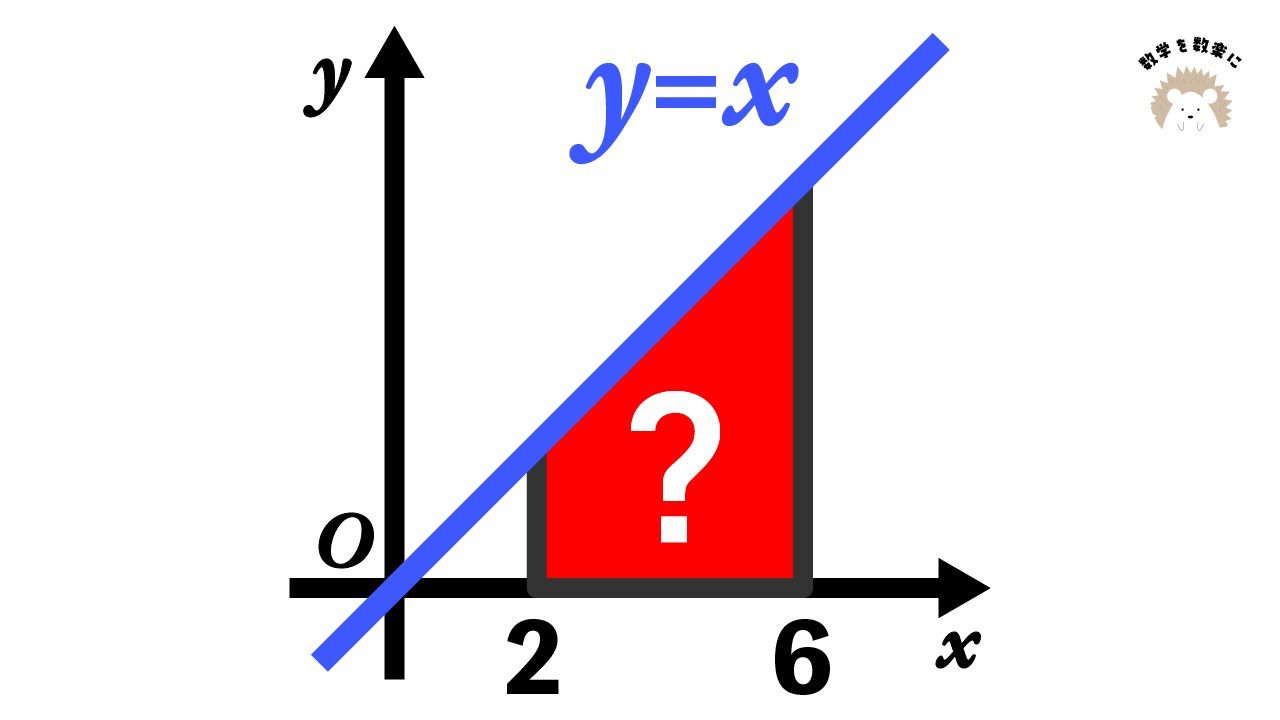
たまには、こんなふうに解いても良いでしょうか?関数と面積
福田の数学〜九州大学2024年文系第1問〜2つの放物線と共通接線で囲まれる図形の面積

単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 2つの放物線
$C_1:y=2x^2$, $C_2:y=2x^2-8x+16$
の両方に接する直線を$l$とする。以下の問いに答えよ。
(1)直線$l$の方程式を求めよ。
(2)2つの放物線$C_1$, $C_2$と直線$l$で囲まれた図形の面積を求めよ。
この動画を見る
$\Large\boxed{1}$ 2つの放物線
$C_1:y=2x^2$, $C_2:y=2x^2-8x+16$
の両方に接する直線を$l$とする。以下の問いに答えよ。
(1)直線$l$の方程式を求めよ。
(2)2つの放物線$C_1$, $C_2$と直線$l$で囲まれた図形の面積を求めよ。
福田の数学〜九州大学2024年理系第1問〜空間における三角形の面積の最大値

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#九州大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ $a$を実数とし、座標空間内の3点P(-1,1,-1), Q(1,1,1), R($a$, $a^2$, $a^3$)を考える。以下の問いに答えよ。
(1)$a$≠-1, $a$≠1 のとき、3点P,Q,Rは一直線上にないことを示せ。
(2)$a$が-1<$a$<1 の範囲を動くとき、三角形PQRの面積の最大値を求めよ。
この動画を見る
$\Large\boxed{1}$ $a$を実数とし、座標空間内の3点P(-1,1,-1), Q(1,1,1), R($a$, $a^2$, $a^3$)を考える。以下の問いに答えよ。
(1)$a$≠-1, $a$≠1 のとき、3点P,Q,Rは一直線上にないことを示せ。
(2)$a$が-1<$a$<1 の範囲を動くとき、三角形PQRの面積の最大値を求めよ。
【高校数学】三角関数を用いる積分(応用編)【数学のコツ】

