 数Ⅱ
数Ⅱ
 数Ⅱ
数Ⅱ
どっちがでかい?僅差!

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2^{\sqrt{5}}と3^{\sqrt{2}}ではどちらが大きいか?$
この動画を見る
$2^{\sqrt{5}}と3^{\sqrt{2}}ではどちらが大きいか?$
福田の数学〜京都大学2023年理系第1問(2)〜整式の割り算と余り

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 問2 整式$x^{2023}$-1 を整式$x^4$+$x^3$+$x^2$+$x$+1 で割った時の余りを求めよ。
2023京都大学理系過去問
この動画を見る
$\Large\boxed{1}$ 問2 整式$x^{2023}$-1 を整式$x^4$+$x^3$+$x^2$+$x$+1 で割った時の余りを求めよ。
2023京都大学理系過去問
【高校数学】恒等式の問題演習~係数比較法と数値代入法を分かりやすく~ 1-7.5【数学Ⅱ】

単元:
#数Ⅱ#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
等式$x^3+5x^2+4x-4=(x+1)^3+p(x+1)^2+q(x+1)+r$が$x$についての恒等式となるように、定数$p,q,r$の値を求めよ
この動画を見る
等式$x^3+5x^2+4x-4=(x+1)^3+p(x+1)^2+q(x+1)+r$が$x$についての恒等式となるように、定数$p,q,r$の値を求めよ
福田の数学〜東京大学2023年文系第4問〜四面体の体積

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#図形と方程式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 半径1の球面上の相異なる4点A,B,C,Dが
AB=1, AC=BC, AD=BD, $\cos\angle ACB$=$\cos\angle ADB$=$\displaystyle\frac{4}{5}$
を満たしているとする。
(1)三角形ABCの面積を求めよ。
(2)四角形ABCDの体積を求めよ。
2023東京大学文系過去問
この動画を見る
$\Large\boxed{4}$ 半径1の球面上の相異なる4点A,B,C,Dが
AB=1, AC=BC, AD=BD, $\cos\angle ACB$=$\cos\angle ADB$=$\displaystyle\frac{4}{5}$
を満たしているとする。
(1)三角形ABCの面積を求めよ。
(2)四角形ABCDの体積を求めよ。
2023東京大学文系過去問
【高校数学】恒等式とは?分かりやすく~どこよりも丁寧に~ 1-7【数学Ⅱ】

【数Ⅱ】図形と方程式:円:円と方程式:円上の点Pにおける接線の方程式を求めよ。例題付き!
単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
教材:
#PRIME数学#PRIME数学Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
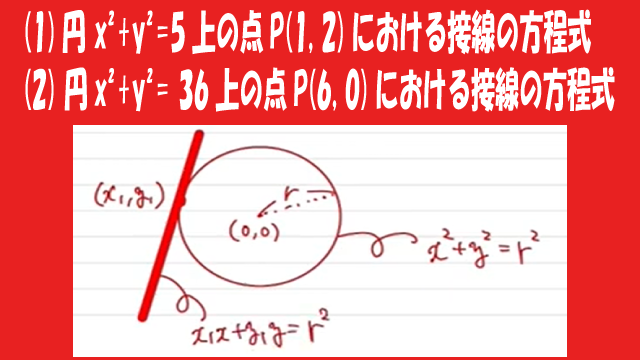
円上の点における接線の方程式の求め方を解説!実際に
(1)円 x²+y²=5上の点P(1, 2)における接線の方程式、
(2) 円x²+y²= 36上の点P(6, 0)における接線の方程式
も求めます。
この動画を見る
円上の点における接線の方程式の求め方を解説!実際に
(1)円 x²+y²=5上の点P(1, 2)における接線の方程式、
(2) 円x²+y²= 36上の点P(6, 0)における接線の方程式
も求めます。
【数Ⅱ】図形と方程式:円と方程式 円上の点Pにおける接線の方程式を求めよ。例題付き!

単元:
#数Ⅱ#図形と方程式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
円上の点における接線の方程式の求め方を解説!実際に(1)円$x^2+y^2=5$上の点P(1, 2)における接線の方程式、(2) 円$x^2+y^2= 36$上の点P(6, 0)における接線の方程式 も求めます。
この動画を見る
円上の点における接線の方程式の求め方を解説!実際に(1)円$x^2+y^2=5$上の点P(1, 2)における接線の方程式、(2) 円$x^2+y^2= 36$上の点P(6, 0)における接線の方程式 も求めます。
【数Ⅱ】図形と方程式:円:円と方程式:円の外にある点から、円に接するような直線を引け!

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
教材:
#PRIME数学#PRIME数学Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
点(2, 6)を通り,円x²+y²=20 に接する直線の方程式を求めよ。
この動画を見る
点(2, 6)を通り,円x²+y²=20 に接する直線の方程式を求めよ。
【数Ⅱ】図形と方程式:円と方程式 円の外にある点から、円に接するような直線を引け!

【数Ⅱ】図形と方程式:円:円と方程式:円x²+y²=5と直線 2x+1=2の2つの交点を結ぶ線分の長さlを求めよ。
単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
教材:
#PRIME数学#PRIME数学Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
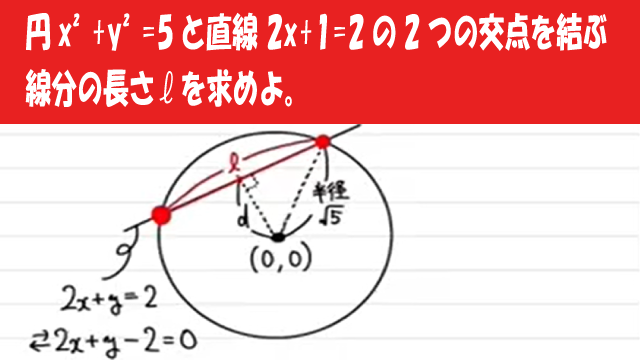
【数Ⅱ】図形と方程式:円:円と方程式:円x²+y²=5と直線 2x+1=2の2つの交点を結ぶ線分の長さlを求めよ。
この動画を見る
【数Ⅱ】図形と方程式:円:円と方程式:円x²+y²=5と直線 2x+1=2の2つの交点を結ぶ線分の長さlを求めよ。
【数Ⅱ】図形と方程式:円と方程式 円x^2+y^2=5と直線 2x+1=2の2つの交点を結ぶ線分の長さlを求めよ。
単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
円$x^2+y^2=5$と直線 $2x+1=2$の2つの交点を結ぶ線分の長さlを求めよ。
この動画を見る
円$x^2+y^2=5$と直線 $2x+1=2$の2つの交点を結ぶ線分の長さlを求めよ。
福田の数学〜東京大学2023年文系第2問〜定積分で表された関数と最大最小

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#点と直線#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#不定積分・定積分#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 座標平面上の放物線y=3$x^2$-4xをCとおき、直線y=2xをlとおく。実数tに対し、C上の点P(t, $3t^2-4t$)とlの距離をf(t)とする。
(1)-1≦a≦2の範囲の実数aに対し、定積分
g(a)=$\displaystyle\int_{-1}^af(t)dt$
を求めよ。
(2)aが0≦a≦2の範囲を動くとき、g(a)-f(a)の最大値および最小値を求めよ。
2023東京大学文系過去問
この動画を見る
$\Large\boxed{2}$ 座標平面上の放物線y=3$x^2$-4xをCとおき、直線y=2xをlとおく。実数tに対し、C上の点P(t, $3t^2-4t$)とlの距離をf(t)とする。
(1)-1≦a≦2の範囲の実数aに対し、定積分
g(a)=$\displaystyle\int_{-1}^af(t)dt$
を求めよ。
(2)aが0≦a≦2の範囲を動くとき、g(a)-f(a)の最大値および最小値を求めよ。
2023東京大学文系過去問
2023年京大数学!整式の割り算!2通りで解説します【京都大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
整式$x^{2023}-1$を整式$x^{4}+x^{3}+x^{2}+x+1$で割ったときの余りを求めよ。
京都大過去問
この動画を見る
整式$x^{2023}-1$を整式$x^{4}+x^{3}+x^{2}+x+1$で割ったときの余りを求めよ。
京都大過去問
福田の数学〜東京大学2023年理系第5問〜整式の割り算と2重因子をもつ条件

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#複素数と方程式#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#剰余の定理・因数定理・組み立て除法と高次方程式#微分とその応用#微分法#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 整式f(x)=$(x-1)^2(x-2)$を考える。
(1)g(x)を実数を係数とする整式とし、g(x)をf(x)で割った余りをr(x)とおく。
$g(x)^7$をf(x)で割った余りと$r(x)^7$をf(x)で割った余りが等しいことを示せ。
(2)a,bを実数とし、h(x)=$x^2$+ax+b とおく。$h(x)^7$をf(x)で割った余りを$h_1(x)$とおき、$h_1(x)^7$をf(x)で割った余りを$h_2(x)$とおく。$h_2(x)$がh(x)に等しくなるようなa,bの組を全て求めよ。
2023東京大学理系過去問
この動画を見る
$\Large\boxed{5}$ 整式f(x)=$(x-1)^2(x-2)$を考える。
(1)g(x)を実数を係数とする整式とし、g(x)をf(x)で割った余りをr(x)とおく。
$g(x)^7$をf(x)で割った余りと$r(x)^7$をf(x)で割った余りが等しいことを示せ。
(2)a,bを実数とし、h(x)=$x^2$+ax+b とおく。$h(x)^7$をf(x)で割った余りを$h_1(x)$とおき、$h_1(x)^7$をf(x)で割った余りを$h_2(x)$とおく。$h_2(x)$がh(x)に等しくなるようなa,bの組を全て求めよ。
2023東京大学理系過去問
福田の数学〜東京工業大学2023年理系第5問(PART1)〜4直線に接する球面の決定

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#図形と方程式#点と直線#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ xyz空間の4点A(1,0,0), B(1,1,1), C(-1,1,-1), D(-1,0,0)を考える。
(1)2直線AB,BCから等距離にある点全体のなす図形を求めよ。
(2)4直線AB, BC, CD, DAに共に接する球面の中心と半径の組を全て求めよ。
2023東京工業大学理系過去問
この動画を見る
$\Large\boxed{5}$ xyz空間の4点A(1,0,0), B(1,1,1), C(-1,1,-1), D(-1,0,0)を考える。
(1)2直線AB,BCから等距離にある点全体のなす図形を求めよ。
(2)4直線AB, BC, CD, DAに共に接する球面の中心と半径の組を全て求めよ。
2023東京工業大学理系過去問
【高校数学】繫分数式の計算~どこよりも分かりやすく丁寧に~ 1-6【数学Ⅱ】

福田の数学〜東京大学2023年理系第3問〜円と放物線と切り取られる弦の長さ

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#円と方程式#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ aを実数とし、座標平面上の点(0,a)を中心とする半径1の円の周をCとする。
(1)Cが不等式$y>x^2$の表す領域に含まれるようなaの範囲を求めよ。
(2)aは(1)で求めた範囲にあるとする。Cのうちx≧0かつy<aを満たす部分をSとする。S上の点Pに対し、点PでのCの接線が放物線$y=x^2$によって切り取られてできる線分の長さを$L_P$とする。$L_Q$=$L_R$となるS上の相異なる2点Q, Rが存在するようなaの範囲を求めよ。
2023東京大学理系過去問
この動画を見る
$\Large\boxed{3}$ aを実数とし、座標平面上の点(0,a)を中心とする半径1の円の周をCとする。
(1)Cが不等式$y>x^2$の表す領域に含まれるようなaの範囲を求めよ。
(2)aは(1)で求めた範囲にあるとする。Cのうちx≧0かつy<aを満たす部分をSとする。S上の点Pに対し、点PでのCの接線が放物線$y=x^2$によって切り取られてできる線分の長さを$L_P$とする。$L_Q$=$L_R$となるS上の相異なる2点Q, Rが存在するようなaの範囲を求めよ。
2023東京大学理系過去問
大学入試問題#467「基本すぎる極限問題」 電気通信大学(2013) #極限

単元:
#大学入試過去問(数学)#三角関数#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{(1-\cos2x)\sin3x}{x^3}$
出典:2013年電気通信大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{(1-\cos2x)\sin3x}{x^3}$
出典:2013年電気通信大学 入試問題
気持ちいい別解あり!これ解ける?【京都大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$a,b,c$を正の数とするとき、不等式
$2\left( -\frac{a+b}{2}-\sqrt{ab}\right)≦3\left(\frac{a+b+c}{2}-\sqrt[3]{abc}\right)$
を証明せよ。
また、等号が成立するのはどんな場合か。
京都大過去問
この動画を見る
$a,b,c$を正の数とするとき、不等式
$2\left( -\frac{a+b}{2}-\sqrt{ab}\right)≦3\left(\frac{a+b+c}{2}-\sqrt[3]{abc}\right)$
を証明せよ。
また、等号が成立するのはどんな場合か。
京都大過去問
大学入試問題#466「絶対に知っておくべき解き方」 電気通信大学(2014) #極限

単元:
#大学入試過去問(数学)#三角関数#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 1 } \displaystyle \frac{x^2log(x+1)-log\ 2}{x-1}$
出典:2014年電気通信大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 1 } \displaystyle \frac{x^2log(x+1)-log\ 2}{x-1}$
出典:2014年電気通信大学 入試問題
福田の数学〜東京大学2023年文系数学第1問〜解と係数の関係と最小値

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#解と判別式・解と係数の関係#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ kを正の実数とし、2次方程式$x^2+x-k$=0 の2つの実数解をα,βとする。
kがk>2の範囲を動くとき、
$\displaystyle\frac{\alpha^3}{1-\beta}$+$\displaystyle\frac{\beta^3}{1-\alpha}$
の最小値を求めよ。
2023東京大学文系過去問
この動画を見る
$\Large\boxed{1}$ kを正の実数とし、2次方程式$x^2+x-k$=0 の2つの実数解をα,βとする。
kがk>2の範囲を動くとき、
$\displaystyle\frac{\alpha^3}{1-\beta}$+$\displaystyle\frac{\beta^3}{1-\alpha}$
の最小値を求めよ。
2023東京大学文系過去問
大学入試問題#465「よくある極限問題」 電気通信大学2009 #極限

単元:
#大学入試過去問(数学)#三角関数#数列の極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sin2x-2\sin\ x}{x\ \sin^2\ x}$
出典:2009年電気通信大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sin2x-2\sin\ x}{x\ \sin^2\ x}$
出典:2009年電気通信大学 入試問題
【高校数学】むやみに代入するな!因数定理のちょっとした裏技! #Shorts

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
因数分解せよ。
$x^3+6x^2-6x+7$
この動画を見る
因数分解せよ。
$x^3+6x^2-6x+7$
2023京都大学 正五角形の一辺の長さ
単元:
#数Ⅱ#三角関数#三角関数とグラフ#加法定理とその応用
指導講師:
鈴木貫太郎
問題文全文(内容文):
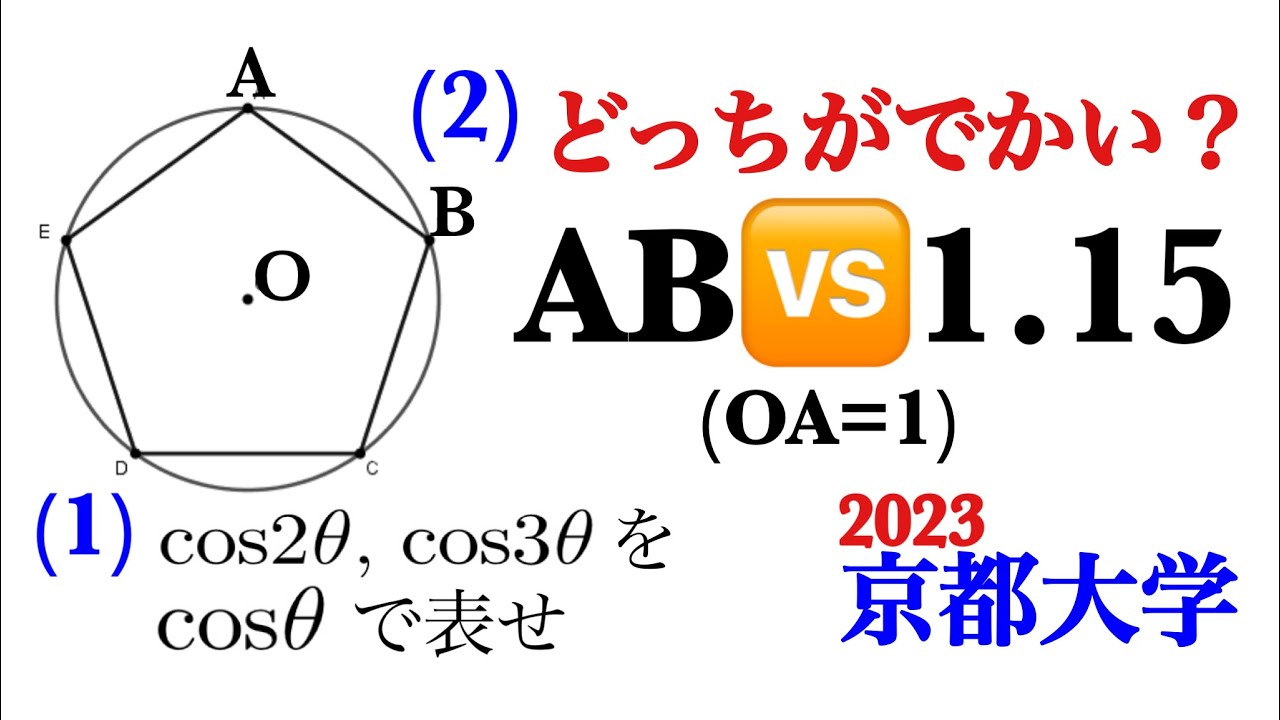
(1)$\cos2\theta,\cos3\theta$を$\cos\theta$を用いて表せ.
(2)半径1の円に内接する正五角形の一辺の長さと1.15の大小比較せよ.
2023京都大過去問
この動画を見る
(1)$\cos2\theta,\cos3\theta$を$\cos\theta$を用いて表せ.
(2)半径1の円に内接する正五角形の一辺の長さと1.15の大小比較せよ.
2023京都大過去問
【高校数学】分数式の計算~どこよりも分かりやすく丁寧に~ 1-5【数学Ⅱ】

福田の1.5倍速演習〜合格する重要問題091〜大阪大学2018年度理系第1問〜不等式の証明と関数の値域

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 次の問に答えよ。
(1)x>0の範囲で不等式
x-$\frac{x^2}{2}$<$\log(1+x)$<$\frac{x}{\sqrt{1+x}}$
が成り立つことを示せ。
(2)xがx>0の範囲を動くとき、
y=$\frac{1}{\log(1+x)}$-$\frac{1}{x}$
のとりうる値の範囲を求めよ。
2018大阪大学理系過去問
この動画を見る
$\Large\boxed{1}$ 次の問に答えよ。
(1)x>0の範囲で不等式
x-$\frac{x^2}{2}$<$\log(1+x)$<$\frac{x}{\sqrt{1+x}}$
が成り立つことを示せ。
(2)xがx>0の範囲を動くとき、
y=$\frac{1}{\log(1+x)}$-$\frac{1}{x}$
のとりうる値の範囲を求めよ。
2018大阪大学理系過去問
2変数関数の値域 日大
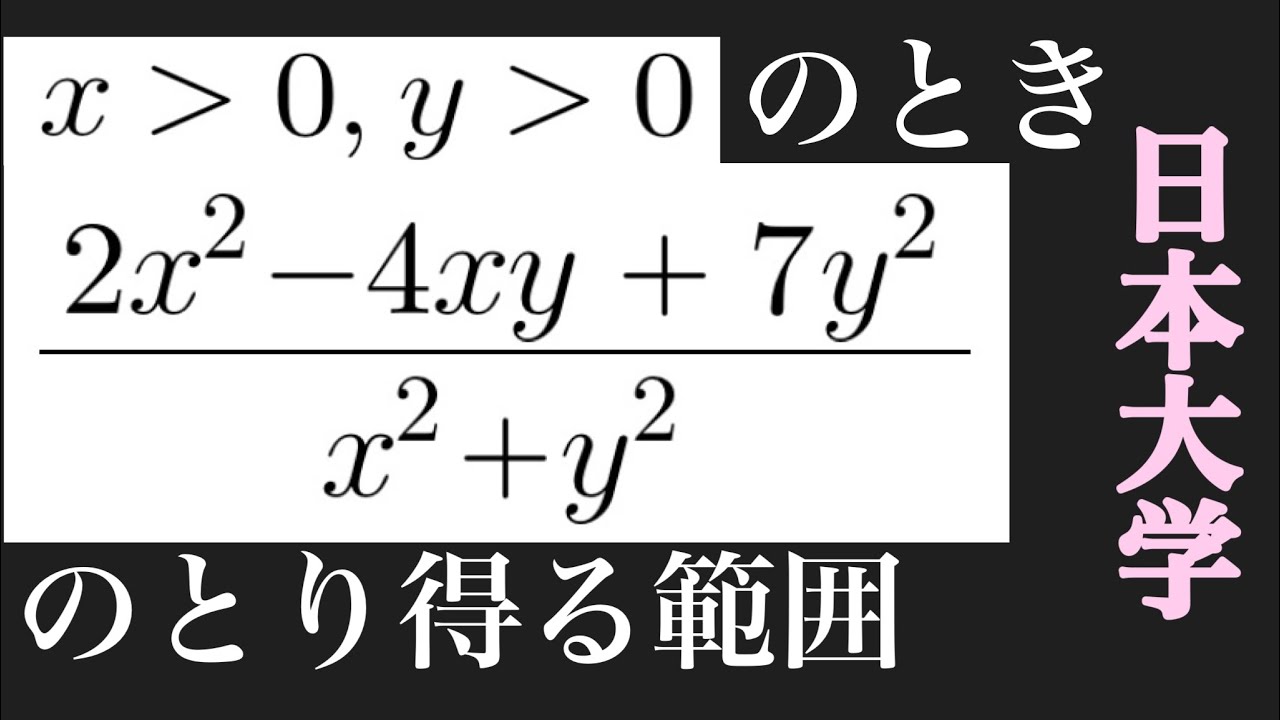
単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#日本大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x\gt 0,y \gt 0$において$\dfrac{2x^2-4xy+7y^2}{x^2+y^2}$のとり得る範囲を求めよ.
日大過去問
この動画を見る
$x\gt 0,y \gt 0$において$\dfrac{2x^2-4xy+7y^2}{x^2+y^2}$のとり得る範囲を求めよ.
日大過去問
大学入試問題#458「これはさすがに落とせない!」 横浜国立大学(2000) #定積分

単元:
#大学入試過去問(数学)#対数関数#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{2} \displaystyle \frac{log\ x}{(1+x)^2} dx$
出典:2000年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{2} \displaystyle \frac{log\ x}{(1+x)^2} dx$
出典:2000年横浜国立大学 入試問題
浜松医大 対数の基本 数3不要

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)2進法で30桁の自然数nを10進法で表すと何桁か,
$\log_{10}=0.3010$
(2)自然数nを2進法で表すと$a_n$桁となる.
$\displaystyle \lim_{ n \to \(x) } \dfrac{\log_{10}n}{a_n}$を求めよ.
浜松医大過去問
この動画を見る
(1)2進法で30桁の自然数nを10進法で表すと何桁か,
$\log_{10}=0.3010$
(2)自然数nを2進法で表すと$a_n$桁となる.
$\displaystyle \lim_{ n \to \(x) } \dfrac{\log_{10}n}{a_n}$を求めよ.
浜松医大過去問
福田の1.5倍速演習〜合格する重要問題088〜一橋大学2018年度文系第4問〜四面体の体積の最大

単元:
#数Ⅱ#大学入試過去問(数学)#空間ベクトル#図形と方程式#軌跡と領域#空間ベクトル#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ p,qを正の実数とする。原点をOとする座標空間内の3点P(p,0,0), Q(0,q,0), R(0,0,1)は$\angle$PRQ=$\frac{\pi}{6}$を満たす。四面体OPQRの体積の最大値を求めよ。
2018一橋大学文系過去問
この動画を見る
$\Large\boxed{4}$ p,qを正の実数とする。原点をOとする座標空間内の3点P(p,0,0), Q(0,q,0), R(0,0,1)は$\angle$PRQ=$\frac{\pi}{6}$を満たす。四面体OPQRの体積の最大値を求めよ。
2018一橋大学文系過去問
