 数Ⅱ
数Ⅱ
 数Ⅱ
数Ⅱ
【因数定理】コツがあるんです【数学 解説動画】

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
次の式を因数分解せよ。
(1)$x^3+4x^2-6x-27$
(2)$x^3+6x^2-6x+7$
この動画を見る
次の式を因数分解せよ。
(1)$x^3+4x^2-6x-27$
(2)$x^3+6x^2-6x+7$
下4桁!でも簡単

cos1°は有理数か【数学 入試問題】【チェビシェフ多項式】

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#集合と命題(集合・命題と条件・背理法)#三角関数#加法定理とその応用#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学#数B
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(1)$n$を自然数とする。
$cos(n+2)\theta+cos n\theta=2cos(n+1)\theta cos\theta$を示せ。
(2)自然数$n$に対し、$cosn\theta=T_n(cos\theta)$を満たす整数係数の$n$次の整式$T_n(x)$が存在することを示せ。
(3)$cos1°$が無理数であることを証明せよ。
数学入試問題過去問
この動画を見る
(1)$n$を自然数とする。
$cos(n+2)\theta+cos n\theta=2cos(n+1)\theta cos\theta$を示せ。
(2)自然数$n$に対し、$cosn\theta=T_n(cos\theta)$を満たす整数係数の$n$次の整式$T_n(x)$が存在することを示せ。
(3)$cos1°$が無理数であることを証明せよ。
数学入試問題過去問
【有名問題】京都大学の伝説の問題です【数学 入試問題】

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#集合と命題(集合・命題と条件・背理法)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$ tan1°$は有理数か?
数学入試問題過去問
この動画を見る
$ tan1°$は有理数か?
数学入試問題過去問
福田の数学〜名古屋大学2022年文系第3問〜放物線と放物線で囲まれた面積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#名古屋大学
指導講師:
福田次郎
問題文全文(内容文):
a,bを実数とし、放物線$y=\frac{1}{2}x^2$を$C_1$、放物線$y=-(x-a)^2+b$を$C_2$とする。
(1)$C_1$と$C_2$が異なる2点で交わるためのa,bの条件を求めよ。
以下、$C_1$と$C_2$は異なる2点で交わるとし、$C_1$と$C_2$で囲まれた図形の面積をSとする。
(2)$S=16$となるためのa,bの条件を求めよ。
(3)a,bは$b \leqq a+3$を満たすとする。このときSの最大値を求めよ。
2022名古屋大学文系過去問
この動画を見る
a,bを実数とし、放物線$y=\frac{1}{2}x^2$を$C_1$、放物線$y=-(x-a)^2+b$を$C_2$とする。
(1)$C_1$と$C_2$が異なる2点で交わるためのa,bの条件を求めよ。
以下、$C_1$と$C_2$は異なる2点で交わるとし、$C_1$と$C_2$で囲まれた図形の面積をSとする。
(2)$S=16$となるためのa,bの条件を求めよ。
(3)a,bは$b \leqq a+3$を満たすとする。このときSの最大値を求めよ。
2022名古屋大学文系過去問
きっと良問

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
P(x)はxの3次式でP(11)=11,P(12)=12,P(13)=14,P(14)=15である.
P(15)のときはいくつであるか求めよ.
この動画を見る
P(x)はxの3次式でP(11)=11,P(12)=12,P(13)=14,P(14)=15である.
P(15)のときはいくつであるか求めよ.
指数。雑談:チャンネル登録しているかどうか。

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$2^{\frac{5}{2}} \times 3^{\frac{3}{2}} \times 6^{\frac{1}{2}}$
を計算せよ
この動画を見る
$2^{\frac{5}{2}} \times 3^{\frac{3}{2}} \times 6^{\frac{1}{2}}$
を計算せよ
【良問】数IIの知識で解けます【山形大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#三角関数#点と直線#円と方程式#加法定理とその応用#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#山形大学#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$T=\dfrac{sin\theta cos\theta}{1+sin^2\theta}$とする。
$\theta$が$0<\theta<\dfrac{\pi}{2}$の範囲を動くとき、$T$の最大値を求めよ。
山形大過去問
この動画を見る
$T=\dfrac{sin\theta cos\theta}{1+sin^2\theta}$とする。
$\theta$が$0<\theta<\dfrac{\pi}{2}$の範囲を動くとき、$T$の最大値を求めよ。
山形大過去問
格子点を通るということは?【山口大学】【数学 入試問題】
単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#集合と命題(集合・命題と条件・背理法)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#数学(高校生)#山口大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
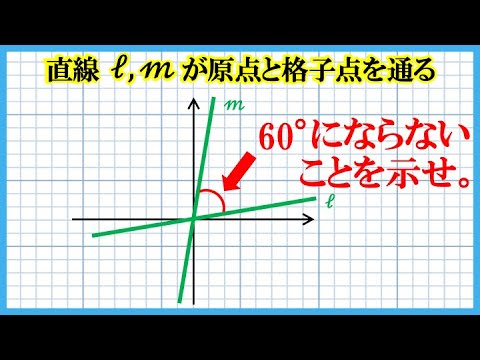
座標平面上で、$x$座標,$y$座標が共に整数である点を格子点という。
原点を通る2直線$l,m$がそれぞれ原点以外にも格子点を通るとき、
$l,m$のなす角は、$60°$にならないことを証明せよ。
ただし、$\sqrt3$が無理数であることを証明なしに用いても良い。
山口大過去問
この動画を見る
座標平面上で、$x$座標,$y$座標が共に整数である点を格子点という。
原点を通る2直線$l,m$がそれぞれ原点以外にも格子点を通るとき、
$l,m$のなす角は、$60°$にならないことを証明せよ。
ただし、$\sqrt3$が無理数であることを証明なしに用いても良い。
山口大過去問
中国Jr 数学Olympic あっと驚く解法も

単元:
#数学検定・数学甲子園・数学オリンピック等#式と証明#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^5=1,x \neq 1$とするとき,
$\dfrac{x}{1+x^2}+\dfrac{x^2}{1+x^4}+\dfrac{x^3}{1+x^6}+\dfrac{x^4}{1+x^8}$の値を求めよ.
中国jr数学オリンピック過去問
この動画を見る
$ x^5=1,x \neq 1$とするとき,
$\dfrac{x}{1+x^2}+\dfrac{x^2}{1+x^4}+\dfrac{x^3}{1+x^6}+\dfrac{x^4}{1+x^8}$の値を求めよ.
中国jr数学オリンピック過去問
福田の数学〜大阪大学2022年理系第3問〜線分の通過範囲

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
正の実数tに対し、座標平面上の2点$P(0,t)$と$Q(\frac{1}{t},0)$を考える。
tが$1 \leqq t \leqq 2$の範囲を動くとき、座標平面内で線分PQが通過する部分を図示せよ。
2022大阪大学理系過去問
この動画を見る
正の実数tに対し、座標平面上の2点$P(0,t)$と$Q(\frac{1}{t},0)$を考える。
tが$1 \leqq t \leqq 2$の範囲を動くとき、座標平面内で線分PQが通過する部分を図示せよ。
2022大阪大学理系過去問
簡単な問題

単元:
#数A#数Ⅱ#複素数と方程式#整数の性質#約数・倍数・整数の割り算と余り・合同式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \omega=1(\omega \neq 1)$であり,
$x=a+b $
$y=a\omega+b\omega^2 $
$z=a\omega^2+b\omega $である.
$ x^3+y^3+z^3$の値をa,bで表せ.
この動画を見る
$ \omega=1(\omega \neq 1)$であり,
$x=a+b $
$y=a\omega+b\omega^2 $
$z=a\omega^2+b\omega $である.
$ x^3+y^3+z^3$の値をa,bで表せ.
【数学Ⅱ/高2の予習】二項定理の基本
単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の式の展開式を求めよ
$(x+3)^4$
この動画を見る
次の式の展開式を求めよ
$(x+3)^4$
円周率の証明問題【2010年大分大学】

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#大分大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
円周率$\pi$に関して次の不等式が成立することを証明せよ。
ただし、数値$\pi=3.141592・・・$を使用して直接比較する解答は0点とする。
$3\sqrt6-3\sqrt2<\pi<24-12\sqrt3$
2010大分大過去問
この動画を見る
円周率$\pi$に関して次の不等式が成立することを証明せよ。
ただし、数値$\pi=3.141592・・・$を使用して直接比較する解答は0点とする。
$3\sqrt6-3\sqrt2<\pi<24-12\sqrt3$
2010大分大過去問
福田の数学〜一橋大学2022年文系第4問〜立方体の内部の点と結んだ線分の通過範囲

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
tを実数とし、座標空間に点$A(t-1,t,t+1)$をとる。また、(0,0,0),(1,0,0),
(0,1,0),(1,1,0),(0,0,1),(1,0,1),(0,1,1),(1,1,1)を頂点とする立方体を
Dとする。点PがDの内部及びすべての面上を動くとき、線分APの動く範囲を
Wとし、Wの体積をf(t)とする。
(1)f(-1)を求めよ。
(2)f(t)のグラフを描き、f(t)の最小値を求めよ。
2022一橋大学文系過去問
この動画を見る
tを実数とし、座標空間に点$A(t-1,t,t+1)$をとる。また、(0,0,0),(1,0,0),
(0,1,0),(1,1,0),(0,0,1),(1,0,1),(0,1,1),(1,1,1)を頂点とする立方体を
Dとする。点PがDの内部及びすべての面上を動くとき、線分APの動く範囲を
Wとし、Wの体積をf(t)とする。
(1)f(-1)を求めよ。
(2)f(t)のグラフを描き、f(t)の最小値を求めよ。
2022一橋大学文系過去問
2分で解ける問題

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^2+\dfrac{1}{x^2}=\sqrt2 $のとき,$ x^{2022}+\dfrac{1}{x^{2022}}$の値を求めよ.
この動画を見る
$ x^2+\dfrac{1}{x^2}=\sqrt2 $のとき,$ x^{2022}+\dfrac{1}{x^{2022}}$の値を求めよ.
二項定理を使ってあることに気付ける?【2017年一橋大学】

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#式の計算(整式・展開・因数分解)#恒等式・等式・不等式の証明#数列#漸化式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数B
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$ P(0)=1,P(x+1)-P(x)=2x$を満たす整式$P(x)$を求めよ。
2017一橋大過去問
この動画を見る
$ P(0)=1,P(x+1)-P(x)=2x$を満たす整式$P(x)$を求めよ。
2017一橋大過去問
中山廉人の数学力を鈴木貫太郎がチェック

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
Morite2 English Channel
問題文全文(内容文):
鈴木貫太郎先生が、「指数対数」と「対数関数」の基本を解説します。
公式や定義を確認しましょう。
この動画を見る
鈴木貫太郎先生が、「指数対数」と「対数関数」の基本を解説します。
公式や定義を確認しましょう。
福田の数学〜大阪大学2022年理系第2問〜三角関数と論証

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#推理と論証#推理と論証#大阪大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\alpha=\frac{2\pi}{7}$とする。以下の問いに答えよ。
(1)$\cos4\alpha=\cos3\alpha$であることを示せ。
(2)$f(x)=8x^3+4x^2-4x-1$とするとき、$f(\cos\alpha)=0$が成り立つことを示せ。
(3)$\cos\alpha$は無理数であることを示せ。
2022大阪大学理系過去問
この動画を見る
$\alpha=\frac{2\pi}{7}$とする。以下の問いに答えよ。
(1)$\cos4\alpha=\cos3\alpha$であることを示せ。
(2)$f(x)=8x^3+4x^2-4x-1$とするとき、$f(\cos\alpha)=0$が成り立つことを示せ。
(3)$\cos\alpha$は無理数であることを示せ。
2022大阪大学理系過去問
【わかりやすく解説】相加相乗平均の関係を使う不等式の証明②(高校数学Ⅱ)

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$a \gt 0,b \gt 0$のとき、不等式$(1+\displaystyle \frac{a}{b})(1+\displaystyle \frac{b}{a}) \geqq 4$が成り立つことを証明せよ
この動画を見る
$a \gt 0,b \gt 0$のとき、不等式$(1+\displaystyle \frac{a}{b})(1+\displaystyle \frac{b}{a}) \geqq 4$が成り立つことを証明せよ
指数不等式

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \dfrac{9^x+4^x}{6^x-9^x} \geqq 5 $
これを解け.
この動画を見る
$ \dfrac{9^x+4^x}{6^x-9^x} \geqq 5 $
これを解け.
福田の数学〜一橋大学2022年文系第3問〜同値関係の証明と不等式の表す領域

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#一次不等式(不等式・絶対値のある方程式・不等式)#図形と方程式#恒等式・等式・不等式の証明#軌跡と領域#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
次の問いに答えよ。
(1)実数x,yについて、$「|x-y| \leqq x+y」$であることの必要十分条件は
「$x \geqq 0$かつ$y \geqq 0$ 」であることを示せ。
(2)次の不等式で定まるxy平面上の領域を図示せよ。
$|1+y-2x^2-y^2| \leqq 1-y-y^2$
2022一橋大学文系過去問
この動画を見る
次の問いに答えよ。
(1)実数x,yについて、$「|x-y| \leqq x+y」$であることの必要十分条件は
「$x \geqq 0$かつ$y \geqq 0$ 」であることを示せ。
(2)次の不等式で定まるxy平面上の領域を図示せよ。
$|1+y-2x^2-y^2| \leqq 1-y-y^2$
2022一橋大学文系過去問
【わかりやすく解説】相加相乗平均の関係を使う不等式の証明①(高校数学Ⅱ)

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$a \gt 0,b \gt 0$のとき、不等式$ab+\displaystyle \frac{4}{ab} \geqq 4$が成り立つことを証明せよ
この動画を見る
$a \gt 0,b \gt 0$のとき、不等式$ab+\displaystyle \frac{4}{ab} \geqq 4$が成り立つことを証明せよ
方程式を解く。
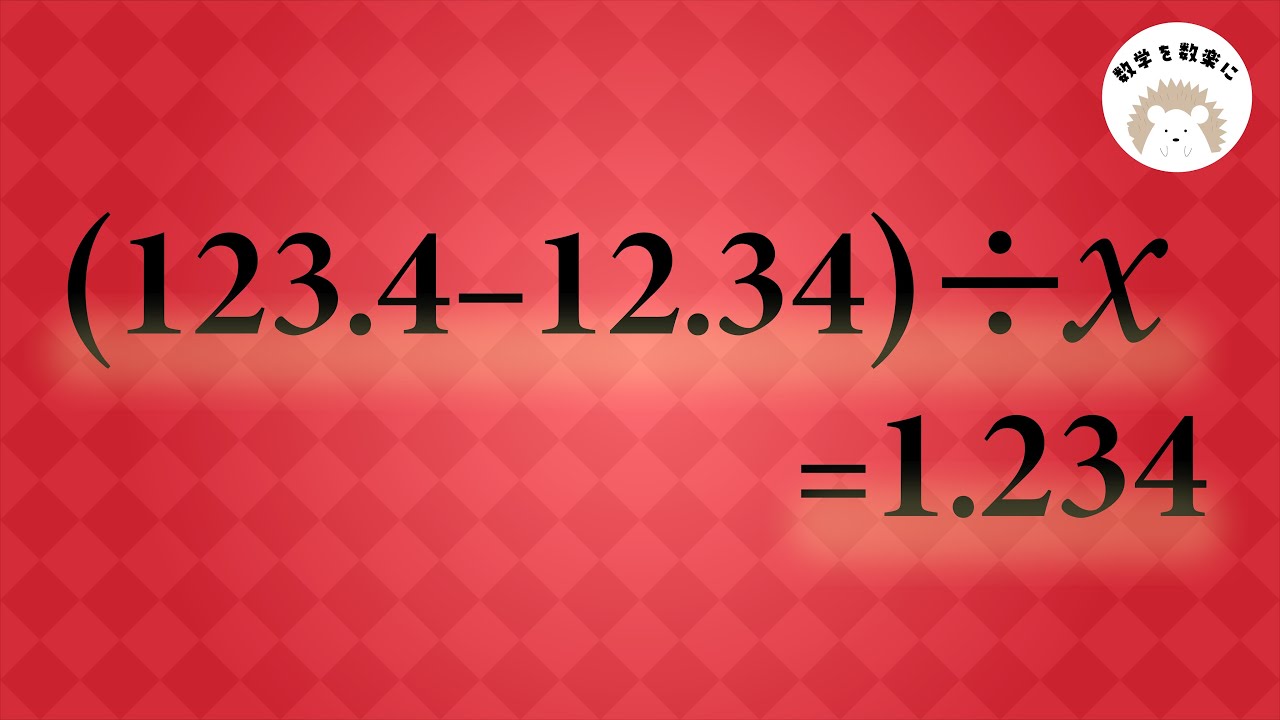
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(123.4-12.34) \div x =1.234$
この動画を見る
$(123.4-12.34) \div x =1.234$
福田の数学〜大阪大学2022年理系第1問〜複素数平面上の点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#軌跡と領域#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
rを正の実数とする。
複素数平面上で点Zが点3/2を中心とする半径rの円周上を動くとき、
$Z+w=Zw$
を満たす点wが描く図形を求めよ。
2022大阪大学理系過去問
この動画を見る
rを正の実数とする。
複素数平面上で点Zが点3/2を中心とする半径rの円周上を動くとき、
$Z+w=Zw$
を満たす点wが描く図形を求めよ。
2022大阪大学理系過去問
どっちがでかい?

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 3^{\sqrt5}$ VS $ 5^{\sqrt3}$ どちらが大きいか?
この動画を見る
$ 3^{\sqrt5}$ VS $ 5^{\sqrt3}$ どちらが大きいか?
【次数が高くても焦るな】対称式 入試問題【2017年昭和大学】

単元:
#数Ⅰ#数Ⅱ#数と式#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$a+b=1,a^2+b^2=3$のとき、$a^7+b^7$の値を求めよ。
2017昭和大過去問
この動画を見る
$a+b=1,a^2+b^2=3$のとき、$a^7+b^7$の値を求めよ。
2017昭和大過去問
福田の数学〜一橋大学2022年文系第2問〜平面上の三角形の面積の最大値

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}\ 0 \leqq \theta \lt 2\pi$とする。
座標平面上の3点O(0,0), $P(\cos\theta,\sin\theta)$, $Q(1,3\sin2\theta)$
が三角形をなすとき、$\triangle OPQ$の面積の最大値を求めよ。
2022一橋大学文系過去問
この動画を見る
${\Large\boxed{2}}\ 0 \leqq \theta \lt 2\pi$とする。
座標平面上の3点O(0,0), $P(\cos\theta,\sin\theta)$, $Q(1,3\sin2\theta)$
が三角形をなすとき、$\triangle OPQ$の面積の最大値を求めよ。
2022一橋大学文系過去問
【数Ⅱ】領域内の点の最大値・最小値【具体例を作って方針を立てよう】

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
不等式$x^2+y^2 \leqq 9$,$y \geqq \dfrac{1}{3}x-1$で表される領域をDとする.
領域D内の点$(x,y)$について,-$x+y$の最大値・最小値を求めよ.
この動画を見る
不等式$x^2+y^2 \leqq 9$,$y \geqq \dfrac{1}{3}x-1$で表される領域をDとする.
領域D内の点$(x,y)$について,-$x+y$の最大値・最小値を求めよ.
中学生向け「どっちがでかい?」

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きいか?
$\dfrac{10^{2021}+1}{10^{2022}+1}$ VS $\dfrac{10^{2022}+1}{10^{2023}+1}$
この動画を見る
どちらが大きいか?
$\dfrac{10^{2021}+1}{10^{2022}+1}$ VS $\dfrac{10^{2022}+1}{10^{2023}+1}$
