 数列とその和(等差・等比・階差・Σ)
数列とその和(等差・等比・階差・Σ)
 数列とその和(等差・等比・階差・Σ)
数列とその和(等差・等比・階差・Σ)
和歌山大 三項間漸化式 半角の公式 高校数学 Japanese university entrance exam questions
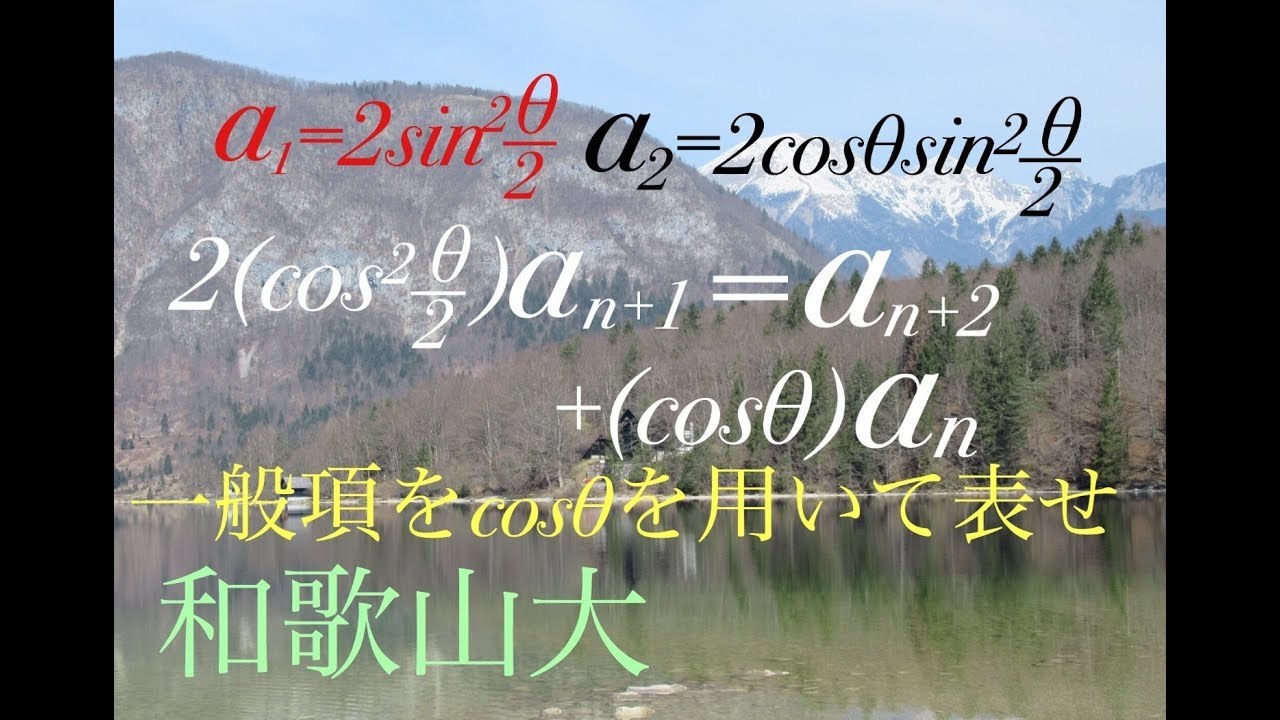
単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#三角関数#三角関数とグラフ#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#和歌山大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
和歌山大学過去問題
$a_1=2\sin^2\frac{θ}{2}$,$a_2=2\cosθ\sin^2\frac{θ}{2}$
$2(cos^2\frac{θ}{2})a_{n+1}=a_{n+2}+(\cosθ)a_n$
$a_n$を$\cosθ$を用いて表せ。
この動画を見る
和歌山大学過去問題
$a_1=2\sin^2\frac{θ}{2}$,$a_2=2\cosθ\sin^2\frac{θ}{2}$
$2(cos^2\frac{θ}{2})a_{n+1}=a_{n+2}+(\cosθ)a_n$
$a_n$を$\cosθ$を用いて表せ。
福田の一夜漬け数学〜数列・漸化式(6)その他色々〜高校2年生

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
次の漸化式を解け。(すべて$a_1=1$とする)
①$a_{n+1}=\displaystyle \frac{a_n}{4a_n-1}$
②$a_{n+1}=2\displaystyle \sqrt{a_n}$
③$a_{n+1}=2(n+1)a_n$
④$a_{n+1}=\displaystyle \frac{4a_n+8}{a_n+6}$
この動画を見る
次の漸化式を解け。(すべて$a_1=1$とする)
①$a_{n+1}=\displaystyle \frac{a_n}{4a_n-1}$
②$a_{n+1}=2\displaystyle \sqrt{a_n}$
③$a_{n+1}=2(n+1)a_n$
④$a_{n+1}=\displaystyle \frac{4a_n+8}{a_n+6}$
福田の一夜漬け数学〜数列・漸化式(5)連立漸化式〜高校2年生

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
次の漸化式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_{n+1}=4a_n+b_n\\
b_{n+1}=a_n+4b_n\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1\\
b_1=2\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_{n+1}=a_n+4b_n\\
b_{n+1}=a_n+b_n\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1\\
b_1=1\\
\end{array}
\right.
\end{eqnarray}$
この動画を見る
次の漸化式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_{n+1}=4a_n+b_n\\
b_{n+1}=a_n+4b_n\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1\\
b_1=2\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_{n+1}=a_n+4b_n\\
b_{n+1}=a_n+b_n\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1\\
b_1=1\\
\end{array}
\right.
\end{eqnarray}$
福田の一夜漬け数学〜数列・漸化式(4)3項間の漸化式〜高校2年生

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
次の漸化式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1, a_2=5\\
a_{n+2}=5a_{n+1}-4a_n\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1, a_2=5\\
a_{n+2}=4a_{n+1}-4a_n\\
\end{array}
\right.
\end{eqnarray}$
この動画を見る
次の漸化式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1, a_2=5\\
a_{n+2}=5a_{n+1}-4a_n\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1, a_2=5\\
a_{n+2}=4a_{n+1}-4a_n\\
\end{array}
\right.
\end{eqnarray}$
福田の一夜漬け数学〜数列・漸化式(3)〜高校2年生

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
次の漸化式を解け。(すべて、$a_1=1$とする)
①$(n+1)a_{n+1}=na_n+2$
②$na_{n+1}=(n+1)a_n+2$
③$(n+2)a_{n+1}=na_n+2$
④$na_{n+1}=(n+2)a_n+2$
この動画を見る
次の漸化式を解け。(すべて、$a_1=1$とする)
①$(n+1)a_{n+1}=na_n+2$
②$na_{n+1}=(n+1)a_n+2$
③$(n+2)a_{n+1}=na_n+2$
④$na_{n+1}=(n+2)a_n+2$
福田の一夜漬け数学〜数列・漸化式(2)〜高校2年生

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
次の漸化式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1\\
a_{n+1}=3a_n+2^n\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1\\
a_{n+1}=2a_n+n^2+2n\\
\end{array}
\right.
\end{eqnarray}$
この動画を見る
次の漸化式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1\\
a_{n+1}=3a_n+2^n\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1\\
a_{n+1}=2a_n+n^2+2n\\
\end{array}
\right.
\end{eqnarray}$
福田の一夜漬け数学〜数列・漸化式(1)〜高校2年生

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
次の漸化式を解け。(すべて、$a_1=1$とする)
①$a_{n+1}=a_n+2$
②$a_{n+1}=2a_n$
③$a_{n+1}=2a_n+2$
④$a_{n+1}=a_n+2n$
⑤$a_{n+1}=2a_n+2^n$
⑥$a_{n+1}=2a_n+2n$
この動画を見る
次の漸化式を解け。(すべて、$a_1=1$とする)
①$a_{n+1}=a_n+2$
②$a_{n+1}=2a_n$
③$a_{n+1}=2a_n+2$
④$a_{n+1}=a_n+2n$
⑤$a_{n+1}=2a_n+2^n$
⑥$a_{n+1}=2a_n+2n$
福田の一夜漬け数学〜数列・群数列(3)〜高校2年生
単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
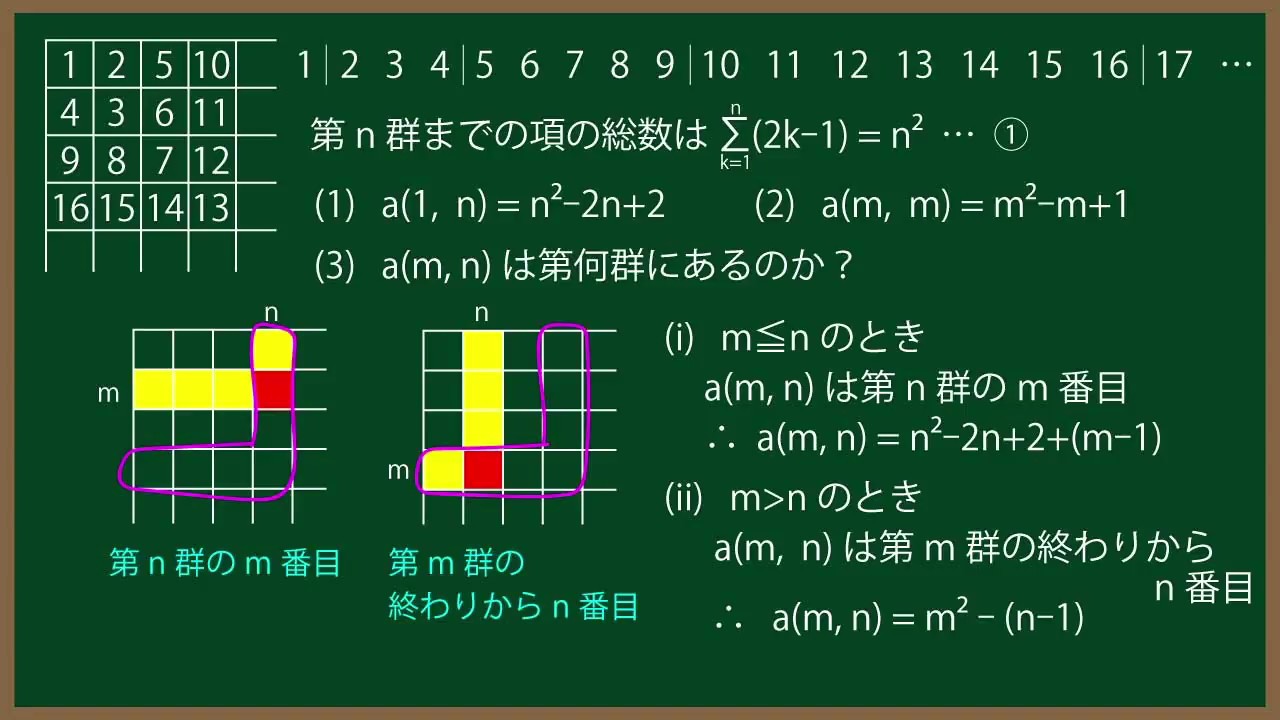
\begin{array}{|c|c|c|c|c}
\hline 1 & 2 & 5 & 10 & \\
\hline 4 & 3 &6 & 11 & \\
\hline 9 & 8 & 7 & 12 & \\
\hline 16 & 15 & 14 & 13 & \\
\hline \\
\end{array}
上図のように自然数を配置していく。
$m$行目、$n$列目にある数を$a(m,n)$と
表すことにする。
例えば、$a(3,2)=8$ である。
次の問いに答えよ。
(1)$a(1,n)$
(2)$a(m,m)$
(3)$a(m,n)$
(4)150は何行目の何列目に出てくるか。
この動画を見る
\begin{array}{|c|c|c|c|c}
\hline 1 & 2 & 5 & 10 & \\
\hline 4 & 3 &6 & 11 & \\
\hline 9 & 8 & 7 & 12 & \\
\hline 16 & 15 & 14 & 13 & \\
\hline \\
\end{array}
上図のように自然数を配置していく。
$m$行目、$n$列目にある数を$a(m,n)$と
表すことにする。
例えば、$a(3,2)=8$ である。
次の問いに答えよ。
(1)$a(1,n)$
(2)$a(m,m)$
(3)$a(m,n)$
(4)150は何行目の何列目に出てくるか。
福田の一夜漬け数学〜数列・群数列(2)〜高校2年生

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
数列 $1 2 1 3 2 $$1 4 $$3 $$2 $$1 $$5\cdots$について次を求めよ。
(1)第100項
(2)初項から第100項までの和
数列 $ \dfrac{2}{3} \dfrac{2}{5} \dfrac{4}{5} \dfrac{2}{7} \dfrac{4}{7} \dfrac{6}{7} \dfrac{2}{9}$$ \dfrac{4}{9}$$ \dfrac{6}{9}$$ \dfrac{8}{9}$$ \dfrac{2}{11}\cdots$について
次の問いに答えよ。
(1)$\displaystyle \frac{4}{15}$は第何項か。
(2)第100項は何か。
この動画を見る
数列 $1 2 1 3 2 $$1 4 $$3 $$2 $$1 $$5\cdots$について次を求めよ。
(1)第100項
(2)初項から第100項までの和
数列 $ \dfrac{2}{3} \dfrac{2}{5} \dfrac{4}{5} \dfrac{2}{7} \dfrac{4}{7} \dfrac{6}{7} \dfrac{2}{9}$$ \dfrac{4}{9}$$ \dfrac{6}{9}$$ \dfrac{8}{9}$$ \dfrac{2}{11}\cdots$について
次の問いに答えよ。
(1)$\displaystyle \frac{4}{15}$は第何項か。
(2)第100項は何か。
福田の一夜漬け数学〜数列・群数列(1)〜高校2年生

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
群数列 $1\ | \ 3 5 \ |\ 7 9 11$$ \ |\ 13 15 17 19$$ \ | \ 21 \cdots$について次を求めよ。
(1)第$n$群の初項
(2)第$n$群の総和
(3)301は第何群の何番目か
正の奇数の列$\left\{a_n\right\}$を次のように第$k$群に$2^{k-1}$個の項を含むように分ける。
$1\ | \ 3 5 \ |\ 7 9 11 13 $$\ | \ 15 17 19 21 $$23 25 27 29 $$\ | \ 31 \cdots$
(1)第$n$群の初項を求めよ。
(2)777は第何群の何番目か。
この動画を見る
群数列 $1\ | \ 3 5 \ |\ 7 9 11$$ \ |\ 13 15 17 19$$ \ | \ 21 \cdots$について次を求めよ。
(1)第$n$群の初項
(2)第$n$群の総和
(3)301は第何群の何番目か
正の奇数の列$\left\{a_n\right\}$を次のように第$k$群に$2^{k-1}$個の項を含むように分ける。
$1\ | \ 3 5 \ |\ 7 9 11 13 $$\ | \ 15 17 19 21 $$23 25 27 29 $$\ | \ 31 \cdots$
(1)第$n$群の初項を求めよ。
(2)777は第何群の何番目か。
福田の一夜漬け数学〜数列・和Snの問題〜高校2年生

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
数列$\left\{a_n\right\}$の初項から第$n$項までの和$S_n$が次のときの一般項$a_n$を求めよ。
(1)$S_n=n^2-2n+3$
(2)$S_n=2^n+3^n-2$
数列$\left\{a_n\right\}$の初項から第$n$項までの和$S_n$が$S_n=2a_n-n$であるとき、
$a_n$を求めよ。
この動画を見る
数列$\left\{a_n\right\}$の初項から第$n$項までの和$S_n$が次のときの一般項$a_n$を求めよ。
(1)$S_n=n^2-2n+3$
(2)$S_n=2^n+3^n-2$
数列$\left\{a_n\right\}$の初項から第$n$項までの和$S_n$が$S_n=2a_n-n$であるとき、
$a_n$を求めよ。
福田の一夜漬け数学〜数列・等差x等比型の和の裏技〜高校2年生

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
次の数列の和を求めよ。
$1・1, 4・3, 7・3^2,$$ 10・3^3,$$ \cdots,$$ (3n-2)・3^{n-1}$
次の和を求めよ。
$S=2・\left(\frac{1}{3}\right)+4・\left(\frac{1}{3}\right)^2$$+6・\left(\frac{1}{3}\right)^3$$+\cdots$$+2n・\left(\frac{1}{3}\right)^n$
この動画を見る
次の数列の和を求めよ。
$1・1, 4・3, 7・3^2,$$ 10・3^3,$$ \cdots,$$ (3n-2)・3^{n-1}$
次の和を求めよ。
$S=2・\left(\frac{1}{3}\right)+4・\left(\frac{1}{3}\right)^2$$+6・\left(\frac{1}{3}\right)^3$$+\cdots$$+2n・\left(\frac{1}{3}\right)^n$
福田の一夜漬け数学〜数列・階差数列と部分分数分解〜高校2年生

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
次の数列の一般項を求めよ。
$2,4,7,13,24,42,69,107,158,\cdots$
次の和を求めよ。
(1)$\displaystyle \sum_{k=1}^n\frac{1}{4k^2-1}$
(2)$\displaystyle \sum_{k=1}^n\frac{1}{k^2+2k}$
(3)$\displaystyle \sum_{k=1}^n\frac{1}{k(k+1)(k+2)}$
この動画を見る
次の数列の一般項を求めよ。
$2,4,7,13,24,42,69,107,158,\cdots$
次の和を求めよ。
(1)$\displaystyle \sum_{k=1}^n\frac{1}{4k^2-1}$
(2)$\displaystyle \sum_{k=1}^n\frac{1}{k^2+2k}$
(3)$\displaystyle \sum_{k=1}^n\frac{1}{k(k+1)(k+2)}$
山形大(医)確率 等比数列の和 高校数学 Japanese university entrance exam questions

単元:
#数A#場合の数と確率#確率#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#山形大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
山形大学過去問題
箱に白玉が3個、赤玉が2個。1個とり出し、白なら戻す。赤なら戻さない。
2個目の赤が出たら終了。n回目に終わる確率を求めよ。
この動画を見る
山形大学過去問題
箱に白玉が3個、赤玉が2個。1個とり出し、白なら戻す。赤なら戻さない。
2個目の赤が出たら終了。n回目に終わる確率を求めよ。
福田の一夜漬け数学〜数列・シグマ記号(2)〜高校2年生

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
次の和を求めよ。
(1)$2^2+4^2+6^2+8^2+\cdots+(2n)^2$
(2)$1・2・3+2・3・5$$+3・4・7+$$4・5・9+$$\cdots+n(n+1)(2n+1)$
次の数列の初項から第n項までの和を求めよ。
(1)$2, 2+4, 2+4+6,$$ 2+4+6+8,\cdots$
(2)$1^2+1・2+2^2,$$ 2^2+2・3+3^2,$$ 3^2+3・4+4^2,\cdots$
(3)$1, 11, 111, 1111,\cdots$
次の数列の和を求めよ。
(1)$1・n, 3(n-1), 5(n-2),$$\cdots$$, (2n-3)・2$$, (2n-1)・1$
(2)$1^2・n, 2^2(n-1), 3^2(n-2),$$\cdots$$, (n-1)^2・2$$, n^2・1$
この動画を見る
次の和を求めよ。
(1)$2^2+4^2+6^2+8^2+\cdots+(2n)^2$
(2)$1・2・3+2・3・5$$+3・4・7+$$4・5・9+$$\cdots+n(n+1)(2n+1)$
次の数列の初項から第n項までの和を求めよ。
(1)$2, 2+4, 2+4+6,$$ 2+4+6+8,\cdots$
(2)$1^2+1・2+2^2,$$ 2^2+2・3+3^2,$$ 3^2+3・4+4^2,\cdots$
(3)$1, 11, 111, 1111,\cdots$
次の数列の和を求めよ。
(1)$1・n, 3(n-1), 5(n-2),$$\cdots$$, (2n-3)・2$$, (2n-1)・1$
(2)$1^2・n, 2^2(n-1), 3^2(n-2),$$\cdots$$, (n-1)^2・2$$, n^2・1$
福田の一夜漬け数学〜数列・シグマ記号(1)〜高校2年生

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
次の和を求めよ。
(1)$\displaystyle \sum_{k=1}^n(3k^2+7k+2)$
(2)$\displaystyle \sum_{k=1}^nk(k^2+1)$
(3)$\displaystyle \sum_{k=1}^n(-2)^{k-1}$
次の和を求めよ。
(1)$\displaystyle \sum_{k=1}^n\frac{1}{k(k+1)}$
(2)$\displaystyle \sum_{k=1}^n\frac{1}{\sqrt k+\sqrt{k+1}}$
この動画を見る
次の和を求めよ。
(1)$\displaystyle \sum_{k=1}^n(3k^2+7k+2)$
(2)$\displaystyle \sum_{k=1}^nk(k^2+1)$
(3)$\displaystyle \sum_{k=1}^n(-2)^{k-1}$
次の和を求めよ。
(1)$\displaystyle \sum_{k=1}^n\frac{1}{k(k+1)}$
(2)$\displaystyle \sum_{k=1}^n\frac{1}{\sqrt k+\sqrt{k+1}}$
福田の一夜漬け数学〜等差数列・等比数列(2)〜高校2年生

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$8,a,b$がこの順に等差数列、$a,b,36$がこの順に等比数列をなすとき、
$a,b$の値を求めよ。
等差数列をなす3つの数がある。その和は$3$で、2乗の和は$35$である。
この3つの数を求めよ。
$10$以上$50$以下の分数で、分母が$3$である既約分数の和を求めよ。
$p$を素数、自然数$m,n$を$m \lt n$とする。$m$と$n$の間にあって$p$を分母と
する既約分数の総和を求めよ。
この動画を見る
$8,a,b$がこの順に等差数列、$a,b,36$がこの順に等比数列をなすとき、
$a,b$の値を求めよ。
等差数列をなす3つの数がある。その和は$3$で、2乗の和は$35$である。
この3つの数を求めよ。
$10$以上$50$以下の分数で、分母が$3$である既約分数の和を求めよ。
$p$を素数、自然数$m,n$を$m \lt n$とする。$m$と$n$の間にあって$p$を分母と
する既約分数の総和を求めよ。
福田の一夜漬け数学〜等差数列・等比数列(1)〜高校2年生

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
初項から第10項までの和が550,初項から第20項までの和が700である
等差数列$\left\{a_n\right\}$について
(1)一般項$a_n$を求めよ。
(2)数列$\left\{a_n\right\}$の第20項から第30項までの和を求めよ。
(3)初項から第$n$項までの和$S_n$の最大値とそのときのnの値を求めよ。
初項から第4項までの和が45,初項から第8項までの和が765である
等比数列$\left\{a_n\right\}$を考える。
(1)一般項$a_n$を求めよ。
(2)数列$\left\{a_n\right\}$の公比が正であるとき、数列$\left\{a_{2n-1}\right\}$はどのような数列か。
この動画を見る
初項から第10項までの和が550,初項から第20項までの和が700である
等差数列$\left\{a_n\right\}$について
(1)一般項$a_n$を求めよ。
(2)数列$\left\{a_n\right\}$の第20項から第30項までの和を求めよ。
(3)初項から第$n$項までの和$S_n$の最大値とそのときのnの値を求めよ。
初項から第4項までの和が45,初項から第8項までの和が765である
等比数列$\left\{a_n\right\}$を考える。
(1)一般項$a_n$を求めよ。
(2)数列$\left\{a_n\right\}$の公比が正であるとき、数列$\left\{a_{2n-1}\right\}$はどのような数列か。
質問に対する返答です。整数問題,数列の和

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$1 \leqq t< u < v \leqq 6m$
$t+u+v=6m$
この動画を見る
$1 \leqq t< u < v \leqq 6m$
$t+u+v=6m$
【高校数学】数Ⅲ-71 数列の極限⑦(無限等比数列)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$a_1=1,a_{n+1}=\dfrac{1}{3}a_n+2(n=1,2,・・・)$によって
定められる数列$\{a_n\}$について、$\displaystyle \lim_{n\to\infty}a_n$を求めよ。
②$a_1=o,a_2=1,a_{n+2}=\dfrac{1}{4}(a_{n+1}+3a_n)(n=1,2,・・・)$によって
定められる数列$\{a_n\}$について、$\displaystyle \lim_{n\to\infty}a_n$を求めよ。
この動画を見る
①$a_1=1,a_{n+1}=\dfrac{1}{3}a_n+2(n=1,2,・・・)$によって
定められる数列$\{a_n\}$について、$\displaystyle \lim_{n\to\infty}a_n$を求めよ。
②$a_1=o,a_2=1,a_{n+2}=\dfrac{1}{4}(a_{n+1}+3a_n)(n=1,2,・・・)$によって
定められる数列$\{a_n\}$について、$\displaystyle \lim_{n\to\infty}a_n$を求めよ。
確率、等比数列 巴戦は平等な優勝決定法か?(類)東大、神戸大

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
確率、等比数列 巴戦は平等な優勝決定法か?
(類)東大、神戸大
この動画を見る
確率、等比数列 巴戦は平等な優勝決定法か?
(類)東大、神戸大
【高校数学】 数B-86 群数列④

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
数列$\dfrac{1}{1},\dfrac{1}{2},\dfrac{2}{1},\dfrac{1}{3},\dfrac{2}{2},\dfrac{3}{1},\dfrac{1}{4},\dfrac{2}{3},\dfrac{3}{2},\dfrac{4}{1},\dfrac{1}{5},\dfrac{2}{4},・・・$
について次の問いに答えよう.
①$\dfrac{5}{22}$は第何項か求めよう.
②この数列の第100項を求めよう.
この動画を見る
数列$\dfrac{1}{1},\dfrac{1}{2},\dfrac{2}{1},\dfrac{1}{3},\dfrac{2}{2},\dfrac{3}{1},\dfrac{1}{4},\dfrac{2}{3},\dfrac{3}{2},\dfrac{4}{1},\dfrac{1}{5},\dfrac{2}{4},・・・$
について次の問いに答えよう.
①$\dfrac{5}{22}$は第何項か求めよう.
②この数列の第100項を求めよう.
【高校数学】 数B-85 群数列③

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
数列$\dfrac{1}{1},\dfrac{1}{2},\dfrac{3}{2},\dfrac{1}{3},\dfrac{3}{3},\dfrac{5}{3},\dfrac{1}{4},\dfrac{3}{4},\dfrac{5}{4},\dfrac{7}{4},\dfrac{1}{5},\dfrac{3}{5},・・・$
について次の問いに答えよう.
①$\dfrac{5}{9}$は第何項か求めよう.
②この数列の第200項を求めよう.
この動画を見る
数列$\dfrac{1}{1},\dfrac{1}{2},\dfrac{3}{2},\dfrac{1}{3},\dfrac{3}{3},\dfrac{5}{3},\dfrac{1}{4},\dfrac{3}{4},\dfrac{5}{4},\dfrac{7}{4},\dfrac{1}{5},\dfrac{3}{5},・・・$
について次の問いに答えよう.
①$\dfrac{5}{9}$は第何項か求めよう.
②この数列の第200項を求めよう.
【高校数学】 数B-84 群数列②

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
奇数の列を,下のように,1個,2個,4個,8個,・・・となるように群に分ける.
$ 1 | 3,5 | 7,9,11,13 | 15,17,・・・$
①第$n$群の奇数の和を求めよう.
②第8群の5番目の数を求めよう.
この動画を見る
奇数の列を,下のように,1個,2個,4個,8個,・・・となるように群に分ける.
$ 1 | 3,5 | 7,9,11,13 | 15,17,・・・$
①第$n$群の奇数の和を求めよう.
②第8群の5番目の数を求めよう.
【高校数学】 数B-83 群数列①

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
1から順に自然数を並べて,下のように1個,2個,4個,8個,・・・となるように群に分ける.
$ 1 | ,3 | 4,5,6,7 | 8,9,・・・$
①第7群の初めの数と終わりの数を求めよう.
②第$n$群の数の和を求めよう.
この動画を見る
1から順に自然数を並べて,下のように1個,2個,4個,8個,・・・となるように群に分ける.
$ 1 | ,3 | 4,5,6,7 | 8,9,・・・$
①第7群の初めの数と終わりの数を求めよう.
②第$n$群の数の和を求めよう.
【高校数学】 数B-82 いろいろな数列の和③

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の数列の初項から第$n$項までの和を求めよう.
①$\dfrac{1}{1+\sqrt2},\dfrac{1}{\sqrt2+\sqrt3},\dfrac{1}{\sqrt3+\sqrt4},・・・$
②$\dfrac{1}{1+\sqrt3},\dfrac{1}{\sqrt3+\sqrt5},\dfrac{1}{\sqrt5+\sqrt7},・・・$
この動画を見る
次の数列の初項から第$n$項までの和を求めよう.
①$\dfrac{1}{1+\sqrt2},\dfrac{1}{\sqrt2+\sqrt3},\dfrac{1}{\sqrt3+\sqrt4},・・・$
②$\dfrac{1}{1+\sqrt3},\dfrac{1}{\sqrt3+\sqrt5},\dfrac{1}{\sqrt5+\sqrt7},・・・$
【高校数学】 数B-81 いろいろな数列の和②

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の数列の初項から第$n$項までの和を求めよう.
①$\dfrac{1}{2・4},\dfrac{1}{4・6},\dfrac{1}{6・8},・・・$
②$\dfrac{1}{1・4},\dfrac{1}{4・7},\dfrac{1}{7・10},・・・$
この動画を見る
次の数列の初項から第$n$項までの和を求めよう.
①$\dfrac{1}{2・4},\dfrac{1}{4・6},\dfrac{1}{6・8},・・・$
②$\dfrac{1}{1・4},\dfrac{1}{4・7},\dfrac{1}{7・10},・・・$
【高校数学】 数B-80 いろいろな数列の和①

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の数列の初項から第$n$項までの和を求めよう.
①$3,5・2,7・2^2,9・2^3・・・$
②$x\neq 1$のとき,$1,3x,5x^2,7x^3,・・・$
この動画を見る
次の数列の初項から第$n$項までの和を求めよう.
①$3,5・2,7・2^2,9・2^3・・・$
②$x\neq 1$のとき,$1,3x,5x^2,7x^3,・・・$
【高校数学】 数B-79 数列の和と一般項②

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
初項から第$n$項までの和$S_n$が
次の式で表される数列$\{a_n\}$の一般項を求めよう.
①$S_n=n^2+2n+2$
②$S_n=a_{n}+(n-1)^2$
この動画を見る
初項から第$n$項までの和$S_n$が
次の式で表される数列$\{a_n\}$の一般項を求めよう.
①$S_n=n^2+2n+2$
②$S_n=a_{n}+(n-1)^2$
【高校数学】 数B-78 数列の和と一般項①

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
数列$\{a_n\}$の初項から第$n$項までの和を$S_n$とすると,
$a_1=S_1,n\geqq 2$のとき,$a_n=①$
初項から第$n$項までの和$S_n$が次の式で表される数列$\{a_n\}$の一般項を求めよう.
②$n^2-4n$
③$3^n-1$
この動画を見る
数列$\{a_n\}$の初項から第$n$項までの和を$S_n$とすると,
$a_1=S_1,n\geqq 2$のとき,$a_n=①$
初項から第$n$項までの和$S_n$が次の式で表される数列$\{a_n\}$の一般項を求めよう.
②$n^2-4n$
③$3^n-1$
