 漸化式
漸化式
 漸化式
漸化式
福田の数学〜北里大学2022年医学部第3問〜確率と漸化式の融合問題

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
1つの箱を置ける台と2つの箱A, Bがある。箱Aには赤玉2個、青玉2個が
入っており、箱Bには白玉3個、青玉1個が入っている。台の上に箱Aを置き、
次の操作を繰り返す。
(操作) 台に置かれている箱から玉を1個取り出して色を調べてから箱に戻し、台
に置かれている箱を台から降ろす。取りだした玉が青球であれば箱Bを台
に置き、それ以外の色の玉であれば箱Aを台に置く。
正の整数nに対し、n回目の操作を終えたときに、台に箱Aが置かれている確率
をa_n、箱Bが置かれている確率をb_nとおく。次の問いに答えよ。
(1) 正の整数nに対し、$b_n$と$a_{n+1}$をそれぞれ $a_n$ を用いて表せ。
(2) 正の整数nに対し、$a_n$をnを用いて表せ。
(3) 正の整数nに対し、1回目からn回目までのn回の操作で白玉を1回も取り出
さない確率をnを用いて表せ。
(4)正の整数nに対し、1回目からn回目までのn回の操作で白玉をちょうど1回
だけ取り出す確率をnを用いて表せ。
2022北里大学医学部過去問
この動画を見る
1つの箱を置ける台と2つの箱A, Bがある。箱Aには赤玉2個、青玉2個が
入っており、箱Bには白玉3個、青玉1個が入っている。台の上に箱Aを置き、
次の操作を繰り返す。
(操作) 台に置かれている箱から玉を1個取り出して色を調べてから箱に戻し、台
に置かれている箱を台から降ろす。取りだした玉が青球であれば箱Bを台
に置き、それ以外の色の玉であれば箱Aを台に置く。
正の整数nに対し、n回目の操作を終えたときに、台に箱Aが置かれている確率
をa_n、箱Bが置かれている確率をb_nとおく。次の問いに答えよ。
(1) 正の整数nに対し、$b_n$と$a_{n+1}$をそれぞれ $a_n$ を用いて表せ。
(2) 正の整数nに対し、$a_n$をnを用いて表せ。
(3) 正の整数nに対し、1回目からn回目までのn回の操作で白玉を1回も取り出
さない確率をnを用いて表せ。
(4)正の整数nに対し、1回目からn回目までのn回の操作で白玉をちょうど1回
だけ取り出す確率をnを用いて表せ。
2022北里大学医学部過去問
見掛け倒し

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \underbrace{777・・・・・・77^7}_{101桁}$を18で割ったあまりを求めよ.
この動画を見る
$ \underbrace{777・・・・・・77^7}_{101桁}$を18で割ったあまりを求めよ.
福田の数学〜上智大学2022年理工学部第3問〜複素数平面上の点列と三角形の相似

単元:
#大学入試過去問(数学)#複素数平面#相似な図形#数列#漸化式#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B#数C
指導講師:
福田次郎
問題文全文(内容文):
複素数からなる数列${z_n}$を、次の条件で定める。
$z_1=0,\ \ \ z_{n+1}=(1+i)z_n-i \ \ \ (i=1,2,3, \ \ ...)$
正の整数nに対し、z_nに対応する負素数平面上の点をA_nとおく。
(1)$z_2=\boxed{ツ }+\boxed{ツ }\ i, \ \ \ z_3=\boxed{ト}+$
$\boxed{ナ}\ i,\ \ \ z_4=\boxed{二}+\boxed{ヌ}\ i $である。
(2)$r \gt 0,\ 0 \leqq θ \lt 2\pi$ を用いて、$1+i=r(\cos θ+i\sin θ)$のように$1+i$を極形式で
表すとき、$r=\sqrt{\boxed{ネ}},\ θ=\frac{\boxed{ノ }}{\boxed{ハ}}\pi$である。
(3)すべての正の整数nに対する$\triangle PA_nA_{n+1}$が互いに相似になる点Pに対応する
複素数は、$\boxed{ヒ}+\boxed{フ }\ i$である。
(4)$|z_n| \gt 1000$となる最小のnは$n=\boxed{へ}$である。
(5)$A_{2022+k}$が実軸上にある最小の正の整数kは$k=\boxed{ホ}$である。
2022上智大学理工学部過去問
この動画を見る
複素数からなる数列${z_n}$を、次の条件で定める。
$z_1=0,\ \ \ z_{n+1}=(1+i)z_n-i \ \ \ (i=1,2,3, \ \ ...)$
正の整数nに対し、z_nに対応する負素数平面上の点をA_nとおく。
(1)$z_2=\boxed{ツ }+\boxed{ツ }\ i, \ \ \ z_3=\boxed{ト}+$
$\boxed{ナ}\ i,\ \ \ z_4=\boxed{二}+\boxed{ヌ}\ i $である。
(2)$r \gt 0,\ 0 \leqq θ \lt 2\pi$ を用いて、$1+i=r(\cos θ+i\sin θ)$のように$1+i$を極形式で
表すとき、$r=\sqrt{\boxed{ネ}},\ θ=\frac{\boxed{ノ }}{\boxed{ハ}}\pi$である。
(3)すべての正の整数nに対する$\triangle PA_nA_{n+1}$が互いに相似になる点Pに対応する
複素数は、$\boxed{ヒ}+\boxed{フ }\ i$である。
(4)$|z_n| \gt 1000$となる最小のnは$n=\boxed{へ}$である。
(5)$A_{2022+k}$が実軸上にある最小の正の整数kは$k=\boxed{ホ}$である。
2022上智大学理工学部過去問
漸化式・対数の利用の融合問題 福井大

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#福井大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a_1=1,a_{n+1}=\dfrac{a_n}{a_n+3},a_{11}$は小数点以下0でない数が初めて表れるのは小数第何位?
福井大過去問
この動画を見る
$ a_1=1,a_{n+1}=\dfrac{a_n}{a_n+3},a_{11}$は小数点以下0でない数が初めて表れるのは小数第何位?
福井大過去問
高知大(医)3項間漸化式

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#高知大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a_1=1,a_2=5,a_{n+2}=4a_{n+1}-3a_n-4$
の一般項$a_n$を求めよ.
高知大(医)過去問
この動画を見る
$ a_1=1,a_2=5,a_{n+2}=4a_{n+1}-3a_n-4$
の一般項$a_n$を求めよ.
高知大(医)過去問
東京女子大 漸化式・数列の最大値

単元:
#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a_1$は7であり,$n^2a_{n+1}-(n+1)^2a_n=-n^2(n+1)^2$である.
(1)$a_n$の一般項を求めよ.
(2)$a_n$の最大値を求めよ.
東京女子大過去問
この動画を見る
$ a_1$は7であり,$n^2a_{n+1}-(n+1)^2a_n=-n^2(n+1)^2$である.
(1)$a_n$の一般項を求めよ.
(2)$a_n$の最大値を求めよ.
東京女子大過去問
室蘭工業大 漸化式基本

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a_1=2,a_{n+1}=\dfrac{1}{2}a_n+\dfrac{4n+2^n}{2^{n+1}}$である.
$a_n\lt a_{n+1}$を満たす最大の自然数$n$を求めよ.
室蘭工業大過去問
この動画を見る
$ a_1=2,a_{n+1}=\dfrac{1}{2}a_n+\dfrac{4n+2^n}{2^{n+1}}$である.
$a_n\lt a_{n+1}$を満たす最大の自然数$n$を求めよ.
室蘭工業大過去問
福田の数学〜明治大学2022年全学部統一入試12AB第3問〜漸化式の図形への応用

単元:
#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数列#漸化式#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
(1)三角形$ABC$の内接円が辺$AB$と接する点をPとし、
辺$BC$と接する点を$Q$とし、辺$CA$と接する点をRとする。
$\angle A$の大きさを$θ$とすると、$\angle APR=\boxed{ア}$であり、
$\angle PQR=\boxed{ア}$である。
$\boxed{ア}$の解答群
$⓪0 ①\frac{\pi}{2} ②θ ③\frac{θ}{2} ④\frac{\pi}{2}-θ ⑤\frac{\pi-θ}{2}$
$⑥\pi-\frac{θ}{2} ⑦\pi-θ ⑧\frac{\pi-3θ}{2} ⑨\frac{\pi}{2}-3θ$
(2)三角形$T_1$の3つの角のうち、角の大きさが最小のものは$\frac{\pi}{6}$で、
最大のものは$\frac{\pi}{2}$であるとする。
$n=1,\ 2,\ 3,\ ...$について、三角形$T_n$の内接円を$O_n$とし、
$T_n$と$O_n$とが接する3つの点を頂点とするような三角形を$T_{n+1}$とする。
このとき、三角形$T_2$の3つの角のうち、
角の大きさが最小のものは$\frac{\pi}{\boxed{イ}}$で、
最大のものは$\frac{\boxed{ウ}\ \pi}{\boxed{エオ}}$である。
$n=1,\ 2,\ 3,\ ...$について、三角形$T_n$の3つの角のうち、
角の大きさが最小のものを$a_n$とし、最大のものを$b_n$とする。三角形$T_{n+1}$について、
$a_{n+1}=\boxed{カ},\ \ \ b_{n+1}=\boxed{キ}$
と表せる。この式より
$a_n+b_n=\frac{\boxed{ク}}{\boxed{ケ}}\pi,$
$b_n-a_n=\frac{\pi}{\boxed{コ}・\boxed{サ}^{n-1}}$
であり、$a_n=\frac{\pi}{\boxed{シ}}(1-\frac{1}{\boxed{ス}^n}) $である。
$\boxed{カ}、\boxed{キ}$の解答群
$⓪\frac{a_n}{2} ①\frac{b_n}{2} ②\frac{\pi}{2}-a_n ③\frac{\pi}{2}-b_n ④\frac{\pi-a_n}{2}$
$⑤\frac{\pi-b_n}{2} ⑥\pi-\frac{a_n}{2} ⑦\pi-\frac{b_n}{2} ⑧\pi-a_n ⑨\pi-b_n$
2022明治大学全統過去問
この動画を見る
(1)三角形$ABC$の内接円が辺$AB$と接する点をPとし、
辺$BC$と接する点を$Q$とし、辺$CA$と接する点をRとする。
$\angle A$の大きさを$θ$とすると、$\angle APR=\boxed{ア}$であり、
$\angle PQR=\boxed{ア}$である。
$\boxed{ア}$の解答群
$⓪0 ①\frac{\pi}{2} ②θ ③\frac{θ}{2} ④\frac{\pi}{2}-θ ⑤\frac{\pi-θ}{2}$
$⑥\pi-\frac{θ}{2} ⑦\pi-θ ⑧\frac{\pi-3θ}{2} ⑨\frac{\pi}{2}-3θ$
(2)三角形$T_1$の3つの角のうち、角の大きさが最小のものは$\frac{\pi}{6}$で、
最大のものは$\frac{\pi}{2}$であるとする。
$n=1,\ 2,\ 3,\ ...$について、三角形$T_n$の内接円を$O_n$とし、
$T_n$と$O_n$とが接する3つの点を頂点とするような三角形を$T_{n+1}$とする。
このとき、三角形$T_2$の3つの角のうち、
角の大きさが最小のものは$\frac{\pi}{\boxed{イ}}$で、
最大のものは$\frac{\boxed{ウ}\ \pi}{\boxed{エオ}}$である。
$n=1,\ 2,\ 3,\ ...$について、三角形$T_n$の3つの角のうち、
角の大きさが最小のものを$a_n$とし、最大のものを$b_n$とする。三角形$T_{n+1}$について、
$a_{n+1}=\boxed{カ},\ \ \ b_{n+1}=\boxed{キ}$
と表せる。この式より
$a_n+b_n=\frac{\boxed{ク}}{\boxed{ケ}}\pi,$
$b_n-a_n=\frac{\pi}{\boxed{コ}・\boxed{サ}^{n-1}}$
であり、$a_n=\frac{\pi}{\boxed{シ}}(1-\frac{1}{\boxed{ス}^n}) $である。
$\boxed{カ}、\boxed{キ}$の解答群
$⓪\frac{a_n}{2} ①\frac{b_n}{2} ②\frac{\pi}{2}-a_n ③\frac{\pi}{2}-b_n ④\frac{\pi-a_n}{2}$
$⑤\frac{\pi-b_n}{2} ⑥\pi-\frac{a_n}{2} ⑦\pi-\frac{b_n}{2} ⑧\pi-a_n ⑨\pi-b_n$
2022明治大学全統過去問
福田の数学〜早稲田大学2022年商学部第1問(3)〜漸化式で与えられた数列の項の値

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(3)$a$を実数とする。
数列$\left\{a_n\right\}$が次の条件を満たしている。
$(\textrm{i})a_1=a$
$(\textrm{ii})a_{n+1}=a_n^2-2a_n-3(n=1,2,3,\ldots)$
このとき、すべての正の整数$n$に対して、$a_n \leqq 10$となるような
$a$の最小値は$\boxed{\ \ ウ\ \ }$である。
2022早稲田大学商学部過去問
この動画を見る
${\large\boxed{1}}$(3)$a$を実数とする。
数列$\left\{a_n\right\}$が次の条件を満たしている。
$(\textrm{i})a_1=a$
$(\textrm{ii})a_{n+1}=a_n^2-2a_n-3(n=1,2,3,\ldots)$
このとき、すべての正の整数$n$に対して、$a_n \leqq 10$となるような
$a$の最小値は$\boxed{\ \ ウ\ \ }$である。
2022早稲田大学商学部過去問
福田の数学〜早稲田大学2022年商学部第1問(1)〜漸化式の解法

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#数列#漸化式#数学的帰納法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(1)数列$\left\{a_n\right\}$が次の条件を満たしている。
$(\textrm{i})a_1=a_2=4$
$(\textrm{ii})a_{n+2}=a_n^{\log_2a_{n+1}} (n=1,2,3,\ldots)$
このとき、$\log_2(\log_2a_{10})=\boxed{\ \ ア\ \ }$である。
2022早稲田大学商学部過去問
この動画を見る
${\large\boxed{1}}$(1)数列$\left\{a_n\right\}$が次の条件を満たしている。
$(\textrm{i})a_1=a_2=4$
$(\textrm{ii})a_{n+2}=a_n^{\log_2a_{n+1}} (n=1,2,3,\ldots)$
このとき、$\log_2(\log_2a_{10})=\boxed{\ \ ア\ \ }$である。
2022早稲田大学商学部過去問
福田の数学〜早稲田大学2022年理工学部第3問〜漸化式と数列の極限

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{3}}\ r$を実数とする。
次の条件によって定められる数列$\left\{a_n\right\},\left\{b_n\right\},\left\{c_n\right\}$を考える。
$a_1=r,a_{n+1}=\frac{[a_n]}{4}+\frac{a_n}{4}+\frac{5}{6}(n=1,2,3,\ldots)$
$b_1=r,b_{n+1}=\frac{b_n}{2}+\frac{7}{12}(n=1,2,3,\ldots)$
$c_1=r,c_{n+1}=\frac{c_n}{2}+\frac{5}{6}(n=1,2,3,\ldots)$
ただし、$[x]$はxを超えない最大の整数とする。以下の問いに答えよ。
(1)$\lim_{n \to \infty}b_n$と$\lim_{n \to \infty}c_n$を求めよ。
(2)$b_n \leqq a_n \leqq c_n (n=1,2,3,\ldots)$を示せ。
(3)$\lim_{n \to \infty}a_n$を求めよ。
2022早稲田大学理工学部過去問
この動画を見る
${\large\boxed{3}}\ r$を実数とする。
次の条件によって定められる数列$\left\{a_n\right\},\left\{b_n\right\},\left\{c_n\right\}$を考える。
$a_1=r,a_{n+1}=\frac{[a_n]}{4}+\frac{a_n}{4}+\frac{5}{6}(n=1,2,3,\ldots)$
$b_1=r,b_{n+1}=\frac{b_n}{2}+\frac{7}{12}(n=1,2,3,\ldots)$
$c_1=r,c_{n+1}=\frac{c_n}{2}+\frac{5}{6}(n=1,2,3,\ldots)$
ただし、$[x]$はxを超えない最大の整数とする。以下の問いに答えよ。
(1)$\lim_{n \to \infty}b_n$と$\lim_{n \to \infty}c_n$を求めよ。
(2)$b_n \leqq a_n \leqq c_n (n=1,2,3,\ldots)$を示せ。
(3)$\lim_{n \to \infty}a_n$を求めよ。
2022早稲田大学理工学部過去問
福田の数学〜慶應義塾大学2022年看護医療学部第2問(2)〜漸化式と和に関する不等式

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{2}}$(2)$a_1=4,\ \ \ 4a_{n+1}=2a_n+3(n=1,2,3,\ldots)$で与えられる
数列$\left\{a_n\right\}$の一般項は$a_n=\boxed{\ \ ア\ \ }$である。
また$\sum_{n=1}^la_n \geqq 20$
を満たす最小の自然数lは$\boxed{\ \ イ\ \ }$である。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{2}}$(2)$a_1=4,\ \ \ 4a_{n+1}=2a_n+3(n=1,2,3,\ldots)$で与えられる
数列$\left\{a_n\right\}$の一般項は$a_n=\boxed{\ \ ア\ \ }$である。
また$\sum_{n=1}^la_n \geqq 20$
を満たす最小の自然数lは$\boxed{\ \ イ\ \ }$である。
2022慶應義塾大学看護医療学科過去問
【よく出る応用問題!】f(n)の絡む漸化式を5分で解説!〔数学、高校数学〕

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
3rd School
問題文全文(内容文):
f(n)の絡む漸化式について解説します。
以下の漸化式で表される数列の一般項を求めよ。
$a_{n+1}=2a_n+3n-3$ $a_1=1$
この動画を見る
f(n)の絡む漸化式について解説します。
以下の漸化式で表される数列の一般項を求めよ。
$a_{n+1}=2a_n+3n-3$ $a_1=1$
大学入試問題#250 福井大学(2012) #定積分
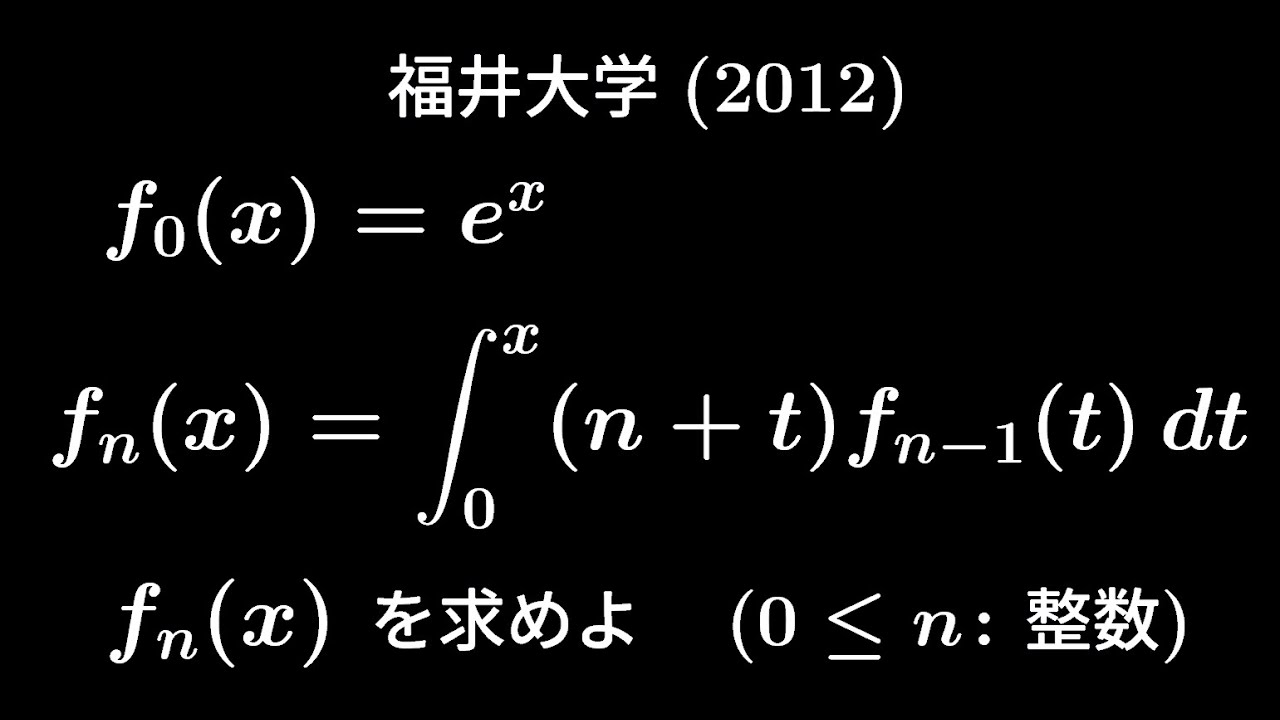
単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#数列#漸化式#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福井大学#数B#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$n$を0以上の整数とする。
次の2つの条件をみたす関数$f_n(x)$を求めよ。
(ⅰ)$f_0(x)=e^x$
(ⅱ)$f_n(x)=\displaystyle \int_{0}^{x}(n+t)f_{n-1}(t)dt$
出典:2012年福井大学 入試問題
この動画を見る
$n$を0以上の整数とする。
次の2つの条件をみたす関数$f_n(x)$を求めよ。
(ⅰ)$f_0(x)=e^x$
(ⅱ)$f_n(x)=\displaystyle \int_{0}^{x}(n+t)f_{n-1}(t)dt$
出典:2012年福井大学 入試問題
【よく出る!】分数型の漸化式はこれで一撃!〔数学、高校数学〕

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
3rd School
問題文全文(内容文):
以下の漸化式で表される数列の一般項を求めよ。
$a_{n+1}=\frac{2a_n}{3a_n+1}$ $a_1=1$
この動画を見る
以下の漸化式で表される数列の一般項を求めよ。
$a_{n+1}=\frac{2a_n}{3a_n+1}$ $a_1=1$
【テストによく出る!】漸化式の典型問題はこう解く!〔数学、高校数学〕

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
3rd School
問題文全文(内容文):
以下の漸化式で表される数列の一般項を求めよ。
$a_{n+1}=2a_n+3$ $a_1=1$
この動画を見る
以下の漸化式で表される数列の一般項を求めよ。
$a_{n+1}=2a_n+3$ $a_1=1$
福田の数学〜慶應義塾大学2022年経済学部第2問〜絶対値を含む漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$数列$\left\{a_n\right\}$は
$a_{n+1}=-|a_n|-\frac{1}{2}a_n+5\hspace{15pt}(n=1,2,3,\ldots)$
を満たしている。
(1)$a_1=\frac{1}{2}$ならば、$a_2=\frac{\boxed{\ \ アイ\ \ }}{\boxed{\ \ ウ\ \ }},\ a_3=-\frac{\boxed{\ \ エオ\ \ }}{\boxed{\ \ カ\ \ }}$である。
(2)$-2 \leqq a_n \leqq -1$ならば$a_{n+1}$および$a_{n+2}$の取り得る値の範囲は、
それぞれ$\boxed{\ \ キ\ \ }\leqq a_{n+1} \leqq \frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }},\ -\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\leqq a_{n+1} \leqq -\boxed{\ \ シ\ \ }$である。
以下、$a_1=2+(\frac{2}{3})^{10}$とする。
(3)$a_n \lt 0$となる自然数nの内最小のものをmとすると、$m=\boxed{\ \ スセ\ \ }$である。
(4)(3)の$m$に対して、自然数kが$2k \geqq m$を満たすとき、
$a_{2k+2}=-\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}\ a_{2k}-\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$
より
$a_{2k}=-\frac{\boxed{\ \ テト\ \ }}{\boxed{\ \ ナ\ \ }}+\frac{3}{\boxed{\ \ ニヌ\ \ }}(-\frac{\boxed{\ \ ネ\ \ }}{\boxed{\ \ ノ\ \ }})^{k-\boxed{\ \ ハ\ \ }}$
が成り立つ。
2022慶應義塾大学経済学部過去問
この動画を見る
${\Large\boxed{2}}$数列$\left\{a_n\right\}$は
$a_{n+1}=-|a_n|-\frac{1}{2}a_n+5\hspace{15pt}(n=1,2,3,\ldots)$
を満たしている。
(1)$a_1=\frac{1}{2}$ならば、$a_2=\frac{\boxed{\ \ アイ\ \ }}{\boxed{\ \ ウ\ \ }},\ a_3=-\frac{\boxed{\ \ エオ\ \ }}{\boxed{\ \ カ\ \ }}$である。
(2)$-2 \leqq a_n \leqq -1$ならば$a_{n+1}$および$a_{n+2}$の取り得る値の範囲は、
それぞれ$\boxed{\ \ キ\ \ }\leqq a_{n+1} \leqq \frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }},\ -\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\leqq a_{n+1} \leqq -\boxed{\ \ シ\ \ }$である。
以下、$a_1=2+(\frac{2}{3})^{10}$とする。
(3)$a_n \lt 0$となる自然数nの内最小のものをmとすると、$m=\boxed{\ \ スセ\ \ }$である。
(4)(3)の$m$に対して、自然数kが$2k \geqq m$を満たすとき、
$a_{2k+2}=-\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}\ a_{2k}-\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$
より
$a_{2k}=-\frac{\boxed{\ \ テト\ \ }}{\boxed{\ \ ナ\ \ }}+\frac{3}{\boxed{\ \ ニヌ\ \ }}(-\frac{\boxed{\ \ ネ\ \ }}{\boxed{\ \ ノ\ \ }})^{k-\boxed{\ \ ハ\ \ }}$
が成り立つ。
2022慶應義塾大学経済学部過去問
大学入試問題#233 岡山県立大学(2012) #数列

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#岡山県立大学
指導講師:
ますただ
問題文全文(内容文):
$a_1=1$
$a_{n+1}=\displaystyle \frac{4}{n}S_n$
一般項$a_n$を求めよ。
出典:2012年岡山県立大学 入試問題
この動画を見る
$a_1=1$
$a_{n+1}=\displaystyle \frac{4}{n}S_n$
一般項$a_n$を求めよ。
出典:2012年岡山県立大学 入試問題
福田の入試問題解説〜慶應義塾大学2022年医学部第1問(4)〜合成関数と漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
(4)数列$\left\{a_n\right\},\left\{b_n\right\}$(ただし$a_1\neq 0$かつ$a_1\neq 1$)に対して1次関数
$f_n(x)=a_nx+b_n (n=1,2,\ldots)$
を定める。また、$\alpha=a_1, \beta=b_1$とおく。すべての自然数nに対して
$(f_n◦f_1)(x)=f_{n+1}(x)$
が成り立つとき、数列$\left\{a_n\right\},\left\{b_n\right\}$の一般項を$\alpha$と$\beta$の式で表すと
$a_n=\boxed{\ \ ク\ \ }, b_n=\boxed{\ \ ケ\ \ }$
となる。
2022慶應義塾大学医学部過去問
この動画を見る
(4)数列$\left\{a_n\right\},\left\{b_n\right\}$(ただし$a_1\neq 0$かつ$a_1\neq 1$)に対して1次関数
$f_n(x)=a_nx+b_n (n=1,2,\ldots)$
を定める。また、$\alpha=a_1, \beta=b_1$とおく。すべての自然数nに対して
$(f_n◦f_1)(x)=f_{n+1}(x)$
が成り立つとき、数列$\left\{a_n\right\},\left\{b_n\right\}$の一般項を$\alpha$と$\beta$の式で表すと
$a_n=\boxed{\ \ ク\ \ }, b_n=\boxed{\ \ ケ\ \ }$
となる。
2022慶應義塾大学医学部過去問
【漸化式ニガテな人は見て!】漸化式の見方の基礎はこれだけです〔数学、高校数学〕

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
3rd School
問題文全文(内容文):
以下の漸化式で表される数列の一般項を求めよ。
(1)$a_{n+1}=a_n+3$ $a_1=2$
(2)$a_{n+1}=2a_n$ $a_1=1$
この動画を見る
以下の漸化式で表される数列の一般項を求めよ。
(1)$a_{n+1}=a_n+3$ $a_1=2$
(2)$a_{n+1}=2a_n$ $a_1=1$
東北大文系 虚数のナイスな問題

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#数列#漸化式#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
pは0でない実数である.$x^2-px+5p=0$の解を$\alpha,\beta$とする.
(1)$\alpha^5+\beta^5=p\5$となるpを求めよ.
(2)$\alpha$は虚数で$\alpha^5$が実数となるpを求めよ.
東北大文系過去問
この動画を見る
pは0でない実数である.$x^2-px+5p=0$の解を$\alpha,\beta$とする.
(1)$\alpha^5+\beta^5=p\5$となるpを求めよ.
(2)$\alpha$は虚数で$\alpha^5$が実数となるpを求めよ.
東北大文系過去問
中学生でも解ける京大の入試問題!解けますか?【数学 入試問題】【京都大学】

単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#数列#漸化式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
1歩で1段または2段のいずれかで階段を昇るとき、1歩で2段昇ることは連続しないものとする。15段の階段を昇る昇り方は何通りあるか。
京都大過去問
この動画を見る
1歩で1段または2段のいずれかで階段を昇るとき、1歩で2段昇ることは連続しないものとする。15段の階段を昇る昇り方は何通りあるか。
京都大過去問
福田の数学〜浜松医科大学2022年医学部第4問〜確率漸化式と誤った答案に対する指摘

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
次の問題
問題
表面と裏面が出る確率がそれぞれであるコインを投げる試行を繰り返し、同
じ面が3回連続して出た時点で試行を終了する。n回投げ終えた段階で試行が
終了する確率 $p_n$を求めよ。
に対する次の答案Aについて以下の問いに答えよ。
(1) もし答案Aに誤りがあれば誤りを指摘し、その理由を述べよ。ただし、すでに
指摘してある誤った結論から論理的に導き出した結論を誤りとして指摘する必要
はない。誤りがないときは「誤りなし」と答えよ。
(2) 答案Aで導かれたp_nと正解の$p_n$とで値が異なるとき、値が異なる最小のnを
求め、そのnに対する正解のpnの値を答えよ。そのようなnがないときは
「すべて一致する」と答えよ。
答案A
自然数nに対して、コインをn回投げ終えた段階で、その後最短で試行が終了するために
必要な回数がk回($k \geqq 0$)である確率を$p_n(k)$とする。このとき、
kは0,1,2のいずれかであるから、確率の総和は
$p_n(0)+p_n(1)+p_n(2)=1$
である。また、$p_n(0)=p_n,p_{n+1}(0)=\frac{1}{2}p_n(1),p_{n+2}(0)=\frac{1}{4}p_n(2)$であるから漸化式
$p_n+2p_{n+1}+4p_{n+2}=1 (n \geqq 1)$
を得る。ここで$\frac{1}{7}+\frac{2}{7}+\frac{4}{7}=1$なので、$q_n=2^n(p_n-\frac{1}{7})$とすれば
$q_n+q_{n+1}+q_{n+2}=0$
である。よって$n \geqq 4$に対して
$q_n=-q_{n-1}-q_{n-2}=(q_{n-2}+q_{n-3})-q_{n-2}=q_{n-3}$
が成立する。以上より、
$Q(x)=
\left\{
\begin{array}{1}q_1 (nを3で割った時の余りが1のとき)\\
q_2 (nを3で割った時の余りが2のとき)\\
q_3 (nが3で割り切れるとき)\\
\end{array}
\right.$
とすれば求める確率は
$p_n=\frac{q_n}{2^n}+\frac{1}{7}=\frac{Q(n)}{2^n}+\frac{1}{7} (n \geqq 4)$
である。また最初の2項は定義より$p_1=p_2=0$であり$p_n$の漸化式で$n=1$とすれば
$p_1+2p_2+4p_3=1$ であるから$p_3=\frac{1}{4}$である。さらに
$q_1=-\frac{2}{7}, q_2=-\frac{4}{7}, q_3=\frac{6}{7}$
である。したがって
$p_1=p_2=0, p_3=\frac{1}{4}, p_n=\frac{Q(n)}{2^n}+\frac{1}{7} (n \geqq 4)$
となる。
2022浜松医科大学医学部過去問
この動画を見る
次の問題
問題
表面と裏面が出る確率がそれぞれであるコインを投げる試行を繰り返し、同
じ面が3回連続して出た時点で試行を終了する。n回投げ終えた段階で試行が
終了する確率 $p_n$を求めよ。
に対する次の答案Aについて以下の問いに答えよ。
(1) もし答案Aに誤りがあれば誤りを指摘し、その理由を述べよ。ただし、すでに
指摘してある誤った結論から論理的に導き出した結論を誤りとして指摘する必要
はない。誤りがないときは「誤りなし」と答えよ。
(2) 答案Aで導かれたp_nと正解の$p_n$とで値が異なるとき、値が異なる最小のnを
求め、そのnに対する正解のpnの値を答えよ。そのようなnがないときは
「すべて一致する」と答えよ。
答案A
自然数nに対して、コインをn回投げ終えた段階で、その後最短で試行が終了するために
必要な回数がk回($k \geqq 0$)である確率を$p_n(k)$とする。このとき、
kは0,1,2のいずれかであるから、確率の総和は
$p_n(0)+p_n(1)+p_n(2)=1$
である。また、$p_n(0)=p_n,p_{n+1}(0)=\frac{1}{2}p_n(1),p_{n+2}(0)=\frac{1}{4}p_n(2)$であるから漸化式
$p_n+2p_{n+1}+4p_{n+2}=1 (n \geqq 1)$
を得る。ここで$\frac{1}{7}+\frac{2}{7}+\frac{4}{7}=1$なので、$q_n=2^n(p_n-\frac{1}{7})$とすれば
$q_n+q_{n+1}+q_{n+2}=0$
である。よって$n \geqq 4$に対して
$q_n=-q_{n-1}-q_{n-2}=(q_{n-2}+q_{n-3})-q_{n-2}=q_{n-3}$
が成立する。以上より、
$Q(x)=
\left\{
\begin{array}{1}q_1 (nを3で割った時の余りが1のとき)\\
q_2 (nを3で割った時の余りが2のとき)\\
q_3 (nが3で割り切れるとき)\\
\end{array}
\right.$
とすれば求める確率は
$p_n=\frac{q_n}{2^n}+\frac{1}{7}=\frac{Q(n)}{2^n}+\frac{1}{7} (n \geqq 4)$
である。また最初の2項は定義より$p_1=p_2=0$であり$p_n$の漸化式で$n=1$とすれば
$p_1+2p_2+4p_3=1$ であるから$p_3=\frac{1}{4}$である。さらに
$q_1=-\frac{2}{7}, q_2=-\frac{4}{7}, q_3=\frac{6}{7}$
である。したがって
$p_1=p_2=0, p_3=\frac{1}{4}, p_n=\frac{Q(n)}{2^n}+\frac{1}{7} (n \geqq 4)$
となる。
2022浜松医科大学医学部過去問
福田の数学〜筑波大学2022年理系第2問〜確率漸化式と常用対数

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数B
指導講師:
福田次郎
問題文全文(内容文):
整数$\ a_1,\ a_2,\ a_3,\ \ldots$を、さいころをくり返し投げることにより、以下のように
定めていく。まず$a_1=1$とする。そして、正の整数$n$に対し、$a_{n+1}$の値を、n回目に
出たさいころの目に応じて、次の規則で定める。
$(\ 規則\ )$ n回目に出た目が1,2,3,4なら$a_{n+1}=a_n、5,6$なら$a_{n+1}=-a_n$
例えば、さいころを3回投げ、その出た目が順に5,3,6であったとすると、
$a_1=1,a_2=-1,a_3=-1,a_4=1$となる。
$a_n=1$となる確率を$p_n$とする。ただし、$p_1=1$とし、さいころのどの目も、
出る確率は$\frac{1}{6}$であるとする。
(1)$p_2,p_3$を求めよ。
(2)$p_{n+1}$を$p_n$を用いて表せ。
(3)$p_n \leqq 0.5000005$を満たす最小の正の整数nを求めよ。
ただし、$0.47 \lt \log_{10}3 \lt 0.48$であることを用いてよい。
2022筑波大学理系過去問
この動画を見る
整数$\ a_1,\ a_2,\ a_3,\ \ldots$を、さいころをくり返し投げることにより、以下のように
定めていく。まず$a_1=1$とする。そして、正の整数$n$に対し、$a_{n+1}$の値を、n回目に
出たさいころの目に応じて、次の規則で定める。
$(\ 規則\ )$ n回目に出た目が1,2,3,4なら$a_{n+1}=a_n、5,6$なら$a_{n+1}=-a_n$
例えば、さいころを3回投げ、その出た目が順に5,3,6であったとすると、
$a_1=1,a_2=-1,a_3=-1,a_4=1$となる。
$a_n=1$となる確率を$p_n$とする。ただし、$p_1=1$とし、さいころのどの目も、
出る確率は$\frac{1}{6}$であるとする。
(1)$p_2,p_3$を求めよ。
(2)$p_{n+1}$を$p_n$を用いて表せ。
(3)$p_n \leqq 0.5000005$を満たす最小の正の整数nを求めよ。
ただし、$0.47 \lt \log_{10}3 \lt 0.48$であることを用いてよい。
2022筑波大学理系過去問
福田の数学〜千葉大学2022年理系第7問〜不定方程式の自然数解と漸化式で与えられた数列

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$x,y$についての方程式
$x^2-6xy+y^2=9 \ldots\ldots(*)$
に関する次の問いに答えよ。
(1)$x,y$がともに正の整数であるような(*)の解のうち、yが最小であるものを
求めよ。
(2)数列$a_1,a_2,a_3,\ldots$が漸化式
$a_{n+2}-6a_{n+1}+a_n=0 (n=1,2,3,\ldots)$
を満たすとする。このとき、$(x,y)=(a_{n+1},a_n)$が(*)を満たすならば、
$(x,y)=(a_{n+2},a_{n+1})$も(*)を満たすことを示せ。
(3)(*)の整数解(x,y)は無数に存在することを示せ。
2022千葉大学理系過去問
この動画を見る
$x,y$についての方程式
$x^2-6xy+y^2=9 \ldots\ldots(*)$
に関する次の問いに答えよ。
(1)$x,y$がともに正の整数であるような(*)の解のうち、yが最小であるものを
求めよ。
(2)数列$a_1,a_2,a_3,\ldots$が漸化式
$a_{n+2}-6a_{n+1}+a_n=0 (n=1,2,3,\ldots)$
を満たすとする。このとき、$(x,y)=(a_{n+1},a_n)$が(*)を満たすならば、
$(x,y)=(a_{n+2},a_{n+1})$も(*)を満たすことを示せ。
(3)(*)の整数解(x,y)は無数に存在することを示せ。
2022千葉大学理系過去問
大阪府立大 漸化式と数学的帰納法・合同式の基本問題

単元:
#大学入試過去問(数学)#漸化式#大阪府立大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 3(a_n+1)+4^{2n-1}$は13の倍数であることを示せ.
大阪府立大(経済)過去問
この動画を見る
$ 3(a_n+1)+4^{2n-1}$は13の倍数であることを示せ.
大阪府立大(経済)過去問
福田の数学〜神戸大学2022年理系第1問〜3項間の漸化式と極限

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数列$\left\{a_n\right\}$を$a_1=1,a_2=2,a_{n+2}=\sqrt{a_{n+1}・a_n} (n=1,2,3,\ldots)$によって定める。
以下の問いに答えよ。
(1)全ての自然数$n$について$a_{n+1}=\frac{2}{\sqrt{a_n}}$が成り立つことを示せ。
(2)数列$\left\{b_n\right\}$を$b_n=\log a_n (n=1,2,3,\ldots)$によって定める。
$b_n$の値を$n$を用いて表せ。
(3)極限値$\lim_{n \to \infty}a_n$を求めよ。
2022神戸大学理系過去問
この動画を見る
数列$\left\{a_n\right\}$を$a_1=1,a_2=2,a_{n+2}=\sqrt{a_{n+1}・a_n} (n=1,2,3,\ldots)$によって定める。
以下の問いに答えよ。
(1)全ての自然数$n$について$a_{n+1}=\frac{2}{\sqrt{a_n}}$が成り立つことを示せ。
(2)数列$\left\{b_n\right\}$を$b_n=\log a_n (n=1,2,3,\ldots)$によって定める。
$b_n$の値を$n$を用いて表せ。
(3)極限値$\lim_{n \to \infty}a_n$を求めよ。
2022神戸大学理系過去問
cos1°は有理数か【数学 入試問題】【チェビシェフ多項式】

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#集合と命題(集合・命題と条件・背理法)#三角関数#加法定理とその応用#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学#数B
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(1)$n$を自然数とする。
$cos(n+2)\theta+cos n\theta=2cos(n+1)\theta cos\theta$を示せ。
(2)自然数$n$に対し、$cosn\theta=T_n(cos\theta)$を満たす整数係数の$n$次の整式$T_n(x)$が存在することを示せ。
(3)$cos1°$が無理数であることを証明せよ。
数学入試問題過去問
この動画を見る
(1)$n$を自然数とする。
$cos(n+2)\theta+cos n\theta=2cos(n+1)\theta cos\theta$を示せ。
(2)自然数$n$に対し、$cosn\theta=T_n(cos\theta)$を満たす整数係数の$n$次の整式$T_n(x)$が存在することを示せ。
(3)$cos1°$が無理数であることを証明せよ。
数学入試問題過去問
福田の数学〜大阪大学2022年理系第4問〜漸化式とはさみうちの原理

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#関数の極限#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$f(x)=\log(x+1)+1$とする。以下の問いに答えよ。
(1)方程式$f(x)=x$は、$x \gt 0$の範囲でただ1つの解を
もつことを示せ。
(2)(1)の解を$\alpha$とする。実数$x$が$0 \lt x \lt \alpha$を満たすならば、
次の不等式が成り立つことを示せ。
$0 \lt \frac{\alpha-f(x)}{\alpha-x} \lt f'(x)$
(3)数列$\left\{x_n\right\}$を
$x_1=1, x_{n+1}=f(x_n) (n=1,2,3,\ldots\ldots)$
で定める。このとき、全ての自然数nに対して
$\alpha -x_{n+1} \lt \frac{1}{2}(\alpha -x_n)$
が成り立つことを示せ。
(4)(3)の数列$\left\{x_n\right\}$について、$\lim_{n \to \infty}x_n=\alpha$を示せ。
2022大阪大学理系過去問
この動画を見る
$f(x)=\log(x+1)+1$とする。以下の問いに答えよ。
(1)方程式$f(x)=x$は、$x \gt 0$の範囲でただ1つの解を
もつことを示せ。
(2)(1)の解を$\alpha$とする。実数$x$が$0 \lt x \lt \alpha$を満たすならば、
次の不等式が成り立つことを示せ。
$0 \lt \frac{\alpha-f(x)}{\alpha-x} \lt f'(x)$
(3)数列$\left\{x_n\right\}$を
$x_1=1, x_{n+1}=f(x_n) (n=1,2,3,\ldots\ldots)$
で定める。このとき、全ての自然数nに対して
$\alpha -x_{n+1} \lt \frac{1}{2}(\alpha -x_n)$
が成り立つことを示せ。
(4)(3)の数列$\left\{x_n\right\}$について、$\lim_{n \to \infty}x_n=\alpha$を示せ。
2022大阪大学理系過去問
福田の数学〜一橋大学2022年文系第5問〜確率漸化式

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
中身の見えない2つの箱があり、1つの箱には赤玉2つと白玉1つが入っており、
もう1つの箱には赤玉1つと白玉2つが入っている。どちらかの箱を選び、選んだ
箱の中から玉を1つ取り出して元に戻す、という操作を繰り返す。
(1) 1回目は箱を無作為に選び、2回目以降は、前回取り出した玉が赤玉なら前回
と同じ箱、前回取り出した玉が白玉なら前回とは異なる箱を選ぶ。n回目に赤玉
を取り出す確率$p_n$を求めよ。
(2)1回目は箱を無作為に選び、2回目以降は、前回取り出した玉が赤玉なら前回
と同じ箱、前回取り出した玉が白玉なら箱を無作為に選ぶ。n回目に赤玉を取り
出す確率 $q_n$を求めよ。
2022一橋大学文系過去問
この動画を見る
中身の見えない2つの箱があり、1つの箱には赤玉2つと白玉1つが入っており、
もう1つの箱には赤玉1つと白玉2つが入っている。どちらかの箱を選び、選んだ
箱の中から玉を1つ取り出して元に戻す、という操作を繰り返す。
(1) 1回目は箱を無作為に選び、2回目以降は、前回取り出した玉が赤玉なら前回
と同じ箱、前回取り出した玉が白玉なら前回とは異なる箱を選ぶ。n回目に赤玉
を取り出す確率$p_n$を求めよ。
(2)1回目は箱を無作為に選び、2回目以降は、前回取り出した玉が赤玉なら前回
と同じ箱、前回取り出した玉が白玉なら箱を無作為に選ぶ。n回目に赤玉を取り
出す確率 $q_n$を求めよ。
2022一橋大学文系過去問
