 関数の極限
関数の極限
 関数の極限
関数の極限
福田のわかった数学〜高校3年生理系032〜極限(32)関数の極限、色々な極限(2)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{III} 色々な極限(2)\\
\lim_{x \to 2}([2x]-[x]) を求めよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{III} 色々な極限(2)\\
\lim_{x \to 2}([2x]-[x]) を求めよ。
\end{eqnarray}
福田のわかった数学〜高校3年生理系031〜極限(31)関数の極限、色々な極限(1)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{III} 色々な極限(1)\\
\lim_{x \to 1}\frac{(x-1)^2}{|x^2-1|} を求めよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{III} 色々な極限(1)\\
\lim_{x \to 1}\frac{(x-1)^2}{|x^2-1|} を求めよ。
\end{eqnarray}
15滋賀県教員採用試験(数学:5番 グラフと極限)
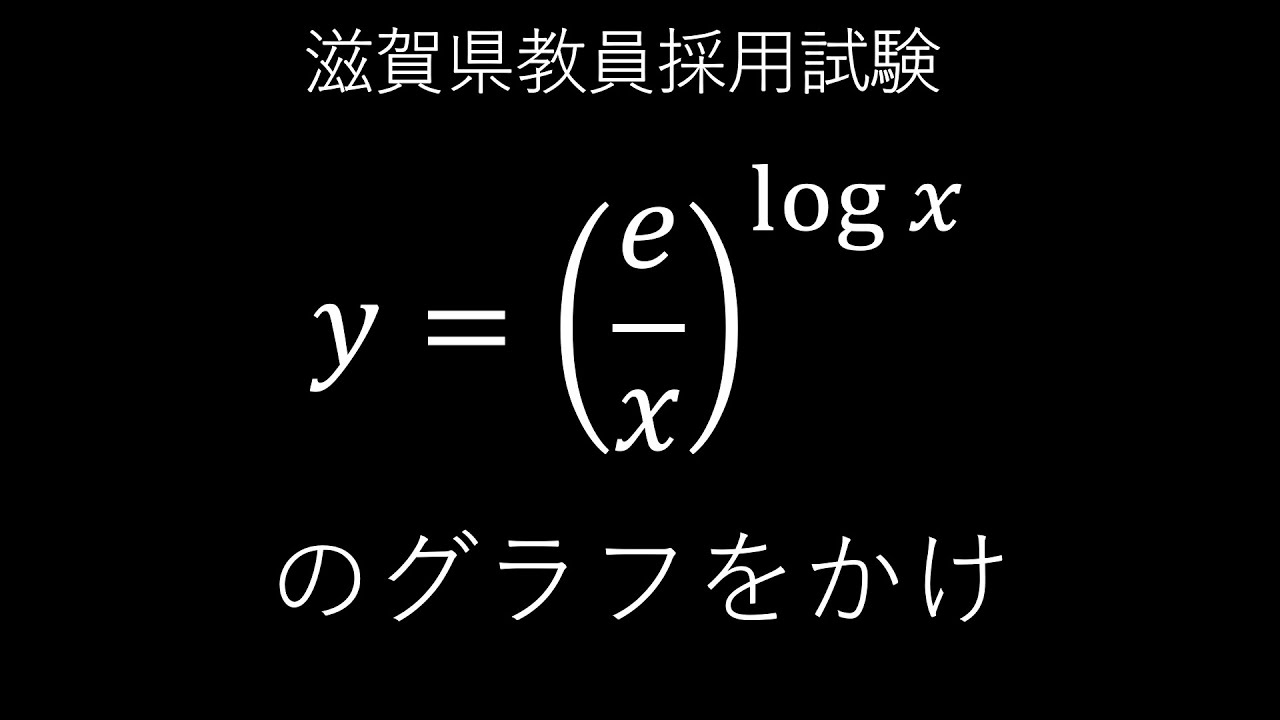
単元:
#関数と極限#微分とその応用#数列の極限#関数の極限#関数の変化(グラフ・最大最小・方程式・不等式)#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{5}$
$y=\left(\dfrac{e}{x}\right)^{\log x}$のグラフをかけ.
この動画を見る
$\boxed{5}$
$y=\left(\dfrac{e}{x}\right)^{\log x}$のグラフをかけ.
福田のわかった数学〜高校3年生理系030〜極限(30)関数の極限、三角関数の極限(10)

単元:
#数Ⅱ#三角関数#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 三角関数の極限(10)
$\displaystyle \lim_{x \to 0}\frac{\sqrt{9-8x+7\cos2x}-(a+bx)}{x^2}$
が有限の値となる$a,b$とそのときの極限値
この動画を見る
数学$\textrm{III}$ 三角関数の極限(10)
$\displaystyle \lim_{x \to 0}\frac{\sqrt{9-8x+7\cos2x}-(a+bx)}{x^2}$
が有限の値となる$a,b$とそのときの極限値
福田のわかった数学〜高校3年生理系029〜極限(29)関数の極限、三角関数の極限(9)
単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
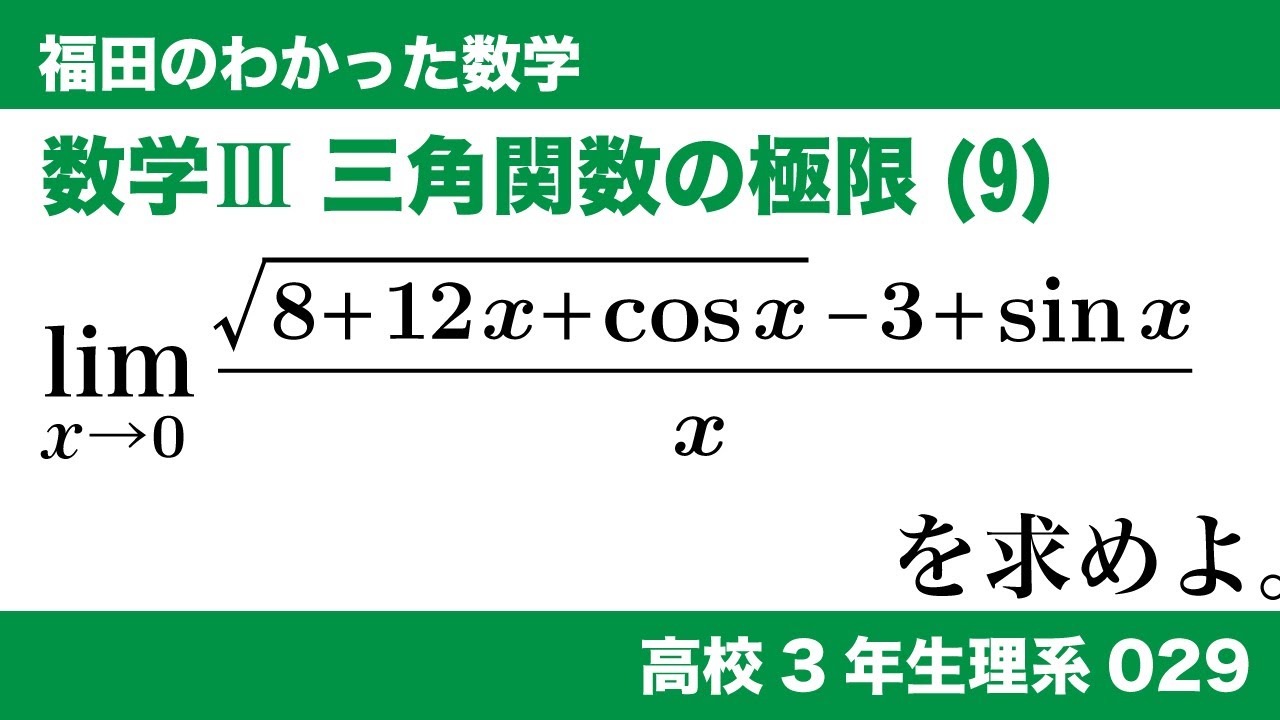
数学$\textrm{III}$ 三角関数の極限$(9)\\
\lim_{x \to 0}\frac{\sqrt{8+12x+\cos x}-3+\sin x}{x}$
を求めよ。
この動画を見る
数学$\textrm{III}$ 三角関数の極限$(9)\\
\lim_{x \to 0}\frac{\sqrt{8+12x+\cos x}-3+\sin x}{x}$
を求めよ。
福田のわかった数学〜高校3年生理系028〜極限(28)関数の極限、三角関数の極限(8)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{III} 三角関数の極限(8)\\
\\
\lim_{x \to 0}(\frac{\sin2x}{2x}-\frac{\sin3x}{3x}) を求めよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{III} 三角関数の極限(8)\\
\\
\lim_{x \to 0}(\frac{\sin2x}{2x}-\frac{\sin3x}{3x}) を求めよ。
\end{eqnarray}
福田のわかった数学〜高校3年生理系027〜極限(27)関数の極限、三角関数の極限(7)

単元:
#数Ⅱ#三角関数#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{III} 三角関数の極限(7)\\
\\
\lim_{x \to 0}\frac{\sin(2\sin x)}{3x(1+2x)} を求めよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{III} 三角関数の極限(7)\\
\\
\lim_{x \to 0}\frac{\sin(2\sin x)}{3x(1+2x)} を求めよ。
\end{eqnarray}
福田のわかった数学〜高校3年生理系026〜極限(26)関数の極限、三角関数の極限(6)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{III} 三角関数の極限(6)\\
\lim_{x \to \frac{\pi}{2}}\frac{1-\sin x}{(2x-\pi)^2} を求めよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{III} 三角関数の極限(6)\\
\lim_{x \to \frac{\pi}{2}}\frac{1-\sin x}{(2x-\pi)^2} を求めよ。
\end{eqnarray}
福田のわかった数学〜高校3年生理系025〜極限(25)関数の極限、三角関数の極限(5)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 三角関数の極限(5)
$\lim_{x \to 0}\displaystyle \frac{\tan x°}{x}$ を求めよ。
この動画を見る
数学$\textrm{III}$ 三角関数の極限(5)
$\lim_{x \to 0}\displaystyle \frac{\tan x°}{x}$ を求めよ。
福田のわかった数学〜高校3年生理系024〜極限(24)関数の極限、三角関数の極限(4)

単元:
#数Ⅱ#三角関数#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 三角関数の極限(4)
次の極限を求めよ。
(1)$\lim_{x \to 0}x\sin\displaystyle \frac{1}{x}$ (2)$\lim_{x \to -\infty}x\sin\displaystyle \frac{1}{x}$
この動画を見る
数学$\textrm{III}$ 三角関数の極限(4)
次の極限を求めよ。
(1)$\lim_{x \to 0}x\sin\displaystyle \frac{1}{x}$ (2)$\lim_{x \to -\infty}x\sin\displaystyle \frac{1}{x}$
福田のわかった数学〜高校3年生理系023〜極限(23)関数の極限、三角関数の極限(3)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 三角関数の極限(3)
$\lim_{\theta \to 0}\displaystyle \frac{\tan\theta-\sin\theta}{\theta^3}$ を求めよ。
この動画を見る
数学$\textrm{III}$ 三角関数の極限(3)
$\lim_{\theta \to 0}\displaystyle \frac{\tan\theta-\sin\theta}{\theta^3}$ を求めよ。
福田のわかった数学〜高校3年生理系022〜極限(22)関数の極限、三角関数の極限(2)

単元:
#関数と極限#微分とその応用#関数の極限#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 三角関数の極限(2)
$\sin x$ を定義に従って微分せよ。
この動画を見る
数学$\textrm{III}$ 三角関数の極限(2)
$\sin x$ を定義に従って微分せよ。
福田のわかった数学〜高校3年生理系021〜極限(21)関数の極限、三角関数の極限(1)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 三角関数の極限(1)
$\lim_{x \to 0}\displaystyle \frac{\sin\theta}{\theta}=1$ を証明せよ。
この動画を見る
数学$\textrm{III}$ 三角関数の極限(1)
$\lim_{x \to 0}\displaystyle \frac{\sin\theta}{\theta}=1$ を証明せよ。
福田のわかった数学〜高校3年生理系020〜極限(20)関数の極限、無理関数の極限(5)

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 無理関数の極限(5)
$\displaystyle\lim_{x \to \infty}(\sqrt{x^2+2x+3}-(ax+b))$
を求めよ。
この動画を見る
数学$\textrm{III}$ 無理関数の極限(5)
$\displaystyle\lim_{x \to \infty}(\sqrt{x^2+2x+3}-(ax+b))$
を求めよ。
福田のわかった数学〜高校3年生理系019〜極限(19)関数の極限、無理関数の極限(4)

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 無理関数の極限(4)
$\displaystyle \lim_{x \to -\infty}(\sqrt{x^2+x+1}-$$\sqrt{x^2-x+1})$ を求めよ。
この動画を見る
数学$\textrm{III}$ 無理関数の極限(4)
$\displaystyle \lim_{x \to -\infty}(\sqrt{x^2+x+1}-$$\sqrt{x^2-x+1})$ を求めよ。
福田のわかった数学〜高校3年生理系018〜極限(18)関数の極限、無理関数の極限(3)

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 無理関数の極限(3)
$\displaystyle \lim_{x \to \infty}(\sqrt{x^2+x+1}-$$\sqrt{x^2-x+1})$ を求めよ。
この動画を見る
数学$\textrm{III}$ 無理関数の極限(3)
$\displaystyle \lim_{x \to \infty}(\sqrt{x^2+x+1}-$$\sqrt{x^2-x+1})$ を求めよ。
福田のわかった数学〜高校3年生理系017〜関数の極限、無理関数の極限(2)

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 無理関数の極限(2)
$\lim_{x \to 1}\displaystyle \frac{\sqrt[3]x-1}{\sqrt x-1}$ を求めよ。
この動画を見る
数学$\textrm{III}$ 無理関数の極限(2)
$\lim_{x \to 1}\displaystyle \frac{\sqrt[3]x-1}{\sqrt x-1}$ を求めよ。
福田のわかった数学〜高校3年生理系016〜極限(16)関数の極限、無理関数の極限

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 極限(16)
$\lim_{x \to 1}\displaystyle \frac{\sqrt{x+8}-3}{\sqrt{x+3}-2}$ を求めよ。
この動画を見る
数学$\textrm{III}$ 極限(16)
$\lim_{x \to 1}\displaystyle \frac{\sqrt{x+8}-3}{\sqrt{x+3}-2}$ を求めよ。
福田のわかった数学〜高校3年生理系012〜極限(12)極限関数

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$f(x)$$=\displaystyle\lim_{ n \to \infty }\displaystyle \frac{\tan^{2n+1} x-\tan^n x+1}{\tan^{2n+2} x+\tan^{2n} x+1}$
$(0 \leqq x \lt \displaystyle\frac{\pi}{2})$のグラフをかけ。
この動画を見る
$f(x)$$=\displaystyle\lim_{ n \to \infty }\displaystyle \frac{\tan^{2n+1} x-\tan^n x+1}{\tan^{2n+2} x+\tan^{2n} x+1}$
$(0 \leqq x \lt \displaystyle\frac{\pi}{2})$のグラフをかけ。
福田のわかった数学〜高校3年生理系011〜極限(10)極限関数

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle\lim_{n \to \infty}\displaystyle \frac{1}{n}\displaystyle\sqrt[n]{{}_{2n}\mathrm{P}_{n}}$を求めよ。
この動画を見る
$\displaystyle\lim_{n \to \infty}\displaystyle \frac{1}{n}\displaystyle\sqrt[n]{{}_{2n}\mathrm{P}_{n}}$を求めよ。
17滋賀県教員採用試験 3番 極限について

単元:
#関数と極限#数列の極限#関数の極限#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{3}$
$\sqrt{\sqrt{3+{\sqrt{3+{\sqrt3+・・・}}}}}$の値を求めよ.
この動画を見る
$\boxed{3}$
$\sqrt{\sqrt{3+{\sqrt{3+{\sqrt3+・・・}}}}}$の値を求めよ.
#12数検1級1次過去問 極限(マクローリン展開)Σn^2/n!

単元:
#数学検定・数学甲子園・数学オリンピック等#関数と極限#数列の極限#関数の極限#数学検定#数学検定準1級#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\boxed{6}$
$\displaystyle \sum_{n=1}^{\infty}\dfrac{n^2}{n!}$を求めよ.
この動画を見る
$\boxed{6}$
$\displaystyle \sum_{n=1}^{\infty}\dfrac{n^2}{n!}$を求めよ.
#9数検準1級1次過去問 極限

単元:
#数学検定・数学甲子園・数学オリンピック等#関数と極限#数列の極限#関数の極限#数学検定#数学検定準1級#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\boxed{7}$
$\displaystyle \lim_{x\to 1}\dfrac{x^2+2x-3}{\sqrt[3]x-1}$を求めよ.
この動画を見る
$\boxed{7}$
$\displaystyle \lim_{x\to 1}\dfrac{x^2+2x-3}{\sqrt[3]x-1}$を求めよ.
慶應(理) 関数の極限

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#関数の極限#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x\gt 0,e a \fallingdotseq 2.71・・・$
(1)$\sqrt x \log_x \gt -1$を示せ.
(2)(1)を利用して$\displaystyle \lim_{x\to +0} x\log x=0$を示せ.
2019慶應(理)過去問
この動画を見る
$x\gt 0,e a \fallingdotseq 2.71・・・$
(1)$\sqrt x \log_x \gt -1$を示せ.
(2)(1)を利用して$\displaystyle \lim_{x\to +0} x\log x=0$を示せ.
2019慶應(理)過去問
【数Ⅲ】極限:ロピタルを使って極限を簡単に求める

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\displaystyle \lim_{x\to\infty}\dfrac{1-\cos 3x}{x^2}$を求めよ
この動画を見る
$\displaystyle \lim_{x\to\infty}\dfrac{1-\cos 3x}{x^2}$を求めよ
数検準1級2次(3番 極限値)

単元:
#数学検定・数学甲子園・数学オリンピック等#関数と極限#関数の極限#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\boxed{3}$
曲線$y=2\sqrt x$上の点$P(t,2\sqrt t)$に対して,
$y$軸上に$OP=OQ$をみたす点$Q$をとる.
直線$PQ$と$x$軸との支点を$R$とする.
$\displaystyle \lim_{t\to 0} \ OR$を求めよ.
図は動画内参照
この動画を見る
$\boxed{3}$
曲線$y=2\sqrt x$上の点$P(t,2\sqrt t)$に対して,
$y$軸上に$OP=OQ$をみたす点$Q$をとる.
直線$PQ$と$x$軸との支点を$R$とする.
$\displaystyle \lim_{t\to 0} \ OR$を求めよ.
図は動画内参照
数検準1級1次過去問【2020年12月】7番:極限値

単元:
#数学検定・数学甲子園・数学オリンピック等#関数と極限#関数の極限#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
7⃣$\displaystyle \lim_{ x \to \infty } x \{ log(x+2) - logx \}$
この動画を見る
7⃣$\displaystyle \lim_{ x \to \infty } x \{ log(x+2) - logx \}$
09愛知県教員採用試験(数学:2番 微積)

単元:
#関数と極限#微分とその応用#積分とその応用#関数の極限#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
2⃣ $0 \leqq x \leqq \frac{1}{\sqrt 3}$
$f(x)=\int_x^{\sqrt 3 x} \sqrt{1-t^2} dt$
(1)f(x)の最大値
(2)$\displaystyle \lim_{ x \to \infty } \frac{f(x)}{x}$
この動画を見る
2⃣ $0 \leqq x \leqq \frac{1}{\sqrt 3}$
$f(x)=\int_x^{\sqrt 3 x} \sqrt{1-t^2} dt$
(1)f(x)の最大値
(2)$\displaystyle \lim_{ x \to \infty } \frac{f(x)}{x}$
一橋大 3次関数の最大値

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#関数の極限#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^3-3ax^2+a$,$x\leqq 2$の範囲で$f(x)$の最大値が$105$となるような$a$の値を求めよ.
一橋大過去問
この動画を見る
$f(x)=x^3-3ax^2+a$,$x\leqq 2$の範囲で$f(x)$の最大値が$105$となるような$a$の値を求めよ.
一橋大過去問
数検準1級1次過去問(7番 極限値)

単元:
#数学検定・数学甲子園・数学オリンピック等#関数と極限#関数の極限#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
7⃣$\displaystyle \lim_{ n \to \infty } n \{ log(n+3) - logn \}$
$\displaystyle \lim_{ n \to \infty } (1+\frac{1}{n})^n = \displaystyle \lim_{ n \to 0 } (1+n)^{\frac{1}{n}}=e$
この動画を見る
7⃣$\displaystyle \lim_{ n \to \infty } n \{ log(n+3) - logn \}$
$\displaystyle \lim_{ n \to \infty } (1+\frac{1}{n})^n = \displaystyle \lim_{ n \to 0 } (1+n)^{\frac{1}{n}}=e$
