 関数と極限
関数と極限
 関数と極限
関数と極限
福田の数学〜ポリアの壺とは逆の試行における確率の極限〜杏林大学2023年医学部第1問後編〜確率漸化式と極限

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#杏林大学#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
複数の玉が人った袋から玉を 1 個取り出して袋に戻す事象を考える。どの玉も同じ確率で取り出されるものとし、nを自然数として、以下の間いに答えよ。
(1) 袋の中に赤玉 1 個と黒玉 2 個が入っている。この袋の中から玉を 1 個取り出し、取り出した玉と同じ色の玉をひとつ加え、合計 2 個の玉を袋に戻すという試行を繰り返す。n回目の試行において赤玉が取り出される確率を$p_{ n }$とすると、$p_{ 2 }=\dfrac{\fbox{ア}}{\fbox{イ}}, p_{ 3 }=\dfrac{\fbox{ウ}}{\fbox{エ}}$
( 2 )袋の中に赤玉 3 個と黒玉 2 個が人っている。この袋の中から玉を 1 個取り出し、赤玉と黒玉を 1 個ずつ、合計 2 個の球を袋に戻す試行を繰り返す。n回目の試行において赤玉が取り出される確率を$p_{ n }$とすると、次式が成り立つ。
$p_{ 2 }=\dfrac{\fbox{オカ}}{\fbox{キク}}, p_{ 3 }=\dfrac{\fbox{ケコ}}{\fbox{サシ}}$
n回目の試行開始時点で袋に人っている玉の個数$M_{ n } はM_{ n }=n+\fbox{ス}$であり、この時点で袋に入っていると期待される赤玉の個数$R_{ n }はR_{ n }=M_{ n }×P_{ n }$と表される。n回目の試行において、黒玉が取り出された場合にのみ、試行後の赤玉の個数が施行前と比べて$\fbox{セ}$個増えるため、n+ 1 回目の試行開始時点で袋に入っていると期待される赤玉の個数は$R_{ n+1 }=R_{ n }+(1-P_{ n })×\fbox{セ}$となる。したがって、
$P_{ n+1 }=\dfrac{n+\fbox{ソ}}{n+\fbox{タ}}×P_{ n }+\dfrac{1}{n+\fbox{チ}}$
が成り立つ。このことから、$(n+3)×(n+\fbox{ツ})×(P_{n}-\dfrac{\fbox{テ}}{\fbox{ト}})$がnに依らず一定となる事が分かり、$\displaystyle \lim_{ n \to \infty } P_n =\dfrac{\fbox{ナ}}{\fbox{ニ}}$と求められる。
2023杏林大学医過去問
この動画を見る
複数の玉が人った袋から玉を 1 個取り出して袋に戻す事象を考える。どの玉も同じ確率で取り出されるものとし、nを自然数として、以下の間いに答えよ。
(1) 袋の中に赤玉 1 個と黒玉 2 個が入っている。この袋の中から玉を 1 個取り出し、取り出した玉と同じ色の玉をひとつ加え、合計 2 個の玉を袋に戻すという試行を繰り返す。n回目の試行において赤玉が取り出される確率を$p_{ n }$とすると、$p_{ 2 }=\dfrac{\fbox{ア}}{\fbox{イ}}, p_{ 3 }=\dfrac{\fbox{ウ}}{\fbox{エ}}$
( 2 )袋の中に赤玉 3 個と黒玉 2 個が人っている。この袋の中から玉を 1 個取り出し、赤玉と黒玉を 1 個ずつ、合計 2 個の球を袋に戻す試行を繰り返す。n回目の試行において赤玉が取り出される確率を$p_{ n }$とすると、次式が成り立つ。
$p_{ 2 }=\dfrac{\fbox{オカ}}{\fbox{キク}}, p_{ 3 }=\dfrac{\fbox{ケコ}}{\fbox{サシ}}$
n回目の試行開始時点で袋に人っている玉の個数$M_{ n } はM_{ n }=n+\fbox{ス}$であり、この時点で袋に入っていると期待される赤玉の個数$R_{ n }はR_{ n }=M_{ n }×P_{ n }$と表される。n回目の試行において、黒玉が取り出された場合にのみ、試行後の赤玉の個数が施行前と比べて$\fbox{セ}$個増えるため、n+ 1 回目の試行開始時点で袋に入っていると期待される赤玉の個数は$R_{ n+1 }=R_{ n }+(1-P_{ n })×\fbox{セ}$となる。したがって、
$P_{ n+1 }=\dfrac{n+\fbox{ソ}}{n+\fbox{タ}}×P_{ n }+\dfrac{1}{n+\fbox{チ}}$
が成り立つ。このことから、$(n+3)×(n+\fbox{ツ})×(P_{n}-\dfrac{\fbox{テ}}{\fbox{ト}})$がnに依らず一定となる事が分かり、$\displaystyle \lim_{ n \to \infty } P_n =\dfrac{\fbox{ナ}}{\fbox{ニ}}$と求められる。
2023杏林大学医過去問
福田の数学〜ポリアの壺は証明を覚えよう〜杏林大学2023年医学部第1問前編〜ポリアの壺

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#杏林大学#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
複数の玉が人った袋から玉を 1 個取り出して袋に戻す事象を考える。どの玉も同じ確率で取り出されるものとし、nを自然数として、以下の間いに答えよ。
(1) 袋の中に赤玉 1 個と黒玉 2 個が入っている。この袋の中から玉を 1 個取り出し、取り出した玉と同じ色の玉をひとつ加え、合計 2 個の玉を袋に戻すという試行を繰り返す。n回目の試行において赤玉が取り出される確率を$p_{ n }$とすると、$p_{ 2 }=\dfrac{\fbox{ア}}{\fbox{イ}}, p_{ 3 }=\dfrac{\fbox{ウ}}{\fbox{エ}}$
( 2 )袋の中に赤玉 3 個と黒玉 2 個が人っている。この袋の中から玉を 1 個取り出し、赤玉と黒玉を 1 個ずつ、合計 2 個の球を袋に戻す試行を繰り返す。n回目の試行において赤玉が取り出される確率を$p_{ n }$とすると、次式が成り立つ。
$p_{ 2 }=\dfrac{\fbox{オカ}}{\fbox{キク}}, p_{ 3 }=\dfrac{\fbox{ケコ}}{\fbox{サシ}}$
n回目の試行開始時点で袋に人っている玉の個数$M_{ n } はM_{ n }=n+\fbox{ス}$であり、この時点で袋に入っていると期待される赤玉の個数$R_{ n }はR_{ n }=M_{ n }×P_{ n }$と表される。n回目の試行において、黒玉が取り出された場合にのみ、試行後の赤玉の個数が施行前と比べて$\fbox{セ}$個増えるため、n+ 1 回目の試行開始時点で袋に入っていると期待される赤玉の個数は$R_{ n+1 }=R_{ n }+(1-P_{ n })×\fbox{セ}$となる。したがって、
$P_{ n+1 }=\dfrac{n+\fbox{ソ}}{n+\fbox{タ}}×P_{ n }+\dfrac{1}{n+\fbox{チ}}$
が成り立つ。このことから、$(n+3)×(n+\fbox{ツ})×(P_{n}-\dfrac{\fbox{テ}}{\fbox{ト}})$がnに依らず一定となる事が分かり、$\displaystyle \lim_{ n \to \infty } P_n =\dfrac{\fbox{ナ}}{\fbox{ニ}}$と求められる。
2023杏林大学医過去問
この動画を見る
複数の玉が人った袋から玉を 1 個取り出して袋に戻す事象を考える。どの玉も同じ確率で取り出されるものとし、nを自然数として、以下の間いに答えよ。
(1) 袋の中に赤玉 1 個と黒玉 2 個が入っている。この袋の中から玉を 1 個取り出し、取り出した玉と同じ色の玉をひとつ加え、合計 2 個の玉を袋に戻すという試行を繰り返す。n回目の試行において赤玉が取り出される確率を$p_{ n }$とすると、$p_{ 2 }=\dfrac{\fbox{ア}}{\fbox{イ}}, p_{ 3 }=\dfrac{\fbox{ウ}}{\fbox{エ}}$
( 2 )袋の中に赤玉 3 個と黒玉 2 個が人っている。この袋の中から玉を 1 個取り出し、赤玉と黒玉を 1 個ずつ、合計 2 個の球を袋に戻す試行を繰り返す。n回目の試行において赤玉が取り出される確率を$p_{ n }$とすると、次式が成り立つ。
$p_{ 2 }=\dfrac{\fbox{オカ}}{\fbox{キク}}, p_{ 3 }=\dfrac{\fbox{ケコ}}{\fbox{サシ}}$
n回目の試行開始時点で袋に人っている玉の個数$M_{ n } はM_{ n }=n+\fbox{ス}$であり、この時点で袋に入っていると期待される赤玉の個数$R_{ n }はR_{ n }=M_{ n }×P_{ n }$と表される。n回目の試行において、黒玉が取り出された場合にのみ、試行後の赤玉の個数が施行前と比べて$\fbox{セ}$個増えるため、n+ 1 回目の試行開始時点で袋に入っていると期待される赤玉の個数は$R_{ n+1 }=R_{ n }+(1-P_{ n })×\fbox{セ}$となる。したがって、
$P_{ n+1 }=\dfrac{n+\fbox{ソ}}{n+\fbox{タ}}×P_{ n }+\dfrac{1}{n+\fbox{チ}}$
が成り立つ。このことから、$(n+3)×(n+\fbox{ツ})×(P_{n}-\dfrac{\fbox{テ}}{\fbox{ト}})$がnに依らず一定となる事が分かり、$\displaystyle \lim_{ n \to \infty } P_n =\dfrac{\fbox{ナ}}{\fbox{ニ}}$と求められる。
2023杏林大学医過去問
【演習】極限の式変形の方針について解説しました!【数学III】

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
3rd School
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 } \frac{cosax-cosbx}{x^2}$を求めよ
この動画を見る
$\displaystyle \lim_{ x \to 0 } \frac{cosax-cosbx}{x^2}$を求めよ
これもオイラーの公式っていうんだ!

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \prod_{n=1}^\infty cos(\frac x{2^n}) = cos\frac x{2}cos\frac x{4} cos\frac x{8} \cdots $
$cos\frac x{2^n} = \frac {sinx}x $
これを証明せよ.
この動画を見る
$\displaystyle \prod_{n=1}^\infty cos(\frac x{2^n}) = cos\frac x{2}cos\frac x{4} cos\frac x{8} \cdots $
$cos\frac x{2^n} = \frac {sinx}x $
これを証明せよ.
福田の数学〜曲線の長さの計算は大丈夫?〜明治大学2023年理工学部第2問〜曲線の長さと極限

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$f(x)=\dfrac{1}{8}x^2-logx(x \gt0)$とし、座標平面上の曲線y=f(x)をCとする。ただし、logxは自然対数を表す。関数f(x)は$x=\fbox{あ}$で最小値をとる。曲線C上の点A(1,f(1))における曲線Cの接線をlとすると、lの方程式は$y=\fbox{い}$である。
曲線Cと接線lおよび直線x=2で囲まれた図形の面積は$\fbox{う}$である。また、点$(t,f(t))(t \lt1)$をPとし、点Aから点Pまでの曲線Cの長さをL(t)とすると$L(2)=\fbox{え}$である。また、$\displaystyle \lim_{ t \to 1+0 } \dfrac{L(t)}{t-1}= \fbox{お}$である。
2023明治大学理工学部過去問
この動画を見る
$f(x)=\dfrac{1}{8}x^2-logx(x \gt0)$とし、座標平面上の曲線y=f(x)をCとする。ただし、logxは自然対数を表す。関数f(x)は$x=\fbox{あ}$で最小値をとる。曲線C上の点A(1,f(1))における曲線Cの接線をlとすると、lの方程式は$y=\fbox{い}$である。
曲線Cと接線lおよび直線x=2で囲まれた図形の面積は$\fbox{う}$である。また、点$(t,f(t))(t \lt1)$をPとし、点Aから点Pまでの曲線Cの長さをL(t)とすると$L(2)=\fbox{え}$である。また、$\displaystyle \lim_{ t \to 1+0 } \dfrac{L(t)}{t-1}= \fbox{お}$である。
2023明治大学理工学部過去問
理系こう聞こえている?

数学どうにかしたい人へ

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#図形の性質#式と証明#複素数と方程式#平面上のベクトル#空間ベクトル#平面上の曲線#複素数平面#図形と計量#データの分析#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#一次不等式(不等式・絶対値のある方程式・不等式)#集合と命題(集合・命題と条件・背理法)#2次方程式と2次不等式#2次関数とグラフ#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#データの分析#整数の性質#場合の数#確率#三角形の辺の比(内分・外分・二等分線)#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#図形と方程式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#円と方程式#軌跡と領域#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数列#確率分布と統計的な推測#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#数列とその和(等差・等比・階差・Σ)#漸化式#数学的帰納法#確率分布#統計的な推測#関数と極限#微分とその応用#積分とその応用#2次曲線#複素数平面#図形への応用#関数(分数関数・無理関数・逆関数と合成関数)#数列の極限#関数の極限#微分法#色々な関数の導関数#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#不定積分#定積分#面積・体積・長さ・速度#空間における垂直と平行と多面体(オイラーの法則)#不定積分・定積分#面積、体積#媒介変数表示と極座標#速度と近似式#数学(高校生)#数B#数C#数Ⅲ
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
数学が共通テストのみの人の勉強法紹介動画です
この動画を見る
数学が共通テストのみの人の勉強法紹介動画です
福田の数学〜無限級数の和は部分和の極限〜明治大学2023年全学部統一Ⅲ第1問(1)〜無限級数の和

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
無限級数
$\displaystyle \sum_{n=1}^{\infty} \log \frac{(n+1)(n+2)}{n(n+3)}$
の和を求めよ。
2023明治大学過去問
この動画を見る
無限級数
$\displaystyle \sum_{n=1}^{\infty} \log \frac{(n+1)(n+2)}{n(n+3)}$
の和を求めよ。
2023明治大学過去問
大学入試問題#627「よくみる形」 横浜市立医学部(2006) #定積分 #極限

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#関数と極限#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \displaystyle \int_{1}^{n} \displaystyle \frac{1}{x^3}e^{-\frac{1}{x}} dx$
出典:2006年横浜市立大学医学部 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \int_{1}^{n} \displaystyle \frac{1}{x^3}e^{-\frac{1}{x}} dx$
出典:2006年横浜市立大学医学部 入試問題
【対数の微分】対数関数の微分の導出について解説しました!【数学III】

大学入試問題#623「えぐいの見た目だけ」 岩手大学(2021) #極限 僚太さんの紹介

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#岩手大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 } (\displaystyle \frac{x\ \tan\ x}{\sqrt{ \cos2x }-\cos\ x}+\displaystyle \frac{x}{\tan2x})$
出典:2021年岩手大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 } (\displaystyle \frac{x\ \tan\ x}{\sqrt{ \cos2x }-\cos\ x}+\displaystyle \frac{x}{\tan2x})$
出典:2021年岩手大学 入試問題
大学入試問題#622「公式にしたがって」 九州歯科大学(2016) #級数 僚太さんの紹介

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#九州歯科大学
指導講師:
ますただ
問題文全文(内容文):
$x^2+8x+c=0$の異なる2つの実数解を$\alpha,\beta$とする
$\displaystyle \sum_{k=1}^\infty (\alpha-\beta)^{2k}=3$のとき$c$の値を求めよ。
出典:2010年九州歯科大学 入試問題
この動画を見る
$x^2+8x+c=0$の異なる2つの実数解を$\alpha,\beta$とする
$\displaystyle \sum_{k=1}^\infty (\alpha-\beta)^{2k}=3$のとき$c$の値を求めよ。
出典:2010年九州歯科大学 入試問題
大学入試問題#621「これは、ぜひ挑戦してほしい」 防衛医科大学(2016) #極限

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#防衛医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to \infty } \{\displaystyle \frac{2x-2}{2x-1}-\displaystyle \frac{2}{(2x-1)^2}\}^{3x}$
出典:2016年防衛医科大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to \infty } \{\displaystyle \frac{2x-2}{2x-1}-\displaystyle \frac{2}{(2x-1)^2}\}^{3x}$
出典:2016年防衛医科大学 入試問題
これどゆこと?

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
五条悟の無下限呪術がアキレスと亀らしんですが,どういうことですか?
この動画を見る
五条悟の無下限呪術がアキレスと亀らしんですが,どういうことですか?
【三角関数の微分】三角関数の微分の導出について解説しました!【数学III】

大学入試問題#617「極限2本」 関西大学(2021) #極限

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#関西大学
指導講師:
ますただ
問題文全文(内容文):
(1)$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{1}{x}(\displaystyle \frac{1}{3-\sin2x}-\displaystyle \frac{1}{3+\sin2x})$
(2)$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{1}{x^2}(\displaystyle \frac{1}{\sqrt{ 3-\sin^22x }}-\displaystyle \frac{1}{\sqrt{ 3+\sin^22x }})$
出典:2021年関西大学 入試問題
この動画を見る
(1)$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{1}{x}(\displaystyle \frac{1}{3-\sin2x}-\displaystyle \frac{1}{3+\sin2x})$
(2)$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{1}{x^2}(\displaystyle \frac{1}{\sqrt{ 3-\sin^22x }}-\displaystyle \frac{1}{\sqrt{ 3+\sin^22x }})$
出典:2021年関西大学 入試問題
工夫が必要な極限問題 By 英語orドイツ語シはBかHか さん #極限
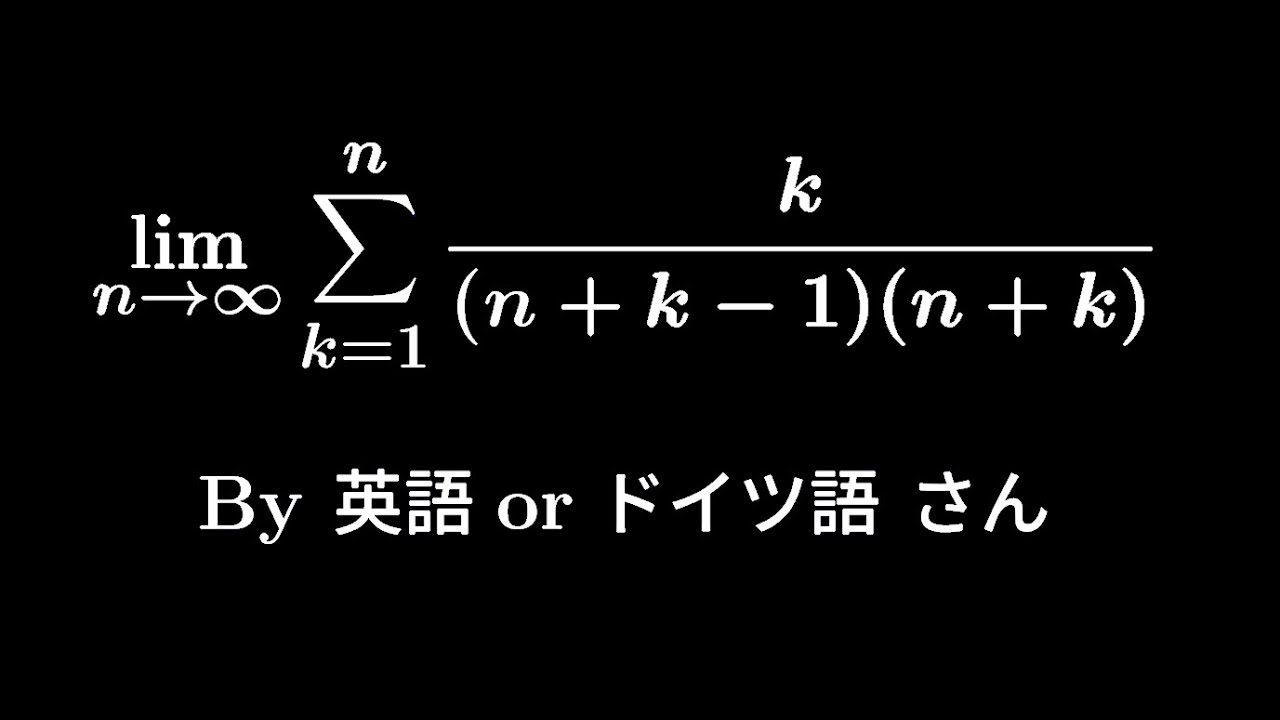
単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{k}{(n+k-1)(n+k)}$
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{k}{(n+k-1)(n+k)}$
福田の数学〜上智大学2023年理工学部第2問〜逆関数の微分積分

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ 関数$f(x)$=$\sin x$ $\left(0≦x≦\frac{\pi}{2}\right)$の逆関数を$g(x)$とする。
(1)関数$g(x)$の定義域は$\boxed{\ \ え\ \ }$である。
(2)$y$=$g(x)$の$x$=$\frac{4}{5}$における接線の傾きは$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$である。
(3)$\displaystyle\int_0^{\frac{1}{2}}g(x)dx$=$\displaystyle\frac{\pi}{\boxed{\ \ キ\ \ }}$+$\boxed{\ \ ク\ \ }$+$\displaystyle\frac{\boxed{\ \ ケ\ \ }}{\boxed{\ \ コ\ \ }}\sqrt{\boxed{\ \ サ\ \ }}$である。
(4)$y$=$g(x)$のグラフと$x$=1および$x$軸で囲まれた図形を$x$軸のまわりに1回転させてできる立体の体積は$\displaystyle\frac{\pi^a}{\boxed{\ \ シ\ \ }}$+$\boxed{\ \ ス\ \ }\pi$ ただし$a$=$\boxed{\ \ セ\ \ }$である。
この動画を見る
$\Large{\boxed{2}}$ 関数$f(x)$=$\sin x$ $\left(0≦x≦\frac{\pi}{2}\right)$の逆関数を$g(x)$とする。
(1)関数$g(x)$の定義域は$\boxed{\ \ え\ \ }$である。
(2)$y$=$g(x)$の$x$=$\frac{4}{5}$における接線の傾きは$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$である。
(3)$\displaystyle\int_0^{\frac{1}{2}}g(x)dx$=$\displaystyle\frac{\pi}{\boxed{\ \ キ\ \ }}$+$\boxed{\ \ ク\ \ }$+$\displaystyle\frac{\boxed{\ \ ケ\ \ }}{\boxed{\ \ コ\ \ }}\sqrt{\boxed{\ \ サ\ \ }}$である。
(4)$y$=$g(x)$のグラフと$x$=1および$x$軸で囲まれた図形を$x$軸のまわりに1回転させてできる立体の体積は$\displaystyle\frac{\pi^a}{\boxed{\ \ シ\ \ }}$+$\boxed{\ \ ス\ \ }\pi$ ただし$a$=$\boxed{\ \ セ\ \ }$である。
福田の数学〜上智大学2023年TEAP利用型理系第1問(3)〜連立漸化式と極限

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (3)$a_1$=0, $b_1$=6とし、
$a_{n+1}$=$\displaystyle\frac{a_n+b_n}{2}$, $b_{n+1}$=$a_n$ ($n$≧1)
で定まる$a_n$, $b_n$を用いて、平面上の点$P_n$($a_n$, $b_n$)($n$=1,2,3,...)を定める。
(i)点$P_n$は常に直線$y$=$\boxed{\ \ ウ\ \ }x$+$\boxed{\ \ エ\ \ }$上にある。
(ii)$n$を限りなく大きくするとき、点$P_n$は点$\left(\boxed{\ \ オ\ \ }, \boxed{\ \ カ\ \ }\right)$に限りなく近づく。
この動画を見る
$\Large{\boxed{1}}$ (3)$a_1$=0, $b_1$=6とし、
$a_{n+1}$=$\displaystyle\frac{a_n+b_n}{2}$, $b_{n+1}$=$a_n$ ($n$≧1)
で定まる$a_n$, $b_n$を用いて、平面上の点$P_n$($a_n$, $b_n$)($n$=1,2,3,...)を定める。
(i)点$P_n$は常に直線$y$=$\boxed{\ \ ウ\ \ }x$+$\boxed{\ \ エ\ \ }$上にある。
(ii)$n$を限りなく大きくするとき、点$P_n$は点$\left(\boxed{\ \ オ\ \ }, \boxed{\ \ カ\ \ }\right)$に限りなく近づく。
極限の基本問題 愛知県立大

単元:
#関数と極限#学校別大学入試過去問解説(数学)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2019愛知県立大学過去問題
$e=\displaystyle \lim_{ h \to 0 } (1+h)^\frac{1}{h} $
aは正の実数
$e=\displaystyle \lim_{ x \to \infty } \frac{1}{x^{x}}(x-a)^{x}$
の値
この動画を見る
2019愛知県立大学過去問題
$e=\displaystyle \lim_{ h \to 0 } (1+h)^\frac{1}{h} $
aは正の実数
$e=\displaystyle \lim_{ x \to \infty } \frac{1}{x^{x}}(x-a)^{x}$
の値
福田の数学〜青山学院大学2023年理工学部第5問〜定積分で定義された数列と極限

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#積分とその応用#数列の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数Ⅲ#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ $a_n$=$\displaystyle\frac{1}{n!}\int_1^e(\log x)^ndx$ ($n$=1,2,3,...)とおく。
(1)$a_1$を求めよ。
(2)不等式0≦$a_n$≦$\frac{e-1}{n!}$ が成り立つことを示せ。
(3)$n$≧2のとき、$a_n$=$\displaystyle\frac{e}{n!}$-$a_{n-1}$ であることを示せ。
(4)$\displaystyle\lim_{n \to \infty}\sum_{k=2}^n\frac{(-1)^k}{k!}$ を求めよ。
この動画を見る
$\Large\boxed{5}$ $a_n$=$\displaystyle\frac{1}{n!}\int_1^e(\log x)^ndx$ ($n$=1,2,3,...)とおく。
(1)$a_1$を求めよ。
(2)不等式0≦$a_n$≦$\frac{e-1}{n!}$ が成り立つことを示せ。
(3)$n$≧2のとき、$a_n$=$\displaystyle\frac{e}{n!}$-$a_{n-1}$ であることを示せ。
(4)$\displaystyle\lim_{n \to \infty}\sum_{k=2}^n\frac{(-1)^k}{k!}$ を求めよ。
林俊介 語りかける東大数学

単元:
#対数関数#関数と極限
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)$n\in Z+$
$g(x):=\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{\cos(\pi x)+1}{2} (\vert x \vert \leq 1) \\
0 (\vert x \vert \gt 1)
\end{array}
\right.
\end{eqnarray}$
$f(x):$連続であり,$p,q \in R$
$\vert x\vert \leq \dfrac{1}{n}$でつねに$p\leq f(x)\leq q$
$p\leq n\dfrac{\displaystyle \int_{-1}^{1} g(nx) f(x) dx\leq q}{I}$を示せ.
(2)$h(x)=:\begin{eqnarray}
\left\{
\begin{array}{l}
-\dfrac{\pi}{2}\sin(\pi x) (\vert x\vert \leq 1) \\
0 (\vert x\vert \gt 1)
\end{array}
\right.
\end{eqnarray}$
次の極限を求めよ.
$\displaystyle \lim_{n\to\infty} n^2\displaystyle \int_{-1}^{1} h(nx)\log(1+e^{x+1})dx $
(1)$g(x)=\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{\cos(\pi x)+1}{2} (\vert x\vert \leq 1) \\
0 (\vert x\vert \gt 1)
\end{array}
\right.
\end{eqnarray}$
$p\leq n \displaystyle \int_{-1}^{1} g(nx) f(x)dx \leq q$
2015東大過去問
この動画を見る
(1)$n\in Z+$
$g(x):=\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{\cos(\pi x)+1}{2} (\vert x \vert \leq 1) \\
0 (\vert x \vert \gt 1)
\end{array}
\right.
\end{eqnarray}$
$f(x):$連続であり,$p,q \in R$
$\vert x\vert \leq \dfrac{1}{n}$でつねに$p\leq f(x)\leq q$
$p\leq n\dfrac{\displaystyle \int_{-1}^{1} g(nx) f(x) dx\leq q}{I}$を示せ.
(2)$h(x)=:\begin{eqnarray}
\left\{
\begin{array}{l}
-\dfrac{\pi}{2}\sin(\pi x) (\vert x\vert \leq 1) \\
0 (\vert x\vert \gt 1)
\end{array}
\right.
\end{eqnarray}$
次の極限を求めよ.
$\displaystyle \lim_{n\to\infty} n^2\displaystyle \int_{-1}^{1} h(nx)\log(1+e^{x+1})dx $
(1)$g(x)=\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{\cos(\pi x)+1}{2} (\vert x\vert \leq 1) \\
0 (\vert x\vert \gt 1)
\end{array}
\right.
\end{eqnarray}$
$p\leq n \displaystyle \int_{-1}^{1} g(nx) f(x)dx \leq q$
2015東大過去問
福田の数学〜慶應義塾大学2023年理工学部第4問〜定積分と不等式Part2
単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#数列の極限#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ (1)0≦$x$≦$\displaystyle\frac{\pi}{2}$において常に不等式|$b$|≦|$b$+1-$b\cos x$|が成り立つような実数$b$の値の範囲は$\boxed{\ \ シ\ \ }$≦$b$≦$\boxed{\ \ ス\ \ }$である。
以下、$b$を$\boxed{\ \ シ\ \ }$≦$b$≦$\boxed{\ \ ス\ \ }$を満たす0でない実数とし、数列$\left\{a_n\right\}$を
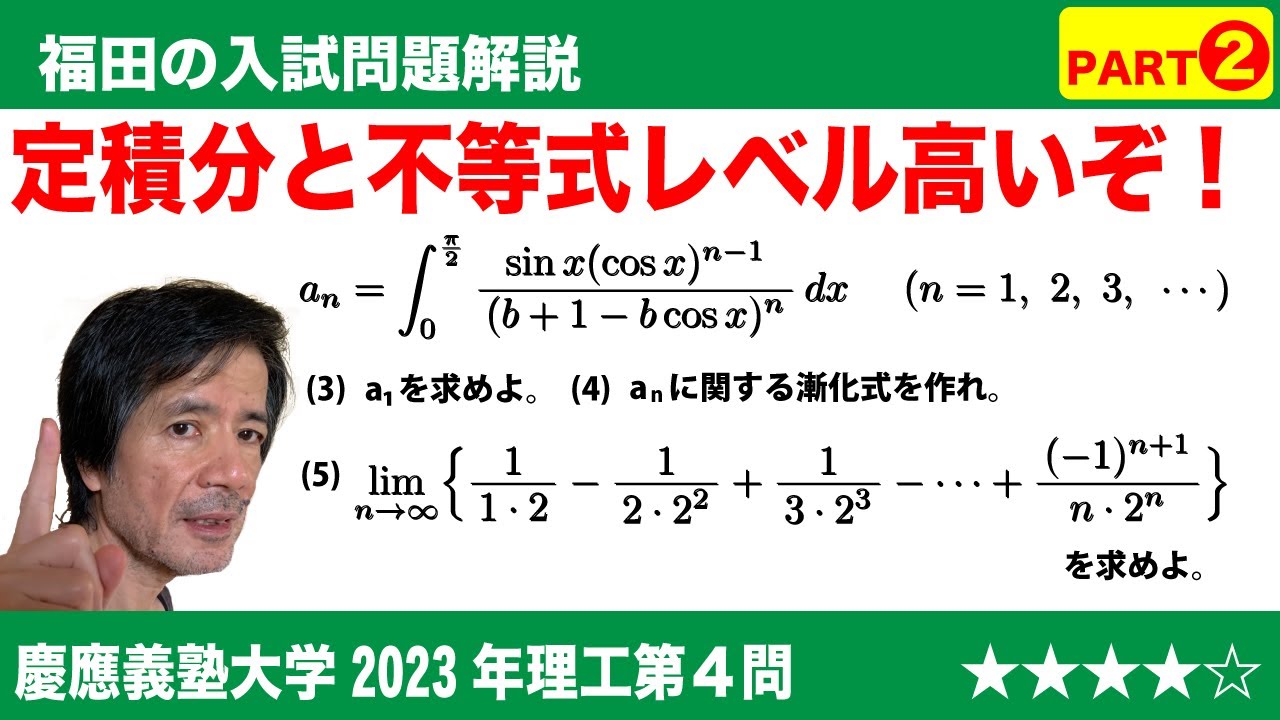
$a_n$=$\displaystyle\int_0^{\frac{\pi}{2}}\frac{\sin x(\cos x)^{n-1}}{(b+1-b\cos x)^n}dx$ (n=1,2,3,...)で定義する。
(2)$\displaystyle\lim_{n \to \infty}b^na_n$=0 が成り立つことを証明しなさい。
(3)$a_1$=$\boxed{\ \ セ\ \ }$である。
(4)$a_{n+1}$を$a_n$,$n$,$b$を用いて表すと$a_{n+1}$=$\boxed{\ \ ソ\ \ }$となる。
(5)$\displaystyle\lim_{n \to \infty}\left\{\frac{1}{1・2}-\frac{1}{2・2^2}+\frac{1}{3・2^3}-...+\frac{(-1)^{n+1}}{n・2^n}\right\}$=$\boxed{\ \ タ\ \ }$である。
この動画を見る
$\Large\boxed{4}$ (1)0≦$x$≦$\displaystyle\frac{\pi}{2}$において常に不等式|$b$|≦|$b$+1-$b\cos x$|が成り立つような実数$b$の値の範囲は$\boxed{\ \ シ\ \ }$≦$b$≦$\boxed{\ \ ス\ \ }$である。
以下、$b$を$\boxed{\ \ シ\ \ }$≦$b$≦$\boxed{\ \ ス\ \ }$を満たす0でない実数とし、数列$\left\{a_n\right\}$を
$a_n$=$\displaystyle\int_0^{\frac{\pi}{2}}\frac{\sin x(\cos x)^{n-1}}{(b+1-b\cos x)^n}dx$ (n=1,2,3,...)で定義する。
(2)$\displaystyle\lim_{n \to \infty}b^na_n$=0 が成り立つことを証明しなさい。
(3)$a_1$=$\boxed{\ \ セ\ \ }$である。
(4)$a_{n+1}$を$a_n$,$n$,$b$を用いて表すと$a_{n+1}$=$\boxed{\ \ ソ\ \ }$となる。
(5)$\displaystyle\lim_{n \to \infty}\left\{\frac{1}{1・2}-\frac{1}{2・2^2}+\frac{1}{3・2^3}-...+\frac{(-1)^{n+1}}{n・2^n}\right\}$=$\boxed{\ \ タ\ \ }$である。
大学入試問題#603「もう飽きた?」 千葉大学(1989) #極限

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$P_n=\sqrt[ n ]{ \displaystyle \frac{(3n)!}{(2n)!} }$とおく
(1)$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{P_n}{n}$を求めよ
(2)$\displaystyle \lim_{ n \to \infty } (\displaystyle \frac{n+2}{n})^{P_n}$を求めよ
出典:1989年千葉大学 入試問題
この動画を見る
$P_n=\sqrt[ n ]{ \displaystyle \frac{(3n)!}{(2n)!} }$とおく
(1)$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{P_n}{n}$を求めよ
(2)$\displaystyle \lim_{ n \to \infty } (\displaystyle \frac{n+2}{n})^{P_n}$を求めよ
出典:1989年千葉大学 入試問題
福田の数学〜千葉大学2023年第4問〜関数の増減と極限

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#関数の極限#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 2つの実数$a$,$b$は0<$b$<$a$を満たすとする。関数
$f(x)$=$\displaystyle\frac{1}{b}\left(e^{-(a-b)x}-e^{-ax}\right)$
の最大値を$M(a,b)$、最大値をとるときの$x$の値を$X(a,b)$と表す。ここで、$e$は自然対数の底である。
(1)$X(a,b)$を求めよ。
(2)極限$\displaystyle\lim_{b \to +0}X(a,b)$ を求めよ。
(3)極限$\displaystyle\lim_{b \to +0}M(a,b)$ を求めよ。
この動画を見る
$\Large\boxed{4}$ 2つの実数$a$,$b$は0<$b$<$a$を満たすとする。関数
$f(x)$=$\displaystyle\frac{1}{b}\left(e^{-(a-b)x}-e^{-ax}\right)$
の最大値を$M(a,b)$、最大値をとるときの$x$の値を$X(a,b)$と表す。ここで、$e$は自然対数の底である。
(1)$X(a,b)$を求めよ。
(2)極限$\displaystyle\lim_{b \to +0}X(a,b)$ を求めよ。
(3)極限$\displaystyle\lim_{b \to +0}M(a,b)$ を求めよ。
大学入試問題#598「計算が大変でした」 関西大学(2009) #区分求積法

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#数列の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#関西大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{n-k}{n\sqrt{ 3n^2+k^2 }}$
出典:2009年関西大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{n-k}{n\sqrt{ 3n^2+k^2 }}$
出典:2009年関西大学 入試問題
福田の数学〜東京医科歯科大学2023年医学部第3問〜積分で定義された関数と極限

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ $a$,$b$を正の実数、$p$を$a$より小さい正の実数とし、すべての実数$x$について
$\displaystyle\int_p^{f(x)}\frac{a}{u(a-u)}du$=$bx$, 0<$f(x)$<$a$
かつ$f(0)$=$p$を満たす関数$f(x)$を考える。このとき以下の問いに答えよ。
(1)$f(x)$を$a$,$b$,$p$を用いて表せ。
(2)$f(-1)$=$\frac{1}{2}$, $f(1)$=1, $f(3)$=$\frac{3}{2}$のとき、$a$,$b$,$p$を求めよ。
(3)(2)のとき、$\displaystyle\lim_{x \to -\infty}f(x)$, $\displaystyle\lim_{x \to \infty}f(x)$ を求めよ。
この動画を見る
$\Large\boxed{3}$ $a$,$b$を正の実数、$p$を$a$より小さい正の実数とし、すべての実数$x$について
$\displaystyle\int_p^{f(x)}\frac{a}{u(a-u)}du$=$bx$, 0<$f(x)$<$a$
かつ$f(0)$=$p$を満たす関数$f(x)$を考える。このとき以下の問いに答えよ。
(1)$f(x)$を$a$,$b$,$p$を用いて表せ。
(2)$f(-1)$=$\frac{1}{2}$, $f(1)$=1, $f(3)$=$\frac{3}{2}$のとき、$a$,$b$,$p$を求めよ。
(3)(2)のとき、$\displaystyle\lim_{x \to -\infty}f(x)$, $\displaystyle\lim_{x \to \infty}f(x)$ を求めよ。
福田の数学〜東京医科歯科大学2023年医学部第2問PART2〜場合分けされた連立漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数Ⅲ#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ xyz空間において、3点(0,0,0),(1,0,0),(0,1,0)を通る平面$\pi_1$と3点(1,0,0),(0,1,0),(0,0,1)を通る平面$\pi_2$を考える。$x_0$=1, $y_0$=2, $z_0$=-2として、点P${}_0$($x_0$,$y_0$,$z_0$)から始めて、次の手順でP${}_1$($x_1$,$y_1$,$z_1$), P${}_2$($x_2$,$y_2$,$z_2$),... を決める。
・$k$が偶数のとき、$\pi_1$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
・$k$が奇数のとき、$\pi_2$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
このとき、次の問いに答えよ。
(1)$\pi_2$に直交するベクトルのうち、長さが1で$x$成分が正のもの$n_2$を求めよ。
(2)$x_{k+1}$,$y_{k+1}$,$z_{k+1}$をそれぞれ$x_k$,$y_k$,$z_k$を用いて表せ。
(3)$\displaystyle\lim_{k\to\infty}x_k$, $\displaystyle\lim_{k\to\infty}y_k$, $\displaystyle\lim_{k\to\infty}z_k$を求めよ。
この動画を見る
$\Large\boxed{2}$ xyz空間において、3点(0,0,0),(1,0,0),(0,1,0)を通る平面$\pi_1$と3点(1,0,0),(0,1,0),(0,0,1)を通る平面$\pi_2$を考える。$x_0$=1, $y_0$=2, $z_0$=-2として、点P${}_0$($x_0$,$y_0$,$z_0$)から始めて、次の手順でP${}_1$($x_1$,$y_1$,$z_1$), P${}_2$($x_2$,$y_2$,$z_2$),... を決める。
・$k$が偶数のとき、$\pi_1$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
・$k$が奇数のとき、$\pi_2$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
このとき、次の問いに答えよ。
(1)$\pi_2$に直交するベクトルのうち、長さが1で$x$成分が正のもの$n_2$を求めよ。
(2)$x_{k+1}$,$y_{k+1}$,$z_{k+1}$をそれぞれ$x_k$,$y_k$,$z_k$を用いて表せ。
(3)$\displaystyle\lim_{k\to\infty}x_k$, $\displaystyle\lim_{k\to\infty}y_k$, $\displaystyle\lim_{k\to\infty}z_k$を求めよ。
電気通信大学2014年 #極限 #Shorts
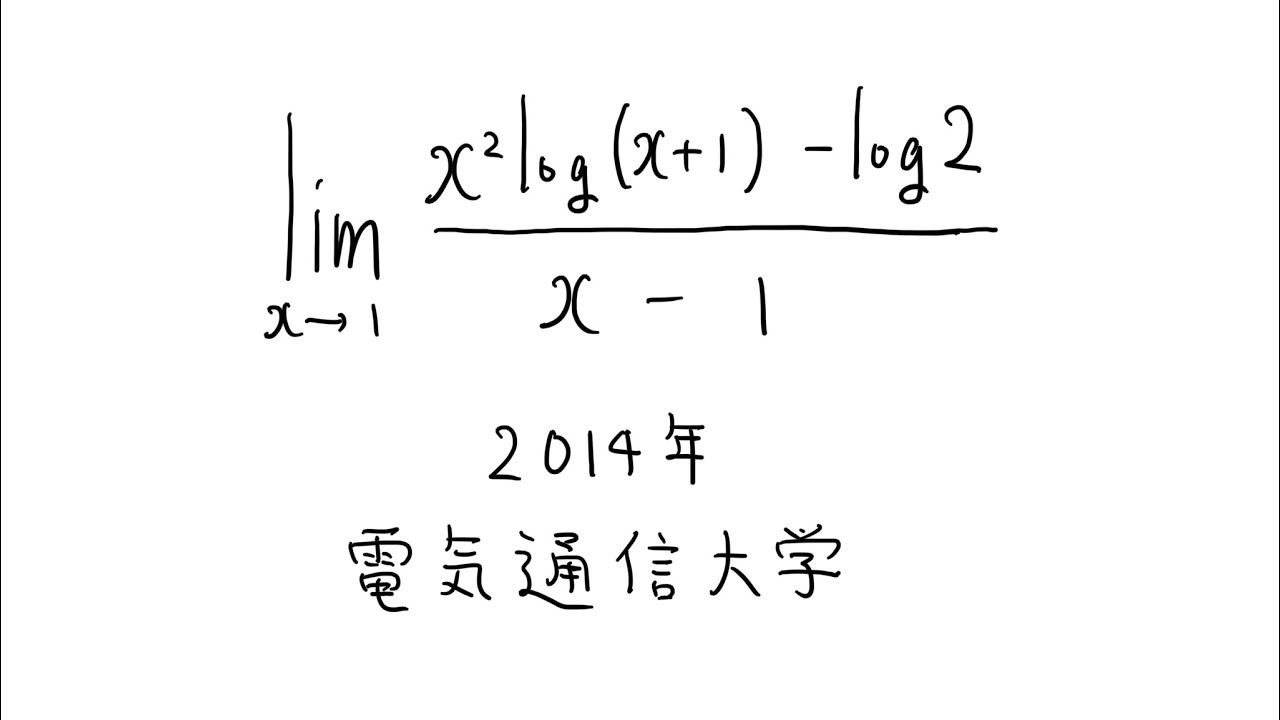
単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 1 } \displaystyle \frac{x^2log(x+1)-log\ 2}{x-1}$
出典:2014年電気通信大学
この動画を見る
$\displaystyle \lim_{ x \to 1 } \displaystyle \frac{x^2log(x+1)-log\ 2}{x-1}$
出典:2014年電気通信大学
福田の数学〜東京医科歯科大学2023年医学部第2問PART1〜場合分けされた連立漸化式

単元:
#大学入試過去問(数学)#漸化式#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数Ⅲ#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ xyz空間において、3点(0,0,0),(1,0,0),(0,1,0)を通る平面$\pi_1$と3点(1,0,0),(0,1,0),(0,0,1)を通る平面$\pi_2$を考える。$x_0$=1, $y_0$=2, $z_0$=-2として、点P${}_0$($x_0$,$y_0$,$z_0$)から始めて、次の手順でP${}_1$($x_1$,$y_1$,$z_1$), P${}_2$($x_2$,$y_2$,$z_2$),... を決める。
・$k$が偶数のとき、$\pi_1$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
・$k$が奇数のとき、$\pi_2$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
このとき、次の問いに答えよ。
(1)$\pi_2$に直交するベクトルのうち、長さが1で$x$成分が正のもの$n_2$を求めよ。
(2)$x_{k+1}$,$y_{k+1}$,$z_{k+1}$をそれぞれ$x_k$,$y_k$,$z_k$を用いて表せ。
(3)$\displaystyle\lim_{k\to\infty}x_k$, $\displaystyle\lim_{k\to\infty}y_k$, $\displaystyle\lim_{k\to\infty}z_k$を求めよ。
この動画を見る
$\Large\boxed{2}$ xyz空間において、3点(0,0,0),(1,0,0),(0,1,0)を通る平面$\pi_1$と3点(1,0,0),(0,1,0),(0,0,1)を通る平面$\pi_2$を考える。$x_0$=1, $y_0$=2, $z_0$=-2として、点P${}_0$($x_0$,$y_0$,$z_0$)から始めて、次の手順でP${}_1$($x_1$,$y_1$,$z_1$), P${}_2$($x_2$,$y_2$,$z_2$),... を決める。
・$k$が偶数のとき、$\pi_1$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
・$k$が奇数のとき、$\pi_2$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
このとき、次の問いに答えよ。
(1)$\pi_2$に直交するベクトルのうち、長さが1で$x$成分が正のもの$n_2$を求めよ。
(2)$x_{k+1}$,$y_{k+1}$,$z_{k+1}$をそれぞれ$x_k$,$y_k$,$z_k$を用いて表せ。
(3)$\displaystyle\lim_{k\to\infty}x_k$, $\displaystyle\lim_{k\to\infty}y_k$, $\displaystyle\lim_{k\to\infty}z_k$を求めよ。
