 関数の変化(グラフ・最大最小・方程式・不等式)
関数の変化(グラフ・最大最小・方程式・不等式)
 関数の変化(グラフ・最大最小・方程式・不等式)
関数の変化(グラフ・最大最小・方程式・不等式)
福田の入試問題解説〜北海道大学2022年理系第3問〜指数不等式の領域が表す面積の最小

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
以下の問いに答えよ。
(1)連立不等式$x \geqq 2, 2^x \leqq x^y \leqq x^2$の表す領域をxy平面上に図示せよ。
ただし、自然対数の底eが$2 \lt e \lt 3$を満たすことを用いてよい。
(2)$a \gt 0$に対して、連立不等式$2 \leqq x \leqq 6, (x^y-2^x)(x^a-x^y) \geqq 0$
の表すxy平面上の領域の面積をS(a)とする。
$S(a)$を最小にするaの値を求めよ。
2022北海道大学理系過去問
この動画を見る
以下の問いに答えよ。
(1)連立不等式$x \geqq 2, 2^x \leqq x^y \leqq x^2$の表す領域をxy平面上に図示せよ。
ただし、自然対数の底eが$2 \lt e \lt 3$を満たすことを用いてよい。
(2)$a \gt 0$に対して、連立不等式$2 \leqq x \leqq 6, (x^y-2^x)(x^a-x^y) \geqq 0$
の表すxy平面上の領域の面積をS(a)とする。
$S(a)$を最小にするaの値を求めよ。
2022北海道大学理系過去問
福田の数学〜京都大学2022年理系第5問〜方程式の解と不等式の証明

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#複素数と方程式#恒等式・等式・不等式の証明#解と判別式・解と係数の関係#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
曲線$C:y=\cos^3x$ $(0 \leqq x \leqq \frac{\pi}{2})$,x軸およびy軸で囲まれる図形の面s系をS
とする。$0 \lt t \lt \frac{\pi}{2}$とし、C上の点Q$(t,\cos^3t)$と原点O,およびP$(t,o),R(0,\cos^3t)$
を頂点にもつ長方形OPQRの面積をf(t)とする。このとき、次の問いに答えよ。
(1)Sを求めよ。
(2)$f(t)$は最大値をただ一つのtでとることを示せ。そのときのtを$\alpha$とすると、
$f(\alpha)=\frac{\cos^4\alpha}{3\sin\alpha}$ であることを示せ。
(3)$\frac{f(\alpha)}{S} \lt \frac{9}{16}$ を示せ。
2022京都大学理系過去問
この動画を見る
曲線$C:y=\cos^3x$ $(0 \leqq x \leqq \frac{\pi}{2})$,x軸およびy軸で囲まれる図形の面s系をS
とする。$0 \lt t \lt \frac{\pi}{2}$とし、C上の点Q$(t,\cos^3t)$と原点O,およびP$(t,o),R(0,\cos^3t)$
を頂点にもつ長方形OPQRの面積をf(t)とする。このとき、次の問いに答えよ。
(1)Sを求めよ。
(2)$f(t)$は最大値をただ一つのtでとることを示せ。そのときのtを$\alpha$とすると、
$f(\alpha)=\frac{\cos^4\alpha}{3\sin\alpha}$ であることを示せ。
(3)$\frac{f(\alpha)}{S} \lt \frac{9}{16}$ を示せ。
2022京都大学理系過去問
2022藤田医科大の簡単な問題 メインはn個の相加相乗平均の証明

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#微分とその応用#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x\gt 0$において$\dfrac{x}{2}+\dfrac{2}{x^2}$の最小値を求めよ.
2022藤田医科大過去問
この動画を見る
$ x\gt 0$において$\dfrac{x}{2}+\dfrac{2}{x^2}$の最小値を求めよ.
2022藤田医科大過去問
2^π VS π^2 どっちがでかい?

単元:
#微分とその応用#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きいか?
$2^{\pi}$ VS $\pi^2$
ただし,$3.14\lt \pi\lt \dfrac{22}{7}$
$2.7\lt e\lt 2.8$であるとする.
この動画を見る
どちらが大きいか?
$2^{\pi}$ VS $\pi^2$
ただし,$3.14\lt \pi\lt \dfrac{22}{7}$
$2.7\lt e\lt 2.8$であるとする.
【全ての問題は概要欄】大学入試問題#79 大阪大学(2020 改) 微分
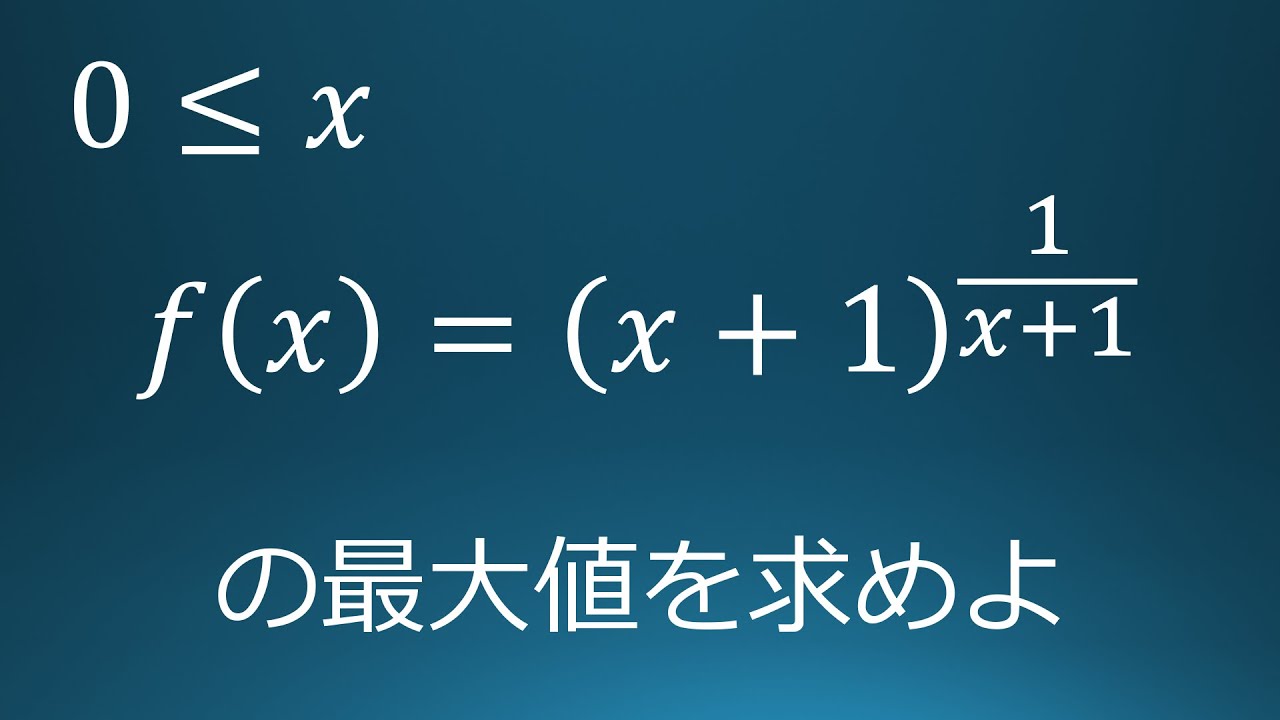
単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq x$
関数$f(x)=(x+1)^{\frac{1}{x+1}}$の最大値を求めよ。
出典:2020年大阪大学 入試問題
この動画を見る
$0 \leqq x$
関数$f(x)=(x+1)^{\frac{1}{x+1}}$の最大値を求めよ。
出典:2020年大阪大学 入試問題
福田のわかった数学〜高校3年生理系108〜変化率(3)水の問題(2)

単元:
#微分とその応用#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 変化率(3) 水の問題(2)
右図(※動画参照)のような直円錐の容器に水が満たされている。下側から$2cm^3$秒
の割合で水が流出する。水面の高さが8cmになった瞬間の水面の下降する
速度と水面の面積が減少する速度を求めよ。
この動画を見る
数学$\textrm{III}$ 変化率(3) 水の問題(2)
右図(※動画参照)のような直円錐の容器に水が満たされている。下側から$2cm^3$秒
の割合で水が流出する。水面の高さが8cmになった瞬間の水面の下降する
速度と水面の面積が減少する速度を求めよ。
福田のわかった数学〜高校3年生理系092〜グラフを描こう(14)三角関数、凹凸、漸近線

単元:
#数Ⅱ#三角関数#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ グラフを描こう(14)
$y=\frac{1}{2}\sin2x-2\sin x+x (0 \leqq x \leqq 2\pi)$のグラフを描け。凹凸、漸近線も調べよ。
この動画を見る
数学$\textrm{III}$ グラフを描こう(14)
$y=\frac{1}{2}\sin2x-2\sin x+x (0 \leqq x \leqq 2\pi)$のグラフを描け。凹凸、漸近線も調べよ。
福田のわかった数学〜高校3年生理系091〜グラフを描こう(13)指数関数、凹凸、漸近線

単元:
#数Ⅱ#指数関数と対数関数#指数関数#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ グラフを描こう(13)
$y=e^{\frac{1}{x^2-1}} (-1 \lt x \lt 1)$
のグラフを描け。凹凸、漸近線を調べよ。
この動画を見る
数学$\textrm{III}$ グラフを描こう(13)
$y=e^{\frac{1}{x^2-1}} (-1 \lt x \lt 1)$
のグラフを描け。凹凸、漸近線を調べよ。
福田のわかった数学〜高校3年生理系090〜グラフを描こう(12)無理関数、凹凸、漸近線

単元:
#関数と極限#微分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ グラフを描こう。(12)
$y=\sqrt[3]{x^3-x^2}$ のグラフを描け。ただし凹凸、漸近線も調べよ。
この動画を見る
数学$\textrm{III}$ グラフを描こう。(12)
$y=\sqrt[3]{x^3-x^2}$ のグラフを描け。ただし凹凸、漸近線も調べよ。
福田のわかった数学〜高校3年生理系089〜グラフを描こう(11)分数関数、凹凸、漸近線

単元:
#関数と極限#微分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ グラフを描こう(11)
$y=\frac{x^3}{x^2-1}$ のグラフを描け。ただし、凹凸、漸近線も調べよ。
この動画を見る
数学$\textrm{III}$ グラフを描こう(11)
$y=\frac{x^3}{x^2-1}$ のグラフを描け。ただし、凹凸、漸近線も調べよ。
福田のわかった数学〜高校3年生理系088〜グラフを描こう(10)分数関数、凹凸、漸近線

単元:
#関数と極限#微分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ グラフを描こう(10)
$y=\frac{e^x}{x-1}$
のグラフを描け。ただし凹凸、漸近線を調べよ。
この動画を見る
数学$\textrm{III}$ グラフを描こう(10)
$y=\frac{e^x}{x-1}$
のグラフを描け。ただし凹凸、漸近線を調べよ。
福田のわかった数学〜高校3年生理系087〜グラフを描こう(9)媒介変数表示のグラフ

単元:
#平面上の曲線#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#媒介変数表示と極座標#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ グラフを描こう(9)
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=t\cos t-\sin t\\
y=t\sin t+\cos t
\end{array}
\right.
(0 \leqq t \leqq 2\pi)
\end{eqnarray}$
のグラフを描け。ただし凹凸は調べなくてよい。
この動画を見る
数学$\textrm{III}$ グラフを描こう(9)
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=t\cos t-\sin t\\
y=t\sin t+\cos t
\end{array}
\right.
(0 \leqq t \leqq 2\pi)
\end{eqnarray}$
のグラフを描け。ただし凹凸は調べなくてよい。
福田のわかった数学〜高校3年生理系086〜グラフを描こう(8)媒介変数表示のグラフ

単元:
#平面上の曲線#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#媒介変数表示と極座標#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ グラフを描こう(8)
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=t^3-3t^2\\
y=t^2-2t
\end{array}
\right.
\end{eqnarray}$
のグラフを描け。
ただし凹凸は調べなくてよい。
この動画を見る
数学$\textrm{III}$ グラフを描こう(8)
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=t^3-3t^2\\
y=t^2-2t
\end{array}
\right.
\end{eqnarray}$
のグラフを描け。
ただし凹凸は調べなくてよい。
福田のわかった数学〜高校3年生理系085〜グラフを描こう(7)媒介変数表示のグラフ

単元:
#平面上の曲線#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#媒介変数表示と極座標#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$グラフを描こう(7)
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=t^2+1\\
y=2-t-t^2
\end{array}
\right.
(-2 \leqq t \leqq 1)
\end{eqnarray}$
のグラフを描け。
凹凸は調べなくてよい。
この動画を見る
数学$\textrm{III}$グラフを描こう(7)
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=t^2+1\\
y=2-t-t^2
\end{array}
\right.
(-2 \leqq t \leqq 1)
\end{eqnarray}$
のグラフを描け。
凹凸は調べなくてよい。
福田の数学〜明治大学2021年理工学部第1問(4)〜定積分で表された関数と変曲点

単元:
#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#大学入試解答速報#数学#明治大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(4)連続関数$f(x)$は区間$x \geqq 0$で正の値をとり、区間$x \gt 0$で微分可能
かつ$f'(x)\neq 0$であるとする。さらに、実数の定数aと関数$f(x)$が
$\int_0^x3t^2f(t)dt-(x^3+3)f(x)+\log f(x)=a (x \geqq 0)$
を満たすとする。このとき
$a=-\boxed{\ \ ヌ\ \ }-\log\boxed{\ \ ネ\ \ }$
である。また、曲線$y=f(x)\ (x \gt 0)$の変曲点のx座標をpとすると
$p^3=\frac{\boxed{\ \ ノ\ \ }}{\boxed{\ \ ハ\ \ }}$である。ただし、$\log x$は$x$の自然対数である。
この動画を見る
${\Large\boxed{1}}$(4)連続関数$f(x)$は区間$x \geqq 0$で正の値をとり、区間$x \gt 0$で微分可能
かつ$f'(x)\neq 0$であるとする。さらに、実数の定数aと関数$f(x)$が
$\int_0^x3t^2f(t)dt-(x^3+3)f(x)+\log f(x)=a (x \geqq 0)$
を満たすとする。このとき
$a=-\boxed{\ \ ヌ\ \ }-\log\boxed{\ \ ネ\ \ }$
である。また、曲線$y=f(x)\ (x \gt 0)$の変曲点のx座標をpとすると
$p^3=\frac{\boxed{\ \ ノ\ \ }}{\boxed{\ \ ハ\ \ }}$である。ただし、$\log x$は$x$の自然対数である。
福田のわかった数学〜高校3年生理系079〜グラフを描こう(1)分数関数のグラフ

単元:
#関数と極限#微分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ グラフを描こう(1)
$y=\frac{x^2}{x-1}$のグラフを描け。
ただし凹凸は調べなくてよい。
この動画を見る
数学$\textrm{III}$ グラフを描こう(1)
$y=\frac{x^2}{x-1}$のグラフを描け。
ただし凹凸は調べなくてよい。
福田のわかった数学〜高校3年生理系078〜極値(2)極値を求める

単元:
#微分とその応用#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 極値(2)
$f(x)=x^2e^{-|x-a|} (a \gt 2)$の極値を求めよ。
この動画を見る
数学$\textrm{III}$ 極値(2)
$f(x)=x^2e^{-|x-a|} (a \gt 2)$の極値を求めよ。
福田の数学〜明治大学2021年全学部統一入試Ⅲ第4問〜極方程式と曲線で囲まれた面積

単元:
#平面上の曲線#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#媒介変数表示と極座標#数学(高校生)#大学入試解答速報#数学#明治大学#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}}$座標平面の原点Oを極、x軸の正の部分を始線とする極座標$(r,\ \theta)$を考える。
$k \gt 0$として、極方程式
$r(\sqrt{\cos\theta}+\sqrt{\sin\theta})^2=k (0 \leqq \theta \leqq \frac{\pi}{2})$
で表される曲線を$C(k)$とする。曲線$C(k)$上の点を直交座標$(x,\ y)$で表せばxの
とりうる値の範囲は、$\boxed{\ \ ア\ \ } \leqq x \leqq \boxed{\ \ イ\ \ }$である。
曲線$C(k)$とx軸、y軸で囲まれた図形の面積を$S(k)$とおけば、$S(k)=\boxed{\ \ ウ\ \ }$
でなる。直交座標が$(\frac{k}{4},\ \frac{k}{4})$である曲線$C(k)$上の点Aにおける曲線$C(k)$の接線l
の方程式は、$y=\boxed{\ \ エ\ \ }$となる。曲線$C(k)$と直線l、およびx軸で囲まれた
図形の面積を$T(k)$とおけば、$S(k)=\boxed{\ \ オ\ \ }\ T(k)$が成り立つ。$0 \lt m \lt n$を
満たす実数$m,n$に対して、$S(n)-S(m)$が$T(n)$と等しくなるのは、
$\frac{m^2}{n^2}=\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ \ \ }}$のときである。
$\boxed{\ \ イ\ \ }\ 、\boxed{\ \ ウ\ \ }$の解答群
$⓪\sqrt k ①k ②k^2 ③\frac{\sqrt 2}{2} ④\frac{\sqrt 2}{3}$
$⑤\frac{k}{2} ⑥\frac{k}{3} ⑦\frac{k^2}{4} ⑧\frac{k^2}{5} ⑨\frac{k^2}{6}$
$\boxed{\ \ エ\ \ }$の解答群
$⓪x+\frac{k}{2} ①x+\frac{k}{4} ②-x+\frac{k}{2} ③-x+\frac{k}{4} ④2x-\frac{k}{2}$
$⑤2x-\frac{k}{4} ⑥2x-\frac{3k}{4} ⑦-2x+\frac{k}{2} ⑧-2x+\frac{k}{4} ⑨-2x+\frac{3k}{4}$
2021明治大学全統過去問
この動画を見る
${\Large\boxed{4}}$座標平面の原点Oを極、x軸の正の部分を始線とする極座標$(r,\ \theta)$を考える。
$k \gt 0$として、極方程式
$r(\sqrt{\cos\theta}+\sqrt{\sin\theta})^2=k (0 \leqq \theta \leqq \frac{\pi}{2})$
で表される曲線を$C(k)$とする。曲線$C(k)$上の点を直交座標$(x,\ y)$で表せばxの
とりうる値の範囲は、$\boxed{\ \ ア\ \ } \leqq x \leqq \boxed{\ \ イ\ \ }$である。
曲線$C(k)$とx軸、y軸で囲まれた図形の面積を$S(k)$とおけば、$S(k)=\boxed{\ \ ウ\ \ }$
でなる。直交座標が$(\frac{k}{4},\ \frac{k}{4})$である曲線$C(k)$上の点Aにおける曲線$C(k)$の接線l
の方程式は、$y=\boxed{\ \ エ\ \ }$となる。曲線$C(k)$と直線l、およびx軸で囲まれた
図形の面積を$T(k)$とおけば、$S(k)=\boxed{\ \ オ\ \ }\ T(k)$が成り立つ。$0 \lt m \lt n$を
満たす実数$m,n$に対して、$S(n)-S(m)$が$T(n)$と等しくなるのは、
$\frac{m^2}{n^2}=\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ \ \ }}$のときである。
$\boxed{\ \ イ\ \ }\ 、\boxed{\ \ ウ\ \ }$の解答群
$⓪\sqrt k ①k ②k^2 ③\frac{\sqrt 2}{2} ④\frac{\sqrt 2}{3}$
$⑤\frac{k}{2} ⑥\frac{k}{3} ⑦\frac{k^2}{4} ⑧\frac{k^2}{5} ⑨\frac{k^2}{6}$
$\boxed{\ \ エ\ \ }$の解答群
$⓪x+\frac{k}{2} ①x+\frac{k}{4} ②-x+\frac{k}{2} ③-x+\frac{k}{4} ④2x-\frac{k}{2}$
$⑤2x-\frac{k}{4} ⑥2x-\frac{3k}{4} ⑦-2x+\frac{k}{2} ⑧-2x+\frac{k}{4} ⑨-2x+\frac{3k}{4}$
2021明治大学全統過去問
福田のわかった数学〜高校3年生理系077〜極値(1)極大値をもつ条件

単元:
#数Ⅱ#三角関数#三角関数とグラフ#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 極値(1)
$f(x)=\frac{a-\cos x}{a+\sin x}\ が0 \lt x \lt \frac{\pi}{2}$の範囲で
極大値をもつように定数aの値の範囲を定めよ。
この動画を見る
数学$\textrm{III}$ 極値(1)
$f(x)=\frac{a-\cos x}{a+\sin x}\ が0 \lt x \lt \frac{\pi}{2}$の範囲で
極大値をもつように定数aの値の範囲を定めよ。
福田の数学〜明治大学2021年全学部統一入試Ⅲ第1問〜関数の増減と面積

単元:
#微分とその応用#積分とその応用#微分法#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#数学(高校生)#大学入試解答速報#数学#明治大学#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$関数$f(x)=\frac{1}{2}(x+\sqrt{2-3x^2})$の定義域は$-\frac{\sqrt{\boxed{\ \ ア\ \ }}}{\boxed{\ \ イ\ \ }} \leqq x \leqq \frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$であり、
$f(x)$は$x=\frac{\sqrt{\boxed{\ \ オ\ \ }}}{\boxed{\ \ カ\ \ }}$のとき、
最大値$\frac{\sqrt{\boxed{\ \ キ\ \ }}}{\boxed{\ \ ク\ \ }}$をとる。曲線$y=f(x)$、
直線$y=2x$およびy軸で囲まれた図形の面積は$\boxed{\ \ ケ\ \ }$となる。
$\boxed{\ \ ケ\ \ }$の解答群
$⓪\frac{\sqrt3}{18}\pi ①\frac{\sqrt3}{36}\pi ②\frac{\sqrt3}{72}\pi ③\frac{1}{6}+\frac{\sqrt3}{36}\pi ④\frac{1}{24}+\frac{\sqrt3}{36}\pi$
$⑤\frac{5}{24}+\frac{\sqrt3}{36}\pi ⑥\frac{1}{3}+\frac{\sqrt3}{18}\pi ⑦\frac{1}{6}+\frac{\sqrt3}{18}\pi ⑧\frac{1}{8}+\frac{\sqrt3}{18}\pi ⑨\frac{7}{24}+\frac{\sqrt3}{18}\pi$
この動画を見る
${\Large\boxed{1}}$関数$f(x)=\frac{1}{2}(x+\sqrt{2-3x^2})$の定義域は$-\frac{\sqrt{\boxed{\ \ ア\ \ }}}{\boxed{\ \ イ\ \ }} \leqq x \leqq \frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$であり、
$f(x)$は$x=\frac{\sqrt{\boxed{\ \ オ\ \ }}}{\boxed{\ \ カ\ \ }}$のとき、
最大値$\frac{\sqrt{\boxed{\ \ キ\ \ }}}{\boxed{\ \ ク\ \ }}$をとる。曲線$y=f(x)$、
直線$y=2x$およびy軸で囲まれた図形の面積は$\boxed{\ \ ケ\ \ }$となる。
$\boxed{\ \ ケ\ \ }$の解答群
$⓪\frac{\sqrt3}{18}\pi ①\frac{\sqrt3}{36}\pi ②\frac{\sqrt3}{72}\pi ③\frac{1}{6}+\frac{\sqrt3}{36}\pi ④\frac{1}{24}+\frac{\sqrt3}{36}\pi$
$⑤\frac{5}{24}+\frac{\sqrt3}{36}\pi ⑥\frac{1}{3}+\frac{\sqrt3}{18}\pi ⑦\frac{1}{6}+\frac{\sqrt3}{18}\pi ⑧\frac{1}{8}+\frac{\sqrt3}{18}\pi ⑨\frac{7}{24}+\frac{\sqrt3}{18}\pi$
福田の数学〜青山学院大学2021年理工学部第5問〜絶対値の付いた関数と面積の最大最小

単元:
#大学入試過去問(数学)#微分とその応用#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{5}}$tを$0 \leqq t \leqq \frac{\pi}{2}$を満たす定数とする。関数
$f(x)=|\sin x-\sin t| (0 \leqq x \leqq \pi)$
について、以下の問いに答えよ。
(1)$t=\frac{\pi}{6}$のとき$y=f(x) (0 \leqq x \leqq \pi)$のグラフを描け。
(2)$y=f(x) (0 \leqq x \leqq \pi)$のグラフとx軸、y軸および直線$x=\pi$
で囲まれた図形の面積をSとする。Sをtを用いて表せ。
(3)tが$\leqq t \leqq \frac{\pi}{2}$の範囲を動くときのSの最大値と最小値を求めよ。
2021青山学院大学理工学部過去問
この動画を見る
${\Large\boxed{5}}$tを$0 \leqq t \leqq \frac{\pi}{2}$を満たす定数とする。関数
$f(x)=|\sin x-\sin t| (0 \leqq x \leqq \pi)$
について、以下の問いに答えよ。
(1)$t=\frac{\pi}{6}$のとき$y=f(x) (0 \leqq x \leqq \pi)$のグラフを描け。
(2)$y=f(x) (0 \leqq x \leqq \pi)$のグラフとx軸、y軸および直線$x=\pi$
で囲まれた図形の面積をSとする。Sをtを用いて表せ。
(3)tが$\leqq t \leqq \frac{\pi}{2}$の範囲を動くときのSの最大値と最小値を求めよ。
2021青山学院大学理工学部過去問
福田の数学〜上智大学2021年TEAP利用理系第4問〜楕円と弦の中点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#平面上の曲線#図形と方程式#軌跡と領域#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}}$Oを原点とする座標平面において、楕円$D:\frac{x^2}{6}+\frac{y^2}{2}=1$ 上に異なる2点$P_1,P_2$
がある。$P_1$における接線$l_1$と$P_2$における接線$l_2$の交点を$Q(a,\ b)$とし、線分$P_1P_2$の
中点をRとする。
(1)$P_1$の座標を$(x_1,\ y_1)$とするとき、$l_1$の方程式は$x_1x+\boxed{\ \ チ\ \ }\ y_1y+\boxed{\ \ ツ\ \ }=0$
と表される。
(2)直線$P_1P_2$の方程式は、a,bを用いて$ax+\boxed{\ \ テ\ \ }\ by+\boxed{\ \ ト\ \ }=0$と表される。
(3)3点O,R,Qは一直線上にあって$\overrightarrow{ OR }=\frac{\boxed{\ \ ナ\ \ }}{a^2+\boxed{\ \ ニ\ \ }\ b^2}\overrightarrow{ OQ }$が成り立つ。
(4)$l_1$と$l_2$のどちらもy軸と平行ではないとする。このとき、$l_1$と$l_2$の傾きは
tの方程式$(a^2+\boxed{\ \ ヌ\ \ })t^2+\boxed{\ \ ネ\ \ }abt+(b^2+\boxed{\ \ ノ\ \ })=0$ の解である。
(5)$l_1$と$l_2$が直交しながら$P_1,P_2$が動くとする。
$(\textrm{i})Q$の軌跡の方程式を求めよ。 $(\textrm{ii})R$のy座標の最大値を求めよ。
$(\textrm{iii})R$の軌跡の概形を描け。
2021上智大学理系過去問
この動画を見る
${\Large\boxed{4}}$Oを原点とする座標平面において、楕円$D:\frac{x^2}{6}+\frac{y^2}{2}=1$ 上に異なる2点$P_1,P_2$
がある。$P_1$における接線$l_1$と$P_2$における接線$l_2$の交点を$Q(a,\ b)$とし、線分$P_1P_2$の
中点をRとする。
(1)$P_1$の座標を$(x_1,\ y_1)$とするとき、$l_1$の方程式は$x_1x+\boxed{\ \ チ\ \ }\ y_1y+\boxed{\ \ ツ\ \ }=0$
と表される。
(2)直線$P_1P_2$の方程式は、a,bを用いて$ax+\boxed{\ \ テ\ \ }\ by+\boxed{\ \ ト\ \ }=0$と表される。
(3)3点O,R,Qは一直線上にあって$\overrightarrow{ OR }=\frac{\boxed{\ \ ナ\ \ }}{a^2+\boxed{\ \ ニ\ \ }\ b^2}\overrightarrow{ OQ }$が成り立つ。
(4)$l_1$と$l_2$のどちらもy軸と平行ではないとする。このとき、$l_1$と$l_2$の傾きは
tの方程式$(a^2+\boxed{\ \ ヌ\ \ })t^2+\boxed{\ \ ネ\ \ }abt+(b^2+\boxed{\ \ ノ\ \ })=0$ の解である。
(5)$l_1$と$l_2$が直交しながら$P_1,P_2$が動くとする。
$(\textrm{i})Q$の軌跡の方程式を求めよ。 $(\textrm{ii})R$のy座標の最大値を求めよ。
$(\textrm{iii})R$の軌跡の概形を描け。
2021上智大学理系過去問
福田のわかった数学〜高校3年生理系070〜接線(2)媒介変数表示の接線

単元:
#平面上の曲線#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#媒介変数表示と極座標#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$接線(2) 媒介変数表示の接線
$\left\{
\begin{array}{1}
x=\theta-\sin\theta\\
y=1-\cos\theta
\end{array}
\right.$
で表される曲線の$\theta=\frac{3\pi}{2}$のときの点Pにおける接線を求めよ。
この動画を見る
数学$\textrm{III}$接線(2) 媒介変数表示の接線
$\left\{
\begin{array}{1}
x=\theta-\sin\theta\\
y=1-\cos\theta
\end{array}
\right.$
で表される曲線の$\theta=\frac{3\pi}{2}$のときの点Pにおける接線を求めよ。
【数Ⅲ】微分法:伝説の静岡大学のグラフの問題を紹介!!どんなグラフになるか予想しよう!(概要欄にネタバレあり)

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#静岡大学#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数$f(x),g(x)$を $f(x)=x^4-x^2+6(\vert x\vert\leqq 1),\dfrac{12}{\vert x\vert +1}(\vert x\vert\gt 1)$,$g(x)=\dfrac{1}{2}\cos2\pi x+\dfrac{7}{2}(\vert x\vert\leqq 2)$ で定義する。このとき次の問いに答えよ。
$f(x),g(x)$の増減を調べ、2曲線$C_1:y=f(x),C_2:y=g(x)$のグラフの概形を同じ座標平面上にかけ。
この動画を見る
関数$f(x),g(x)$を $f(x)=x^4-x^2+6(\vert x\vert\leqq 1),\dfrac{12}{\vert x\vert +1}(\vert x\vert\gt 1)$,$g(x)=\dfrac{1}{2}\cos2\pi x+\dfrac{7}{2}(\vert x\vert\leqq 2)$ で定義する。このとき次の問いに答えよ。
$f(x),g(x)$の増減を調べ、2曲線$C_1:y=f(x),C_2:y=g(x)$のグラフの概形を同じ座標平面上にかけ。
福田のわかった数学〜高校3年生理系068〜微分(13)関数方程式

単元:
#微分とその応用#微分法#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 微分(13) 関数方程式
$x \gt 0$ で定義された微分可能な関数$f(x)$において、$f(xy)=f(x)+f(y)$
が正の数$x,\ y$に対して常に成り立ち、$f'(1)=1$とする。
(1)$f(1)$ を求めよ。
(2)$f'(x)=\frac{1}{x}$ を示せ。
この動画を見る
数学$\textrm{III}$ 微分(13) 関数方程式
$x \gt 0$ で定義された微分可能な関数$f(x)$において、$f(xy)=f(x)+f(y)$
が正の数$x,\ y$に対して常に成り立ち、$f'(1)=1$とする。
(1)$f(1)$ を求めよ。
(2)$f'(x)=\frac{1}{x}$ を示せ。
福田の数学〜上智大学2021年理工学部第2問(1)〜条件を満たす関数と命題の否定

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#微分とその応用#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$(1)実数全体で定義され、実数の値をとる関数$f(x)$に対する次の条件$p$を考える。
$p:「K以上の全ての実数xに対してf(x) \geqq 1」$が成り立つような実数Kが存在する。
$(\textrm{i})$次に挙げた関数$(\textrm{a})~(\textrm{d})$のそれぞれについて、pを満たすならばo、pを
満たさないならばxをマークせよ。
$(\textrm{a})f(x)=xe^{-x} (\textrm{b})f(x)=\frac{2x^2+1}{x^2+1} (\textrm{c})f(x)=x+\sin x (\textrm{d})f(x)=x\sin x$
$(\textrm{ii})$次の条件がpの否定になるように、$\boxed{\ \ あ\ \ }~\boxed{\ \ え\ \ }$のそれぞれの選択肢から、
あてはまるものを選べ。
・$「\boxed{\ \ あ\ \ }\ \boxed{\ \ い\ \ }$実数に対して$\boxed{\ \ う\ \ }」が\boxed{\ \ え\ \ }$
$\boxed{\ \ あ\ \ }$の選択肢$:(\textrm{a})K$以上の $(\textrm{b})K$未満の
$\boxed{\ \ い\ \ }$の選択肢:$(\textrm{a})$すべての $(\textrm{b})$ある
$\boxed{\ \ う\ \ }$の選択肢$:(\textrm{a})f(x) \geqq 1 (\textrm{b})f(x) \lt 1$
$\boxed{\ \ え\ \ }$の選択肢$:(\textrm{a})$どんな実数Kについても成り立つ $\\(\textrm{b})$成り立つような実数Kが存在する
$(\textrm{iii})$関数$f(x)$に対して、$g(x)=2f(x)$で関数$g(x)$を定める。次に挙げた命題$(\textrm{A})~(\textrm{D})$
のそれぞれについて、正しければoを、正しくなければxを、マークせよ。
$(\textrm{A})f(x)$が$p$を満たすならば、$g(x)$も$p$を満たす。
$(\textrm{B})g(x)$が$p$を満たすならば、$f(x)$もpを満たす。
$(\textrm{C})f(x)$が$p$を満たさないならば、$g(x)$もpを満たさない。
$(\textrm{D})f(x)$がpを満たさないならば、$g(x)$も$p$を満たす。
2021上智大学理工学部過去問
この動画を見る
${\Large\boxed{2}}$(1)実数全体で定義され、実数の値をとる関数$f(x)$に対する次の条件$p$を考える。
$p:「K以上の全ての実数xに対してf(x) \geqq 1」$が成り立つような実数Kが存在する。
$(\textrm{i})$次に挙げた関数$(\textrm{a})~(\textrm{d})$のそれぞれについて、pを満たすならばo、pを
満たさないならばxをマークせよ。
$(\textrm{a})f(x)=xe^{-x} (\textrm{b})f(x)=\frac{2x^2+1}{x^2+1} (\textrm{c})f(x)=x+\sin x (\textrm{d})f(x)=x\sin x$
$(\textrm{ii})$次の条件がpの否定になるように、$\boxed{\ \ あ\ \ }~\boxed{\ \ え\ \ }$のそれぞれの選択肢から、
あてはまるものを選べ。
・$「\boxed{\ \ あ\ \ }\ \boxed{\ \ い\ \ }$実数に対して$\boxed{\ \ う\ \ }」が\boxed{\ \ え\ \ }$
$\boxed{\ \ あ\ \ }$の選択肢$:(\textrm{a})K$以上の $(\textrm{b})K$未満の
$\boxed{\ \ い\ \ }$の選択肢:$(\textrm{a})$すべての $(\textrm{b})$ある
$\boxed{\ \ う\ \ }$の選択肢$:(\textrm{a})f(x) \geqq 1 (\textrm{b})f(x) \lt 1$
$\boxed{\ \ え\ \ }$の選択肢$:(\textrm{a})$どんな実数Kについても成り立つ $\\(\textrm{b})$成り立つような実数Kが存在する
$(\textrm{iii})$関数$f(x)$に対して、$g(x)=2f(x)$で関数$g(x)$を定める。次に挙げた命題$(\textrm{A})~(\textrm{D})$
のそれぞれについて、正しければoを、正しくなければxを、マークせよ。
$(\textrm{A})f(x)$が$p$を満たすならば、$g(x)$も$p$を満たす。
$(\textrm{B})g(x)$が$p$を満たすならば、$f(x)$もpを満たす。
$(\textrm{C})f(x)$が$p$を満たさないならば、$g(x)$もpを満たさない。
$(\textrm{D})f(x)$がpを満たさないならば、$g(x)$も$p$を満たす。
2021上智大学理工学部過去問
福田の数学〜上智大学2021年理工学部第1問〜双曲線の方程式と回転体の体積

単元:
#大学入試過去問(数学)#平面上の曲線#微分とその応用#2次曲線#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#上智大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 媒介変数表示
$x=\frac{2}{\cos\theta}, y=3\tan\theta+1$
で表される図形Cを考える。
(1)Cは頂点$(±\boxed{\ \ ア\ \ },\ \boxed{\ \ イ\ \ })$、焦点$(±\sqrt{\boxed{\ \ ウ\ \ }},\ \boxed{\ \ エ\ \ })$、
漸近線$y=±\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}x+\boxed{\ \ キ\ \ }$をもつ双曲線である。
(2)双曲線Cと直線$x=4$は、2点$(4,\ \boxed{\ \ ク\ \ }±\boxed{\ \ ケ\ \ }\sqrt{\boxed{\ \ コ\ \ }})$
で交わる。\\
(3)双曲線Cと直線x=4で囲まれる部分をy軸の周りに1回転\\
させてできる立体の体積は\ \boxed{\ \ サ\ \ }\sqrt{\boxed{\ \ シ\ \ }}\ \pi である。
\end{eqnarray}
2021上智大学理工学部過去問
この動画を見る
${\Large\boxed{1}}$ 媒介変数表示
$x=\frac{2}{\cos\theta}, y=3\tan\theta+1$
で表される図形Cを考える。
(1)Cは頂点$(±\boxed{\ \ ア\ \ },\ \boxed{\ \ イ\ \ })$、焦点$(±\sqrt{\boxed{\ \ ウ\ \ }},\ \boxed{\ \ エ\ \ })$、
漸近線$y=±\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}x+\boxed{\ \ キ\ \ }$をもつ双曲線である。
(2)双曲線Cと直線$x=4$は、2点$(4,\ \boxed{\ \ ク\ \ }±\boxed{\ \ ケ\ \ }\sqrt{\boxed{\ \ コ\ \ }})$
で交わる。\\
(3)双曲線Cと直線x=4で囲まれる部分をy軸の周りに1回転\\
させてできる立体の体積は\ \boxed{\ \ サ\ \ }\sqrt{\boxed{\ \ シ\ \ }}\ \pi である。
\end{eqnarray}
2021上智大学理工学部過去問
【数Ⅲ】微分法:対数微分、この計算式をどうしますか?

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$f(x)=(1+a^x)^{\frac{1}{x}}$は,$0<a<1$の時単調である
[上級問題精講数学Ⅲ、416(1)]
この動画を見る
$f(x)=(1+a^x)^{\frac{1}{x}}$は,$0<a<1$の時単調である
[上級問題精講数学Ⅲ、416(1)]
福田の数学〜中央大学2021年理工学部第4問〜定積分と不等式、極限

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#積分とその応用#関数の極限#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$自然数$n$に対し,$f_n(x)=x^{-1+\frac{1}{n}}(x\gt 0)$とおく.
また,正の実数$a_n$は$\displaystyle \int_{1}^{a_n}f_n(x)dx=1$満たすものとする.次の問い
答えよ.
(1)関数$f_n(x)$の不定積分を求めよ.
(2)$a_n$の値と極限$\displaystyle \lim_{n\to\infty}a_n$を求めよ.また,正の実数$b_n$が$\displaystyle \int_{1}^{b_n}f_{n+1}(x)dx=-1$を満たすとき,$b_n$の値と極限$\displaystyle \lim_{n\to\infty}b_n$を求めよ.
(3)2以上の自然数$k$に対して$\displaystyle \int_{k-1}^{k}f_n(x)dx \gt \dfrac{1}{k}$を示し,これを利用して$a_n\lt 4$を証明せよ.
(4)$\displaystyle \int_{1}^{a_n}f_{n+1}(x)dx\lt 1$を示し,これを利用して$a_n\lt a_{n+1}$を証明せよ.
2021中央大理工学部過去問
この動画を見る
$\boxed{4}$自然数$n$に対し,$f_n(x)=x^{-1+\frac{1}{n}}(x\gt 0)$とおく.
また,正の実数$a_n$は$\displaystyle \int_{1}^{a_n}f_n(x)dx=1$満たすものとする.次の問い
答えよ.
(1)関数$f_n(x)$の不定積分を求めよ.
(2)$a_n$の値と極限$\displaystyle \lim_{n\to\infty}a_n$を求めよ.また,正の実数$b_n$が$\displaystyle \int_{1}^{b_n}f_{n+1}(x)dx=-1$を満たすとき,$b_n$の値と極限$\displaystyle \lim_{n\to\infty}b_n$を求めよ.
(3)2以上の自然数$k$に対して$\displaystyle \int_{k-1}^{k}f_n(x)dx \gt \dfrac{1}{k}$を示し,これを利用して$a_n\lt 4$を証明せよ.
(4)$\displaystyle \int_{1}^{a_n}f_{n+1}(x)dx\lt 1$を示し,これを利用して$a_n\lt a_{n+1}$を証明せよ.
2021中央大理工学部過去問
練習問題41 微分方程式(数研1級1次 高専数学 教員採用試験)

単元:
#数学検定・数学甲子園・数学オリンピック等#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#その他#数学検定#数学検定1級#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$(1-x)y+(1+y)x\dfrac{dy}{dx}=0$の
一般解を求めよ.
この動画を見る
$(1-x)y+(1+y)x\dfrac{dy}{dx}=0$の
一般解を求めよ.
