 不定積分
不定積分
 不定積分
不定積分
名古屋大学2024年の確率と積分の融合問題をその場で解きながら解説してみた!#shorts #高校数学 #名古屋大学
単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
名古屋大学2024年の確率と積分の融合問題をその場で解きながら解説してみた!
この動画を見る
名古屋大学2024年の確率と積分の融合問題をその場で解きながら解説してみた!
【積分】「積分って結局なにしてるの?」について解説しました!【数学III】

【高校数学】毎日積分43日目【難易度:★★】【毎日17時投稿】

高校数学:数学検定準1級1次:問題5 :部分積分

単元:
#積分とその応用#不定積分#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_0^2 (\frac{x^2}{2}+3x)e^{\frac{x}{2}} dx$
不定積分、定積分を求めよ
この動画を見る
$\int_0^2 (\frac{x^2}{2}+3x)e^{\frac{x}{2}} dx$
不定積分、定積分を求めよ
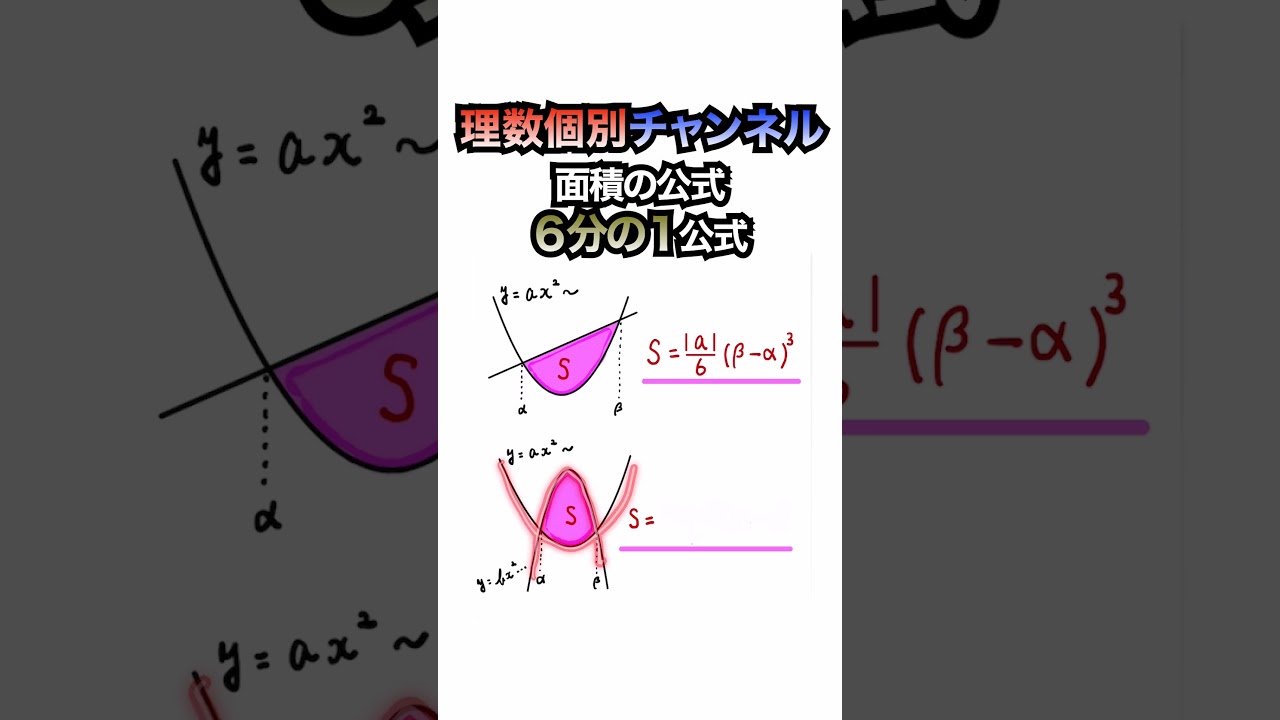
積分による面積計算の公式③【3分の1公式】#shorts
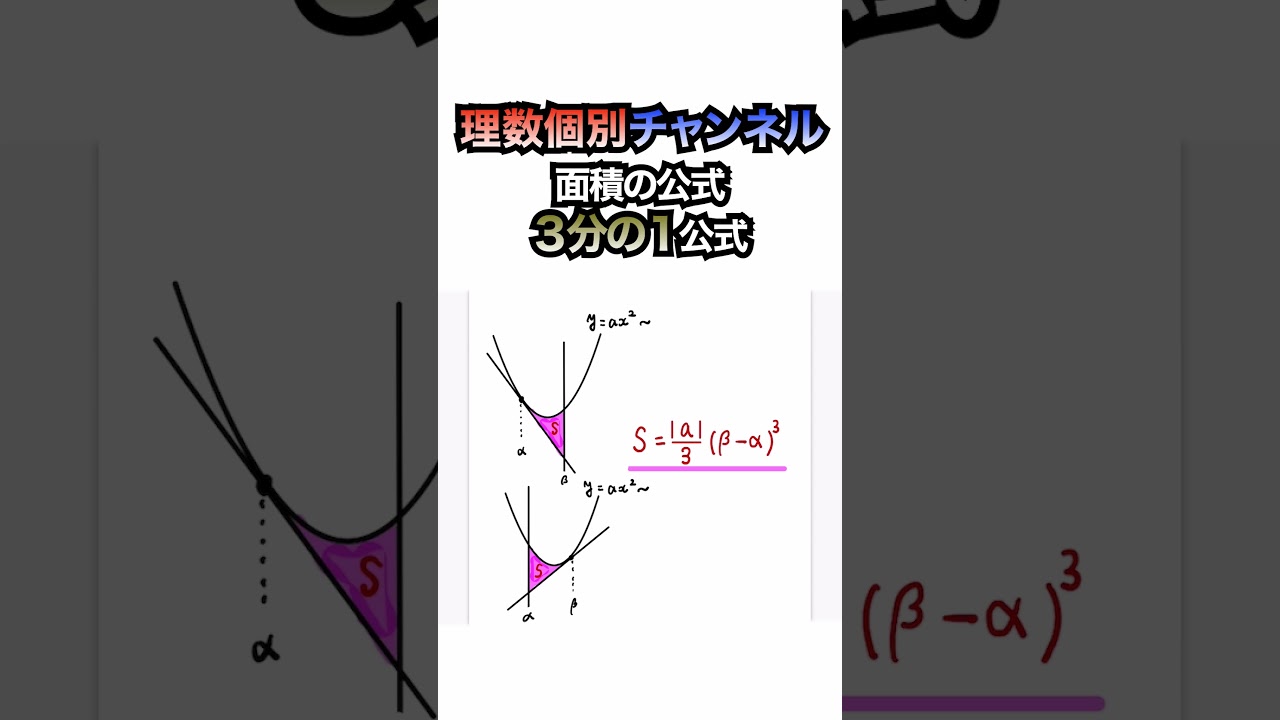
積分による面積計算の公式②【12分の1公式】#shorts
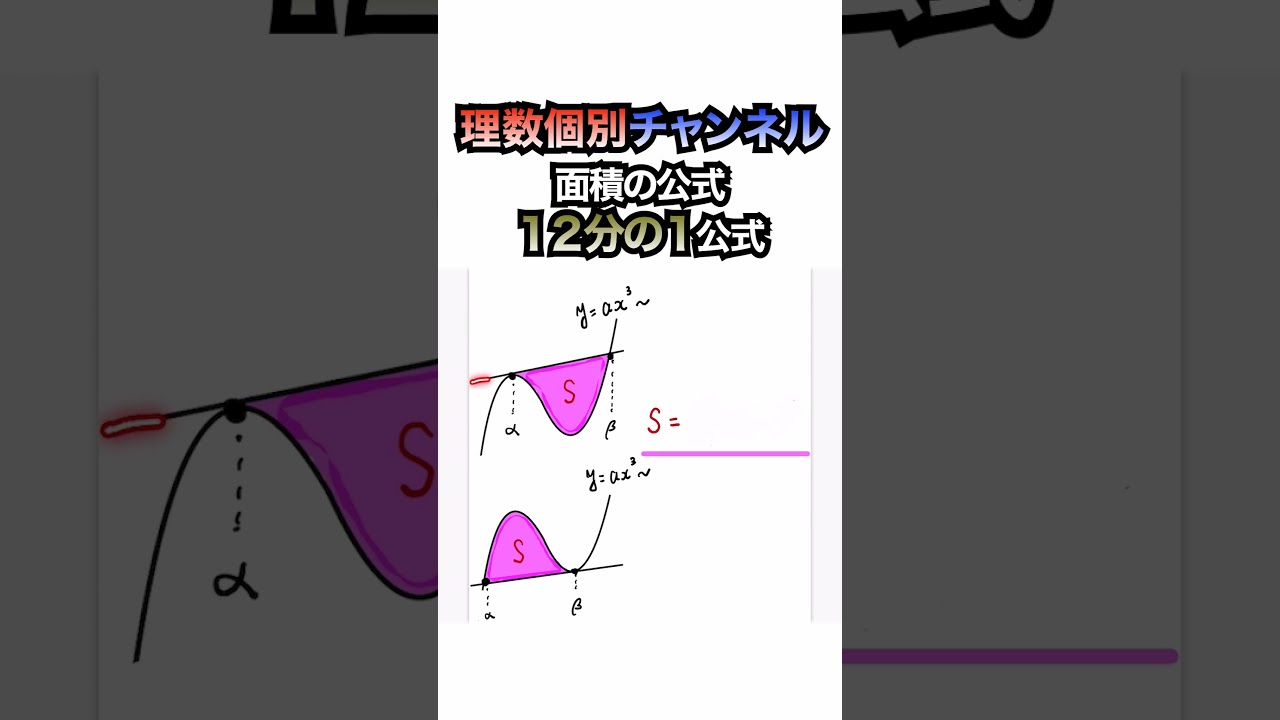
積分による面積計算の公式①【6分の1公式】#shorts
数学どうにかしたい人へ

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#図形の性質#式と証明#複素数と方程式#平面上のベクトル#空間ベクトル#平面上の曲線#複素数平面#図形と計量#データの分析#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#一次不等式(不等式・絶対値のある方程式・不等式)#集合と命題(集合・命題と条件・背理法)#2次方程式と2次不等式#2次関数とグラフ#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#データの分析#整数の性質#場合の数#確率#三角形の辺の比(内分・外分・二等分線)#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#図形と方程式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#円と方程式#軌跡と領域#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数列#確率分布と統計的な推測#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#数列とその和(等差・等比・階差・Σ)#漸化式#数学的帰納法#確率分布#統計的な推測#関数と極限#微分とその応用#積分とその応用#2次曲線#複素数平面#図形への応用#関数(分数関数・無理関数・逆関数と合成関数)#数列の極限#関数の極限#微分法#色々な関数の導関数#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#不定積分#定積分#面積・体積・長さ・速度#空間における垂直と平行と多面体(オイラーの法則)#不定積分・定積分#面積、体積#媒介変数表示と極座標#速度と近似式#数学(高校生)#数B#数C#数Ⅲ
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
数学が共通テストのみの人の勉強法紹介動画です
この動画を見る
数学が共通テストのみの人の勉強法紹介動画です
大学入試問題#637「朝のトーストと一緒にどうぞ!」埼玉大学
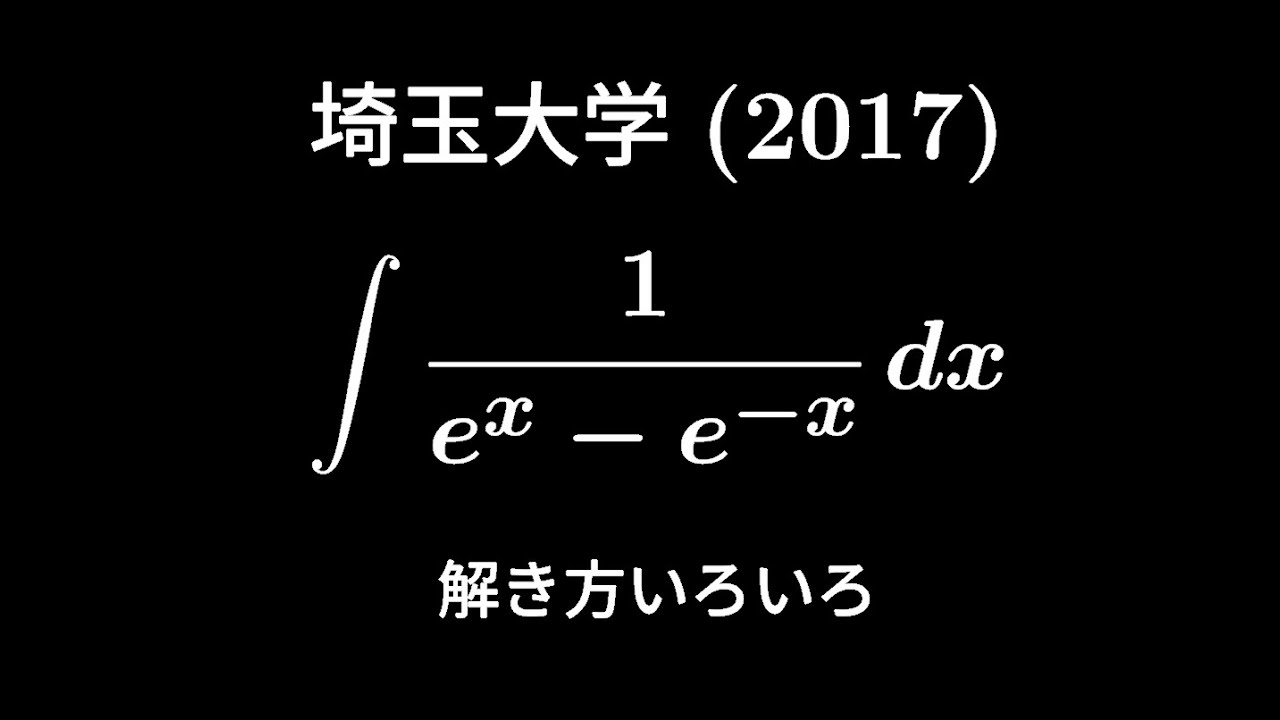
単元:
#大学入試過去問(数学)#不定積分#数学(高校生)#埼玉大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{1}{e^x-e^{-x}} dx$
出典:2017年埼玉大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{1}{e^x-e^{-x}} dx$
出典:2017年埼玉大学 入試問題
大学入試問題#636「ミスなく」 東京電機大学(2020) #不定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#東京電機大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} x^3log(x^2+1) dx$
出典:2020年東京電機大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} x^3log(x^2+1) dx$
出典:2020年東京電機大学 入試問題
大学入試問題#635「意外と簡単」 公立諏訪東京理科大学 #不定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#東京理科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
(1)$\displaystyle \int e^x\{f'(x)+f(x)\} dx$
(2)$\displaystyle \int e^x \displaystyle \frac{1+\sin\ x}{1+\cos\ x}\ dx$
出典:2023年公立諏訪東京理科大学 入試問題
この動画を見る
(1)$\displaystyle \int e^x\{f'(x)+f(x)\} dx$
(2)$\displaystyle \int e^x \displaystyle \frac{1+\sin\ x}{1+\cos\ x}\ dx$
出典:2023年公立諏訪東京理科大学 入試問題
大学入試問題#626「一直線だが、最後まで気を抜かない」 横浜市立大学医学部(2007)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#横浜市立大学
指導講師:
ますただ
問題文全文(内容文):
$n$:自然数
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin\{(2n+1)\theta\}\cos\theta d\theta$
出典:2007年横浜市立大学 入試問題
この動画を見る
$n$:自然数
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin\{(2n+1)\theta\}\cos\theta d\theta$
出典:2007年横浜市立大学 入試問題
会津大学2014 #Shorts #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{dx}{x(log\ x)^2}$
出典:2014年会津大学
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{x(log\ x)^2}$
出典:2014年会津大学
広島市立大学 2016 #不定積分 #Shorts

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{\cos^3\ x}{\sin^2\ x} dx$
出典:2016年広島市立大学
この動画を見る
$\displaystyle \int \displaystyle \frac{\cos^3\ x}{\sin^2\ x} dx$
出典:2016年広島市立大学
大学入試問題#586「見た目が美しい」 広島市立大学(2009) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{dx}{x+\sqrt{ x }}$
出典:2009年広島市立大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{x+\sqrt{ x }}$
出典:2009年広島市立大学 入試問題
大学入試問題#584「これは落としたくない!!」 京都帝国大学(1937) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{2x+3}{x^3+x^2-2x} dx$
出典:1937年京都帝国大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{2x+3}{x^3+x^2-2x} dx$
出典:1937年京都帝国大学 入試問題
広島市立大学(2009) #不定積分 #Shorts

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int log(1+2x) dx$
出典:2009年広島市立大学
この動画を見る
$\displaystyle \int log(1+2x) dx$
出典:2009年広島市立大学
大学入試問題#581「最後まで落ち着いて!」 東京帝国大学(1940) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{3x^2-3x+2}{x^3-3x^2+x-3} dx$
出典:1940年東京帝国大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{3x^2-3x+2}{x^3-3x^2+x-3} dx$
出典:1940年東京帝国大学 入試問題
大学入試問題#579「技のかけ方は好みでしょうか」 京都帝国大学(1939) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{\sin^4\ x}{\cos^3\ x} dx$
出典:1939年京都帝国大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{\sin^4\ x}{\cos^3\ x} dx$
出典:1939年京都帝国大学 入試問題
大学入試問題#576「逆に閃かないと苦戦」 京都帝国大学(1938) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{\sin\theta+\cos\theta}{3+\sin2\theta} d\theta$
出典:1938年京都帝国大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{\sin\theta+\cos\theta}{3+\sin2\theta} d\theta$
出典:1938年京都帝国大学 入試問題
大学入試問題#574「なにかありそう」 東京帝国大学(1938) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{1+\sin\ x}{\sin\ x(1+\cos\ x)}\ dx$
出典:1938年東京帝国大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{1+\sin\ x}{\sin\ x(1+\cos\ x)}\ dx$
出典:1938年東京帝国大学 入試問題
大学入試問題#573「沼にはまらないように!!」 京都帝国大学(1937) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{dx}{x(a^3+x^3)}$
出典:1937年京都帝国大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{x(a^3+x^3)}$
出典:1937年京都帝国大学 入試問題
大学入試問題#572「初手どうすべきか」 By 英語orドイツ語さん #不定積分
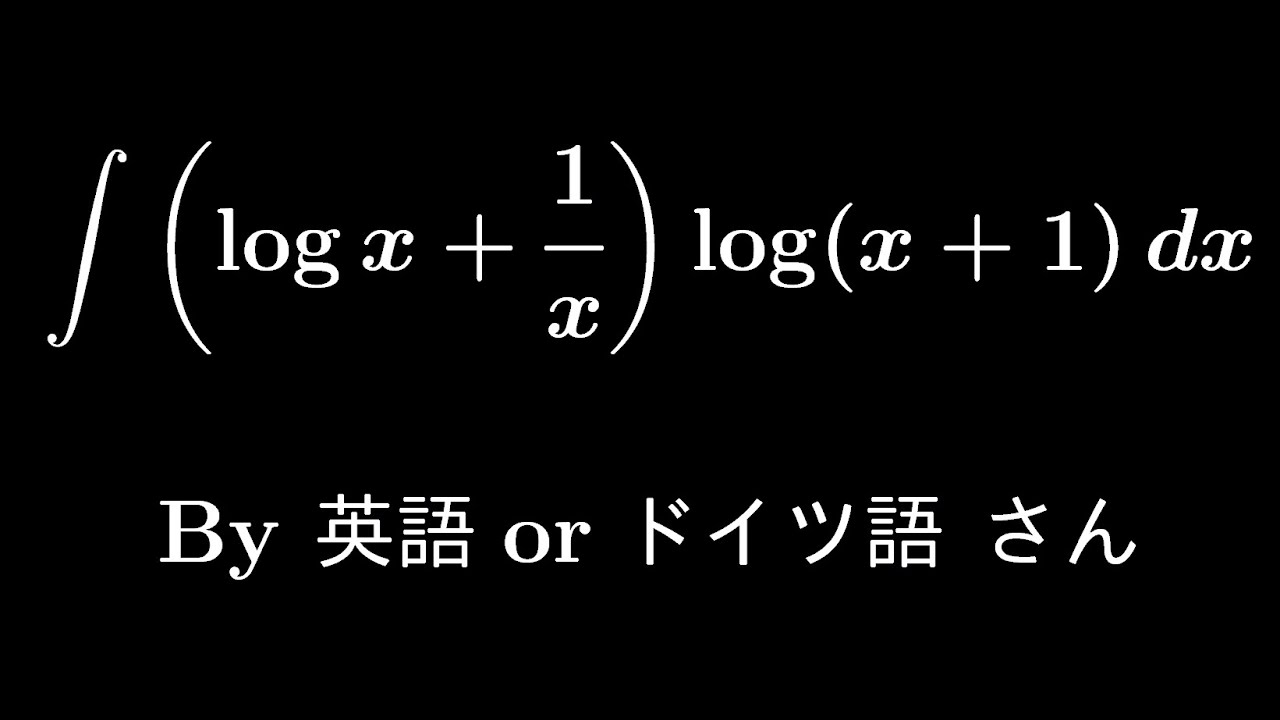
単元:
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int (log\ x+\displaystyle \frac{1}{x})log(x+1) dx$
この動画を見る
$\displaystyle \int (log\ x+\displaystyle \frac{1}{x})log(x+1) dx$
大学入試問題#569「これは至高の積分」 By Picmin3daisukiさん #不定積分
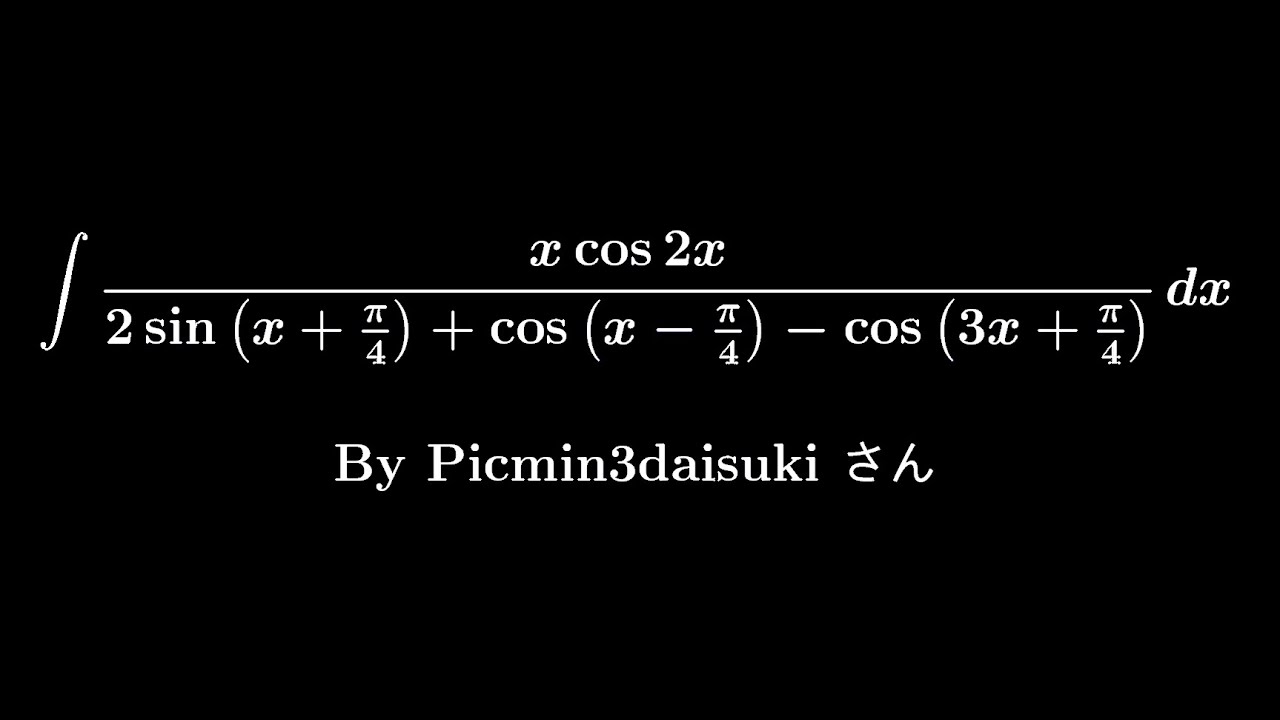
単元:
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x\ \cos\ 2x}{2\sin(x+\displaystyle \frac{\pi}{4})+\cos(x-\displaystyle \frac{\pi}{4})-\cos(3x+\displaystyle \frac{\pi}{4})}\ dx$
この動画を見る
$\displaystyle \int \displaystyle \frac{x\ \cos\ 2x}{2\sin(x+\displaystyle \frac{\pi}{4})+\cos(x-\displaystyle \frac{\pi}{4})-\cos(3x+\displaystyle \frac{\pi}{4})}\ dx$
大学入試問題#567「定数aの処理の難しさ」 東京大学1938 #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int x^2(x^2+a^2)^{\frac{1}{2}}\ dx$
出典:1938年東京帝国大学 入試問題
この動画を見る
$\displaystyle \int x^2(x^2+a^2)^{\frac{1}{2}}\ dx$
出典:1938年東京帝国大学 入試問題
大学入試問題#566「計算力勝負」 京都帝国大学(1936) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x^3}{x^2-3x+2}\ dx$
出典:1936年京都帝国大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{x^3}{x^2-3x+2}\ dx$
出典:1936年京都帝国大学 入試問題
大学入試問題#565「これは落とせない」 京都帝国大学(1935) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{e^x-1}{e^x+1}\ dx$
出典:1935年京都帝国大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{e^x-1}{e^x+1}\ dx$
出典:1935年京都帝国大学 入試問題
大学入試問題#564「構想力が鍛えられる問題!」 東京帝国大学(1934) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{3x+4}{\sqrt{ x^2+2x+5 }}\ dx$
出典:1934年東京帝国大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{3x+4}{\sqrt{ x^2+2x+5 }}\ dx$
出典:1934年東京帝国大学 入試問題
大学入試問題#560「初手が大事」 同志社大学(2016) #不定積分
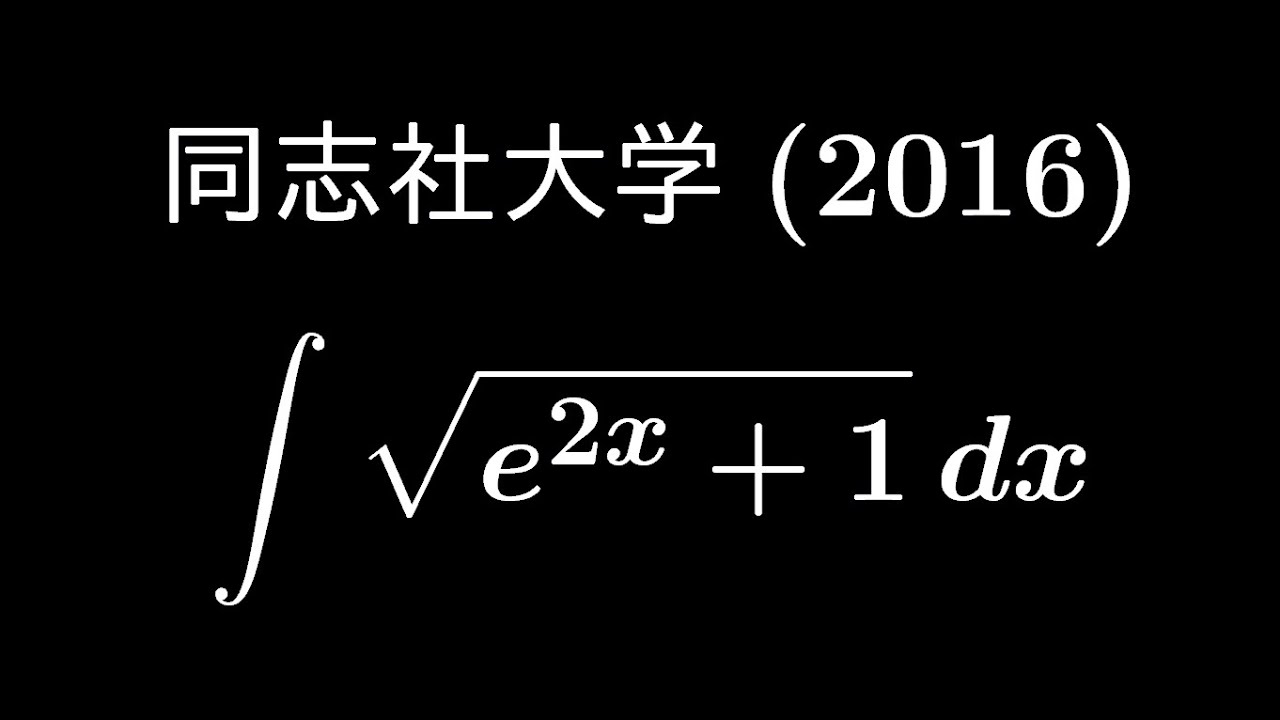
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#同志社大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \sqrt{ e^{2x}+1 }\ dx$
出典:2016年同志社大学 入試問題
この動画を見る
$\displaystyle \int \sqrt{ e^{2x}+1 }\ dx$
出典:2016年同志社大学 入試問題
大学入試問題#556「技はかかりそうだけど、正面突破」 東京帝国大学大正14年 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{x+\sin\ x}{1+\cos\ x} dx$
出典:大正14年東京大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{x+\sin\ x}{1+\cos\ x} dx$
出典:大正14年東京大学 入試問題
