 定積分
定積分
 定積分
定積分
大学入試問題#624「手抜きです。すみません」 横浜市立医学部(2004)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#横浜市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} log\displaystyle \frac{x+2}{x+1}dx$
出典:2004年横浜市立大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} log\displaystyle \frac{x+2}{x+1}dx$
出典:2004年横浜市立大学医学部 入試問題
大学入試問題#620「ほぼ一択」 横浜国立大学(2023) #定積分 僚太さんの紹介

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{log\frac{\pi}{4}}^{log\frac{\pi}{2}} \displaystyle \frac{e^{2x}}{\{\sin(e^x)\}^2} dx$
出典:2023年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{log\frac{\pi}{4}}^{log\frac{\pi}{2}} \displaystyle \frac{e^{2x}}{\{\sin(e^x)\}^2} dx$
出典:2023年横浜国立大学 入試問題
大学入試問題#619「正面突破」 福岡女子大学(2021) #定積分 僚太さんの紹介

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{2} \displaystyle \frac{1}{x^2}log\sqrt{ 9-x^2 }\ dx$
出典:2021年福岡女子大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{2} \displaystyle \frac{1}{x^2}log\sqrt{ 9-x^2 }\ dx$
出典:2021年福岡女子大学 入試問題
大学入試問題#618「とりあえず置換積分かな」 福岡大学医学部(2016) #定積分 僚太さんの紹介

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#福岡大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{\frac{5}{2}} (x-1)\sqrt{ -x^2+4x-3 }\ dx$
出典:2016年福岡大学医学部 入試問題
この動画を見る
$\displaystyle \int_{1}^{\frac{5}{2}} (x-1)\sqrt{ -x^2+4x-3 }\ dx$
出典:2016年福岡大学医学部 入試問題
工夫が必要な回転体の体積 By にっし~Diaryさん

単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$C_1:y=x^2$と$C_2:y=a\ log\ x$は$x=k$で接する
(1)$a$の値を求めよ
(2)$C_1,C_2,x$軸で囲まれた部分を、直線$x=k$を中心に回転させてできる体積を求めよ
この動画を見る
$C_1:y=x^2$と$C_2:y=a\ log\ x$は$x=k$で接する
(1)$a$の値を求めよ
(2)$C_1,C_2,x$軸で囲まれた部分を、直線$x=k$を中心に回転させてできる体積を求めよ
福田の数学〜上智大学2023年理工学部第3問〜対数関数の積分と数学的帰納法

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#数列#数学的帰納法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ $e$を自然定数の底とする。自然数$n$に対して、
$S_n$=$\displaystyle\int_1^e(\log x)^n dx$
とする。
(1)$S_1$の値を求めよ。
(2)すべての自然数$n$に対して、
$S_n$=$a_n e$+$b_n$, ただし$a_n$, $b_n$はいずれも整数
と表されることを証明せよ。
この動画を見る
$\Large\boxed{3}$ $e$を自然定数の底とする。自然数$n$に対して、
$S_n$=$\displaystyle\int_1^e(\log x)^n dx$
とする。
(1)$S_1$の値を求めよ。
(2)すべての自然数$n$に対して、
$S_n$=$a_n e$+$b_n$, ただし$a_n$, $b_n$はいずれも整数
と表されることを証明せよ。
福田の数学〜上智大学2023年TEAP利用型理系第4問Part2〜不等式の証明と近似値計算

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{4}}$ $e$を自然対数の底とする。$e$=2.718...である。
(1)0≦$x$≦1において不等式1+$x$≦$e^x$≦1+2$x$が成り立つことを示せ。
(2)$n$を自然数とするとき、0≦$x$≦1において不等式
$\displaystyle\sum_{k=0}^n\frac{x^k}{k!}$≦$e^x$≦$\displaystyle\sum_{k=0}^n\frac{x^k}{k!}+\frac{x^n}{n!}$
が成り立つことを示せ。
(3)0≦$x$≦1を定義域とする関数$f(x)$を
$f(x)$=$\left\{\begin{array}{1}
1 (x=0)\\
\displaystyle\frac{e^x-1}{x} (0<x≦1)
\end{array}\right.$
と定義する。(2)の不等式を利用して、定積分$\displaystyle\int_0^1f(x)dx$ の近似値を小数第3位まで求め、求めた近似値と真の値との誤差が$10^{-3}$以下である理由を説明せよ。
この動画を見る
$\Large{\boxed{4}}$ $e$を自然対数の底とする。$e$=2.718...である。
(1)0≦$x$≦1において不等式1+$x$≦$e^x$≦1+2$x$が成り立つことを示せ。
(2)$n$を自然数とするとき、0≦$x$≦1において不等式
$\displaystyle\sum_{k=0}^n\frac{x^k}{k!}$≦$e^x$≦$\displaystyle\sum_{k=0}^n\frac{x^k}{k!}+\frac{x^n}{n!}$
が成り立つことを示せ。
(3)0≦$x$≦1を定義域とする関数$f(x)$を
$f(x)$=$\left\{\begin{array}{1}
1 (x=0)\\
\displaystyle\frac{e^x-1}{x} (0<x≦1)
\end{array}\right.$
と定義する。(2)の不等式を利用して、定積分$\displaystyle\int_0^1f(x)dx$ の近似値を小数第3位まで求め、求めた近似値と真の値との誤差が$10^{-3}$以下である理由を説明せよ。
福田の数学〜上智大学2023年TEAP利用型理系第4問Part1〜不等式の証明と近似値計算

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{4}}$ $e$を自然対数の底とする。$e$=2.718...である。
(1)0≦$x$≦1において不等式1+$x$≦$e^x$≦1+2$x$が成り立つことを示せ。
(2)$n$を自然数とするとき、0≦$x$≦1において不等式
$\displaystyle\sum_{k=0}^n\frac{x^k}{k!}$≦$e^x$≦$\displaystyle\sum_{k=0}^n\frac{x^k}{k!}+\frac{x^n}{n!}$
が成り立つことを示せ。
(3)0≦$x$≦1を定義域とする関数$f(x)$を
$f(x)$=$\left\{\begin{array}{1}
1 (x=0)\\
\displaystyle\frac{e^x-1}{x} (0<x≦1)
\end{array}\right.$
と定義する。(2)の不等式を利用して、定積分$\displaystyle\int_0^1f(x)dx$ の近似値を小数第3位まで求め、求めた近似値と真の値との誤差が$10^{-3}$以下である理由を説明せよ。
この動画を見る
$\Large{\boxed{4}}$ $e$を自然対数の底とする。$e$=2.718...である。
(1)0≦$x$≦1において不等式1+$x$≦$e^x$≦1+2$x$が成り立つことを示せ。
(2)$n$を自然数とするとき、0≦$x$≦1において不等式
$\displaystyle\sum_{k=0}^n\frac{x^k}{k!}$≦$e^x$≦$\displaystyle\sum_{k=0}^n\frac{x^k}{k!}+\frac{x^n}{n!}$
が成り立つことを示せ。
(3)0≦$x$≦1を定義域とする関数$f(x)$を
$f(x)$=$\left\{\begin{array}{1}
1 (x=0)\\
\displaystyle\frac{e^x-1}{x} (0<x≦1)
\end{array}\right.$
と定義する。(2)の不等式を利用して、定積分$\displaystyle\int_0^1f(x)dx$ の近似値を小数第3位まで求め、求めた近似値と真の値との誤差が$10^{-3}$以下である理由を説明せよ。
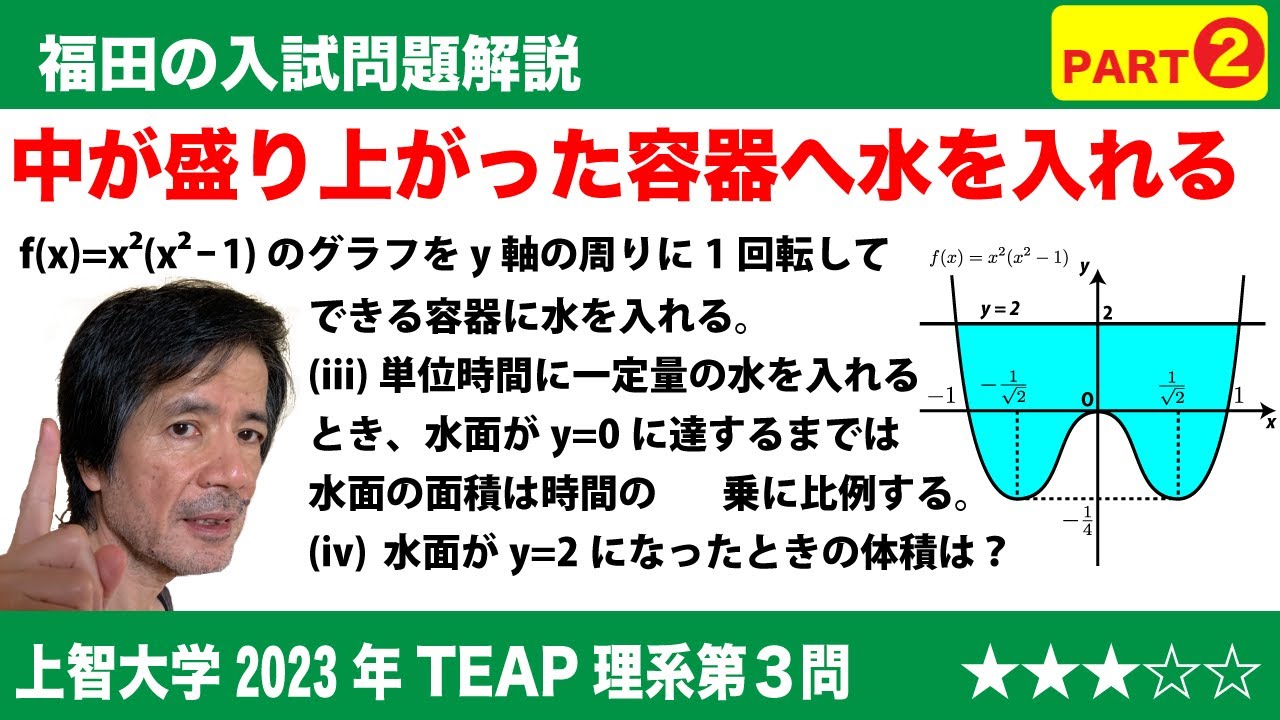
福田の数学〜上智大学2023年TEAP利用型理系第3問Part2〜容器に水を入れる
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ $\pi$を円周率とする。$f(x)$=$x^2(x^2-1)$とし、$f(x)$の最小値を$m$とする。
(1)$m$=$\displaystyle\frac{\boxed{\ \ シ\ \ }}{\boxed{\ \ ス\ \ }}$ である。
(2)$y$=$f(x)$で表される曲線を$y$軸の周りに1回転させてできる曲面でできた器に、$y$軸方向から静かに水を注ぐ。
(i)水面が$y$=$a$(ただし$m$≦$a$≦0)になったときの水面の面積は$\boxed{\ \ セ\ \ }$である。
(ii)水面が$y$=0になったときの水の体積は$\displaystyle\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}\pi$ である。
(iii)上方から注ぐ水が単位時間あたり一定量であるとする。水面が$y$=0に達するまでは、水面の面積は、水を注ぎ始めてからの時間の$\displaystyle\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$ 乗に比例して大きくなる。
(iv)水面が$y$=2になったときの水面の面積は$\boxed{\ \ テ\ \ }\pi$であり、水の体積は$\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}\pi$ である。
この動画を見る
$\Large{\boxed{3}}$ $\pi$を円周率とする。$f(x)$=$x^2(x^2-1)$とし、$f(x)$の最小値を$m$とする。
(1)$m$=$\displaystyle\frac{\boxed{\ \ シ\ \ }}{\boxed{\ \ ス\ \ }}$ である。
(2)$y$=$f(x)$で表される曲線を$y$軸の周りに1回転させてできる曲面でできた器に、$y$軸方向から静かに水を注ぐ。
(i)水面が$y$=$a$(ただし$m$≦$a$≦0)になったときの水面の面積は$\boxed{\ \ セ\ \ }$である。
(ii)水面が$y$=0になったときの水の体積は$\displaystyle\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}\pi$ である。
(iii)上方から注ぐ水が単位時間あたり一定量であるとする。水面が$y$=0に達するまでは、水面の面積は、水を注ぎ始めてからの時間の$\displaystyle\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$ 乗に比例して大きくなる。
(iv)水面が$y$=2になったときの水面の面積は$\boxed{\ \ テ\ \ }\pi$であり、水の体積は$\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}\pi$ である。
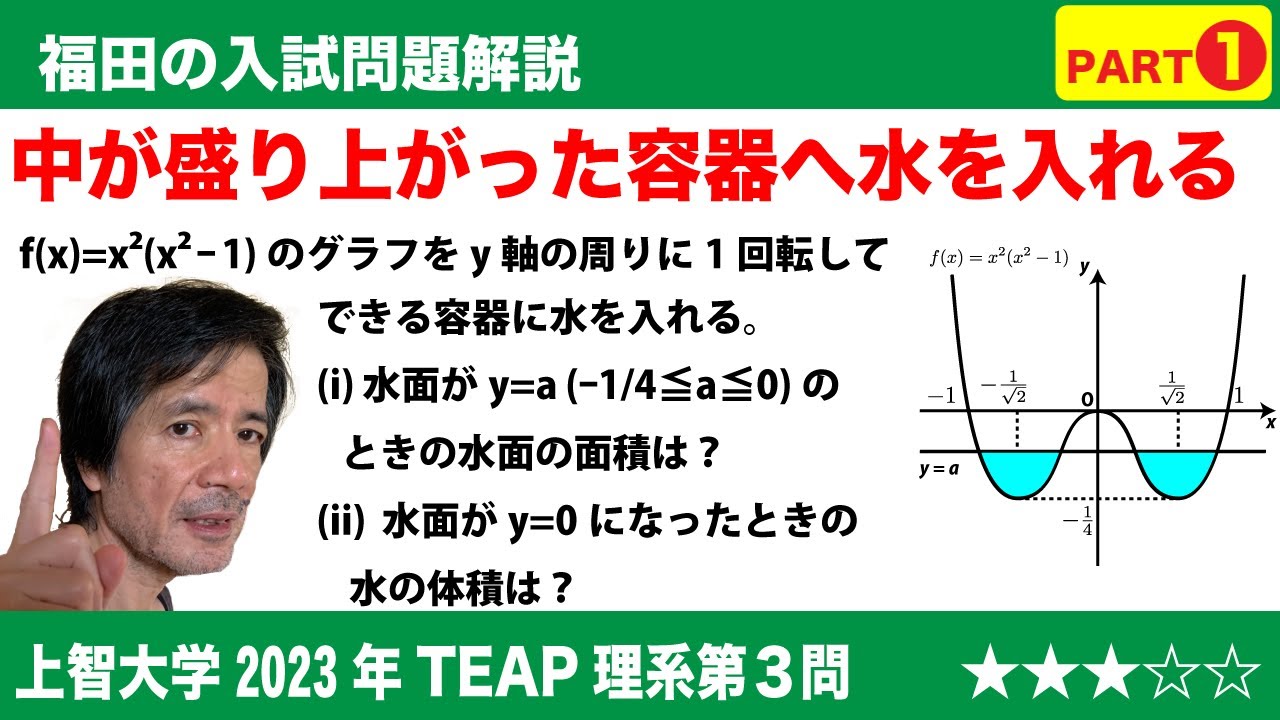
福田の数学〜上智大学2023年TEAP利用型理系第3問Part1〜容器に水を入れる
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ $\pi$を円周率とする。$f(x)$=$x^2(x^2-1)$とし、$f(x)$の最小値を$m$とする。
(1)$m$=$\displaystyle\frac{\boxed{\ \ シ\ \ }}{\boxed{\ \ ス\ \ }}$ である。
(2)$y$=$f(x)$で表される曲線を$y$軸の周りに1回転させてできる曲面でできた器に、$y$軸方向から静かに水を注ぐ。
(i)水面が$y$=$a$(ただし$m$≦$a$≦0)になったときの水面の面積は$\boxed{\ \ セ\ \ }$である。
(ii)水面が$y$=0になったときの水の体積は$\displaystyle\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}\pi$ である。
(iii)上方から注ぐ水が単位時間あたり一定量であるとする。水面が$y$=0に達するまでは、水面の面積は、水を注ぎ始めてからの時間の$\displaystyle\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$ 乗に比例して大きくなる。
(iv)水面が$y$=2になったときの水面の面積は$\boxed{\ \ テ\ \ }\pi$であり、水の体積は$\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}\pi$ である。
この動画を見る
$\Large{\boxed{3}}$ $\pi$を円周率とする。$f(x)$=$x^2(x^2-1)$とし、$f(x)$の最小値を$m$とする。
(1)$m$=$\displaystyle\frac{\boxed{\ \ シ\ \ }}{\boxed{\ \ ス\ \ }}$ である。
(2)$y$=$f(x)$で表される曲線を$y$軸の周りに1回転させてできる曲面でできた器に、$y$軸方向から静かに水を注ぐ。
(i)水面が$y$=$a$(ただし$m$≦$a$≦0)になったときの水面の面積は$\boxed{\ \ セ\ \ }$である。
(ii)水面が$y$=0になったときの水の体積は$\displaystyle\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}\pi$ である。
(iii)上方から注ぐ水が単位時間あたり一定量であるとする。水面が$y$=0に達するまでは、水面の面積は、水を注ぎ始めてからの時間の$\displaystyle\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$ 乗に比例して大きくなる。
(iv)水面が$y$=2になったときの水面の面積は$\boxed{\ \ テ\ \ }\pi$であり、水の体積は$\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}\pi$ である。
福田の数学〜青山学院大学2023年理工学部第5問〜定積分で定義された数列と極限

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#積分とその応用#数列の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数Ⅲ#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ $a_n$=$\displaystyle\frac{1}{n!}\int_1^e(\log x)^ndx$ ($n$=1,2,3,...)とおく。
(1)$a_1$を求めよ。
(2)不等式0≦$a_n$≦$\frac{e-1}{n!}$ が成り立つことを示せ。
(3)$n$≧2のとき、$a_n$=$\displaystyle\frac{e}{n!}$-$a_{n-1}$ であることを示せ。
(4)$\displaystyle\lim_{n \to \infty}\sum_{k=2}^n\frac{(-1)^k}{k!}$ を求めよ。
この動画を見る
$\Large\boxed{5}$ $a_n$=$\displaystyle\frac{1}{n!}\int_1^e(\log x)^ndx$ ($n$=1,2,3,...)とおく。
(1)$a_1$を求めよ。
(2)不等式0≦$a_n$≦$\frac{e-1}{n!}$ が成り立つことを示せ。
(3)$n$≧2のとき、$a_n$=$\displaystyle\frac{e}{n!}$-$a_{n-1}$ であることを示せ。
(4)$\displaystyle\lim_{n \to \infty}\sum_{k=2}^n\frac{(-1)^k}{k!}$ を求めよ。
三重大学(2016) #Shorts
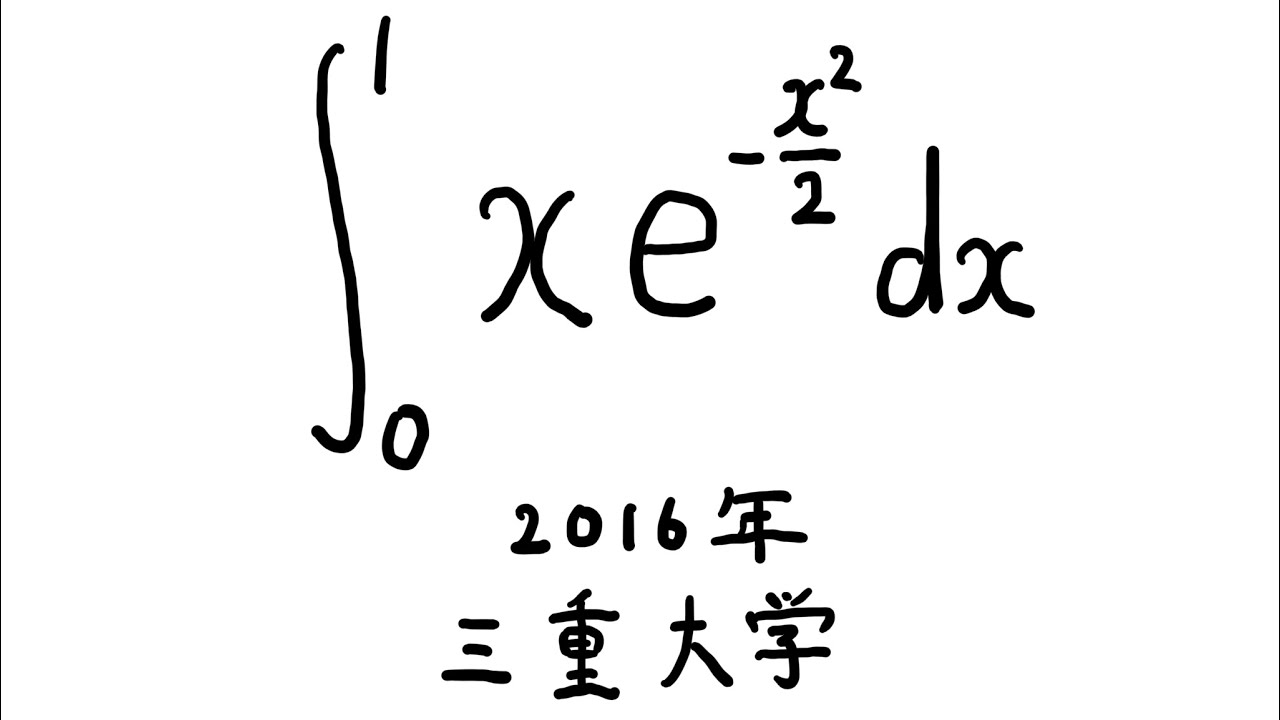
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} xe^{-\frac{1}{2}x^2} dx$
出典:2016年三重大学
この動画を見る
$\displaystyle \int_{0}^{1} xe^{-\frac{1}{2}x^2} dx$
出典:2016年三重大学
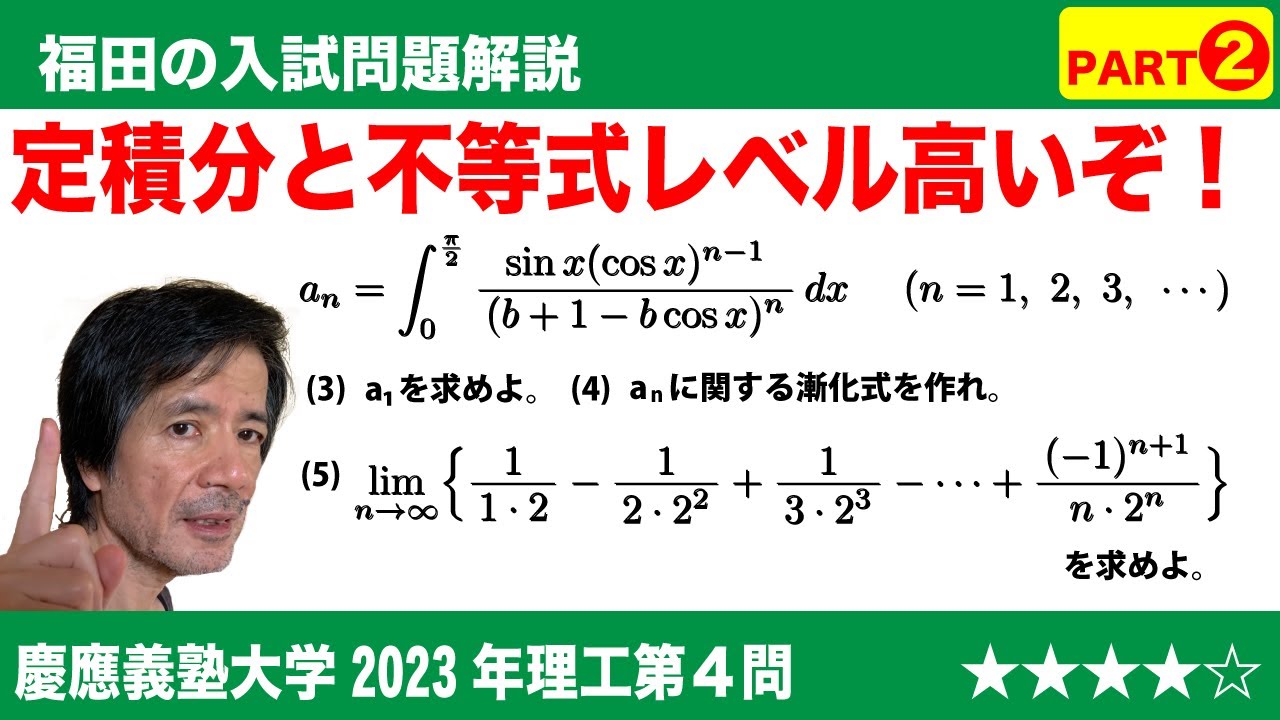
福田の数学〜慶應義塾大学2023年理工学部第4問〜定積分と不等式Part2
単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#数列の極限#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ (1)0≦$x$≦$\displaystyle\frac{\pi}{2}$において常に不等式|$b$|≦|$b$+1-$b\cos x$|が成り立つような実数$b$の値の範囲は$\boxed{\ \ シ\ \ }$≦$b$≦$\boxed{\ \ ス\ \ }$である。
以下、$b$を$\boxed{\ \ シ\ \ }$≦$b$≦$\boxed{\ \ ス\ \ }$を満たす0でない実数とし、数列$\left\{a_n\right\}$を
$a_n$=$\displaystyle\int_0^{\frac{\pi}{2}}\frac{\sin x(\cos x)^{n-1}}{(b+1-b\cos x)^n}dx$ (n=1,2,3,...)で定義する。
(2)$\displaystyle\lim_{n \to \infty}b^na_n$=0 が成り立つことを証明しなさい。
(3)$a_1$=$\boxed{\ \ セ\ \ }$である。
(4)$a_{n+1}$を$a_n$,$n$,$b$を用いて表すと$a_{n+1}$=$\boxed{\ \ ソ\ \ }$となる。
(5)$\displaystyle\lim_{n \to \infty}\left\{\frac{1}{1・2}-\frac{1}{2・2^2}+\frac{1}{3・2^3}-...+\frac{(-1)^{n+1}}{n・2^n}\right\}$=$\boxed{\ \ タ\ \ }$である。
この動画を見る
$\Large\boxed{4}$ (1)0≦$x$≦$\displaystyle\frac{\pi}{2}$において常に不等式|$b$|≦|$b$+1-$b\cos x$|が成り立つような実数$b$の値の範囲は$\boxed{\ \ シ\ \ }$≦$b$≦$\boxed{\ \ ス\ \ }$である。
以下、$b$を$\boxed{\ \ シ\ \ }$≦$b$≦$\boxed{\ \ ス\ \ }$を満たす0でない実数とし、数列$\left\{a_n\right\}$を
$a_n$=$\displaystyle\int_0^{\frac{\pi}{2}}\frac{\sin x(\cos x)^{n-1}}{(b+1-b\cos x)^n}dx$ (n=1,2,3,...)で定義する。
(2)$\displaystyle\lim_{n \to \infty}b^na_n$=0 が成り立つことを証明しなさい。
(3)$a_1$=$\boxed{\ \ セ\ \ }$である。
(4)$a_{n+1}$を$a_n$,$n$,$b$を用いて表すと$a_{n+1}$=$\boxed{\ \ ソ\ \ }$となる。
(5)$\displaystyle\lim_{n \to \infty}\left\{\frac{1}{1・2}-\frac{1}{2・2^2}+\frac{1}{3・2^3}-...+\frac{(-1)^{n+1}}{n・2^n}\right\}$=$\boxed{\ \ タ\ \ }$である。
福田の数学〜慶應義塾大学2023年理工学部第4問〜定積分と不等式Part1

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ (1)0≦$x$≦$\displaystyle\frac{\pi}{2}$において常に不等式|$b$|≦|$b$+1-$b\cos x$|が成り立つような実数$b$の値の範囲は$\boxed{\ \ シ\ \ }$≦$b$≦$\boxed{\ \ ス\ \ }$である。
以下、$b$を$\boxed{\ \ シ\ \ }$≦$b$≦$\boxed{\ \ ス\ \ }$を満たす0でない実数とし、数列$\left\{a_n\right\}$を
$a_n$=$\displaystyle\int_0^{\frac{\pi}{2}}\frac{\sin x(\cos x)^{n-1}}{(b+1-b\cos x)^n}dx$ (n=1,2,3,...)で定義する。
(2)$\displaystyle\lim_{n \to \infty}b^na_n$=0 が成り立つことを証明しなさい。
(3)$a_1$=$\boxed{\ \ セ\ \ }$である。
(4)$a_{n+1}$を$a_n$,$n$,$b$を用いて表すと$a_{n+1}$=$\boxed{\ \ ソ\ \ }$となる。
(5)$\displaystyle\lim_{n \to \infty}\left\{\frac{1}{1・2}-\frac{1}{2・2^2}+\frac{1}{3・2^3}-...+\frac{(-1)^{n+1}}{n・2^n}\right\}$=$\boxed{\ \ タ\ \ }$である。
この動画を見る
$\Large\boxed{4}$ (1)0≦$x$≦$\displaystyle\frac{\pi}{2}$において常に不等式|$b$|≦|$b$+1-$b\cos x$|が成り立つような実数$b$の値の範囲は$\boxed{\ \ シ\ \ }$≦$b$≦$\boxed{\ \ ス\ \ }$である。
以下、$b$を$\boxed{\ \ シ\ \ }$≦$b$≦$\boxed{\ \ ス\ \ }$を満たす0でない実数とし、数列$\left\{a_n\right\}$を
$a_n$=$\displaystyle\int_0^{\frac{\pi}{2}}\frac{\sin x(\cos x)^{n-1}}{(b+1-b\cos x)^n}dx$ (n=1,2,3,...)で定義する。
(2)$\displaystyle\lim_{n \to \infty}b^na_n$=0 が成り立つことを証明しなさい。
(3)$a_1$=$\boxed{\ \ セ\ \ }$である。
(4)$a_{n+1}$を$a_n$,$n$,$b$を用いて表すと$a_{n+1}$=$\boxed{\ \ ソ\ \ }$となる。
(5)$\displaystyle\lim_{n \to \infty}\left\{\frac{1}{1・2}-\frac{1}{2・2^2}+\frac{1}{3・2^3}-...+\frac{(-1)^{n+1}}{n・2^n}\right\}$=$\boxed{\ \ タ\ \ }$である。
福田の数学〜早稲田大学2023年人間科学部第7問〜空間ベクトルと回転体の体積

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#積分とその応用#定積分#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{7}$ 座標空間に点C(0,1,1)を中心とする半径1の球面Sがある。点P(0,0,3)からSに引いた接線と$xy$平面との交点をQとする。$\overrightarrow{PC}・\overrightarrow{PQ}$=$t|\overrightarrow{PQ}|$と表すとき、
$t$=$\boxed{\ \ テ \ \ }$である。点Qは楕円状にあり、この楕円を
$\displaystyle\frac{(x+b)^2}{a}$+$\displaystyle\frac{(y+d)^2}{c}$=1
とするとき、$a$=$\boxed{\ \ ト\ \ }$, $b$=$\boxed{\ \ ナ\ \ }$, $c$=$\boxed{\ \ ニ\ \ }$, $d$=$\boxed{\ \ ヌ\ \ }$ である。
また、点Pに光源があるとき、球面Sで光が当たる部分を点Rが動く。ただし、
球面Sは光を通さない。このとき線分PRが通過してできる図形の体積は
2$\pi$・$\displaystyle\frac{\boxed{ネ}+\boxed{ノ}\sqrt{\boxed{ハ}}}{\boxed{ヒ}}$
である。
この動画を見る
$\Large\boxed{7}$ 座標空間に点C(0,1,1)を中心とする半径1の球面Sがある。点P(0,0,3)からSに引いた接線と$xy$平面との交点をQとする。$\overrightarrow{PC}・\overrightarrow{PQ}$=$t|\overrightarrow{PQ}|$と表すとき、
$t$=$\boxed{\ \ テ \ \ }$である。点Qは楕円状にあり、この楕円を
$\displaystyle\frac{(x+b)^2}{a}$+$\displaystyle\frac{(y+d)^2}{c}$=1
とするとき、$a$=$\boxed{\ \ ト\ \ }$, $b$=$\boxed{\ \ ナ\ \ }$, $c$=$\boxed{\ \ ニ\ \ }$, $d$=$\boxed{\ \ ヌ\ \ }$ である。
また、点Pに光源があるとき、球面Sで光が当たる部分を点Rが動く。ただし、
球面Sは光を通さない。このとき線分PRが通過してできる図形の体積は
2$\pi$・$\displaystyle\frac{\boxed{ネ}+\boxed{ノ}\sqrt{\boxed{ハ}}}{\boxed{ヒ}}$
である。
兵庫医科大学(2021) #Shorts
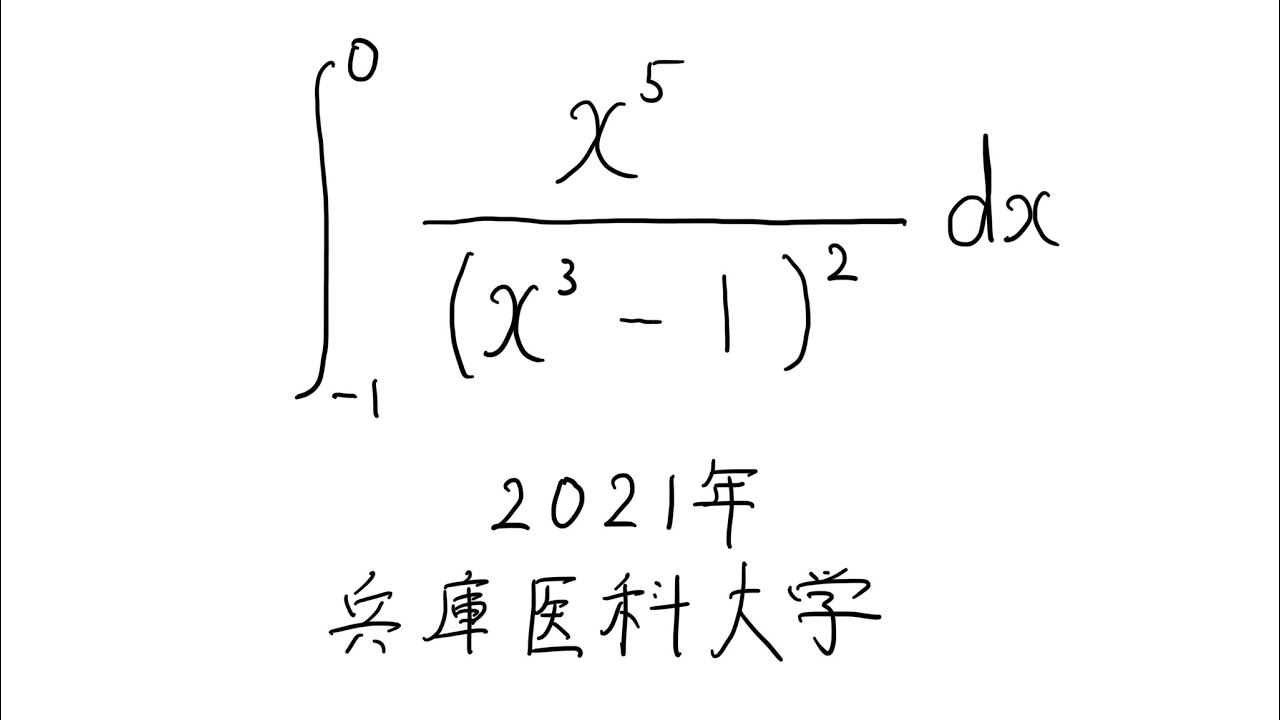
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#兵庫医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{0} \displaystyle \frac{x^5}{(x^3-1)^2} dx$
出典:2021年兵庫医科大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{0} \displaystyle \frac{x^5}{(x^3-1)^2} dx$
出典:2021年兵庫医科大学 入試問題
大学入試問題#615「ラッキー問題?」 東京工業大学(1976) #積分方程式
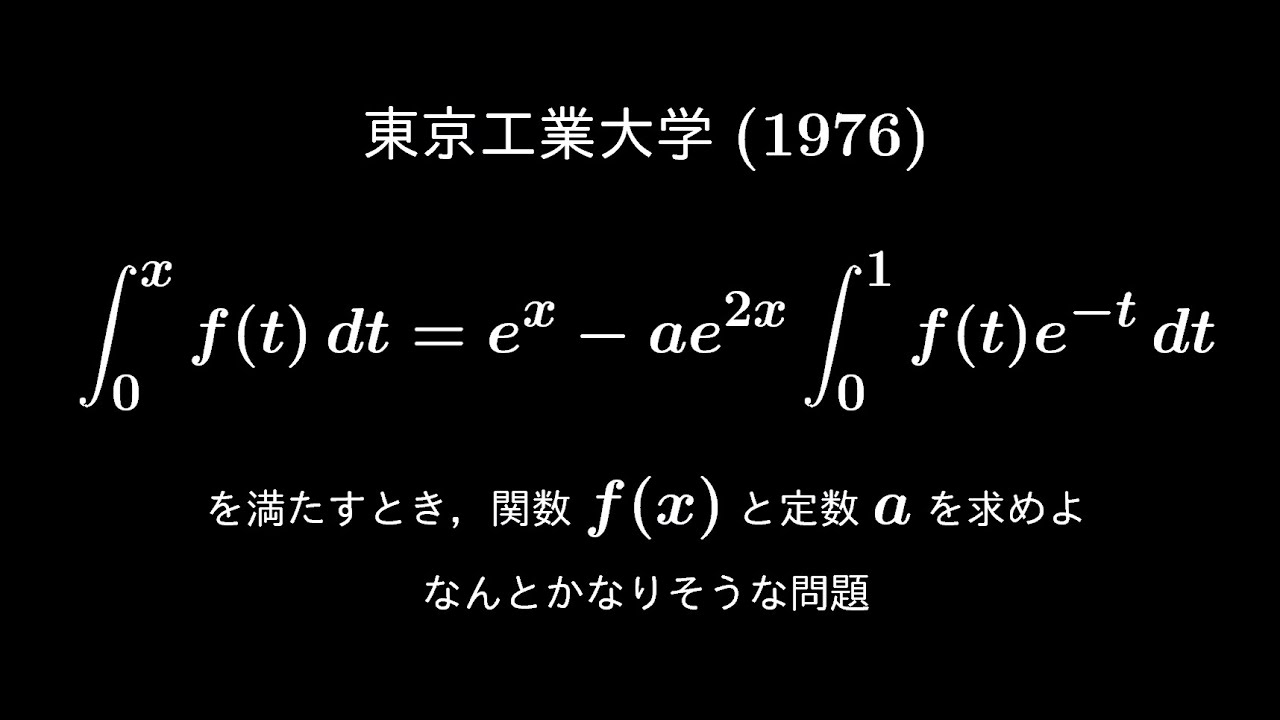
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{x} f(t)dt=e^x-ae^{2x}\displaystyle \int_{0}^{1} f(t)e^{-t}dt$のとき
関数$f(x),$定数$a$を求めよ。
出典:1976年東京工業大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{x} f(t)dt=e^x-ae^{2x}\displaystyle \int_{0}^{1} f(t)e^{-t}dt$のとき
関数$f(x),$定数$a$を求めよ。
出典:1976年東京工業大学 入試問題
大学入試問題#613「微分してたら、時間かかるだろうな~~」 慶應義塾大学(1996)

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \frac{10x-x^2}{(10+10x-x^2)^2}$の最大値を求めよ
出典:1996年慶應義塾大学 入試問題
この動画を見る
$\displaystyle \frac{10x-x^2}{(10+10x-x^2)^2}$の最大値を求めよ
出典:1996年慶應義塾大学 入試問題
大学入試問題#612 早稲田大学(2021)

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
正の実数$x,y,z$が
$\displaystyle \frac{1}{x}+\displaystyle \frac{2}{y}+\displaystyle \frac{3}{z}=1$を満たすとき
$(x-1)(y-2)(z-3)$の最小値を求めよ
出典:2021年早稲田大学 入試問題
この動画を見る
正の実数$x,y,z$が
$\displaystyle \frac{1}{x}+\displaystyle \frac{2}{y}+\displaystyle \frac{3}{z}=1$を満たすとき
$(x-1)(y-2)(z-3)$の最小値を求めよ
出典:2021年早稲田大学 入試問題
大学入試問題#608「絶対値・・・・」 横浜市立大学(2009) #定積分

単元:
#数Ⅰ#数Ⅱ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#三角関数#三角関数とグラフ#加法定理とその応用#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{\pi}{6}}^{\frac{\pi}{2}} |\sin2\ x| \sin\ x\ dx$
出典:2009年横浜市立大学 入試問題
この動画を見る
$\displaystyle \int_{-\frac{\pi}{6}}^{\frac{\pi}{2}} |\sin2\ x| \sin\ x\ dx$
出典:2009年横浜市立大学 入試問題
大学入試問題#607「やばい、忙しすぎる」 青山学院大学(2007) #定積分

単元:
#数Ⅱ#三角関数#三角関数とグラフ#微分とその応用#積分とその応用#微分法#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{2}}^{\pi} x(\cos2x-\sin2x) dx$
出典:2007年青山学院大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{2}}^{\pi} x(\cos2x-\sin2x) dx$
出典:2007年青山学院大学 入試問題
福田の数学〜千葉大学2023年第7問〜三角関数と定積分の最大Part2

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{7}$ 関数
$f(x)$=$\displaystyle\left|\cos x-\sqrt5\sin x-\frac{3\sqrt2}{2}\right|$
について、以下の問いに答えよ。
(1)$f(x)$の最大値を求めよ。
(2)$\displaystyle\int_0^{2\pi}f(x)dx$ を求めよ。
(3)$S(t)$=$\displaystyle\int_t^{t+\frac{\pi}{3}}f(x)dx$ とおく。このとき$S(t)$の最大値を求めよ。
この動画を見る
$\Large\boxed{7}$ 関数
$f(x)$=$\displaystyle\left|\cos x-\sqrt5\sin x-\frac{3\sqrt2}{2}\right|$
について、以下の問いに答えよ。
(1)$f(x)$の最大値を求めよ。
(2)$\displaystyle\int_0^{2\pi}f(x)dx$ を求めよ。
(3)$S(t)$=$\displaystyle\int_t^{t+\frac{\pi}{3}}f(x)dx$ とおく。このとき$S(t)$の最大値を求めよ。
福田の数学〜千葉大学2023年第7問〜三角関数と定積分の最大Part1

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#積分とその応用#定積分#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{7}$ 関数
$f(x)$=$\displaystyle\left|\cos x-\sqrt5\sin x-\frac{3\sqrt2}{2}\right|$
について、以下の問いに答えよ。
(1)$f(x)$の最大値を求めよ。
(2)$\displaystyle\int_0^{2\pi}f(x)dx$ を求めよ。
(3)$S(t)$=$\displaystyle\int_t^{t+\frac{\pi}{3}}f(x)dx$ とおく。このとき$S(t)$の最大値を求めよ。
この動画を見る
$\Large\boxed{7}$ 関数
$f(x)$=$\displaystyle\left|\cos x-\sqrt5\sin x-\frac{3\sqrt2}{2}\right|$
について、以下の問いに答えよ。
(1)$f(x)$の最大値を求めよ。
(2)$\displaystyle\int_0^{2\pi}f(x)dx$ を求めよ。
(3)$S(t)$=$\displaystyle\int_t^{t+\frac{\pi}{3}}f(x)dx$ とおく。このとき$S(t)$の最大値を求めよ。
高校の範囲で解ける積分 By 英語orドイツ語シはBかHか さん #定積分

単元:
#複素数平面#積分とその応用#複素数平面#定積分#数学(高校生)#数C#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} arg(1+\sqrt{ -x }) dx$
$-\pi \leqq arg(1+\sqrt{ -x }) \lt \pi$
この動画を見る
$\displaystyle \int_{0}^{1} arg(1+\sqrt{ -x }) dx$
$-\pi \leqq arg(1+\sqrt{ -x }) \lt \pi$
青山学院大学(2007年) #Shorts

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{4} \displaystyle \frac{x^2+1}{x+1} dx$
出典:2007年青山学院大学
この動画を見る
$\displaystyle \int_{0}^{4} \displaystyle \frac{x^2+1}{x+1} dx$
出典:2007年青山学院大学
大学入試問題#昭和大#604「nの計算丁寧に」 昭和大学医学部(2014) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#昭和大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} x^2(1-x)^n dx$
$n$自然数
出典:2014年昭和大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} x^2(1-x)^n dx$
$n$自然数
出典:2014年昭和大学 入試問題
大学入試問題#601「これは落としたくないかも」 広島大学後期(2014) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#広島大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$f(x)=x\ log\ x$のとき
$(\displaystyle \frac{1}{e} \leqq x \leqq )$
$\displaystyle \int_{0}^{e} f^{-1}(x) dx$を求めよ
出典:2014年広島大学後期 入試問題
この動画を見る
$f(x)=x\ log\ x$のとき
$(\displaystyle \frac{1}{e} \leqq x \leqq )$
$\displaystyle \int_{0}^{e} f^{-1}(x) dx$を求めよ
出典:2014年広島大学後期 入試問題
大学入試問題#599「King-propertyは使ってません」 南山大学(2013) 定積分
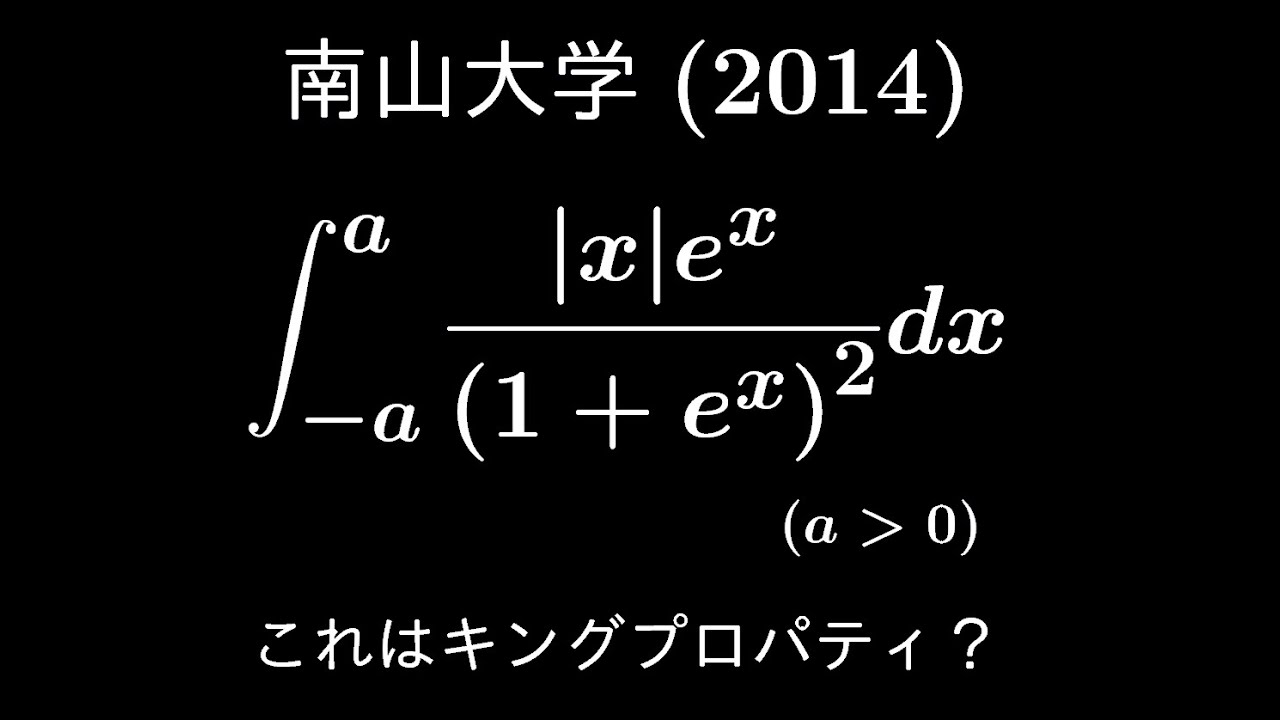
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#南山大学
指導講師:
ますただ
問題文全文(内容文):
$a \gt 0$
$\displaystyle \int_{-a}^{a} \displaystyle \frac{|x|e^x}{(1+e^x)^2} dx$
出典:2013年南山大学 入試問題
この動画を見る
$a \gt 0$
$\displaystyle \int_{-a}^{a} \displaystyle \frac{|x|e^x}{(1+e^x)^2} dx$
出典:2013年南山大学 入試問題
大学入試問題#598「計算が大変でした」 関西大学(2009) #区分求積法

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#数列の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#関西大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{n-k}{n\sqrt{ 3n^2+k^2 }}$
出典:2009年関西大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{n-k}{n\sqrt{ 3n^2+k^2 }}$
出典:2009年関西大学 入試問題
福田の数学〜東京医科歯科大学2023年医学部第3問〜積分で定義された関数と極限

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ $a$,$b$を正の実数、$p$を$a$より小さい正の実数とし、すべての実数$x$について
$\displaystyle\int_p^{f(x)}\frac{a}{u(a-u)}du$=$bx$, 0<$f(x)$<$a$
かつ$f(0)$=$p$を満たす関数$f(x)$を考える。このとき以下の問いに答えよ。
(1)$f(x)$を$a$,$b$,$p$を用いて表せ。
(2)$f(-1)$=$\frac{1}{2}$, $f(1)$=1, $f(3)$=$\frac{3}{2}$のとき、$a$,$b$,$p$を求めよ。
(3)(2)のとき、$\displaystyle\lim_{x \to -\infty}f(x)$, $\displaystyle\lim_{x \to \infty}f(x)$ を求めよ。
この動画を見る
$\Large\boxed{3}$ $a$,$b$を正の実数、$p$を$a$より小さい正の実数とし、すべての実数$x$について
$\displaystyle\int_p^{f(x)}\frac{a}{u(a-u)}du$=$bx$, 0<$f(x)$<$a$
かつ$f(0)$=$p$を満たす関数$f(x)$を考える。このとき以下の問いに答えよ。
(1)$f(x)$を$a$,$b$,$p$を用いて表せ。
(2)$f(-1)$=$\frac{1}{2}$, $f(1)$=1, $f(3)$=$\frac{3}{2}$のとき、$a$,$b$,$p$を求めよ。
(3)(2)のとき、$\displaystyle\lim_{x \to -\infty}f(x)$, $\displaystyle\lim_{x \to \infty}f(x)$ を求めよ。
