 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
【数Ⅱ】微分法と積分法:ax+bの積分、∫(x+8)³dxの不定積分を求めよ。

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\displaystyle \int_{}^{}(x+8)^3dx$の不定積分を求めよ。
この動画を見る
$\displaystyle \int_{}^{}(x+8)^3dx$の不定積分を求めよ。
【数B】数列:第10項が50、第15項が30の等差数列{an}では、第何項が初めて負となるか。

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
第10項が50、第15項が30の等差数列{an}では、第何項が初めて負となるか。
この動画を見る
第10項が50、第15項が30の等差数列{an}では、第何項が初めて負となるか。
【数B】数列: 次の条件を満たす等差数列anの一般項を求めよ。a1+a4=12,a1+a7=18

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の条件を満たす等差数列anの一般項を求めよ。
a1+a4=12,a1+a7=18
この動画を見る
次の条件を満たす等差数列anの一般項を求めよ。
a1+a4=12,a1+a7=18
東大(類題)整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
3桁の整数を2乗したら下3桁が元の数と同じをすべて求めよ.
2005類題東大過去問
この動画を見る
3桁の整数を2乗したら下3桁が元の数と同じをすべて求めよ.
2005類題東大過去問
【数Ⅲ】微分法: 微分係数の利用! f'(a)が存在するとき、次の極限をf(a),f'(a)で表せ。(1)lim(h→0){f(a+4h)-f(a+2h)}/h

単元:
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$f'(a)$が存在するとき、次の極限を$f(a),f'(a)$で表せ。
(1)$\displaystyle \lim_{h\to 0}\dfrac{f(a+4h)-f(a+2h)}{h}$
この動画を見る
$f'(a)$が存在するとき、次の極限を$f(a),f'(a)$で表せ。
(1)$\displaystyle \lim_{h\to 0}\dfrac{f(a+4h)-f(a+2h)}{h}$
【高校数学】絶対値を含む方程式・不等式~考え方を学ぼう~ 1-14【数学Ⅰ】

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
絶対値を含む方程式・不等式の説明動画です
この動画を見る
絶対値を含む方程式・不等式の説明動画です
【数A】整数の性質:aを自然数とする。a+2は3の倍数であり、a+4は7の倍数であるとき、a+11は21の倍数であることを証明しましょう。

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
教材:
#高校ゼミスタンダード#高校ゼミスタンダード数A#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
aを自然数とする。a+2は3の倍数であり、a+4は7の倍数であるとき、a+11は21の倍数であることを証明しなさい。
この動画を見る
aを自然数とする。a+2は3の倍数であり、a+4は7の倍数であるとき、a+11は21の倍数であることを証明しなさい。
整数問題 最大公約数と最小公倍数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$A$と$B$の最大公約数を$G$,最小公倍数を$L$とする.
$(A+B)^2-2LG=3600$,$A,B$を求めよ.
この動画を見る
$A$と$B$の最大公約数を$G$,最小公倍数を$L$とする.
$(A+B)^2-2LG=3600$,$A,B$を求めよ.
【高校数学】1次不等式の利用~ただの文章題です~ 1-13 【数学Ⅰ】

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1)Aさんの通う学校から自宅までの道のりは24kmである。
この道のりを初めは時速4km,途中から時速3kmで歩いたら、
所要時間は7時間以内であった。
時速4kmで歩いた道のりはどれほどか。
(2)連続する3つの整数の和が37以上になるもののうち、
その和が最小となる3つの数を求めよ。
この動画を見る
(1)Aさんの通う学校から自宅までの道のりは24kmである。
この道のりを初めは時速4km,途中から時速3kmで歩いたら、
所要時間は7時間以内であった。
時速4kmで歩いた道のりはどれほどか。
(2)連続する3つの整数の和が37以上になるもののうち、
その和が最小となる3つの数を求めよ。
6次方程式の6つの解

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
複数の解法でこれを解け.
$z^6+1=0$
この動画を見る
複数の解法でこれを解け.
$z^6+1=0$
【数Ⅰ】中高一貫校問題集3(数式・関数編)43:数と式:因数分解:次の式を因数分解せよ。6x²+5xy-6y²+x-5y-1

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
教材:
#TK数学#TK数学問題集3(数式・関数編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の式を因数分解せよ。
6x²+5xy-6y²+x-5y-1
この動画を見る
次の式を因数分解せよ。
6x²+5xy-6y²+x-5y-1
【数学A】接弦定理の覚え方と証明【このやり方なら、来週も忘れない】

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【数学A】接弦定理の覚え方と証明紹介動画です
この動画を見る
【数学A】接弦定理の覚え方と証明紹介動画です
【数学】中学生でも分かるマイナス乗~指数がマイナスのとき~

一橋大 整式の剰余

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#複素数平面#整式の除法・分数式・二項定理#複素数平面#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(z)=z^{2n}+z^n+1$を
$z^2+z+1$で割ったあまり
$z^2-z+1$で割ったあまり
を求めよ.$n$は自然数である.
一橋大学過去問
この動画を見る
$f(z)=z^{2n}+z^n+1$を
$z^2+z+1$で割ったあまり
$z^2-z+1$で割ったあまり
を求めよ.$n$は自然数である.
一橋大学過去問
N進法と倍数判定

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$7$進法,$6$進法,$5$進法で表された$4$桁の整数である.
$ABCD_{(7)}$,$ABCD_{(6)}$,$ABCD_{(5)}$はすべて$6$の倍数$ABCD$をすべて求めよ.
この動画を見る
$7$進法,$6$進法,$5$進法で表された$4$桁の整数である.
$ABCD_{(7)}$,$ABCD_{(6)}$,$ABCD_{(5)}$はすべて$6$の倍数$ABCD$をすべて求めよ.
慶應志木高校入試問題 約数の逆数の総和

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$N$の約数の和は$120$であり,$N$の約数の逆数の和は$\dfrac{15}{7}$である.
$N$を求めよ.
慶応志木高過去問
この動画を見る
$N$の約数の和は$120$であり,$N$の約数の逆数の和は$\dfrac{15}{7}$である.
$N$を求めよ.
慶応志木高過去問
20年5月数学検定1級1次試験(微分)
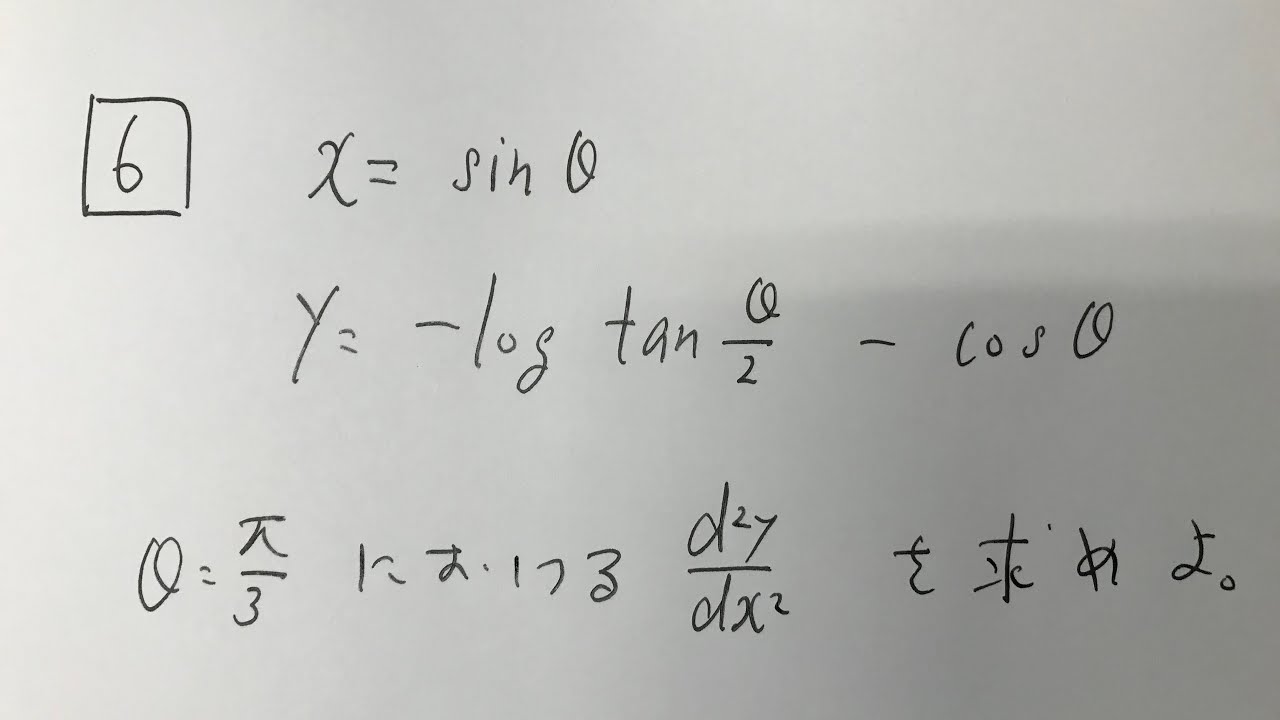
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{6}$
$x=\sin\theta$
$y=-1\log\tan\dfrac{\theta}{2}-\cos\theta$
$\theta=\dfrac{\pi}{3}$における$\dfrac{d^2y}{dx^2}$を求めよ.
20年5月数学検定1級1次試験(微分)過去問
この動画を見る
$\boxed{6}$
$x=\sin\theta$
$y=-1\log\tan\dfrac{\theta}{2}-\cos\theta$
$\theta=\dfrac{\pi}{3}$における$\dfrac{d^2y}{dx^2}$を求めよ.
20年5月数学検定1級1次試験(微分)過去問
20年5月数学検定1級1次試験(微分)
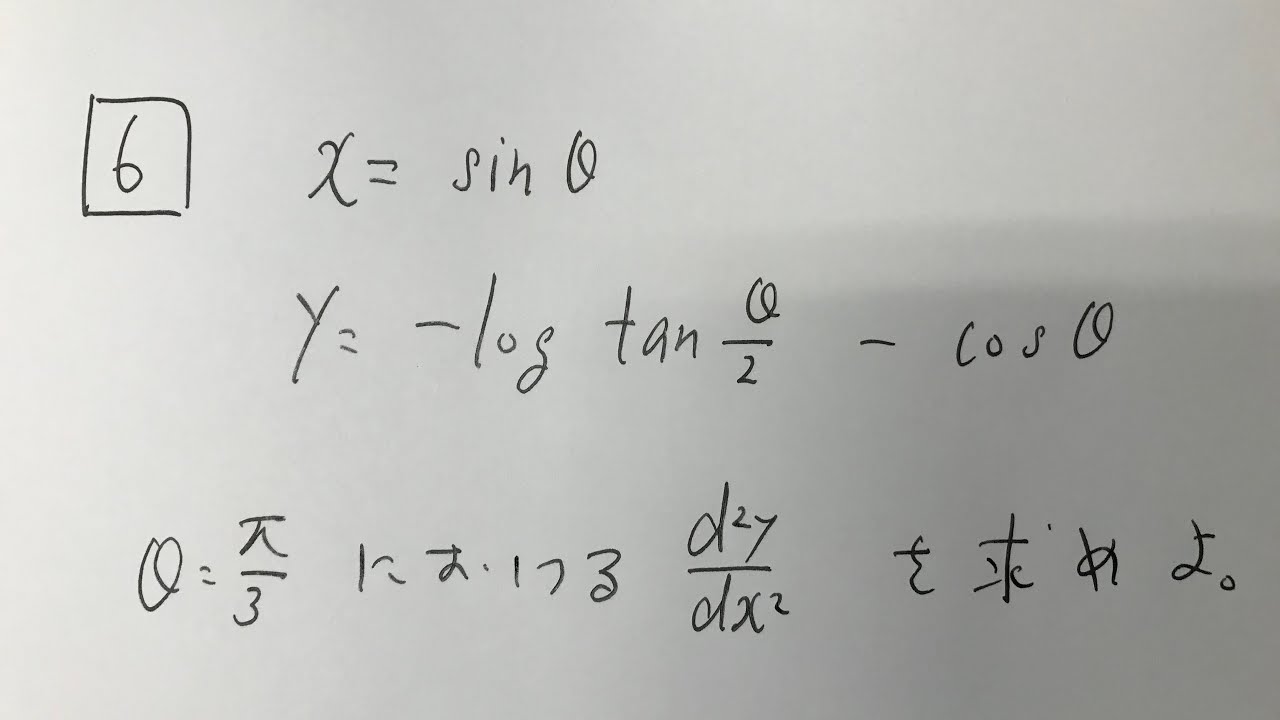
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#三角関数#三角関数とグラフ#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
6⃣
x=sinθ
$y=-log tan \frac{θ}{2}-cosθ$
$θ=\frac{\pi}{3}$における$\frac{dy}{dx^2}$を求めよ。
この動画を見る
6⃣
x=sinθ
$y=-log tan \frac{θ}{2}-cosθ$
$θ=\frac{\pi}{3}$における$\frac{dy}{dx^2}$を求めよ。
合同式の応用

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$6$桁の整数である.
$n=1234A5$であり,$n^2+4n+1$が$11$の倍数となる$A$をすべて求めよ.
この動画を見る
$6$桁の整数である.
$n=1234A5$であり,$n^2+4n+1$が$11$の倍数となる$A$をすべて求めよ.
【高校数学】組合せの例題~最低でもこれはできるように~ 1-10.5【数学A】

単元:
#数Ⅰ#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1)正六角形の6個の頂点のうち3点を結んで三角形を作るとき、
三角形は何個作れるか。
(2)6本の平行線と、それらに交わる7本の平行線によってできる
平行四辺形は何個か。
(3)7人を次のようにする方法は何通りあるか。
(a)部屋A、B、Cに2人ずつ入れ、部屋Dに1人入れる。
(b)2人,2人,2人,1人の4組に分ける
この動画を見る
(1)正六角形の6個の頂点のうち3点を結んで三角形を作るとき、
三角形は何個作れるか。
(2)6本の平行線と、それらに交わる7本の平行線によってできる
平行四辺形は何個か。
(3)7人を次のようにする方法は何通りあるか。
(a)部屋A、B、Cに2人ずつ入れ、部屋Dに1人入れる。
(b)2人,2人,2人,1人の4組に分ける
20年5月数学検定1級1次試験(四面体の体積)

単元:
#数学検定・数学甲子園・数学オリンピック等#空間ベクトル#空間ベクトル#数学検定#数学検定1級#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
3⃣4点 A(1,-4,1),B(2,2,2),C(2,-6,-3),D(3,-2,-1)とする。
四面体ABCDの体積Vを求めよ。
この動画を見る
3⃣4点 A(1,-4,1),B(2,2,2),C(2,-6,-3),D(3,-2,-1)とする。
四面体ABCDの体積Vを求めよ。
20年5月数学検定1級1次試験(三角関数)

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#三角関数#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{2}$
$\tan(2Arc\tan\dfrac{1}{3}+Arc\tan\dfrac{1}{12})$
$Arc\tan a=\tan^{-1}a=t\Leftrightarrow t=\tan a$
$\tan(\tan^{-1}a)=a$
$\tan(\alpha+\beta)=\dfrac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}$
20年5月数学検定1級1次試験(三角関数)過去問
この動画を見る
$\boxed{2}$
$\tan(2Arc\tan\dfrac{1}{3}+Arc\tan\dfrac{1}{12})$
$Arc\tan a=\tan^{-1}a=t\Leftrightarrow t=\tan a$
$\tan(\tan^{-1}a)=a$
$\tan(\alpha+\beta)=\dfrac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}$
20年5月数学検定1級1次試験(三角関数)過去問
20年5月数学検定1級1次試験(三角関数)

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#三角関数#三角関数とグラフ#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
2⃣
$tan(2Arctan \frac{1}{3} + Arctan \frac{1}{12} )$
この動画を見る
2⃣
$tan(2Arctan \frac{1}{3} + Arctan \frac{1}{12} )$
【数Ⅰ】2次関数:2次方程式が重解を持つ条件をわかりやすく解説!

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$4x²+(m-1)x+1=0$が重解を持つように、定数mの値を定めよ。
この動画を見る
$4x²+(m-1)x+1=0$が重解を持つように、定数mの値を定めよ。
指数関数 2次関数 大分大

単元:
#数Ⅰ#数Ⅱ#2次関数#2次関数とグラフ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$y=9^x+\dfrac{1}{9^x}-4a\left(3^x+\dfrac{1}{3^x}\right)$である.
$y$の最小値とそのときの$x$の値を$a$を用いて表せ.
2018大分大過去問
この動画を見る
$y=9^x+\dfrac{1}{9^x}-4a\left(3^x+\dfrac{1}{3^x}\right)$である.
$y$の最小値とそのときの$x$の値を$a$を用いて表せ.
2018大分大過去問
たまには高校入試問題 市川高校 整数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$5xy-10x-y^2+y=5$を満たす整数$(x,y)$をすべて求めよ.
2009市川高校過去問
この動画を見る
$5xy-10x-y^2+y=5$を満たす整数$(x,y)$をすべて求めよ.
2009市川高校過去問
18大阪府教員採用試験(数学:整数)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#その他
指導講師:
ますただ
問題文全文(内容文):
$2018$
$x\gt 0$の小数部分を$b$とし,$x^2+b^2=40$を満たす.
このとき,$b$の範囲と$x$の値を求めよ.
18大阪府教員採用試験(数学:整数)過去問
この動画を見る
$2018$
$x\gt 0$の小数部分を$b$とし,$x^2+b^2=40$を満たす.
このとき,$b$の範囲と$x$の値を求めよ.
18大阪府教員採用試験(数学:整数)過去問
18大阪府教員採用試験(数学:整数)

単元:
#数A#整数の性質#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
2018
x>0の小数部分をbとし、$x^2+b^2 =40$を満たす。
このとき、bの範囲とxの値を求めよ。
この動画を見る
2018
x>0の小数部分をbとし、$x^2+b^2 =40$を満たす。
このとき、bの範囲とxの値を求めよ。
20年5月数学検定1級1次試験(合同式)

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}$
$2018n \equiv 2(mod 1000)$をみたす最小の自然数$n$を求めよ.
20年5月数学検定1級1次試験(合同式)過去問
この動画を見る
$\boxed{1}$
$2018n \equiv 2(mod 1000)$をみたす最小の自然数$n$を求めよ.
20年5月数学検定1級1次試験(合同式)過去問
20年5月数学検定1級1次試験(合同式)

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
1⃣
2018 $n ≡ 2$ (mod 1000)をみたす最小の自然数nを求めよ
この動画を見る
1⃣
2018 $n ≡ 2$ (mod 1000)をみたす最小の自然数nを求めよ
