 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
福田のおもしろ数学278〜等差数列の和に関する問題

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$a_1,a_2,a_3,\cdots$は公差$1$の等差数列であり、$a_1+a_2+a_3+\cdots+a_{98}=137$を満たす。
このとき、$a_2+a_4+a_6+\cdots+a_{98}$の値を求めよ。
この動画を見る
$a_1,a_2,a_3,\cdots$は公差$1$の等差数列であり、$a_1+a_2+a_3+\cdots+a_{98}=137$を満たす。
このとき、$a_2+a_4+a_6+\cdots+a_{98}$の値を求めよ。
福田の数学〜東京理科大学2024創域理工学部第1問(3)〜条件を満たす点の個数

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a,b$を正の実数とする。座標平面上に点$\textrm{A}(a,1)$をとり、自然数$n=1,2,3,\cdots$に対して点$\textrm{P}_n(n,0)$をとる。集合$U$を次で定める。
$U=\{n|n$は自然数かつ2点$\textrm{A}, \textrm{P}_n$間の距離は$b$以下$\}$
(a) $a=2$とする。$b=1$のとき、$U$の要素の個数は?また、$b=\sqrt{3}$のとき、$U$の要素の個数は?
(b) $a=\dfrac72$とする。$b=\sqrt2$のとき、$U$の要素の個数は?また、$b=2\sqrt2$のとき、$U$の要素の個数は?
(c) $b=2$のとき、$U$の要素の個数が2個となる正の整数$a$は?また、$b=5$のとき、$U$の要素の個数が9個となる最小の正の整数$a$は?
この動画を見る
$a,b$を正の実数とする。座標平面上に点$\textrm{A}(a,1)$をとり、自然数$n=1,2,3,\cdots$に対して点$\textrm{P}_n(n,0)$をとる。集合$U$を次で定める。
$U=\{n|n$は自然数かつ2点$\textrm{A}, \textrm{P}_n$間の距離は$b$以下$\}$
(a) $a=2$とする。$b=1$のとき、$U$の要素の個数は?また、$b=\sqrt{3}$のとき、$U$の要素の個数は?
(b) $a=\dfrac72$とする。$b=\sqrt2$のとき、$U$の要素の個数は?また、$b=2\sqrt2$のとき、$U$の要素の個数は?
(c) $b=2$のとき、$U$の要素の個数が2個となる正の整数$a$は?また、$b=5$のとき、$U$の要素の個数が9個となる最小の正の整数$a$は?
【数学】2023年度 第3回 高2模試 全問解説

単元:
#大学入試過去問(数学)#全統模試(河合塾)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
大問1:小問集合
(1)実数xの2次方程式$2x^2-3x+1<0$を解け。
(2)$(3x+y)^4$を展開したときの$x^2y^2$の係数を答えよ。
(3)5つの文字A,B,C,D,Eを円形に並べる方法は何通りか。
(4)次のデータの平均値は3であるとする。1,2,3,7,a。aの値を求めよ。また、このデータの分散を求めよ。
(5)mは実数の定数とする。xy平面上の2直線$l_1:3x-y+5=0,l_2:mx+2y+4=0$が垂直になるとき、mの値を求めよ。
(6)実数xの方程式$4^x=2\sqrt{2}$を解け。
(7)実数x,yについて、x>0かつy>0であることは、xy>0であるための何条件か?
(選択肢)①必要十分条件である。②必要条件であるが、十分条件ではない。③十分条件であるが、必要条件ではない。④必要条件でも、十分条件でもない
大問2-1:高次方程式
a,bを実数の定数とする。xの3次式$P(x)=x^3+(2a-1)x^2-(a^2+2a-2)x+b$があり、3次方程式 P(x)=0がx=1を解にもつ。
(1)bをaを用いて表せ。
(2)P(x)を1次式x−1で割ったときの商をaを用いて表せ。
(3)3次方程式P(x)=0において、異なる実数解の個数が2となるようなaの値を求めよ。
大問2-2:確率
赤球1個と白球1個と青球1個の合計3個の球が入った袋がある。この袋から 1個の球を取り出しその色を確認して袋に戻すことを、繰り返し5回行う。
(1)5回とも赤球が取り出される確率を求めよ。
(2)5回のうち、赤球が2回取り出され、かつ白球が3回取り出される確率を求めよ。
(3)3種類の色の球が取り出される確率を求めよ。
大問3:図形と方程式
mを実数の定数とする。Oを原点とするxy平面上に点(2,3)を通り、傾きがmの直線がある。また、2点A(1,0),B(-1,0)があり、軸上のy>0の部分にある点Cが∠ACB=90°を満たしている。
(1)lの方程式を求めよ。また、Cの座標を求めよ。
(2)点Cと直線の距離をdとする。dをmを用いて表せ。
(3)不等式y>0の表す領域内の点Pが∠APB=45°を満たして動くとき、Pが描く図形をKとする。
(i)Kはある円の一部である。その円の中心の座標と半径を求めよ。
(ii)aを正の定数とし、Kと線分AB (両端を含む)で囲まれる領域(境界を含む)をDとする。点(x,y)がD上を動くとき、$\displaystyle\frac{y-a}{x-2}$の最大値をM(a)とする。M($\frac{1}{2}$)とM(3)をそれぞれ求めよ。
大問4:三角関数
kはk≧1を満たす定数とする。下の図のように、OB=1,∠OAB=$\frac{π}{2}$,∠AOB=θ(0<θ<$\frac{π}{4}$)である直角三角形OABがある。また、半直線OA上に点Pを、OP=2kABを満たすようにとる。
(1)辺OAの長さをを用いて表せ。また、線分OPの長さをk、θを用いて表せ。
(2)sinθcosθをsin2θを用いて表せ。また、sin²θをcos2θを用いて表せ。
(3) $BP^2$をk, sin2θ,cos2θを用いて表せ。
(4-i) k=1とする。θが0<θ<$\frac{π}{4}$の範囲を変化するとき、$BP^2$の最小値を求めよ。また、そのときのθの値を求めよ。
(4-ii) k>1とする。θが0<θ<$\frac{π}{4}$の範囲を変化するとき、$BP^2$のとり得る値の範囲をkを用いて表せ。
大問5:微分法
3次関数 $f(x)=x^3+kx^2-kx+k^2$がある。ただし、kは実数とする。
(1)f'(−1)=0とする。
(i)kの値を求めよ。
(ii)0≦x≦1におけるf(x)の最大値と最小値を求めよ。
(2)f(x)はx>0の範囲に極大値と極小値をもつとする。
(i)kのとり得る値の範囲を求めよ。
(ii)f(x)の極大値と極小値の和をS(k)とする。kの値が(2-i)で求めた範囲を変化するとき、S(k)の最大値を求めよ。
大問6:数列
数列{$a_n$}を$a_1=\frac{1}{\sqrt{2}},a_2=\sqrt{2},a_{n+2}a_{n+1}-a_{n+1}a_{n}=n+1(n=1,2,3,...)$により定める。また、数列{$b_n$}を$b_n=a_{n+1}a_{n}(n=1,2,3,・・・)$により定める。
(1)$b_1$を求めよ。また、$b_{n+1}$を$b_n$を用いて表せ。
(2)数列{$b_n$}の一般項を求めよ。
(3)$c_n=\displaystyle\frac{\sqrt{2}a_n}{n}(n=1,2,3,…)$とおく。$c_{n+1}$を$c_n$を用いて表せ。また、数列{$c_n$}の一般項を求めよ。
(4)$a_n>50$を満たす最小の正の整数の値をNとするとき、$\displaystyle \sum_{k=1}^N\frac{2k+1}{{a_{n+1}}^2{a_n}²}$を求めよ。
この動画を見る
大問1:小問集合
(1)実数xの2次方程式$2x^2-3x+1<0$を解け。
(2)$(3x+y)^4$を展開したときの$x^2y^2$の係数を答えよ。
(3)5つの文字A,B,C,D,Eを円形に並べる方法は何通りか。
(4)次のデータの平均値は3であるとする。1,2,3,7,a。aの値を求めよ。また、このデータの分散を求めよ。
(5)mは実数の定数とする。xy平面上の2直線$l_1:3x-y+5=0,l_2:mx+2y+4=0$が垂直になるとき、mの値を求めよ。
(6)実数xの方程式$4^x=2\sqrt{2}$を解け。
(7)実数x,yについて、x>0かつy>0であることは、xy>0であるための何条件か?
(選択肢)①必要十分条件である。②必要条件であるが、十分条件ではない。③十分条件であるが、必要条件ではない。④必要条件でも、十分条件でもない
大問2-1:高次方程式
a,bを実数の定数とする。xの3次式$P(x)=x^3+(2a-1)x^2-(a^2+2a-2)x+b$があり、3次方程式 P(x)=0がx=1を解にもつ。
(1)bをaを用いて表せ。
(2)P(x)を1次式x−1で割ったときの商をaを用いて表せ。
(3)3次方程式P(x)=0において、異なる実数解の個数が2となるようなaの値を求めよ。
大問2-2:確率
赤球1個と白球1個と青球1個の合計3個の球が入った袋がある。この袋から 1個の球を取り出しその色を確認して袋に戻すことを、繰り返し5回行う。
(1)5回とも赤球が取り出される確率を求めよ。
(2)5回のうち、赤球が2回取り出され、かつ白球が3回取り出される確率を求めよ。
(3)3種類の色の球が取り出される確率を求めよ。
大問3:図形と方程式
mを実数の定数とする。Oを原点とするxy平面上に点(2,3)を通り、傾きがmの直線がある。また、2点A(1,0),B(-1,0)があり、軸上のy>0の部分にある点Cが∠ACB=90°を満たしている。
(1)lの方程式を求めよ。また、Cの座標を求めよ。
(2)点Cと直線の距離をdとする。dをmを用いて表せ。
(3)不等式y>0の表す領域内の点Pが∠APB=45°を満たして動くとき、Pが描く図形をKとする。
(i)Kはある円の一部である。その円の中心の座標と半径を求めよ。
(ii)aを正の定数とし、Kと線分AB (両端を含む)で囲まれる領域(境界を含む)をDとする。点(x,y)がD上を動くとき、$\displaystyle\frac{y-a}{x-2}$の最大値をM(a)とする。M($\frac{1}{2}$)とM(3)をそれぞれ求めよ。
大問4:三角関数
kはk≧1を満たす定数とする。下の図のように、OB=1,∠OAB=$\frac{π}{2}$,∠AOB=θ(0<θ<$\frac{π}{4}$)である直角三角形OABがある。また、半直線OA上に点Pを、OP=2kABを満たすようにとる。
(1)辺OAの長さをを用いて表せ。また、線分OPの長さをk、θを用いて表せ。
(2)sinθcosθをsin2θを用いて表せ。また、sin²θをcos2θを用いて表せ。
(3) $BP^2$をk, sin2θ,cos2θを用いて表せ。
(4-i) k=1とする。θが0<θ<$\frac{π}{4}$の範囲を変化するとき、$BP^2$の最小値を求めよ。また、そのときのθの値を求めよ。
(4-ii) k>1とする。θが0<θ<$\frac{π}{4}$の範囲を変化するとき、$BP^2$のとり得る値の範囲をkを用いて表せ。
大問5:微分法
3次関数 $f(x)=x^3+kx^2-kx+k^2$がある。ただし、kは実数とする。
(1)f'(−1)=0とする。
(i)kの値を求めよ。
(ii)0≦x≦1におけるf(x)の最大値と最小値を求めよ。
(2)f(x)はx>0の範囲に極大値と極小値をもつとする。
(i)kのとり得る値の範囲を求めよ。
(ii)f(x)の極大値と極小値の和をS(k)とする。kの値が(2-i)で求めた範囲を変化するとき、S(k)の最大値を求めよ。
大問6:数列
数列{$a_n$}を$a_1=\frac{1}{\sqrt{2}},a_2=\sqrt{2},a_{n+2}a_{n+1}-a_{n+1}a_{n}=n+1(n=1,2,3,...)$により定める。また、数列{$b_n$}を$b_n=a_{n+1}a_{n}(n=1,2,3,・・・)$により定める。
(1)$b_1$を求めよ。また、$b_{n+1}$を$b_n$を用いて表せ。
(2)数列{$b_n$}の一般項を求めよ。
(3)$c_n=\displaystyle\frac{\sqrt{2}a_n}{n}(n=1,2,3,…)$とおく。$c_{n+1}$を$c_n$を用いて表せ。また、数列{$c_n$}の一般項を求めよ。
(4)$a_n>50$を満たす最小の正の整数の値をNとするとき、$\displaystyle \sum_{k=1}^N\frac{2k+1}{{a_{n+1}}^2{a_n}²}$を求めよ。
#北海道大学1957#因数分解_64

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
ますただ
問題文全文(内容文):
$2x^2-xy-y^2-7x+y+6$を因数分解せよ.
1957北海道大学過去問題
この動画を見る
$2x^2-xy-y^2-7x+y+6$を因数分解せよ.
1957北海道大学過去問題
福田のおもしろ数学277〜ガウス記号の等式の証明

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$n$は正の整数とする。
$[\sqrt{n}+\sqrt{n+1}]=[\sqrt{ 4n+2 }]$であることを証明して下さい。
$[n]$は$x$を超えない最大の整数を表します。
この動画を見る
$n$は正の整数とする。
$[\sqrt{n}+\sqrt{n+1}]=[\sqrt{ 4n+2 }]$であることを証明して下さい。
$[n]$は$x$を超えない最大の整数を表します。
福田の数学〜東京理科大学2024創域理工学部第1問(2)〜三角不等式の解法

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#加法定理とその応用#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}(2)0 \leqq θ \lt 2π$のとき、次の不等式を解こう。
$sin2θ \gt 2cos(θ+\frac{π}{6})+\frac{\sqrt{3}}{2}・・・③$
$a=cosθ,b=sinθ$とおくと、次の不等式$③$は
$\boxed{キ}ab-\boxed{ク}\sqrt{\boxed{ケ}}a+\boxed{コ}b-\sqrt{2}\gt0 ・・・④$
となる。不等式$④$の左辺は
$(\boxed{サ}a+\boxed{シ})(\boxed{ス}b-\sqrt{セ})$
と因数分解できる。これより、不等式$③$の解は
$\frac{π}{\boxed{ソ}} \lt θ \lt \frac{\boxed{タ}}{\boxed{チ}}π$または$\frac{\boxed{ツ}}{\boxed{テ}}π \lt θ \lt\frac{\boxed{ト}}{\boxed{ナ}}π$
と求まる。
この動画を見る
$\boxed{1}(2)0 \leqq θ \lt 2π$のとき、次の不等式を解こう。
$sin2θ \gt 2cos(θ+\frac{π}{6})+\frac{\sqrt{3}}{2}・・・③$
$a=cosθ,b=sinθ$とおくと、次の不等式$③$は
$\boxed{キ}ab-\boxed{ク}\sqrt{\boxed{ケ}}a+\boxed{コ}b-\sqrt{2}\gt0 ・・・④$
となる。不等式$④$の左辺は
$(\boxed{サ}a+\boxed{シ})(\boxed{ス}b-\sqrt{セ})$
と因数分解できる。これより、不等式$③$の解は
$\frac{π}{\boxed{ソ}} \lt θ \lt \frac{\boxed{タ}}{\boxed{チ}}π$または$\frac{\boxed{ツ}}{\boxed{テ}}π \lt θ \lt\frac{\boxed{ト}}{\boxed{ナ}}π$
と求まる。
福田のおもしろ数学276〜一般項が求まらない数列の極限

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$a_1=a(\gt 0),a_{n+1}=\frac{1}{6}cosa_n+\frac{1}{2}a_n+\frac{π}{4}$のとき、$\displaystyle \lim_{ n \to \infty } a_n$を求めて下さい。
この動画を見る
$a_1=a(\gt 0),a_{n+1}=\frac{1}{6}cosa_n+\frac{1}{2}a_n+\frac{π}{4}$のとき、$\displaystyle \lim_{ n \to \infty } a_n$を求めて下さい。
#1 微分空間の圏について: The category of diffeological spaces

福田の数学〜東京理科大学2024創域理工学部第1問(1)〜複素数と三角形の外接円

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}(1)a$を正の実数とする。$x$についての方程式
$(x^2+ax+2)(x^2-ax-1)=0・・・①$
が異なる2つの実数解と異なる2つの虚数解をもつのは
$\boxed{ア} \lt a \lt \boxed{イ}\sqrt{\boxed{ウ}}・・・②$
のときである。
以下では、$a$は不等式$②$を満たす最大の整数とし、$i$は虚数単位とする。このとき、複素数平面上において、方程式$①$の異なる2つの虚数解と$3+i$を頂点とする三角形の面積は$\boxed{エ}$であり、この三角形の外接円を複素数zの方程式で表すと
$|x-\boxed{オ}|=\sqrt{\boxed{カ}}$
である。
この動画を見る
$\boxed{1}(1)a$を正の実数とする。$x$についての方程式
$(x^2+ax+2)(x^2-ax-1)=0・・・①$
が異なる2つの実数解と異なる2つの虚数解をもつのは
$\boxed{ア} \lt a \lt \boxed{イ}\sqrt{\boxed{ウ}}・・・②$
のときである。
以下では、$a$は不等式$②$を満たす最大の整数とし、$i$は虚数単位とする。このとき、複素数平面上において、方程式$①$の異なる2つの虚数解と$3+i$を頂点とする三角形の面積は$\boxed{エ}$であり、この三角形の外接円を複素数zの方程式で表すと
$|x-\boxed{オ}|=\sqrt{\boxed{カ}}$
である。
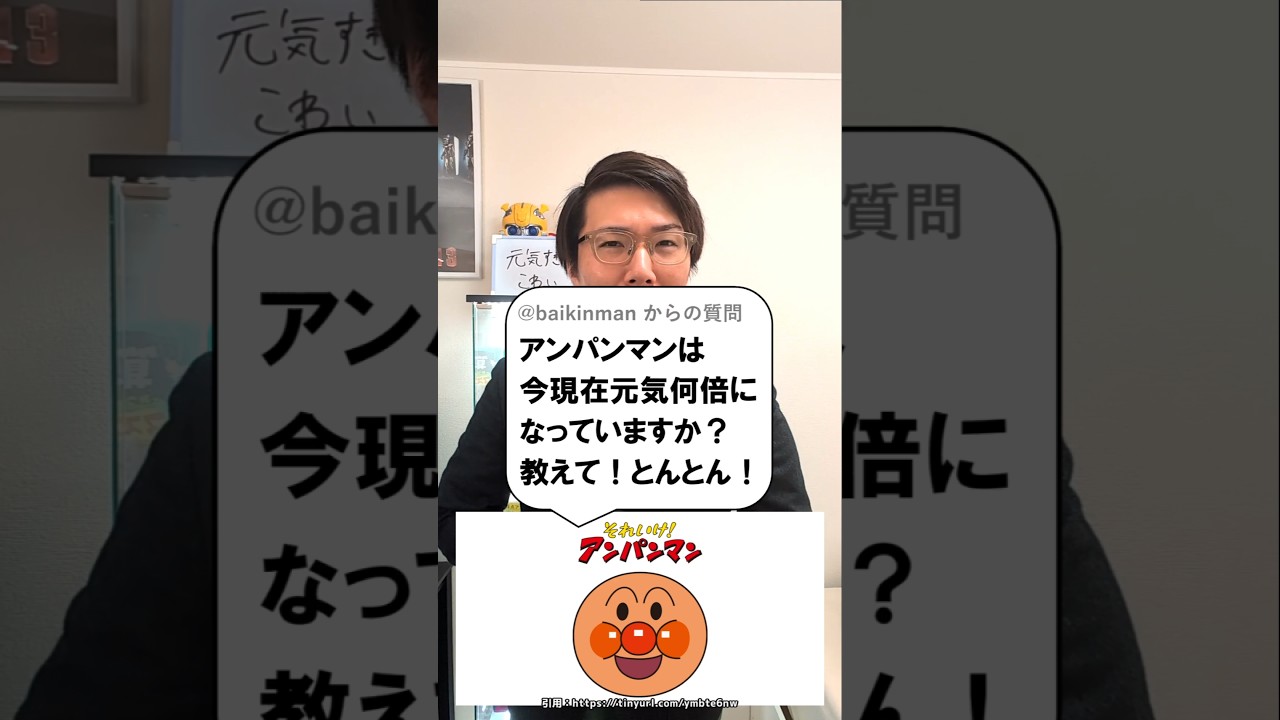
アンパンマンは今元気何倍ですか?
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
アンパンマンは今現在元気何倍になっていますか
この動画を見る
アンパンマンは今現在元気何倍になっていますか
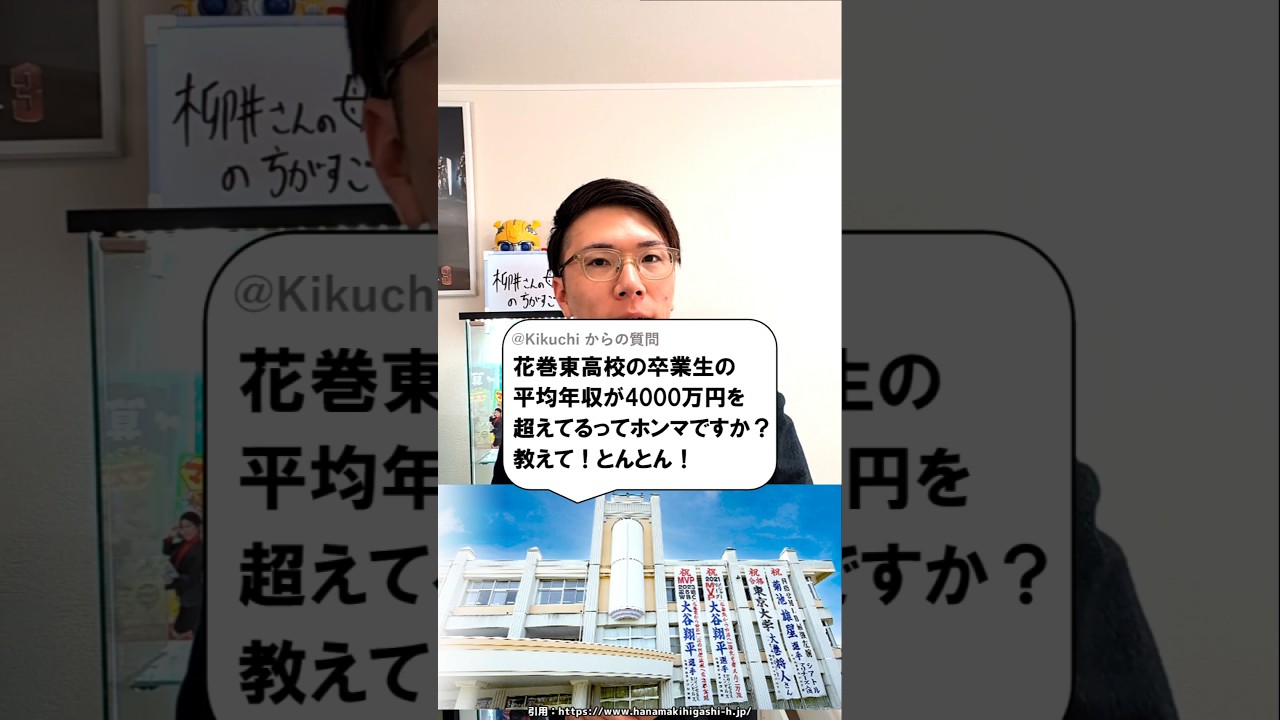
花巻東高校の平均年収4000万円なん?
単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
大谷翔平選手のおかげで花巻東高校の卒業生の年収が上がっているみたいなので計算しました
この動画を見る
大谷翔平選手のおかげで花巻東高校の卒業生の年収が上がっているみたいなので計算しました
福田のおもしろ数学275〜分母の違う項がたくさん並んだ方程式の解

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
次の方程式を満たす$x$を求めて下さい。
$\frac{x-2020}{1}+\frac{x-2019}{2}+\cdots+\frac{x-2000}{21} = \frac{x-1}{2020}+\frac{x-2}{2019}+\cdots+\frac{x-21}{2000} $
この動画を見る
次の方程式を満たす$x$を求めて下さい。
$\frac{x-2020}{1}+\frac{x-2019}{2}+\cdots+\frac{x-2000}{21} = \frac{x-1}{2020}+\frac{x-2}{2019}+\cdots+\frac{x-21}{2000} $
福田の数学〜上智大学2024理工学部第3問〜円の内部を反射しながら進む点の通過範囲

単元:
#大学入試過去問(数学)#平面上のベクトル#数列#平面上のベクトルと内積#漸化式#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B#数C
指導講師:
福田次郎
問題文全文(内容文):
点$O$を中心とし半径が$1$の円形のビリヤード台がある。台の縁の点$P_1$に大きさが無視できる球$Q$を置き、半径$P_1O$とのなす角が$\frac{\pi}{8}$の方向へ球$Q$を打ち出す。
球$Q$は、ビリヤード台の縁に当たると、図のように入射角と反射角が等しくなるように反射し、一度打ち出されたら止まらないものとする。
$i=1,2,3,\cdots$に対し、点$P_i$の次に球$Q$が縁に当たる点を$P_{i+1}$とし、$\overrightarrow{OP_i}=\overrightarrow{p_i}$とする。
(1)$\overrightarrow{p_3}=\fbox{あ}\overrightarrow{p_1}+\fbox{い}\overrightarrow{p_2},\overrightarrow{p_4}=\fbox{う}\overrightarrow{p_1}+\fbox{え}\overrightarrow{p_2}$である。
(2)$P_i=P_1となるiのうち、 i\geqq 2で最小のものは\fbox{ソ}である。$
(3)$線分P_1P_2とP_3P_4 との交点をA、線分P_1P_2とP_6P_7との交点をBとすると$
$\overrightarrow{OA}=\fbox{お}\overrightarrow{p_1}+\fbox{か}\overrightarrow{p_2},\overrightarrow{OB}=\fbox{き}\overrightarrow{p_1}+\fbox{く}\overrightarrow{p_2}$である。
(4)球$Q$が点$P_1$から打ち出されてから初めて再び点$P_1$に到達するまでに、中心$O$と球$Q$とを結ぶ線分$OQ$がちょうど2回通過する領域の面積は$\fbox{タ}+\fbox{チ}\sqrt{2}$である。
この動画を見る
点$O$を中心とし半径が$1$の円形のビリヤード台がある。台の縁の点$P_1$に大きさが無視できる球$Q$を置き、半径$P_1O$とのなす角が$\frac{\pi}{8}$の方向へ球$Q$を打ち出す。
球$Q$は、ビリヤード台の縁に当たると、図のように入射角と反射角が等しくなるように反射し、一度打ち出されたら止まらないものとする。
$i=1,2,3,\cdots$に対し、点$P_i$の次に球$Q$が縁に当たる点を$P_{i+1}$とし、$\overrightarrow{OP_i}=\overrightarrow{p_i}$とする。
(1)$\overrightarrow{p_3}=\fbox{あ}\overrightarrow{p_1}+\fbox{い}\overrightarrow{p_2},\overrightarrow{p_4}=\fbox{う}\overrightarrow{p_1}+\fbox{え}\overrightarrow{p_2}$である。
(2)$P_i=P_1となるiのうち、 i\geqq 2で最小のものは\fbox{ソ}である。$
(3)$線分P_1P_2とP_3P_4 との交点をA、線分P_1P_2とP_6P_7との交点をBとすると$
$\overrightarrow{OA}=\fbox{お}\overrightarrow{p_1}+\fbox{か}\overrightarrow{p_2},\overrightarrow{OB}=\fbox{き}\overrightarrow{p_1}+\fbox{く}\overrightarrow{p_2}$である。
(4)球$Q$が点$P_1$から打ち出されてから初めて再び点$P_1$に到達するまでに、中心$O$と球$Q$とを結ぶ線分$OQ$がちょうど2回通過する領域の面積は$\fbox{タ}+\fbox{チ}\sqrt{2}$である。
福田の数学〜上智大学2024理工学部第3問〜円の内部を反射しながら進む点の通過範囲

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$O$ を中心とする半径1の円周上の点 $P_1$ から図のように (図は動画内参照) 点 $Q$ を発射すると円の中を $P_2, \, P_3, \, \ldots $ と反射しながら止まることなく動き続けるとする。$\vec{OP_i}=\vec{p_i}$ とおく。$\vec{p_3}, \, \vec{p_4}$ を $\vec{p_1}, \, \vec{p_2}$ で表せ。$\vec{p_i}=\vec{p_1}$ となる最小の $i\ge2$ を求めよ。点 $Q$ が再び点 $P_1$ に到達するまでに、線分 $OQ$ がちょうど2回通過する領域の面積は?
この動画を見る
$O$ を中心とする半径1の円周上の点 $P_1$ から図のように (図は動画内参照) 点 $Q$ を発射すると円の中を $P_2, \, P_3, \, \ldots $ と反射しながら止まることなく動き続けるとする。$\vec{OP_i}=\vec{p_i}$ とおく。$\vec{p_3}, \, \vec{p_4}$ を $\vec{p_1}, \, \vec{p_2}$ で表せ。$\vec{p_i}=\vec{p_1}$ となる最小の $i\ge2$ を求めよ。点 $Q$ が再び点 $P_1$ に到達するまでに、線分 $OQ$ がちょうど2回通過する領域の面積は?
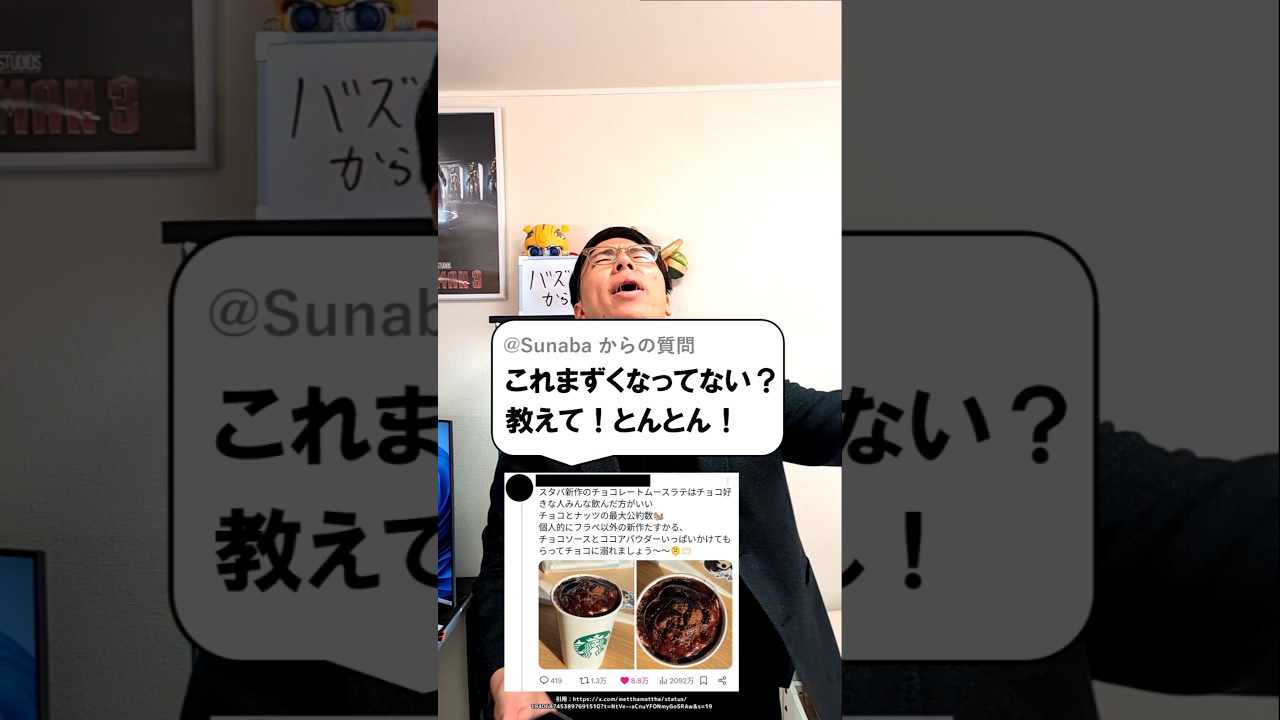
最大公約数ってまずいってこと?
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
スタバ新作のチョコレートムースラテはチョコ好きな人みんな飲んだ方がいい
チョコとナッツの最大公約数
と紹介していたツイートについて
この動画を見る
スタバ新作のチョコレートムースラテはチョコ好きな人みんな飲んだ方がいい
チョコとナッツの最大公約数
と紹介していたツイートについて
なんて書いた?黒板ASMRと思いきや...

福田のおもしろ数学274〜底が2の対数のガウスの和が2024を超えるのはいつか

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
次の式を満たす最小の整数 $n$ を求めて下さい。
$[\log_2{1}]+[\log_2{2}]+[\log_2{3}]+\cdots+[\log_2{n}]>2024$
$[x]$ は $x$ を超えない最大の整数を表します。
この動画を見る
次の式を満たす最小の整数 $n$ を求めて下さい。
$[\log_2{1}]+[\log_2{2}]+[\log_2{3}]+\cdots+[\log_2{n}]>2024$
$[x]$ は $x$ を超えない最大の整数を表します。
3次不等式を解け

3次不等式を解け

福田の数学〜上智大学2024理工学部第2問〜漸化式と約数倍数の証明

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
次の条件によって定められる数列 ${a_n}$ を考える。
$a_1=2, \, a_{n+1}=a_n^2+a_n+1$
$(1)$ $a_n-2$ は $5$ で割り切れることを証明せよ。
$(2)$ $a_n^2+1$ は $5^n$ で割り切れることを証明せよ。
この動画を見る
次の条件によって定められる数列 ${a_n}$ を考える。
$a_1=2, \, a_{n+1}=a_n^2+a_n+1$
$(1)$ $a_n-2$ は $5$ で割り切れることを証明せよ。
$(2)$ $a_n^2+1$ は $5^n$ で割り切れることを証明せよ。
福田のおもしろ数学273〜命題の真偽を確認するにはどのカードを裏返すか

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
表にアルファベット、裏に数字が書かれた5枚のカード $\rm P,Q,1,3,6$が机に置かれている。命題「表が$\rm P$ならば裏は素数である」の真偽を確認するにはどれを裏返せばいい?
この動画を見る
表にアルファベット、裏に数字が書かれた5枚のカード $\rm P,Q,1,3,6$が机に置かれている。命題「表が$\rm P$ならば裏は素数である」の真偽を確認するにはどれを裏返せばいい?
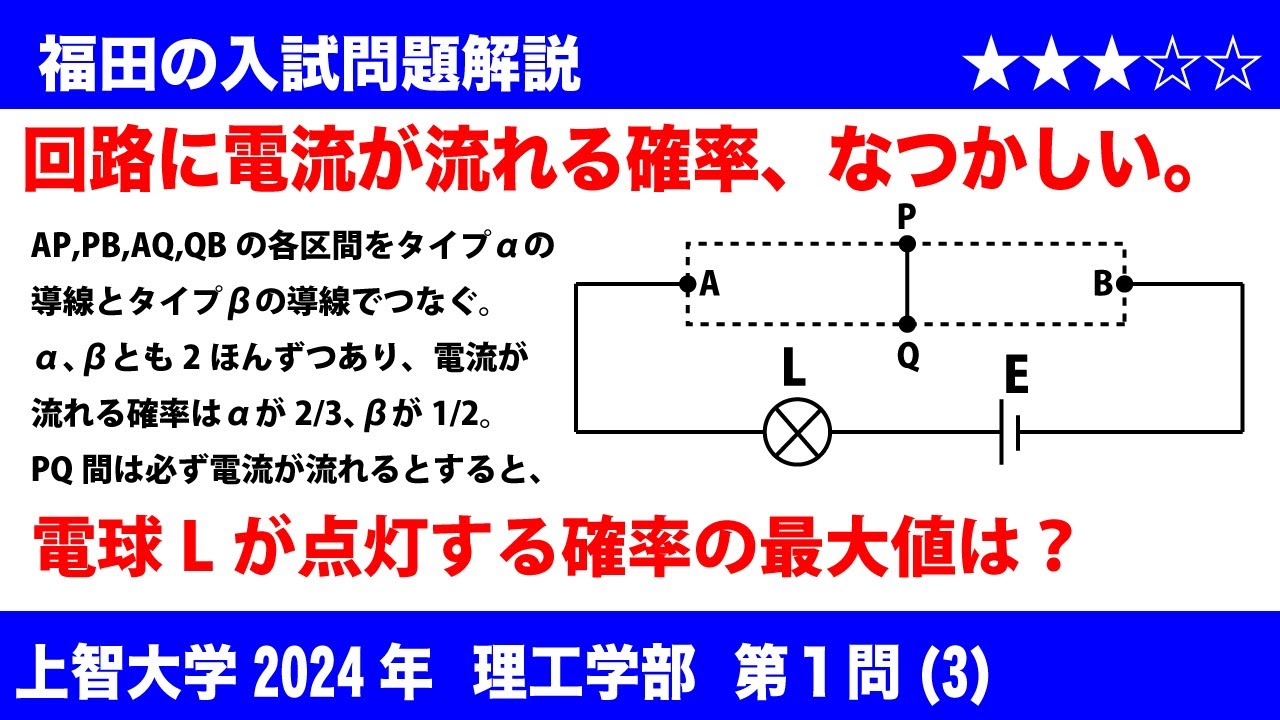
福田の数学〜上智大学2024理工学部第1問(3)〜回路に電流が流れて電球が点灯する確率の最大
単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
次の図で表される回路は、$\rm AP$間、$\rm AQ$間、$\rm PB$間、$\rm QB$間がつながっておらず、それぞれの区間を1本の導線でつなぐことができる。$\rm P$または$\rm Q$を経由して$\rm AB$間がつながり電流が流れると電球が点灯する。導線にはタイプαが2本、タイプβが2本ある。それぞれの導線に電流が流れる確率はタイプαが$\dfrac23$、タイプβが$\dfrac12$である。
(i) $\rm AP$間、$\rm PB$間を2本のタイプαの導線でそれぞれつなぐとき、$\rm L$が点灯する確率は?
(ii) $\rm AP$間、$\rm AQ$間、$\rm PB$間、$\rm QB$間でそれぞれつなぐすべてのパターンを考える。$\rm L$が点灯する確率が最も大きくなるときの確率は?
(iii) $\rm PQ$間を確実に電流が流れる別の導線でつなぎ、$\rm AP$間、$\rm AQ$間、$\rm PB$間、$\rm QB$間を4本の導線でそれぞれつなぐすべてのパターンを考える。$\rm L$が点灯する確率が最も大きくなるときの確率は?
この動画を見る
次の図で表される回路は、$\rm AP$間、$\rm AQ$間、$\rm PB$間、$\rm QB$間がつながっておらず、それぞれの区間を1本の導線でつなぐことができる。$\rm P$または$\rm Q$を経由して$\rm AB$間がつながり電流が流れると電球が点灯する。導線にはタイプαが2本、タイプβが2本ある。それぞれの導線に電流が流れる確率はタイプαが$\dfrac23$、タイプβが$\dfrac12$である。
(i) $\rm AP$間、$\rm PB$間を2本のタイプαの導線でそれぞれつなぐとき、$\rm L$が点灯する確率は?
(ii) $\rm AP$間、$\rm AQ$間、$\rm PB$間、$\rm QB$間でそれぞれつなぐすべてのパターンを考える。$\rm L$が点灯する確率が最も大きくなるときの確率は?
(iii) $\rm PQ$間を確実に電流が流れる別の導線でつなぎ、$\rm AP$間、$\rm AQ$間、$\rm PB$間、$\rm QB$間を4本の導線でそれぞれつなぐすべてのパターンを考える。$\rm L$が点灯する確率が最も大きくなるときの確率は?
微分法と積分法 数Ⅱ 最大最小を利用した関数の決定【マコちゃんねるがていねいに解説】

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
a,bは定数で、a<0とする。関数f(x)=ax³-3ax²+b (1≦x≦3) の最大値が10,最小値が-2になるように,定数a,bの値を定めよ。
この動画を見る
a,bは定数で、a<0とする。関数f(x)=ax³-3ax²+b (1≦x≦3) の最大値が10,最小値が-2になるように,定数a,bの値を定めよ。
福田のおもしろ数学272〜複雑な分数計算どうやって約分するか

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\dfrac{(10^4+324)(22^4+324)(34^4+324)(46^4+324)(58^4+324)}{(4^4+324)(16^4+324)(28^4+324)(40^4+324)(52^4+324)}$
を計算してください。
この動画を見る
$\dfrac{(10^4+324)(22^4+324)(34^4+324)(46^4+324)(58^4+324)}{(4^4+324)(16^4+324)(28^4+324)(40^4+324)(52^4+324)}$
を計算してください。
2次方程式のすごい解法見つけた

福田の数学〜上智大学2024理工学部第1問(2)〜定積分の計算

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\dfrac{2\sin x}{x^3}dx=-\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\dfrac{\sin x}{x}dx+\fbox{エ}\pi^p+\fbox{オ}\sqrt{\fbox{カ}}\pi^q$
ただし、$p=\fbox{キ},q=\fbox{ク}$である。
この動画を見る
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\dfrac{2\sin x}{x^3}dx=-\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\dfrac{\sin x}{x}dx+\fbox{エ}\pi^p+\fbox{オ}\sqrt{\fbox{カ}}\pi^q$
ただし、$p=\fbox{キ},q=\fbox{ク}$である。
#北海道大学1919#因数分解_63

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
ますただ
問題文全文(内容文):
$a^4+b^4+c^4-2b^2c^2-2c^2a^2-2a^2b^2$を因数分解せよ.
1919北海道帝国大学過去問題
この動画を見る
$a^4+b^4+c^4-2b^2c^2-2c^2a^2-2a^2b^2$を因数分解せよ.
1919北海道帝国大学過去問題
5つの文字を求めよ!?東大の整数問題【東京大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
n,a,b,c,dは0または正の整数であって、
a^2+b^2+c^2+d^2=n^2-6
a+b+c+d≦n
a≧b≧c≧d
を満たすものとする。このような整数の組(n,a,b,c,d)をすべて求めよ。
この動画を見る
n,a,b,c,dは0または正の整数であって、
a^2+b^2+c^2+d^2=n^2-6
a+b+c+d≦n
a≧b≧c≧d
を満たすものとする。このような整数の組(n,a,b,c,d)をすべて求めよ。
福田のおもしろ数学271〜再帰関数の値を計算する

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
整数を定義域とする関数が次のように定義されている。
\begin{eqnarray}
f(n)
=
\begin{cases}
n-3 & ( n \geqq 1000 ) \\
f(f(n+5)) & ( n \lt 1000 )
\end{cases}
\end{eqnarray}
このとき$f(84)$を求めよ
この動画を見る
整数を定義域とする関数が次のように定義されている。
\begin{eqnarray}
f(n)
=
\begin{cases}
n-3 & ( n \geqq 1000 ) \\
f(f(n+5)) & ( n \lt 1000 )
\end{cases}
\end{eqnarray}
このとき$f(84)$を求めよ
福田の数学〜上智大学2024理工学部第1問(1)〜複素数の絶対値と三角関数の計算

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
複素数 $z=(-3+2 \cos\theta )+(4+2 \sin \theta)i$ の絶対値は、$\theta = \theta_1$ のとき最小値 $\fbox{ア}$ をとる。このとき、 $\sin{\theta_1} = \frac{\fbox{イ}}{\fbox{ウ}}$ である。
この動画を見る
複素数 $z=(-3+2 \cos\theta )+(4+2 \sin \theta)i$ の絶対値は、$\theta = \theta_1$ のとき最小値 $\fbox{ア}$ をとる。このとき、 $\sin{\theta_1} = \frac{\fbox{イ}}{\fbox{ウ}}$ である。
