 高校入試過去問(数学)
高校入試過去問(数学)
 高校入試過去問(数学)
高校入試過去問(数学)
【…で、実際の解き方は?】二次方程式:法政大学第二高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2次方程式$(2x+3)^2=(3x-8)^2$を解きなさい.
法政大第二高校過去問
この動画を見る
2次方程式$(2x+3)^2=(3x-8)^2$を解きなさい.
法政大第二高校過去問
コメント欄が荒れそうな解き方してしまった🙇♂️中学受験の知識だけでは解けません。東北学院
単元:
#数学(中学生)#中3数学#円#三平方の定理#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
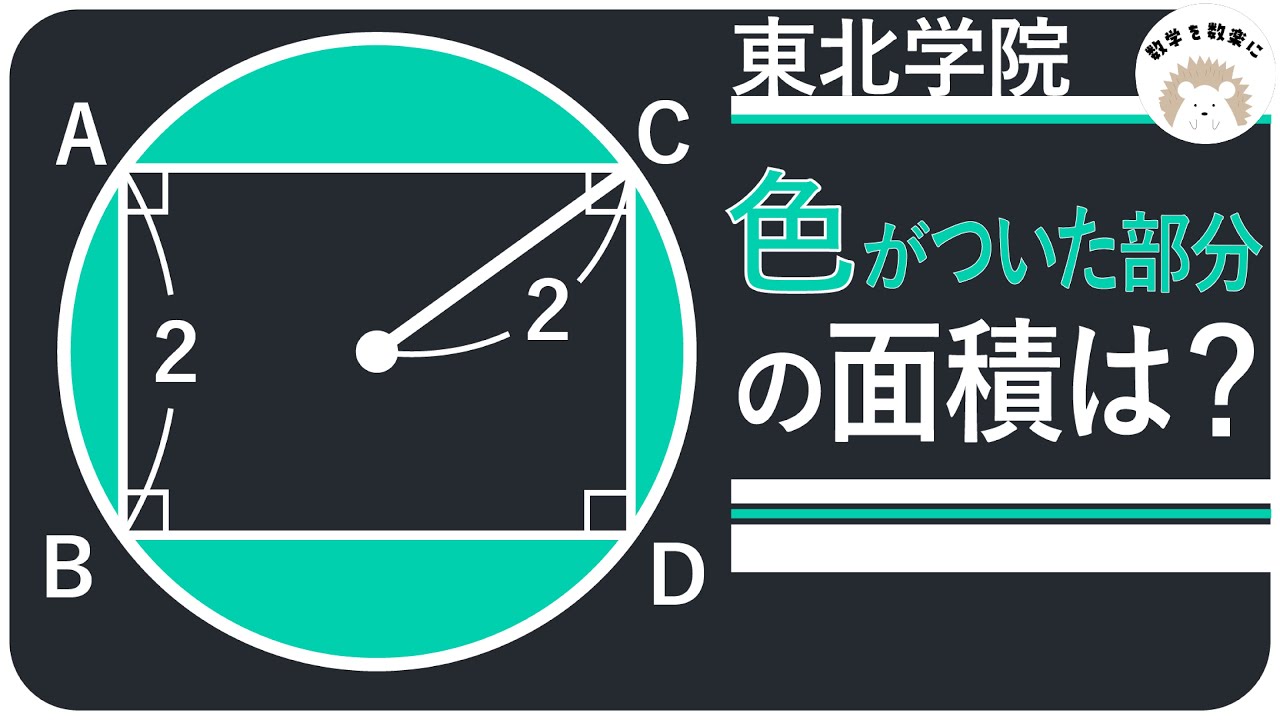
半径=2
斜線部の面積は?
*図は動画内参照
東北学院高等学校
この動画を見る
半径=2
斜線部の面積は?
*図は動画内参照
東北学院高等学校
筆算した人いる?いないか。四天王寺高校

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
N=1234×17+35
Nを17で割ったときの商と余りを求めよ。
四天王寺高等学校
この動画を見る
N=1234×17+35
Nを17で割ったときの商と余りを求めよ。
四天王寺高等学校
【中学数学】高校入試:2022年度神奈川県立高校入試数学大問6(ウ)

単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
AB=5cm,BC=1cm,AD=4m,∠ADC=∠BCD=90°の台形ABCDを底面とし,AE=BF=CG=DH=1cmを高さとする四角柱である。
点Iが辺CD上の点で,CI:ID=7:3であるとき,この四角柱の表面上に,図2のように点Aから辺EF,辺GHと交わるように,点Iまで線を引く。このような線のうち,長さが最も短くなるように引いた線の長さは√□cmである。
この動画を見る
AB=5cm,BC=1cm,AD=4m,∠ADC=∠BCD=90°の台形ABCDを底面とし,AE=BF=CG=DH=1cmを高さとする四角柱である。
点Iが辺CD上の点で,CI:ID=7:3であるとき,この四角柱の表面上に,図2のように点Aから辺EF,辺GHと交わるように,点Iまで線を引く。このような線のうち,長さが最も短くなるように引いた線の長さは√□cmである。
【ケアレスミスを減らすために】文字式:江戸川学園取手高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\dfrac{a-5b+2}{5}-\dfrac{4a-3b-2}{3}+2a-1$を計算しなさい.
江戸川学園取手高等学校過去問
この動画を見る
$\dfrac{a-5b+2}{5}-\dfrac{4a-3b-2}{3}+2a-1$を計算しなさい.
江戸川学園取手高等学校過去問
【「分かったつもり」が命取り!】文字式:大阪星光学院高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
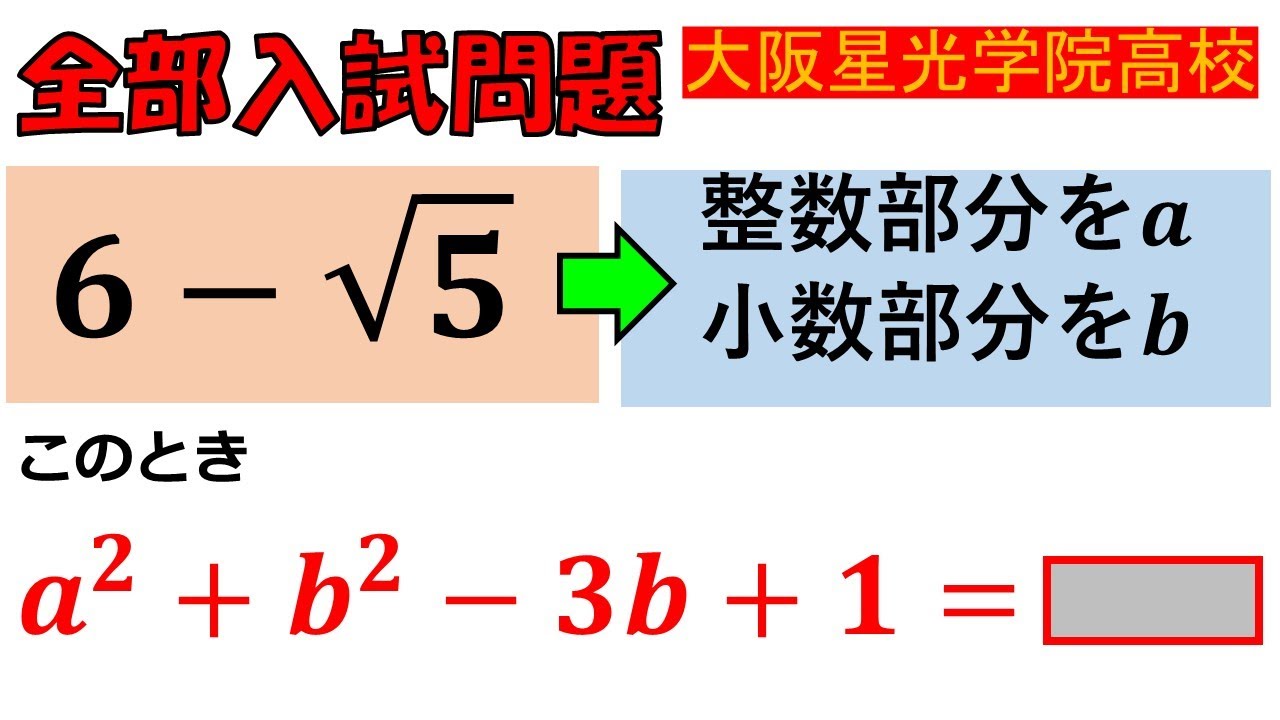
$6-\sqrt5$の整数部分を$a$とし,小数部分を$b$とする.
このとき,$a^2+b^2-3b+1=\Box$である.$\Box$の値を求めよ.
大阪星光学院高等学校過去問
この動画を見る
$6-\sqrt5$の整数部分を$a$とし,小数部分を$b$とする.
このとき,$a^2+b^2-3b+1=\Box$である.$\Box$の値を求めよ.
大阪星光学院高等学校過去問
代入するの? 四天王寺高校
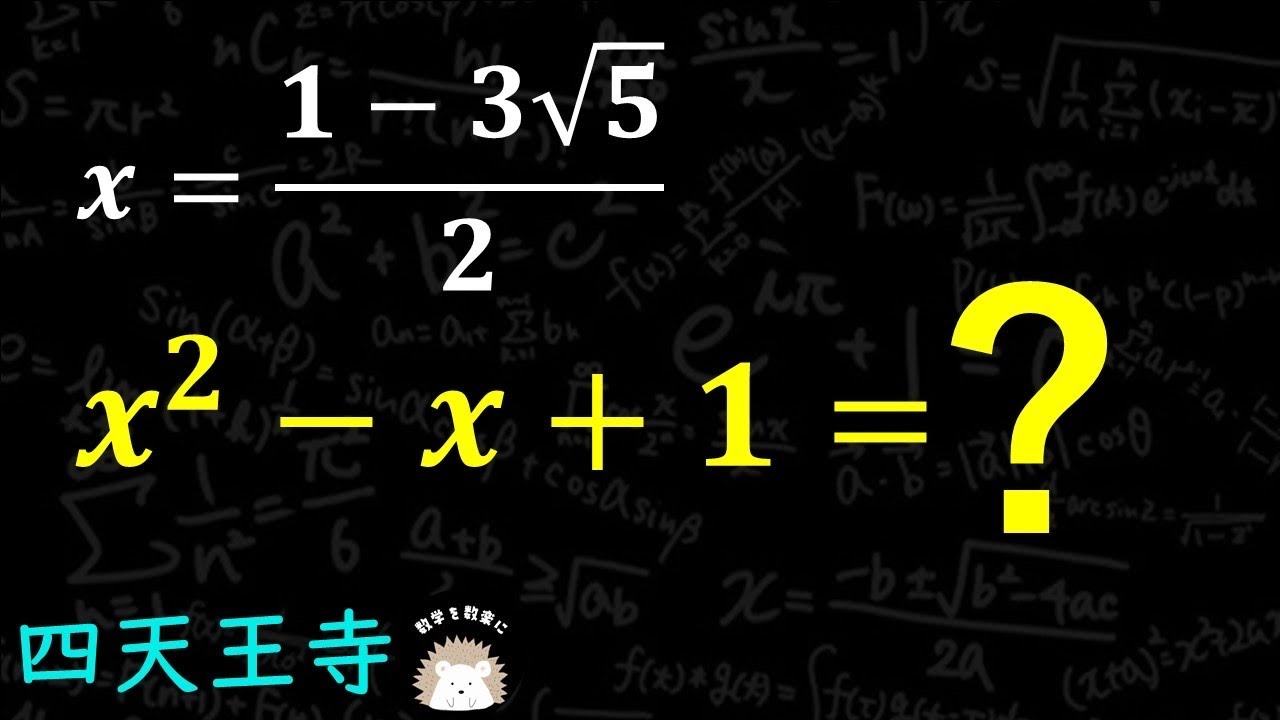
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x= \frac{1-3 \sqrt 5}{2}$
$x^2-x+1 =?$
四天王寺高等学校
この動画を見る
$x= \frac{1-3 \sqrt 5}{2}$
$x^2-x+1 =?$
四天王寺高等学校
気付けば一瞬!!普連土学園
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
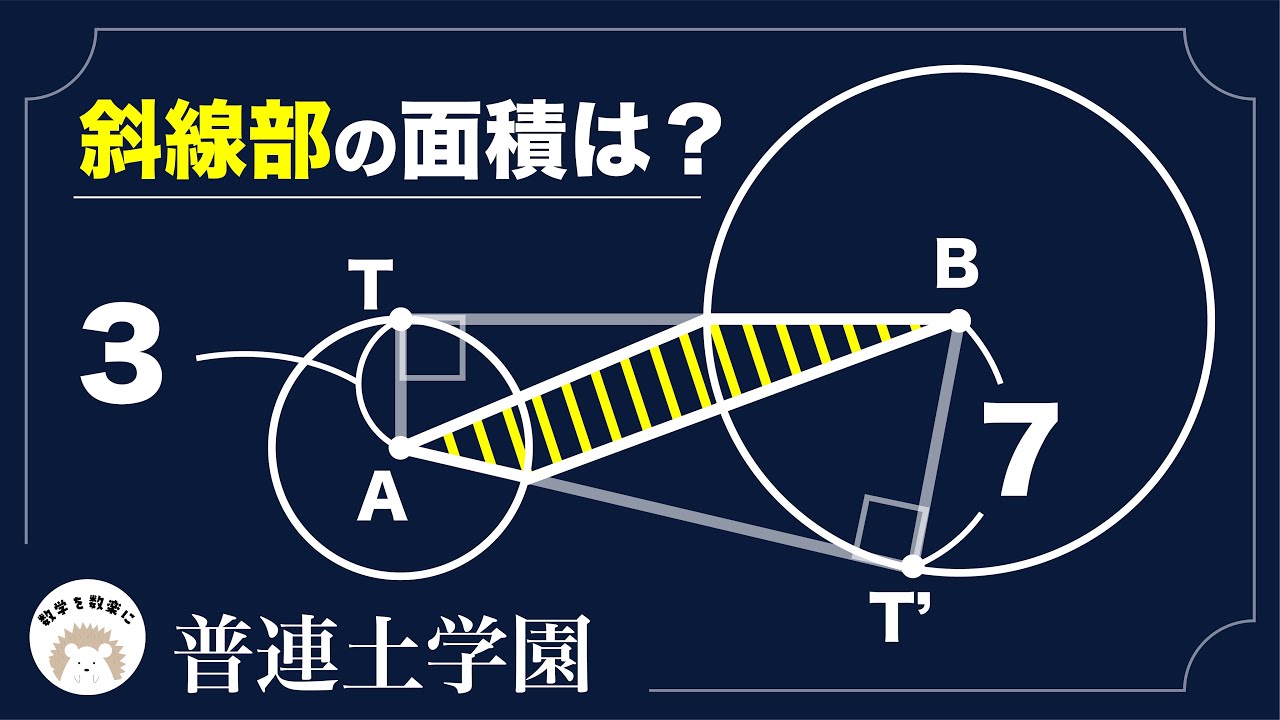
斜線部の面積は?
*図は動画内参照
普連土学園高等学校
この動画を見る
斜線部の面積は?
*図は動画内参照
普連土学園高等学校
【ただ一つ言えることは…】連立方程式:城北高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
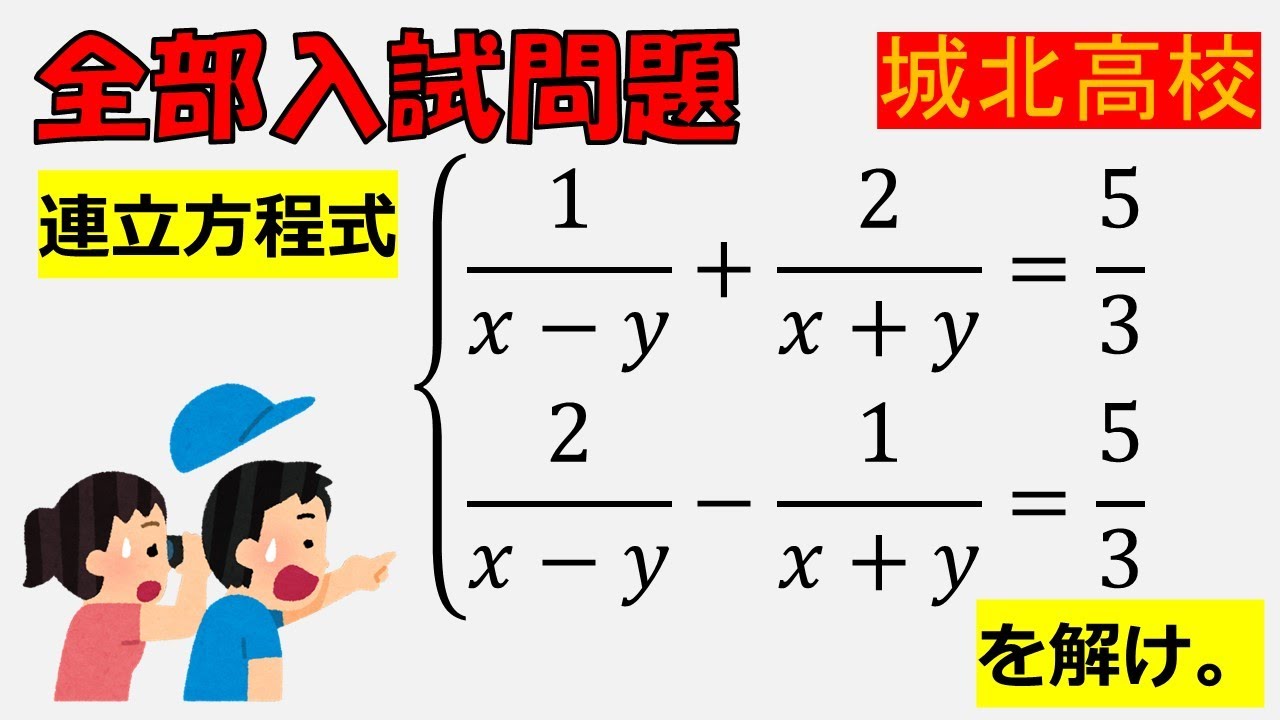
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{1}{x-y}+\dfrac{2}{x+y}=\dfrac{5}{3} \\
\dfrac{2}{x-y}-\dfrac{1}{x+y}=\dfrac{5}{3}
\end{array}
\right.
\end{eqnarray}$
を解け.
城北高校過去問
この動画を見る
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{1}{x-y}+\dfrac{2}{x+y}=\dfrac{5}{3} \\
\dfrac{2}{x-y}-\dfrac{1}{x+y}=\dfrac{5}{3}
\end{array}
\right.
\end{eqnarray}$
を解け.
城北高校過去問
連立方程式だけど、2次式 四天王寺

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式を解け(x>0 , y<0)
$
\begin{eqnarray}
\left\{
\begin{array}{l}
3x^2 + y^2 = 9 \\
2x^2 - 3y^2 = -5
\end{array}
\right.
\end{eqnarray}
$
四天王寺高等学校
この動画を見る
連立方程式を解け(x>0 , y<0)
$
\begin{eqnarray}
\left\{
\begin{array}{l}
3x^2 + y^2 = 9 \\
2x^2 - 3y^2 = -5
\end{array}
\right.
\end{eqnarray}
$
四天王寺高等学校
二次方程式 解一つ 立命館高校

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式$ax^2+2x+b=0$の解がx=2のただ1つであるとき定数a,bの値をそれぞれ求めよ。
立命館高等学校
この動画を見る
2次方程式$ax^2+2x+b=0$の解がx=2のただ1つであるとき定数a,bの値をそれぞれ求めよ。
立命館高等学校
等式の変形 西大和学園

単元:
#数学(中学生)#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
aについて解け
$\frac{1}{a}+\frac{2}{b} = \frac{1}{ca}$
2022西大和学園高等学校
この動画を見る
aについて解け
$\frac{1}{a}+\frac{2}{b} = \frac{1}{ca}$
2022西大和学園高等学校
【その場で「考える力」を身に付ける!】整数:大阪星光学院高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2数$a,b$の最大公約数を$[a\odot b]$と表すと・・・
$[1\odot 2]+[2\odot 3]+[3\odot 4]+・・・+[100\odot 101]=\Box$であり,
$[1\odot 3]+[2\odot 4]+[3\dot 5]+・・・+[99\odot 101]+[100\odot 102]=\box$である.
大阪星光高校過去問
この動画を見る
2数$a,b$の最大公約数を$[a\odot b]$と表すと・・・
$[1\odot 2]+[2\odot 3]+[3\odot 4]+・・・+[100\odot 101]=\Box$であり,
$[1\odot 3]+[2\odot 4]+[3\dot 5]+・・・+[99\odot 101]+[100\odot 102]=\box$である.
大阪星光高校過去問
【この形!どの形?】平方根:渋谷教育学園幕張高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
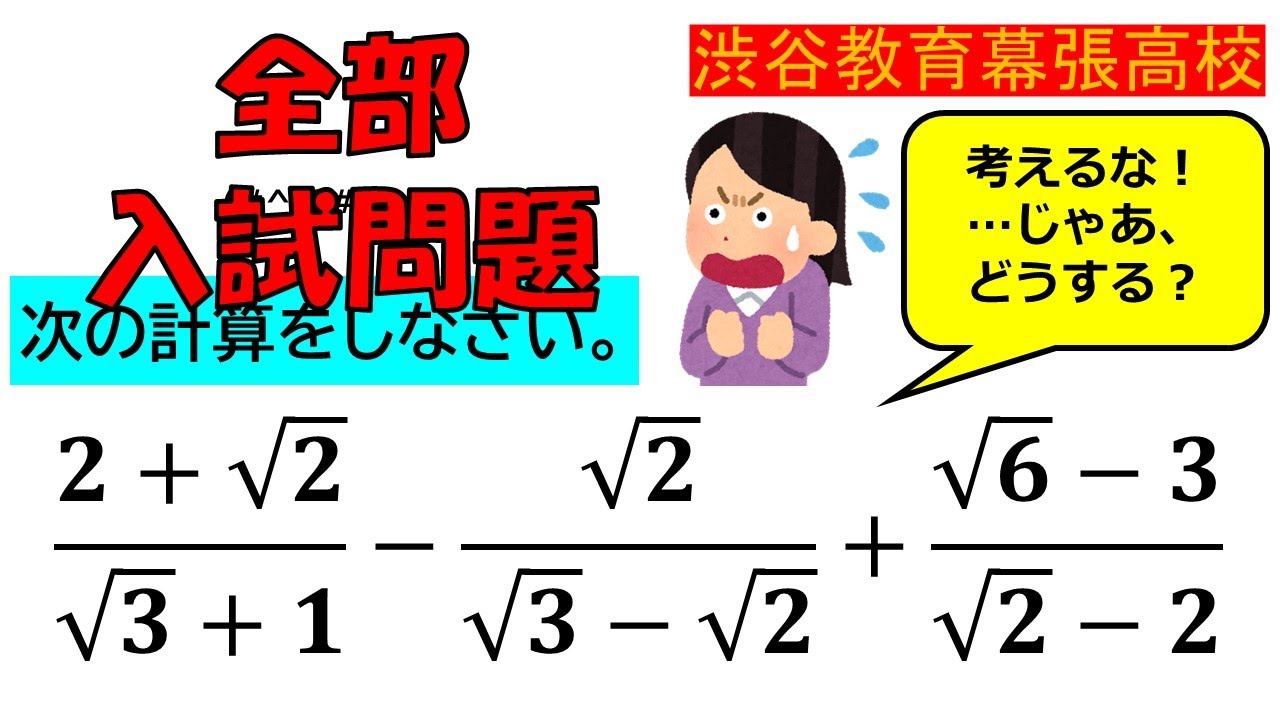
次の計算をしなさい.
$\dfrac{2+\sqrt2}{\sqrt3+1}-\dfrac{\sqrt2}{\sqrt3-\sqrt2}+\dfrac{\sqrt6-3}{\sqrt2-2}$
渋谷教育学園幕張高等学校過去問
この動画を見る
次の計算をしなさい.
$\dfrac{2+\sqrt2}{\sqrt3+1}-\dfrac{\sqrt2}{\sqrt3-\sqrt2}+\dfrac{\sqrt6-3}{\sqrt2-2}$
渋谷教育学園幕張高等学校過去問
和と差の積は二乗の差? 四天王寺

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
二次方程式を解け
$(x-\frac{1}{2})^2 - 3(x+\frac{1}{2})(1-2x) = 0$
四天王寺高等学校
この動画を見る
二次方程式を解け
$(x-\frac{1}{2})^2 - 3(x+\frac{1}{2})(1-2x) = 0$
四天王寺高等学校
【一度は解きたい!典型問題!】図形:埼玉県高等学校~全国入試問題解法
単元:
#数学(中学生)#平面図形#平面図形その他#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
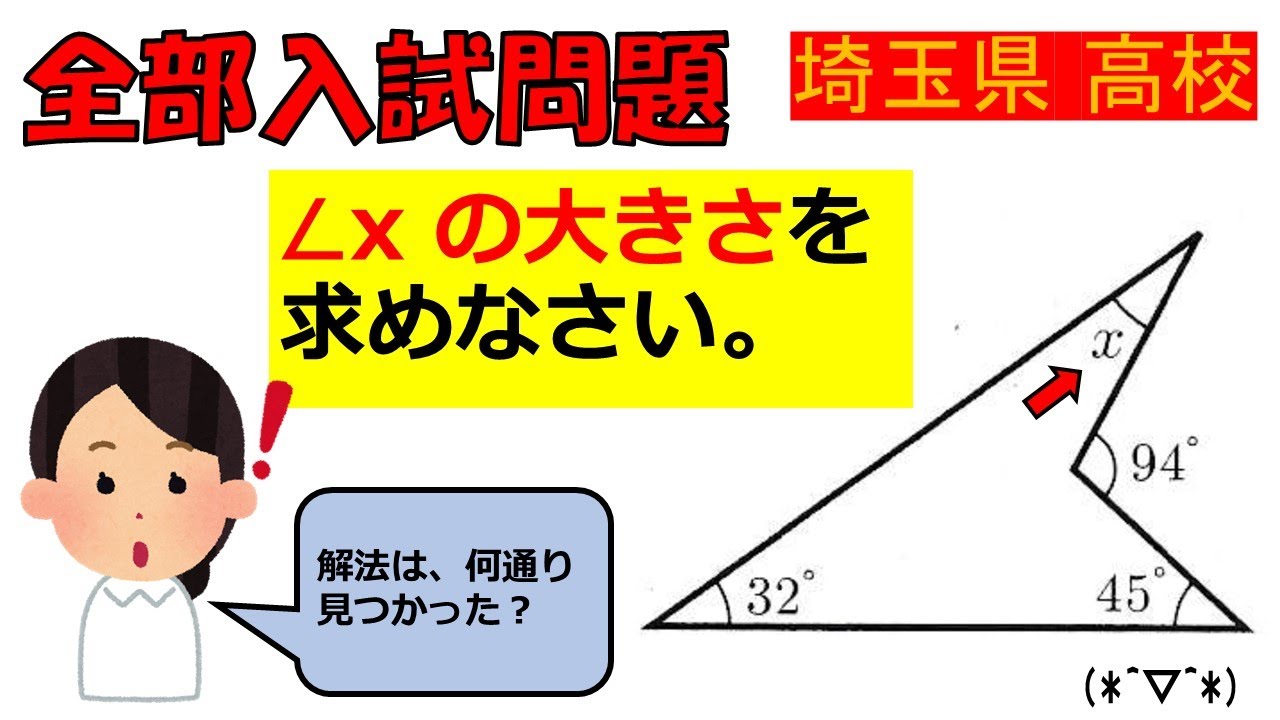
$\angle x$の大きさを求めなさい.
埼玉県高校過去問
この動画を見る
$\angle x$の大きさを求めなさい.
埼玉県高校過去問
斜めの正方形はやること決まっている 土浦日大
【数学】高校入試:2022年度神奈川県立高校入試数学大問6(イ)

単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
AB=5cm,BC=1cm,AD=4m,∠ADC=∠BCD=90°の台形ABCDを底面とし,AE=BF=CG=DH=1cmを高さとする四角柱である。
(イ)この四角柱において,3点B,D,Gを結んでできる三角形の面積として正しいものを答えなさい。
この動画を見る
AB=5cm,BC=1cm,AD=4m,∠ADC=∠BCD=90°の台形ABCDを底面とし,AE=BF=CG=DH=1cmを高さとする四角柱である。
(イ)この四角柱において,3点B,D,Gを結んでできる三角形の面積として正しいものを答えなさい。
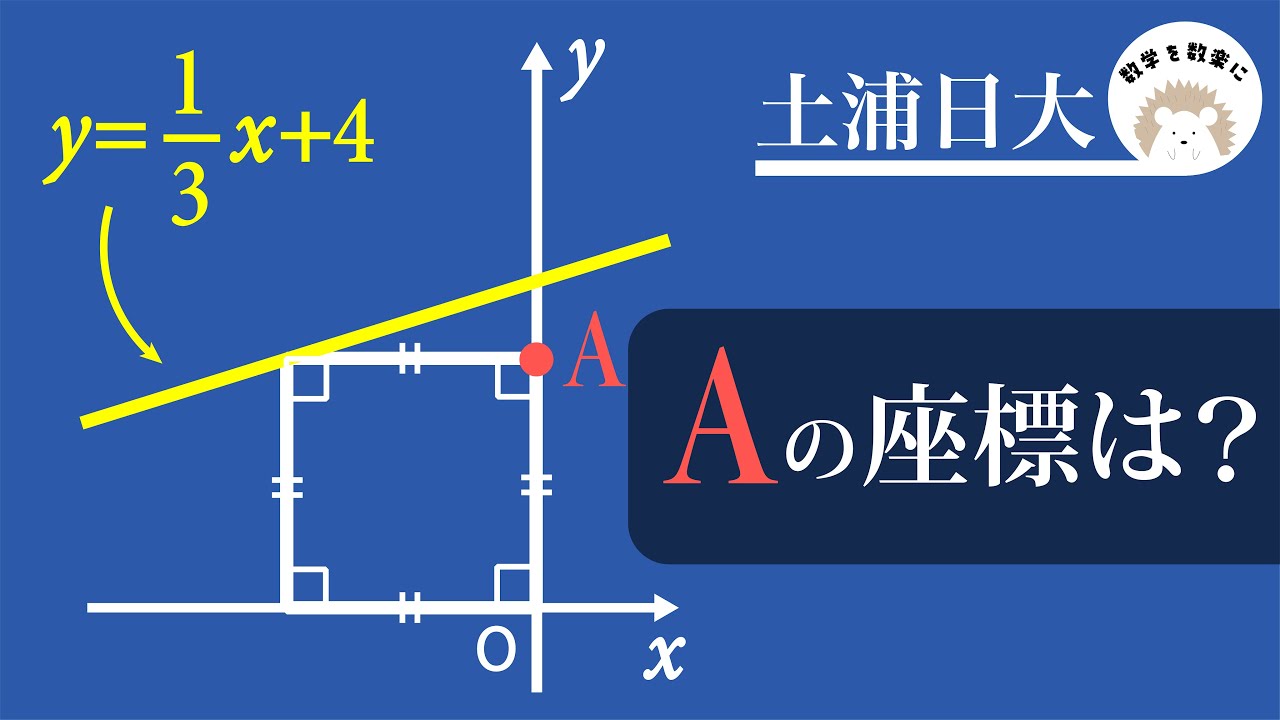
気付け一瞬!!関数嫌いな人、集まれ! 土浦日大
単元:
#数学(中学生)#中1数学#平面図形#図形の移動#平面図形その他#平面図形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
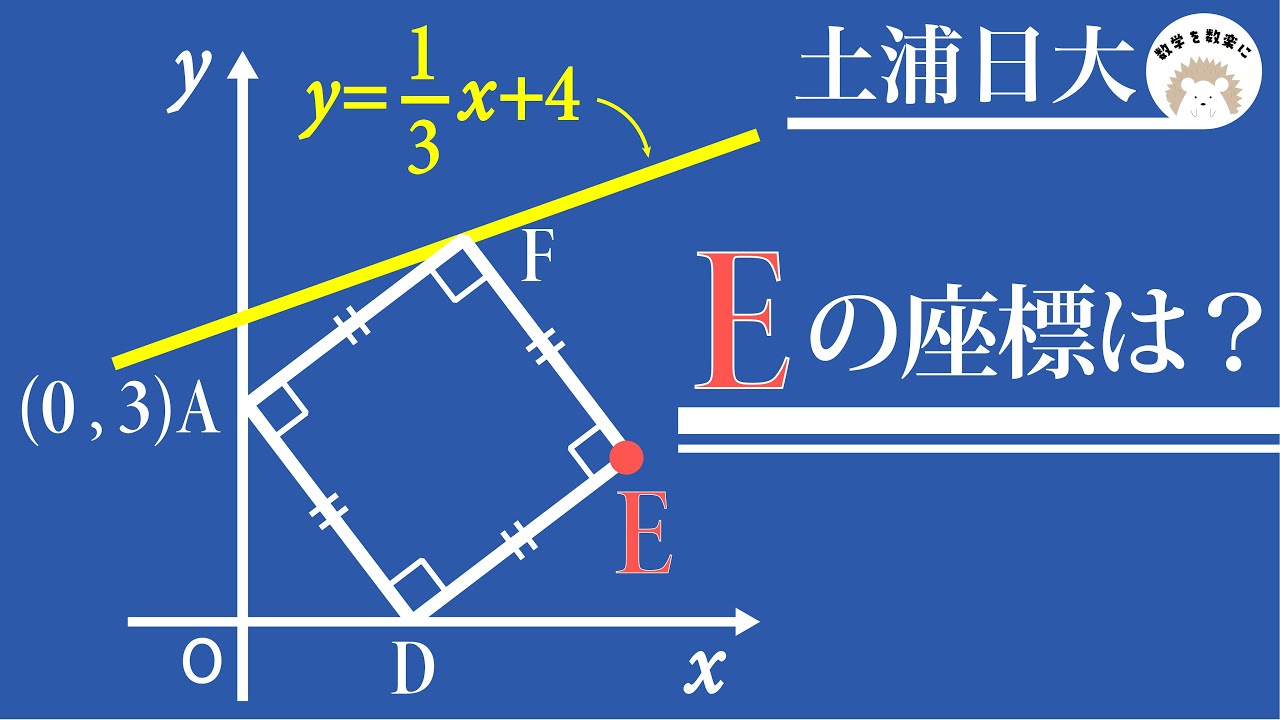
Aの座標は?
*図は動画内参照
土浦日本大学高等学校
この動画を見る
Aの座標は?
*図は動画内参照
土浦日本大学高等学校
【条件を数式に変えよ!】整数:新潟県高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
この2つの自然数の積は,この2つの自然数の和より55大きい.
連続する2つの自然数を求めなさい.
新潟県高校過去問
この動画を見る
この2つの自然数の積は,この2つの自然数の和より55大きい.
連続する2つの自然数を求めなさい.
新潟県高校過去問
【1分30秒で大切なものが見える!】図形:新潟県高等学校~全国入試問題解法
単元:
#数学(中学生)#平面図形#平面図形その他#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
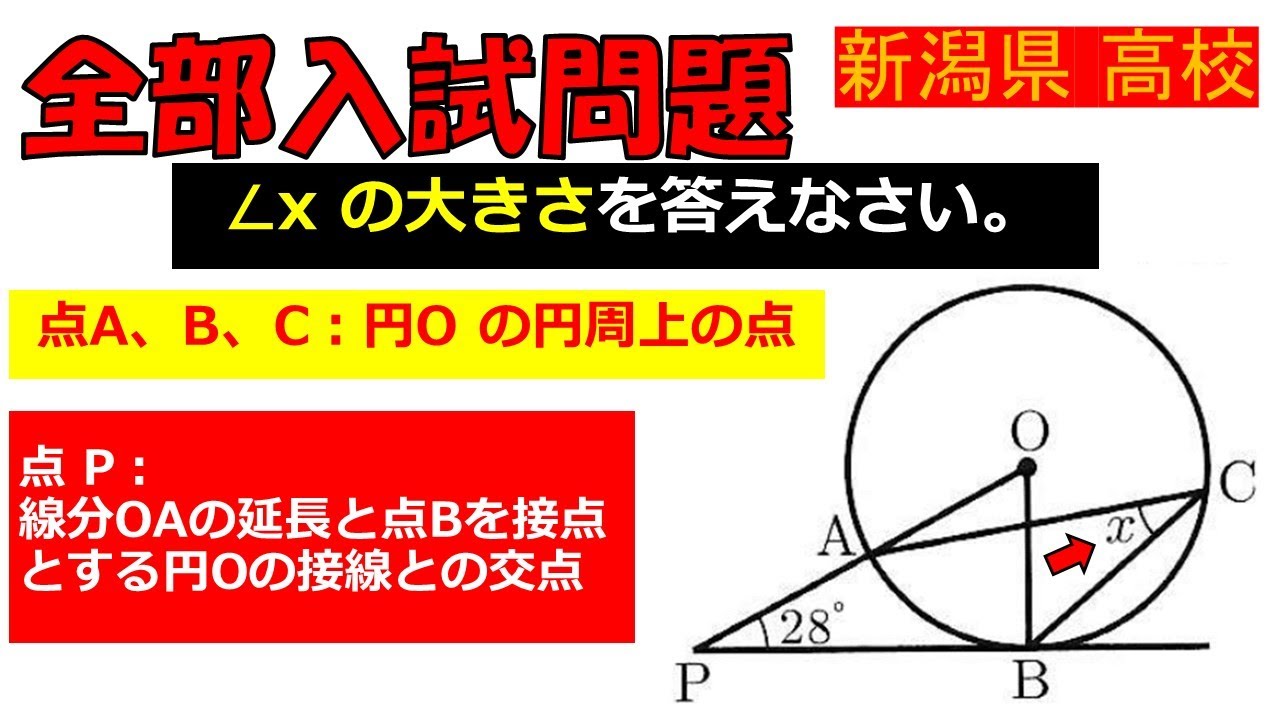
点$A,B,C$は円$O$の円周上の点であり,
点$P$は線分$OA$の延長と点$B$を接点とする円$O$の接線との交点である.
$\angle x$の大きさを求めなさい.
新潟県高校過去問
この動画を見る
点$A,B,C$は円$O$の円周上の点であり,
点$P$は線分$OA$の延長と点$B$を接点とする円$O$の接線との交点である.
$\angle x$の大きさを求めなさい.
新潟県高校過去問
知っていれば、気づけば一瞬!!立命館高校11
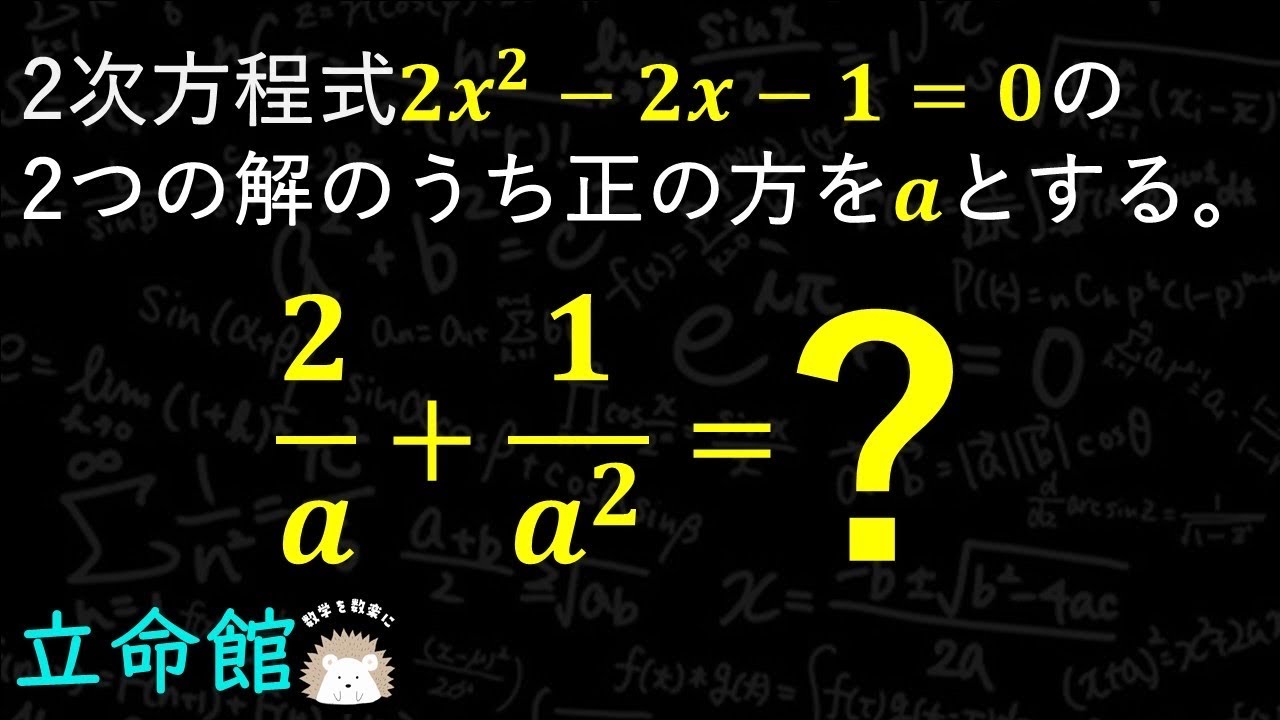
単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式$2x^2-2x-1 = 0$の2つの解のうち正の方をaとする。
$\frac{2}{a}+\frac{1}{a^2}=?$
立命館高等学校
この動画を見る
2次方程式$2x^2-2x-1 = 0$の2つの解のうち正の方をaとする。
$\frac{2}{a}+\frac{1}{a^2}=?$
立命館高等学校
【高校生になると見方が変わる!】二次方程式:東京都立国立高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の二次方程式を解け.
$2\left(x-\dfrac{1}{4}\right)^2-3=x^2+\dfrac{1}{8}$
都立国立高校過去問
この動画を見る
次の二次方程式を解け.
$2\left(x-\dfrac{1}{4}\right)^2-3=x^2+\dfrac{1}{8}$
都立国立高校過去問
【基礎力は身に付いているのか】計算:和洋国府台女子高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の式を計算せよ.
$\left(\dfrac{1}{3}-\dfrac{1}{2}\right)\div \left(-\dfrac{2^2}{5}+\dfrac{1}{2}\right)$
和洋国府台女子高等学校過去問
この動画を見る
次の式を計算せよ.
$\left(\dfrac{1}{3}-\dfrac{1}{2}\right)\div \left(-\dfrac{2^2}{5}+\dfrac{1}{2}\right)$
和洋国府台女子高等学校過去問
因数分解 東大寺学園

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$x^2-4x^2y^2+y^2z^2+2xyz$
東大寺学園高等学校
この動画を見る
因数分解せよ
$x^2-4x^2y^2+y^2z^2+2xyz$
東大寺学園高等学校
整数問題 筑波大附属

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
4ケタの数字3,4,5,6を並べ替えてできる4ケタの数をmとし、mの各位の数を逆順に並べてできる数をnとするとm+nは必ずpの倍数となる。
(ただしpは考えられる最大の整数)
p=?
筑波大学附属高等学校
この動画を見る
4ケタの数字3,4,5,6を並べ替えてできる4ケタの数をmとし、mの各位の数を逆順に並べてできる数をnとするとm+nは必ずpの倍数となる。
(ただしpは考えられる最大の整数)
p=?
筑波大学附属高等学校
【3分で好きになる!】連立方程式:近畿大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 近畿大学附属高等学校
aの値を求めよ。
【連立方程式】
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x + y = 5a-13 \\
3x - 2y = -2a+1
\end{array}
\right.
\end{eqnarray}$
の解は、$y$が$x$の$2$倍になっている。
この動画を見る
入試問題 近畿大学附属高等学校
aの値を求めよ。
【連立方程式】
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x + y = 5a-13 \\
3x - 2y = -2a+1
\end{array}
\right.
\end{eqnarray}$
の解は、$y$が$x$の$2$倍になっている。
気付けば爽快!! 立命館高校 12
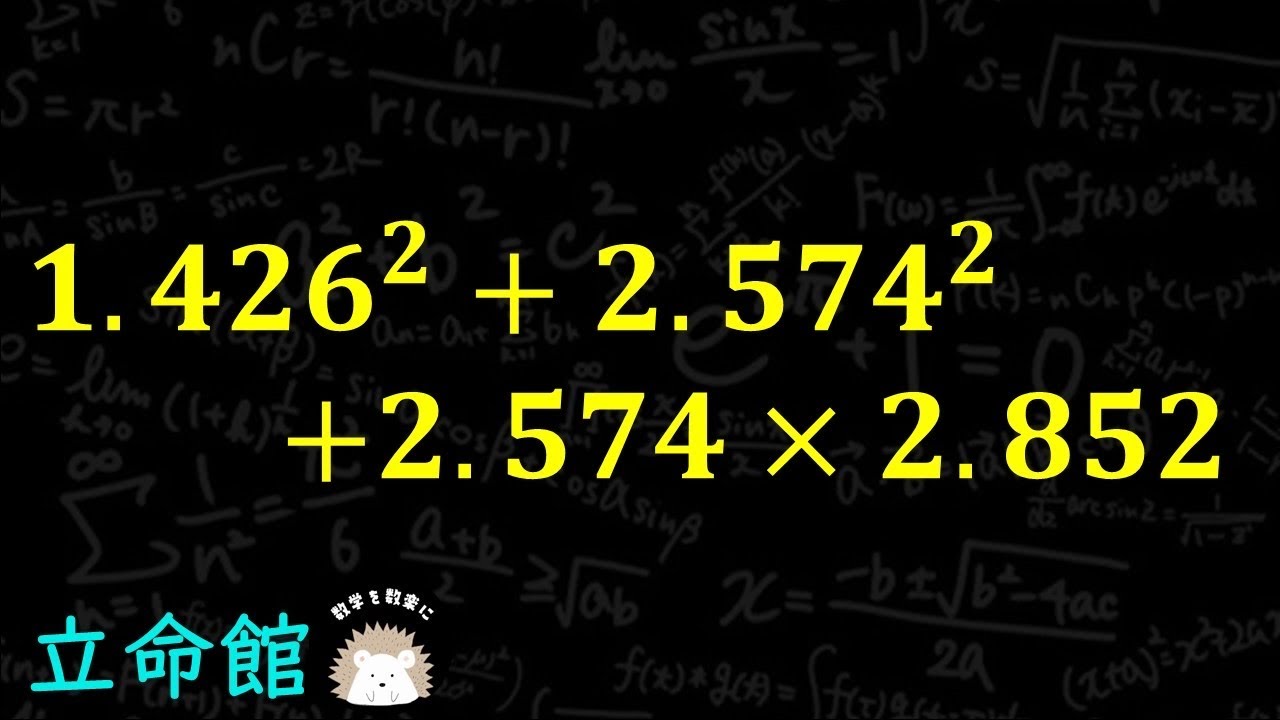
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$1.426^2+2.574^2+2.574 \times 2.852$
立命館高等学校
この動画を見る
$1.426^2+2.574^2+2.574 \times 2.852$
立命館高等学校
【数学】高校入試:2022年度神奈川県立高校入試数学大問6(ア)

単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
AB=5cm,BC=1cm,AD=4m,∠ADC=∠BCD=90°の台形ABCDを底面とし,AE=BF=CG=DH=1cmを高さとする四角柱である。
(ア) この四角柱の体積として正しいものを選びなさい
この動画を見る
AB=5cm,BC=1cm,AD=4m,∠ADC=∠BCD=90°の台形ABCDを底面とし,AE=BF=CG=DH=1cmを高さとする四角柱である。
(ア) この四角柱の体積として正しいものを選びなさい
【3分で理解を深める!】二次方程式:東京都立新宿高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
二次方程式$(x+2)(x-3)=(2x+4)(3x-5)$を解け.
都立新宿高校過去問
この動画を見る
二次方程式$(x+2)(x-3)=(2x+4)(3x-5)$を解け.
都立新宿高校過去問
