 中3数学
中3数学
 中3数学
中3数学
【『盾』印 二重…!】解の公式の使い方:二次方程式(その2)~中学からの二次方程式

単元:
#数学(中学生)#中3数学#2次方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x^2+px-(4+2p)=0 $を公式を使って解け.
この動画を見る
$ x^2+px-(4+2p)=0 $を公式を使って解け.
平方根を含む計算は手際よくこなそう!~全国入試問題解法 #shorts, #高校入試, #頭の体操, #数学,
単元:
#数学(中学生)#中3数学#平方根
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
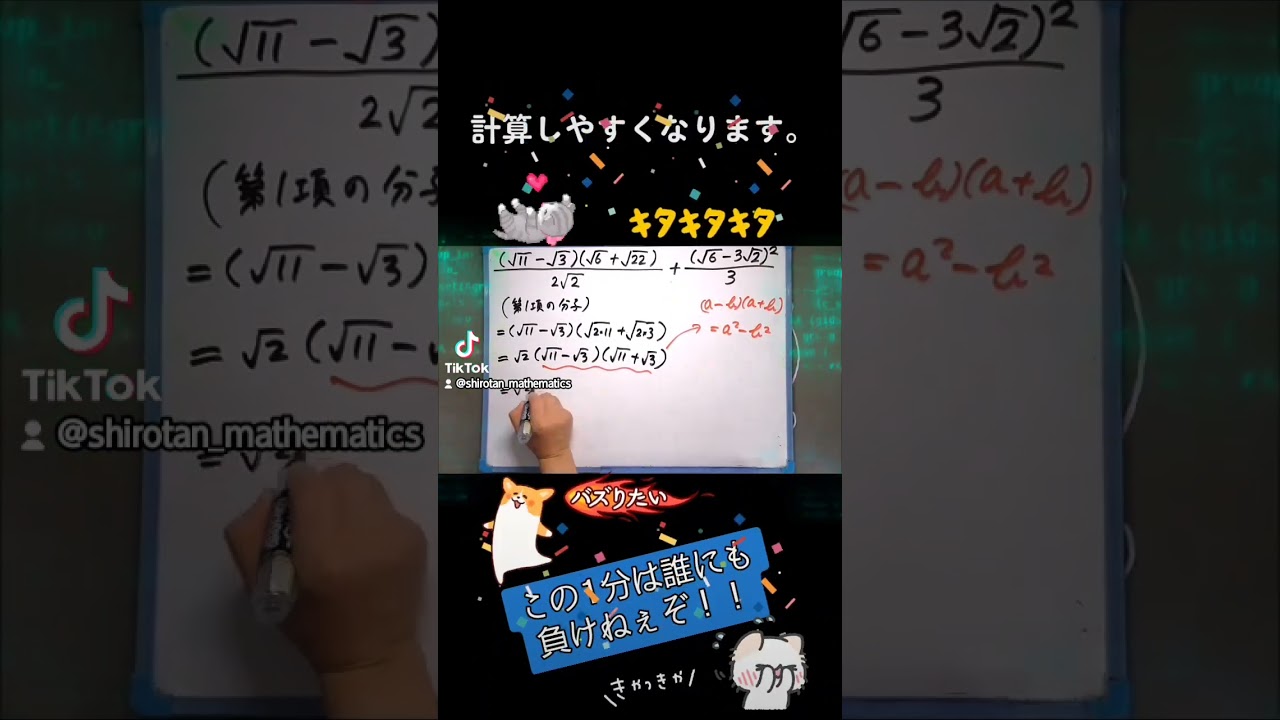
$ \dfrac{(\sqrt{11}-\sqrt3)(\sqrt6+\sqrt{22})}{2\sqrt2}+\dfrac{(\sqrt6-3\sqrt2)^2}{3}$の値を求めよ.
都立立川高校過去問
この動画を見る
$ \dfrac{(\sqrt{11}-\sqrt3)(\sqrt6+\sqrt{22})}{2\sqrt2}+\dfrac{(\sqrt6-3\sqrt2)^2}{3}$の値を求めよ.
都立立川高校過去問
【「勝ち」に必要なら…!】解の公式:二次方程式(その1)~中学からの二次方程式

単元:
#数学(中学生)#中3数学#2次方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x^2+4x-5=0$
解の公式を使って,次の2次方程式を解け.
この動画を見る
$ x^2+4x-5=0$
解の公式を使って,次の2次方程式を解け.
2つの円と正方形
福田のおもしろ数学083〜長方形内の正方形の一辺の長さ
福田のおもしろ数学082〜正方形の面積は
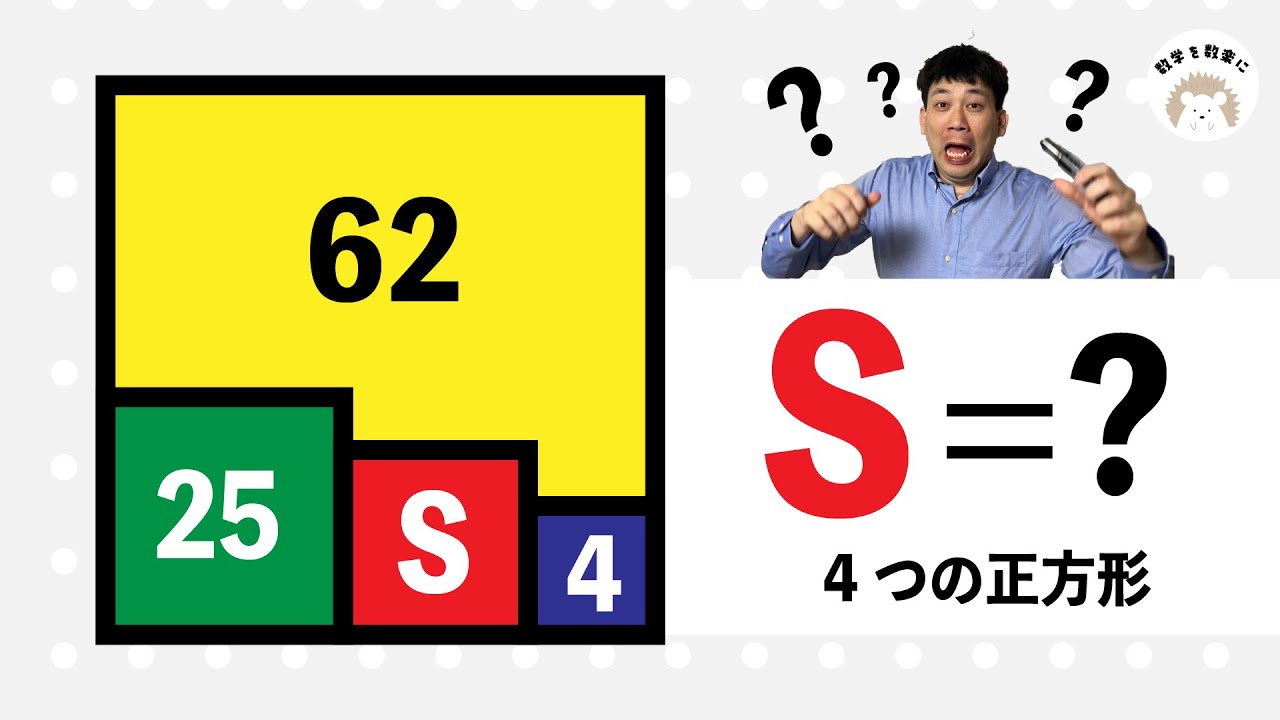
4つの正方形
補助線引けるかな?円の面積=?

平方根と整数の典型問題は大切!~全国入試問題解法 #shorts, #数学, #高校入試, #サウンド, #不等式,

単元:
#数学(中学生)#中3数学#平方根
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \sqrt5 \leqq n \leqq \sqrt{11}$となるような自然数$ n $の値は$ n=\Box $である.
沖縄県入試問題過去問
この動画を見る
$ \sqrt5 \leqq n \leqq \sqrt{11}$となるような自然数$ n $の値は$ n=\Box $である.
沖縄県入試問題過去問
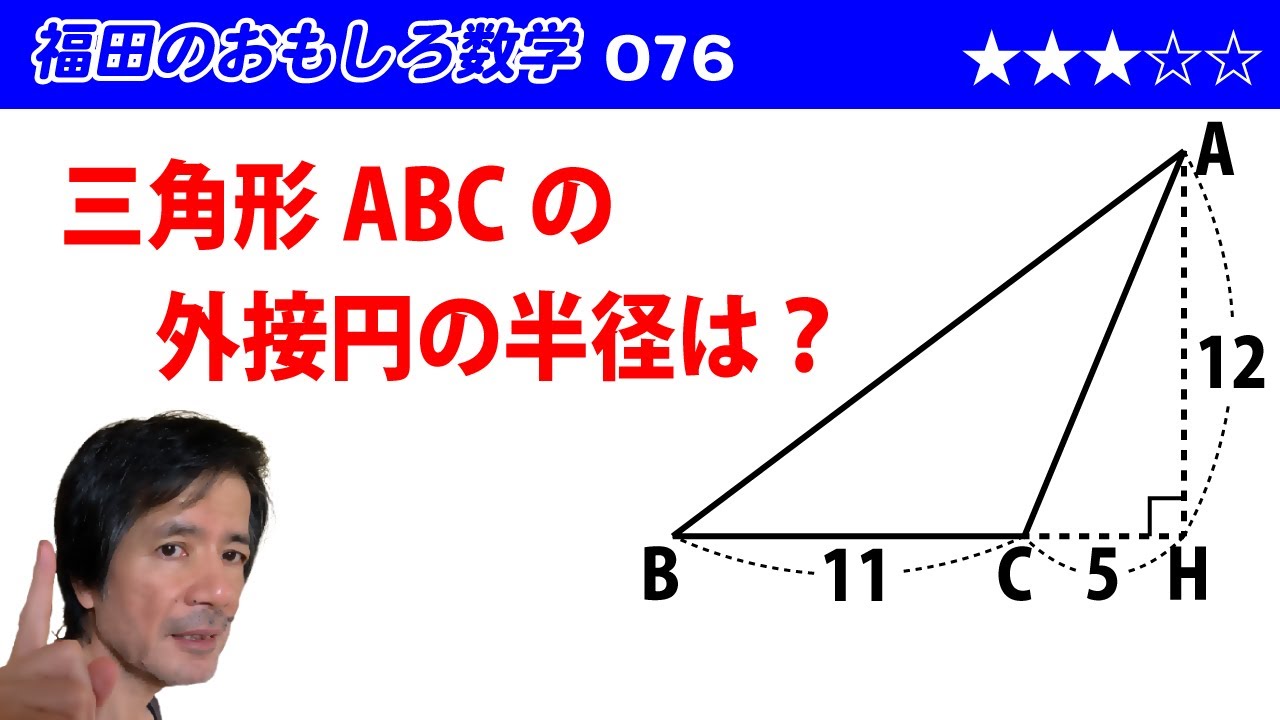
福田のおもしろ数学076〜三角形の外接円の半径は
因数分解は別解が存在する動画~全国入試問題解法 #shorts #数学 #高校入試 #サウンド

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ 3a(a-2b)-(a-2b)-(6b+2)$を因数分解せよ.
ラ・サール高校過去問
この動画を見る
$ 3a(a-2b)-(a-2b)-(6b+2)$を因数分解せよ.
ラ・サール高校過去問
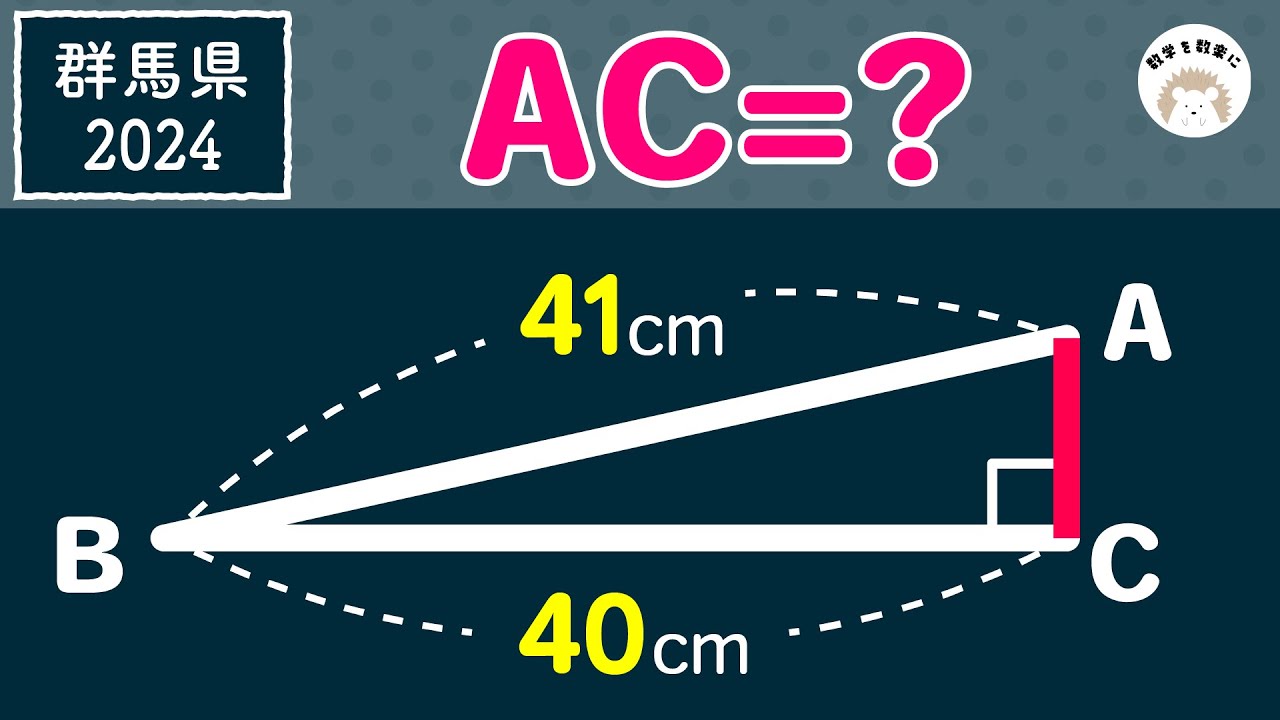
三平方の定理だけど。。。2024群馬県
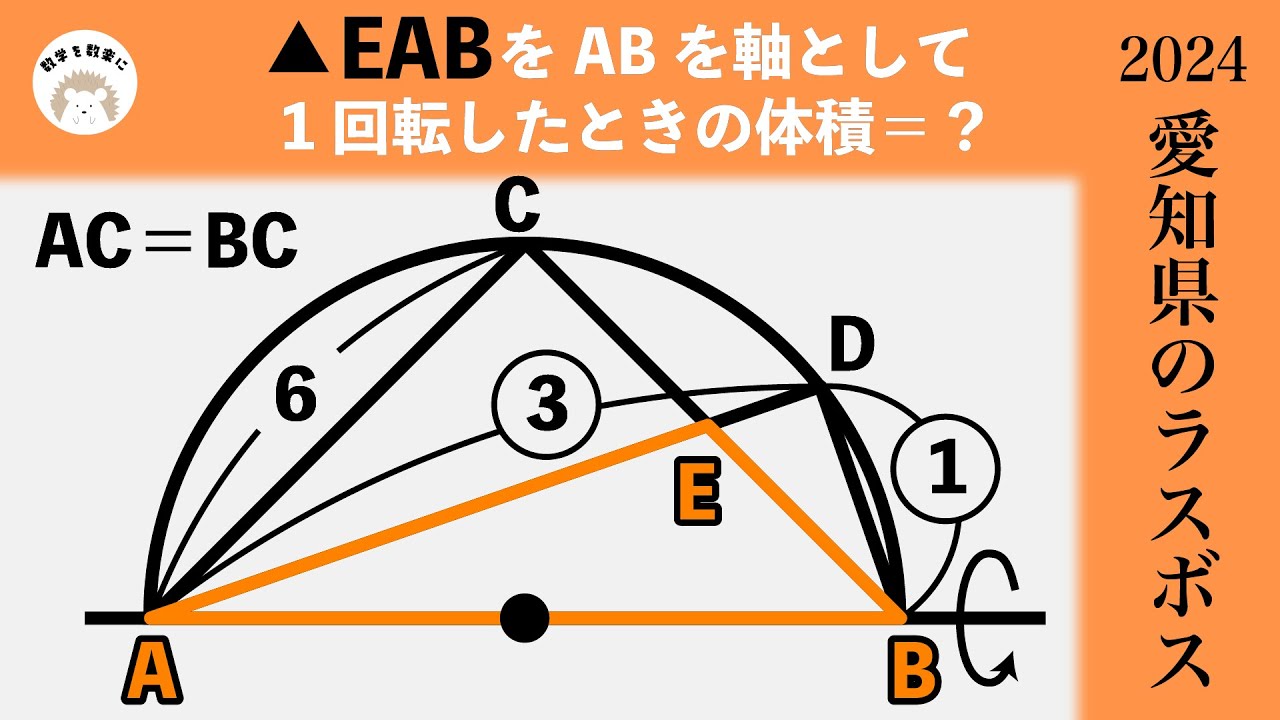
円と回転体 2024愛知県のラスボス
【まず手を付けよう…!】二次方程式:法政大学第二高等学校~全国入試問題解法

単元:
#中3数学#2次方程式#高校入試過去問(数学)#法政大学第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2次方程式$ (x+2)^2+x^2=(x+4)^2-12 $を解きなさい.
法政大学第二高等学校過去問
この動画を見る
2次方程式$ (x+2)^2+x^2=(x+4)^2-12 $を解きなさい.
法政大学第二高等学校過去問
【な、長い…!】平方根:洛南高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#洛南高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ (1+\sqrt2+\sqrt4+\sqrt8+\sqrt{16}+\sqrt{32})$
$ \times (1-\sqrt2+\sqrt4-\sqrt8+\sqrt{16}-\sqrt{32}$
を計算しなさい.
洛南高等学校過去問
この動画を見る
$ (1+\sqrt2+\sqrt4+\sqrt8+\sqrt{16}+\sqrt{32})$
$ \times (1-\sqrt2+\sqrt4-\sqrt8+\sqrt{16}-\sqrt{32}$
を計算しなさい.
洛南高等学校過去問
平方根を含む応用問題~全国入試問題解法 #shorts #高校入試 #数学 #頭の体操 #サウンド

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \sqrt{65}-5 $の整数部分を$ n $とし,小数部分を$ t $とする.
(1)$ n $はいくつか?
(2)$ \dfrac{1}{4}t^2+4t=\Box $である.
東海高校過去問
この動画を見る
$ \sqrt{65}-5 $の整数部分を$ n $とし,小数部分を$ t $とする.
(1)$ n $はいくつか?
(2)$ \dfrac{1}{4}t^2+4t=\Box $である.
東海高校過去問
この問題一瞬で解ける?
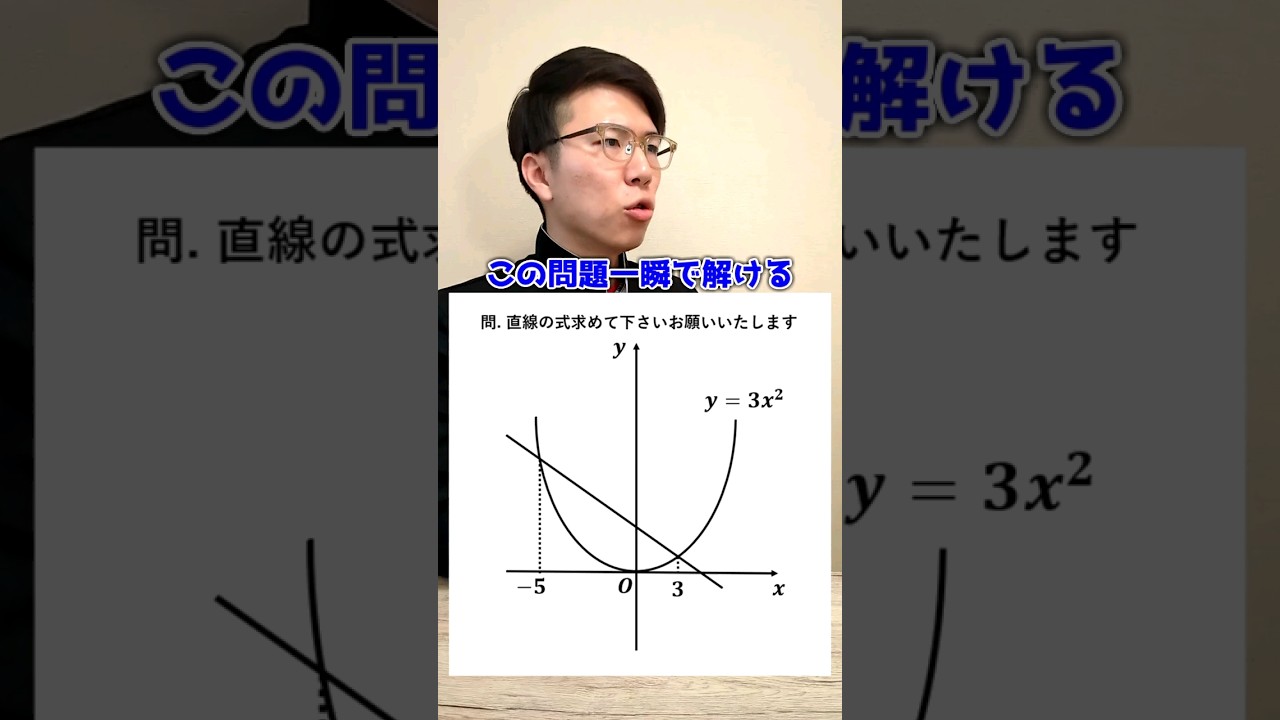
この問題一瞬で解ける?

【次の一手を読め…!】文字式:東海高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#平方根#高校入試過去問(数学)#東海高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ a=2(\sqrt{13}-2)$の$ b $は整数部分であり,$ c $は小数部分である.
このとき,$ (a+3b+1)(c+1)$の値は$ \Box $である.
東海高等学校過去問
この動画を見る
$ a=2(\sqrt{13}-2)$の$ b $は整数部分であり,$ c $は小数部分である.
このとき,$ (a+3b+1)(c+1)$の値は$ \Box $である.
東海高等学校過去問
【イメージできるか…!】法政大学第二高等学校:二次関数~全国入試問題解法
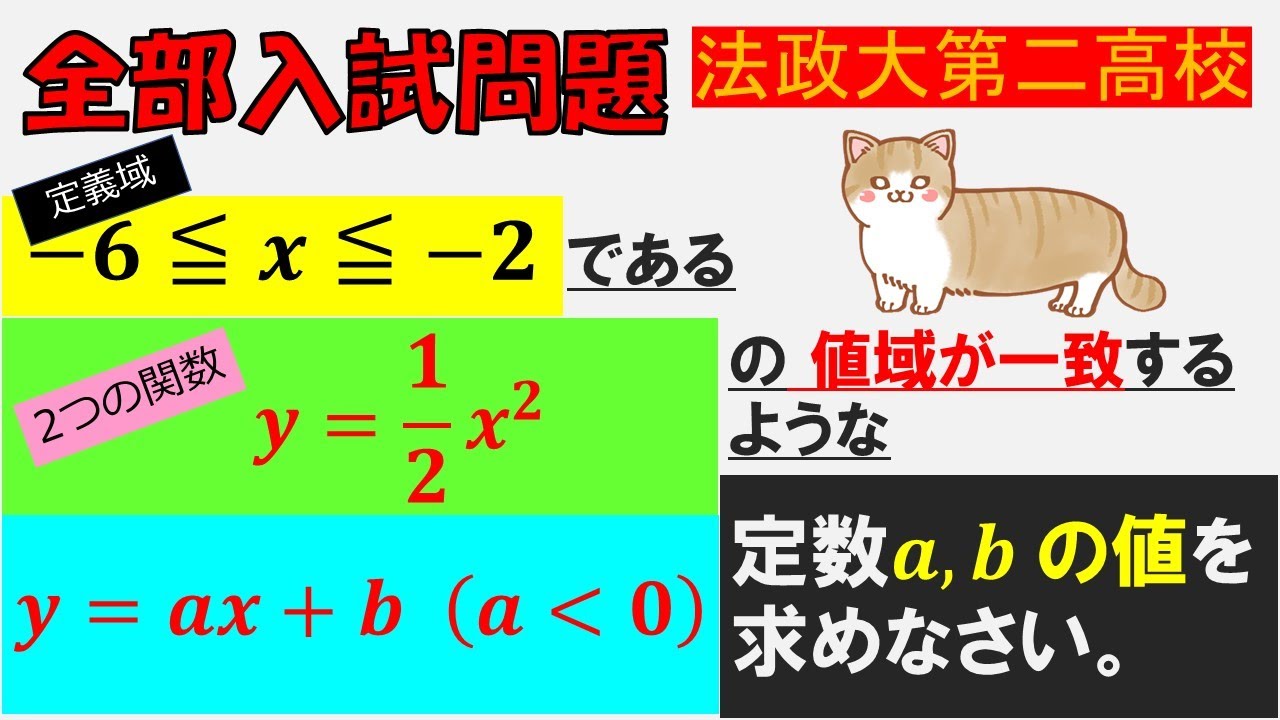
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#法政大学第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
定義域$ -6 \leqq x \leqq -2 $である2つの関数
$ y=\dfrac{1}{2}x^2, y=ax+b(a \lt 0)$の値域が一致するような
定数$ a,b $の値を求めなさい.
法政大第二高校過去問
この動画を見る
定義域$ -6 \leqq x \leqq -2 $である2つの関数
$ y=\dfrac{1}{2}x^2, y=ax+b(a \lt 0)$の値域が一致するような
定数$ a,b $の値を求めなさい.
法政大第二高校過去問
正八角形と円

【理解すれば一瞬…!】方程式:法政大学国際高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#法政大学国際高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x(x+1)(2x+1)=0 $を満たす$ x $の値をすべて求めよ.
法政大国際高校過去問
この動画を見る
$ x(x+1)(2x+1)=0 $を満たす$ x $の値をすべて求めよ.
法政大国際高校過去問
福田のおもしろ数学043〜1分で求まったら天才〜四角形の面積
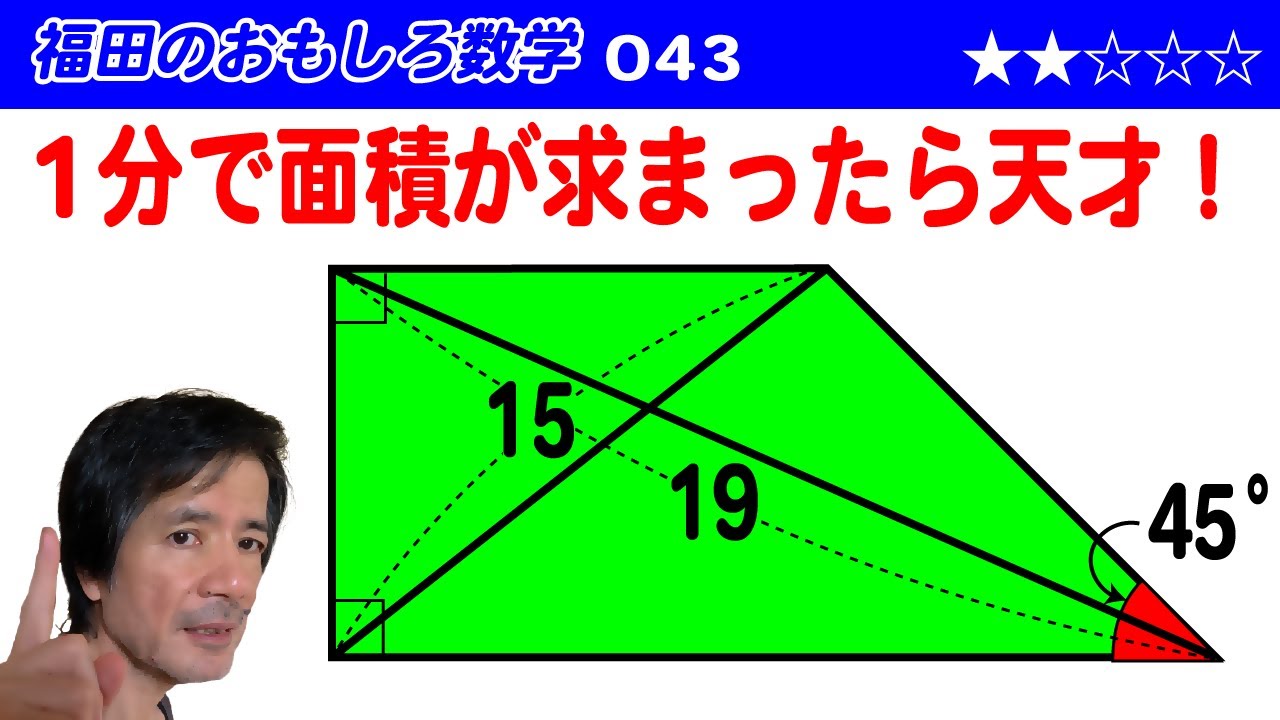
単元:
#算数(中学受験)#数学(中学生)#中2数学#中3数学#三平方の定理#平面図形#角度と面積#三角形と四角形
指導講師:
福田次郎
問題文全文(内容文):
$AC=19,BD=15,\angle A=\angle B=90°,\angle C=45°$の四角形$ABCD$の面積を求めよ.
この動画を見る
$AC=19,BD=15,\angle A=\angle B=90°,\angle C=45°$の四角形$ABCD$の面積を求めよ.
【ミスしやすい構造とは…!】二次方程式:東京都立八王子東高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#東京都立八王子東高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2次方程式$ 3(3-x)=2(x-2)^2$を解け.
都立八王子東高校過去問
この動画を見る
2次方程式$ 3(3-x)=2(x-2)^2$を解け.
都立八王子東高校過去問
大切な因数分解の応用!~全国入試問題解法 #shorts #数学 #高校受験 #頭の体操 #サウンド
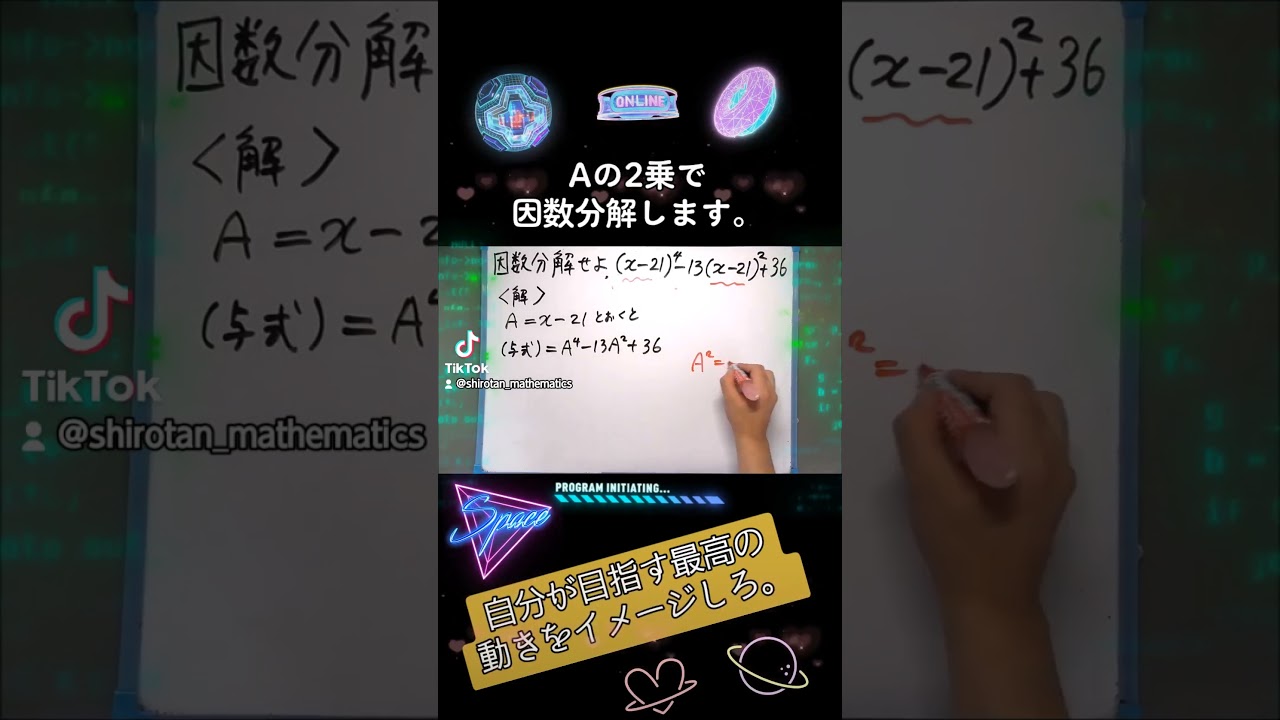
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の式を因数分解せよ.
$ (x-21)^2-13(x-21)^2+36 $
開成高校過去問
この動画を見る
次の式を因数分解せよ.
$ (x-21)^2-13(x-21)^2+36 $
開成高校過去問
さすがに知ってる?

【高校入試で4次の項…!?】文字式:ラ・サール高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#平方根#高校入試過去問(数学)#ラ・サール高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x=\sqrt7+\sqrt2 $
$ y=\sqrt7-\sqrt2 $ のとき
$ x^4-6x^2y^2+y^4 $の値を求めよ.
ラ・サール高校過去問
この動画を見る
$ x=\sqrt7+\sqrt2 $
$ y=\sqrt7-\sqrt2 $ のとき
$ x^4-6x^2y^2+y^4 $の値を求めよ.
ラ・サール高校過去問
【スマートに行こう…!】因数分解:立命館高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#立命館高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ (2x+3y)^2-3(x-3y)\times (x+3y)-4y^2 $
を因数分解しなさい.
立命館高校過去問
この動画を見る
$ (2x+3y)^2-3(x-3y)\times (x+3y)-4y^2 $
を因数分解しなさい.
立命館高校過去問
福田のおもしろ数学034〜各面が合同な三角形でできた四面体の体積〜等面四面体
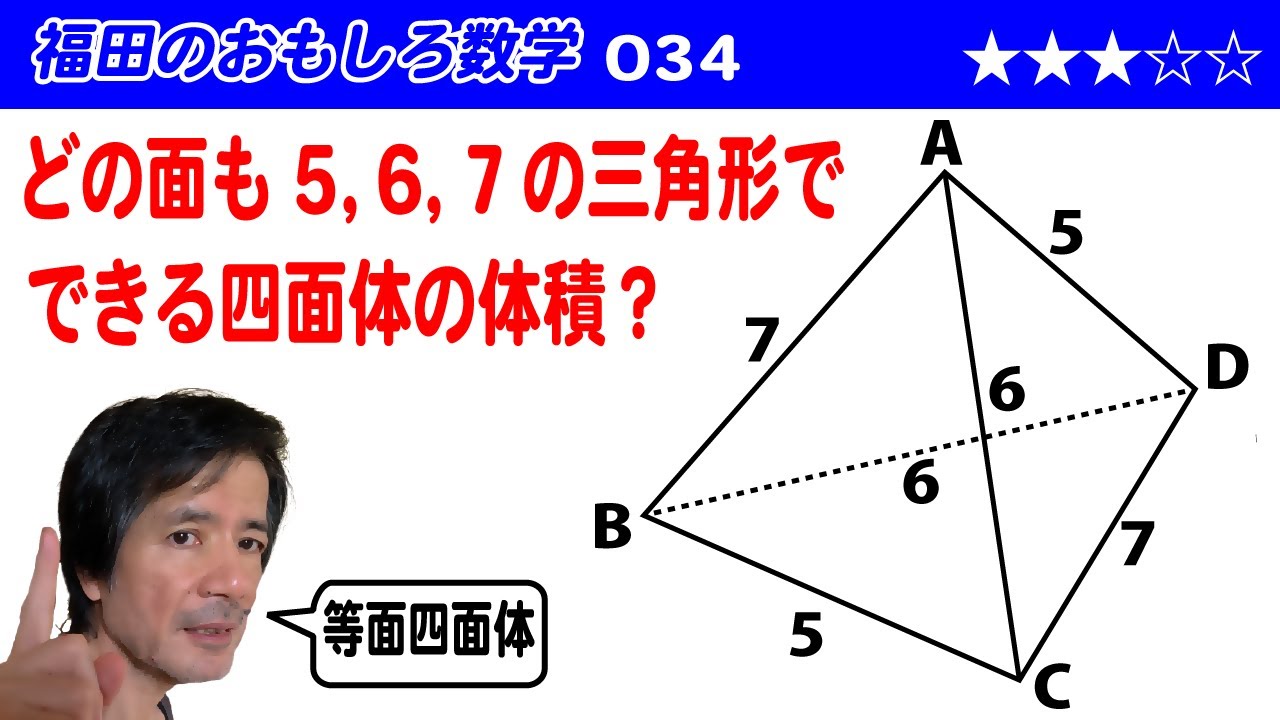
単元:
#数学(中学生)#中3数学#数A#図形の性質#三平方の定理#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
どの面も、5,6,7の長さの三角形でできている四面体の体積を求めよ
この動画を見る
どの面も、5,6,7の長さの三角形でできている四面体の体積を求めよ
この問題一瞬で解ける?

