数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
連立方程式は知ってるカタチに直せ…!~全国入試問題解法 #shorts, #数学, #高校入試, #頭の体操, #連立方程式,
単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
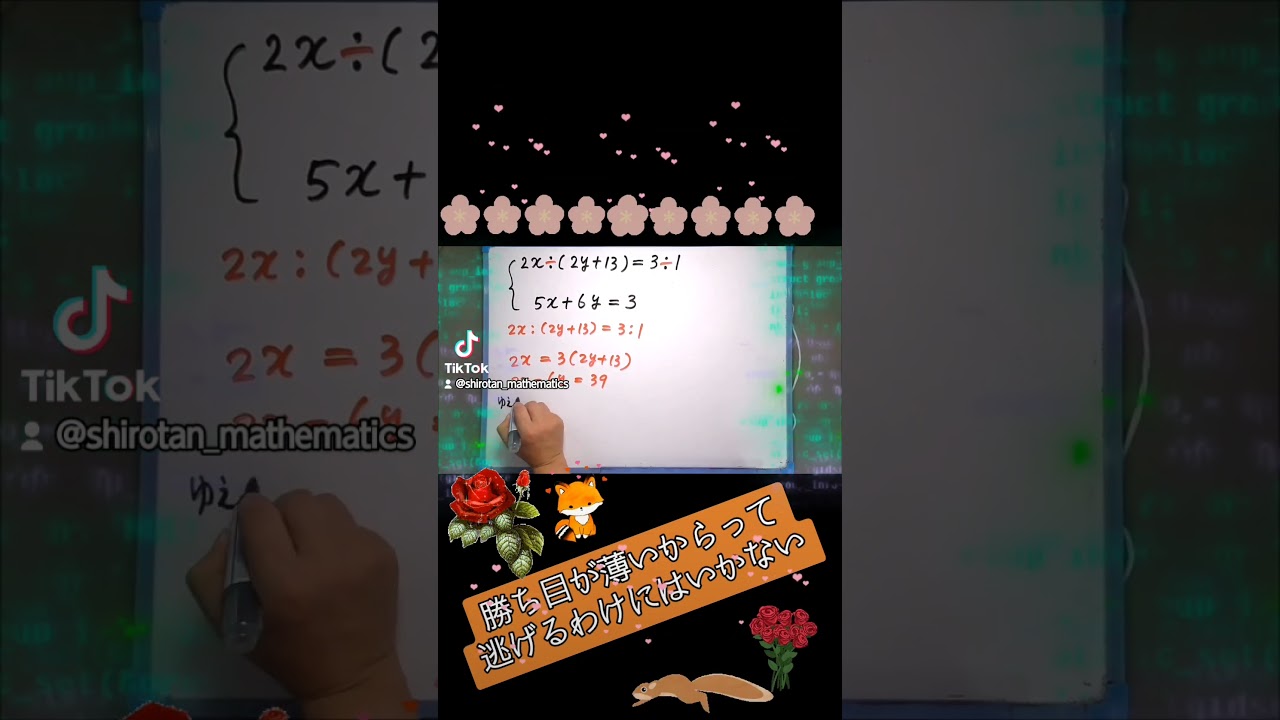
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x\div(2y+13)=3:1 \\
5x+6y=3
\end{array}
\right.
\end{eqnarray}$
次の連立方程式を解きなさい.
広大付属高校過去問
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x\div(2y+13)=3:1 \\
5x+6y=3
\end{array}
\right.
\end{eqnarray}$
次の連立方程式を解きなさい.
広大付属高校過去問
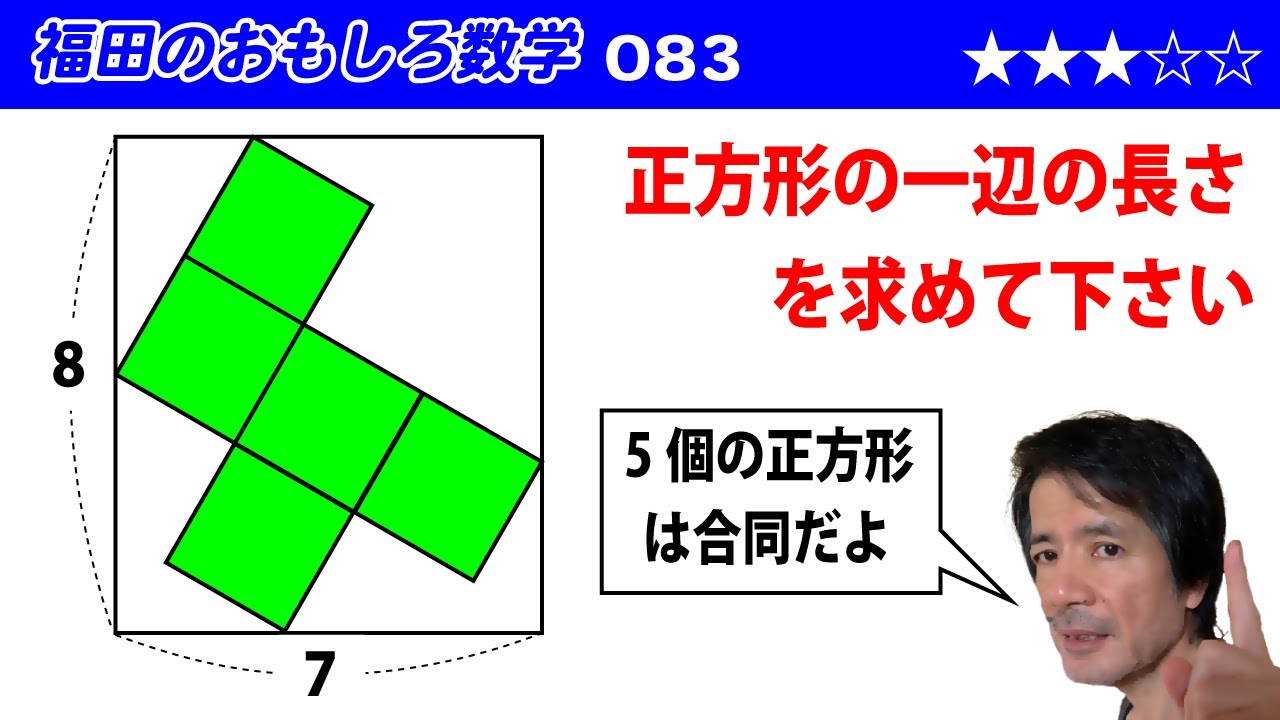
福田のおもしろ数学083〜長方形内の正方形の一辺の長さ
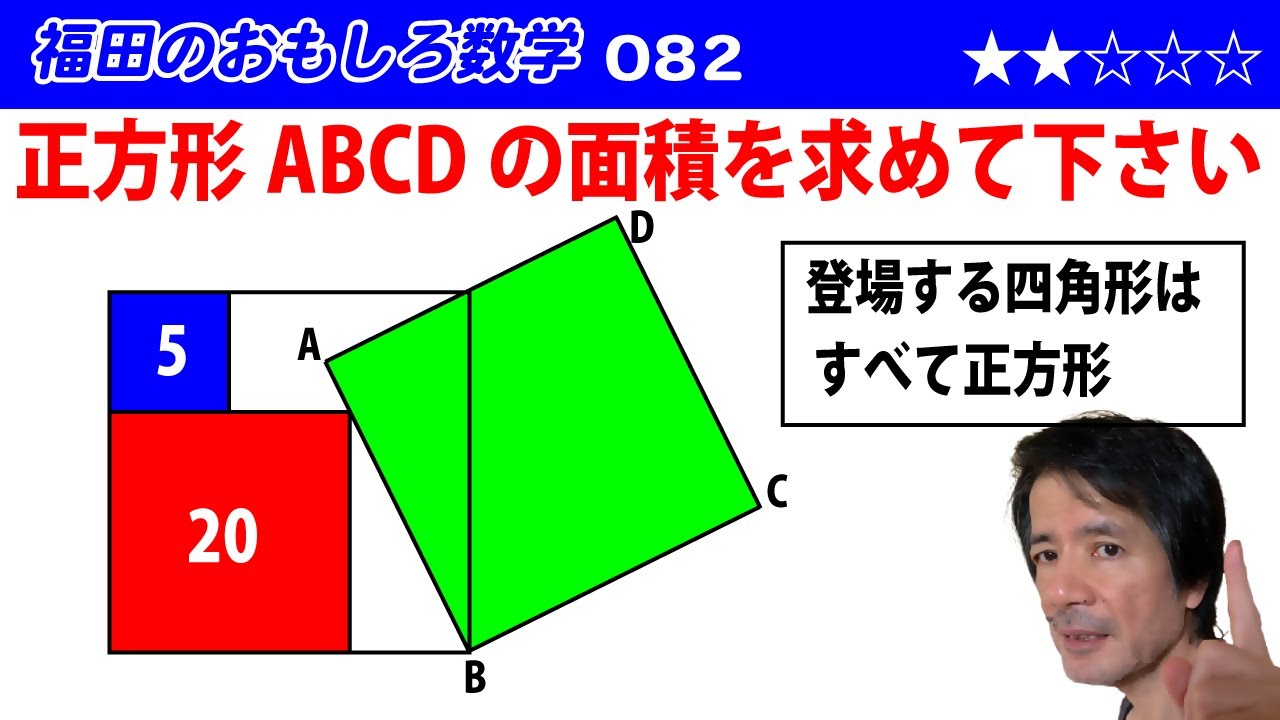
福田のおもしろ数学082〜正方形の面積は
【スッキリするには…!】文字式:江戸川学園取手高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#江戸川学園取手高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ A=x^2+x+1 $
$ B=x^2-x-1 $
$ C=x^3-1 $ のとき,$ 2A-{A-(2B-C)}-(B-C)$を計算しなさい.
江戸川取手高校過去問
この動画を見る
$ A=x^2+x+1 $
$ B=x^2-x-1 $
$ C=x^3-1 $ のとき,$ 2A-{A-(2B-C)}-(B-C)$を計算しなさい.
江戸川取手高校過去問
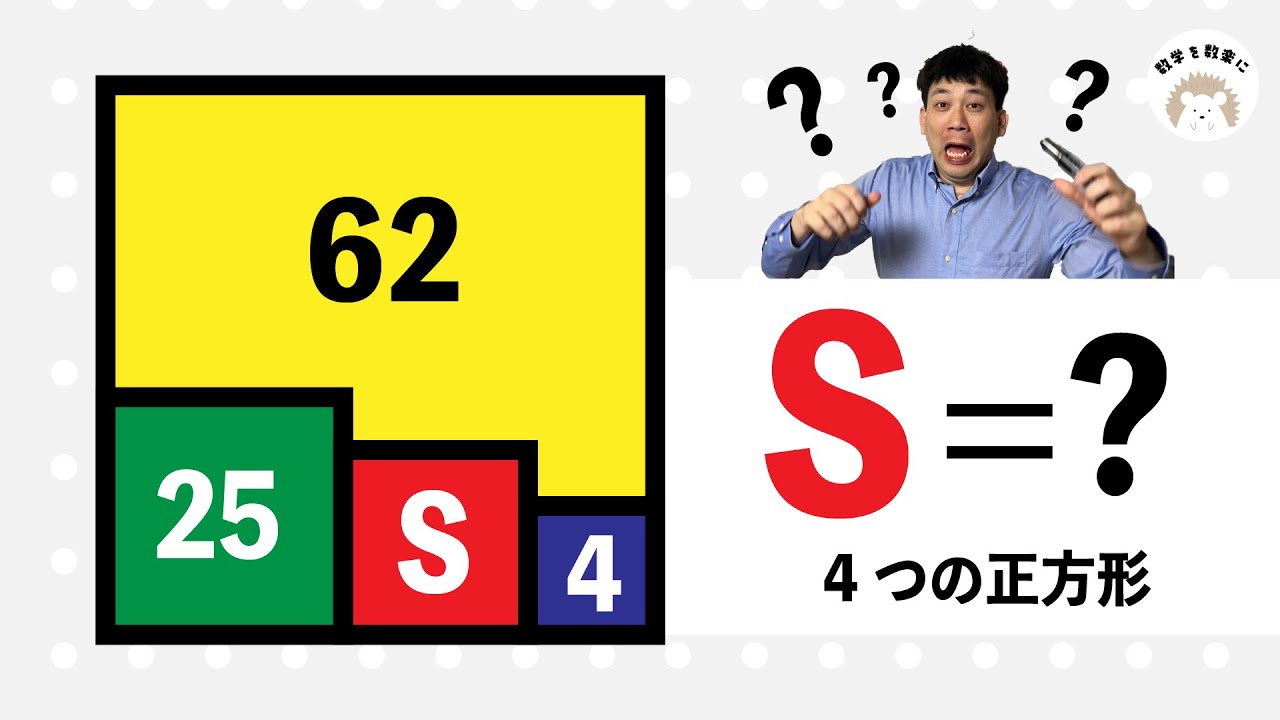
4つの正方形
🍭【峠を越えれば…!】整数:慶応義塾高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ 7^{123}$を$100$で割ると,余りは$ \Box $である.
次の空欄をうめよ.
慶應義塾高校過去問
この動画を見る
$ 7^{123}$を$100$で割ると,余りは$ \Box $である.
次の空欄をうめよ.
慶應義塾高校過去問
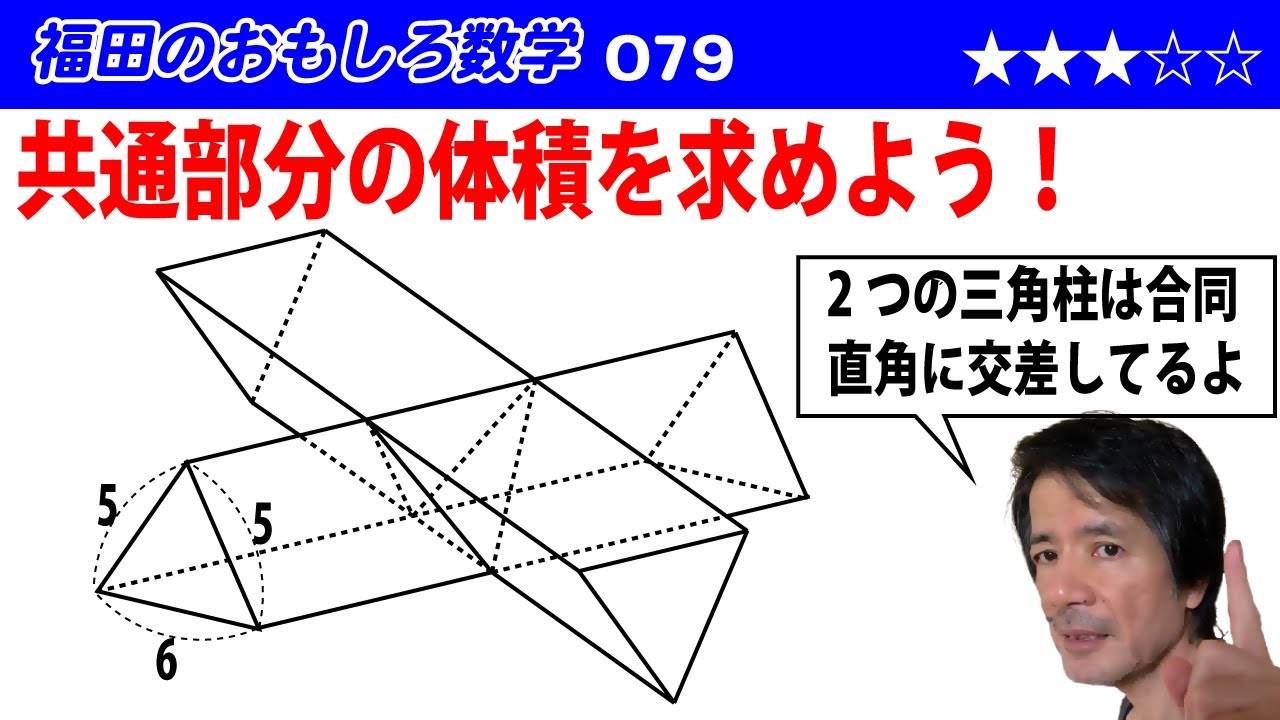
福田のおもしろ数学079〜交差する三角柱の共通部分の体積
補助線引けるかな?円の面積=?

【信じて進め…!】連立方程式:関西学院高等部~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#関西学院高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{4}x+0.3y=3 \\
0.7x+\dfrac{2}{7}y=1
\end{array}
\right.
\end{eqnarray}$
次の連立方程式を解け.
関西学院高等学校過去問
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{4}x+0.3y=3 \\
0.7x+\dfrac{2}{7}y=1
\end{array}
\right.
\end{eqnarray}$
次の連立方程式を解け.
関西学院高等学校過去問
平方根と整数の典型問題は大切!~全国入試問題解法 #shorts, #数学, #高校入試, #サウンド, #不等式,

単元:
#数学(中学生)#中3数学#平方根
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \sqrt5 \leqq n \leqq \sqrt{11}$となるような自然数$ n $の値は$ n=\Box $である.
沖縄県入試問題過去問
この動画を見る
$ \sqrt5 \leqq n \leqq \sqrt{11}$となるような自然数$ n $の値は$ n=\Box $である.
沖縄県入試問題過去問
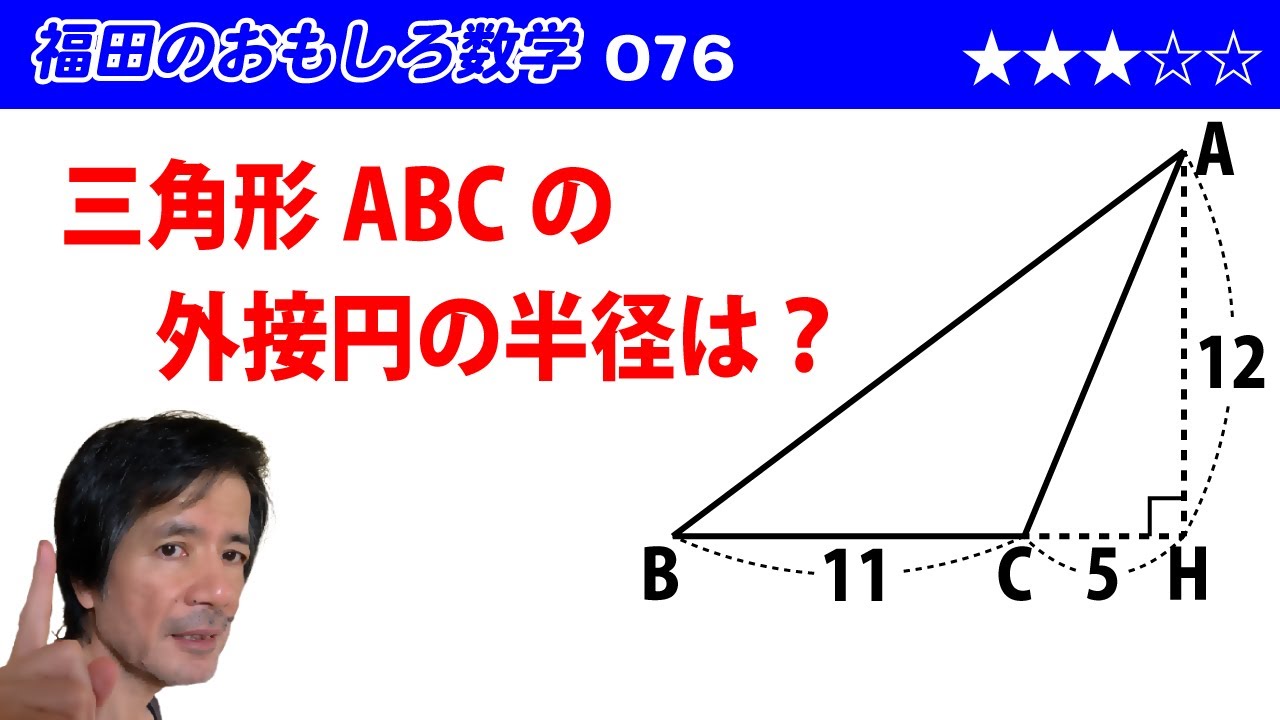
福田のおもしろ数学076〜三角形の外接円の半径は
福田のおもしろ数学075〜1分チャレンジ〜扇形から作る円錐の体積

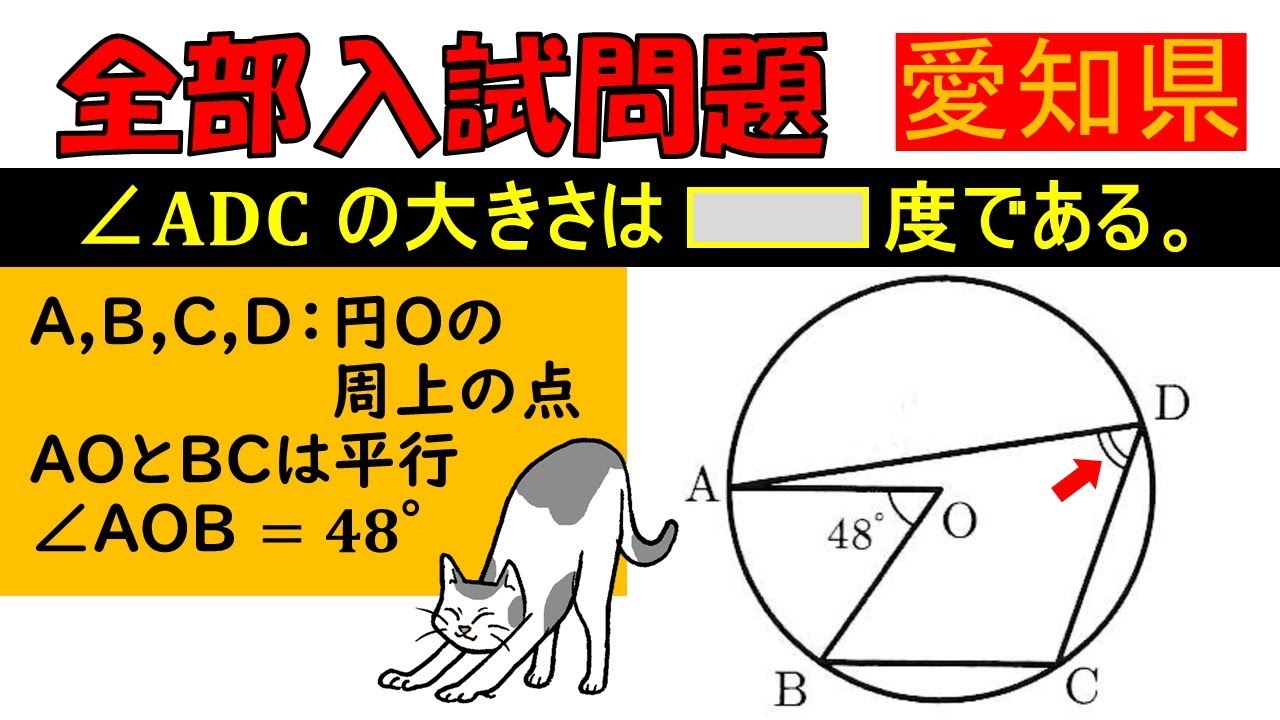
【条件をよく見て…!】図形:愛知県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#愛知県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ A,B,C,D$は円$O$の周上の点である.
$ AO $と$ BC $は平行であり, $ \angle AOB=48°$である.
$ \angle ADC $の大きさは$ \Box $度である.
愛知県入試問題過去問
この動画を見る
$ A,B,C,D$は円$O$の周上の点である.
$ AO $と$ BC $は平行であり, $ \angle AOB=48°$である.
$ \angle ADC $の大きさは$ \Box $度である.
愛知県入試問題過去問
千葉県の難問!?平面図形2024

式の値 2通りで解説
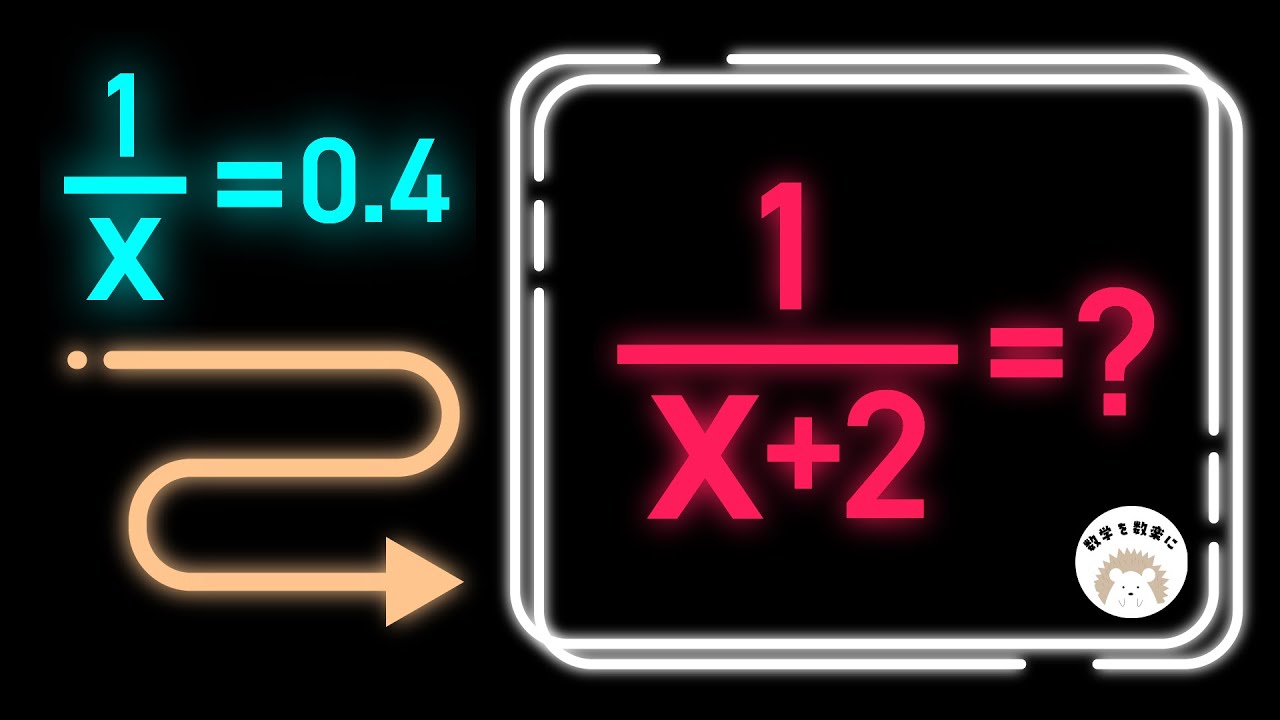
単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1}{x}=0.4$のとき$\frac{1}{x+2}=$
この動画を見る
$\frac{1}{x}=0.4$のとき$\frac{1}{x+2}=$
【よく見てやれば…!】平方根:青山学院高等部~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#青山学院高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \left(\dfrac{1}{2\sqrt2}+\sqrt3 \right)\left(\sqrt2-\dfrac{1}{2\sqrt3}\right)$
次の計算をせよ.
青山学院高等部過去問
この動画を見る
$ \left(\dfrac{1}{2\sqrt2}+\sqrt3 \right)\left(\sqrt2-\dfrac{1}{2\sqrt3}\right)$
次の計算をせよ.
青山学院高等部過去問
【ルールに忠実に…!】平方根:東京学芸大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#東京学芸大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \dfrac{\sqrt{(-2)^2}(\sqrt2+\sqrt3)^2}{\sqrt2}+\dfrac{(3-\sqrt6)^2}{\sqrt3}$
を計算しなさい.
東京学芸大附属高校過去問
この動画を見る
$ \dfrac{\sqrt{(-2)^2}(\sqrt2+\sqrt3)^2}{\sqrt2}+\dfrac{(3-\sqrt6)^2}{\sqrt3}$
を計算しなさい.
東京学芸大附属高校過去問
因数分解は別解が存在する動画~全国入試問題解法 #shorts #数学 #高校入試 #サウンド

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ 3a(a-2b)-(a-2b)-(6b+2)$を因数分解せよ.
ラ・サール高校過去問
この動画を見る
$ 3a(a-2b)-(a-2b)-(6b+2)$を因数分解せよ.
ラ・サール高校過去問
【条件をフル活用…!】図形:兵庫県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)#兵庫県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
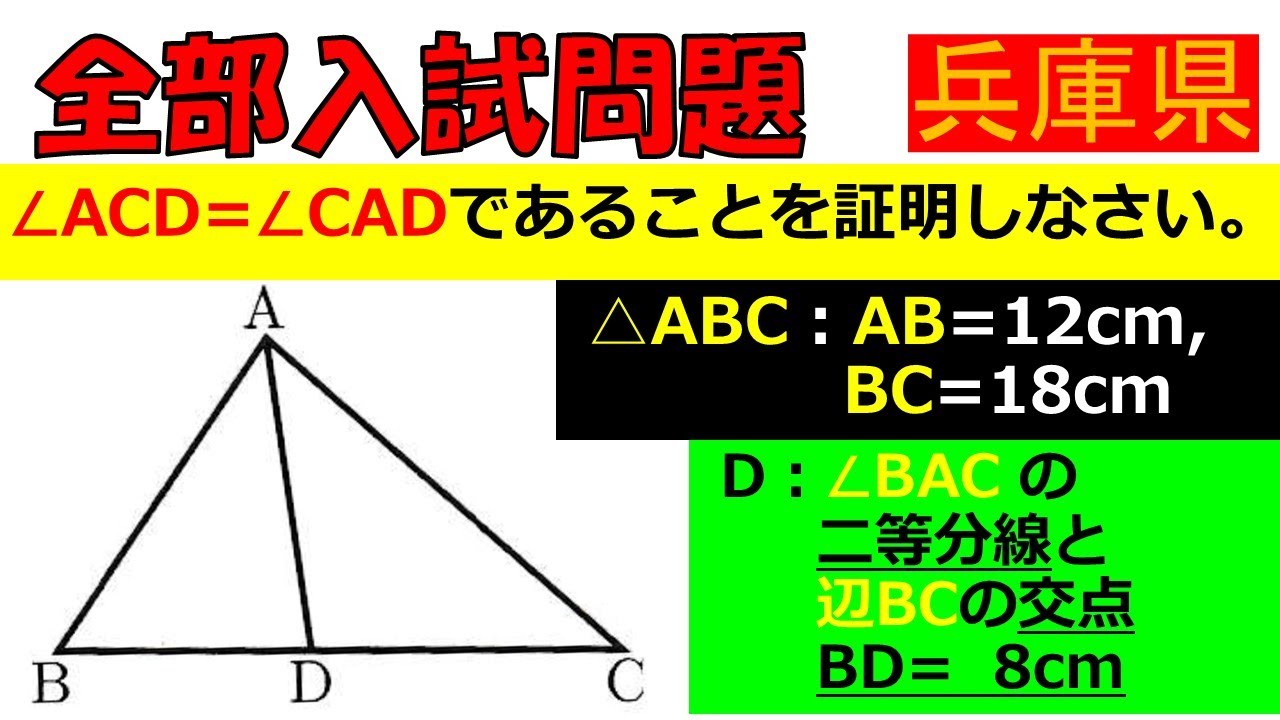
$ \triangle ABC $の$ AB$は12cmであり,$ BC $は18cmである.
$ D $は$ \angle BAC $の二等分線と辺$ BC $の交点である.
$ \angle ACD=\angle CAD $であることを証明しなさい.
兵庫県公立高等学校過去問
この動画を見る
$ \triangle ABC $の$ AB$は12cmであり,$ BC $は18cmである.
$ D $は$ \angle BAC $の二等分線と辺$ BC $の交点である.
$ \angle ACD=\angle CAD $であることを証明しなさい.
兵庫県公立高等学校過去問
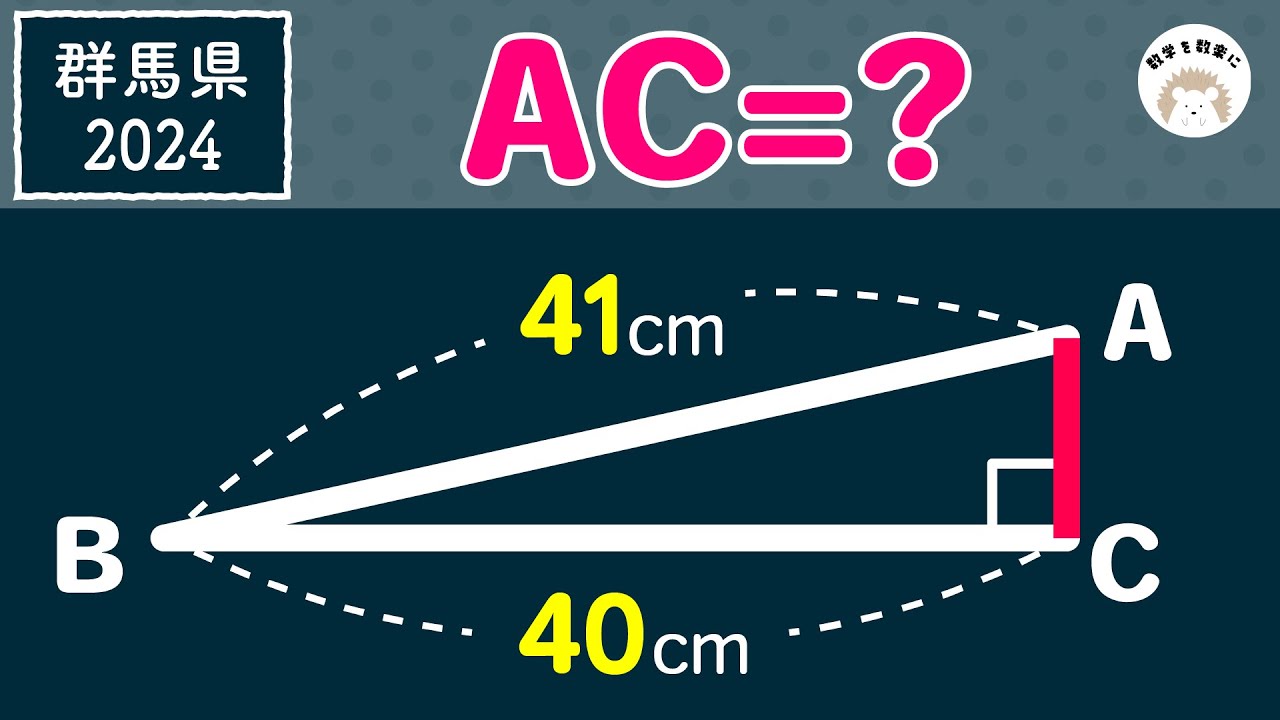
三平方の定理だけど。。。2024群馬県
【それを決めるのは…!】整数:大阪府公立高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#大阪府公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ n $を自然数とするとき,$ 5-\dfrac{78}{n}$の値が自然数となるような
最も小さい自然数$ n $の値を求めなさい.
大阪府公立高等学校過去問
この動画を見る
$ n $を自然数とするとき,$ 5-\dfrac{78}{n}$の値が自然数となるような
最も小さい自然数$ n $の値を求めなさい.
大阪府公立高等学校過去問
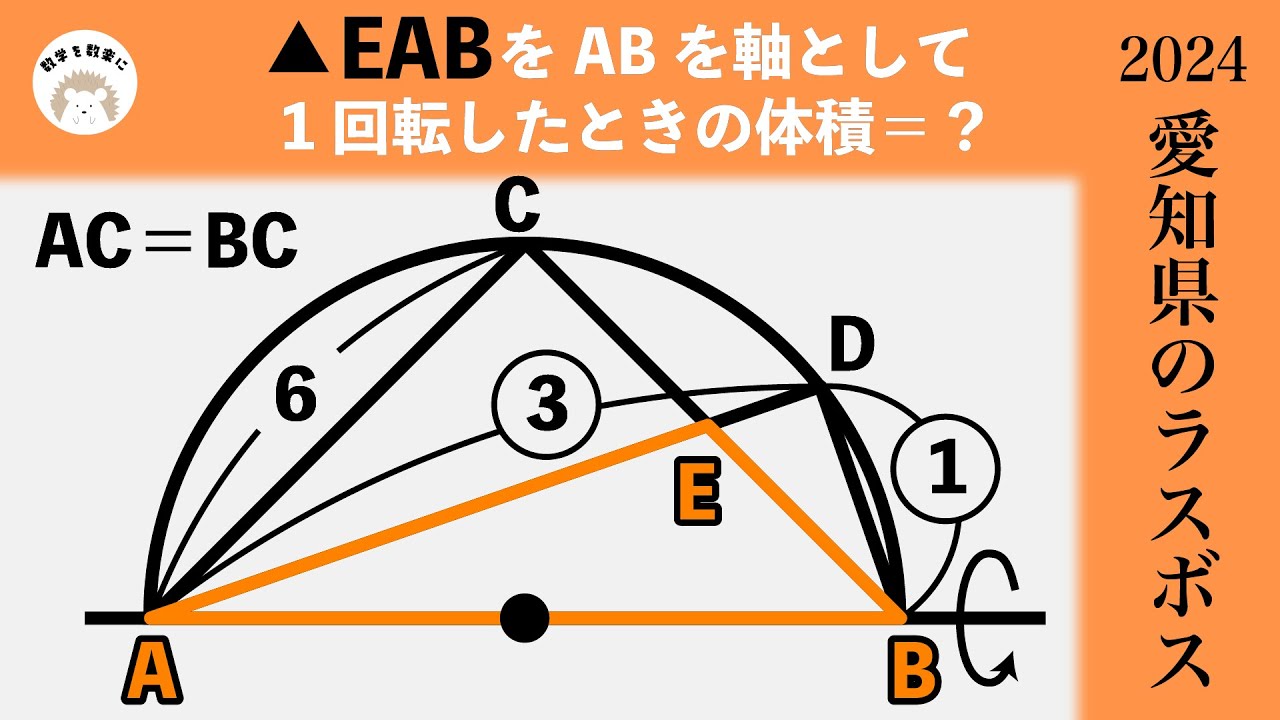
円と回転体 2024愛知県のラスボス
【まず手を付けよう…!】二次方程式:法政大学第二高等学校~全国入試問題解法

単元:
#中3数学#2次方程式#高校入試過去問(数学)#法政大学第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2次方程式$ (x+2)^2+x^2=(x+4)^2-12 $を解きなさい.
法政大学第二高等学校過去問
この動画を見る
2次方程式$ (x+2)^2+x^2=(x+4)^2-12 $を解きなさい.
法政大学第二高等学校過去問
証明がわからない人へ

単元:
#数学(中学生)#中2数学#平行と合同
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
三角形の合同の証明の動画です
$AB=AD,\angle ABC= \angle ADE$ならば$\triangle ABC \equiv \triangle ADE$となることを証明してください
この動画を見る
三角形の合同の証明の動画です
$AB=AD,\angle ABC= \angle ADE$ならば$\triangle ABC \equiv \triangle ADE$となることを証明してください
【これなら「分かる」…!】整数:大阪府公立高等学校~全国入試問題解法

単元:
#高校入試過去問(数学)#大阪府公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ n $を自然数とする.
$ n \leqq \sqrt x \leqq n+1 $を満たす自然数$ x $の個数が100であるときの
$ n $の値を求めなさい.
大阪府公立高等学校過去問
この動画を見る
$ n $を自然数とする.
$ n \leqq \sqrt x \leqq n+1 $を満たす自然数$ x $の個数が100であるときの
$ n $の値を求めなさい.
大阪府公立高等学校過去問
こんな学校知ってる?

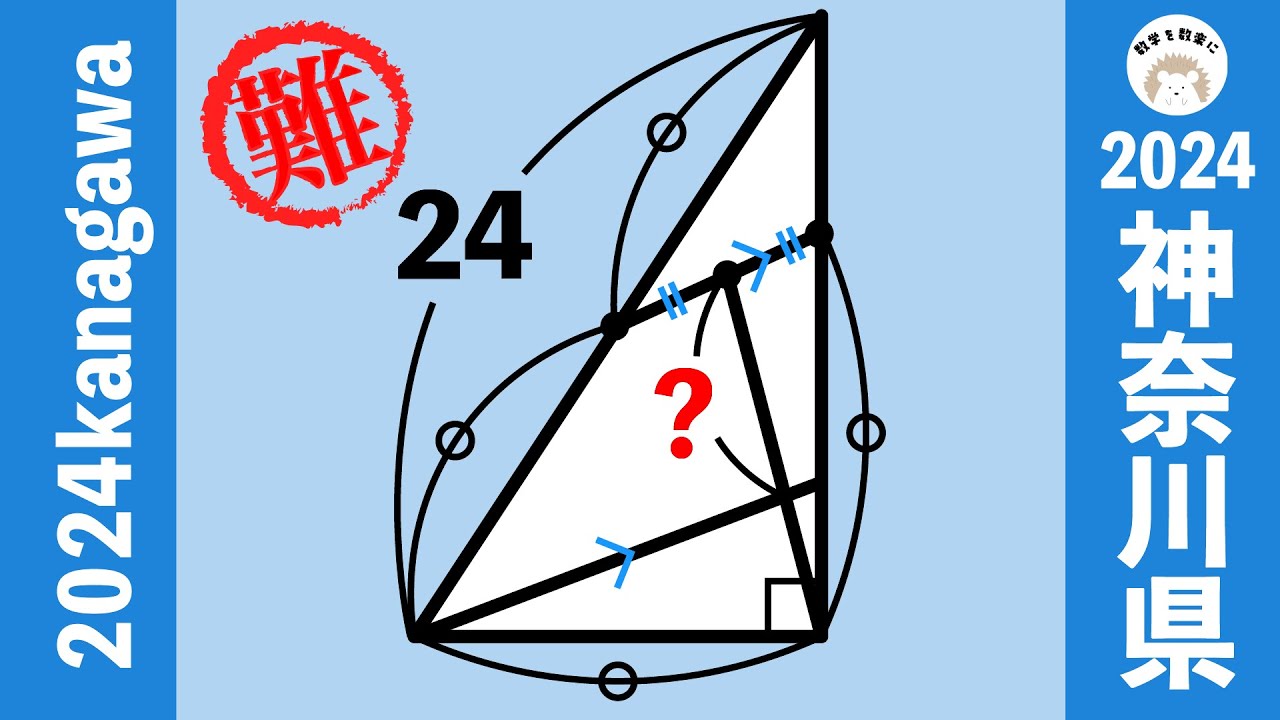
2024神奈川県の平面図形の難問
【学んだことを活かせ…!】連立方程式:明治大学付属中野高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#明治大学付属中野高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x,y $についての連立方程式 $ \begin{eqnarray}
\left\{
\begin{array}{l}
4x+3y=11 \\
x-ky=-\dfrac{1}{2}k
\end{array}
\right.
\end{eqnarray}$ の解が $\begin{eqnarray}
\left\{
\begin{array}{l}
x=p \\
y=q
\end{array}
\right.
\end{eqnarray}$ であり,
$ p+q=3 $が成り立つ.$ k $の値を求めなさい.
明治大学付属中野高等学校過去問
この動画を見る
$ x,y $についての連立方程式 $ \begin{eqnarray}
\left\{
\begin{array}{l}
4x+3y=11 \\
x-ky=-\dfrac{1}{2}k
\end{array}
\right.
\end{eqnarray}$ の解が $\begin{eqnarray}
\left\{
\begin{array}{l}
x=p \\
y=q
\end{array}
\right.
\end{eqnarray}$ であり,
$ p+q=3 $が成り立つ.$ k $の値を求めなさい.
明治大学付属中野高等学校過去問
【な、長い…!】平方根:洛南高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#洛南高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ (1+\sqrt2+\sqrt4+\sqrt8+\sqrt{16}+\sqrt{32})$
$ \times (1-\sqrt2+\sqrt4-\sqrt8+\sqrt{16}-\sqrt{32}$
を計算しなさい.
洛南高等学校過去問
この動画を見る
$ (1+\sqrt2+\sqrt4+\sqrt8+\sqrt{16}+\sqrt{32})$
$ \times (1-\sqrt2+\sqrt4-\sqrt8+\sqrt{16}-\sqrt{32}$
を計算しなさい.
洛南高等学校過去問
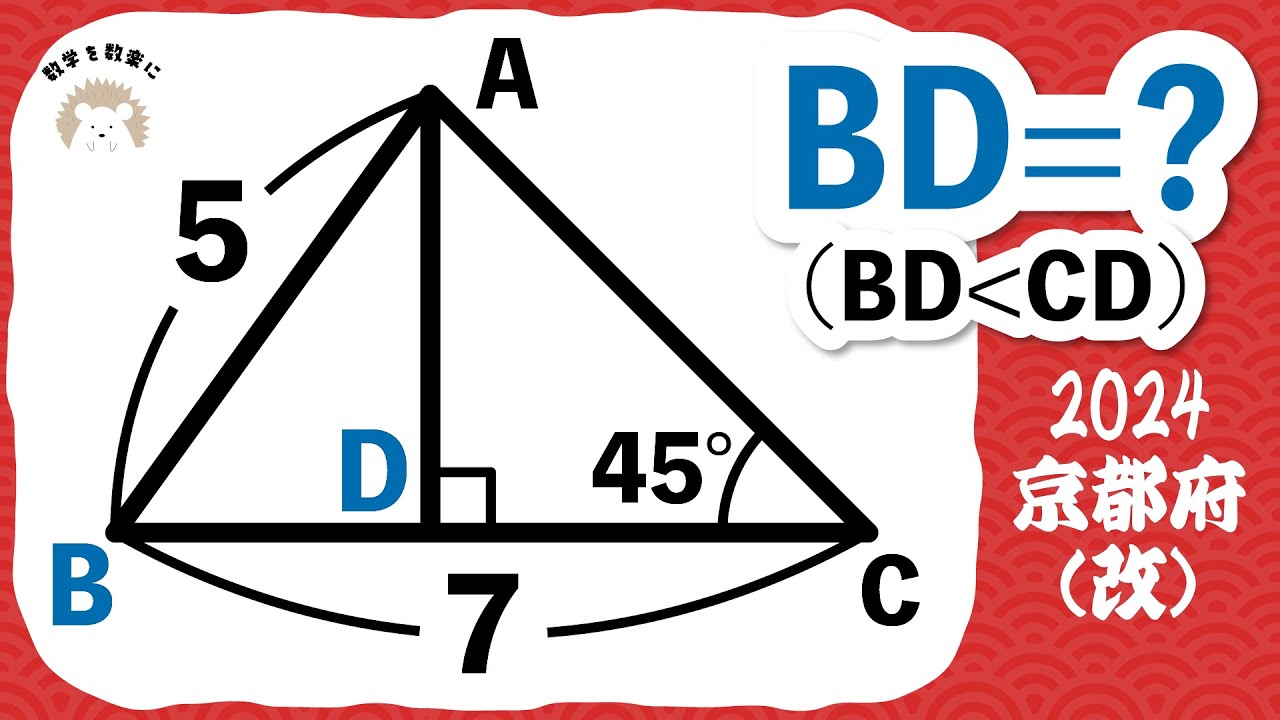
平面図形 2024京都府(改)